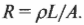Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
C= Q U .
2. Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,
здесь
S — поверхность каждой пластины конденсатора;
d — расстояние между ними;
εa = εr·ε0 — абсолютная диэлектрическая проницаемость среды;
εr — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C= C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
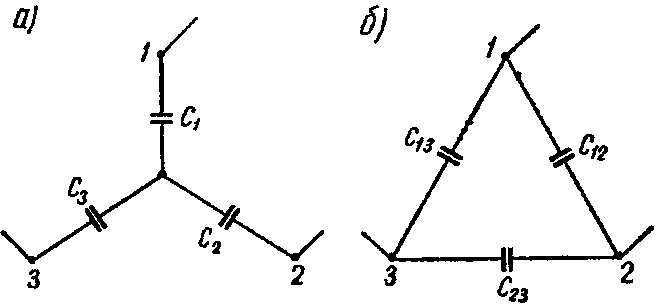
Рис. 0
осуществляется по формулам:
Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .
6. Энергия электростатического поля конденсатора:
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ .
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
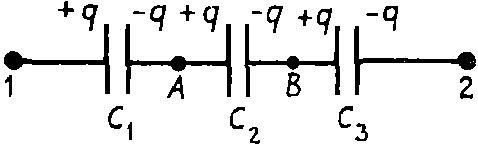
Рис. 1
Решение
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .
Воспользовавшись формулой напряжения на конденсаторе
U= q C ,
запишем
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
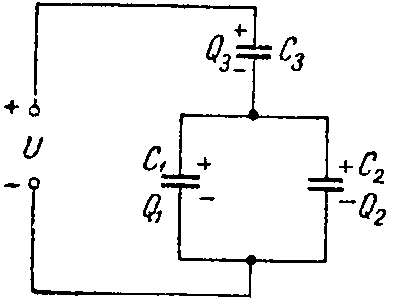
Рис. 2
Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.
Решение
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
C12 = C1 + C2 = 200 мкФ,
эквивалентная емкость всей цепи равна
C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.
Заряд на эквивалентной емкости
Q = C·U = 120·10–6·240 = 288·10–4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.
Напряжение на конденсаторах C1 и C2 равно
U1 = U2 = U — U3 = 240 — 96 = 144 В.
их заряды имеют следующие значения
Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;
Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
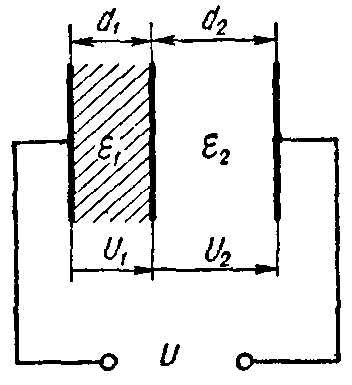
Рис. 3
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = εr1·ε0 и εa2 = εr2·ε0, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Даны: C1 = 30 мкФ; C2 = 20 мкФ; r1 = 100 Ом. r2 = 400 Ом. r3 = 600 Ом, U = 20 В.
Решение
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.
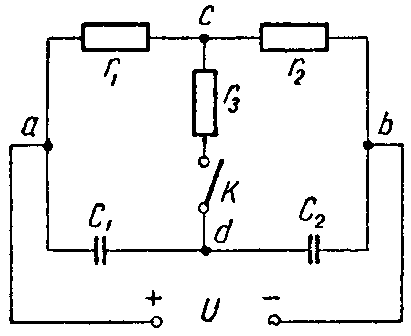
Рис. 4
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I= U r 1 + r 2 = 20 500 =0,04 А,
а через сопротивление r3 ток не протекает.
Поэтому точки c и d равнопотенциальны (φc = φd). Следовательно, напряжение между точками a и c (Uac = φa — φc) равно напряжению между точками a и d (Uad = φa — φd).
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
UC1 = I·r1 = 0,04·100 = 4 В.
Аналогично напряжение на втором конденсаторе равно
UC2 = I·r2 = 0,04·400 = 16 В.
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
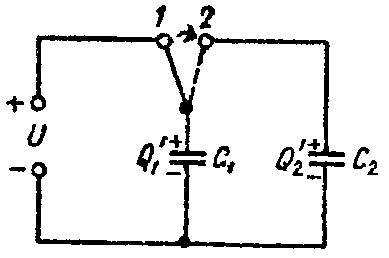
Рис. 5
Решение
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
Q = C1·U = 5·10–6·25 = 125·10–6 Кл.
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
Q = Q’1 + Q’2 = 125 10–6 Кл. (1)
По второму закону Кирхгофа имеем
0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
или
Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)
Решая уравнения (1) и (2), найдем
Q’1 = 5 10–6 Кл; Q’2 = 120 10–6 Кл.
Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..
Напряжение на зажимах конденсаторов станет равным
U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.
Энергия обоих конденсаторов будет равна
W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10–6 — 62,5·10–6 = 1500·10–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
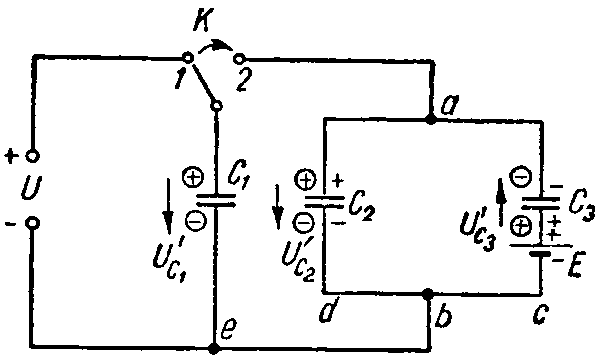
Рис. 6
Решение
Рубильник находится в положении 1. Заряд конденсатора C1 равен
Q1 = C1·U = 10·10–6·30 = 0,3·10–3 Кл.
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
откуда
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для узла a
Q’1 + Q’2 — Q’3 = Q1 + Q2 — Q3. (1)
Для контура 2ebda2
0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) — (3), после подстановки числовых значений величин, примут вид
Q’1 + Q’2 — Q’3 = 0,3·10–3; (4)
3Q’1 — Q’2 = 0; (5)
2Q’2 + Q’3 = 3·10–3. (6)
Решая совместно уравнения (4) — (6), получим
Q’1 = 0,33·10–3 Кл; Q’2 = 0,99·10–3 Кл; Q’3 = 1,02·10–3 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.
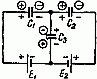
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
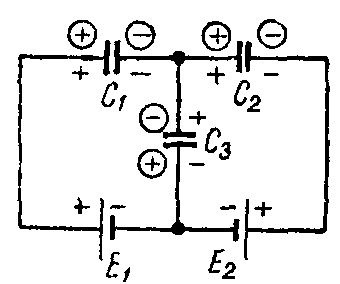
Рис. 7
Решение
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 — противоположна выбранной.
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
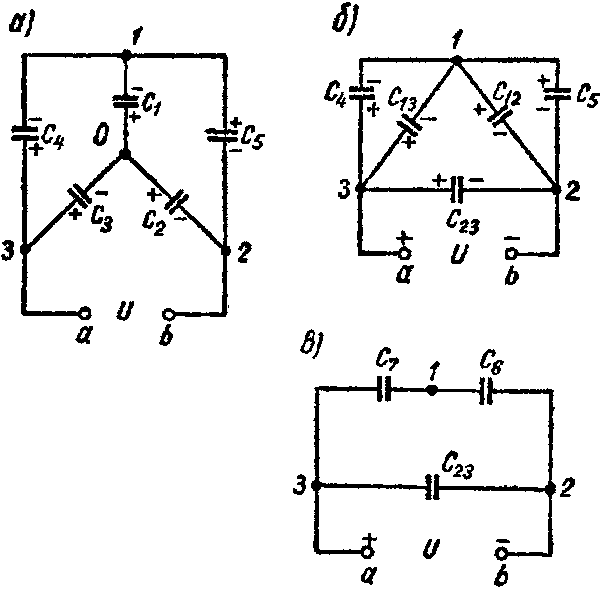
Рис. 8
Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
Решение
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
C6 = C12 + C5 = 3 мкФ.
Аналогично
C7 = C13 + C4 = 2 мкФ.
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅U=6 В.
Таково же напряжение и на конденсаторах C4 и C13
U4 = U31 = 6 В.
Напряжение на конденсаторе C6 равно
U6 = U — U7 = 4 В;
U5 = U12 = 4 В.
Вычислим заряды
Q4 = C4·U4 = 6·10–6 Кл;
Q5 = C5·U5 = 9,6·10–6 Кл;
Q12 = C12·U12 = 6·10–6 Кл;
Q13 = C13·U31 = 2,4·10–6 Кл.
По закону сохранения электричества для узла 1 схем 8, а и б имеем
–Q4 — Q1 + Q5 = –Q4 — Q13 + Q12 + Q5,
отсюда
Q1 = Q13 — Q12 = 3,6·10–6 Кл,
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 =1,8 В.
Далее находим напряжения и заряды на остальных конденсаторах
U31 = U1 + U3,
отсюда
U3 = U31 — U1 = 4,2 В;
Q3 = C3·U3 = 21·10–6 Кл,
также
U12 = U2 — U1 = 4,2 В,
откуда
U2 = U12 + U1 = 5,8 В;
Q2 = C2·U2 = 17,4·10–6 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
для узла 1
Q5 — Q1 — Q4 = 0; (1)
для узла О
Q1 + Q2 — Q3 = 0; (2)
для контура О13О
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)
для контура О12О
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)
для контура a3О2b
Q 3 C 3 + Q 2 C 2 =U. (5)
Система уравнений (1) — (5) — содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
C ab = Q U ,
где Q = Q3 + Q4, или Q = Q2 + Q5.
Задача 9. В схеме рис. 9 найти распределение зарядов, если E1 = 20 В; E2 = 7 В; C1 = 7 мкФ; C2 = 1 мкФ; C3 = 3 мкФ; C4 = 4 мкФ; C5 = C6 = 5 мкФ.
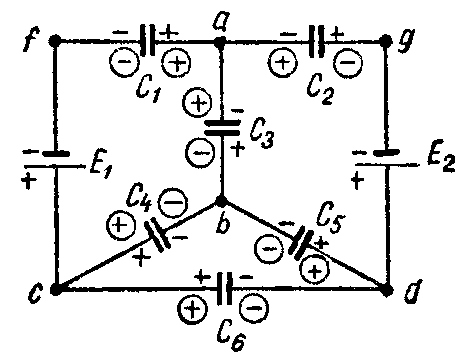
Рис. 9
Решение
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для узла а
Q1 + Q2 + Q3 = 0;
для узла b
–Q3 — Q4 — Q5 = 0;
для узла c
–Q1 + Q4 + Q6 = 0;
для контура afcba
E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Q1 = 35 мкКл; Q2 = –5 мкКл; Q3 = –30 мкКл;
Q4 = 20 мкКл; Q5 = 10 мкКл; Q6 = 15 мкКл.
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
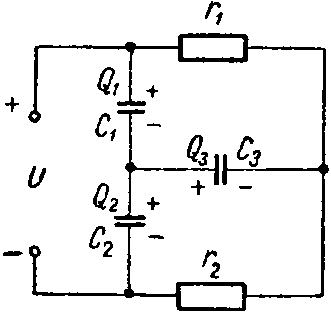
Рис. 10
Решение
Через сопротивления протекает ток
I= U r 1 + r 2 =0,05 А.
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,
или
Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .
Решив эту систему уравнений, найдем, что
Q1 = 90 мкКл; Q2 = 60 мкКл; Q3 = 30 мкКл.
 последовательное соединение конденсаторов,
последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами
Комментарии

В этой главе…
- Исследуем движение электронов и электрический ток
- Вычисляем напряжение и сопротивление по закону Ома
- Оцениваем мощность электрического тока
- Разбираемся с параллельными и последовательными цепями
- Знакомимся с правилами Кирхгофа
Статическое электричество возникает при избытке либо недостатке электронов, т.е. когда имеются отрицательно или положительно заряженные тела. А в привычном электричестве, т.е. в текущем по проводам электрическом токе, избыточного заряда нет, и, следовательно, нет и общего заряда. Есть лишь напряжение, подобное тому, которое создается батарейкой или настенной розеткой. Оно создается в проводах электрическим полем, в ответ на которое возникает движение электронов — электрический ток. (Более подробно о напряжении рассказывается в главе 16.)
Эта глава посвящена электронам, т.е. заряженным частицам, движущимся в электрических контурах, с которыми вы уже знакомы. В главе 16 рассказывается о статическом, а в этой — только о динамическом проявлении электричества. Здесь описываются сходства и различия между ними, носители и источники электрического тока, закон Ома, мощности электрического тока и, наконец, электрические контуры и их элементы.
Содержание
- Марширующие электроны: ток
- Знакомимся с силой тока
- Вычисляем силу тока, идущего через батарейку
- Оцениваем сопротивление: закон Ома
- Вычисляем силу тока
- Проверка удельного сопротивления
- Измеряем мощность: ватт
- От одного к другому: последовательные цепи
- Разделение тока: параллельные цепи
- Создаем электрические цепи по правилам Кирхгофа
- Используем правило контуров
- Исследуем многоконтурные цепи
- Разбираемся с параллельно и последовательно соединенными конденсаторами
- Конденсаторы в параллельных цепях
- Конденсаторы в последовательных цепях
- Соединяем резисторы с конденсаторами: RC-цепи
Марширующие электроны: ток
Электрический ток возникает при направленном движении электронов. Но как заставить их двигаться именно так, чтобы получился электрический ток? Ответ: нужно создать и поддерживать электродвижущую силу, или э.д.с. Э.д.с. обеспечивает разность потенциалов (напряжение), благодаря которой электроны чувствуют силовое воздействие.
Итак, чем именно создается э.д.с.? Батарейкой? Или настенной розеткой? Э.д.с. — это то, что дает напряжение, ведь напряжение — это все, что нужно для создания электрического поля в проводе, которое заставляет электроны двигаться. (В главе 16 говорится, что электрическое поле характеризуется своей напряженностью ( E ), которая равна отношению силы ( F ) и заряда ( q ): ( Е = F/q ).)
В физике величина электрического тока (сила тока) обозначается буквой ( I ) и измеряется в амперах (А).
Знакомимся с силой тока
Как правильно определить силу тока? Это величина заряда, проходящего через некоторую часть контура за некоторое время. А вот то же самое определение, но в виде формулы:
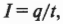
где ( q ) и ( t ) — это соответственно электрический заряд и время. Если за 1 с через контур проходит заряд в 1 Кл, то величина электрического тока равна 1 А.
Вычисляем силу тока, идущего через батарейку
Зная величину заряда в контуре с батарейкой и время, можно вычислить силу тока, идущего через батарейку: ( I=q/t ). Посмотрите на рис. 17.1; две вертикальные черты, расположенные сверху, означают батарейку. (Эти линии напоминают о разных металлических пластинах в первых батарейках, которые подвергались воздействию химических веществ и соединялись вместе.)
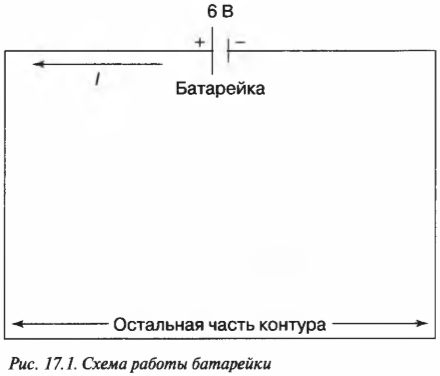
Батарейка обеспечивает электродвижущую силу величиной 6 В, которая гонит ток по контуру. Если за 30 с по контуру проходит заряд 19 Кл, то чему равна сила тока?
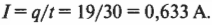
В данном случае по контуру течет 0,633 ампера. Обратите внимание, что ток идет от положительной части батарейки, обозначаемой на значке батарейки более длинной чертой, к отрицательной части, обозначаемой на значке батарейки более короткой линией.
Полезно считать, что в цепи батарейка является ступенькой напряжения. Иначе говоря, батарейка как бы “поднимает” ток, поступающий в ее отрицательную часть (в случае рис. 17.1 на уровень 6 В), а затем электрический ток снова “спускается” и течет по контуру.
Хотя ток всегда изображается движущимся по контуру от положительного к отрицательному знаку батарейки, но в действительности электроны движутся в противоположном направлении. Почему возникло такое различие? Причина здесь историческая: первые исследователи думали, что по контуру текут именно положительные заряды, но на самом деле все происходит наоборот. Впрочем, это не проблема, если вы будете придерживаться единообразия и всегда считать, что ток выходит с положительного конца батарейки.
Оцениваем сопротивление: закон Ома
Сопротивление — это величина, которая связывает приложенное напряжение с созданной им силой тока. Вот как выглядит формула, которая связывает напряжение, силу тока и сопротивление:
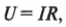
где ( U ), ( I ) и ( R ) — это соответственно напряжение, сила тока и сопротивление. Сопротивление измеряется в омах (Ом), 1 Ом = 1 В/1 А. Таким образом, прикладывая напряжение ( U ) на участке цепи с некоторым сопротивлением ( R ), получим силу тока ( I ). Это и есть закон Ома, названный так по фамилии своего открывателя Георга Симона Ома (сделавшего свое открытие в XIX веке).
Вычисляем силу тока
С помощью закона Ома можно найти силу тока, идущего от положительной к отрицательной клемме батарейки. Посмотрите на цепь, показанную на рис. 17.2, где батарейка с напряжением 6 В создает электрический ток, идущий через резистор ( R ) с сопротивлением 2 Ом.
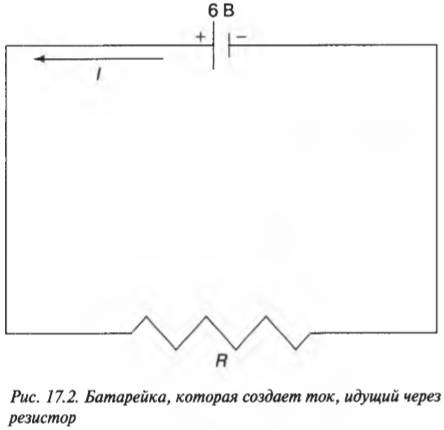
Из закона Ома следует, что:
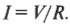
Подстановка числовых значений дает:
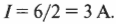
Итак, ток силой 3 А течет по контуру против часовой стрелки.
Проверка удельного сопротивления
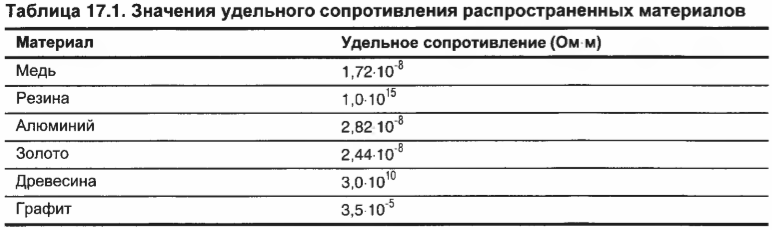
При изучении электричества часто приходится иметь дело с величиной ( rho ) называемой удельным сопротивлением, т.е. сопротивлением на единицу длины и площади, и измеряемой в Ом·м. Зная силу тока через определенный материал, можно с помощью удельного сопротивления материала узнать его сопротивление. Физики вычислили значения удельного сопротивления многих распространенных материалов; некоторые из этих значений перечислены в табл. 17.1.
Сопротивление материала ( R ) можно найти, умножив его удельное сопротивление ( rho ) на его длину ( L ) (чем она больше, тем большее сопротивление вызывает) и поделив на площадь ( A ) поперечного сечения этого материала (чем больше площадь, которую должен пересекать ток, тем сопротивление меньше):
Измеряем мощность: ватт
Некоторые предметы домашнего обихода, например, лампочки накаливания или сушилки для волос, используют электроэнергию. Мощность таких электроприборов измеряется в ваттах (Вт). Как определить ее величину? Работа по перемещению заряда ( q ) по цепи равна ( qU ), где ( U ) — это электродвижущая сила. Если поделить эту работу на время ее выполнения, получится мощность:
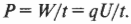
Впрочем, заряд ( q ), деленный на время ( t ), равняется силе тока ( I ), таким образом:
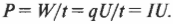
Мощность, которая обеспечивается в цепи источником э.д.с., в частности батарейкой, вычисляется по формуле ( P = IU ). Например, батарейка при 10 В создает в лампочке накаливания силу тока 0,5 А. Какова мощность этой лампочки? ( P = IU ), т.е. мощность равна 0,5·10 = 5 Вт. Впрочем, ( I = U/R ), поэтому мощность, обеспечиваемую в цепи определенным напряжением, можно вычислять несколькими способами:
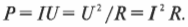
От одного к другому: последовательные цепи
В предыдущих разделах этой главы говорилось о токе, идущем через один резистор; впрочем, как показано на рис. 17.3, в цепи может быть и два резистора.
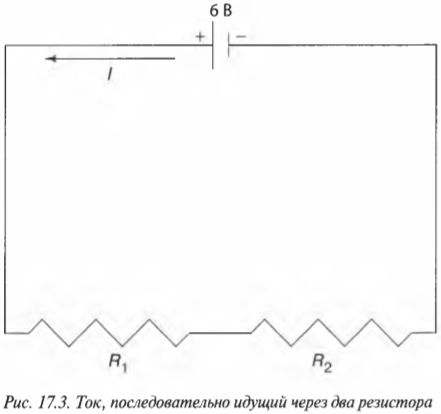
Два резистора могут быть подключены последовательно, когда, перед тем как вернуться к источнику электродвижущей силы (см. первый раздел этой главы), ток в цепи течет сначала через один из них, а затем — через другой. Рассмотрим последовательное подключение двух резисторов с сопротивлениями ( R_1 ) и ( R_2 ), когда один и тот же ток, перед тем как вернуться к батарейке, должен пройти через оба резистора. Тогда общее сопротивление ( R ) должно равняться сумме этих двух сопротивлений:
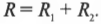
Итак, чтобы получить общее сопротивление двух последовательно соединенных резисторов, надо сложить их сопротивления ( R_1 ) и ( R_2 ). Например, если ( R_1 ) = 10 Ом и ( R_2 ) = 20 Ом, батарейка создает напряжение 6 В, то ток какой силы будет проходить через цепь? Общее сопротивление должно равняться 30 Ом, тогда:
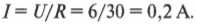
Разделение тока: параллельные цепи
Если в одной и той же цепи имеется множество резисторов, то совсем не обязательно, чтобы у них было только последовательное соединение (см. предыдущий раздел), когда ток идет от одного резистора к другому. Два резистора ( R_1 ) и ( R_2 ) можно соединить таким образом, чтобы ток разветвлялся, как на рис. 17.4. Какая-то часть тока идет через первый резистор, а другая — через второй.
Резисторы на рис. 17.4 являются параллельными, т.е. на концах каждого из них одно и то же напряжение, но ток, идущий через эти резисторы, не обязательно одинаковый.
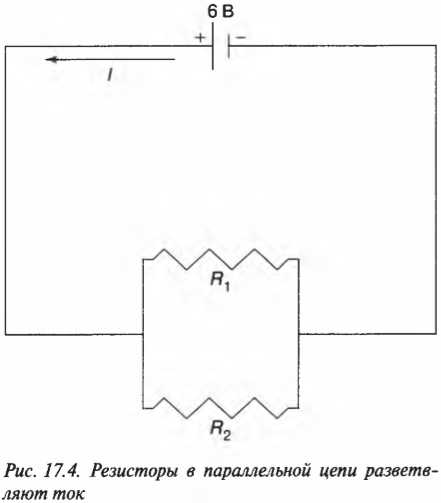
Напряжение на концах каждого из параллельных резисторов одинаково и равно 6 В, т.е. напряжению, создаваемому батарейкой. Этим и отличаются последовательно и параллельно соединенные резисторы. Через последовательно соединенные резисторы идет один и тот же ток. А когда резисторы соединены параллельно, на концах каждого из них одинаковое напряжение.
Итак, чему равно общее сопротивление резисторов ( R_1 ) и ( R_2 ) соединенных параллельно? Общая сила тока ( I ) — это сила тока, идущего через два резистора:
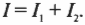
И поскольку ( I=U/R ) (см. выше раздел о законе Ома), то можно записать:
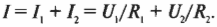
Дело в том, что при параллельном соединении ( U_1=U_2 ), поэтому если обозначить это общее напряжение как ( U ), то можно сказать, что:
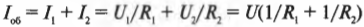
Это равенство еще записывается как ( I=U/R ), и в итоге мы получаем:
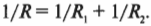
Эта формула показывает, как надо вычислять общее сопротивление двух параллельно соединенных резисторов. Если говорить о произвольном количестве резисторов, то получится такой способ вычисления общего сопротивления:
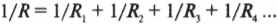
Например, если на рис. 17.4 ( R_1 ) = 10 Ом и ( R_2 ) = 30 Ом, а напряжение батарейки составляет 6 В, то ток какой силы идет через эту цепь? Величина, обратная общему сопротивлению цепи, равна
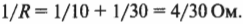
Чтобы найти общее сопротивление при параллельном соединении, надо сложить величины, обратные значениям сопротивления, а затем взять величину, обратную полученному результату. Таким образом, общее сопротивление равно 30/4 Ом, т.е. сила тока равна 6/(30/4) = 0,8 А.
Создаем электрические цепи по правилам Кирхгофа
К сожалению, электрические цепи не всегда можно разбить на последовательные и параллельные составляющие, поэтому важную роль играют правила Кирхгофа, названные так в честь своего открывателя, Густава Кирхгофа. Эти два простых правила позволяют анализировать цепи самой разной сложности, поскольку представляют собой неизменные соотношения целостности, которые выполняются между токами и напряжениями на участках любой электрической цепи. (Для корректной формулировки этих правил в цепи выделяются узлы, т.е. точки соединения трех и более проводников, и контуры, т.е. замкнутые пути из проводников. — Примеч. ред.)
- Правило соединения. Общий ток, притекающий в любой узел цепи, должен равняться общему току, вытекающему из него.
- Правило контуров. В любом замкнутом контуре сети сумма увеличений потенциала (например, от батарейки) должна равняться сумме падений потенциала (например, от резистора). (Иначе говоря, суммарная э.д.с. равна суммарному напряжению. — Примеч. ред.)
Правило соединения достаточно легко понять: сила тока, входящего в любой узел, должна равняться силе тока, выходящего из этого узла. Ну а как насчет правила контуров, которое гласит, что в любом замкнутом контуре суммарное увеличение и суммарное падение потенциала должны быть равны? Правило контуров означает, что насколько движущиеся по контуру электроны “спускаются”, настолько они и “поднимаются”, и приходят туда, откуда пришли. Например, увеличение потенциала выполняется батарейками; когда электроны входят в ее отрицательную часть и выходят из положительной, напряжение батарейки возрастает. С другой стороны, когда электрон входит в резистор, требуется определенное усилие для того, чтобы провести его через этот резистор (вот почему резистор еще называют сопротивлением), отсюда и понижение потенциала при выходе из него электрона.
Используем правило контуров
На рис. 17.5 показан пример использования правила контуров для цепи из двух резисторов и двух батареек. Ток какой силы идет по этой цепи?
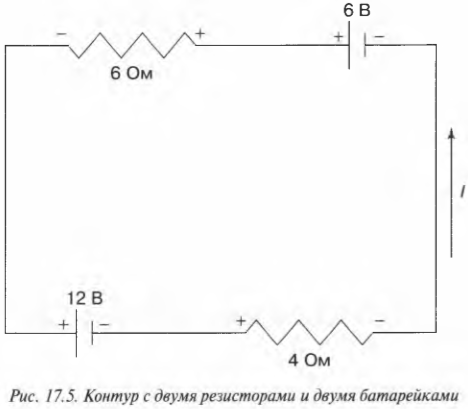
Правило контуров гласит, что вдоль всего контура:
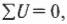
где ( sum!U ) — это сумма напряжений вдоль всего контура. Как можно использовать это правило?
Чтобы решить эту задачу, выберите направление тока, начертив стрелку, как показано на рис. 17.5. В действительности ток может идти в противоположном направлении, но здесь нет ничего плохого, ведь тогда полученная отрицательная сила тока будет показывать, что ток идет не в том направлении, которое было выбрано. Выбор направления тока — в данном примере против часовой стрелки — помогает начертить знаки + и — там, где ток соответственно заходит в резистор и выходит из него (эти действия в правило Кирхгофа не входят; я просто использую приемы, которые считаю полезными).
Известно, что вдоль всего контура ( sum!U ) = 0 и что в резисторе падение потенциала ( U = IR ). Остается только двигаться вдоль контура в одном направлении (не имеет значения, по часовой или против часовой стрелки), и когда встретится знак “+” или “-” (на резисторе или батарейке), нужно записать этот знак, а за ним — соответствующее ему падение или возрастание потенциала. Если, к примеру, начать с батарейки с э.д.с. 6 В и идти по часовой стрелке, то в соответствии с правилом контуров получим следующее равенство:
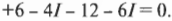
Сгруппировав его члены, получим:
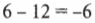
и
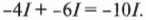
Таким образом:
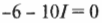
или
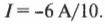
Итак, сила тока равна —0,6 А.
Из того, что сила тока имеет отрицательную величину, следует, что на самом деле ток идет в направлении, противоположном тому, которое выбрано сначала и показано на рис. 17.4.
Исследуем многоконтурные цепи
Если вам кажется, что правила Кирхгофа исчерпали все свои возможности уже на одноконтурных цепях, то попробуйте решить новую задачу, показанную на рис. 17.6.
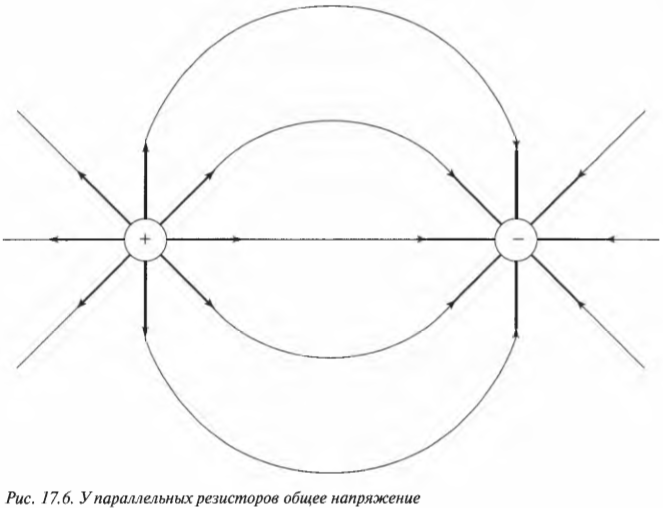
На рисунке показаны три ответвления цепи и три разных тока. Найдите соответствующие значения сил тока ( I_1 ), ( I_2 ) и ( I_3 ) с применением обоих правил Кирхгофа. Правило соединения гласит, что в любом узле ( sum!I ) = 0, где ( sum!I ) — это сумма всех сил токов (втекающих и вытекающих). Рассмотрим точку А, которая находится в левой части рис. 17.6. Токи, соответствующие значениям ( I_1 ) и ( I_2 ), в нее втекают, а ток, соответствующий значению ( I_3 ), из нее вытекает, поэтому:
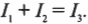
Теперь обратимся к правилу контуров, которое гласит, что ( sum!I ) = 0. В нашем примере три контура: два внутренних и один внешний, т.е. огибающий контур. Так как неизвестных у нас три (это значения силы тока ( I_1 ), ( I_2 ) и ( I_3 )), то все, что нам нужно, — это три уравнения. Согласно правилу ( sum!I ) = 0, одно из них у нас уже есть. Поэтому, чтобы получить два оставшихся уравнения, надо разобраться с двумя внутренними контурами. Верхний контур дает:
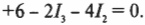
А из нижнего контура получается:
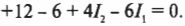
Итак, получено три уравнения с тремя неизвестными:
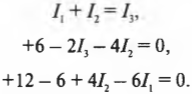
Если значение ( I_3 ), полученное из первого уравнения, подставить во второе, тогда можно получить:
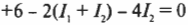
и
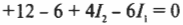
или
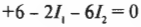
и
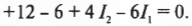
Используя первое из этих уравнений, можно ( I_1 ) выразить через ( I_2 ):
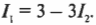
Подставив это значение ( I_1 ) во второе уравнение, получим:
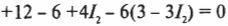
или
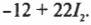
Таким образом:
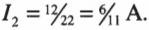
Теперь у нас есть одно из значений силы тока: ( I_2 ) = 6/11 А. Эту дробь можно вставить в уравнение:
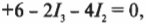
чтобы получить:
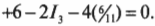
После деления на 2 получим:
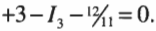
Тогда:
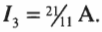
Теперь нам известны два значения сил токов ( I_2 ) и ( I_3 ). А как насчет ( I_1 )? Так как:
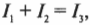
то:
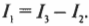
Отсюда легко получить, что:
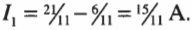
Итак, благодаря правилам Кирхгофа, теперь нам известны все значения силы тока: ( I_1 ) = 15/11 А, ( I_2 ) = 6/11 А и ( I_3 ) = 21/11 А.
В подобных задачах доя поиска решения часто требуется потратить много времени и выполнить много вычислений, но, справившись с ними, можно полностью определить значения основных параметров электрических цепей.
Разбираемся с параллельно и последовательно соединенными конденсаторами
Параллельные и последовательные цепи можно создавать не только из резисторов, но и из конденсаторов. Как известно (подробнее см. главу 16), конденсатор — это физическая система, способная сохранять электрический заряд. Чтобы найти общую емкость конденсаторов, используемых в параллельной цепи, надо просто сложить их емкости:
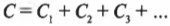
Конденсаторы в параллельных цепях
Когда конденсаторы подключены параллельно, то напряжение, создаваемое батарейкой, будет одинаковым для всех этих конденсаторов. Посмотрите на рис. 17.7, где показаны два конденсатора, подключенные в параллельную цепь.
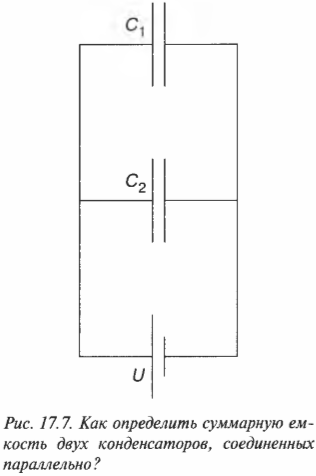
Что же делать в подобной ситуации? Найдите общий заряд ( Q ), хранящийся на обоих конденсаторах ( C_1 ) и ( C_2 ); он равен сумме зарядов, хранящихся на каждом из них:
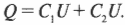
Так как батарейка подает на концы каждого конденсатора одно и то же напряжение ( U ), оно у конденсаторов одинаково, поэтому предыдущее равенство можно переписать как бы для одного конденсатора с емкостью ( C_1+C_2 ):
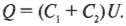
Иначе говоря, если заменить два конденсатора ( C_1 ) и ( C_2 ) одним ( C ), имеющим емкость ( C_1+C_2 ), то значение ( Q ) не изменится:
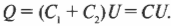
Конденсаторы в последовательных цепях
Когда конденсаторы включены параллельно, батарейка поддерживает одинаково напряжение на концах обоих конденсаторов.
На рис. 17.8 показаны два конденсатора в последовательной цепи. Что же делать в такой ситуации?
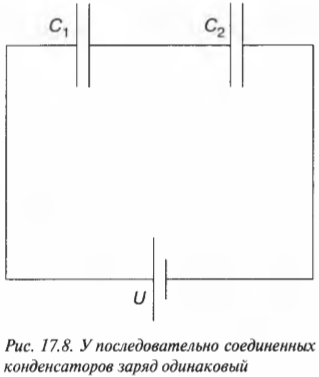
Как видно на рис. 17.8, самая правая пластина конденсатора ( C_1 ) и самая левая пластина конденсатора ( C_2 ) соединены друг с другом, но не с остальной цепью. Иначе говоря, две пластины от остальной цепи изолированы, и вначале они электрически нейтральны (с суммарным общим зарядом, равным нулю).
Любой отрицательный заряд ( -q ), появившийся на самой правой пластине конденсатора ( C_1 ), должен быть равен по величине любому положительному заряду ( q ), появившемуся на самой левой пластине конденсатора ( C_2 ), поскольку суммарный заряд на обеих этих пластинах должен быть равен нулю. А так как суммарный заряд на двух пластинах одного конденсатора тоже должен быть равен нулю, то заряд на самой левой пластине конденсатора ( C_1 ) и на самой правой пластине конденсатора ( C_2 ) должен быть равен соответственно ( q ) и ( -q ). Поэтому величины зарядов (хоть отрицательных, хоть положительных) на каждой пластине одинаковы и равны ( q ).
Итак, заряд на каждом конденсаторе одинаковый. Кроме того, известно, что общее напряжение на концах двух конденсаторов вычисляется по формуле:
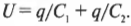
Так как заряд на каждом конденсаторе один и тот же, то это равенство принимает следующий вид:
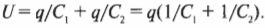
Если вписать в равенство общую емкость ( C ), то получится:
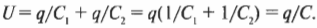
Иначе говоря, последовательно подключенные емкости складываются так же, как и параллельно подключенные резисторы (см. выше раздел о параллельно подключенных резисторах): складываются обратные значения и берется значение .обратное результату:
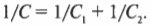
Если конденсаторов больше двух, то сложение для них надо делать следующим образом:
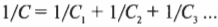
Соединяем резисторы с конденсаторами: RC-цепи
В предыдущих разделах этой главы речь шла о работающих отдельно друг от друга резисторах (электронных компонентах, затрудняющих движение тока в электрической цепи) и конденсаторах (телах, которые хранят заряд, держа его положительные и отрицательные компоненты отдельно, чтобы те притягивали друг друга, но при этом не могли самостоятельно соединиться). Теперь настало время собрать воедино резисторы и конденсаторы. Посмотрите на резистор и конденсатор, показанные на рис. 17.9. Допустим, что конденсатор в исходном состоянии имел напряжение ( U_0 ). Посмотрим, что произойдет после замыкания цепи с помощью выключателя. Может в цепи появится постоянный ток?
Но на самом деле ток ведет себя иначе: так, как показано на графике (рис. 17.10). Исходное значение силы тока равно (как и положено) ( U_0/R ) (где ( R ) означает сопротивление), но затем сила тока уменьшается. Что же происходит?
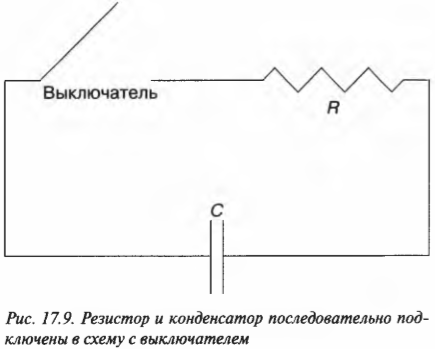
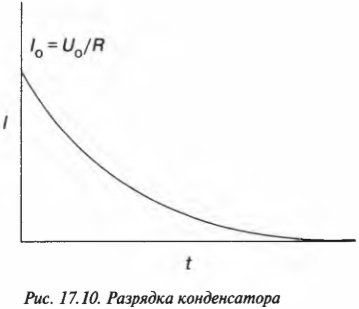
Дело в том, что с течением времени заряд конденсатора уменьшается и соответственно уменьшается ток. Конденсатор не является батарейкой и может подавать ток только тогда, когда на нем остается хоть какой-то заряд. Начальное значение силы тока равно ( U_0/R ), так как у конденсатора напряжение равно ( U_0 ), а ток идет через резистор ( R ). Но со временем ток слабеет по следующей формуле:
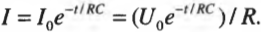
Здесь ( I ) — сила тока, ( e ) — основание натуральных логарифмов, равное 2,71828 (клавишу для вычисления значения функции ( e^{x} ) всегда можно найти на инженерном калькуляторе), ( t ) — время, ( R ) — сопротивление и ( C ) — это емкость. Подобно кривой, показанной на рис. 17.10, ведет себя и заряд конденсатора:
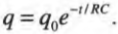
Глава 17. Летим вслед за электронами по проводам
3 (60%) 1 vote
На этой странице вы узнаете
- Что общего у электрического тока с водой?
- В чем отличие сопротивления от удельного сопротивления?
- Почему нежелательно использовать телефон, подключенный к зарядке?
- Фамилия какого ученого стоит миллион?
«Все, кина не будет. Электричество кончилось». Наверное, никого не оставит равнодушным популярная фраза из широко известного фильма «Джентльмены удачи». Ведь действительно: бесит, когда сидишь за просмотром любимого сериальчика, вдруг — бамс! Вырубили свет, и зарядки ноута, как назло, не хватило. И не выработаешь электричество в домашних условиях, а жаль… Но вот понять, как оно работает — это мы сможем сделать в статье.

Электрический ток
В наше время трудно себе представить жизнь без электричества. Телевизор не посмотреть, телефон не зарядить, чай не попить… Ни один электроприбор в доме не будет работать без электричества. А объявление об отключении электроэнергии, вызывает тихий ужас.
Электричество — это форма энергии, которая существует в виде статических или подвижных электрических зарядов.
Поток. И то и другое представляет собой направленное движение частиц. Из чего состоит вода? Из молекул. Когда эти молекулы движутся в одном направлении, то они образуют поток воды, который течет, например, по трубам.
Так же и электрический ток. Он образуется потоком заряженных частиц, которые движутся по проводам.
Сформулируем определение:
Электрический ток — это упорядоченное движение заряженных частиц.
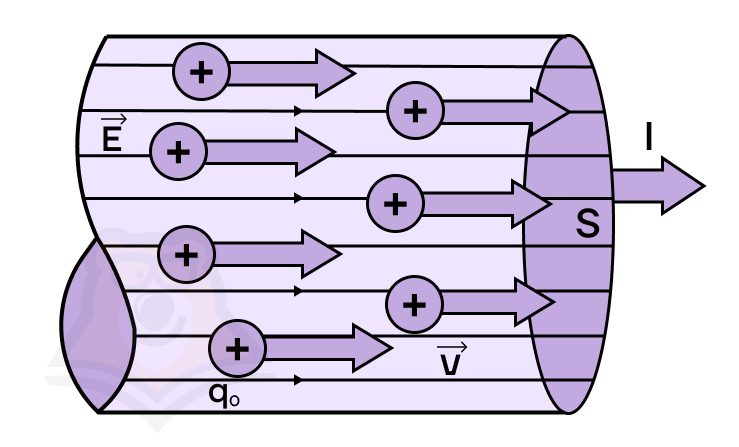
Чтобы электрический ток существовал, необходимо выполнение следующих условий:
- наличие свободных заряженных частиц;
- наличие электрического поля;
- наличие замкнутой электрической цепи.
Основными количественными характеристиками электрического тока являются сила тока и напряжение.
Напряжение
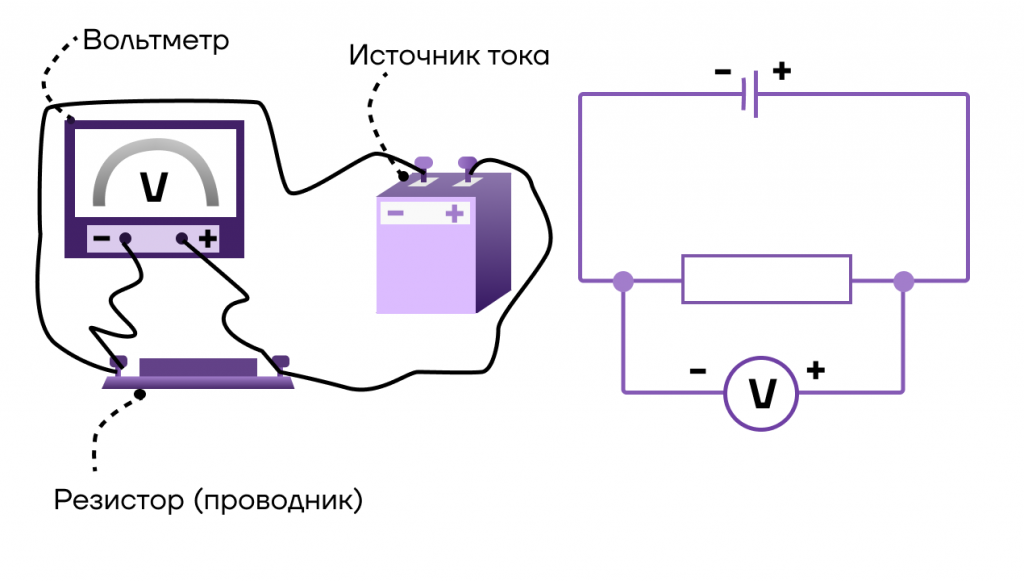
Чтобы внутри цепи существовал электрический ток, цепь должна быть замкнута и между концами участка цепи должно существовать напряжение.
Напряжение — скалярная (не имеющая направления) физическая величина, значение которой равно работе тока на участке цепи, совершаемой при переносе единичного электрического заряда из одной точки в другую.
U — напряжение (В),
A — работа тока на участке цепи (Дж),
q — электрический заряд (Кл).
Единица измерения U — В (Вольт) = (frac{Дж}{Кл})

Электрический ток – результат “труда” множества частиц. Они любят работать – не ленятся перемещаться из одного конца цепи в другой. И чем больше они будут работать, тем большее напряжение получится. Так запоминаем связь напряжения (U) с работой (A).
Услышав слова из известной песни Димы Билана «Это ты, это я, между нами молния, С электрическим разрядом 220 Вольт…» любой физик (и электрик) приобретает новую пару седых волосинок. Такое напряжение очень опасно для человека. Однако, 220 Вольт — это то самое напряжение в наших розетках!
Прибор для измерения напряжения — вольтметр. Он включается в цепь параллельно. Пример подключения представлен на рисунке:
Сила тока
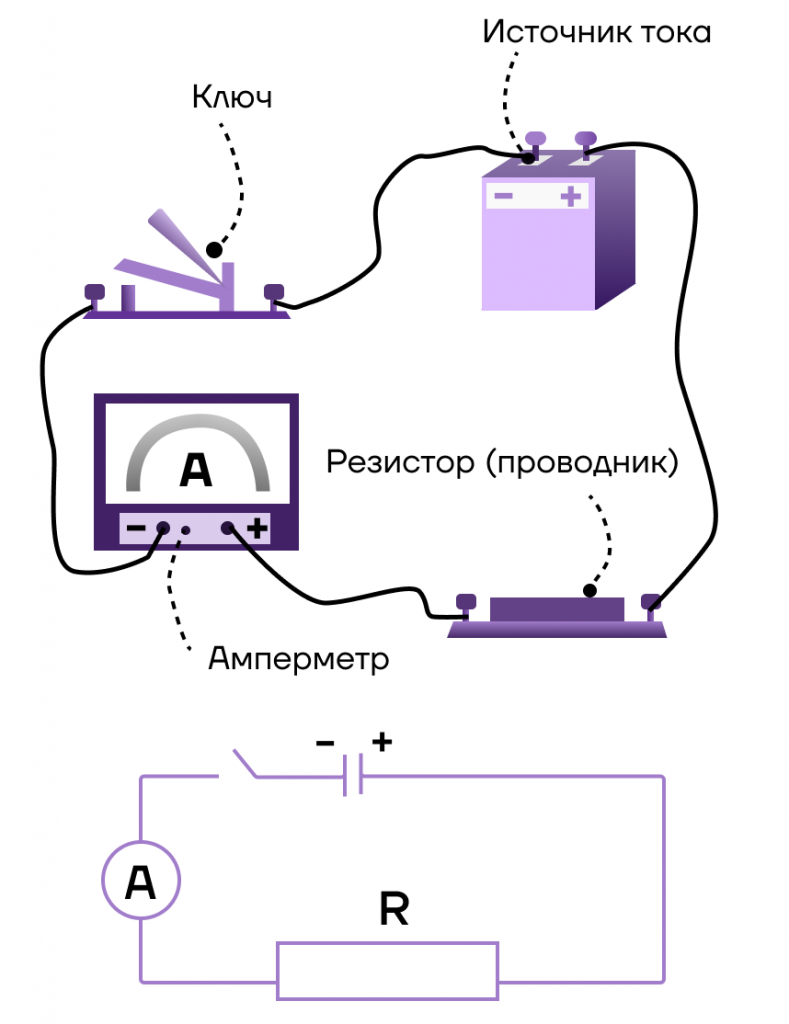
Это еще одна немаловажная характеристика электрического тока.
Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени .
I — сила тока (А),
q — электрический заряд (Кл),
t — время (с).
Единица измерения I — А (ампер) = (frac{Кл}{с}).
Представим, что внутри проводника «бежит» в одном направлении огромное количество заряженных частиц. Так вот, чем больше общий заряд частиц, пробегающих через поперечное сечение проводника за единицу времени, тем больше будет значение силы тока. Это поможет вам запомнить зависимость силы тока (I) от электрического заряда (q).
Прибор для измерения силы тока — амперметр. Он включается в цепь последовательно. Пример подключения представлен на рисунке:
Направление тока совпадает с направлением движения положительно заряженных частиц.
Давайте разберемся, как можно определить направление тока в цепи на примере.
Задача. На рисунке изображена электрическая цепь с источником тока и сопротивлением R. Определите направление тока в данной цепи (по часовой стрелке/против часовой стрелки).
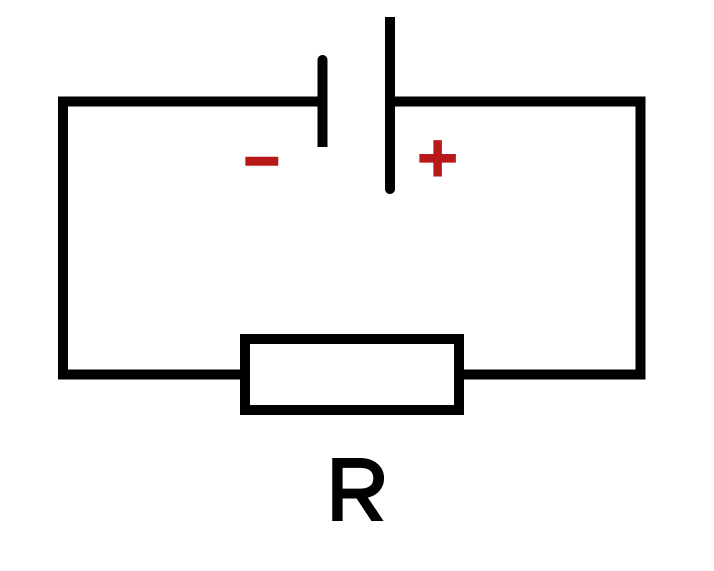
Решение:
Обратите внимание, «большая» пластина реостата расположена справа (именно она и направляет ток), а «маленькая» слева. Положительно заряженные частицы двигаются от катода к аноду (от положительно заряженной пластинки к отрицательно заряженной), а направление тока всегда совпадает с направлением положительно заряженных частиц. Значит, ток в цепи направлен по часовой стрелке.
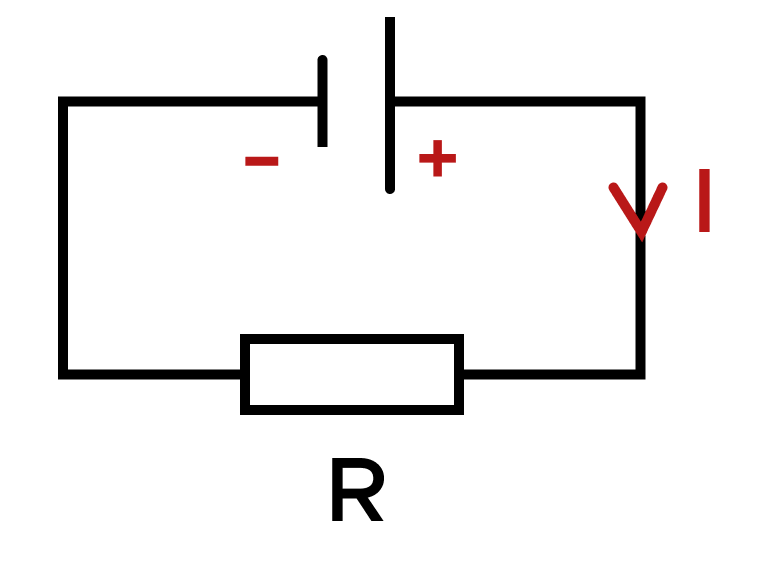
Ответ: по часовой стрелке
Электрическое сопротивление
Оно является электрической характеристикой проводника.
Сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
R — сопротивление (Ом),
p — удельное сопротивление проводника,
l — длина проводника (м),
S — площадь поперечного сечения проводника (мм²).
Единица измерения R — Ом.
Удельное сопротивление проводника (p) можно посмотреть в специальной таблице в справочнике или в интернете. Для каждого материала будет свое значение. Мы приведем для примера лишь фрагмент такой таблицы.
Таблица удельных сопротивлений проводников
| Металл | Удельное сопротивление, Ом * (мм^2)/ м |
| Серебро | 0,0015 |
| Медь | 0,018 |
| Золото | 0,023 |
| Алюминий | 0,029 |
| Вольфрам | 0,055 |
| Железо | 0,098 |
Сопротивление — это внешнее свойство, зависящее от количества присутствующего материала, от геометрических характеристик проводника и от самого материала, из которого сделан проводник.
Удельное сопротивление — это внутреннее свойство проводника, которое не зависит от его размера, а зависит от химического состава вещества и температуры.
Условно можно сказать, что сопротивление — это свойство проводника, а удельное сопротивление — свойство материала.
Получается, что прежде всего на то, каким будет сопротивление, влияют размеры проводника, его форма, материал, из которого он сделан.
Удельное сопротивление проводника зависит также от температуры. Когда температура твердых тел увеличивается, то удельное сопротивление возрастает. А в растворах и расплавах — наоборот, уменьшается. В экзаменационных задачах случаи с изменением удельного сопротивления не рассматриваются, а вот в олимпиадных задачах такое встретить можно.
Давайте поразмышляем: что чему сопротивляется?
Причина электрического сопротивления кроется во взаимодействии зарядов разного знака при протекании тока по проводнику. Это взаимодействие можно сравнить с силой трения, стремящейся остановить движение заряженных частиц.
Чем сильнее взаимодействие свободных электронов с положительными ионами в узлах кристаллической решетки проводника, тем больше сопротивление проводника.
Проводник с определенным постоянным сопротивлением называется резистор.
Вернемся к сравнению электрического тока с водой: как молекулы воды из крана движутся сверху вниз, так и электрический ток имеет определенное направление — от катода к аноду. Электрический заряд условно в нашем примере аналогичен массе воды, а напряжение — напору воды из крана.
Закон Ома
Сила тока, напряжение и сопротивление связаны между собой соотношением, которое называется закон Ома:
I — сила тока (А),
U — напряжение (В),
R — сопротивление (Ом).
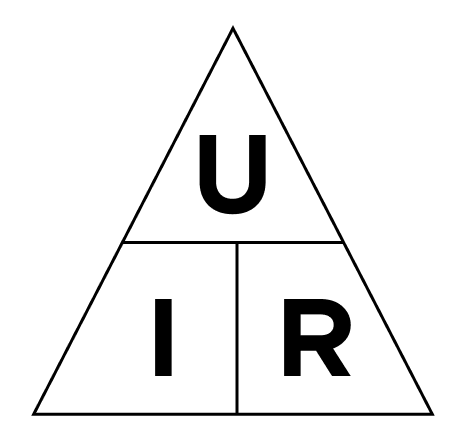
Для упрощенного понимания закона Ома можно использовать данный треугольник. Чтобы вспомнить формулу для нахождения той или иной величины, нужно ее закрыть рукой. Если оставшиеся открытыми величины стоят бок о бок, то они перемножаются друг с другом (U=IR). А если одна величина стоит выше другой, то в таком случае мы делим их друг на друга (I=U/R или R=U/I)
Данный закон справедлив для участка цепи, на который не действуют сторонние силы.
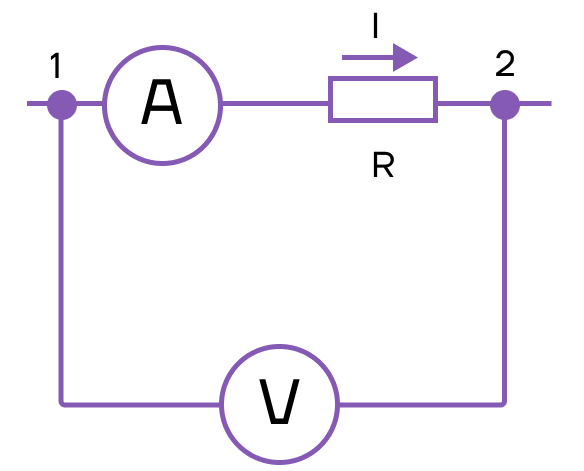
Разберем задачу из контрольно-измерительных материалов ЕГЭ (номер 12).
Ниже на рисунке приведена схема электрической цепи, в которой провода можно считать идеальными. Определите сопротивление резистора, если показания амперметра 0,2 А, а вольтметра — 8 В.
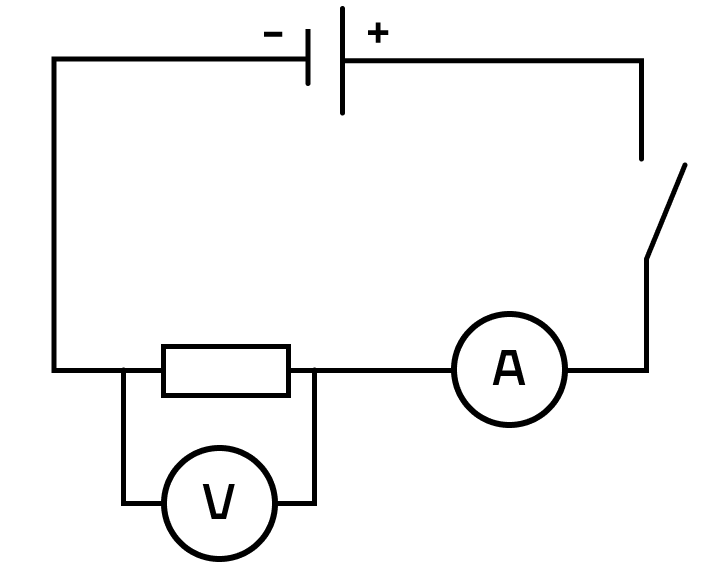
Решение:
Вольтметр подключен параллельно резистору. Следовательно, он показывает напряжение на резисторе U.
Амперметр подключен последовательно. Следовательно, он показывает силу тока I на всей цепи.
Чтобы найти сопротивление на резисторе, воспользуемся законом Ома:
I=(frac{U}{R}), где R — сопротивление резистора.
Выразим R и подставим значения:
R=(frac{U}{I})
R=(frac{8}{0,2})=40 (Ом)
Ответ: 40
Работа и мощность электрического тока
Вернемся к понятию работы. Мы говорили, при перемещении заряда по проводнику электрическое поле совершает работу (А):
A = qU
Если мы выразим заряд из формулы силы тока q=It, то получим, формулу для расчета работы электрического поля (А) при протекании постоянного тока (или просто работа тока):
A — работа электрического тока (Дж),
U — напряжение (В),
I — сила тока (А),
t — время прохождения тока (с).
Единица измерения А — Дж (Джоуль).
В быту ток совершает работу длительное время, поэтому при определении затраченной электрической энергии используют единицу измерения кВт * ч. Киловатт в час — это энергия, которая потребляется устройством мощностью 1 кВт в течении 1 часа. Учитывая, что 1 ч=3600 с, получим:
1 кВт*ч = 1000 Вт * 3600 с = 3600000 Дж = 3600 кДж
Если же работу тока рассчитать за единицу времени, то мы получим мощность постоянного электрического тока.
Мощность — величина, обозначающая интенсивность передачи электрической энергии.
P — мощность (Вт),
A — работа электрического тока (Дж),
t — время прохождения тока (с).
Единица измерения P — Вт (Ватт).
Средняя мощность тока равна:
(P = frac{A}{t} = frac{qU}{t} = IU = frac{U^2}{R} = I^2R)
Теперь мы знаем все про мощность и работу тока, а значит, нужно отработать это на практике. Тем более что такие задачи встречаются в ЕГЭ (номер 12).
Задача.
Какую работу совершит электрический ток в электродвигателе вентилятора за 20 мин., если сила тока в цепи 0,2 А, а напряжение 12 В?
Решение.
Вспомним формулу для работы тока A=U*I*t , где U=12 В — напряжение в электродвигателе, I=0,2 A — сила тока, t=20 мин=1200 с — время.
Все данные нам уже известны, поэтому можем подставить их в формулу для работы тока и получить ответ.
A=12*0,2*1200=2880 Дж
Ответ: 2880 Дж
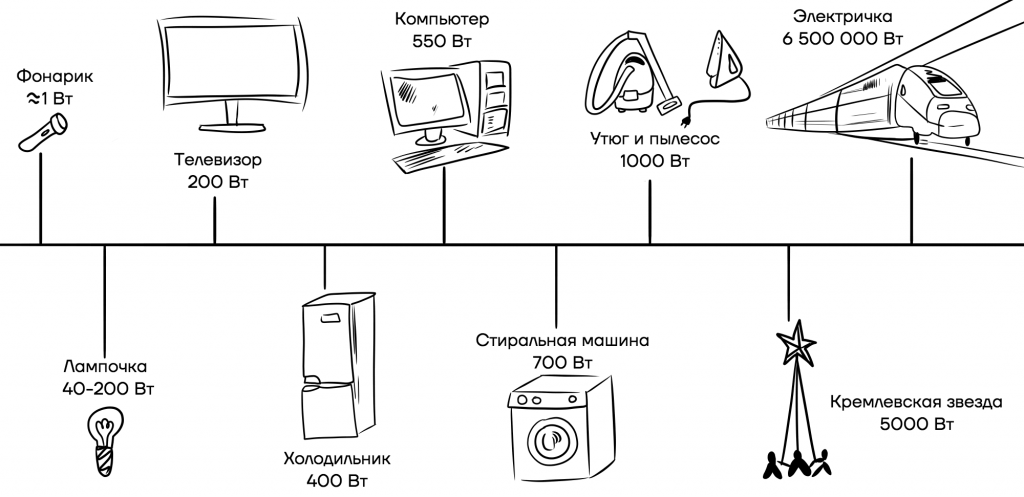
Мощность электроприбора всегда указывается в документации, прилагающейся к нему. Кроме того, нередко ее пишут на самом приборе. Давайте посмотрим на утюг, или стиральную машину дома. Мы увидим, что утюг имеет мощность 1000 Вт, а обычная энергосберегающая лампочка, всего 40 Вт (на то она и сберегающая). Чем больше мощность прибора, тем больше энергии он будет потреблять. Примеры мощностей различных приборов представлены на рисунке.
Закон Джоуля — Ленца
Теперь же свяжем работу тока и теплоту, которая выделяется на проводнике за некоторое время t.
Когда приборы подключены в сеть, мы можем заметить, что они нагреваются. Очень часто это наблюдается, когда телефон подключен на зарядку, а мы продолжаем по нему звонить, использовать интернет и прочее. Это плохо влияет на телефон: перегрев батареи и корпуса могут быстрее привести девайс в негодность.

Почему так происходит?
Электрический ток оказывает тепловое действие на проводник. Количество теплоты, которое при этом выделяется, будет рассчитываться по закону Джоуля — Ленца:
Количество теплоты, выделяемое за время в проводнике с током, пропорционально произведению квадрата силы тока на этом участке и сопротивления проводника:
Q — количество теплоты (Дж),
I — работа электрического тока (Дж),
R — сопротивление (Ом),
t — время прохождения тока (с).
Единица измерения Q — Дж (Джоуль).
В электронагревательных приборах используются проводники с высоким сопротивлением, что обеспечивает выделение тепла на определенном участке.
Так, проволоку из нихрома (сплав никеля с хромом) применяют в электронагревательных элементах, работающих при температуре до 1000 ℃ (резисторах, например). Нихром относится к классу сплавов с высоким электрическим сопротивлением, что определяет его применение в качестве электрических нагревателей. Этот сплав используется также в печах обжига и сушки и различных аппаратах теплового воздействия, например, в фенах, паяльниках или обогревателях.

Кто первый ввел понятие «электрический ток» в науку? Ответ: Андре-Мари Ампер.
Такой был финальный вопрос (ценой в 1 000 000) в игре «Кто хочет стать миллионером?» от 20 января 2018 г. Но участники не смогли ответить на него, и мечту получить свой миллион не исполнили.

Еще немного про электричество…
- Постоянный электрический ток используется в работе двигателей электротранспорта, схемах автомобилей, электронике и др.
- Электричество есть и в нашем организме. Мышечные клетки сердца при сокращении производят электроэнергию, эти импульсы можно измерить с помощью электрокардиограммы (ЭКГ).
- Бенджамин Франклин (да-да, президент Америки) провел множество опытов в 18 веке и создал громоотвод. Также он является человеком, который вывел закон сохранения электрического заряда.
- В древности люди считали, что, если молния ударила в курган, значит, там зарыто сокровище.
Термины
Источник тока — устройство, разделяющее положительные и отрицательные заряды.
Сторонние силы — силы неэлектрического происхождения, вызывающие разделение зарядов в источнике тока.
Фактчек
- Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени: (I = frac{q}{t})
- Напряжение — скалярная физическая величина, равная отношению полной работы кулоновских и сторонних сил А при перемещении положительного заряда на участке цепи к значению этого заряда: (U = frac{A}{q})
- Сопротивление — физическая величина, характеризующая электрические свойства участка цепи: (R = frac{pl}{S})
- Мощность — величина, обозначающая интенсивность передачи электрической энергии: (P = frac{A}{t})
- Закон Ома: сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении и обратно пропорциональна сопротивлению участка при постоянном напряжении: (I = frac{U}{R}).
- Закон Джоуля— Ленца: количество теплоты Q, выделяемое за время t в проводнике с током, пропорционально произведению квадрата силы тока I на этом участке и сопротивления R проводника: Q = I2Rt.
- Работа электрического поля при протекании постоянного тока (или просто работа тока): А = UIt.
Проверь себя
Задание 1.
Упорядоченное движение заряженных частиц — это:
- электрическое поле
- электрический ток
- электрическая мощность
- работа тока
Задание 2.
Удельное сопротивление проводника:
- зависит от температуры
- не зависит от температуры
- зависит от силы протекающего через проводник тока
- не зависит от напряжения
Задание 3.
Формула для расчета силы тока:
- I = Ut
- I = UIt
- I = I2Rt
- (I = frac{q}{t})
Задание 4.
Что такое мощность электрического тока:
- работа за единицу времени
- отношение заряда к единице времени
- произведение силы тока на сопротивление
- тепло, выделяемое на резисторе
Задание 5.
Причина электрического сопротивления:
- во взаимодействии зарядов одинакового знака
- в отсутствии взаимодействия между зарядами
- во взаимодействии зарядов разного знака
- в передаче тепла
Ответы: 1.— 2; 2. — 1; 3.— 4; 4.— 1; 5. — 3.
[math]C_1 – C_4 = 8мкФ, [math]C_5 = C_6 = 12мкФ, [math]Q_2 = Q_6 = 5cdot 10^{-5}Кл. Найти напряжение U на всей цепочке конденсаторов и заряд всей цепи Q.
Напряжение на участке 4-5 на конденсаторах С5 и С6. Это напряжение находится как отношение заряда к емкости:
После замены параллельных пар конденсатор на эквивалентные емкости, получили упрощенную схему, показанную на рисунке ниже
В данном эквивалентном соединении на всех элементах (конденсаторах) заряд одинаковый и равен общему заряду, т.е. [math]10^{-4}Кл
Поэтому можем легко найти напряжения на остальных участках при [math]Q=10^{-4}Кл:
[math]U_{1-2}=U_{C1}=frac{Q}{C_1}=frac{10^{-4}}{8cdot 10^{-6}}=12,5Вольт
[math]U_{3-4}=U_{C1}=frac{Q}{C_4}=frac{10^{-4}}{8cdot 10^{-6}}=12,5Вольт
Таким образом мы нашли, что весь общий заряд цепи равен [math]Q=10^{-4}Кулон. Соответственно, можем найти общее напряжение [math]U_{1-6} на зажимах заданной схемы:
[math]U_{1-6}=U_{1-2}+U_{2-3}+U_{3-4}+U_{4-5}=35,4Вольт
Получили, что общий заряд цепи [math]Q=10^{-4}Кулон, напряжение на зажимах 1-6 [math]U_{1-6}=35,4Вольт
А можно решить немного по-другому
Упрощаем схему, сведя ее к последовательному соединению конденсаторов (см. рис. выше)
Получили, что общий заряд цепи [math]Q=10^{-4}Кулон, напряжение на зажимах 1-6 [math]U_{1-6}=35,4Вольт
Как видим, вычисления и первым и вторым способом сошлись
Содержание:
- Последовательное соединение конденсаторов
- Параллельное соединение конденсаторов
- Смешанное соединение конденсаторов
- Пример расчета
В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.
-
Последовательное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.
Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:
Qобщ=Q1=Q2=Q3,
где: Q1, Q2, Q3 — соответственно заряд на первом, втором, третьем и т.д. конденсаторах
Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:
U1=Q/C1; U2=Q/C2; U3=Q/C3, где:
- U1, U2, U3 — соответственно напряжение на первом, втором, третьем конденсаторах
- C1, C2, C3 — соответственно емкости первого, второго, третьего конденсаторов
При этом общее напряжение составит:
Uобщ=U1+U2+U3+…+Un
Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:
- При последовательном соединении двух конденсаторов:
Собщ=(C1*C2)/(C1+C2)
- При последовательном соединении трех и более конденсаторов:
1/Собщ=1/C1+1/C2+1/C3+…+1/Cn
-
Параллельное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.
Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:
U=U1=U2=U3
Заряд же на каждом из конденсаторов будет зависеть от его емкости:
Q1=U*C1; Q2=U*C2; Q3=U*C3
При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:
Qобщ=Q1+Q2+Q3…+…Qn.
Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:
Собщ=C1+C2+C3+…+Cn
-
Смешанное соединение конденсаторов
Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.
Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.
Для наглядности приведем пример расчета общей емкости данной схемы.
-
Пример расчета
Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.
Произведем расчет каждой группы:
- Группа 1 — последовательное соединение трех конденсаторов:
1/C1,2,3 = 1/C1+1/C2+1/C3 = 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C1,2,3 = 1/0,367 = 2,72 мкФ
- Группа 2 — последовательное соединение двух конденсаторов:
С4,5 = (C4*C5)/(C4+C5)= (20*30)/(20+30) = 600/50 = 12 мкФ
- Группа 3 — параллельное соединение трех конденсаторов:
С6,7,8 = C6+C7+C8 = 5+25+30 = 60 мкФ
В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:
- Группа 4 — параллельное соединение двух групп конденсаторов:
С1,2,3,4,5 = C1,2,3+C4,5 = 2,72+12 = 14,72 мкФ
В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:
Собщ = (C1,2,3,4,5*C6,7,8)/(C1,2,3,4,5+C6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ
Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!
Не нашли на сайте ответа на интересующий Вас вопрос? Задайте его на форуме! Наши специалисты обязательно Вам ответят.
↑ Наверх