В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя – верхней части, и знаменателя – нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34 умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.
Приведение дробей к общему знаменателю – это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель дробей – это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Можно ди дроби 13, 216, 512 привести к общему знаменателю, который равен 150?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12. Другими словами, число 150 должно без остатка делиться на 3, 6, 12. Проверим:
150÷3=50, 150÷6=25, 150÷12=12,5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель дробей – это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел – это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Нужно найти наименьший общий знаменатель для дробей 110 и 12728.
Ищем НОК чисел 10 и 28. Разложим их на простые множители и получим:
10=2·528=2·2·7НОК(15, 28)=2·2·5·7=140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Есть дроби 314 и 518. Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14=2·718=2·3·3НОК(14, 18)=2·3·3·7=126
Вычисляем дополнительные множители для каждой дроби. Для 314 дополнительный множитель находится как 126÷14=9, а для дроби 518 дополнительный множитель будет равен 126÷18=7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3·914·9=27126, 5·718·7=35126.
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Привести дроби 32, 56,38 и 1718 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
НОК(2, 6)=6НОК(6, 8)=24НОК(24, 18)=72НОК(2, 6, 8, 18)=72
Далее вычислим дополнительные множители для каждой дроби.
Для 32 дополнительный множитель равен 72÷2= 36, для 56 дополнительный множитель равен 72÷6= 12, для 38 дополнительный множитель равен 72÷8= 9, наконец, для 1718 дополнительный множитель равен 72÷18= 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
32·36=1087256·12=607238·9=27721718·4=6872
Как привести дробь к наименьшему общему знаменателю (пример)
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Общий знаменатель и дополнительный множитель.
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
(frac{17}{5}, frac{1}{5})
Пример разных знаменателей у дробей:
(frac{8}{3}, frac{2}{13})
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
(frac{8}{3} = frac{8 times color{red} {13}}{3 times color{red} {13}} = frac{104}{39})
Вторую дробь умножаем на дополнительный множитель 3.
(frac{2}{13} = frac{2 times color{red} {3}}{13 times color{red} {3}} = frac{6}{39})
Мы привели к общему знаменателю дроби:
(frac{8}{3} = frac{104}{39}, frac{2}{13} = frac{6}{39})
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби (frac{5}{8}) и (frac{7}{12}) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
(begin{align}&frac{5}{8} = frac{5 times color{red} {3}}{8 times color{red} {3}} = frac{15}{24}\\&frac{7}{12} = frac{7 times color{red} {2}}{12 times color{red} {2}} = frac{14}{24}\\ end{align})
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби (frac{1}{4}) и (frac{9}{16}) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
(begin{align}&frac{1}{4} = frac{1 times color{red} {4}}{4 times color{red} {4}} = frac{4}{16}\\&frac{9}{16} = frac{9 times color{red} {1}}{16 times color{red} {1}} = frac{9}{16}\\ end{align})
Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.
К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.
Пример №1:
Для дроби (frac{1}{2}) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?
Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.
(frac{1}{2} = frac{1 times color{red} {6}}{2 times color{red} {6}} = frac{6}{12})
б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.
(frac{1}{2} = frac{1 times color{red} {9}}{2 times color{red} {9}} = frac{9}{18})
в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.
(frac{1}{2} = frac{1 times color{red} {25}}{2 times color{red} {25}} = frac{25}{50})
При нахождении наименьшего общего знаменателя при сложении (вычитании) обыкновенных дробей учащиеся часто поступают нерационально, принимая в качестве общего знаменателя произведение знаменателей исходных дробей.
Можно использовать следующий прием, использующий навык сокращения дробей
Пример 1. Найти сумму дробей с разными знаменателями
Составили дробь из знаменателей дробей слагаемых и после ее сокращения на 7 получили дополнительные множители к дробям слагаемым:
2 – дополнительный множитель к дроби со знаменателем 21,
3 – дополнительный множитель к дроби со знаменателем 14
Т.е. дополнительные множители соответствуют исходным знаменателям “крест-накрест”
Пример 2. Найти разность дробей с разными знаменателями
Составили дробь из знаменателей, сократили ее и получили дополнительные множители, которые соответствуют исходным знаменателям “крест-накрест”, как в пропорции
Способ можно применять для нахождения наименьшего общего кратного двух чисел (это очевидно, т.к. наименьший общий знаменатель является наименьшим общим кратным исходных знаменателей)
Пример 3. Найти наименьшее общее кратное
Составили дробь из чисел, для которых надо найти наименьшее общее кратное, сократили ее последовательно (сначала на 2, потом на 7, потом на 3) – получили несократимую дробь.
Числитель составленной дроби умножаем на знаменатель дроби после сокращения (84 умножаем на 3).
Знаменатель составленной дроби умножаем на числитель дроби после сокращения (126 умножаем на 2).
В обоих случаях получаем наименьшее общее кратное при условии, что получена именно несократимая дробь.
Алгоритм усложняется, если надо найти общий знаменатель трех и более дробей. В этом случае надо найти общий знаменатель первых двух дробей, потом найти общий знаменатель результата и следующей дроби и т.д.
Алгоритм можно применять также при сложении (вычитании) алгебраических дробей.
Математика
5 класс
Урок № 51
Приведение дробей к общему знаменателю
Перечень рассматриваемых вопросов:
- основное свойство дроби;
- общий знаменатель дробей;
- дополнительный множитель;
- НОК двух чисел;
- наименьший общий знаменатель.
Тезаурус
Общий знаменатель – это число всегда положительное, на которое делятся знаменатели данных дробей.
Наименьший общий знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.
Дополнительный множитель – это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель.
Обязательная литература:
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Вы уже знаете, что дробь в математике – это число, состоящее из одной или нескольких частей единиц, и умеете определять и называть часть целого.
Вопрос: какая часть яблока на картинке?
Ответ: 
Вопрос: какая часть пиццы осталась на тарелке?
Ответ: 
.
Или, например, круг разделили на восемь частей. Четыре части закрасили в другой цвет: значит, закрашено 
части круга.
Но, если посмотреть внимательнее, четыре доли круга, разделённого на восемь частей, – это ровно половина. Значит, дробь 
равна дроби 
.
Вспомним основное свойство дроби.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Дроби 
и 
имеют разные знаменатели, но их можно привести к общему знаменателю.
Для этого найдём число, которое делится на 8 и 3, – например, число 24.
Дополнительный множитель обычно пишут слева над числителем:
Приведём дроби к знаменателю 24. Для этого умножим числитель и знаменатель дроби 
на дополнительный множитель 3.
Теперь умножим числитель и знаменатель дроби 
на дополнительный множитель 8.
Дроби
и
приведены к общему знаменателю.
Далее приведём дроби 
и 
к наименьшему общему знаменателю.
Так как наименьшее общее кратное (НОК) чисел 36 и 54 равно 108, то наименьший общий знаменатель этих дробей также равен 108.
Соответственно, чтобы привести дробь
к знаменателю 108, необходимо и числитель, и знаменатель дроби умножить на 3:
Чтобы привести дробь 
к тому же знаменателю, умножаем и числитель, и знаменатель этой дроби на 2:
Таким образом, алгоритм приведения дробей к наименьшему
- деление на простые множители знаменателей дробей;
- поиск наименьшего общего кратного(НОК)для знаменателей этих дробей;
- приведение дроби к общему знаменателю, то есть умножение и числителя, и знаменателя дроби на множитель.
Итак, сегодня мы научились находить наименьший общий знаменатель дробей двумя способами:
- первый способ – перемножить знаменатели этих дробей;
- второй способ – найти наименьшее общее кратное этих дробей.
Тренировочные задания
№ 1. Для дроби 
выберите из представленных равную ей дробь со знаменателем 6; 15; 102:
Чтобы привести дробь
к знаменателю 6, нужно числитель и знаменатель дроби умножить на дополнительный множитель 2:
Чтобы привести дробь 
к знаменателю 15, нужно числитель и знаменатель дроби умножить на дополнительный множитель 5:
Чтобы привести дробь 
к знаменателю 102, нужно числитель и знаменатель дроби умножить на дополнительный множитель 34:
Следовательно, правильный ответ: 
№ 2. Какое число является наименьшим общим знаменателем дробей 
и 
?
12
24
96
35
Чтобы найти наименьший общий знаменатель дробей 
и 
, нужно:
- разложить на простые множители знаменатели дробей: 8 = 2 ∙ 2 ∙ 2 и 12 = 2 ∙ 2 ∙ 3;
- найти НОК (8, 12) = 24.
Следовательно, правильный ответ: 24.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Сложение дробей
Поддержать сайт
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
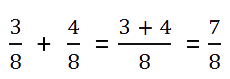
C помощью букв это правило сложения можно записать так:
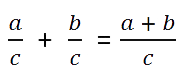
Запомните!
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
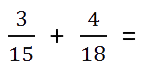
Как найти общий знаменатель
Находим НОК (15, 18).
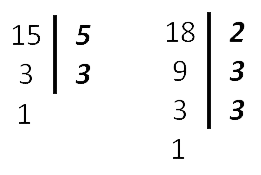
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
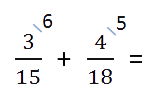
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
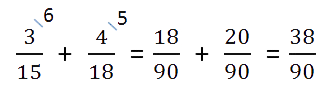
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
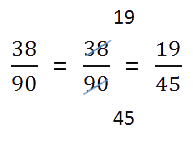
- Eсли в результате получилась
- Ещё раз весь пример целиком.
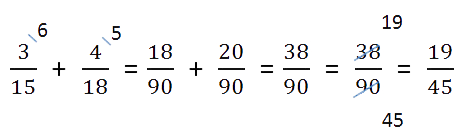
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
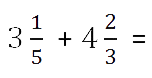
Складываем целые части.
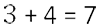
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем.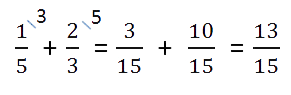
- Сложить полученные результаты из пунктов 1 и 2.
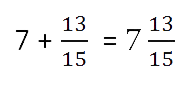
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
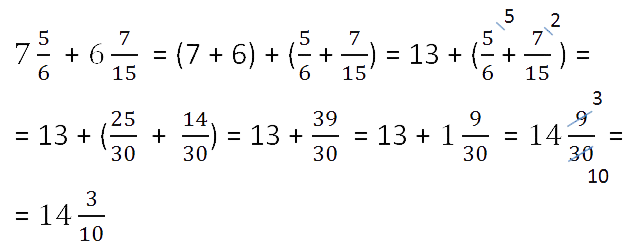
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( – ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + + 
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
