Нахождение наименьшего общего знаменателя бывает нужно для сложения, вычитания и сравнения дробей.
Наименьший общий знаменатель – это наименьшее число, которое нацело делится и на первый, и на второй знаменатель двух дробей.
Правило нахождения наименьшего знаменателя следующее:
Для того, чтобы найти наименьший общий знаменатель двух дробей, нужно найти методом подбора наименьшее общее число, которое бы делилось и на первый, и на второй знаменатель. После этого нужно умножить каждую дробь на такое число, чтобы в знаменателе этих дробей получилось найденное нами наименьшее общее число.
Найти наименьший общий знаменатель двух дробей: 56frac{5}{6} и 34frac{3}{4}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 6, и на 4. Это число 12. Далее умножаем каждую дробь на такие числа, чтобы в знаменателе получилось 12. Первую дробь умножаем на 2, а вторую на 3:
56=5⋅26⋅2=1012frac{5}{6}=frac{5cdot2}{6cdot2}=frac{10}{12}
34=3⋅34⋅3=912frac{3}{4}=frac{3cdot3}{4cdot3}=frac{9}{12}
Дроби приведены к наименьшему общему знаменателю: 12.
Ответ
12
Найти наименьший общий знаменатель двух дробей: 521frac{5}{21} и 27frac{2}{7}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 21, и на 7. В этом случае это – один из знаменателей, число 21. Далее нужно умножить вторую дробь на такое число, чтобы в знаменателе получилось 21. Умножаем вторую дробь на 3:
27=2⋅37⋅3=621frac{2}{7}=frac{2cdot3}{7cdot3}=frac{6}{21}
Дроби приведены к наименьшему общему знаменателю: 21.
Ответ
21
Решение задач по алгебре онлайн от экспертов Студворк!
Тест по теме “Наименьший общий знаменатель”
Загрузить PDF
Загрузить PDF
Для сложения или вычитания дробей с разными знаменателями (числа, стоящие под дробной чертой) сначала необходимо найти их наименьший общий знаменатель (НОЗ). Таким числом будет наименьшее кратное, которое встречается в списке кратных каждого знаменателя, то есть число, делящееся нацело на каждый знаменатель.[1]
Также вы можете вычислить наименьшее общее кратное (НОК) двух или более знаменателей. В любом случае речь идет о целых числах, методы нахождения которых весьма схожи. Определив НОЗ, вы сможете привести дроби к общему знаменателю, что в свою очередь позволит вам складывать и вычитать их.
-

1
Перечислите кратные каждого знаменателя. Составьте список из нескольких кратных для каждого знаменателя в уравнении. Каждый список должен состоять из произведения знаменателя на 1, 2, 3, 4 и так далее.
- Пример: 1/2 + 1/3 + 1/5
- Кратные 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; и так далее.
- Кратные 3: 3 * 1 = 3; 3 * 2 = 6; 3 *3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; и так далее.
- Кратные 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; и так далее.
-

2
Определите наименьшее общее кратное. Просмотрите каждый список и отметьте любые кратные числа, которые являются общими для всех знаменателей. После выявления общих кратных определите наименьший знаменатель.
- Обратите внимание, что если общий знаменатель не найден, возможно, потребуется продолжить выписывать кратные до тех пор, пока не появится общее кратное число.
- Лучше (и легче) пользоваться этим методом в том случае, когда в знаменателях стоят небольшие числа.
- В нашем примере общим кратным всех знаменателей является число 30: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
- НОЗ = 30
-

3
Перепишите исходное уравнение. Для того чтобы привести дроби к общему знаменателю, при этом не изменив их значения, умножьте каждый числитель (число, стоящее над дробной чертой) на число, равное частному от деления НОЗ на соответствующий знаменатель.
- Пример: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
- Новое уравнение: 15/30 + 10/30 + 6/30
-

4
Решите полученное уравнение. После нахождения НОЗ и изменения соответствующих дробей, просто решите полученное уравнение. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30
Реклама
-

1
Перечислите делители каждого знаменателя. Делитель – это целое число, которое делит нацело данное число.[4]
Например, делителями числа 6 являются числа 6, 3, 2, 1. Делителем любого числа является 1, потому что любое число делится на единицу.- Пример: 3/8 + 5/12
- Делители 8: 1, 2, 4, 8
- Делители 12: 1, 2, 3, 4, 6, 12
-

2
Найдите наибольший общий делитель (НОД) обоих знаменателей. Перечислив делители каждого знаменателя, отметьте все общие делители. Самый большой общий делитель является наибольшим общим делителем, который понадобится вам для решения задачи.
- В нашем примере общими делителями для знаменателей 8 и 12 являются числа 1, 2, 4.
- НОД = 4.
-

3
Перемножьте знаменатели между собой. Если вы хотите использовать НОД для решения задачи, сначала перемножьте знаменатели между собой.
- Пример: 8 * 12 = 96
-

4
Разделите полученное значение на НОД. Получив результат перемножения знаменателей, разделите его на вычисленный вами НОД. Полученное число будет наименьшим общим знаменателем (НОЗ).
- Пример: 96 / 4 = 24
-

5
Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.
- Пример: 24 / 8 = 3; 24 / 12 = 2
- (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
- 9/24 + 10/24
-

6
Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 9/24 + 10/24 = 19/24
Реклама
-

1
Разложите каждый знаменатель на простые множители. Разложите каждый знаменатель на простые множители, то есть простые числа, которые при перемножении дают исходный знаменатель. Напомним, что простые множители – это числа, которые делятся только на 1 или самих себя.[6]
- Пример: 1/4 + 1/5 + 1/12
- Простые множители 4: 2 * 2
- Простые множители 5: 5
- Простые множители 12: 2 * 2 * 3
-

2
Подсчитайте число раз каждый простой множитель есть у каждого знаменателя. То есть определите, сколько раз каждый простой множитель появляется в списке множителей каждого знаменателя.
- Пример: Есть две 2 для знаменателя 4; нуль 2 для 5; две 2 для 12
- Есть нуль 3 для 4 и 5; одна 3 для 12
- Есть нуль 5 для 4 и 12; одна 5 для 5
-

3
Возьмите только наибольшее число раз для каждого простого множителя. Определите наибольшее число раз наличия каждого простого множителя в любом знаменателе.
- Например: наибольшее число раз для множителя 2 – 2 раза; для 3 – 1 раз; для 5 – 1 раз.
-

4
Запишите по порядку найденные в предыдущем шаге простые множители. Не записывайте число раз наличия каждого простого множителя во всех исходных знаменателях – делайте это с учетом наибольшего числа раз (как описано в предыдущем шаге).
- Пример: 2, 2, 3, 5
-

5
Перемножьте эти числа. Результат произведения этих чисел равен НОЗ.
- Пример: 2 * 2 * 3 * 5 = 60
- НОЗ = 60
-

6
Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.
- Пример: 60/4 = 15; 60/5 = 12; 60/12 = 5
- 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
- 15/60 + 12/60 + 5/60
-

7
Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 15/60 + 12/60 + 5/60 = 32/60 = 8/15
Реклама
-

1
Преобразуйте каждое смешанное число в неправильную дробь. Для этого умножьте целую часть смешанного числа на знаменатель и сложите с числителем – это будет числитель неправильной дроби. Целое число тоже превратите в дробь (просто поставьте 1 в знаменателе).
- Пример: 8 + 2 1/4 + 2/3
- 8 = 8/1
- 2 1/4, 2 * 4 + 1 = 8 + 1 = 9; 9/4
- Переписанное уравнение: 8/1 + 9/4 + 2/3
-

2
Найти наименьший общий знаменатель. Вычислите НОЗ любым способом, описанным в предыдущих разделах. Для этого примера мы будем использовать метод “перечисление кратных”, в котором выписываются кратные каждого знаменателя и на их основе вычисляется НОЗ.
- Обратите внимание, что вам не нужно перечислять кратные для 1, так как любое число, умноженное на 1, равно самому себе; иными словами, каждое число является кратным 1.
- Пример: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; т.д.
- 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; т.д.
- НОЗ = 12
-

3
Перепишите исходное уравнение. Числители и знаменатели исходных дробей умножьте на число, равное частному от деления НОЗ на соответствующий знаменатель.
- Например: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
- 96/12 + 27/12 + 8/12
-

4
Решите уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (по желанию)
Об этой статье
Эту страницу просматривали 223 321 раз.
Была ли эта статья полезной?
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
Что такое общий знаменатель?
Кроме понятия “общий знаменатель“, есть еще такое понятие как – “Наименьший общий знаменатель (НОЗ)” – это… тоже самое, что и “НОК”. Поэтому, мы не будем это разбирать здесь второй раз.
Но что такое общий знаменатель простыми словами?
Общий знаменатель – это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗ
Пример общего знаменателя :
Для того, чтобы понять, “что такое общий знаменатель” нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение – “+”.
Для таких маленьких чисел, как 2 и 3 – “нок” будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 – 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае – “+” – 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли “общий знаменатель” мы смогли выполнить необходимое действие с дробями.
1 2 + 1 3 =
1*3 2*3 + 1*2 3*2 =
3 6 + 2 6 =
3 + 2 6 =
5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос – “в каком случае ноз двух дробей будет являться произведением знаменателей?“, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.
И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :
Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
A B + C D =
A*D B*D + C*B D*B =
A*D + C*B DB
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом “НОК” для двух чисел, которые здесь – знаменатели.
Если вы не сходили по ссылке, то давайте вкратце попробуем разобраться в формуле подбора общего знаменателя.
Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный “НОК” – только может называться по другому…
смайлы
Этот способ может называться как “нахождение общего знаменателя методом разложения на множители”
Либо “метод нахождения наименьшего общего знаменателя” или просто “НОЗ”
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель – это 8 и разложить его на множители:
8 = 2 * 2 * 2
Ниже раскладываем меньший знаменатель :
6 = 2 * 3
Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
8 * 3 = 24
Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
10 = 2 * 5
Раскладываем меньший знаменатель :
4 = 2 * 2
Виртуально исключаем повторяющиеся множители из второго знаменателя – это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
10 * 2 = 20
Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находить общий знаменатель дробей онлайн!
Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
20 = 2 * 2 * 5
Раскладываем на множители второй знаменатель :
8 = 2 * 2 * 2
Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
20 * 2 = 40
Итого получаем их общий знаменатель 40.
Переходим к нахождению общего знаменателя онлайн
Открываем наш калькулятор.
Вводим первый знаменатель 20.
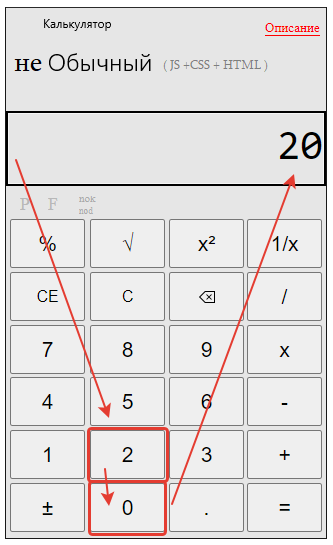
Нажимаем кнопку “НОК”
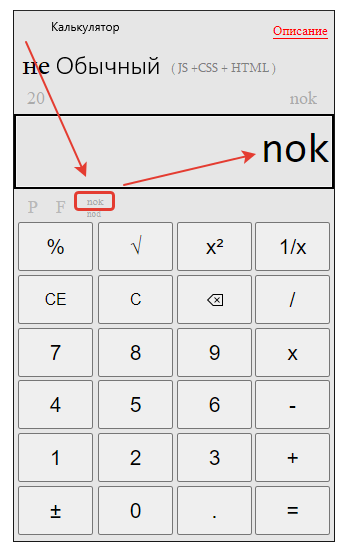
Набираем второй знаменатель 8.
Нажимаем равно – “=”
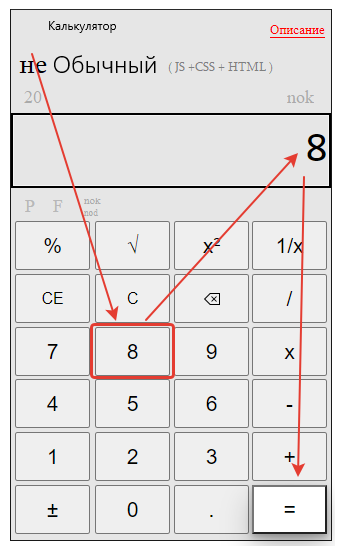
Получаем результат нахождения общего знаменателя онлайн :

Далее вы можете сравнить два результата нахождения общего знаменателя.
Что такое наименьший общий знаменатель?
Разница между “общим знаменателем“(1) и “наименьшим общим знаменателем“(2) в том, что первое может быть бесконечное количество… а второе “НОЗ”, только один!
Но, что же такое “наименьший общий знаменатель”
НОЗ – это абсолютно тоже самое, что и “НОК”.
Определение, что же такое “наименьший общий знаменатель”
Наименьший общий знаменатель двух знаменателей – это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Формула наименьшего общего кратного
Для нахождения “наименьшего общего знаменателя” двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Для понимания формулы наименьшего общего кратного нам нужен пример!
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
10 = 2 * 5
Разложим второй знаменатель на множители :
6 = 2 * 3
Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
10 * 3 = 30
Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Как найти наименьший общий знаменатель на калькуляторе
Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12
Прежде чем приступать к нахождению “нок” двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
18 = 2 * 3 * 3
Раскладываем меньшее число на множители :
12 = 2 * 2 * 3
Исключаем повторяющиеся цифры – это одна 2 и 3, остается 2.
Умножаем большее число на 2.
18 * 2 = 36
Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
Теперь проверим правильность нахождения “нок” на калькуляторе.
Открываем калькулятор.
Набираем первое число – пусть это будет число 12

Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
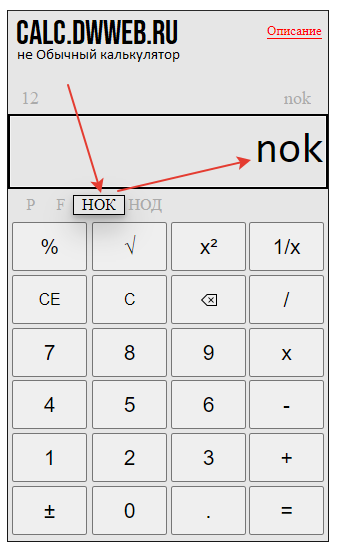
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.

И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
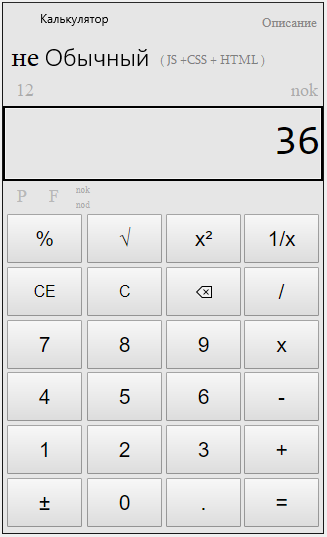
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса – давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать… перебором…, а потом подтвердим наше решение через “НОК”.
5 – не подходит – не делится на 3.
10 – не подходит – не делится на 3.
15 – не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 – не подходит, не делится на 2.
30 – подходит
, делится на все без остатка… мы нашли общий знаменатель для трех дробей, методом перебора
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель – 2.
Нажимаем кнопку – “НОК”.

Набираем второй знаменатель – 3.
Нажимаем равно – “=”.

Далее опять нажимаем – “НОК”.
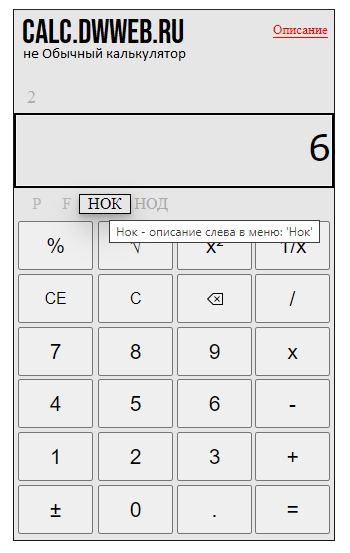
Набираем третий знаменатель – 6.
Нажимаем равно – “=”.
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
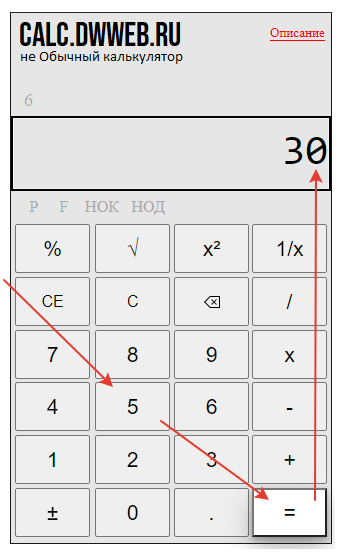
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели – иначе, зачем искать общий знаменатель – ведь знаменатели одинаковые.
Выше были рассмотрены варианты нахождения общего знаменателя дробей с разными знаменателями.
Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.д
При нахождении наименьшего общего знаменателя при сложении (вычитании) обыкновенных дробей учащиеся часто поступают нерационально, принимая в качестве общего знаменателя произведение знаменателей исходных дробей.
Можно использовать следующий прием, использующий навык сокращения дробей
Пример 1. Найти сумму дробей с разными знаменателями
Составили дробь из знаменателей дробей слагаемых и после ее сокращения на 7 получили дополнительные множители к дробям слагаемым:
2 – дополнительный множитель к дроби со знаменателем 21,
3 – дополнительный множитель к дроби со знаменателем 14
Т.е. дополнительные множители соответствуют исходным знаменателям “крест-накрест”
Пример 2. Найти разность дробей с разными знаменателями
Составили дробь из знаменателей, сократили ее и получили дополнительные множители, которые соответствуют исходным знаменателям “крест-накрест”, как в пропорции
Способ можно применять для нахождения наименьшего общего кратного двух чисел (это очевидно, т.к. наименьший общий знаменатель является наименьшим общим кратным исходных знаменателей)
Пример 3. Найти наименьшее общее кратное
Составили дробь из чисел, для которых надо найти наименьшее общее кратное, сократили ее последовательно (сначала на 2, потом на 7, потом на 3) – получили несократимую дробь.
Числитель составленной дроби умножаем на знаменатель дроби после сокращения (84 умножаем на 3).
Знаменатель составленной дроби умножаем на числитель дроби после сокращения (126 умножаем на 2).
В обоих случаях получаем наименьшее общее кратное при условии, что получена именно несократимая дробь.
Алгоритм усложняется, если надо найти общий знаменатель трех и более дробей. В этом случае надо найти общий знаменатель первых двух дробей, потом найти общий знаменатель результата и следующей дроби и т.д.
Алгоритм можно применять также при сложении (вычитании) алгебраических дробей.
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Основное свойство рациональных чисел гласит:
(frac{p}{q}=frac{p times n}{q times n})
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Рассмотрим пример:
(frac{1}{2}=frac{1 times 4}{2 times 4}=frac{4}{8})
Получаем,
(frac{1}{2}=frac{4}{8})
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Приведите дроби с разными знаменателями к наименьшему общему знаменателю .
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
НОК(14,20)= 2⋅5⋅2⋅7=140
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь (frac{1}{20}) домножить на 7, чтобы получить знаменатель 140.
(frac{1}{20}=frac{1 times 7}{20 times 7}=frac{7}{140})
А вторую дробь умножить на 10.
(frac{3}{14}=frac{3 times 10}{14 times 10}=frac{30}{140})
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
- Нужно разложить на простые множители знаменатели дробей.
- Нужно найти наименьшее общее кратное (НОК) для знаменателей данных дробей.
- Привести дроби к общему знаменателю, то есть умножить и числитель и знаменатель дроби на множитель.
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей (frac{2}{11}, frac{1}{15}, frac{3}{22})
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби (frac{2}{11}, frac{1}{15}, frac{3}{22}) к общему знаменатели равному 330.
(begin{align}
frac{2}{11}=frac{2 times 30}{11 times 30}=frac{60}{330} \\
frac{1}{15}=frac{1 times 22}{15 times 22}=frac{22}{330} \\
frac{3}{22}=frac{3 times 15}{22 times 15}=frac{60}{330} \\
end{align})
Вопросы по теме:
Какой общий знаменатель у дробей (bf frac{2}{25}) и (bf frac{1}{14})?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
( begin{align}
frac{2}{25}=frac{2 times 14}{25 times 14}=frac{28}{350} \\
frac{1}{14}=frac{1 times 25}{14 times 25}=frac{25}{350} \\
end{align})
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей (frac{2}{25}) и (frac{1}{14}) знаменателем может быть число 700, 1400 и т.д.
