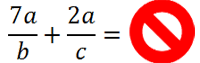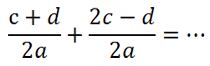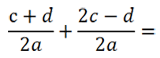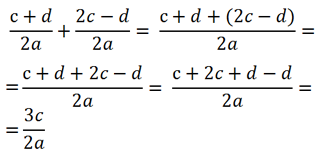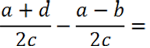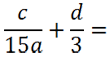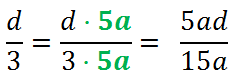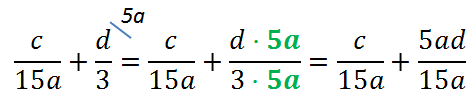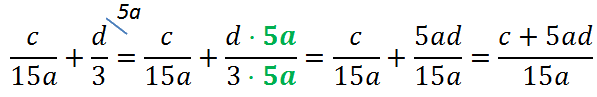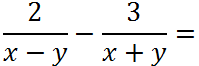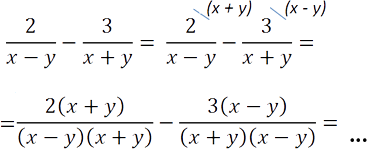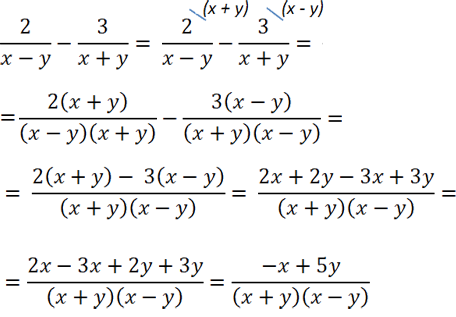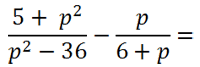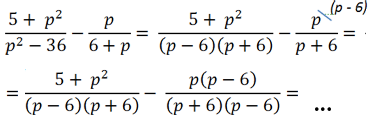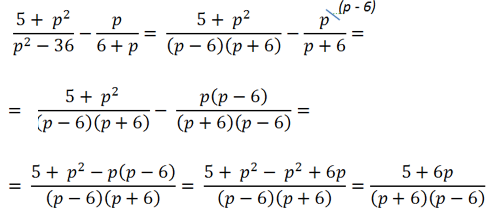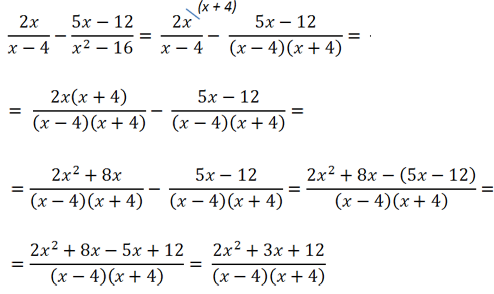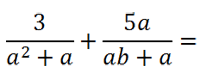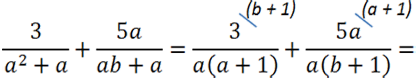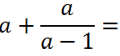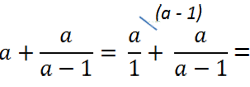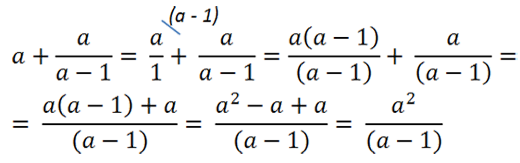Как найти общий знаменатель многочлена - Сайт, где вы сможете решить свои вопросы

Большинство действий с алгебраическими дробями, такие, например, как сложение и вычитание, требуют предварительного приведения этих дробей к одинаковым знаменателям. Такие знаменатели также часто обозначаются словосочетанием «общий знаменатель». В данной теме мы рассмотрим определение понятий «общий знаменатель алгебраических дробей» и «наименьший общий знаменатель алгебраических дробей (НОЗ)», рассмотрим по пунктам алгоритм нахождения общего знаменателя и решим несколько задач по теме.

Общий знаменатель алгебраических дробей

Если говорить про обыкновенные дроби, то общим знаменателем является такое число, которое делится на любой из знаменателей исходных дробей. Для обыкновенных дробей 12 и 59 число 36 может быть общим знаменателем, так как без остатка делится на 2 и на 9.

Общий знаменатель алгебраических дробей определяется похожим образом, только вместо чисел используются многочлены, так как именно они стоят в числителях и знаменателях алгебраической дроби.

Определение 1

Общий знаменатель алгебраической дроби – это многочлен, который делится на знаменатель любой из дробей.

В связи с особенностями алгебраических дробей, речь о которых пойдет ниже, мы чаще будем иметь дело с общими знаменателями, представленными в виде произведения, а не в виде стандартного многочлена.

Пример 1

Многочлену, записанному в виде произведения 3·x2·(x+1), соответствует многочлен стандартного вида 3·x3+3·x2. Этот многочлен может быть общим знаменателем алгебраических дробей 2x, -3·x·yx2 и y+3x+1 , в связи с тем, что он делится на x, на x2 и на x+1. Информация о делимости многочленов есть в соответствующей теме нашего ресурса.

Наименьший общий знаменатель (НОЗ)

Для заданных алгебраических дробей количество общих знаменателей может быть бесконечное множество.

Пример 2

Возьмем для примера дроби 12·x и x+1×2+3 . Их общим знаменателем является 2·x·(x2+3), как и −2·x·(x2+3), как и x·(x2+3), как и 6,4·x·(x2+3)·(y+y4), как и −31·x5·(x2+3)3, и т.п.

При решении задач можно облегчить себе работу, используя общий знаменатель, который среди всего множества знаменателей имеет самый простой вид. Такой знаменатель часто обозначается как наименьший общий знаменатель.

Определение 2

Наименьший общий знаменатель алгебраических дробей – это общий знаменатель алгебраических дробей, который имеет самый простой вид.

К слову, термин «наименьший общий знаменатель» не является общепризнанным, потому лучше ограничиваться термином «общий знаменатель». И вот почему.

Ранее мы сфокусировали ваше внимание на фразе «знаменатель самого простого вида». Основной смысл этой фразы следующий: на знаменатель самого простого вида должен без остатка делиться любой другой общий знаменатель данных в условии задачи алгебраических дробей. При этом в произведении, которое является общим знаменателем дробей, можно использовать различные числовые коэффициенты.

Пример 3

Возьмем дроби 12·x и x+1×2+3 . Мы уже выяснили, что проще всего работать нам будет с общим знаменателем вида 2·x·(x2+3). Также общим знаменателем для этих двух дробей может быть x·(x2+3), который не содержит числового коэффициента. Вопрос в том, какой из этих двух общих знаменателей считать наименьшим общим знаменателем дробей. Однозначного ответа нет, потому правильнее говорить просто об общем знаменателе, а в работу брать тот вариант, с которым работать будет удобнее всего. Так, мы можем использовать и такие общие знаменатели как x2·(x2+3)·(y+y4) или −15·x5·(x2+3)3, которые имеют более сложный вид, но проводить с ними действия может быть сложнее.

Нахождение общего знаменателя алгебраических дробей: алгоритм действий

Предположим, что у нас имеется несколько алгебраических дробей, для которых нам необходимо отыскать общий знаменатель. Для решения этой задачи мы можем использовать следующий алгоритм действий. Сначала нам необходимо разложить на множители знаменатели исходных дробей. Затем мы составляем произведение, в которое последовательно включаем:

все множители из знаменателя первой дроби вместе со степенями;
все множители, присутствующие в знаменателе второй дроби, но которых нет в записанном произведении или их степень недостаточно;
все недостающие множители из знаменателя третьей дроби, и так далее.

Полученное произведение и будет общим знаменателем алгебраических дробей.

В качестве множителей произведения мы можем взять все знаменатели дробей, данных в условии задачи. Однако множитель, который мы получим в итоге, по смыслу будет далек от НОЗ и использование его будет иррациональным.

Пример 4

Определите общий знаменатель дробей 1×2·y, 5x+1 и y-3×5·y .

Решение

В данном случае у нас нет необходимости раскладывать знаменатели исходных дробей на множители. Потому начнем применять алгоритм с составления произведения.

Из знаменателя первой дроби возьмем множитель x2·y, из знаменателя второй дроби множитель x+1. Получаем произведение x2·y·(x+1).

Знаменатель третьей дроби может дать нам множитель x5·y, однако в составленном нами ранее произведении уже есть множители x2 и y. Следовательно, добавляем еще x5−2=x3. Получаем произведение x2·y·(x+1)·x3, которое можно привести к виду x5·y·(x+1). Это и будет наш НОЗ алгебраических дробей.

Ответ: x5·y·(x+1).

Теперь рассмотрим примеры задач, когда в знаменателях алгебраических дробей есть целые числовые множители. В таких случаях мы также действуем по алгоритму, предварительно разложив целые числовые множители на простые множители.

Пример 5

Найдите общий знаменатель дробей 112·x и 190·x2 .

Решение

Разложив числа в знаменателях дробей на простые множители, получаем 122·3·x и 12·32·5·x2 . Теперь мы можем перейти к составлению общего знаменателя. Для этого из знаменателя первой дроби возьмем произведение 22·3·x и добавим к нему множители 3, 5 и x из знаменателя второй дроби. Получаем 22·3·x·3·5·x=180·x2. Это и есть наш общий знаменатель.

Ответ: 180·x2.

Если внимательно посмотреть на результаты двух разобранных примеров, то можно заметить, что общие знаменатели дробей содержат все множители, присутствующие в разложениях знаменателей, причем если некоторый множитель имеется в нескольких знаменателях, то он берется с наибольшим из имеющихся показателей степени. А если в знаменателях имеются целые коэффициенты, то в общем знаменателе присутствует числовой множитель, равный наименьшему общему кратному этих числовых коэффициентов.

Пример 6

В знаменателях обеих алгебраических дробей 112·x и 190·x2 есть множитель x. Во втором случае множитель x возведен в квадрат. Для составления общего знаменателя это множитель нам необходимо взять в наибольшей степени, т.е. x2. Других множителей с переменными нет. Целые числовые коэффициенты исходных дробей 12 и 90, а их наименьшее общее кратное равно 180. Получается, что искомый общий знаменатель имеет вид 180·x2.

Теперь мы можем записать еще один алгоритм нахождения общего множителя алгебраических дробей. Для этого мы:

раскладываем знаменатели всех дробей на множители;
составляем произведение всех буквенных множителей (при наличии множителя в нескольких разложениях, берем вариант с наибольшим показателем степени);
добавляем НОК числовых коэффициентов разложений к полученному произведению.

Приведенные алгоритмы равноценны, так что использовать в решении задач можно любой из них. Важно уделять внимание деталям.

Встречаются случаи, когда общие множители в знаменателях дробей могут быть незаметны за числовыми коэффициентами. Здесь целесообразно сначала вынести числовые коэффициенты при старших степенях переменных за скобки в каждом из множителей, имеющихся в знаменателе.

Пример 7

Какой общий знаменатель имеют дроби 35-x и 5-x·y22·x-10 .

Решение

В первом случае за скобки необходимо вынести минус единицу. Получаем 3-x-5 . Умножаем числитель и знаменатель на -1 для того, чтобы избавиться от минуса в знаменателе: -3x-5 .

Во втором случае за скобку выносим двойку. Это позволяет нам получить дробь 5-x·y22·x-5 .

Очевидно, что общий знаменатель данных алгебраических дробей -3x-5 и 5-x·y22·x-5 это 2·(x−5).

Ответ: 2·(x−5).

Данные в условии задачи дроби могут иметь дробные коэффициенты. В этих случаях необходимо сначала избавиться от дробных коэффициентов путем умножения числителя и знаменателя на некоторое число.

Пример 8

Упростите алгебраические дроби 12·x+1114·x2+17 и -223·x2+113 , после чего определите их общий знаменатель.

Решение

Избавимся от дробных коэффициентов, умножив числитель и знаменатель в первом случае на 14, во втором случае на 3. Получаем:

12·x+1114·x2+17=14·12·x+114·114·x2+17=7·x+14×2+2 и -223·x2+113=3·-23·23·x2+43=-62·x2+4=-62·x2+2 .

После проведенных преобразований становится понятно, что общий знаменатель – это 2·(x2+2).

Ответ: 2·(x2+2).

Источник

Как привести дроби к общему знаменателю

Как привести алгебраические (рациональные) дроби к общему знаменателю?

1) Если в знаменателях дробей стоят многочлены, нужно попытаться разложить эти многочлены на множители одним из известных способов.

2) Наименьший общий знаменатель (НОЗ) состоит из всех множителей, взятых в наибольшей степени.

Наименьший общий знаменатель для чисел устно ищем как наименьшее число, которое делится на остальные числа.

3) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.

4) Числитель и знаменатель первоначальной дроби умножаем на дополнительный множитель.

Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.

$[1)frac{{2a}}{{15b}}ufrac{{7b}}{{9c}}]$

Чтобы найти общий знаменатель для чисел, выбираем большее число и проверяем, делится ли оно на меньшее. 15 на 9 не делится. Умножаем 15 на 2 и проверяем, делится ли полученное число на 9. 30 на 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9. 45 на 9 делится, значит, общий знаменатель для чисел равен 45.

Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель данных дробей равен 45 bc (буквы принято записывать в алфавитном порядке).

Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:

$[frac{{2{a^{backslash 3c}}}}{{15b}} = frac{{6ac}}{{45bc}};frac{{7{b^{backslash 5b}}}}{{9c}} = frac{{35{b^2}}}{{45bc}};]$

$[2)frac{b}{{6{a^3}c}}ufrac{7}{{8{a^2}bc}}]$

Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8∙2=16 на 6 не делится, 8∙3=24 на 6 делится. Каждую из переменных нужно включить в общий знаменатель один раз. Из степеней берем степень с большим показателем.

Таким образом, общий знаменатель данных дробей равен 24a³bc.

Чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый: 24a³bc:(6a³c)=4b, 24a³bc:(8a²bc)=3a.

Дополнительный множитель умножаем на числитель и знаменатель:

$[frac{{{b^{backslash 4b}}}}{{6{a^3}c}} = frac{{4{b^2}}}{{24{a^3}bc}};frac{{{7^{backslash 3a}}}}{{8{a^2}bc}} = frac{{21a}}{{24{a^3}bc}};]$

$[3)frac{{2x + 1}}{{{x^2} - 18x + 81}}ufrac{3}{{{x^2} - 81}}]$

Многочлены, стоящие в знаменателях данных дробей, нужно разложить на множители. В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):

$[frac{{2x + 1}}{{{x^2} - 18x + 81}} = frac{{2x + 1}}{{{{(x - 9)}^2}}},]$

$[frac{3}{{{x^2} - 81}} = frac{3}{{(x - 9)(x + 9)}}.]$

Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, то есть равен (x-9)²(x+9). Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:

$[frac{{2x + {1^{backslash (x + 9)}}}}{{{{(x - 9)}^2}}} = frac{{(2x + 1)(x + 9)}}{{{{(x - 9)}^2}(x + 9)}} = ]$

$[ = frac{{2{x^2} + 18x + x + 9}}{{{{(x - 9)}^2}(x + 9)}} = frac{{2{x^2} + 19x + 9}}{{{{(x - 9)}^2}(x + 9)}},]$

$[frac{{{3^{backslash (x - 9)}}}}{{(x - 9)(x + 9)}} = frac{{3(x - 9)}}{{{{(x - 9)}^2}(x + 9)}} = ]$

$[ = frac{{3x - 27}}{{{{(x - 9)}^2}(x + 9)}};]$

$[4)frac{5}{{{x^2} - 5x}}ufrac{{3x}}{{4x - 20}}]$

Многочлены, стоящие в знаменателях, раскладываем на множители. В знаменателе первой дроби выносим за скобки общий множитель x, из второй — 4:

$[frac{5}{{{x^2} - 5x}} = frac{5}{{x(x - 5)}},]$

$[frac{{3x}}{{4x - 20}} = frac{{3x}}{{4(x - 5)}}.]$

Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, а значит, равен 4x(x-5).

Находим дополнительные множители и умножаем их на числитель и знаменатель:

$[frac{{{5^{backslash 4}}}}{{x(x - 5)}} = frac{{20}}{{4x(x - 5)}},]$

$[frac{{3{x^{backslash x}}}}{{4(x - 5)}} = frac{{3{x^2}}}{{4x(x - 5)}}.]$

Необходимость в приведении рациональных дробей к общему знаменателю в алгебре возникает при сложении и вычитании дробей. Как складывать и как вычитать дроби с разными знаменателями, рассмотрим в следующий раз.

Источник

☰

Общий знаменатель для алгебраических дробей

При сложении и вычитании алгебраический дробей с разными знаменателями сначала дроби приводят к общему знаменателю. Это значит, находят такой один знаменатель, который делится на исходный знаменатель каждой алгебраической дроби, входящей в состав данного выражения.

Как известно, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, отличное от нуля, то значение дроби не изменится. Это является основным свойством дроби. Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).

Например, дана такая сумма алгебраических дробей:

Требуется упростить выражение, т. е. сложить две алгебраические дроби. Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.

Для числовых коэффициентов и переменных НОК ищется отдельно. НОК(3, 2) = 6, а НОК(x, y) = xy. Далее найденные значения перемножаются: 6xy.

Теперь надо определить, на какой множитель надо умножить 3x, чтобы получить 6xy:
6xy ÷ 3x = 2y

Значит, при приведении первой алгебраической дроби к общему знаменателю ее числитель надо умножить на 2y (знаменатель уже был умножен при приведении к общему знаменателю). Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.

Таким образом, получаем:

Далее уже можно действовать как с дробями с одинаковыми знаменателями: складываются числители, а в знаменателе пишется один общий:

После преобразований получается упрощенное выражение, представляющее собой одну алгебраическую дробь, являющуюся суммой двух исходных:

Алгебраические дроби в исходном выражении могут содержать знаменатели, представляющие собой многочлены, а не одночлены (как в приведенном выше примере). В таком случае, перед поиском общего знаменателя следует разложить знаменатели на множители (если это возможно). Далее общий знаменатель собирается из разных множителей. Если множитель есть в нескольких исходных знаменателях, то его берут единожды. Если множитель имеет разные степени в исходных знаменателях, то его берут с большей. Например:

Здесь многочлен a² – b² можно представить как произведение (a – b)(a + b). Множитель 2a – 2b раскладывается как 2(a – b). Таким образом, общий знаменатель будет равен 2(a – b)(a + b).

Источник

Алгебраические дроби складывают и вычитают по
правилам сложения и вычитания
обыкновенных дробей.

Сложение алгебраических дробей

Запомните!

Складывать можно только дроби с одинаковыми знаменателями!

Нельзя складывать дроби без преобразований

Можно складывать дроби

При сложении алгебраических дробей с одинаковыми знаменателями:

числитель первой дроби складывается с числителем второй дроби;
знаменатель остаётся прежним.

Рассмотрим пример сложения алгебраических дробей.

Так как знаменатель у обеих дробей «2а», значит, дроби можно сложить.

Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним.
При сложении дробей в полученном числителе
приведем подобные.

Вычитание алгебраических дробей

Запомните!

Вычитать можно только дроби с одинаковыми знаменателями!

При вычитании алгебраических дробей с одинаковыми знаменателями:

из числителя первой дроби вычитается числитель второй дроби.
знаменатель остаётся прежним.

Важно!

Обязательно заключите в скобки весь числитель вычитаемой дроби.

Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель «2с», значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби «(a + d)» числитель второй дроби
«(a − b)».
Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем
правило раскрытия скобок.

Приведение алгебраических дробей к общему знаменателю

Рассмотрим другой пример. Требуется сложить алгебраические дроби.

В таком виде сложить дроби нельзя, так как у них разные знаменатели.

Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.

Правила приведения алгебраических дробей к общему знаменателю очень похожи на
правила приведения к общему знаменателю
обыкновенных дробей.
.

В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.

Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.

Работаем с числовыми коэффициентами. Определяем
НОК
(наименьшее общее кратное) для всех числовых коэффициентов.
Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.

Вернемся к нашему примеру.

Рассмотрим знаменатели «15a» и «3» обеих дробей и найдем для них общий знаменатель.

Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка
делится на каждый числовый коэффициент).
Для «15» и «3» — это «15».
Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях.
В знаменателях «15a» и «5» есть только
один одночлен — «а».
Перемножим НОК из п.1 «15» и одночлен «а» из п.2. У нас получится «15a». Это и будет общим знаменателем.
Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a»?».

Рассмотрим первую дробь. В этой дроби и так знаменатель «15a», значит, ее не требуется ни на что умножать.

Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3», чтобы получить «15a»?»
Ответ — на «5a».

При приведении к общему знаменателю дроби умножаем на «5a»
и числитель, и знаменатель.

Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через
«домики».

Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.

Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.

Рассмотрим пример вычитания дробей с разными знаменателями.

В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.

Рассмотрим знаменатели «(x − y)» и «(x + y)» обеих дробей и найдем для них общий знаменатель.

Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.

Важно!

Многочлены необходимо рассматривать целиком!
Для удобства заключайте целый многочлен в скобки.

У нас есть два различных многочлена в знаменателях «(x − y)» и «(x + y)».
Их произведение будет общим знаменателем, т.е. «(x − y)(x + y)» — общий знаменатель.

Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать
формулы сокращенного умножения.

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

В первой алгебраической дроби знаменатель «(p² − 36)». Очевидно, что к нему можно
применить формулу разности квадратов.

После разложения многочлена «(p² − 36)» на произведение
многочленов
«(p + 6)(p − 6)»
видно, что в дробях повторяется многочлен «(p + 6)».
Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6)».

Важно!

Прежде чем приводить многочлены к общему знаменателю, попытайтесь
использовать формулы сокращённого умножения или вынесение общего множителя за скобки.

Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.

Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

На первый взгляд одинаковых многочленов в обеих дробях нет.

Вынесем общий множитель
«а» за скобки в обоих знаменателях.

После вынесения общего множителя «а» за скобки, в
обоих знаменателях появился одинаковый одночлен «а».
Значит, общий знаменатель для обеих дробей будет выглядеть так: «а(а + 1)(b + 1)».

Сложение алгебраической дроби с одночленом или числом

Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).

Чтобы сложить одночлен или число с алгебраической дробью,
нужно представить одночлен в виде дроби со знаменателем «1».

Представим одночлен «а» как алгебраическую дробь со знаменателем «1».

Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.

Теперь приведем алгебраические дроби к общему знаменателю «(а − 1)» и решим пример.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

$begingroup$

I am solving a limit and am stuck with finding the common denominator. This is the limit that I have:

$$lim_{x to 1} left( frac{1}{1-x} – frac{3}{1-x^3} right)$$

Since $x to 1$, the limit is $frac{1}0 – frac{3}0$ – or $infty – infty$.

So, I think the next thing I need to do is find the common denominator and continue from there on.

I would very much appreciate an answer. Thank you all and have a nice day.

asked Jul 23, 2017 at 21:43

$endgroup$

$begingroup$

Hint:

This might help you.

$$1-x^3= (1-x)(1+x+x^2)$$

answered Jul 23, 2017 at 21:44

Siong Thye GohSiong Thye Goh

147k20 gold badges86 silver badges149 bronze badges

$endgroup$

$begingroup$

Hint: $;1-x^3=(1-x)(1+x+x^2),$, then by partial fraction decomposition:

$$
frac{1}{1-x^3} = frac{1}{3}left(frac{1}{1-x}+frac{x+2}{1+x+x^2}right)
$$

It follows that:

$$require{cancel}
frac{1}{1-x} – frac{3}{1-x^3} = cancel{frac{1}{1-x}} – left(cancel{frac{1}{1-x}} + frac{x+2}{1+x+x^2}right) = – ,frac{x+2}{1+x+x^2}
$$

answered Jul 23, 2017 at 23:03

dxivdxiv

74.8k6 gold badges63 silver badges119 bronze badges

$endgroup$

$begingroup$

$$frac{1}{1-x}-frac{3}{1-x^3}=frac{1}{1-x}-frac{3}{(1-x)(x^2+x+1)}=frac{1}{1-x}left(1-frac{3}{x^2+x+1}right)=frac{1}{1-x}left(frac{x^2+x-2}{x^2+x+1}right)=frac{1}{1-x}left(frac{(x-1)(x+2)}{x^2+x+1}right)=frac{-(x+2)}{x^2+x+1}$$

answered Jul 23, 2017 at 22:22

dromastyxdromastyx

2,7481 gold badge9 silver badges20 bronze badges

$endgroup$

$begingroup$

HINT: note that $$1-x^3=- left( -1+x right) left( {x}^{2}+x+1 right) $$
and $$frac{1}{1-x}-frac{3}{1-x^3}=-{frac {x+2}{{x}^{2}+x+1}}$$
$$frac{1}{1-x}-frac{3}{1-x^3}=frac{-x^3+3x-2}{(1-x)(1-x^3}=frac{-(x+2)(x-1)^2}{(1-x)(1-x^3)}$$

answered Jul 23, 2017 at 21:46

$endgroup$

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Общий знаменатель алгебраических дробей

Наименьший общий знаменатель (НОЗ)

Нахождение общего знаменателя алгебраических дробей: алгоритм действий

Общий знаменатель для алгебраических дробей

Сложение алгебраических дробей

Нельзя складывать дроби без преобразований

Можно складывать дроби

Вычитание алгебраических дробей

Приведение алгебраических дробей к общему знаменателю

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

Сложение алгебраической дроби с одночленом или числом

Ваши комментарии

Not the answer you’re looking for? Browse other questions tagged .

Вам также может понравиться

Как найти приложение по адресу ошибки

Как найти уведомление фсс

Как найти сфинкса на улице

Добавить комментарий Отменить ответ

Not the answer you’re looking for? Browse other questions tagged

.