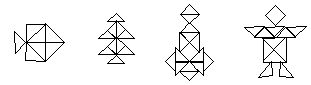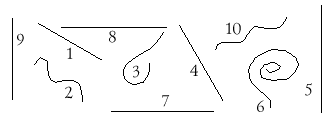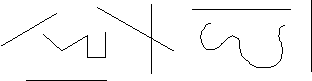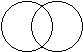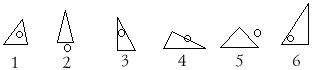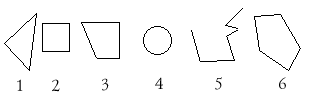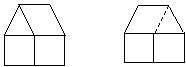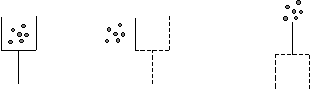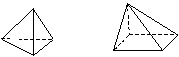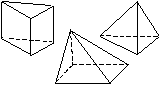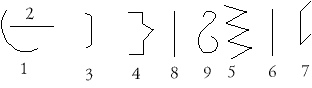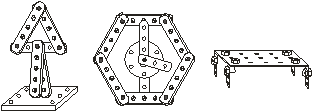Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
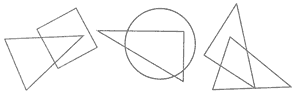
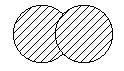
Раскрась общую часть треугольника, круга и квадрата.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,287
- гуманитарные 33,620
- юридические 17,900
- школьный раздел 607,113
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Раскрась общую часть треугольника, квадрата и круга?
Математика | 1 – 4 классы
Раскрась общую часть треугольника, квадрата и круга.
Пошаговое объяснение : Смотри приложение.
Начерти треугольник и круг так, чтобы их общей частью был а)круг?
Начерти треугольник и круг так, чтобы их общей частью был а)круг.
Поменяйтесь тетрадями и проверь работу друк у друга.
Зарисовать общую часть квадрата и круга (задание7)?
Зарисовать общую часть квадрата и круга (задание7).
Нарисуйте два квадрата так что бы их пересечением(общей частью)был треугольник?
Нарисуйте два квадрата так что бы их пересечением(общей частью)был треугольник.
Начерти окружность радиусом 3 см?
Начерти окружность радиусом 3 см.
Отметь на окружности три точки и соедини их отрезками так, чтобы получился треугольник.
Раскрась его желтым карандашом.
Какие фигуры являются общей частью окружности и треугольника ; круга и треугольника?
Раскрась седьмую часть круга?
Раскрась седьмую часть круга.
Найди закономерность и продолжи последовательность фигур (указать не менее четырех фигур) : треугольник круг квадрат треугольник треугольник круг квадрат треугольник круг круг квадрат?
Найди закономерность и продолжи последовательность фигур (указать не менее четырех фигур) : треугольник круг квадрат треугольник треугольник круг квадрат треугольник круг круг квадрат.
Как начертить треугольник и кругтак, чтобы их общей частью был?
Как начертить треугольник и кругтак, чтобы их общей частью был.
Назови общую часть : треугольника АВК и квадрата КАЕМ ; треугольника АВК и квадрата АВКС?
Назови общую часть : треугольника АВК и квадрата КАЕМ ; треугольника АВК и квадрата АВКС.
Начерти треугольник и круг, так чтобы их общей частью был а)круг б)треугольник?
Начерти треугольник и круг, так чтобы их общей частью был а)круг б)треугольник.
На столе лежат вырезанные из цветной бумаги синий квадрат, красный треугольник и желтый круг?
На столе лежат вырезанные из цветной бумаги синий квадрат, красный треугольник и желтый круг.
Раскрась фигуры так , чтобы : а) треугольник был сверху, под ним был квадрат, а круг в самом низу.
На этой странице находится вопрос Раскрась общую часть треугольника, квадрата и круга?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 1 – 4 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
Измерение времени – Ответы (ГДЗ) к рабочей тетради по математике 3 класс 2 часть (Рудницкая, Юдачева)
УЗНАЕМ НОВОЕ
102. Нарисуй стрелки так, чтобы часы показывали указанное время.
103. Заполни пропуски.
104. Дорога в музыкальную школу занимает у Кати 25 мин. В какое время Катя должна выйти из дома, если в школе нужно быть в 16 ч 15 мин.
105. Закончи предложения.
106. Запиши, какое время показывают часы, если сейчас вторая половина суток.
107. Дополни предложения.
108. Выполни действия.
109. Прочитай названия месяцев: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь. Подчеркни название каждого месяца, в котором 31 день. Выпиши названия всех летних месяцев.
110. Ответь на вопросы.
111. Дополни предложения, используя календарь.
ВСПОМИНАЕМ ПРОЙДЕНОЕ
112. Прочитай буквы с помощью зеркала и запиши получившееся слово.
Получилось слово Москва.
113. Выполни умножение.
114. Реши задачу по краткой записи.
115. Построй точки, симметричные данным относительно оси.
116. Раскрась общую часть треугольника, круга и квадрата.
117. Разгадай математический кроссворд.
По горизонтали:
1. Сумма чисел 999 и 1.
По вертикали:
2. Произведение чисел 200 и 2.
3. Разность чисел 1000 и 100.
118. Сколько концов у двух палок? 4 конца
А у двух с половиной? 6 концов.
[spoiler title=”источники:”]
http://matematika.my-dict.ru/q/4003376_raskras-obsuu-cast-treugolnika-kvadrata-i/
http://matem-gdz.ru/3-klass/otvety-gdz-k-rabochej-tetradi-po-matematike-3-klass-2-chast-rudnickaya-yudacheva/izmerenie-vremeni.html
[/spoiler]
Анна БЕЛОШИСТАЯ,
г. Мурманск
Наглядная геометрия1
Статья опубликована при поддержке интернет-магазина Westwing, в котором Вы найдете широчайший выбор товаров, так или иначе связанных с дизайном окружающего пространства, обустройством дома и интерьером. Что бы Вы не искали — бельевой шкаф в уютную спальню или большой кожаный диван в просторную гостиную загородного коттеджа, определяетесь ли вы с обстановкой ванной комнаты или подыскиваете навесной шкаф для небольшой кухни в городской квартире — у Вас есть прекрасная возможность приобрести не просто качественную мебель в Вествинг, а стать обладателем дизайнерских предметов интерьера и аксессуаров по уникально низким ценам. Прямое сотрудничество Westwing с лучшими производителями позволяет интернет-магазину предоставлять своим клиентам скидки на товары до 70%, устраивать распродажи и проводить совместные акции с известными брендами. С подробной информацией об ассортименте предлагаемых товаров и ценах на них, о проводимых акциях и распродажах можно ознакомиться на сайте westwing.ru.
геометрия в начальных классах” представляет
собой дополнительный к учебнику математики
материал, который может быть использован в
сочетании с любым существующим учебником, а
также для проведения факультативных или
кружковых занятий в начальной школе.
Курс “Наглядная геометрия” в 1-м
классе четырехлетней начальной школы
ориентирован на типовую подготовку детей
дошкольного возраста, но с учетом того, что дети,
подготовленные по альтернативным дошкольным
программам “Математика и конструирование”,
“Школа 2100”, “Детство” и “Радуга”,
имеют расширенную геометрическую подготовку.
Для работы с более подготовленными детьми
учитель может использовать задания, отмеченные в
тетрадях звездочкой (*).
Для проведения уроков по наглядной
геометрии учитель может использовать 1 час в
неделю из часов предмета “Технология” или 1
час школьного компонента. Программа и содержание
курса “Наглядная геометрия” находятся в
полном согласовании с системой изучения
геометрического материала в средней школе.
Методической особенностью курса
является разработка системы учебных заданий1 для
каждого урока и для всего курса в целом. Задания
непосредственно адресованы ученику,
обусловливая характер его учебных действий.
Поэтому содержание, формулировка и система
учебных заданий в данном курсе имеют целый ряд
отличительных особенностей по сравнению с
системой заданий, реализованных в привычных
учителю пособиях по математике.
Последовательность заданий выстраивается таким
образом: в начале предлагается
организационно-подготовительное задание, цель
которого – подготовить ребенка к той
деятельности, которую он будет выполнять в
следующих – основных – заданиях (это может быть
активизация внимания и восприятия, развитие
зрительно-моторной координации, разработка
мелких мышц руки и т.п.), затем предлагается
задание, обязательно носящее частично поисковый
характер или содержащее элементы творчества.
Процесс выполнения такого задания связан с
необходимостью проведения зрительного анализа
или синтеза, активизацией пространственного
анализа, активизацией интуиции ребенка,
опирающейся на его опыт и продуцирующей догадку
или на ранее усвоенные знания, умения и навыки,
позволяющие включить в активную познавательную
деятельность всех учеников класса. Цель такого
задания – организация осознания детьми той
учебной задачи, на решение которой должна быть
направлена их последующая деятельность. Форма
подачи задания – проблемно-поисковая,
реализованная посредством вещественной или
графической модели, воспринимаемой ребенком
визуально, что позволяет максимально привлечь
внимание и обеспечить принятие учебной задачи
всеми учениками класса.
Далее следует этап закрепления, на котором
также предлагаются задания, в определенной мере
отличные от привычных “тренировочных”
заданий. Во-первых, они, как правило, уже
оформлены так чтобы позволить максимально
опираться на зрительное восприятие, зрительный
анализ и синтез, что немаловажно для ребенка
этого возраста; во-вторых, они отличаются
вариативностью способов выполнения,
необходимостью активно привлекать ранее
усвоенные знания, умения, навыки, а также требуют
использования приемов умственных действий.
Иными словами, даже тренировочные задания в
приведенном курсе имеют продуктивный характер.
Таким образом, любое задание в
предлагаемой системе является одновременно и
обучающим, и развивающим. Ту же функцию выполняет
и система дополнительных практических
(конструктивных) и логических
(логико-конструктивных) заданий. Они могут
выполняться как фронтально, так и отдельными
детьми – самостоятельно, по их выбору. Но при
этом учитель не занимает позицию объясняющего
или контролирующего субъекта – он сам активно
включается в процесс выполнения заданий.
Контролирующие задания используются
только в контрольных тестах, приведенных в конце
каждой тетради. Их цель – сделать вывод об уровне
усвоения материала.
Использование простейшей (но максимально
вариабельной) предметной наглядности на уроках
наглядной геометрии позволяет реализовать этот
курс в любых условиях. В качестве раздаточного
материала используются счетные палочки и
стандартный “Дидактический набор”,
содержащий двусторонние фигурки трех основных
форм: круг, треугольник, равный половине
квадрата, и квадрат, затем простейшая
геометрическая мозаика (размер фигур – 16 х 16 см,
для работы на фланелеграфе – 32 х 32 см). Из этих
основных форм дети конструируют как фигуры, так и
различные композиции по образцу, по заданию, по
замыслу, развивая конструктивное и
пространственное мышление. Для работы в тетрадях
дети используют специальную рамку-трафарет с
геометрическими прорезями. Такие рамки
заводского изготовления имеются в продаже.
Используемая рамка позволяет организовать не
только работу по распознаванию геометрических
форм, но и разработку моторики, а также является
основой для формирования конструктивной
моделирующей деятельности через прием
конструктивного рисования и конструктивной
аппликации.
МОЗАИКА
РАМКА
ДИДАКТИЧЕСКИЙ НАБОР
(если нет образца, то фигурки надо
вырезать и сложить в конверт)
1-й класс
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ (9 часов)
Уточнение представлений о форме
геометрических фигур: простые задания на
распознавание (знакомство с рамкой, игра
“Закрой окошки”, выполнение рисунка из
геометрических форм и его закрашивание).
Выполнение геометрического орнамента
с помощью рамки-трафарета.
Квадрат и его распознавание. Получение
квадрата методом загибания “от угла”.
Геометрические орнаменты в квадрате.
Конструирование геометрических фигур
из отдельных частей (работа с геометрической
мозаикой, наборами “Сложи фигуру”).
НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ ПОНЯТИЯ (14
часов)
Точка. Прямая. Кривая. Получение прямой
сгибанием листа неправильной формы.
Сходство и различие прямой и кривой.
Понятие о пересекающихся и
непересекающихся прямых. Количество прямых,
проведенных через одну и две точки на плоскости.
Линии на плоскости. Ломаная.
Моделирование линий из шнура и палочек и их
отношения на плоскости. Сходство и различие
прямой и кривой, кривой и ломаной. Их
распознавание.
Отрезок как часть прямой.
Распознавание отрезков в плоских и объемных
фигурах. Сравнение длин отрезков с помощью
наложения и с помощью циркуля.
Конструирование геометрических фигур
(круга, квадрата, треугольника, прямоугольника)
из плоских частей и заданного количества
элементов (квадрат из 2, 4, 8 треугольников;
прямоугольник из 4, 6, 8 треугольников; треугольник
из 4, 9 треугольников и т. д.) и выполнение эскизов
собранных композиций (от руки на клетчатой
бумаге). Конструирование узоров из
геометрической мозаики и их эскизы.
Циркуль. Начальные приемы работы с
циркулем. Окружность и круг. Представление о
радиусе на основе строения циркуля. Деление
круга пополам и на четыре части сгибанием.
Распознавание окружности (в орнаменте).
Самостоятельное вычерчивание и вырезание круга
с дальнейшим его использованием для
конструктивной деятельности.
Использование циркуля для получения
деталей аппликации (“Снеговик”,
“Слоненок” и др.). Простые орнаменты с
использованием циркуля.
Диаметр круга и его свойства. Радиус
круга и его свойства.
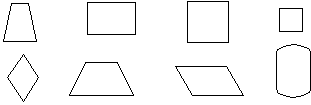
Представление о симметрии:
распознавание фигур, имеющих ось симметрии, и
проверка этого свойства перегибанием фигуры
пополам (круг, квадрат, треугольник,
прямоугольник, равнобедренная трапеция,
звездочка, лист, груша и т. д.).
Симметричный орнамент в круге и
квадрате.
РАБОТА С КОНСТРУКТОРОМ (6 часов)
Ознакомление с деталями конструктора
и инструментами (ключ, отвертка).
Конструирование букв с ориентацией на
их графическую модель.
Знакомство с разными видами
соединения полос: встык с накладкой и внахлест.
Примеры сборки простейших моделей: лесенка.
Понятие о техническом задании и
техническом рисунке.
Понятие о функциональной и
технологической целесообразности модели (для
чего делаем; какую работу будет выполнять данная
модель и в связи с этим какими свойствами и
качествами она должна обладать; целесообразное
использование имеющихся деталей; дизайн
конструкции; ее прочность и устойчивость).
Изготовление моделей многоугольников.
Изготовление конструкции на основе
многоугольника: часы (шестиугольник) и дорожный
знак (треугольник).
Решение простых конструктивных задач.
Соединение “под углом”. Изготовление мебели:
стол, стул, кресло, кровать (диван).
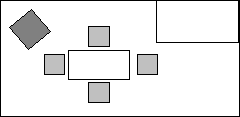
Знакомство с понятием “план”. План
комнаты: расстановка мебели.
ОБЪЕМНЫЕ ФИГУРЫ*
Представление о геометрическом теле.
Классификация простых геометрических
тел по некоторым признакам сходства и различия
(основной признак – форма). Моделирование куба,
прямой призмы и пирамиды из палочек и пластилина.
Распознавание плоских геометрических
фигур в объемных телах (представление о трех
проекциях объемной фигуры). Соотнесение объемной
фигуры с плоским чертежом: игры “Угадай, какая
фигура, как она стояла?” и “Поставь так же,
как на рисунке”.
Знакомство и работа с кубиками
Никитиных (“Сложи узор”).
В конце первого года обучения дети
должны:
1) иметь представление о точке, прямой,
кривой, ломаной, отрезке, квадрате, треугольнике,
круге;
2) знать отличие прямой от кривой (уметь
выделять их и обосновывать свой выбор), отличие
прямой от отрезка, отрезка от ломаной;
3) различать основные формы фигур в
различных положениях: треугольник,
четырехугольник, круг;
4) различать внутреннюю и внешнюю часть
в замкнутых фигурах основных форм;
5) уметь построить модель квадрата
загибанием “от угла”; уметь начертить
окружность с помощью циркуля;
6) уметь найти центр круга,
прямоугольника, квадрата (сгибанием). Уметь
пользоваться рамкой для выполнения рисунков и
орнаментов из геометрических фигур и для
получения деталей аппликации;
7) уметь пользоваться циркулем при
сравнении длин отрезков и изготовлении модели
круга;
8) уметь чертить и измерять отрезок с
помощью линейки.
В конце тетрадей № 1 и 2 приводятся
тестовые задания для проверки сформированности
перечисленных выше знаний и умений.
Для проверки сформированности умений
5, 6 и 7 следует предложить детям выполнить
практическую работу, требующую применения этих
умений: начертить и вырезать круг, найти в нем
центр сгибанием и выполнить симметричный
орнамент с рамкой. Получить квадрат загибанием
“от угла” листа бумаги, найти в нем центр
перегибанием и выполнить симметричный орнамент
(или аппликацию) с рамкой.
I ЧЕТВЕРТЬ
Тема: “Геометрические фигуры”.
Цели: сформировать первичные
представления о геометрических фигурах: круге,
квадрате, треугольнике; сформировать умение
видеть и узнавать эти фигуры, умение работать по
образцу, начать работу по формированию внимания
и самоконтроля; на основе выполнения простейших
заданий на классификацию начать работу над
формированием основных логических приемов
мышления: анализа, сравнения, обобщения.
Планируя уроки данной темы, учитель
ориентируется на результаты входной проверочной
работы. В зависимости от уровня подготовки
класса эта тема может занимать от 2 до 8 уроков.
Содержание входной проверочной работы
подобрано таким образом, что по качеству
выполнения заданий учитель может судить об
умении ребенка воспринимать геометрические
фигуры (сформированность представлений), умении
слушать и слышать инструкцию учителя, умении
самостоятельно распознавать геометрическую
фигуру (адекватность восприятия), выполнять
рисунок с помощью рамки (умение работать по
образцу, сформированность внимания и
самоконтроля, уровень развития мелкой моторики и
зрительно-моторной координации), а также об
интуитивных представлениях о преобразованиях
плоскости (чтобы рисунок получился точным, рамку
надо двигать, переворачивать, координировать
составные части рисунка) и разработанности
мелких мышц руки (закрашивание рисунка по рамке).
Работа проводится дважды: в начале изучения темы
и в конце. Сравнивая две работы одного и того же
ученика, учитель может судить о его продвижении в
процессе обучения.
Для проведения проверочной работы
понадобятся карандаши и лист бумаги каждому
ребенку, а также рамка-трафарет. Учитель работает
со всем классом сразу. Обработка результатов
осуществляется по двум уровням: сделал – не
сделал (нашел – не нашел нужную фигуру, обвел –
не обвел четкой линией контур, ровно – неровно
закрасил фигуру и т.д.).
Проверочная работа
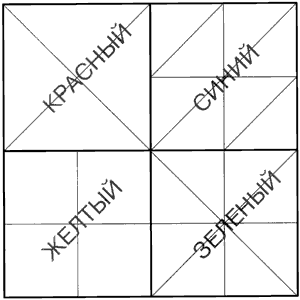
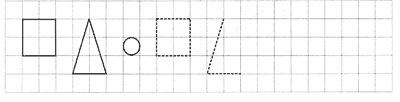
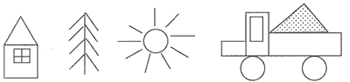
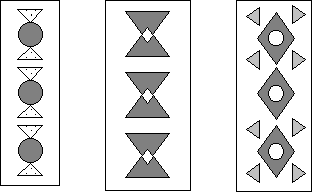
Задание 1. Найдите на рамке и
обведите: круг, квадрат, треугольник,
четырехугольник. Закрасьте круг красным цветом,
квадрат – синим, треугольник – зеленым,
четырехугольник – желтым.
Учитель делает паузу после каждого
указания, давая детям возможность найти и
нарисовать нужную фигуру. Если ребенок видит на
рамке несколько вариантов заданной фигуры,
учитель просит его выбрать один вариант и
нарисовать.
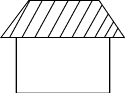
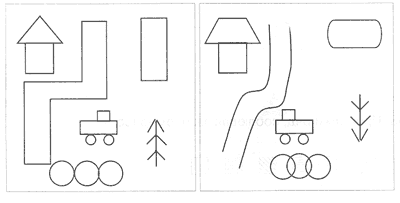
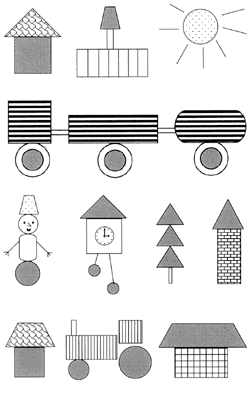
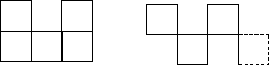
Задание 2. Нарисуйте по рамке такой
домик, как у меня, и раскрасьте его.
Учитель объясняет детям, что
закрашивать фигуру следует используя рамку:
ребенок рисует фигуру и закрашивает ее внутри
соответствующей формы, не снимая рамку. Такая
технология раскрашивания позволяет
раскрепостить руку в кистевом сгибе, избежать
накопления усталости (что провоцирует кистевой
спазм) и подготовить мелкие мышцы кисти к письму.
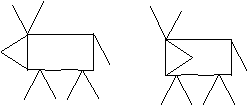
Задание 3. К домику едет трактор.
Нарисуйте его по рамке таким, как у меня, и
закрасьте.
Задание 4. С помощью рамки
повторите мой рисунок и закрасьте его, как вам
хочется.
Задание позволяет проверить не только
точность восприятия и воспроизведения, но и
интуитивное чувство симметрии.
УРОК 1
Тема: “Сравнение фигур по различным
признакам”.
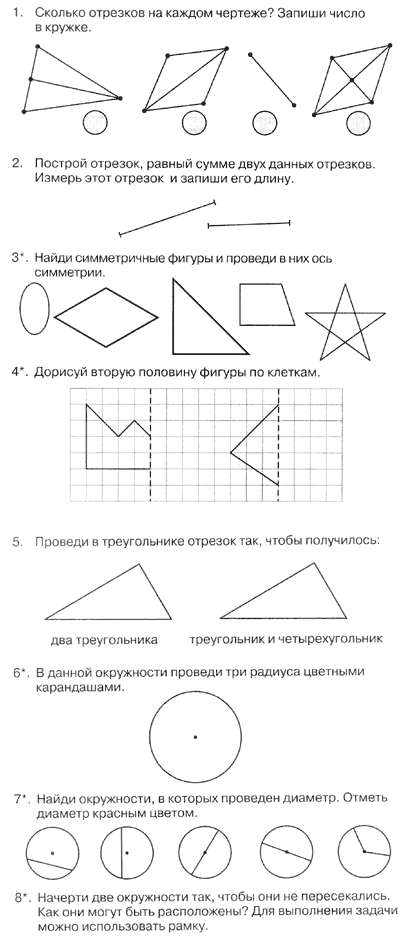
Упражнение 1
Материал: модели фигур, фланелеграф,
дидактический набор у детей.
Способ выполнения: учитель использует
сюжет, сопровождая рассказ изображением любого
сказочного персонажа, например:
– Сегодня я познакомлю вас со своим
другом Ежиком. Он очень любит собирать грибы и
ягоды, а потом развешивает их на веточках
сушиться. Получается похоже на бусы:
– С какой фигуры начинаются бусы?
Какой заканчиваются?
Это упражнение удобно и для формирования
навыка счета: сколько кругов, сколько квадратов,
какая фигура стоит первой, третьей, шестой и т. д.
– Чем похожи все круги? (Они
одинакового размера, все зеленые).
– Чем похожи все квадраты? (Одинакового
размера, все красные).
– Выложите у себя на парте такие же бусы.
Дети используют фигурки из
дидактического набора. Образец дан в тетради.
Учитель следит за единством цвета и
чередованием фигур.
Упражнение 2
Материал: тетрадь, фланелеграф, модели
фигур.
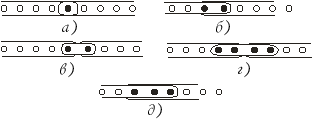
Способ выполнения: однажды Ежик
встретился в лесу с Гусеницей (Гусеницу можно
сконструировать на втором фланелеграфе либо
использовать рисунок в тетради № 1 на с. 5, но в
этом случае детям будет труднее сравнивать).
– Гусеница, ты похожа на мои бусы, –
сказал Ежик.
– Чем же я похожа? – спросила Гусеница.
– Ребята, кто ей ответит?
Рассматривается сходство и различие
конструкций (одинаковая и разная форма фигур,
цвет, размер, возможно, и количество;считающим
детям учитель предлагает сосчитать фигуры).
– Эта Гусеница нарисована у вас в
тетради. Откройте тетрадь. Расскажите, из каких
фигур составлена Гусеница.
Упражнение 3
Материал: тетрадь, рамка, карандаши.
Задание: на верхней строке с. 7
нарисованы бусы (задание 4). Какая фигура первая?
Найдите ее на рамке. Найдите на рамке вторую
фигуру. Что это? (Квадрат. Маленький).
Совместите прорезь рамки с фигурой в тетради и
раскрасьте фигуры первой строки. Продолжите
бусы, рисуя и раскрашивая фигуры по рамке.
Здесь учитель может использовать либо
прием наблюдения за самостоятельной работой
детей и индивидуальной помощи, либо
комментирование при выборе следущей фигуры.
Детям, быстро закончившим выполнение
этого задания, учитель предлагает выполнить
задание 2 на складывание изображенных фигур из
палочек.
Упражнение 4
Материал: конструкции узоров с
ошибками на фланелеграфе.
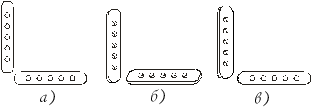
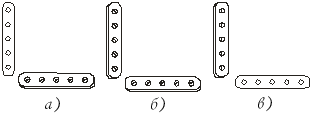
Задание: найдите ошибки в моих бусах:
– Исправьте ошибки. Выложите такие же
бусы на парте. Нарисуйте их в тетради, продолжив
рисунок с помощью рамки. Раскрасьте бусы по
рамке.
Рисунок этих бус представляет для
некоторых детей трудность, так как для того,
чтобы узор был верным, рамку надо поворачивать –
квадрат должен стоять не так: , а так:
.
Если дети путают эту фигуру с фигурой
ромба (она есть на
рамке), надо сначала обговорить нужную операцию и
выполнить ее не в тетради, а на столе (“Положите
рамку так, чтобы получить квадрат в указанном
положении, а я посмотрю, все ли правильно это
сделали”).
– Что надо было сделать с рамкой? (Повернуть.)
Упражнение 5
Материал: набор фигур и карточки с
символами.
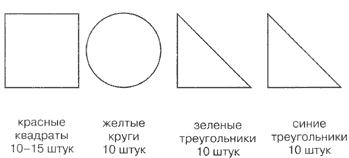
Для игры понадобится набор фигур и
символов в количестве до 10 штук. Например, такой:
Способ выполнения: игра
“Внимание”. Для игры сначала используют 4–5
фигур и карточек с символами, затем можно
увеличить их количество в зависимости от того,
сколько дети могут запомнить. Игра развивает
внимание, память, самоконтроль, расширяет объем
внимания, формирует точность восприятия.
Игра может проходить так: учитель
выставляет в ряд на фланелеграфе 4–5 фигур и
предлагает детям запомнить, как они стоят. Затем
дети закрывают глаза, а учитель меняет две фигуры
местами. Дети должны ответить на вопрос: “Что
изменилось?” При ответах учитель помогает
детям правильно употреблять предлоги за,
между, перед, после.
Варианты:
– фигуры стоят не в ряд, а вразброс;
– учитель убирает одну из фигур и заменяет ее
другой;
– учитель выставляет на фланелеграф 3–5 фигур на
5–6 секунд, затем отворачивает фланелеграф от
детей. Дети рисуют фигуры от руки по памяти на
листочке.
Постепенно (к концу четверти)
количество фигур увеличивается до 10. К этому
заданию удобно подключить счетные операции
(количество, порядок: назовите первую, вторую
справа, какая по счету последняя и т.п.).
Дополнительные упражнения
Упражнение 6
Материал: счетные палочки.
Задание: сложите из палочек (образец
либо предлагается на фланелеграфе, либо
используется задание 2 в тетради № 1). К этому
заданию также можно подключить счет.
Упражнение 7
Материал: рисунок на доске
Задание: найти лишнего человечка.
Дополнительно на столе можно
разложить набор геометрических тел:
– Какая фигура лишняя? (Шар, так как
он без углов.)
Дети могут просто показать пальцем на
лишнюю фигуру, но если им хочется услышать
название фигур, учитель называет их.
В качестве домашнего задания можно
предложить раскрасить Гусеницу (используя
рамку).
УРОК 2
Тема: “Сравнение фигур по различным
признакам”.
Упражнение 1
Материал: набор фигур.
Задание: все фигуры надо разделить на
две группы по какому-нибудь признаку.
Дети выполняют различные разделения:
по цвету, по размеру, по форме. Учитель помогает
им сформулировать обобщение: “По какому
признаку мы разделили фигуры?” (По цвету).
“А по другому признаку можно разделить эти
фигуры?” и т. д.
Упражнение 2
Материал: модели фигур у учителя,
дидактический набор у детей.
Задание: учитель составляет на
фланелеграфе конструкцию из деталей, а дети
повторяют ее на парте, используя дидактический
набор. Можно использовать задание 5 в тетради № 1.
Затем дети зарисовывают конструкции
по клеткам в тетрадь.
Упражнение 3
Игра “Внимание”.
Упражнение 4
Материал: рисунок на доске.
Задание: одна из фигурок в каждом ряду
лишняя. Найдите ее и объясните свой выбор.
Упражнение 5
Материал: тетрадь.
Задание: разбирается и выполняется
задание 7 в тетради № 1. При сравнении фигур дети
опираются на подсчет клеток. Цель задания –
обратить внимание детей на то, что изменение
положения фигуры не изменяет ее форму и размер.
Дополнительные упражнения
Задания 8–10 выполняются в тетради
№ 1.
УРОК 3
Тема: “Классификация фигур по
размеру и форме”.
Упражнение 1
Материал: набор фигур одного цвета.
Задание: разделите фигуры на две
группы. (Большие и маленькие или треугольники и
четырехугольники.)
Упражнение 2
Материал: дидактический набор.
Задание: выложить орнамент
последовательно под диктовку учителя.
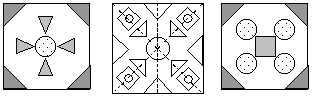
Учитель диктует: в центре – красный
квадрат; сверху, внизу, справа и слева – зеленые
круги; по краям между кругами – треугольники.
Двое учеников конструируют орнаменты
на двух фланелеграфах, повернутых от класса.
Точность выполнения узора проверяется и
сравнивается. Затем орнамент зарисовывается на
нелинованном листе с помощью рамки и
закрашивается.
Упражнение 3
Игра “Внимание”.
Упранение 4
Материал: рисунок на доске.
Задание: найдите лишнюю фигуру и
объясните свой выбор.
В тетради задание 11: а теперь сами
найдите лишний домик.
Упражнение 5
В задании 15 продолжите ряд человечков.
При объяснении порядка чередования
человечков учитель побуждает детей использовать
слова следом за, между, перед ним, после него.
Упражнение 6
Материал: счетные палочки.
Способ выполнения: работа с палочками
задается учителем образцами на фланелеграфе, где
вместо палочек удобно использовать узкие
полоски бумаги размером с карандаш.
Задания:
а) сколько палочек достаточно
взять, чтобы сделать треугольник? (Три.)
Возьмите три палочки и сделайте треугольник;
б) сколько палочек достаточно
добавить, чтобы сделать четырехугольник? (Одну.)
Добавьте одну и сделайте четырехугольник. На что
похож ваш четырехугольник? (На квадрат.);
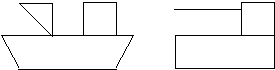
в) сложите такую лампу: . На что это еще похоже?
г) сложите такую лодку: ;
д) cложите такую вазу: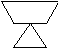
е) сложите такую конфету: ;
ж) сложите телевизор: ;
з) придумайте свою фигуру и сложите
ее из палочек.
Дополнительные упражнения
Задания 12–14 в тетради № 1.
Задание 13 может быть предложено
для домашней работы.
УРОК 4
Тема: “Классификация фигур по
форме”.
Упражнение 1
Материал: набор фигур.
Задание: найдите ошибку в узоре.
Упражнение 2
Материал: рамка, карандаши, набор
фигур, лист бумаги.
Задание: найдите на рамке такую же
фигуру и нарисуйте ее.
Способ выполнения: учитель выставляет
на фланелеграф одну за другой фигуры, а дети
находят их на рамке и рисуют на листе бумаги.
– Дайте название каждой фигуре.
Если учащиеся называют
прямоугольник, учитель пользуется этим
названием. Если слово “прямоугольник” дети
не называют, учитель предлагает придумать
название для фигур 3 и 5 (если дети знают слово
“прямоугольник”, то тогда только для 5).
Возможен такой вариант:
– Ребята, как называют фигуру 1? (Треугольник.)
Сколько у него углов? (Три.) А сколько углов у
этой фигуры? (Четыре.) Как же можно ее назвать?
(Четырехугольник.) Правильно.
– А теперь попробуйте ответить на
такой вопрос: из этих пяти фигур одна очень
сильно отличается от всех других. О какой фигуре
я говорю? Кто догадался?
После нескольких попыток дети обычно
выделяют круг. (У него нет углов.)
– Верно. Я его уберу. Осталось четыре
фигуры. Но одна из них снова отличается от других.
Кто догадался, о какой фигуре я говорю?
Возможны два варианта: дети выделяют
фигуру 1 или 5. Верный выбор – треугольник.
Объяснение: у него три угла, а у остальных –
четыре угла.
Чтобы дети понимали, почему верный
выбор – треугольник, им предлагается последний
вопрос: “Попробуйте дать одно название всем
оставшимся фигурам”.
Если выбрана фигура 5, то тогда такое
название дать невозможно (понятие
“многоугольник” детям незнакомо), если
выбрана фигура 1, то общее название –
четырехугольники.
Упражнение 3
Учитель предлагает детям провести
анализ рисунков (Сколько треугольников? Сколько
четырехугольников? Покажите эти фигуры на рамке).
Задание 16. Составь из четырех
треугольников эти фигуры.
Задание 17. Сосчитай треугольники
на рисунке “Кошка”. Впиши в окошко домика
столько палочек, сколько треугольников.
Упражнение 4
Материал: образец орнамента в полосе,
рамка, полоска бумаги у каждого ученика, цветные
карандаши.
Способ выполнения: учитель проводит
знакомство с орнаментом в полосе. Орнамент
располагается от центра по осевой линии. Центр
находится сгибанием полосы пополам. Линия сгиба
пересекает осевую линию в центре.
Для выполнения орнамента дети
получают треть обычного альбомного листа (в
длину) – полоса. Дети выполняют орнамент в полосе
по рамке с раскрашиванием, осевая линия на
полосках у детей заранее нарисована. Они могут по
желанию либо следовать образцу, либо составить
свой орнамент, следуя правилам его составления,
используя рамку.
Дополнительные упражнения
Задания 16 и 17 дети могут выполнять
самостоятельно в тетради.
УРОК 5
Тема: “Треугольник”.
Упражнение 1
Материал: набор фигур или рисунок на
доске.
Задание: найти лишнюю фигуру и
объяснить свой выбор. При обяснении фиксируются
признаки фигур: количество сторон и углов.
Упражнение 2
Материал: рамка, карандаши, лист
бумаги.
Задание: найти в рамке все
треугольники и обвести их на листе бумаги.
Сколько их? (Если дети обвели фигуру , эту ошибку надо обсудить: у
нее четыре угла).
Упражнение 3
Материал: счетные палочки, карточки с
рисунками фигурок.
Задание: сложите фигуру из палочек.
Способ выполнения: учитель показывает
каждый контур на карточке 2–3 секунды и убирает.
Дети складывают конструкцию по памяти. Затем
сверяют ее с образцом. Упражнение развивает
внимание, образную память и рефлексию.
Упражнение 4
Задание: сложитетреугольник из:
а) трех палочек;
б) пяти палочек (следует дать время на решение
этой конструктивной задачи и обязательно
дождаться хотя бы одного самостоятельного
варианта);
в) шести палочек;
г) семи палочек.
Упражнение требует преодоления
шаблонного восприятия треугольника в виде .
Аналогично выполняется следующее
задание.
Сложите четырехугольник из:
а) четырех палочек;
б) пяти палочек;
в) шести палочек;
г) семи палочек;
д) восьми палочек.
– Можно ли сложить из палочек круг? (Нет,
из палочек получаются только фигуры с углами.)
Упражнение 5
Материал: рамка, цветная бумага,
ножницы, клей, альбомные листы.
Способ выполнения: учитель предлагает
игровую ситуацию:
– Пятачок идет на день рождения к Иа-Иа
и несет в подарок шарики. Разноцветные шарики мы
с вами сейчас сделаем.
Учитель показывает образец аппликации
и помогает детям провести ее анализ (“Сколько
шариков? Какие шарики? Сколько одинаковых?” – и
т.п.).
– Найдите на рамке круг для большего шарика.
– Обведите его на цветной бумаге.
Дети обводят по рамке несколько
разноцветных шариков, вырезают их и крепят на
лист клеевым карандашом. Ниточки дорисовывают.
По качеству вырезанных шариков учитель легко
может судить об уровне владения ножницами.
Дополнительные упражнения
Задания 18 и 19 предлагаются детям,
быстро правившимся с упражнением 5.
УРОК 6
Тема: “Геометрические фигуры” (обобщение).
Упражнение 1
На этом занятии повторяется входная
проверочная работа (домик и трактор). Сравнение
результатов даст учителю возможность определить
степень продвижения ребенка.
В качестве задания более высокого
уровня сложности можно использовать задание 20 из
тетради: “Дорисуй вторую половину
Тянитолкая”. Следует заранее познакомить
детей со сказкой “Айболит” и ее героями (у
Тянитолкая две головы, поэтому справа рисуется
зеркальное отражение левой части рисунка).
Детям, быстро справившимся с рисунком,
предлагается задание 21 из тетради: сложи из
деталей мозаики домик, машину и елочки.
Упражнение 2
Измени рисунок по заданию. Нарисуй
свой вариант.
Примечание: задание
“Перекодировка” показывает уровень
сформированности учебной самостоятельности,
распределения внимания и умения самостоятельно
понимать и воспринимать инструкцию. Можно
сначала предложить детям выполнить задание на
листке бумаги с последующим разбором. Не следует
предварительно объяснять детям способ
выполнения задания, поскольку в этом случае дети
проявят не уровень учебной самостоятельности, а
исполнительность и прилежание.
При анализе результата выполнения задания
учитель помогает детям связно выразить суть
“инструктивного письма”: круг заменяется на
треугольник, а квадрат ни на что не заменяется,
потому что в задании он не обозначен.
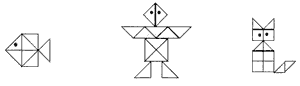
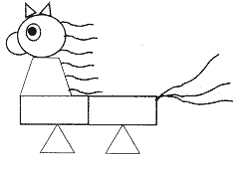
Задание 26 “Нарисуй коня” можно
использовать для домашней работы. Можно
использовать задание 31 “Клоун”. Следует
попросить детей обвести на кальке нужные фигуры
к заданию 31, а затем вырезать их из цветной бумаги
и приклеить на рисунок “Клоун”.
Задание 23. Найди лишнюю фигуру и
закрась ее синим карандашом.
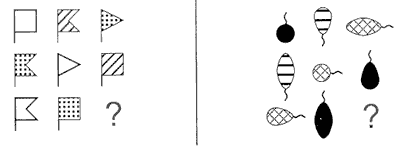
Задание 24. Среди фигур справа найди
такие же, как и слева. Одинаковые фигуры закрась
одним цветом.
Задание 25. Сложи из деталей мозаики
рыбку, робота и кошку.
Задание 26. Сложи из деталей мозаики
лошадь.
УРОК 7
Тема: “Сравнение фигур. Круг”.
Упражнение 1
Материал: на фланелеграфе несколько
кругов одинакового размера, но разного цвета (два
цвета).
Задание: разделите круги на две группы.
По какому признаку это можно сделать? (По цвету.)
Упражнение 2
Способ выполнения: учитель добавляет
несколько квадратов тех же цветов (два цвета) и
примерно тех же размеров, перемешивает фигуры.
Задание: попробуйте снова разделить
фигуры на две группы. (Два варианта: цвет, форма.)
Упражнение 3
Материал: набор фигур.
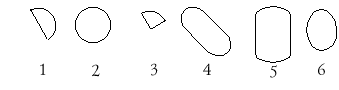
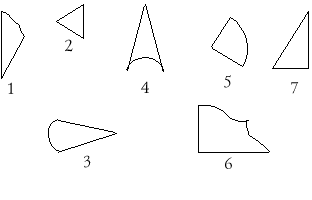
Задание: выберите круг из группы фигур.
– Почему только вторая фигура – круг?
Как можно назвать фигуры 1, 3 и 6? (Полукруг, часть
круга, овал.)
Упражнение 4
Материал: у детей на столе два круга из
плотной бумаги или картона – большой красный и
маленький зеленый.
Задание: давайте попробуем рассказать
про этот круг. Возьмите его в руки. Что можно
рассказать о нем? (Он из бумаги, красный.)
Учитель показывает мяч.
– Можно сказать, что это круг? (Нет.)
Но что-то похожее есть? (Да.)
– Возьмите круг пальцами вот так: . Говорят, что круг плоский.
– Можно сказать, что мяч плоский? (Нет.) Мяч не
будет кругом. Мяч имеет форму шара.
Упражнение 5
Материал: два круга на фланелеграфе.
Задание: посмотрите на эти две фигуры.
– Чем они похожи? (Обе круглые. Круги.)
Чем отличаются? (Цветом: красный и зеленый.
Размером: большой и маленький.)
Упражнение 6
Задание: посмотрите на эти яблоки.
Учитель выставляет на фланелеграф
модели двух яблок: большого зеленого и
маленького красного.
– Какой из ваших кругов похож на это
яблоко? Чем?
Учитель показывает маленькое
красное яблоко. Дети могут показать и тот и
другой круг. Разбирают оба варианта: похож
цветом, похож размером. Тот же вопрос с другим
яблоком.
Упражнение 7
Материал: игра “Сложи круг”.
Способ выполнения: детям раздают
конверты с разрезанным на части кругом. Его надо
сложить. Все варианты разные. Учитель проверяет
результаты, подходя к каждому ребенку. Сложив
свой круг, дети меняются конвертами. Каждый
складывает 5–6 вариантов.
Упражнение 8
Материал: образец закладки с узором из
кругов, рамка, цветные карандаши, полоски бумаги.
Способ выполнения: учитель показывает
детям закладку для книг с узором из кругов. Узор
анализируется. Используя рамку, дети рисуют его
на готовых полосках бумаги (картона). Закрашивают
по рамке.
Это задание можно заменить
выполнением задания “Две гусеницы”: нарисуй
таких же гусениц, используя рамку. Раскрась
правую зеленым цветом, левую – красным.
Дополнительные упражнения
Задания 27–30 в тетради выполняются
на выбор.
Задание 29 “Кто где живет”
желательно рассмотреть в классе .
Задания 28, 32–33 можно предложить
для домашней работы . При этом штриховку следует
заменить раскраской.
Задание 29. Догадайся, какой шарик
где живет.
УРОК 8
Тема: “Сравнение фигур. Квадрат”.
Упражнение 1
Материал: набор фигур.
Задание: одна из фигур в этом наборе
лишняя. Какая? (Квадрат.) Почему? (Все
остальные – круги.)
Упражнение 2
Задание: оставшиеся круги разделите на
две группы. Объясните, почему так разделили. (По
цвету и по размеру.)
Упражнение 3
Задание: что может означает число 2 для
этих кругов? (Два больших круга, два зеленых
круга.) Число 3? (Три синих круга, три маленьких
круга.)
Упражнение 4
Материал: дидактический набор.
Задание: кто помнит, какого цвета был
квадрат, который мы убрали? (Красного.)
Возьмите дидактический набор. У кого квадраты
красные? У кого не красные? Какого цвета?
Отсчитайте шесть квадратов. Что из них можно
сконструировать? (Дорожку, башню, лестницу, поезд,
прямоугольник и т. д.).
Все варианты складывают на
фланелеграфе. Дети дают им названия.
Упражнение 5
Задание: можно ли из всех этих
квадратов сложить один большой квадрат? (Нет.)
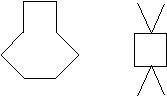
– Сложите такую фигуру:
– Кто-нибудь знает, как она называется?
На что она похожа? (Ящик, коробка, дом…) Дом, но
без крыши. Сложите крышу дома. Какие фигуры надо
взять? (Треугольники или трапецию.)
Дети складывают крышу самостоятельно,
результат выносят на фланелеграф.
Может быть два варианта:
.
Упражнение 6
Материал: образец аппликации
“Кошка”, рамка, ножницы, клей.
Способ выполнения: используя рамку в
качестве шаблона для составляющих модулей, дети
вырезают детали и конструируют на альбомном
листе аппликацию “Кошка”. Детали удобно
крепить клеящим карандашом.
Дополнительные упражнения
Задания 34–38 используются для
организации индивидуальной работы в тетради.
Задания 38. В качестве домашней
работы предлагается раскрашивание рисунка
“Машина”.
УРОК 9
Тема: “Геометрические фигуры”
(обобщающий урок).
Упражнение 1
Материал: набор фигур.
Задание: из данного набора уберите
лишнюю фигуру. (Лишняя фигура – круг.)
– Разделите все квадраты на две
группы. По какому признаку это можно сделать? (По
цвету, по размеру.) Что может означать число 2
для этих фигур? (Два маленьких квадрата.)
Число 4? (Четыре больших квадрата.) Число 3? (Три
красных, три зеленых.) А всего их сколько? (Шесть.)
Упражнение 2
Задание: поиграем в такую игру: вы
закроете глаза, я уберу один квадрат, а вы должны
сказать, какой квадрат я убрала – маленький или
большой, красный или зеленый?
Игра повторяется 3-4 раза. Такая игра
хорошо влияет на развитие внимания и
наблюдательности.
Упражнение 3
Материал: набор фигур.
Способ выполнения: учитель выставляет
на фланелеграфе фигуры, которым дети дают
названия по мере их появления. (Используется
название “четырехугольник” для трапеции).
Затем детям предлагается зарисовать на листке
бумаги все эти фигуры в том же порядке и в таком
же расположении, как на фланелеграфе. Рисунок
выполняется “от руки”.
Для усложнения задания можно
предложить выполнить задание по памяти, отвернув
от детей фланелеграф. Затем правильность
выполнения проверяется.
Упражнение 4
Сложи из деталей мозаики гуся. Нарисуй
его по клеткам.
Упражнение 5
Измени картинку по заданию.
Учитель может предложить выполнить
это задание детям самостоятельно, после его
выполнения отмечается, в какой клетке рисунок не
изменился. (В левой нижней.)
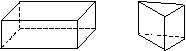
Задании 47. При обводке объемных
фигур полезно предложить детям найти такие же на
столе учителя; показать те части фигуры, которые
мы видим на рисунке; найти фигуру, которая
отличается от двух других (цилиндр).
Задание 48 “Найди
треугольники” нужно перенести на доску и
показать все найденные треугольники. (Их
четыре.)
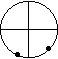
Задание 50 “Найди лишнюю
фигурку” дано для введения в активный словарь
детей терминов “внутри” и “снаружи”. (У
всех точка внутри, а у одного – снаружи.)
Задание 51 “Чем похожи и чем
отличаются рисунки” дано не только для
развития восприятия и внимания, но и для
формирования активного математического словаря
ребенка. Задание лучше выполнять в классе
фронтально, чтобы несколько детей могли отметить
сходные и различные детали рисунка.
Задание 45 может быть предложено
для домашней работы.
Примечание: к концу I четверти
дети достаточно освоились с тетрадью и во многих
случаях догадываются сами, что надо сделать в
задании, даже не умея его прочитать. Именно это
предполагает методика графического решения
тетради. Если это так, то учитель может
использовать тетрадь в свободном режиме для
дополнения урока, для домашних заданий, для
индивидуальной работы (разным детям можно
предлагать разные задания, соответствующие
уровню требуемой сложности и желанию ребенка).
Автор не считает необходимым в 1-м классе жестко
регламентировать работу учителя с тетрадью (то
есть указывать упражнения и страницы к уроку),
так как это легко сделать, сопоставляя текст
урока и страницы тетради, где материал дан
последовательно в соответствии с текстами
уроков. Таким образом, ссылки на тетради в 1-м
классе не являются обязательными для учителя.
Более разумной будет его ориентация на
индивидуальные особенности и уровень развития
детей в классе.
Например, некоторые дети смогут и захотят
выполнить на уроке больше заданий, а некоторые
предпочтут выполнить их дома. Некоторым детям
нужно больше заданий на развитие моторики, а
другим – на развитие логических приемов, третьим
– на развитие внимания и т. п. Медленно
работающим детям можно предложить выполнить
пропущенные задания на каникулах. Такой подход
не является перегрузкой для детей этого типа,
поскольку мыслительная деятельность у них
замедленна, догадка появляется не сразу, а сам
мыслительный процесс обладает большой инерцией.
Иными словами, они все равно додумывают задания
“долго после”, и это додумывание должно
обязательно завершиться продуктивным
результатом, иначе у ребенка будет формироваться
безнадежное чувство “напрасности” всяких
мыслительных усилий: все равно он не успевает
сообразить вовремя, а когда он сообразит, это уже
никого не интересует. С такими детьми нужно
обязательно обсуждать результаты их работы
тогда, когда они сумели выполнить задания сами,
пусть это и будет как бы “вдогонку”, но
ребенок будет знать, что его умственную работу
тоже оценили и заметили, а это в свою очередь
будет стимулировать его к дальнейшей умственной
работе.
Быстро работающим детям можно разрешить
“забегать” вперед, но при этом настаивать на
рефлексии всех своих умственных действий, то
есть просить каждый раз объяснять ход своих
мыслей, чтобы не формировать у ребенка привычку
работать “методом тыка”.
II ЧЕТВЕРТЬ
УРОК2
Тема: “Геометрические фигуры”
(повторение).
Цели: уточнить представления детей
о форме геометрических фигур; развивать
пространственное и логическое мышление.
Упражнение 1
Материал: на фланелеграфе несколько
(8–10) геометрических фигур.
Задание: назовите те, которые вы
знаете. Какого они цвета? Какого размера? (Большая,
маленькая.)
Упражнение 2
Задание: разделите эти фигуры на две
группы. По какому признаку это можно сделать?
Примечание: фигуры выполнены
в двух цветах, поэтому их делят: а) по форме
(треугольники и четырехугольники, закругленные
фигуры); б) по цвету; в) по размеру, то есть
возможно составление трех вариантов
“разделений”. Это задание на классификацию
лучше выполнять в таком порядке: сначала дети
составляют группы, а затем с помощью учителя
формулируют характеристику свойства, по
которому проведена классификация.
Упражнение 3
Материал: рамка, карандаш, лист бумаги.
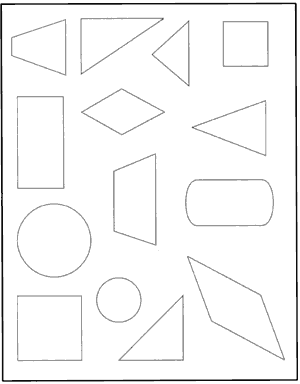
Задание: рассмотрите рамку и назовите
фигуры, которые вы знаете. Возьмите карандаш и
обведите изнутри по рамке: большой круг,
маленький квадрат, треугольник, прямоугольник,
маленький круг, большой квадрат.
Задание проверяет умение различать
фигуры по форме и по размеру; анализируя его,
учитель выявляет ошибки восприятия и различения
формы.
Упражнение 4
Задание: закрасьте красным цветом
(используя для штриховки рамку) большой круг и
маленький квадрат; синим – треугольник и
прямоугольник; зеленым – маленький круг и
большой квадрат.
– Какая фигура у вас осталась
незакрашенной? (Таких не осталось.)
Упражнение 5
Задание: найдите на рамке все
треугольники и обведите их. Закрасьте одним
цветом. Сколько их? (Три.)
Упражнение 6
Задание: найдите на рамке все фигуры, у
которых четыре угла. Обведите их. Закрасьте одним
цветом. Сколько их? (Семь.)
Фигуры считают те дети, которые
умеют.
Если учитель видит, что дети включили в
эту группу такую фигуру: , предлагается следующее задание:
Упражнение 7
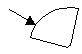
Ребята, Незнайка выполнил это задание
так:
Знайка ему говорит: “У тебя одна
фигура не похожа на все остальные”. А Незнайка
не видит, какая это фигура.
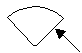
Помогите Незнайке найти лишнюю фигуру.
В процессе выполнения задания учитель
помогает детям найти фигуру с двумя кривыми
сторонами: она похожа на четырехугольник, но у
нее в отличие от других стороны кривые. На этом
уроке достаточно выполнения задания такого
уровня.
Упражнение 8
Материал: детям раздают конверты с
геометрическими фигурами, точно подходящими к
размеру отверстий в рамке. Они выполнены из
цветного картона или тонкого пластика. Хорошо,
если к каждой прикреплена маленькая “ручка”,
за которую удобно брать фигурку.
Такие наборы могут сделать
четвероклассники в подарок первоклассникам,
тогда вместо конвертов дети делают коробочки в
стиле оригами, которые очень удобны для хранения
фигурок.
Способ выполнения: игра “Закрой
окошки”.
Ученики кладут рамки перед собой и
“закрывают” окошки (“Дождь пошел, в
сказочном домике надо быстро закрыть все
окошки”). На следующем уроке эту игру можно
проводить на скорость по секундомеру.
Упражнение 9
Материал: рисунки, выполненные с
помощью рамки.
Способ выполнения: учитель предлагает
детям рассмотреть рисунки, выполненные с помощью
рамки. Они должны определить, какие прорези были
использованы. Можно полистать тетрадь,
рассмотреть ее рисунки. Затем дети выбирают
любую фигурку и выполняют свой рисунок
аналогично. При желании ребенок составляет свой
вариант и раскрашивает его.
Это задание можно дать детям для
выполнения дома.
Задания 52–58 используются для
индивидуальной работы в тетради.
Задание 56 можно усложнить
раскраской фигур, например, задать сохранение
порядка цвета вне перемещения фигур. При этом
сочетание двух закономерностей сделает задание
достаточно сложным: в каждой следующей рамке
первая фигура перемещается на последнее место,
но цвет можно определить как постоянно
сохраняющийся порядок (первая фигура в любом
случае остается красной, вторая – синей и т.п.).
УРОК 10
Тема: “Симметричный орнамент”.
Цели: научить получать квадрат из
прямоугольного листа бумаги; дать представление
о центре квадрата и симметричном построении
орнамента.
Упражнение 1
Материал: несколько симметричных
орнаментов в квадрате. Один из рисунков должен
быть сделан с нарушением симметрии.
Способ выполнения: учитель предлагает
детям рассмотреть несколько орнаментов.
– Какой формы основа орнамента? (Квадрат.)
Из каких геометрических фигур он составлен?
Упражнение 2
Задание: найдите среди этих орнаментов
“неправильный”. В чем его
“неправильность”?
Упражнение 3
Материал: стандартный лист
нелинованной бумаги каждому ребенку.
Задание: чтобы сделать такой орнамент,
нужен квадрат для основы. Можно ли сказать, что
стандартный альбомный лист бумаги имеет форму
квадрата? (Нет.) Сейчас я покажу вам, как
получать квадрат из прямоугольного листа бумаги.
Учитель объясняет, как получить
квадрат загибанием “от угла”. Лишнюю часть
загибают и отрезают или аккуратно отрывают.
Упражнение 4
Задание: для того чтобы узор получился
красивый, его надо начинать от центра квадрата.
Как найти центр нашего квадрата? (Перегнуть его
пополам еще раз.)
Упражнение 5
Материал: рамка, цветные карандаши.
Способ выполнения: дети выполняют
рисунок симметричного орнамента по образцу,
предложенному учителем, используя рамку.
Раскрасить его можно карандашами с помощью рамки
или фломастерами.
Упражнение 6
Задание: тем, кто быстро справился с
работой, учитель предлагает составить орнамент
самостоятельно, предварительно сделав новый
квадрат для основы.
Такую же работу можно предложить всем
детям выполнить дома, но уже в виде аппликации.
Образцы простейших орнаментов:
Задания 59–63 используются для
индивидуальной работы в тетради.
УРОК 11
Тема: “Начальные геометрические
понятия: точка и прямая”.
Цели: Познакомить с
неопределяемыми понятиями геометрии: точка,
прямая, кривая; научить получать прямую способом
перегибания листа; познакомить с геометрической
мозаикой и развивать умение выполнять
конструктивные задания на ее основе.
Упражнение 1
Материал: рисунки на доске.
Способ выполнения: сегодня я хочу
познакомить вас со своими друзьями – цветными
мелками. Они будут трудиться для нас весь год –
чертить и писать на доске. Но для того чтобы мы
знали, что хотят сказать мелки, надо понимать их
язык. Они говорят рисунком. Вот я беру красный
мелок и рисую так:
Что это? Как это назвать? (Точка.) А
теперь мелок побежал по доске, оставляя такой
след:
Как назвать его? Что это?
Чаще всего дети после нескольких
попыток говорят слово “линия”. Если этого не
произошло, учитель сообщает название сам.
Поскольку понятия “точка” и “линия”
являются неопределяемыми в геометрии, не стоит
пытаться объяснять детям, что это такое.
Достаточно просто дать визуальный образ и
сообщить название. Эти понятия будут
формироваться на следующих уроках путем
выполнения заданий на классификацию, сравнение и
обобщение.
Упражнение 2
Материал: рисунок на доске.
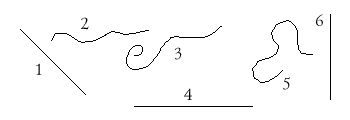
(1, 4, 6 – прямые линии; 2, 3, 5 – кривые
линии.)
Задание: здесь нарисовано несколько
линий. Посмотрите на них. Есть ли среди них
похожие? Чем они похожи? Как можно
охарактеризовать их форму?
В процессе выполнения этого задания
дети быстрее всего находят название для прямой,
но обычно говорят “ровная линия”. Учитель
сообщает, что математики называют эти линии прямыми.
Прежде чем сообщить название
“кривая”, учитель выслушивает предложения
детей. Затем предлагает показать рукой форму
(“ход”) прямой линии и кривой.
Упражнение 3
Задание: учитель просит детей
поставить на доске две точки (расстояние между
ними не менее 50 см).
– А теперь давайте проведем на доске
кривую так, чтобы она прошла через эти две точки.
Ученик проводит кривую от руки.
Учитель следит, чтобы точки оказались на кривой.
В случае необходимости чертеж подправляют.
Упражнение 4
Материал: небольшой лист нелинованной
бумаги, лучше с неправильными краями. На урок
понадобится три таких листка.
– Возьмите лист бумаги. Поставьте
точку в любом месте. Чтобы потом эту точку не
потерять, проткните на этом месте дырочку
стержнем ручки. Теперь поставьте еще одну точку
так, чтобы между вашими точками помещалась
ладошка (иначе дети ставят точки совсем рядом). А
теперь проведите на своем листе кривую линию так,
чтобы она прошла через обе точки.
– Трудно ли это было сделать? (Нет.)
Посмотрите, правильно ли выполнил задание ваш
сосед.
Упражнение 5
Задание: возьмите второй лист бумаги.
Снова поставьте на нем две точки. Проведите через
них прямую линию. Получилась ли у вас прямая?
Дети выполняют задание от руки,
поэтому прямая у них не получается.
– Может быть, это удастся сделать на
доске?
Учитель ставит две точки (достаточно
далеко друг от друга) и предлагает провести через
них прямую. Дети убеждаются, что сделать это
“от руки” невозможно.
Упражнение 6
Задание: может быть, нам легче будет
провести прямую через одну точку?
Учитель предлагает детям взять новый
листок и поставить на нем точку (проткнуть).
– Проведите через нее прямую.
Дети убеждаются, что “от руки”
это сделать нельзя.
Обычно к этому моменту многие
догадываются, что надо воспользоваться
инструментом – линейкой.
Учитель может спросить: “А как вы
сразу догадались, что начерченные мной линии на
доске прямые? В жизни они вам часто встречаются.
Как же люди чертят прямые?”
Затем учитель знакомит детей с новыми
помощниками: Карандашом и Линейкой. Их забавные
“портреты” можно укрепить над доской, и в
дальнейшем их появление будет напоминать детям о
необычном – путешествии в страну Геометрию,
которое дети начинают на этом уроке.
– В этой стране живут геометрические
фигуры, там все имеет геометрическую форму, даже
деревья. А провожать Карандаша и Линейку будет
маленькая смешная Резинка, лучшая подружка
Карандаша. (“Как вы думаете, почему Карандаш
дружит с Резинкой?”)
Введение такого сюжета позволяет
учителю в дальнейшем составлять урок как
путешествие в страну Геометрию, облекать любую
геометрическую задачу в форму приключений
постоянных героев.
Упражнение 7
Задание: как нам провести прямую хотя
бы через одну точку? Сейчас я вам открою
маленький секрет – научу вас делать это без
линейки и карандаша.
Возьмите лист. Поставьте точку
(проткните стержнем). А теперь согните листок так,
чтобы точка оказалась на линии сгиба. Разверните
листок. Какая линия у вас получилась? (Прямая.)
Согните лист по этой линии и проведите пальцем по
сгибу. Какая получилась линия? (Прямая.) Вот мы
с вами и провели прямую линию через точку.
Проведя пальцем по сгибу, дети
закрепляют понятие прямой на тактильном уровне
– на уровне “ощущения на кончике пальцев”.
Дальше учитель может построить урок
так:
– А теперь я вас познакомлю с любимой
игрой детей в стране Геометрии. Это
геометрическая мозаика. Из ее деталей можно
складывать разные предметы и даже растения и
животных. И еще из нее можно складывать очень
красивые орнаменты.
Учитель знакомит детей с набором
“Геометрическая мозаика”.
Упражнение 8
Способ выполнения: знакомство с
деталями мозаики, их классификация по цвету,
размеру, форме.
Упражнение 9
Задания.
1) Из деталей мозаики сложить четыре
квадрата одинакового размера, но разного цвета.
красный желтый голубой зеленый
2) Из деталей красного квадрата сложить
треугольник.
3) Из деталей желтого квадрата сложить
прямоугольник.
4) Из четырех деталей голубого квадрата
сложить прямоугольник и из остальных четырех
деталей – треугольник.
5) Сложить фигуры “Рыбка”,
“Робот”, “Елочка”.
6) Сложить детали в коробку в
соответствии с узором.
Это задание выполняется в том случае,
если есть набор в заводской коробке. Если его нет,
то дети складывают фигуру “Ракета” или
придумывают свою конструкцию.
Для индивидуальной работы
используются задания 64–73 в тетради.
УРОК 12
Тема: “Прямая и кривая. Понятие о
пересекающихся и непересекающихся прямых.
Количество прямых, проведенных через одну точку
и через две точки”.
Цели: научить различать и строить
прямые и кривые линии; познакомить с различными
случаями взаимного расположения прямых на
плоскости.
Упражнение 1
Материал: рисунок на доске.
Задание: разделить все линии на две
группы. Дать названия группам. (Прямые и кривые.)
Упражнение 2
Задание: найдите на рисунке к
упражнению 1 прямую, которая идет точно сверху
вниз. Она называется вертикальной.
Найдите вертикальное направление прямых вокруг
себя (в классе).
– Кто видел, как мастера проверяют
вертикальность стены, ножки стула, забора?
Если никто из детей не видел отвес, учитель
показывает его и рассказывает, как им пользуются
для определения вертикальности.
– Прямая 7 идет точно справа налево (или слева
направо), ее называют горизонтальной.
Найдите в классе горизонтальные прямые.
– Как тогда можно назвать прямые 4 и 1? (Наклонные.)
Если дети не могут назвать эти прямые,
то название “наклонная” учитель
подсказывает детям сам.
Упражнение 3
Материал: небольшие листы
нелинованной бумаги с неровными краями.
Задание: возьмите клочок бумаги .
– Как получить на нем прямую линию без
линейки и карандаша? (Согнуть.) Покажите, как
надо расположить лист, чтобы ваша прямая была
вертикальной (горизонтальной, наклонной).
Упражнение 4
Задание: возьмите ручку и поставьте
точно на своей прямой точку (проколите ее
стержнем).
– Можно ли поставить на прямой еще
одну точку? Как вы думаете, сколько точек можно
поставить на прямой? (Сколько угодно.)
– Верно. Математики говорят, что на
прямой можно поставить бесконечное множество
точек. (Не следует ставить множество точек,
лист может порваться. Достаточно 3–4-х точек.)
Но чтобы их ставить, надо и линию иметь
бесконечной длины. Поэтому математики
договорились: когда говорят слово “прямая”,
имеют в виду, что начертить у себя на листе мы
можем только ее часть (и на доске тоже).
Бесконечную линию невозможно изобразить всю. Мы
чертим часть прямой, а сами про нее представляем
в уме, что она бесконечна и продолжается в любую
сторону сколь угодно далеко. То же самое
математики договорились думать и о кривой. Любая
линия бесконечна.
Но посмотрите на линию 1 и линию 6. Если я захочу
продолжить линию 1, то я точно знаю, куда она
должна пойти (здесь удобно использовать пару
длинных тонких указок, с их помощью дети
моделируют продолжение прямых).
– А продолжая линию 6 (кривую), могу ли я
точно сказать, куда она пойдет дальше? (Нет.)
Есть целая наука, которая изучает прямые и кривые
линии. Она называется аналитическая
геометрия.
Это очень интересная и сложная наука, вы
познакомитесь с ней в старших классах.
Оказывается, про некоторые кривые линии можно
сказать, как они пойдут дальше, и с некоторыми из
них мы познакомимся уже очень скоро.
А сейчас попробуйте ответить на такой вопрос.
Упражнение 5
Задание: как вы думаете, линии 4 и 5
встретятся когда-нибудь? Можно ли найти место их
встречи?
В этом упражнении можно дать сюжет:
Карандаш побежал по линии 4, а Резинка – по линии
5. Встретятся ли они, если побегут так:

– Где они встретятся? Куда должна
подойти Линейка, чтобы не разминуться с ними в
стране Геометрии?
Чертеж на доске достраивается
пунктиром, на месте встречи ставится яркая точка.
Учитель говорит: “Эти две прямые
встретятся в этой точке, – а математики говорят:
пересекутся.”
Упражнение 6
Задание: какие еще две прямые
пересекутся? (1 и 4, 4 и 5, 5 и 7, 1 и 7, 9 и 7 и т. д.).
Это упражнение очень важно для
осознания понятия бесконечности прямой: обычно
дети его не понимают, а запоминают. С другой
стороны, это упражнение закладывает первый
камень в основу изучения стереометрии – оно
является пропедевтическим для формирования
умения находить точки пересечения ребер
многогранников, прямой и плоскости и т. д.
Упражнение 7
Задание: как вы думаете, пересекаются
ли прямые 9 и 5? Что можно сказать о двух
вертикальных прямых? Могут ли они встретиться? (Нет.)
– Найдите на рисунке еще пару прямых,
которые никогда не встретятся. Как они
называются? (Горизонтальные: 8 и 7.)
Упражнение 8
Задание: посмотрите внимательно на
рисунок и скажите: на какие три группы мы
разделили прямые по направлению их “хода”? (Горизонтальные,
вертикальные и наклонные.) А на какие две
группы их можно разбить по возможности встречи? (На
встречающиеся и невстречающиеся.)
– Математики говорят: пересекающиеся
и непересекающиеся.
– Какие две прямые никогда не встретятся (не
пересекутся)? (Две вертикальные прямые, две
горизонтальные прямые.) Найдите в классе пары
прямых, которые никогда не пересекутся, как бы
далеко их ни продолжать.
Дети находят пары горизонтальных и
вертикальных прямых. Если кто-нибудь покажет
скрещивающиеся прямые (например, вертикальную в
начале класса и горизонтальную в конце), учитель
отмечает, что эти прямые тоже никогда не
встретятся, но их нельзя обе назвать
горизонтальными или вертикальными. Это другая
группа прямых, и их название – скрещивающиеся.
Упражнение 9
Задание: возьмите чистый лист.
Поставьте на нем точку (проколите). Начертите
кривую так, чтобы она прошла через эту точку.
Можно ли начертить еще одну кривую так, чтобы она
прошла через ту же точку? Еще одну?
Дети рисуют несколько кривых (лучше
разным цветом), проходящих через данную точку.
Аналогичная работа проводится на доске.
– Сколько кривых можно провести через
одну точку? (Сколько угодно.)
Упражнение 10
Задание: возьмите другой лист .
– Поставьте точку в любом месте
(проколите).
– Согните лист так, чтобы линия сгиба прошла
через эту точку. Проведите пальцем по линии
сгиба. Какая линия? (Прямая.)
– Разверните лист. Какую линию мы провели через
точку? (Прямую.) Можно ли по-другому согнуть
лист, но так, чтобы линия сгиба опять прошла через
ту же точку? Сделайте это. Разверните лист.
Сколько прямых вы провели через одну точку? (Две.)
Важно следить, чтобы дети каждый раз разворачивали
лист.
После того как ученики построят третью и
четвертую прямые, учитель предлагает им ответить
на вопрос: “Сколько прямых можно провести
через одну точку?” (Сколько угодно, множество.)
Упражнение 11
Задание: возьмите новый лист .
Поставьте на нем две точки в любых
местах.
Попробуйте согнуть лист так, чтобы линия сгиба
прошла через обе точки. Проведите пальцем по
сгибу. Какая получилась линия? (Прямая.)
Разверните лист. Какую линию мы провели через две
точки? (Прямую.)
– А теперь попробуйте согнуть лист по-другому, но
так, чтобы линия сгиба прошла снова через те же
две точки.
Учитель дает детям время убедиться в
том, что сделать это невозможно.
– Можно ли провести вторую прямую
линию через те же самые две точки? (Нет.)
Упражнение 12
Задание: возьмите чистый лист.
Поставьте на нем две точки. Проведите кривую
линию так, чтобы она прошла через эти точки.
– А теперь вторую кривую, третью,
четвертую… Получается? (Да.) А еще можно? (Да.)
Сколько кривых можно провести через две точки? (Сколько
угодно.)
Затем подводится итог:
– Сколько кривых можно провести через
одну точку? (Множество.) Прямых? (Множество.)
– Сколько кривых можно провести через две точки?
(Множество.) А прямых? (Только одну.)
Упражнение 13
Материал: кусочки шнура.
Способ выполнения: из кусочков шнура
(40–50 см) дети моделируют по заданию учителя
разные отношения между прямыми на плоскости.
На каждой парте два куска веревки или шнура. (Шнур
должен быть мягким, типа бельевой веревки,
сохраняющим ту форму, которую ему придадут дети.)
– Сделайте модель кривой.
– Сделайте модель прямой.
– Сделайте горизонтальную прямую.
– Сделайте вертикальную прямую.
– Сделайте наклонную прямую.
– Постройте две прямые так, чтобы они не
встретились (не пересеклись).
– Можно ли построить две прямые так, чтобы у них
были две общие точки? (Нет.)
– Можно ли построить две кривые так, чтобы у них
были две точки пересечения? (Да.) Сделайте
такое построение из своих шнуров.
– Поставьте мелом две точки на парте. Проведите
через каждую из них по одной прямой так, чтобы
они:
1) не встретились никогда;
2) чтобы точка их встречи была видна уже сейчас.
Как их тогда можно будет назвать? (Пересекающиеся.);
3) так, чтобы точка встречи не была видна, но чтобы
ее можно было найти, продолжив эти прямые (прямые
моделируются из шнура).
Либо все эти задания, либо их часть
можно параллельно моделировать на фланелеграфе,
используя вместо шнура узкие полоски цветной
бумаги. Такая иллюстрация наглядней, чем чертеж,
и занимает меньше времени. Кроме того, делать
чертеж приходится самому учителю – дети пока с
инструментами не справляются, а собирать модель
отношений на фланелеграфе они могут сами, что
очень им нравится. Шнуры можно растягивать по
полу кабинета.
Примечание: если класс слабый,
материал данного урока можно разбить на два
урока (задания 1–8 и задания 9–13). Оставшееся
время посвящается работе с мозаикой и тетрадью:
– Сложи узор по заданию (варианты см. в тетради).
– Найдите ошибку в узоре (учитель составляет на
фланелеграфе узор из полного набора мозаики с
нарушением симметрии в двух-трех местах; дети
должны найти и исправить ошибку).
Задания 72–78 используются для
индивидуальной работы в тетради.
Задание 76. Сложи из палочек цифры:
УРОК 13
Тема: “Линии на плоскости. Ломаная.
Отрезок”.
Цели: Закрепить представление о
кривой и прямой; познакомить с новым типом линий
– ломаной; познакомить с понятием “отрезок”.
Упражнение 1
Материал: рисунок на доске.
Задание: на данном рисунке найдите и
покажите:
1) две пересекающиеся прямые (разные
варианты);
2) две прямые, которые никогда не пересекутся (“Как
они называются?”);
3) кривую;
4) линию, которая встречается нам впервые (дети
должны показать ломаную линию, названия которой
они не знают).
Учитель сообщает детям название и
предлагает подумать, на какую линию – прямую или
кривую – будет похожа ломаная линия по своим
свойствам.
Упражнение 2
Материал: кусочки шнура.
Задание: у вас на партах есть шнурок и
палочки. Как вы думаете, что удачнее поможет нам
построить модель ломаной?
Пробуя оба варианта, дети видят, что
шнурок удобнее для моделирования кривой, а
палочки – для ломаной. Из палочек строят
произвольную модель ломаной. Один из вариантов
моделируют на фланелеграфе. Не стоит
использовать для этой работы проволоку. Опыт
показывает, что дети часто получают
пространственные модели кривых и ломаных, что
создает для учителя определенные
теоретико-понятийные сложности, перегружающие
урок, хотя разницу между плоской кривой и
пространственной дети улавливают практически
сразу.
Упражнение 3
Задание: поставьте на парте мелом
точку (можно использовать маленький
пластилиновый шарик). Проведите через нее прямую.
Чем лучше воспользоваться? (Шнуром – это
быстрее.) Сколько прямых можно провести через
одну точку? (Сколько угодно.)
– Проведите через эту точку кривую.
Чем лучше воспользоваться? (Шнуром.) Сколько
кривых можно провести через эту точку? (Множество.)
– Проведите через эту точку ломаную. Чем лучше
воспользоваться? (Палочками.) Можно провести
через ту же точку еще одну ломаную? (Можно.)
Сколько ломаных можно провести через точку? (Сколько
угодно.)
Упражнение 4
Задание: поставьте на парте мелом
вторую точку. Дети проводят аналогичную работу,
делая вывод о количестве прямых, кривых и
ломаных, проведенных через две точки.
Учитель помогает детям сделать
обощение: следовательно, по своим свойствам
ломаная ближе к кривой, чем к прямой.
Упражнение 5
Материал: рисунки персонажей, рисунок
на доске.
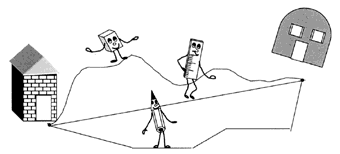
Способ выполнения: учитель предлагает
детям сказочную ситуацию:
– Однажды Карандаш, Линейка и Резинка
отправились в гости к Лесному Гному. Вышли они на
крылечко своего дома и заспорили, какой дорогой
идти. Заспорили так, что поссорились и каждый
пошел своей дорогой. Кто из них раньше доберется
до домика Гнома?
Чтобы не давать определение понятию
“расстояние между двумя точками”, учитель
употребляет слово путь:
– Какой же путь между двумя точками
самый короткий? (По прямой.)
Упражнение 6
Способ выполнения: учитель организует
беседу:
– Посмотрите на рисунок: видно ли, где
Линейка начала свой путь и где закончила? (Да.)
Что стоит на моем рисунке в начале пути? (Точка.)
А в конце? (Точка.) Значит, путь, по которому
шла Линейка, имеет начало и конец. Но мы с вами
говорили, что прямая бесконечна. Можно ли
сказать, что между этими двумя точками
поместилась целая прямая? (Нет.) Математики
говорят, что это часть прямой между двумя
точками. Такой кусочек прямой, заключенный
между двумя точками, называется отрезок.
Слово “отрезок” как бы говорит: “Меня
отрезали от прямой”.
– В жизни мы встречаемся именно с
отрезками – ведь начертить бесконечную прямую
невозможно, для этого нужно бесконечно много
места. Поэтому бесконечную прямую мы можем
только вообразить, а вот отрезок, у которого есть
концы, вполне можно изобразить.
Найдите отрезки на этом рисунке:
Упражнение 7
Материал: рисунок к упр. 1.
Вопрос: о какой из известных вам линий
можно сказать, что она составлена из отрезков? (О
ломаной.) Сколько отрезков на этой ломаной? (Пять.)
Упражнение 8
Материал: рисунок на доске или модель
на фланелеграфе.
Задание: отрезки, как и прямые, бывают
вертикальные, горизонтальные и наклонные, бывают
пересекающиеся и непересекающиеся.
– Найдите на флажке вертикальные и
горизонтальные отрезки.
– Какие отрезки пересекаются (имеют общие точки)?
– Какие отрезки не имеют общих точек (не
пересекаются)?
Флажки составлены на фланелеграфе:
и
.
Упражнение 9
Материал: счетные палочки.
Задание: по заданию учителя дети
составляют из палочек буквы Г, П, А, Н; определяют
в них количество отрезков, их виды, пересечения.
Работа дублируется на фланелеграфе.
Особое внимание обращается на определение точек
пересечения. В данном случае это скорее точка
касания, но в математике для отрезков такого
термина нет, эти точки тоже называются точками
пересечения. Дети должны понять, что термины
“общие точки” и “точки пересечения” –
синонимы. Все эти точки учитель показывает на
фланелеграфе указкой, а ученики в своих моделях и
на парте – пальцем.
Оставшаяся часть урока посвящена
работе с тетрадью и геометрической мозаикой.
Используют задания 79–90.
Задание 89*. Найди и отметь красным
цветом точки пересечения фигур.
УРОК 14
Тема: “Отрезок. Длина отрезка.
Отрезок как элемент фигуры”.
Цели: Уточнить представление детей
об отрезке; учить измерять длину отрезка и
строить отрезок заданной длины.
Упражнение 1
Материал: рисунок на доске.
Задание: на этом рисунке найдите
лишнюю фигуру.
В процессе обсуждения уточняются
представления детей о прямой, кривой, ломаной,
горизонтальной и вертикальной прямых. Дети
выделяют отрезок, имеющий два конца в отличие от
бесконечных линий. Можно предложить детям такой
образ:
– Пошел человечек по прямой, думает:
“Дойду до конца и отдохну…”
Скоро ли он сможет отдохнуть?
Упражнение 2
Материал: рисунок на доске.
Задание: посмотрите на эти две фигуры.
Можно ли их назвать отрезками? (Учитель
показывает еще две фигуры, ранее прикрытые
занавесками.)
– У этих фигур тоже два конца (они тоже
ограничены). Можно ли назвать их отрезками?
В процессе обсуждения дети с помощью
учителя уточняют определение отрезка: это часть
прямой линии, поэтому он должен быть прямым.
Упражнение 3
Материал: рисунок на доске.
Задание: найдите отрезки на рисунке.
Упражнение 4
Материал: модели объемных фигур.
Способ выполнения: учитель показывает
детям куб.
– Как это назвать? (Кубик, куб.)
– Найдите отрезки на кубе. Сколько их?
– Эти отрезки называются “ребра”.
(Пересчет ребер куба сопровождается
скольжением пальца по ребру от вершины до
вершины.)
Упражнение 5
Задание: учитель показывает детям
цилиндр и предлагает найти отрезки на нем. (Их
нет. На цилиндре есть только кривые. Дети
убеждаются в этом, обводя пальцем границу
верхнего и нижнего оснований.)
Упражнение 6
Задание: что представляет собой
боковая сторона куба? Его “дно”? Его
“крыша”? (Квадрат.) Сколько отрезков
ограничивают квадрат? (Четыре.) Что можно
сказать об их длинах? (Они одинаковые.)
Учитель предлагает детям проверить
это измерением длин сторон кубов.
Упражнение 7
Начерти отрезок больше данного
зеленым карандашом, меньше данного – синим.
Далее выполняются задания в тетради на
с. 38–39. Можно сделать аппликацию “Собачка в
будке”, выполнив собачку в стиле оригами.
Учитель показывает, как сделать
собачку.
С помощью рамки дети рисуют и
раскрашивают будку для собачки на листе бумаги.
Клеящим карандашом прикрепляют собачку и
дорисовывают фломастером блюдце с косточкой.
Композицию “Кошка с котятами”
можно выполнить на уроке труда.
УРОК 15
Тема: “Квадрат. Диагональ
квадрата”.
Цели: знакомство с диагональю
квадрата; конструирование из частей квадрата;
развитие конструктивных умений.
Упражнение 1
Материал: рисунок на доске.
Задание: найдите все квадраты на
каждом рисунке.
Упражнение 2
Материал: полоски бумаги шириной 10–12
см.
Задание: сделайте квадрат из своей
полоски. Оторвите лишнее.
Упражнение 3
Способ выполнения: учитель предлагает
детям рассмотреть свою модель и сообщает, что
линия сгиба, разбившая квадрат на две части,
называется диагональ. На какие две части
разбит квадрат? (Равные.) Почему вы думаете,
что они равные? (Они совпали, когда квадрат
согнули.) Как называется эта геометрическая
фигура? (Треугольник.)
Упражнение 4
Задание: разверните свой квадрат и
снова сложите его пополам, но в другом
направлении. На какие две фигуры разбился
квадрат диагональю? (На треугольники.) Какие
они между собой? (Равные.)
Упражнение 5
Задание: разверните свой квадрат. На
сколько частей он разбит линиями сгиба? (На
четыре.) Какими фигурами являются все эти
части? (Треугольниками.) Продолжите мою фразу:
диагональ разбивает квадрат…(на два равных
треугольника);
Квадрат имеет… (сколько диагоналей?) (две
диагонали).
Диагонали квадрата имеют… (какие
длины?) (равные). Проверьте это измерением.
Упражнение 6
Задание: разорвите квадрат очень
аккуратно по диагоналям. Какие между собой все
треугольники? Как проверить, будут ли все
треугольники равны между собой? (Наложить их
один на другой.)
Упражнение 7
Задание: вспомните, какая фигура была у
нас в начале? (Квадрат.) Сложите из этих
треугольников квадрат.
Упражнение 8
Задание: сложите из них же
прямоугольник.
Упражнение 9
Задание: сложите из них треугольник.
В этом упражнении предлагаются
дополнительные задания: сложи указанные
конструкции из 4 треугольников.
Упражнение 10
Материал: образец аппликации
“Бабочка”, цветные основы для аппликации,
кусочки цветной бумаги, клей.
Задание: посмотрите на аппликацию у
меня в руках. Что это? (Бабочка.) Какие детали
этой бабочки у нас уже есть? Какие надо добавить? (Есть
треугольники для крыльев. Нужны круглая головка
и туловище – полоска.)
Дети собирают “Бабочку” на листе
цветной бумаги из четырех треугольников, добавив
головку и туловище (при нехватке времени их можно
дорисовать фломастером). Детали крепятся клеящим
карандашом. Усики и украшения на крыльях
дорисовывают фломастером.
Примечание: упражнения 7–9
проверяются на фланелеграфе или магнитной доске
учителем. Каждый ученик собирает фигуру у себя на
парте. Учитель должен быстро реагировать на
поднятую руку, чтобы похвалить справившегося и
быстро смешать его построение, не давая соседям
скопировать. Трудность такой работы, как и работы
с мозаикой, в том, что каждый ученик должен
работать в своем индивидуальном темпе,
“дозревая” до решения конструктивной задачи
самостоятельно. В связи с этим учителю надо
готовить на доске серию из 4–8 заданий-рисунков,
чтобы не тормозить работу успевающих.
УРОК 3
Тема: “Геометрические фигуры”
(повторение)
Цель: Повторение понятий
“точка”, “отрезок”, “прямая”,
“ломаная”, “кривая”. Закрепление умения
получить квадрат загибанием “от угла” из
полосы и полного листа. Из него делают
“Рыбку”, “Лодочку”, “Котенка”,
“Цветок”.
Детям предлагают следующие задания:
1) на классификацию: “Найди лишнюю”
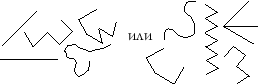
2) на распознавание: “Найди все
квадраты”
3) на построение из отдельных частей:
“Сложи квадрат”
;
4) на смекалку и развитие логического
мышления: “Придумай еще один предмет и заполни
таблицу так, чтобы ни в ряду, ни в столбике они не
повторялись”.
Используя рамку в качестве шаблона для
деталей аппликации или используя способ
разрывания квадрата по осям симметрии, дети
делают себе узорные закладки для учебников.
Прямоугольники для закладок получают, складывая
стандартный лист вчетверо и разрезая его по
сгибам.
Для организации индивидуальной работы
используют задания в тетради. Можно предложить
детям итоговый тест в конце тетради № 1.
Тест по итогам первого полугодия
Оставшиеся задания из тетради дети
могут выполнять по желанию в свободное время или
на каникулах. Учителю следует поощрять желание
детей выполнить побольше заданий в тетради
самостоятельно.
III ЧЕТВЕРТЬ
Если в школе есть наборы
конструкторов, то первые два урока после зимних
каникул проводят с конструкторами (см. блок
“Работа с конструктором”). Если их нет, то
первый урок III четверти строится на материале
последнего урока первого полугодия (повторение),
а затем сразу переходим к уроку 18 данного
полугодия. В этом полугодии используется тетрадь
№ 2.
УРОК 16
Тема: “Конструирование букв”.
Цели: познакомить детей с деталями
конструктора и инструментами; научить собирать
буквы, ориентируясь на их графическую модель;
развивать конструктивные умения.
См. урок 1 раздела “Работа с конструктором”.
УРОК 17
Тема: “Конструирование лесенки”.
Цели: познакомить детей с
простейшими способами соединения деталей (встык
с накладкой и внахлест); развивать
конструктивное мышление.
См. урок 2 раздела “Работа с конструктором”.
УРОК 18
Тема: “Окружность и круг”.
Цели: познакомить с понятиями
“окружность” и “круг”. Учить
пользоваться циркулем для вычерчивания
окружности.
Примечание:
На этом уроке дети знакомятся с новым
чертежным инструментом – циркулем. Удобнее
всего приобрести комплект циркулей для класса,
так как дети часто забывают их дома. Поскольку
циркули будут нужны постоянно, то их следует
приобретать хорошего качества – металлические,
с удобным креплением стержня и иглы.
Циркуль можно хранить в папке для работ. Для
урока “Наглядная геометрия” надо иметь
специальную папку с завязками для хранения
работ, рамки, карандаша, резинки, ножниц, бумаги. В
дальнейшем сюда добавляют два угольника (45° и 30°)
и линейку. Сюда же дети складывают свои поделки
(если не дарят их кому-то). Такая папка в конце
года представляет для учителя своеобразный итог
курса – по качеству и количеству работ можно
судить о степени успешности ученика в изучении
предмета, об уровне сформированности
практических умений и навыков.
Упражнение 1
Материал: рисунок на доске, бумага,
циркули, металлическая крышка для
консервирования с резинкой.
Способ выполнения: учитель предлагает
игру-путешествие в страну Геометрию.
– Сегодня мы снова отправимся в
страну Геометрию с нашими старыми знакомыми –
Линейкой, Карандашом и Резинкой. Они идут по
улице и видят, что жители Геометрии
рассматривают на стене одного дома такую
картинку:
– Ну, это я знаю, – сказал Карандаш.
– Это кривые.
– Красивый рисунок, хороший мастер его делал,
– говорит Линейка, – смотри, Карандаш, здесь есть
одна кривая удивительной формы: вся такая
одинаково плавная, гладкая…
– Про какую кривую говорит Линейка? Каким
инструментом можно начертить такую правильную,
всю одинаково плавную кривую? (Дети называют
циркуль. Если не называют, сюжет знакомит их с
этим инструментом.)
– Кто же нарисовал эту замечательную кривую?
– спросил Карандаш.
– Это мастер Циркуль, – ответили ему жители
Геометрии.
Познакомились наши друзья с Циркулем. Спрашивает
Линейка:
– Как вам удается такие плавные линии
рисовать?
– А вот так, – говорит Циркуль. – Встаю на
острую ножку и кручусь на ней, как балерина. Р-раз!
Учитель берет большой циркуль и быстро
рисует на доске окружность.
– О, какая красивая линия! – говорит
Карандаш. – Что это?
– Это окружность, – говорит Циркуль. –
Линию, которую рисует мой грифель, называют
словом окружность. Если вы начертите
окружность на бумаге и вырежете ее, то эта линия
останется на границе выреза. А то, что останется у
вас в руках, называется круг. (Учитель
показывает бумажный круг.) Окружность – это
граница круга.
Пока Циркуль объяснял Линейке, что
такое окружность, Карандаш наклонился и что-то
поднял с
тротуара.
– Смотрите! – закричал он. – У меня есть и
окружность, и круг.
– И показал всем вот это (учитель показывает
детям металлическую крышку для консервирования
и вынимает из нее круглую резинку).
– Ребята, что здесь окружность, а что – круг?
– Я знаю, как легко запомнить, чем отличается
окружность от круга, – говорит Карандаш. –
Резинка, иди сюда, прыгай!
Карандаш подставил Резинке то, что держал в одной
руке. Резинка весело прыгнула. Но когда Карандаш
предложил ей прыгнуть сквозь предмет в другой
руке, Резинка обиделась и сказала:
– Ты что, Карандаш, думаешь, ты один запомнил
разницу между окружностью и кругом?
– Сквозь что Резинка прыгнула? (Сквозь
окружность. Сквозь круг прыгнуть нельзя: он
сплошной.)
– А что вы еще умеете, мастер Циркуль? –
спросила Линейка.
– О, я могу многое, – ответил Циркуль,
– смотрите!
Учитель показывает несколько красивых
орнаментов и аппликаций, выполненных с помощью
циркуля. Детям обычно эти рисунки очень нравятся,
и они с охотой работают циркулем.
– Ой, как сложно! – говорит
Карандаш. – Я, наверное, не смогу так.
– Это совсем не сложно, – говорит мастер
Циркуль, – и я ребят этому научу очень быстро.
Самое главное – научиться правильно держать
меня в руках.
Упражнение 2
Способ выполнения: учитель предлагает
детям взять в руки циркуль, рассмотреть его,
найти и потрогать пальцем острие, на котором
циркуль “крутится”, найти “хвостик”,
подвигать “ноги”.
Затем беседа может строиться так:
– Какая ножка циркуля стоит в
центре окружности – игла или грифель?
Центр учитель отмечает и показывает на
чертеже.
– Какой ножкой циркуль рисует? (Грифелем.)
– Ноги циркуля двигаются. Что надо сделать,
чтобы нарисовать большую окружность, – развести
их или сдвинуть ближе?
– Попробуйте нарисовать самую большую
окружность, какая поместится на вашем листе.
– А теперь самую маленькую, какая у вас только
получится (на том же листе в любом месте, можно
внутри большой).
Цель этих упражнений – дать детям
возможность почувствовать инструмент в руках,
примериться к его “степеням свободы”.
Если окружность не получается, лист
переворачивают и чертят ее с другой стороны
заново. Детям надо сразу дать несколько листов,
чтобы они не занимались стиранием неудачных
вариантов, а набивали руку, повторяя попытки.
Циркуль – сложный инструмент, им плохо владеют
даже третьеклассники. Обучая детей работе с
циркулем, учитель обращает внимание на то, как
дети держат его в руках (за хвостик, а не за ногу!),
учит вращать циркуль, а не лист бумаги вокруг
циркуля. На первых порах удобно подкладывать под
лист бумаги старую газету, чтобы игла циркуля не
соскальзывала.
Упражнение 3
Материал: образец аппликации, циркуль,
цветная бумага для основы, клей, ножницы.
Задание: дети делают аппликацию
“Снеговик” на листе цветной бумаги.
Ведро, метлу, нос, пуговицы, глаза
дорисовывают фломастером. Ведро можно вырезать
из бумаги. Аппликация крепится к листу клеящим
карандашом.
Для индивидуальной работы используют
задания 1–5 в тетради № 2. Рисунок задания 5
“Кукла” желательно дорисовывать с циркулем.
Если учитель проводил уроки 16 и 17 с
конструктором, то, возможно, эти задания дети уже
выполнили.
Задание 5. Нарисуй вторую половину
куклы симметрично данной. Используй рамку.
УРОК 19
Тема: “Диаметр круга и его свойства”.
Цели: познакомить с понятием
“диаметр”; продолжить работу над
формированием умения работать с циркулем;
развивать конструктивные умения.
Упражнение 1
Материал: циркуль, бумага, ножницы.
Задание: начертите окружность.
Вырежьте круг, отметив центр (проколите его
грифелем). Согните круг так, чтобы центр оказался
на линии сгиба. Круг разделился на две части.
Какие они? (Равные.) Почему вы думаете, что они
равные? (Они совмещаются.)
Упражнение 2
Задание: проведите пальцем по линии
сгиба. Какая она? (Прямая.) Есть ли у нее начало
и конец? (Есть.) Как она называется? (Отрезок.)
– А теперь посмотрите, я построю еще
несколько отрезков в этом круге: тоже от края до
края круга. Чем отличается первый отрезок от
всех?
Учитель делает в своем круге еще
несколько сгибов параллельно диаметру:
Если дети предлагают воспользоваться
линейкой, учитель должен отклонить этот вариант
и предложить воспользоваться циркулем.
– А чем еще интересен этот отрезок?
Чем он еще отличается от всех других? (Он
проходит через центр.)
Подводя итог проведенной работы,
учитель сообщает, что у этого отрезка, который
проходит от края круга до другого края через
центр, есть свое название – диаметр. Из
всех отрезков, соединяющих два противоположных
края круга, диаметр – самый длинный.
Упражнение 3
Задание: можно ли в этом круге провести
другой диаметр? Как должен пройти диаметр? (Через
центр.) Проведите его сгибанием.
– Возьмите циркуль и сравните длины
этих двух диаметров. Какие они? (Равные.)
– Можно ли провести еще один диаметр? Как он
должен пройти? Проведите его сгибанием. Сравните
их длины.
Дети проводят сгибанием несколько
диаметров в круге и с помощью циркуля убеждаются,
что они имеют равные длины.
Учитель подводит итог работы:
– Сколько диаметров можно провести
в круге? (Сколько угодно.) Какие по длине все
диаметры в круге? (Равные.) На какие части
диаметр разбивает круг? (На две равные половины.)
Эти половины назовем словом полукруг.
Упражнение 4
Материал: образец аппликации, циркуль,
ножницы, цветная бумага, клей.
Задание: посмотрите на эту аппликацию.
Из каких деталей сделана божья коровка? (Из
большого полукруга и маленького круга.)
Ориентируясь на образец, дети делают
детали аппликации, причем один ученик чертит
циркулем большой круг и делит его пополам – себе
и соседу по парте, а второй делает два маленьких
круга, используя рамку. Ветка, черные крапинки,
усики, ножки и листочки дорисовываются
фломастером. Детали крепятся на лист клеящим
карандашом.
Упражнение 5
Материал: игра “Сложи круг”.
Способ выполнения: урок можно
завершить игрой “Сложи круг” (из разных
деталей складываем круг). Ее можно проводить
фронтально – на фланелеграфе, но полезнее –
индивидуально на партах. Для этого учителю надо
иметь 15–20 наборов с вариантами сборки (в
конвертах). Дети, справившиеся с заданием,
меняются конвертами. Детали должны различаться
по цвету и быть пронумерованы с обратной стороны
(во избежание путаницы).
Для индивидуальной работы
используются задания 1–26 в тетради.
УРОК 20
Тема: “Радиус круга и его свойства”.
Цели: познакомить с понятием
“радиус”; учить работать с циркулем; учить
составлять симметричный орнамент в круге.
Упражнение 1
Материал: лист бумаги, циркуль,
ножницы.
Задание: начертите окружность.
Отложите циркуль, не двигая его ноги. Вырежьте
фигуру. Проведите в ней диаметр сгибанием. Чем
интересен диаметр? (Он проходит через центр.)
Упражнение 2
Материал: рисунок на доске.
Задание: выберите на рисунке на доске
те окружности, в которых проведен диаметр.
– Сколько диаметров можно провести
в окружности? (Сколько угодно.) Какие они все
по длине? (Равные.)
Упражнение 3
Задание: согните ваш круг по диаметру.
Как называется фигура, которую вы получили? (Полукруг.)
А теперь сложите полукруг пополам. Где оказался
центр круга? Покажите его пальцем. Можно ли
назвать треугольником ту фигуру, которую вы
получили?
Этот вопрос обычно вызывает
оживленное обсуждение: есть три угла, три
стороны. Учитель помогает детям осознать тот
факт, что этих условий недостаточно, стороны
должны быть прямые.
– Проведите пальцем по этой стороне.
Какая она? (Прямая.)
– Теперь по этой стороне. Какая она? (Прямая.)
– Теперь по этой стороне. Какая она?
(Кривая.)
– Как вы думаете, может ли быть у
треугольника кривая сторона? (Нет.) Можно ли
назвать эту фигуру треугольником? (Нет.)
Верно, у этой фигуры есть свое название – сектор.
Сектор – это часть круга. Он похож на
треугольник, но одна сторона у него кривая. А
теперь посмотрите на рисунок. Какая из этих фигур
– сектор, а какая – треугольник?
(Фигуры 3 и 5 – секторы, 2 и 7 –
треугольники; остальные фигуры нельзя назвать ни
сектором, ни треугольником.)
Обращаем внимание детей на фигуру 4 –
она похожа на сектор, но не выпуклая (дети
говорят: “Кривая ушла внутрь”).
Это упражнение не является обязательным, оно
пропедевтическое, то есть не требует заучивания
понятий сектор, вогнутость, выпуклость и т. д.
Его цель – дать образ треугольника в сравнении.
Все эти фигуры похожи на треугольники по
признаку “количество сторон и углов”.
Выполняя это упражнение, дети учатся
анализировать не только количественные
характеристики фигуры, но и качественные – форму
углов и сторон.
Упражнение 4
Задание: разверните ваш круг.
Проведите пальцем от центра круга до его края по
сгибу. Этот отрезок называют словом радиус.
– Сколько радиусов на вашем круге? (Четыре.)
Какие по длине все радиусы? Проверьте с
помощью циркуля. (Все одинаковые.)
Упражнение 5
Задание: можно еще провести в этом
круге радиус? (Учитель помогает учащимся
провести несколько радиусов на доске.)
Если дети затрудняются с ответом,
можно просто предложить: “Соедините центр с
этой точкой” (учитель ставит на окружности
точку красным мелом).
– Будет ли этот отрезок радиусом?
Дети проверяют размеры нового отрезка,
повторяют определение: это отрезок,
соединяющий центр круга с его краем. И делают
вывод, что это тоже радиус.
Аналогично строится еще несколько
радиусов: детей надо подвести к выводу, что
радиусов можно провести сколько угодно, как и
диаметров, и что длины всех радиусов равны между
собой.
Упражнение 6
Задание: найдите на рисунке на доске
диаметр круга. Покажите диаметр вашего круга. (Учитель
обводит свой диаметр красным мелом).
Упражнение 7
Материал: образцы симметричных
орнаментов в круге, рамка, циркуль, ножницы.
Способ выполнения: учитель показывает
несколько орнаментов в круге, выполненных с
помощью рамки. Первый вариант орнамента дети
выполняют в той модели круга, что уже есть у них в
руках. Так как в ней проведены две центральные
оси, многие дети интуитивно располагают
орнамент, ориентируясь на них (располагать
образцы на доске следует так, чтобы
необходимость проведения центральных осей не
сразу бросалась в глаза).
Наблюдая за работой детей, учитель
отмечает, кто из них почувствовал принцип
составления симметричного орнамента.
На необходимость предварительного проведения
центральных осей учитель обращает внимание
детей при анализе готовых работ, отмечает, что
узор получился красивее (ровнее) у тех, кто это
заметил сам. Так как работа с помощью рамки идет
быстро, дети успевают выполнить еще один
орнамент, составив его самостоятельно. Работу
можно закончить дома.
Задания 28–30 используют для
индивидуальной работы в тетрадях.
Рассмотри рисунок “Медвежонок”.
Сколько кружков тебе понадобится? 6 7 8 9
C помощью рамки нарисуй на цветной бумаге
маленькие круги. Измерь циркулем радиус большого
круга и начерти его на цветной бумаге. Вырежи все
детали и наклей на рисунок.
УРОК 21
Тема: “Окружность и ее элементы.
Взаимное расположение окружностей”.
Цели: закрепить знания о диаметре и
радиусе; познакомить с понятием “точки
пересечения окружностей”; учить составлять
простой орнамент с помощью циркуля.
Упражнение 1
Материал: рисунок на доске.
Задание: дети могут предлагать разные
варианты, в зависимости от этого учитель строит
беседу, в результате которой приходят к
следующим выводам:
а) если вторую окружность рисовать
внутри первой, ее радиус должен быть меньше (рис.
1);
б) если снаружи – радиус любой (рис.
2);
в) окружности, имеющие общий центр
и не имеющие общих точек (не пересекающиеся),
называются концентрическими (рис. 3).
Если дети начертили концентрические
окружности, учитель просто сообщает название;
если не начертили – показывает такое
расположение окружностей сам.
Упражнение 2
Задание: попробуйте нарисовать вторую
окружность так, чтобы у них было две точки
пересечения.
Дети чертят вторую окружность и
отмечают точки пересечения двух окружностей
(рис. 2).
Упражнение 3
Задание: можно ли начертить две
окружности так, чтобы у них было три точки
пересечения? (Нет.) Одна? (Да.)
Работа выполняется на доске.
Примечание: одной точкой
пересечения можно считать точку касания.
Упражнение 4
Материал: образцы орнаментов.
Способ выполнения: учитель показывает
простой орнамент и предлагает детям сосчитать,
сколько в нем окружностей, где их центры.
Орнамент должен быть выполнен на
достаточно большом листе и раскрашен либо
акварелью, либо негустой гуашью, чтобы можно было
различить основные линии.
Дальше, если класс сильный, учитель либо может
предложить детям “расшифровать” орнамент,
то есть восстановить порядок его построения на
доске, а затем предложить выполнить его
самостоятельно, либо объясняет детям, как
построен орнамент, и класс строит его вместе с
учителем пошаговым методом.
Примечание: орнамент
раскрашивают фломастерами или карандашами. Дома
можно предложить детям составить орнамент
самостоятельно. Некоторые дети очень быстро
понимают принципы составления таких орнаментов
и выполняют дома красивые композиции.
На следующих уроках можно ориентироваться на
работы детей, предлагать остальным
самостоятельно расшифровать их или обогатить
дополнительными деталями. На с. 25 и 35 тетради есть
варианты простых орнаментов, нарисованных с
помощью циркуля.
Задания 31–44 используют для
индивидуальной работы в тетради.
УРОК 22
Тема: “Симметричные фигуры”.
Цели: познакомить с понятием
“симметричная фигура” (осесимметричная);
научить распознавать эти фигуры и практически
проверять их на симметричность.
Упражнение 1
Материал: елочные фонарики из бумаги
симметричной структуры.
Способ выполнения: учитель показывает
детям игрушку (фонарик), сделанную из трех или
четырех кругов разного цвета (круги перегнуты по
диаметру и склеены).
Упражнение 2
Материал: рисунок на доске.
Задание: выберите на рисунке
геометрические фигуры, из которых можно было бы
сделать фонарик по такому же принципу.
Дети выбирают соответствующие фигуры,
при этом учитель предлагает им показать рукой
линию сгиба. Поскольку из некоторых фигур можно
сделать два разных фонарика, все случаи
обсуждаются, точкой помечается место, куда
приклеивается ниточка.
Учитель должен иметь бумажные модели всех фигур,
чтобы дети могли практически проверить верность
своей догадки. Например, некоторые дети не сразу
понимают, что такое “перегибы” квадрата и
равностороннего шестиугольника, и делают
фонарики одинаковой формы.
Особенный интерес вызывают
прямоугольник и параллелограмм, которые не
являются симметричными относительно диагоналей.
Здесь обычно дети ошибаются, эти случаи надо
проверить практически.
Параллелограмм вообще не является
осесимметричной фигурой, а у прямоугольника –
две оси симметрии.
Затем учитель стирает с доски все
несимметричные фигуры и говорит детям, что те
фигуры, которые они выбрали, называют симметричными.
Линию, которая делит такую фигуру на две
совпадающие при перегибе части, называют осью
симметрии. Эта линия делит фигуру так, что
при перегибе обе половины совпадают.
Здесь можно привести разные примеры из
окружающей жизни: лист дерева, лицо человека,
правая и левая руки и т. д.
Учитель показывает несколько орнаментов: в
круге, в квадрате – и предлагает детям
определить, будут ли они симметричными
относительно оси.
– Многие вещи мы считаем красивыми именно
потому, что они симметричны, например снежинку. (Учитель
показывает несколько снежинок). Такие снежинки
мы научимся вырезать, пользуясь свойством
симметрии. Приглядитесь к окружающим вас
предметам – мы живем в мире симметрии. И человек,
и природа стремятся к ней.
Упражнение 3
Материал: цветная бумага, ножницы,
циркуль, клей.
Задание: дети делают фонарики круглой
и квадратной форм (из трех деталей). Окружности
чертят циркулем. Квадраты получают загибанием
“от угла” полосы цветной бумаги. Желательно,
чтобы каждый сделал два разных фонарика:
Тем, кто справляется с работой быстро,
учитель предлагает сделать фонарики из 5–6
деталей, украсить их вырезами или аппликацией.
Примечание: понятие о симметрии
дается на ознакомительном уровне. Не следует
требовать запоминания терминов. Дети должны
получить представление о симметрии, уметь
узнавать симметричную фигуру и проверять
свойство симметрии практически.
В качестве домашней работы можно
использовать задания из тетради № 2 либо
предложить детям сделать рисунки дворцов,
используя рамку. Дворцы рисуются с соблюдением
симметрии правой и левой половин. Дети
рассматривают образцы учителя и по аналогии
составляют собственные композиции, придумывая
им названия (“дворец Гудвина в Изумрудном
городе”, “дворец феи Фата-Морганы” и т.п.).
Это задание можно выполнить на уроке рисования
либо в виде аппликации на уроке труда.
Задания 45–49 используют для
индивидуальной работы в тетради.
УРОК 23
Тема: “Внутри и снаружи”.
Цели: уточнить представления детей
о внутренней и внешней частях плоской фигуры;
познакомить с термином “граница фигуры”.
Упражнение 1
Материал: рамка, нелинованный лист
бумаги, карандаши.
Задание: детям предлагаем обвести по
рамке круг.
– Поставьте три точки красным
карандашом внутри круга.
Проходя по классу, учитель
просматривает работы, и после этого задание
выполняется на доске (круг заранее начерчен
циркулем).
– Поставьте три точки зеленым
карандашом снаружи круга.
Упражнение 2
Способ выполнения: посмотрите, где я
поставлю точку.
Учитель ставит точку на границе круга.
– Как вы скажете, где я поставила
точку: внутри или снаружи?
Обсуждая ответ, дети приходят к выводу,
что в данном случае точка не внутри и не снаружи.
Учитель помогает им, подсказывая слово граница.
Можно напомнить о линии, разделяющей два
государства.
Делается вывод: граница круга –
окружность.
Примечание: с понятиями
“круг” и “окружность” дети к этому
времени уже познакомились, умеют работать с
циркулем, но на данном уроке целесообразно
использовать рамку. Рамка с прорезями в виде
геометрических фигур используется для быстрого
рисования фигуры нужной формы и ее закрашивания.
Упражнение 3
Задание: закрасьте внутреннюю
часть круга красным цветом, внешнюю
– зеленым, а границу круга обведите по
рамке синим.
Упражнение 4
Материал: рисунок на доске.
Задание: начертите по рамке две
окружности так, как у меня. Обведите одну красным
карандашом, другую – синим.
– Поставьте красную точку так,
чтобы она попала только в красный круг, но не в
синий (учитель просматривает работы, затем
задание выполняется на доске).
– Теперь поставьте синюю точку так, чтобы она
попала только в синий круг, но не в красный.
– Теперь зеленым цветом поставьте точку так,
чтобы она оказалась одновременно и в красном
круге, и в синем.
– Поставьте еще три точки таким же образом. Где
они оказались?
(Это место – пересечение двух
кругов. Дети показывают его, обводя рукой
на доске. Термин пересечение учитель не дает,
отмечает, что это место на чертеже – общее
для двух кругов.)
Дети закрашивают эту область зеленым, отмечая,
что любая точка из этой области попадает
одновременно и в красный круг, и в синий.
Упражнение 5
Задание: закрасьте красным то место на
чертеже, где все точки попадают только в красный
круг, но не в синий. Аналогично – в синий, но не в
красный (синим цветом).
Упражнение 6
Задание: повторяются упражнения 4 и 5,
используется квадрат (рамка). Когда рисунок
полностью раскрашен, учитель задает вопрос:
– Какой формы получилась общая
часть двух квадратов (то есть зеленая фигура)?
Упражнение 7
Задание: используя рамку, начертите
два квадрата так, чтобы их общая часть имела
форму треугольника. Закрасьте эту общую часть.
Упражнение 8
Задание: начертите два квадрата так,
чтобы у них была только одна общая сторона. Общую
сторону отметьте красным карандашом.
– Начертите два квадрата так, чтобы
у них была только одна общая точка. Отметьте эту
точку красным карандашом.
Упражнение 9
Материал: счетные палочки.
Задание: сложите из пяти палочек два
треугольника. Как они должны быть расположены? (У
них общая сторона.) Общую сторону отметьте
красной палочкой.
– Сложите из семи палочек три
треугольника. Как они должны быть расположены?
Можно ли отодвинуть один от другого?
Упражнение 10
Задание: сколько минимально нужно
палочек, чтобы сложить три квадрата? Как они
должны быть расположены? Можно ли отодвинуть
один от другого? Почему нельзя?
Задания 50–52 используют для
индивидуальной работы в тетрадях.
Задание 53*. Найди общую часть трех
фигур и закрась ее красным цветом.
УРОК 24
Тема: “Замкнутая и незамкнутая”.
Цели: Дать детям представление о
замкнутости геометрической фигуры; уточнить
представление о границе, о внутренней и внешней
частях фигуры.
Упражнение 1
Материал: рамка, лист бумаги,
карандаши.
Задание: нарисуйте с рамкой:
а) большой круг, внутри круга квадрат;
б) большой квадрат, внутри квадрата треугольник.
– Какая фигура больше: та, что
внутри, или та, что снаружи? Какие отношения
должны быть между фигурами, чтобы одна
поместилась внутри другой? (Одна больше, другая
меньше.)
Упражнение 2
Материал: рисунок на доске.
Задание: найдите лишнюю фигуру.
(Лишняя фигура – 4, так как пузырек
находится на границе фигуры, а в остальных он
находится внутри или снаружи.)
Упражнение 3
Материал: рисунок на доске.
Задание: найдите лишнюю фигуру.
(Лишняя фигура – 5, так как она
незамкнутая.)
Чтобы дети правильно поняли данный выбор, можно
предложить им такой образ:
– Чтобы вам было легче сделать
выбор, представьте, что я посадила внутрь фигуры
мышку (птичку и т.п.). Что вы мне скажете теперь? (Из
фигуры 5 мышка легко убежит, так как дверца
открыта.)
Учитель подсказывает детям, что такие
фигуры математики чаще называют незамкнутыми.
А такие фигуры, как треугольник, квадрат, круг, –
это замкнутые фигуры.
– Будет ли фигура 6 замкнутой? (Да.)
Упражнение 4
Задание: учитель стирает с доски
фигуру 5 и снова предлагает выбрать лишнюю среди
оставшихся. (Это круг, так как он без углов.)
Упражнение 5
Материал: рисунок на доске.
Задание: учитель предлагает детям
другой рисунок:
– Что это за фигуры? (Окружность и
спираль.)
– Чем они похожи? (Образованы кривой линией,
без углов.)
– Чем отличаются? (Окружность – замкнутая,
спираль – незамкнутая.)
Упражнение 6
Материал: циркуль, лист плотной бумаги,
ножницы, цветная бумага.
Задание: начертить круг с помощью
циркуля на листе плотной бумаги.
– Покажите, где внутренняя часть
круга.
– Что является границей круга? Где внешняя
часть круга?
Дети вырезают круг.
– Что похоже на круг? (Солнце,
озеро, круглое окошко в заледенелом стекле…)
Педагог показывает детям, как сделать
весенний букет (цветы в стиле “оригами”).
Цветы крепятся на вырезанный круг. Можно
прикрепить к листу несколько травинок,
получается весенняя лужайка.
Если вырезать круги из цветной бумаги – синей,
зеленой и т.п., то можно сделать разные варианты
аппликаций: на синей (озеро) – лебеди или
кувшинки, на зеленой (лужайка) – тюльпаны, на
желтой (цветы) – бабочка и т.п.
Задания 54–59 используют для
индивидуальной работы в тетрадях.
IV ЧЕТВЕРТЬ
В IV четверти 5–6 учебных недель. Если в
школе есть конструкторы, проводятся уроки 2–3 из
темы “Работа с конструктором” (практическая
работа по конструированию замкнутых и
незамкнутых фигур, а также по изготовлению
конструкции на основе многоугольников).
Затем проводится 2–3 урока обобщения и
повторения материала, изученного в течение года.
Рекомендуется подключать к работе на уроке
анализ объемных фигур, задания на распознавание
геометрических фигур в геометрических телах,
задания на конструирование многогранников из
палочек и пластилина, задания вида “Угадай, как
стояла” (на соотнесение геометрического тела и
его плоского изображения). Если учитель не
работает с конструктором, то освободившееся
время максимально заполняется заданиями
преимущественно этого вида. Конструктивную
часть заданий можно частично заменить работой на
конструирование из палочек и работой с
различными мозаиками. В конце тетради приводится
содержание теста на усвоение материала II
полугодия. Приводим описания перечисленных выше
видов упражнений.
Задания на конструирование и
трансформацию
Упражнение 1
Задание: переложить одну палочку так,
чтобы домик повернулся в другую сторону.
Упражнение 2
Задание: в фигуре, похожей на ключ,
переложить четыре палочки так, чтобы получилось
три квадрата.
Упражнение 3
Задание: какое наименьшее количество
палочек нужно переложить, чтобы убрать мусор из
совочка?
Упражнение 4
Задание: переложить две палочки так,
чтобы корова смотрела в другую сторону.
Упражнение 5
Задание: в данной фигуре переложить
три палочки так, чтобы получилось четыре равных
четырехугольника.
Упражнение 6
Задание: в фигуре, изображающей стрелу,
переложить четыре палочки так, чтобы получилось
четыре треугольника.
Упражнение 7
Задание: в фигуре, состоящей из четырех
квадратов, переложить три палочки так, чтобы
получилось три таких же квадрата.
Упражнение 8
Задание: перестроить корабль в танк,
переложив шесть палочек.
Упражнение 9
Задание: перестроить вазу в телевизор,
переложив пять палочек.
Упражнение 10
Задание: в фигуре из шести квадратов
убрать три палочки так, чтобы осталось четыре
квадрата.
Задание на конструирование из деталей
мозаики приводятся в тетрадях № 1 и № 2.
Задания на конструирование из
“Танграма” являются часто употребляемыми,
поэтому здесь не приводятся. При этом следует
иметь в виду, что обычно дети шести-семи лет не
справляются с ними самостоятельно. Учитель
расчерчивает основу (шаблон) по форме деталей,
стараясь облегчить ребенку выполнение заданий,
но это резко снижает развивающую возможность
головоломки. Если задания не получаются без
подобного расчерчивания, то их лучше отложить до
2–3-го класса.
Отсутствие конструкторов можно в
определенной мере восполнить работой с кубиками
Никитиных, которая описана в их книгах (см. Никитин
Б. Развивающие игры. Любое издание).
Задания на распознавание
геометрических фигур в объемных телах
Упражнение 1
Материал: куб и квадрат.
Способ выполнения: учитель показывает
куб и квадрат. Чем они похожи? (На кубе есть
квадраты.) Можно ли сказать, что это одно и то
же? (Нет.) Как называется это геометрическое
тело? (Кубик, куб.) Математики называют его
куб. Чем отличается куб от квадрата?
В процессе обсуждения выясняется, что основное
их различие заключается в том, что квадрат
плоский, а куб – нет. Детям понятно, например,
такое объяснение: “Если квадрат приложить к
доске, то он весь к ней приложится вплотную. Такую
фигуру называют плоской”.
– Можно ли куб полностью прижать к
доске? Можно ли назвать его плоской фигурой? (Нет.)
Куб называют геометрическим телом. У него
есть объем, внутрь него можно налить воду. А можно
ли налить воду в квадрат? (Нет.)
Этот образ обычно легко и прочно
запоминается детьми. На базе этого упражнения
строятся и другие упражнения на распознавание
геометрических тел и геометрических фигур:
прямой призмы и прямоугольника (не стоит
сообщать первоклассникам слово параллелепипед,
оно труднопроизносимо в этом возрасте,
достаточно термина призма), треугольника и
пирамиды, круга и шара (с конусом и цилиндром дети
познакомятся во 2-м классе).
Упражнение 2
Материал: геометрические тела куб,
прямая треугольная призма, параллелепипед, 2–3
пирамиды, конус, шар, цилиндр.
Задание: детям предлагается разделить
геометрические тела на две группы и объяснить
причину своего выбора.
Можно выделить группу многогранников
и группу тел вращения. Дети проводят
классификацию, не используя термины. Они просто
объясняют свой выбор, как могут. Если
классификацию провели, объединив в одну группу
конус и пирамиды, а все остальное – в другую
группу, учитель обращает внимание детей на то,
что шар во вторую группу не вписывается. Дети
могут использовать определения “эти без
углов”, “эти с углами” и т. д.
Упражнение 3
Задание: сколько вершин у куба?
Педагог обращает внимание детей на
то, что вершиной называются все точки
“начала” углов.
– Сколько отрезков на кубе? (Двенадцать
–имеются в виду ребра.)
– Сколько квадратов? (Шесть – имеются в виду
грани).
– Сколько вершин, отрезков, треугольников на
этой призме?
– Сколько прямоугольников?
– На этой?
– На пирамиде?
При выполнении этих заданий
результаты подсчетов обязательно проверяются,
все элементы пересчитываются и отмечаются
верные ответы.
Это упражнение предваряет следующее.
Упражнение 4
Материал: проволочная модель куба,
счетные палочки (деревянные) или очищенные от
серы спички, пластилин.
Способ выполнения: учитель показывает
проволочную модель куба.
– Сколько отрезков на кубе? (12).
Какой они все длины? (Равной.) Как это
проверить? (С помощью циркуля дети убеждаются,
что все ребра куба равны).
После этого учитель предлагает взять
столько палочек, сколько надо, чтобы сделать
модель куба. Можно взять счетные палочки или
попросить родителей очистить спички от серы и
использовать их вместо палочек, так как после
этой работы палочки будут испачканы пластилином
и использовать их для других целей уже будет
нельзя.
Учитель накрывает свою модель салфеткой,
оставляя ее на столе. Детям предлагается собрать
куб из палочек и пластилина по памяти. Необходимо
дать детям время (не меньше пяти минут) для
выполнения задания. Его можно считать
контрольным (высокой степени сложности) для
проверки сформированности представления о
геометрическом теле. Задание по силам только тем
детям, у которых достаточно развито
пространственное мышление.
Затем учитель дает возможность выполнить
задание всем остальным, глядя на модель. Дети,
справившиеся с заданием без модели, помогают
товарищам.
Моделирование параллелепипеда (кроме
куба) невозможно из палочек одинаковой длины. Его
моделируют при наличии палочек разной длины,
отмечая, что в основании и сверху – отрезки
одинаковой длины, а по бокам – длиннее. При
наличии палочек разной длины следует повторить
моделирование всех фигур, кроме куба, с учетом
большей длины боковых ребер.
Задания на формирование умения
распознавать три проекции объемного тела
Упражнение 1
Способ выполнения: эти задания лучше
всего предварить игрой “В Обезьянку”,
предложенной Б. Никитиным, с использованием
различных геометрических тел.
Например: у детей имеются два кирпичика и конус.
Учитель говорит: “Сегодня играем в Обезьянку.
Обезьянка должна все за мной повторять.
Посмотрим, кто из вас не ошибется.
После этого на подставке в центре класса учитель
строит разные композиции из трех имеющихся тел.
Задача детей – скопировать их, в том числе и по
цвету, если есть такая возможность.
Упражнение повторяется 3–4 раза по 5–6
минут на нескольких уроках с разными наборами.
При выполнении задания дети видят в основном
фронтальную проекцию, поэтому у них постепенно
формируется умение узнавать ее и домысливать по
ней композицию в объеме.
Упражнение 2
Способ выполнения: на втором этапе
детям предлагаются такие варианты заданий:
а) узнайте по чертежу, какая фигура
изображена:
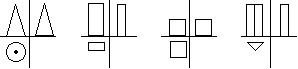
б) определите, как она стояла:
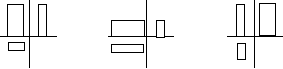
в) какие фигуры изображены и как
они стояли:
Перед тем как предлагать эти задания,
следует провести такую работу.
Учитель показывает детям куб, держа его перед
собой на ладони. Один ребенок становится слева у
двери, другой – справа у окна, остальные дети
видят перед собой фронтальную проекцию.
– Мы все смотрим на этот куб с разных
сторон: вы – спереди, я – сверху, Ваня – справа,
Маша – слева. Как вы думаете, мы все видим одно и
то же? (Да.)
– Что видите вы? (Квадрат.)
– Как вы думаете, что видит Ваня? (Квадрат.)
Ваня подтверждает, что он действительно видит
квадрат.
– Как вы думаете, что видит Маша? (Квадрат.)
– Что вижу я (сверху)? (Квадрат.)
Учитель показывает, что он действительно видит
квадрат. Для такого задания лучше всего иметь
геометрическое тело с гранями, окрашенными в
разный цвет. (Удачным вариантом будет
последующее выполнение трех проекций на доске
разноцветным мелом в соответствии с окраской
граней.)
Аналогичная работа проводится с другими
геометрическими телами.
Задания на формирование логических
приемов мышления содержатся в большом объеме в
тетрадях. Приводим примерные планы-конспекты
уроков повторения и обобщения
УРОК 1
Тема: “Фигуры и линии”.
Цели: уточнить и обобщить
представления детей о линиях разного вида;
развивать геометрическое видение и
конструктивные умения.
Упражнение 1
Материал: рисунок на доске.
Задание: назовите каждую линию на
рисунке.
– Разделите все линии на рисунке так,
чтобы в каждой группе были только схожие между
собой линии. Дайте название каждой группе. Как
называют линию 2? Линию 8? (Горизонтальная и
вертикальная прямые.) Найдите точку
пересечения линий 2 и 8.
Упражнение 2
Материал: рисунок на доске.
Задание: сколько треугольников на
каждом чертеже?
Показывая треугольник, ученик обводит
его указкой.
Упражнение 3
Материал: счетные палочки.
Задание: возьмите четыре палочки.
Какую фигуру можно сложить из четырех палочек? Из
пяти? (Треугольник, четырехугольник.) Из семи?
Из шести?
Упражнение 4
Задание:
а) сложите два треугольника из пяти
палочек;
б) сложите три треугольника из семи палочек.
Упражнение 5
Задание: а) сложите два квадрата из
семи палочек; б) сложите четыре квадрата из 12
палочек.
Упражнение 6
Задание: cложите квадрат и треугольник
из шести палочек.
Упражнение 7
Способ выполнения: игра “Внимание”.
Упражнение 8
Задание: используя палочки и
пластилин, дети конструируют модель куба, при
этом разбирают и повторяют вопросы:
– Сколько вершин у куба?
– Сколько отрезков (ребер)?
– Сколько понадобится палочек, чтобы сделать
куб?
Модель куба учитель накрывает
салфеткой. Дети работают по представлению. Если
кто-то из учеников не может работать без образца,
ему разрешается подойти и посмотреть еще, а затем
желательно работать без опоры.
Задание 60*. Дорисуй флажок и шарик,
сохраняя закономеронсть.
Задания 61–68 используют для
индивидуальной работы в тетрадях.
УРОК 2
Тема: “Геометрические фигуры”.
Цели: уточнить представления о
треугольнике и четырехугольнике; развивать
конструктивные умения.
Упражнение 1
Материал: рисунок на доске.
Задание: одна из фигур лишняя. Какая? (Фигура
4, она незамкнутая.)
Фигуру 4 стирают. Учитель просит детей
снова выбрать одну лишнюю фигуру. (Круг – у него
нет углов.) После того как исключили круг, снова
можно выбрать лишнюю фигуру – это треугольник.
– Как можно назвать все оставшиеся
фигуры одним словом? (Четырехугольники.)
Упражнение 2
Способ выполнения: учитель возвращает
на доску треугольник и круг и просит учеников
запомнить фигуры. На запоминание дается 5–6 сек.
Затем рисунок на доске закрывается, и дети по
памяти рисуют все пять фигур. Рисунок
выполняется от руки (набросок). Успешно
справившимся считается тот, кто нарисует все
пять фигур, и они будут узнаваемы.
Упражнение 3
Материал: циркуль, цветная бумага,
ножницы, клей.
Задание: можно ли сделать из палочек
круг? (Нет.). Какой нужен инструмент, чтобы
начертить круг? (Циркуль.)
Детям демонстрируется аппликация
“Заяц” или любая другая из задания 80 в
тетради. Оставшаяся часть урока посвящается ее
изготовлению.
Примечание: не следует задавать
радиусы: дети в процессе анализа должны отметить,
что туловище – больше, голова – меньше, мордочка
и лапки – одинаковы; чтобы сделать уши, надо
начертить такой же круг, как для головы,
разрезать его пополам и т. д. Самостоятельное
решение проблемы выбора радиусов помогает
формировать глазомер и самоконтроль.
Аппликация крепится на картон клеящим
карандашом. Морковку и хвост дорисовывают
фломастером.
Дети могут по желанию делать разные аппликации
из задания 80 в своих тетрадях. Для индивидуальной
работы учитель использует любые оставшиеся
задания в тетради.
УРОК 3
Тема: “Треугольник”.
Цель: обобщить представление о
треугольнике.
Упражнение 1
Материал: рисунок на доске.
Задание: найти лишнюю фигуру.
Упражнение 2
Материал: лист бумаги в клетку.
Способ выполнения: дети работают на
листе в клетку, на котором обозначена красная
точка.
– Найдите красную точку. Отсчитайте
две клетки вниз и три клетки вправо. Поставьте
точку. Соедините точки красным карандашом.
Отсчитайте шесть клеток вниз, поставьте точку.
Соедините точки синим карандашом. Соедините
первую и последнюю точки зеленым карандашом.
Какая фигура получилась? Что о ней можно
рассказать?
Упражнение 3
Задание: измерьте красную сторону,
зеленую сторону, синюю сторону. Повторяется
техника работы с линейкой.
Упражнение 4
Задание: закрасьте внутреннюю часть
этого треугольник красным карандашом. Используя
рамку, начертите второй треугольник так, чтобы у
этих треугольников была общая сторона.
Обозначьте общую сторону синим цветом. (Ответы
могут быть разные.)
Упражнение 5
Материал: рамка, карандаши.
Задание: начертите произвольный
треугольник (используя рамку). Проведите в нем
отрезок так, чтобы этот треугольник был разбит на
два треугольника.
Упражнение 6
Задание: начертите такой же
треугольник еще раз. Проведите в нем отрезок так,
чтобы этот треугольник был разбит на треугольник
и четырехугольник.
Упражнение 7
Материал: несколько геометрических
тел, среди которых есть конус, пирамиды (с разными
основаниями), призмы (в том числе с треугольным
основанием).
Задание: выберите из этих фигур такие,
в которых вы видите треугольники.
Фигуры рассматривают с разных сторон,
треугольники на них обводят пальцем. Обращают
внимание на конус, в котором издалека можно вроде
бы увидеть треугольник (фронтальная проекция), но
если взять его в руки, то видно, что треугольника
нет.
Примечание: если ребенок
видит треугольник в конусе, то это проективное
виRдение, значит, здесь педагогу следует быть
очень аккуратным при обсуждении этого вопроса.
Нельзя говорить категорично: “Нет
треугольника”. Следует уточнить, что в самой
фигуре треугольников как таковых нет. Чтобы
убедиться в этом, надо взять ее в руки, ощупать
гладкие поверхности, ощутить ладонью отсутствие
ребер (конус – это тело вращения, его поверхность
гладкая, но не плоская). Но в то же время
если смотреть на конус с некоторого
расстояния, то сбоку и спереди мы действительно
видим треугольники. “Так нам видится, так видят
наши глаза. Поэтому если я спрошу, что вы видите,
вы, конечно, ответите: треугольник. Потому что я
спросила, что вы видите. Но если я спрошу, можно ли
на конусе найти и показать треугольник, вы мне
скажете: нет”.
Ребенку довольно сложно ориентироваться в
данной ситуации, так как здесь происходит
разделение двух позиций: стереометрической и
проективной. Если этот вопрос не возник на уроке,
специально его можно не обсуждать.
Упражнение 8
Материал: две объемные фигуры.
(Конус и правильная пирамида с
треугольным основанием – тетраэдр; эти термины
не для детей, а для педагога.)
Задание: сделайте модели этих фигур из
палочек.
Примечание: здесь неизбежно
возникает вопрос, затронутый ранее, и в процессе
его обсуждения педагог подводит детей к выводу,
что модель конуса сделать из палочек невозможно,
а пирамиды – можно.
Используя палочки, дети делают модель пирамиды.
Затем подсчитывают и определяют по модели число
и положение вершин и ребер, показывают
треугольники (грани), обводя их пальцем.
Для индивидуальной работы учитель использует
любые оставшиеся задания в тетради.
УРОК 4
Тема: “Окружность и круг”.
Цель: обобщить представление детей
о круге и окружности.
Упражнение 1
Материал: модели фигур на фланелеграфе.
Задание: найдите лишнюю фигуру. (Все
фигуры – это части круга, 4 – целый круг, поэтому
она лишняя.)
Упражнение 2
Материал: модели недостающих частей
фигур из упр. 1.
Задание: среди данных кусочков найти
недостающие части фигур 1–6 и достроить их до
кругов.
Не следует помогать выбору
соответствием цвета, то есть выбор должен идти не
по цвету, а по форме. Среди этих кусочков должны
быть и похожие, но неподходящие, то есть их должно
быть больше, чем фигур.
Упражнение 3
Материал: циркуль, бумага, ножницы.
Задание: каким инструментом можно
нарисовать окружность? Удобно ли делать это от
руки?
– Начертить циркулем большую
окружность на листе плотной бумаги (повторяется
техника работы с циркулем, зависимость размера
окружности от “раствора” циркуля).
Вырезается круг.
Упражнение 4
Задание: возьмите в руки фигуру,
которую вы вырезали. Можно ли назвать ее
окружностью? (Нет.) Как ее правильно назвать? (Круг.)
Чем же отличается окружность от круга? (Окружность
– граница круга.) Обведите окружность пальцем.
Будет ли она замкнутой? (Да.)
Упражнение 5
Материал: образец аппликации, цветная
бумага, ножницы, клей.
Задание: сегодня мы представим себе,
что у нас есть аквариум. Пустим в аквариум рыбок.
Педагог демонстрирует аппликацию
“Рыбки”.
Круги для рыбок рисуем на цветной бумаге
циркулем и вырезаем. Хвосты и плавники
дорисовываем фломастером. “Воду”
подкрашиваем, можно акварелью. Водоросли можно
дорисовать или приклеить. Для рисования
маленьких кругов можно использовать рамку.
Можно изготовить рыбок в технике
оригами.
УРОК 5
Тема: “Квадрат”.
Цели: уточнить представление о
квадрате; развивать геометрическое видение и
конструктивные умения.
Упражнение 1
Материал: рисунок на доске.
Задание: разделите фигуры на две
группы.
При разделении фигур на группы дети не
могут еще оперировать терминами “ромб”,
“прямой угол”. Но интуитивно они обычно
правильно разделяют фигуры на группы, говоря так:
это квадрат, а это не квадрат.
Примечание: обобщение в данном
случае опирается на интуитивное представление,
на мыслительный образ. Не следует добиваться
каких-то определений, поскольку в 1-м классе
работа идет на дологическом уровне. Цель этого
упражнения – узнать квадрат (проверка
адекватности мысленного образа).
Упражнение 2
Материал: счетные палочки.
Задание: сложите четырехугольник из
четырех палочек. (Учитель просматривает
результаты.) Обязательно ли должен получиться
квадрат? Какая другая фигура может получиться? (Ромб.)
Дети могут и не знать это название, но чаще всего
они сами говорят “ромбик”. Термин дается не
для запоминания, а для введения в активный
словарь ребенка.
– Чем похож ромб на квадрат? (У
него стороны тоже равной длины.)
Примечание: не следует
спрашивать, чем отличается ромб от квадрата, так
как ребенок еще не владеет понятием прямой угол.
Упражнение 3
Материал: лист цветной бумаги.
Задание: можно ли сказать, что этот
лист (лист цветной бумаги стандартного размера)
имеет форму квадрата? Почему? (Стороны разной
длины.)
– Мы с вами уже учились получать
квадрат из такого листа и учились делать
забавных зверят из квадратика бумаги.
Учитель показывает собачку в стиле
оригами. (Хорошо, если учитель сделал заранее
2–3 различные композиции на тему “Собачка”:
такие аппликации очень нравятся детям.)
“Собачку” дети делают, повторяя
действия педагога. При желании можно дополнить
аппликацию дорисовкой.
Если в школе есть конструкторы, то
проводятся уроки 5 и 6 из раздела “Работа с
конструктором” (уголковые соединения и план).
Если конструкторов нет, оставшиеся часы
посвящаем работе с циркулем, выполнению заданий
из тетради и упражнениям с объемными фигурами.
Тестовые задания по результатам
второго полугодия
РАБОТА С КОНСТРУКТОРОМ (6 часов)
Уроки с использованием конструктора
чаще всего вызывают затруднения у учителей.
Анализ практики позволяет выделить несколько
причин.
1. Школа не всегда имеет нужные
конструкторы, в результате чего приносимые
детьми на урок наборы оказываются разными.
Проводить уроки в таких условиях трудно или
почти невозможно.
2. Так как количество деталей велико,
а размеры их небольшие, при сборке изделия часто
падают на пол, теряются. К концу занятия в
коробках с деталями наблюдается такой
беспорядок, что первоклассникам приходится по
10–15 минут после урока раскладывать детали по
своим местам.
3. Дети очень дифференцированно по
времени собирают изделия (от 6 до 35 минут), поэтому
учителю особенно трудно планировать и проводить
вторую половину урока, когда одни уже закончили
работу, а другие еще на полпути.
4. Ребята неохотно разбирают
сделанное своими руками, что необходимо для
проведения последующих уроков. Наличие
нескольких видов тематических конструкторов
облегчило бы работу учителя, но в сегодняшних
условиях для многих семей это трудновыполнимо.
5. Быстрее всех обычно справляются с
заданием дети, имеющие опыт работы с
конструктором. Такие дети, как правило, быстрее
других ориентируются в решении конструктивных
задач. Это является следствием соответствующей
работы дома. У таких детей, как правило, дома есть
несколько наборов конструкторов.
Создающееся противоречие заключается
в том, что этим детям уже неинтересна работа с
примитивным металлическим конструктором типа
“Школьник”, на который, как правило,
опирается учитель (все методические разработки
выполняются именно с опорой на этот самый
дешевый и наиболее доступный набор).
Дети же, которые не имеют опыта
домашней работы с конструктором, работают с этим
набором с трудом – в нем очень мелкие, не всегда
подходящие к резьбе гайки, детали тусклые,
некрасивые, негибкие, получаемые изделия лишены
всякой эстетической привлекательности.
В этом разделе мы приводим основные
положения по организации работы на уроке и по
системе построения заданий, являющейся, на наш
взгляд, наиболее целесообразной в рамках курса
“Наглядная геометрия”.
Работу с конструктором мы планируем
следующим образом: 5-6 занятий в 1-м классе, 4-3
занятия во 2-м классе.
Тематика уроков в 1-м классе
1. Знакомство с конструктором:
название деталей и инструментов. Изготовление
букв. Понятие о жесткости конструкции.
2. Виды соединений: встык с
накладкой, внахлест. Изготовление лесенки.
3–4. Изготовление многоугольников.
Изготовление модели на основе многоугольника:
дорожный знак, часы.
5–6. Виды соединений: под углом.
Изготовление мебели: стол, стул,
кресло, кровать. Знакомство с понятием план.
План комнаты: расстановка мебели.
Практика показывает, что сборке машин
и других механизмов должна предшествовать
сборка более простых изделий, на которых дети
могли бы освоить приемы работы с инструментами,
ознакомиться с основными видами соединений и пр.
При этом нецелесообразно отрабатывать приемы в
специальных тренировочных упражнениях, так как
они лишены для детей практического смысла.
Лучше использовать вопросы-задания, требующие
технического осмысления изученного материала:
1) В какую сторону вращать отвертку,
чтобы завинтить винт в гайку, – по часовой или
против часовой стрелки?
2) В какую сторону вращать гаечный
ключ, чтобы отвинтить гайку?
3) Что удобнее и быстрее
развинчивать – винт отверткой (гайку при этом
удерживать неподвижно) или гайку ключом (винт при
этом удерживать неподвижно отверткой)?
4) Какими способами можно соединить
две полосы, чтобы сделать одну длинную? Какое
наименьшее число винтов и гаек требуется при
различных способах соединения?
5) Чем отличается соединение полос
внахлест одним винтом от соединения двумя
винтами? В каких случаях удобнее первое
соединение, а в каких – второе и почему?
6) Как соединить две полосы под
углом, если они расположены по отношению друг к
другу следующим образом? (Учитель показывает по
очереди варианты, изображенные на рисунке).
7) Почему формы мостов и кранов,
мачты линий электропередачи и другие жесткие
конструкции составлены из балок, соединенных в
треугольники, а не в прямоугольники?
Собери из полос треугольник и
четырехугольник и попробуй изменить их форму.
Какая особенность у треугольника по сравнению с
другими фигурами?
8) Как можно соединить уголки
(уголковые профили), чтобы:
а) удлинить уголок (что лучше:
внахлест или встык с накладкой?);
б) три уголка, сходясь в одной точке,
образовали вершину мачты или фермы (призмы или
пирамиды);
в) четыре уголка, сходясь в одной точке,
образовали вершину пирамиды (мачты)?
9) Как прикрепить на ось колёса,
чтобы они свободно вращались, но с оси не спадали?
10) Каким способом можно закрепить на
оси колесо, чтобы оно вращалось вместе с осью?
11) Как сделать шарнирное (то есть
подвижное) соединение двух полос, чтобы вращение
всегда было свободным (гайка не затягивалась)?
Годится ли для этого контргайка?
12) Что произойдет, если две гайки на
винте туго поджать одну к другой? Почему одну из
гаек в этом случае называют контргайкой?
Эти вопросы могут быть заданы как в
процессе закрепления темы, так и перед ее
изучением, тогда они сыграют роль проблемных, то
есть будут представлять собой конструкторскую
задачу.
Часть таких задач можно давать
желающим для решения дома (возможно, с помощью
родителей).
Система постановки конструкторских
задач является основным условием использования
различных конструкторов для развития
технического конструктивного мышления ребенка.
К каждому набору конструктора
обязательно приложен альбом рисунков или
фотографий, а иногда еще и таблицы, где
перечислено, каких и сколько деталей надо взять,
чтобы собрать изображенную на рисунке модель.
Учитель обычно ориентируется на эти альбомы и
таблицы.
Ребенку надо внимательно рассмотреть
картинку в альбоме, взять из коробки детали и
соединить их согласно образцу, то есть он
выступает в роли исполнителя. Тут ему надо быть
внимательным, точным и аккуратным работником,
но… только исполнителем, только сборщиком кем-то
придуманной модели.
Таким же образом методика рекомендует
строить урок работы с конструктором: в начале
урока непременно производится анализ образца,
выбор деталей и инструментов, а затем сборка
аналогичной модели. Конечно, при таком
построении урока ребенок знакомится с
устройством и работой машин и механизмов,
постигает секреты соединения деталей друг с
другом, узнает их свойства, развивает свои
способности, но в основном исполнительские.
Творческая работа (конструирование и
придумывание нового) на таких уроках обычно
связана с внесением улучшений и добавлений в
готовую модель, причем цель внесения улучшений и
добавлений не оговаривается.
В жизни подобных положений не бывает:
каждый конструктор и целое конструкторское бюро
получают конкретное техническое задание на
разработку нового станка, автомобиля или
самолета. В таком задании бывают перечислены все
требования, которым должен удовлетворять,
например, новый самолет: его скорость,
грузоподъемность, дальность полета, посадочная
скорость и т.п. Тогда конструкторы получают ясную
цель, осуществить которую и стремятся всеми
силами и средствами. При таких условиях
исполнительская деятельность ребенка
становится частью всего творческого процесса и
способствует формированию активного
технического мышления.
В связи с таким подходом учителю
рекомендуется начинать урок не с демонстрации
образца и его анализа, а строить свою работу
таким образом:
1. После выбора модели, которую
предполагается сделать на данном уроке,
проводится обсуждение технических требований к
ней – какой она должна быть.
2. Если имеются альбомы к
конструктору и там есть несколько вариантов
выбранной модели, надо просмотреть все рисунки и
оценить видимые их достоинства и недостатки. Эту
часть работы конструкторы обычно называют ознакомлением
с существующими конструкциями. Если таких
рисунков нет, учителю надо сделать несколько
моделей самому.
3. Разработка конструкции. Это
самая ответственная часть работы. Надо
рассмотреть все имеющиеся детали и выбрать те,
которые пригодятся для данной конструкции (то
есть оценить материалы и возможности, которыми
располагает конструктор).
4. Первоначальную (предварительную)
сборку лучше сделать, не закрепляя деталей
винтами и гайками (“на живую нитку”). Это дает
возможность в ходе сборки производить замену
деталей на более удобные (больше соответствующие
конструктивному замыслу).
5. Собранная и отлаженная модель
теперь должна выдержать испытание по всем
пунктам технических требований. Если требуется,
чтобы дорожный знак не терял равновесие, а крепко
стоял, где поставили, его проверяют на различных
ровных поверхностях. Если требуется, чтобы
тележка сама катилась с наклонной доски, то ее
ставят на доску с нужным уклоном и наблюдают,
катится ли она, и т.д.
6. Если испытания покажут, что
конструкция еще несовершенна и у модели есть
недостатки, то ее отправляют “на доводку”:
изменяют, усовершенствуют, устраняют недостатки.
В этом случае рекомендация “внести
улучшения и усовершенствования” является
обоснованной, логически вытекающей из
результатов испытаний.
7. Когда модель окончательно готова,
ее “принимают в эксплуатацию”, то есть
необходимо дать возможность ребятам поиграть со
своей моделью – “проверить ее в
эксплуатации”.
Все модели хранятся до следующего
урока в специально отведенном для этого месте.
Место лучше выбрать так, чтобы дети имели к нему
доступ и родители, приходя за детьми, могли
видеть их изделия. В условиях отдельного от всей
параллели обучения шестилеток это вполне можно
предусмотреть. Разборку деталей можно
произвести в начале следующего урока, при этом
дети учатся раскладывать детали по своим местам
быстро и аккуратно.
Для шестилеток нецелесообразно
планировать создание модели, на которую они
затрачивают два или три урока. Ребенок
испытывает радость, когда он видит модель,
сделанную своими руками, поэтому и стремится
закончить ее за один урок.
Конструируя модель, испытывая ее и
усовершенствуя, ребенок узнает массу
технических сведений. А так как все это
происходит в процессе целенаправленной
практической деятельности, приобретаемые знания
формируются прочно и служат долго.
Возможны случаи, когда сразу получить
совершенную конструкцию трудно, что-то не
выходит. Тогда лучше остановиться на достигнутом
и отложить решение на некоторое время, до
следующего урока. Не следует сразу подсказывать
верное решение задачи, лучше дождаться, пока идея
“созреет”. Если дети сами просят не
подсказывать им, стремясь самостоятельно решить
проблему, такое желание надо всячески
поддерживать.
Хорошо работать над конструкцией или
композицией вдвоем или втроем. Тогда можно
сделать два или три варианта одной и той же
модели или одну модель достаточно высокой
степени сложности (поезд, ракета и т.д.).
По одному техническому заданию можно
собрать совершенно разные по конструктивному
решению модели. А “защита” проекта или
модели, когда “автор” или “авторский
коллектив” должен доказывать выгодность и
целесообразность того или иного узла или
конструкции в целом, является для ребенка
настоящей школой технического мышления, а также
формирует умение отстаивать свою правоту,
мужественно выдерживать критику и неудачи,
умение в случае необходимости возвращаться
назад, чтобы начать все сначала, но в конце концов
добиться победы над трудной задачей, а
фактически – над самим собой.
УРОК 1
Тема: “Конструирование букв”.
Цели: Познакомить детей с деталями
конструктора и способами их соединения;
развивать конструктивное мышление.
Техническое задание 1
Сконструировать из деталей
конструктора буквы: Л; А; Т; П; К; М; И; Д; У.
1. Буква должна быть легко узнаваема
(похожа на оригинал).
2. Должны быть соблюдены пропорции,
то есть высота “ножек” должна быть
пропорциональна размеру “перекладины”.
3. На каждую букву надо
израсходовать как можно меньше деталей.
Примечание: составляя
техническое задание для шестилеток, надо иметь в
виду, что им необходимо будет его запомнить
(прочитать текс на доске в этот период могут лишь
немногие), поэтому оно должно быть исчерпывающим
и коротким.
Первый этап урока посвящается ознакомлению с
правилами работы и с деталями набора. Он занимает
5–6 минут.
Затем учитель знакомит детей с техническим
заданием (“Наше КБ начинает свою работу, вот
первое задание” или любая другая игровая
ситуация).
Большинство методик рекомендуют при работе с
конструктором выполнять задание по имеющемуся
образцу. Безусловно, совсем уйти от этого очень
трудно и со всеми детьми практически невозможно,
особенно на первых порах. Однако, ставя перед
собой цель – сформировать техническое мышление,
надо понимать, что систематически используя
репродуктивную деятельность, развить
техническое мышление невозможно. Поэтому там,
где есть возможность уйти от образца, это следует
сделать обязательно.
Например, на данном уроке учитель может
использовать такой вариант постановки задачи:
“Сегодня мы познакомимся с конструктором и
будем делать из него буквы”.
После знакомства с конструктором
учитель предлагает детям посмотреть на список
букв и определить, какие из них можно сделать из
деталей конструктора. Буквы четко написаны на
клетчатом поле доски:
Анализируя перечень букв, дети
должны догадаться, что буквы О, С, Р из деталей
конструктора сделать нельзя (в них есть круглые
элементы). Для того чтобы дети самостоятельно
ответили на такой вопрос, накануне (на уроке
чтения или письма) можно предложить такие
упражнения:
а) одна из этих букв отличается
по форме от остальных. Какая это буква? (Найдите
лишнюю букву.)
М, Л, О, Д, Е, Ж
П, У, И, В, К
б) Разделите эти буквы на две
группы по внешнему виду, по форме их элементов:
М, Л, О, Д, Е, Ж, П, В, У, Р, И, Ю, С, К
После того как произведен выбор букв,
учитель сообщает техническое задание. Здесь же
сразу можно спросить: на какую букву пойдет
меньше всего деталей, на какую больше всего,
сколько именно?
Детально задерживаться на этой части
урока не следует, так как именно этот этап – этап
выбора соответствующих форм деталей для
конструирования буквы – является как бы тестом
на проверку сформированности восприятия.
Наблюдая за работой детей, учитель сразу заметит
тех, кто не приступает к работе, так как
затрудняется в выборе полос нужной длины.
Второй момент, на который обратит
внимание учитель, – это несформированность
самоконтроля: ребенок не соблюдает пропорции –
длины полос не соответствуют форме букв, причем
явное несоответствие “конструктора” не
волнует.
Методика работы с этими детьми иная.
Для первых необходим образец и его
анализ (это можно сделать, собрав несколько таких
детей у учительского стола, где лежат
заготовленные заранее образцы; иногда
приходится дать такой образец с собой на парту,
поэтому их надо иметь несколько).
Вторым необходимо посоветовать
внимательно сравнить свою модель с начертанием
буквы на доске: разве “перекладина” у буквы П
такой же длины, как ее “ноги”? и т. д. Если
ребенок может сам оценить соответствие своей
конструкции образу буквы, значит, причина ошибки
действительно в несформированности
самоконтроля. Таких детей надо активно
привлекать к работе на этапе обсуждения качества
изготовления букв.
Если ребенок не видит несоответствия
своей модели образу буквы, то это, как правило,
результат каких-то нарушений восприятия, и они
требуют специфической коррекции.
На этом уроке полезно использовать
парную работу: дети делают буквы вдвоем, не
дублируя друг друга. Это исключит копирование
работы соседа и внесет определенный азарт и дух
партнерства. Тот, кто работает быстрее, закончив
свое задание, поможет напарнику.
После того как весь набор букв
изготовлен, проводятся обсуждение и выявление
ошибок выполнения. Ошибки могут быть следующие:
1) нарушение пропорций буквы;
2) винты, соединяющие детали, выбраны
слишком длинные и царапают руки, буква на парту
не ложится или ложится неровно (винты разной
длины). Эта ошибка скорее дизайнерского
характера, а не конструктивного, но конструктор
должен стремиться к целесообразности, не забывая
о гармоничности и красоте изделия;
3) гайки плохо закручены и буква
“складывается”.
В процессе обсуждения и исправления
конструктивных ошибок учитель обращает внимание
детей на сходство и различие букв Л и А:
– Чем похожи конструкции этих букв?
– Чем они различаются?
Затем учитель предлагает детям
произвести такой опыт: потянуть буквы за
“ноги”. Дети замечают, что Л при этом форму
теряет, но А – сохраняет и деформации не
поддается.
Учитель сообщает детям, что такое
свойство конструкции – сохранение формы,
устойчивость от деформаций – называется жесткостью.
Сравнивая конструкцию всех остальных
букв с конструкцией буквы А, дети выясняют, что
этим свойством обладает только она.
На четвертом этапе урока учитель
организует ситуацию “эксплуатации”
конструкций. Например, так:
– А сейчас мы поиграем в слова:
какие слова можно составить из данных букв?
Сколько слов мы сумеем составить? Кто составит
больше всех?
Дети составляют слова на парте
(вдвоем). Учитель записывает их на доске
столбиком печатными буквами (соответствующими
моделям из конструктора), например:
ЛАК
КИТ
ЛУК
ТАМ
ТАК
ДАЛ и т.д.
Затем можно предложить детям найти
пары похожих по конструкции слов: ЛАК – ЛУК, ТАК
– ТУК (разница – в одной букве).
Интересно предложить такое
упражнение: попробуй получить из данного слова
новое, меняя по одной букве.
Учитель демонстрирует образец
составления цепочки:
ДАЛ – – – ДЫМ (ДАЛ – ДАМ – ДЫМ)
ЛАК – – – – – СОК (ЛАК – МАК – МОК – СОК)
Эта увлекательная игра очень полезна
для развития речи и чувства слова.
Список слов из заданных букв не
ограничивается трехбуквенными словами.
Переносную доску со списком слов лучше оставить
в классе, чтобы дети могли добавлять новые слова.
Игра может превратиться в увлекательное
соревнование (она заставляет детей обратиться к
изучению словарей). Вместо доски (чтобы случайно
не стереть надписи) можно использовать большой
лист бумаги, на который дети крепят пластилином
листочки со своими словами. Через неделю можно
подвести итог игры.
УРОК 2
Тема: “Конструирование лесенки”.
Цели: познакомить с соединениями
внахлест и встык с накладкой; развивать
конструктивное мышление.
Техническое задание 2
“Лесенка”
Сконструировать из деталей
конструктора лесенку.
1. Лесенка должна доставать до крыши
дома (дом может быть игрушечным или нарисованным
на доске, его размеры должны быть такими, чтобы
для изготовления лесенки надо было соединить 2–3
полосы в длину).
2. При ослаблении гаек лесенка не
должна подгибаться (складываться).
3. Ступеньки лестницы не должны
проваливаться (складываться).
4. На лесенку нужно израсходовать
как можно меньше деталей.
Прежде чем приступить к работе,
обсуждается, какие детали следует взять для
лесенки: это полосы. Учитель выбирает самую
длинную полосу и спрашивает, хватит ли ее длины
для изготовления лестницы нужной высоты (чтобы
достать до крыши). Дети замечают, что этой длины
недостаточно, полосы придется соединить.
В процессе обсуждения вопроса, какой
вид соединения является в данном случае лучшим,
учитель может предложить разные виды соединений,
но дети могут и сами придумать варианты
соединения. Потом их следует обсудить.
После обсуждения ученики приходят к
выводу, что: варианты а) и в) не держат
форму, могут деформироваться (нежесткие
соединения); вариант д) содержит лишний болт,
не усиливающий крепость конструкции, а лишь
утяжеляющий ее; наиболее целесообразны варианты б)
и г). Учитель сообщает их названия: внахлест
и встык с накладкой.
Можно обсудить вопрос о том, какой из
вариантов наиболее экономичен и при
использовании какого из них конструкция
получается легче.
Затем дети собирают лесенку.
Урок заканчивается обсуждением
полученных конструкций: выявлением их
достоинств и недостатков, способов устранения
недостатков и – главное – их соответствием
техническому заданию.
Для тех, кто справляется с работой
быстрее, можно предложить усложненный вариант:
лесенка-стремянка.
УРОКИ 3–4
Тема: “Конструкции на основе
многоугольника”.
Цели: уточнить представление о
многоугольнике; познакомить с понятием
“жесткость конструкции”; развивать
конструктивное мышление
Поскольку одна из целей урока –
формирование представления о многоугольнике,
этот урок проводится после изучения темы
“Замкнутые и незамкнутые фигуры”.
Техническое задание сообщается после повторения
геометрического содержания.
Упражнение 1
Материал: рисунок на доске.
Задание: чем похожи все эти линии, как
их можно назвать? (Ломаные.) Выберите любую из
них и сделайте ее модель из конструктора.
Упражнение 2
Задание: посмотрите на мою ломаную. Чем
она отличается от ваших?
Учитель показывает свою модель – она
замкнутая. (“Ваша – замкнутая, у нас –
незамкнутые”.)
Упражнение 3
Задание: сделайте свои ломаные
замкнутыми.
– Как теперь можно назвать все наши
модели?
Если дети начинают перечислять:
треугольники, четырехугольники и т. д., то учитель
просит подобрать одно слово для всех моделей. (Это
многоугольники.)
Упражнение 4
Задание: поднимите свои модели те, у
кого треугольники. Теперь те, у кого
четырехугольники. (Если кто-то сделал квадрат,
следует обратить на это внимание и спросить
название этого четырехугольника.) Теперь –
пятиугольники, шестиугольники, семиугольники (больше
обычно не делают).
Упражнение 5
Задание: у какого многоугольника
меньше всего углов? Сторон? (У треугольника.)
Упражнение 6
Задание: а можно сделать многоугольник
с двумя углами? С одним углом? Попробуйте сделать
это.
Учитель дает время (2–3 минуты обычно
достаточно) на прикидку вариантов. Дети видят,
что это невозможно. Для решения этой задачи нужен
конструктор, так как жесткие полосы наглядно
показывают, что ломаная с одним или двумя углами
не замыкается без деформации сторон, а стороны
многоугольника должны быть прямыми.
Упражнение 7
Задание: можно ли сказать, у какого
многоугольника больше всего сторон и углов? (Нет,
их может быть сколько угодно.)
Упражнение 8
Способ выполнения: учитель выбирает
3–4 модели, среди которых обязательно есть
треугольная форма, и предлагает детям
внимательно следить за его действиями и
догадаться, на что он хочет обратить их внимание.
После этого он демонстрирует неустойчивость
всех многоугольных форм на сжатие и растяжение
(дети обычно делают здесь соединения внахлест
одним винтом, такое соединение форму не держит) и
устойчивость к деформации треугольной
конструкции (хотя в ней те же соединения).
Затем делается вывод о жесткости треугольной
конструкции.
Можно показать детям заготовленные заранее
буквы Л и А и напомнить эпизод из первого урока,
спросив, чем же можно объяснить жесткость
конструкции буквы А. Дети замечают, что эта
конструкция заключает в себе треугольник, что
делает ее жесткой, устойчивой к деформациям.
Некоторые дети вспомнят, что использовали
треугольную конструкцию при изготовлении
лесенки-стремянки.
Упражнение 9
Способ выполнения: учитель показывает
две модели: “Дорожный знак” и “Часы”.
– Какие многоугольники лежат в
основе каждой конструкции? (Треугольник и
шестиугольник.)
Упражнение 10
Способ выполнения: учитель проносит
обе модели по классу, затем ставит их на
подставку и предлагает определить, какие новые,
ранее не использованные элементы конструктора
применяются в этих моделях. (Здесь используются
“уголки”, они обеспечивают вертикальность
моделей.)
Дальше урок можно планировать таким образом:
либо сообщить техническое задание к дорожному
знаку и выполнить это задание всем, либо
попросить часть детей сделать часы по образцу,
дав им минимальное техническое задание (это те
дети, которым на первых порах необходим образец:
они выявлены на первом занятии с конструктором),
а более самостоятельным предложить сделать
дорожный знак по рисунку на доске (или плакату).
Образец при этом убирают за ширму.
При недостатке времени можно
предложить сделать часы всем, у кого модель по
форме ближе к шестиугольнику (у пятиугольника
сторону добавить, у семиугольника – убрать), а
дорожный знак – тем, у кого треугольники и
четырехугольники (убрать одну сторону). Работа
проводится по образцу традиционным способом.
Техническое задание 3
“Дорожный знак”
Сконструировать дорожный знак из
деталей конструктора.
1. Дорожный знак должен прочно
стоять на ровной поверхности.
2. Его размер должен быть пропорционален длине
стойки.
3. Он не должен терять равновесия и не должен
подгибаться (складываться) при ослаблении гаек.
Техническое задание 4
“Часы”
1. Часы должны иметь форму
шестиугольника с равными сторонами
(правильного).
2. Они должны стоять с легким наклоном назад на
ровной поверхности, не падая.
3. Минутная стрелка должна быть длиннее
часовой, и они обе должны сохранять то положение,
которое попеременно им придают, определяя время
(то есть они не должны падать вниз).
С этими часами можно затем провести
игру:
– Покажите, который час. (12 часов
дня, 3 часа дня, 9 часов вечера/утра, 6 часов
вечера/утра. Это расположение стрелок на часах
узнаваемо.)
В конце урока можно предложить детям
решить такую конструктивную задачу:
– Как соединить две полосы под
углом, если они расположены по отношению друг к
другу под прямым углом? (Так как понятие прямого
угла еще не вводилось, то можно просто показать,
как расположить полосы, и сказать: под таким
углом.)
Чтобы детям было интереснее выполнять
такие задания, можно предложить их как загадку и
т. д. Такие соединения понадобятся на следующем
уроке при конструировании мебели.
УРОК 5
Тема: “План. Конструирование мебели”.
Цели: познакомить с понятием план;
научить использовать в конструкции уголковые
соединения; развивать конструктивное мышление.
На этом уроке учитель знакомит детей с
понятием план на примере плана
расстановки мебели в комнате. Можно принести
макет кукольной комнаты, можно использовать
рисунок, на котором изображены нужная мебель и
кукла. Куклу в любом случае надо иметь, так как
размеры и крепость мебели проверяют сажая на нее
куклу.
Можно использовать такой вариант:
ориентируясь на макет (или рисунок), дети
“расставляют” мебель на прямоугольной схеме
комнаты на доске. Каждый предмет изображается
схематически в виде цветного прямоугольника
(диван – красный, стол – синий) и квадрата (стулья
– зеленые квадраты, кресло – желтый).
После этого детям предлагается
сконструировать мебель для куклы. Технический
рисунок стула есть почти в любом конструкторе.
Начать лучше с него. Анализ проводится по альбому
рисунков.
Техническое задание 6
“Стул”
Сконструировать и собрать из деталей
конструктора стул для куклы.
1. Сиденье стула должно быть таким,
чтобы куклу можно было посадить на него.
2. Высота ножек и спинки стула должна быть
пропорциональна размеру сиденья.
3. Стул должен быть устойчивым и не
опрокидываться.
4. Ножки стула не должны подгибаться
(складываться) при ослаблении гаек.
5. Стул должен быть прост по конструкции и
удобен для сидения.
6. На стул нужно израсходовать как можно меньше
деталей.
Аналогичные технические задания
учитель составляет для стола (чтобы за ним можно
было сидеть на этом стуле); для кресла (оно должно
быть с подлокотниками); для дивана (на него кукла
должна лечь) или кровати.
Работу лучше всего организовать по бригадам:
каждый делает свой объект. Это позволит
распределить модели по сложности изготовления
соответственно возможностям детей.
В конце урока каждая бригада по очереди
расставляет свою мебель в комнате. В качестве
макета комнаты удобно использовать посылочную
картонную коробку с удаленной стенкой (стенку
вырезают не по сгибу, а отступив 2–3 см,
остается как бы рама). Внутри коробку оклеивают
обоями и прорезают окошки.
Дети потом долго и с удовольствием играют с этой
комнатой и мебелью. Этот набор можно
использовать затем на уроке чтения – для
составления сюжетных рассказов, на уроке
иностранного языка – для изучения тем
“Комната” и “Мебель”.
От редакции
Ваши пожелания, вопросы и сомнения по
поводу прочитанной работы присылайте по адресу:
121165, Москва, ул. Киевская, д. 24, редакция
“Начальная школа” с пометкой “для А.В.
Белошистой”.
1 В этой
публикации задания к урокам даны выборочно.
Более подробно см. Белошистая А.В. Наглядная
геометрия в 1-м классе. Тетрадь № 1. Тетрадь № 2. М.:
Классикс Стиль, 2003.
2 Урок проводится при
наличии дополнительных часов у учителя.
3 Урок проводится при
наличии у учителя свободных часов.
− А как мы строим работу на таких уроках? (Мы должны понять, что мы не
знаем и сами находим способ.)
− С чего вы начинаете каждый урок? (С повторения.)
2. Актуализация знаний и фиксация индивидуального затруднения в
пробном действии.
1 ЦОР – связь частей и целого на схемах
2. Устный счёт. Приготовили веер, начнём наш урок с устного счета.
(всем по 1 снежку)
3 Новый материал. Объявление темы урока. Давайте посмотрим на слайд.
Что вы тут видите? (геометрические фигуры).
Сегодня на уроке мы продолжим работу с геометрическими фигурами.
Научимся делить их на части, находить часть от фигуры и получать целую
фигуру из частей.
Перед вами лежат конверты с геометрическими фигурами.
4. Постановка проблемы. Открытие нового.
– Откройте конверты (в конверте 4 треугольника).
– Перед вами на партах части какой фигуры? Ваши предположения…
(Прямоугольник, квадрат)
– Как это доказать? (Соединить части)
– Как по–другому можно назвать квадрат (прямоугольник)? (Целое)
– Как получить только красную (желтую, зеленую, синюю) часть.
Получите квадрат из 4 треугольников. Сколько частей в целом?
Из 2х. Сколько теперь частей в целом?
Составьте из данных фигур треугольник. Сколько частей использовали?
УБЕРИТЕ треугольники в конверт
Теперь попробуйте составить круг. Сколько частей вам понадобилось?
А как получить часть круга? Например, половину? (убрать 2 части)
Работаем по командам 1 команда из этих частей моделирует бабочку, 2
команда змейку, а 3 команда (родителей) получает задание в паре из
геометрических фигур сконструировать любой объект, животное или
растение и приклеить на белый лист. В 1 файле фигуры на 2х их надо
поделить.
Вывод: Как найти целое? Как найти часть?
Молодцы ребята! Смело пририсовываем еще 1 снежок. Из такого
количества снега мы можем слепить большой комок для снеговика.
5а. Проектирование и фиксация нового знания. Первичное закрепление
(проговаривание).
Давайте теперь проверим по учебнику на стр. 28 полученные фигуры (№1 и
2)
А в задании №3 мы попробуем составить все возможные равенства по
рисунку.
– На сколько частей разбит квадрат? (на 2, на а и б)
– Объясните задание.
– Выполнить с комментированием.
– 1 ученик работает с места с частями фигуры.
– Из чего можно вычитать? (Только из целого)