Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
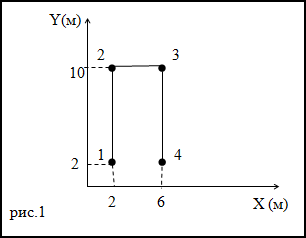
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
#1 11 мая 2005г. 16:29:43

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Тема: Как найти общую длину всех выделенных отрезков?
Мне часто приходится чертить раскладки прогонов, у которых различная длина, и что бы узнать общую длину всех прогонов я выделяю каждый, смотрю в свойствах его длину и на калькуляторе складываю. Подскажите пожалуста, может это можно как либо ускорить. Заранее спасибо,
#2 Ответ от Умник 11 мая 2005г. 17:04:36
- Умник
- Восстановленный участник
- На форуме с 17 июня 2004г.
- Сообщений: 206
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
не помню толи сам накарябал то ли на форуме срисовал используйте этот лисп:
(defun c:ln (/)
(apply '+
(mapcar '(lambda
(x)
(vlax-curve-getDistAtParam
(vlax-ename->vla-object x)
(vlax-curve-getEndParam x)
)
)
(vl-remove-if
'listp
(mapcar 'cadr (ssnamex (ssget)))
)
)
)
)
#3 Ответ от diz 11 мая 2005г. 17:15:13

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Большое спасибо. Только если честно, я ещё не профессионал и не знаю куда это писать. Но буду искать. Если не трудно подскажите
#4 Ответ от VK 11 мая 2005г. 19:51:13
- VK
- Восстановленный участник
- На форуме с 8 июня 2002г.
- Сообщений: 224
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
#5 Ответ от Евгений Елпанов 11 мая 2005г. 21:08:43

- Евгений Елпанов
- Активный участник
- Откуда: Москва
- На форуме с 2 июля 2004г.
- Сообщений: 2,538
- Спасибо: 10
Re: Как найти общую длину всех выделенных отрезков?
> Умник
Програмка отличная, но как-то непонятно:
(vlax-curve-getDistAtParam (vlax-ename->vla-object x);вызов через vla-obj (vlax-curve-getEndParam x);вызов через ent-name )
В хелпе сказано, обе эти функции вызывать через vla-obj
но
(vlax-curve-getDistAtParam x ;вызов через ent-name (vlax-curve-getEndParam x);вызов через ent-name )
Тоже отлично работает…
Может ли кто-нибудь прокаментировать?
#6 Ответ от Евгений Елпанов 11 мая 2005г. 21:43:59

- Евгений Елпанов
- Активный участник
- Откуда: Москва
- На форуме с 2 июля 2004г.
- Сообщений: 2,538
- Спасибо: 10
Re: Как найти общую длину всех выделенных отрезков?
Попробовал запустить все vlax-curve с параметром ent-name
(car (entsel))
Все отработали без ошибок! Хотя хелп напоминает, что надо
(vlax-ename->vla-object (car (entsel)))
Интересно, это недокументированная возможность или…
#7 Ответ от diz 12 мая 2005г. 10:51:49

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Нашёл на подсказанной вами ссылке програмку
(vl-load-com)
(defun entLen ( / set:entities int:allEntities int:curveEntities int:l rea:length)
(setq set:entities (ssget))
(if set:entities
(progn
(setq int:allEntities (sslength set:entities) ; количество выбранных примитивов
int:curveEntities 0 ; счетчик линейных примитивов
int:l 0 ; счетчик
rea:length 0.0 ; общая длина линейных примитивов
) ;_ setq
(while (< int:l (sslength set:entities))
(if (not
(vl-catch-all-error-p
(vl-catch-all-apply
‘vlax-curve-getStartPoint
(list (vlax-ename->vla-object (ssname set:entities int:l)))
) ;_ vl-catch-all-apply
) ;_ vl-catch-all-error-p
) ;_ not
(setq int:curveEntities (1+ int:curveEntities)
rea:length (+ rea:length
(vlax-curve-getDistAtParam
(vlax-ename->vla-object (ssname set:entities int:l))
(vlax-curve-getEndParam (ssname set:entities int:l))
) ;_ vlax-curve-getDistAtParam
) ;_ +
) ;_ setq
) ;_ if
(setq int:l (1+ int:l))
) ;_ while
(princ (strcat “n Выбрано примитивов: ” (itoa int:allEntities)
“, из них линейных: ” (itoa int:curveEntities)
“n Общая длина линейных примитивов: ” (rtos rea:length)
)
)
) ;_ progn
(alert “Примитивы не выбраны!”)
) ;_ if
(prin1)
) ;_ defun
Создал файл с расширением LSP
Загрузил приложение
После ввода в командную строку (entLen), следует предложение выбора объекта. Но после его выбора, хоть я нажимаю на Enter, хоть на првую кнопку мыши, всё сбрасывается.
Что делать?
P.S. Точно так же загружаю програмку подсказанную Умником, набираю c:ln и полное молчание.
#8 Ответ от Александр Ривилис 12 мая 2005г. 12:03:45

- Александр Ривилис
- Активный участник
- Откуда: Украина / Киев
- На форуме с 15 апреля 2005г.
- Сообщений: 8,661
- Спасибо: 158
Re: Как найти общую длину всех выделенных отрезков?
Какая верисия AutoCAD?
#9 Ответ от diz 12 мая 2005г. 13:18:59

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
2005
#10 Ответ от diz 12 мая 2005г. 13:26:53

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Кстати, программа
(vl-load-com)
(defun entLen ( / set:entities int:allEntities int:curveEntities int:l rea:length)
(setq set:entities (ssget))
(if set:entities
(progn
(setq int:allEntities (sslength set:entities) ; количество выбранных примитивов
int:curveEntities 0 ; счетчик линейных примитивов
int:l 0 ; счетчик
rea:length 0.0 ; общая длина линейных примитивов
) ;_ setq
(while (< int:l (sslength set:entities))
(if (not
(vl-catch-all-error-p
(vl-catch-all-apply
'vlax-curve-getStartPoint
(list (vlax-ename->vla-object (ssname set:entities int:l)))
) ;_ vl-catch-all-apply
) ;_ vl-catch-all-error-p
) ;_ not
(setq int:curveEntities (1+ int:curveEntities)
rea:length (+ rea:length
(vlax-curve-getDistAtParam
(vlax-ename->vla-object (ssname set:entities int:l))
(vlax-curve-getEndParam (ssname set:entities int:l))
) ;_ vlax-curve-getDistAtParam
) ;_ +
) ;_ setq
) ;_ if
(setq int:l (1+ int:l))
) ;_ while
(princ (strcat "n Выбрано примитивов: " (itoa int:allEntities)
", из них линейных: " (itoa int:curveEntities)
"n Общая длина линейных примитивов: " (rtos rea:length)
)
)
) ;_ progn
(alert "Примитивы не выбраны!")
) ;_ if
(prin1)
) ;_ defun
пошла без проблем. Большое спсибо “kos”-у
#11 Ответ от Владимир Громов 12 мая 2005г. 14:06:30

- Владимир Громов
- Активный участник
- На форуме с 10 июля 2004г.
- Сообщений: 8,349
- Спасибо: 4
Re: Как найти общую длину всех выделенных отрезков?
Может, следует в последней программе заменить слово “примитив” на слово “объект”?
#12 Ответ от Александр Ривилис 12 мая 2005г. 14:28:29

- Александр Ривилис
- Активный участник
- Откуда: Украина / Киев
- На форуме с 15 апреля 2005г.
- Сообщений: 8,661
- Спасибо: 158
Re: Как найти общую длину всех выделенных отрезков?
diz пишет:
P.S. Точно так же загружаю програмку подсказанную Умником, набираю c:ln и полное молчание.
Только сейчас до меня дошло! 
В командной строке нужно было набирать ln, а не c:ln
А по поводу версии AutoCAD я спросил, т.к. в вериях до AutoCAD 2000 эти функции не работают.
#13 Ответ от diz 12 мая 2005г. 16:39:53

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Если набираю ln, то следует предложение выбора объекта. Но после его выбора, хоть я нажимаю на Enter, хоть на првую кнопку мыши, всё сбрасывается. Но всё таки лучше чем раньше
#14 Ответ от Fantomas 12 мая 2005г. 18:49:55
- Fantomas
- Восстановленный участник
- На форуме с 7 декабря 2003г.
- Сообщений: 392
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Мой вариант:
(defun c:elen(/ fList firSet entSet filOut entList totLen)
(vl-load-com)
(setq fList '((-4 . "<OR")(0 . "*LINE")
(0 . "CIRCLE")(0 . "ARC")
(0 . "ELLIPSE")(-4 . "OR>")
(-4 . "<NOT")(0 . "MLINE")
(-4 . "NOT>"))
filOut 0
); end setq
(if
(not
(and
(setq firSet(ssget "_I")
entSet(ssget "_I" fList)
); end setq
); end and
); end not
(setq entSet(ssget fList))
(setq filOut(-(sslength firSet)(sslength entset)))
); end if
(if entSet
(progn
(setq entList
(mapcar 'vlax-ename->vla-object
(vl-remove-if 'listp
(mapcar 'cadr(ssnamex entSet))))
totLen
(apply '+
(mapcar '(lambda (x)
(vlax-curve-getDistAtParam x
(vlax-curve-getEndParam x)))
entList); end mapcar
); end apply
); end setq
(if(/= 0 filOut)
(princ(strcat "n" (itoa filout)
" were filtered out (unsupported type)"))
); end if
(princ(strcat "nTotal entities: "(itoa(length entList))
" Total length: "(rtos totLen)); end strcat
); end princ
); end progn
(progn
(if(/= 0 filOut)
(princ(strcat "n" (itoa filout)
" were filtered out (unsupported type)"))
(princ "nNothing selected")
); end if
); end progn
); end if
(princ)
); end c:elen
#15 Ответ от Геннадий aka PG 12 мая 2005г. 20:13:00

- Геннадий aka PG
- Восстановленный участник
- На форуме с 4 апреля 2002г.
- Сообщений: 1,348
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Я поюзал первую функцию Умника– нормально работает для линий и дуг.
#16 Ответ от Евгений Елпанов 12 мая 2005г. 20:24:26

- Евгений Елпанов
- Активный участник
- Откуда: Москва
- На форуме с 2 июля 2004г.
- Сообщений: 2,538
- Спасибо: 10
Re: Как найти общую длину всех выделенных отрезков?
> diz
Вопрос, с которого надо было начинать…
Мне часто приходится чертить раскладки прогонов, у которых различная длина, и что бы узнать общую длину всех прогонов я выделяю каждый, смотрю в свойствах его длину и на калькуляторе складываю.
У какого типа примитива ты смотришь длинну?
Что есть прогон – отрезок, полилиния, сплайн или может быть блок?
#17 Ответ от Александр Ривилис 12 мая 2005г. 21:25:16

- Александр Ривилис
- Активный участник
- Откуда: Украина / Киев
- На форуме с 15 апреля 2005г.
- Сообщений: 8,661
- Спасибо: 158
Re: Как найти общую длину всех выделенных отрезков?
… или может быть твердое тело, мультилиния и т.д…
#18 Ответ от Евгений Елпанов 13 мая 2005г. 10:38:42

- Евгений Елпанов
- Активный участник
- Откуда: Москва
- На форуме с 2 июля 2004г.
- Сообщений: 2,538
- Спасибо: 10
Re: Как найти общую длину всех выделенных отрезков?
> Александр Ривилис
Твердое тело наврятли… У него не посмотришь длинну (или что-то выражающее длинну) в свойствах…
Хотя можно передавать в названии слоя или в названии цвета, но не думаю – тогда проще выделить и посмотреть на слой или цвет…
Скорее всего прогон – примитив не имеющий свойства окончания…
#19 Ответ от diz 13 мая 2005г. 10:39:42

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
Мне в основном нужно находить сумму длин прямых линий, и это хорошо выполнияется программой, которрую выложил kos (я писал об этом), но почему то все остальные предложенные программы не идут. Следует предложение выбора объекта, и после выбора хоть я жму на Enter, хоть на правую кнопку, всё сбрасывается. Просто интересно почему?
И ещё вопрос. Я создал кнопку для работающего лиспа, но после перезагрузки компьютера, что бы она работала нужно нужно каждый раз загружать этот лисп. Нельзя ли зделать так, что бы это происходило автоматически?
#20 Ответ от Умник 13 мая 2005г. 10:57:14
- Умник
- Восстановленный участник
- На форуме с 17 июня 2004г.
- Сообщений: 206
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
> diz
Я использую запосщенную приблуду на 2004 и на 2005 (англ. версии) все работает чудесно… У вас случаем в командной сторке сколько строчек – если 2 то результата видно не будет – надо увеличить количество строк до 3-х – результат выводиться в командную строку или воспользуйтесь такой прогой:
(defun c:ln (/)
(alert
(strcat "Total Length is "
(rtos (apply '+
(mapcar '(lambda
(x)
(vlax-curve-getDistAtParam
(vlax-ename->vla-object x)
(vlax-curve-getEndParam x)
)
)
(vl-remove-if
'listp
(mapcar 'cadr (ssnamex (ssget)))
)
)
)
2
2
)
)
)
)
кстати говоря, если вы не использовали раньше лиспов то нужно дописать строчку:
(vl-load-com)
второй после defun
у меня подгружено больше двух сотен функций и загружать с каждой функцией (vl-load-com) смысла нет …
#21 Ответ от Александр Ривилис 13 мая 2005г. 11:28:28

- Александр Ривилис
- Активный участник
- Откуда: Украина / Киев
- На форуме с 15 апреля 2005г.
- Сообщений: 8,661
- Спасибо: 158
Re: Как найти общую длину всех выделенных отрезков?
> diz
Чтобы не нужно было загружать вручную lsp-файл, впришите в макрос для кнопки:
^C^C^P(if (null entLen) (load "entlen.lsp")) (entlen) ^P
Подразумевается, что имя lsp-файла entlen.lsp и он находится в путях доступа AutoCAD.
#22 Ответ от diz 13 мая 2005г. 11:37:05

- diz
- Восстановленный участник
- На форуме с 18 октября 2004г.
- Сообщений: 107
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
У меня действительно была 1 строка в командной строке. Теперь всё получается. Всем большое спасибо!!!
#23 Ответ от Геннадий aka PG 13 мая 2005г. 11:37:05

- Геннадий aka PG
- Восстановленный участник
- На форуме с 4 апреля 2002г.
- Сообщений: 1,348
- Спасибо: 0
Re: Как найти общую длину всех выделенных отрезков?
> diz
> Александр Ривилис
Лучше сделать свое отдельное меню (пусть даже пока из обной кнопки) и подгрузить егою
Подробнее
http://cadhlp.kulichki.com/pdmnu.htm
Посмотри там же сборник CADHLP там есть свое меню и в разделе Расчеты аналогичная прога, взятая тут
/*
https://www.caduser.ru/forum/topic11823.html
*/
(defun C:Dlina (/ Nab Sum i Curve Param)
(vl-load-com)
(if (setq Nab (ssget))
(progn
(setq Sum 0 i 0)
(repeat (sslength Nab)
(setq Curve (vlax-ename->vla-object (ssname Nab i))
i (1+ i)
Param (vl-catch-all-apply 'vlax-curve-getEndParam
(list Curve))
)
(if (not (vl-catch-all-error-p Param))
(setq Sum (+ Sum (vlax-curve-getDistAtParam Curve Param)))
)
)
)
)
(princ (strcat "nСумма длин выбранных элементов равна: " (rtos Sum 2 2)))
(prin1)
)
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
|
По какой формуле высчитать? Если знаю только, что диаметр равен 40 см.
Существует одна и на все времена формула для определения длины окружности и это все проходили по геометрии. Длина окружности(L) равна 2*Пи*R или просто Пи*D, где Пи постоянное число и равно 3,14 ; D – диаметр окружности. По условию задания нам известен диаметр D=40 см. Решение: L = Пи*D = 3,14 х 40 = 125,6 см. Ответ: длина окружности равна 125,6 сантиметра. автор вопроса выбрал этот ответ лучшим
Елленна 4 года назад Диаметр круга: D (BC) = 40 см Диаметр равняется двум радиусам: D = 2R (или АС+АВ)
Формула для вычисления длины окружности: L = 2πR или L = πD Значение постоянного числа π ≈ 3,14 D = 40 см Решение: Длина окружности L = 3,14 × 40 ≈ 125,6 см Если вычисления производить на калькуляторе, на котором встроено значение π, т. е. использовать клавишу с буквой π, то результат будет несколько иной: L = π × 40 = 125,6637061436 ≈ 125,7 см Ответ: при диаметре круга 40 см длина окружности приблизительно равна 125,7 см.
dred70 5 лет назад Зная диаметр окружности или круга, найти её общую протяженность-длину-периметр легко. Нужно всего лишь перемножить две цифры: тот диаметр, который мы знаем, с числом “пи”. Соответственно, если известен лишь радиус круга, формула несколько меняется: радиус мы умножаем на цифру 2 два, а затем на число “пи”, приблизительно равное значению 3,14.
SunnyDeidre 3 года назад Сразу пришла на ум загадка сфинкса из книги “Гарри Поттер и Кубок огня”: Число Пи константа равная отношению длины окружности к диаметру: π = L/D = 3,14. Если диаметр равен 40 см, то длина окружности составит: L = π*D = 3,14 * 40 = 125,6 (см). Ответ: длина окружности равна 125,6 см.
Ilanamo 5 лет назад Есть формула вычисления длинны окружности. Ее можно найти в гугле. Ее изучают в школе на уроках геометрии. Длинна окружности равна 2 пи R. То есть половину диаметра ( радиус) надо умножить на постоянное число ПИ ( греческая буква) равное 3,1415 и умножить на два. это по формуле.
Skarlet 5 лет назад Зная диаметр находишь радиус окружности. Радиус равен половине диаметра 40/2=20 см. А затем по формуле длины окружности находишь её длину. 2*3,14*20=125,6 см, где 3,14 это число Пи, а 20 это радиус окружности. Простейшая задачка.
AHTOXA89 5 лет назад Если вам известен диаметр окружности,то длину окружности найти довольно легко.Зная что число Пи равно 3.14 то можно просто умножить диаметр на число Пи а именно умножаем 40 на 3.14 из этого получаем 125.6 вот и все.
АЛЕКСАНДР 71 5 лет назад Диаметр круга умножается на Пи и вы узнаете длину окружности. В вашем случае 40*3,14=125.6. Длинна окружности будет 125.6 см. Знаете ответ? |
Как находить длину
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.

Инструкция
Если вам нужно найти длину стороны квадрата, то это не составит труда, если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют одинаковую длину, вычислить величину одной из них можно по формуле: a = √S.
В случае, когда требуется просчитать длину стороны прямоугольника, воспользуйтесь значениями его площади s и длины другой стороны b. Из формулы a=S/b вы получите искомое значение.
Чтобы определить длину окружности, то есть замкнутой линии, которая образует круг, воспользуйтесь значениями: r – ее радиусом и D – диаметром. Диаметр можно вычислить, умножив радиус окружности на 2. Известные вам значения подставьте в формулу определения длины окружности: C=2πr=πD, где π=3,14.
Для вычисления длины обычного отрезка воспользуйтесь методом эксперимента. То есть возьмите линейку и измеряйте.
Для того чтобы вычислить длину стороны такой фигуры, как треугольник, вам понадобятся размеры двух других сторон, а также величины углов. Если вы имеете дело с прямоугольным треугольником, и один из его углов равен 60 градусам, то величину его катета можно определить по формуле a=c*cosα, где c – гипотенуза треугольника, а α – угол между гипотенузой и катетом.
Помимо этого, если вы располагаете такими известными величинами, как высота b и площадь S треугольника, то длину стороны, которая является основанием, можно узнать благодаря формуле a=2√S/√√b.
Что касается правильного многоугольника, то длину его стороны можно просчитать, руководствуясь формулой an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности, n – количество углов.
Если вы хотите вычислить длину равносторонней фигуры, вокруг которой описана окружность, то сделать это можно по формуле an=R√3, где R – радиус окружности, n – количество углов фигуры.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей


Расстояние между центрами окружностей равно разности их радиусов


Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
|
| Каждая из окружностей лежит вне другой |  |
|
| Внешнее касание двух окружностей |  |
|
| Внутреннее касание двух окружностей |  |
|
| Окружности пересекаются в двух точках |  |
 |
| Каждая из окружностей лежит вне другой | ||
 |
||
| Внешнее касание двух окружностей | ||
 |
||
| Внутреннее касание двух окружностей | ||
 |
||
| Окружности пересекаются в двух точках | ||
 |
||
 |
||
| Каждая из окружностей лежит вне другой | ||

Расстояние между центрами окружностей больше суммы их радиусов |
||
| Внешнее касание двух окружностей | ||

Расстояние между центрами окружностей равно сумме их радиусов |
||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой |
||
| Внутренняя касательная к двум окружностям |  |
|
| Внутреннее касание двух окружностей |  |
|
| Окружности пересекаются в двух точках |  |
|
| Внешнее касание двух окружностей |  |
|
 |
||
 |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
 |
| Внутренняя касательная к двум окружностям |
 |
| Внутреннее касание двух окружностей |
 |
| Окружности пересекаются в двух точках |
 |
| Внешнее касание двух окружностей |
 |
 |
| Каждая из окружностей лежит вне другой |
 |


Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.


Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.


Существует единственная общая внешняя касательная. Других общих касательных нет.


Существуют две общих внешних касательных. Других общих касательных нет.




Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.


Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Формулы для длин общих касательных и общей хорды двух окружностей
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям |  |
|
| Внутренняя касательная к двум окружностям |  |
|
| Общая хорда двух пересекающихся окружностей |  |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

| Внешняя касательная к двум окружностям |
 |
| Внутренняя касательная к двум окружностям |
 |
| Общая хорда двух пересекающихся окружностей |
 |


Длина общей внешней касательной к двум окружностям вычисляется по формуле



Длина общей внутренней касательной к двум окружностям вычисляется по формуле

| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |

Длина общей хорды двух окружностей вычисляется по формуле
Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Взаимное расположение окружностейВыясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки. Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: II. Не пересекающиеся окружности не имеет общих точек. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов: Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: R + r]” title=”Rendered by QuickLaTeX.com”/> III. Касающиеся окружности имеют одну общую точку — точку касания. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами равно разности радиусов: Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. Расстояние между центрами двух пересекающихся окружностей, если даны радиусы и общая длина хордыДаны два круга с заданными радиусами, которые пересекаются и имеют общий аккорд. Длина общего аккорда дается. Задача состоит в том, чтобы найти расстояние между центрами двух окружностей. Примеры: Подход :
Ниже приведена реализация вышеуказанного подхода: // C ++ программа для поиска [spoiler title=”источники:”] [/spoiler] |













