Ольга Копотева
Знаток
(493)
7 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
Юрий Гринькин
Знаток
(327)
6 лет назад
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Панкратова Татьяна
Знаток
(260)
4 года назад
как найти сумму длин всех ребер параллелепипеда
Кариночка Ученик (158), Вопрос решён 5 лет назад
11 Нравится Ответить
ЛУЧШИЙ ОТВЕТ
Анна Храпко 7 лет назад
Знаток (276)
L=4(a+b+c)
26 Нравится Пожаловаться
16 ОТВЕТОВ
ЛИЛИЯ Шевченко 3 года назад
Ученик (103)
L=4a+4b+4c
8 Нравится Пожаловаться
Ян Серебряков 3 года назад
Ученик (136)
L=4a+4b+4
2 Нравится Пожаловаться
Артём Фризен 3 года назад
Знаток (309)
L=4(a+b+c)
2 Нравится Пожаловаться
Ольга Копотева 2 года назад
Ученик (230)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Подробнее: http://www.kakprosto.ru/kak-68111-kak-nayti-summu-dlin-vseh-ryober-parallelepipeda#ixzz442A3268u
5 Нравится Пожаловаться
Юлия Моисеева 2 года назад
Ученик (133)
L=4(a+b+c)
2 Нравится Пожаловаться
katja maslova 2 года назад
Ученик (204)
L=4(a+b+c)
1 Нравится Пожаловаться
Eekler 2 года назад
Профи (633)
L=4(a+b+c)
Нравится Пожаловаться
Яна Подосенова 2 года назад
Ученик (166)
L=4(a+b+c)
Нравится Пожаловаться
Юрий Гринькин 2 года назад
Знаток (302)
1
Для удобства введем обозначения: А и В стороны основания параллелепипеда; С – его боковая грань.
2
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С) Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение з
Как найти сумму длин всех рёбер параллелепипеда
У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.
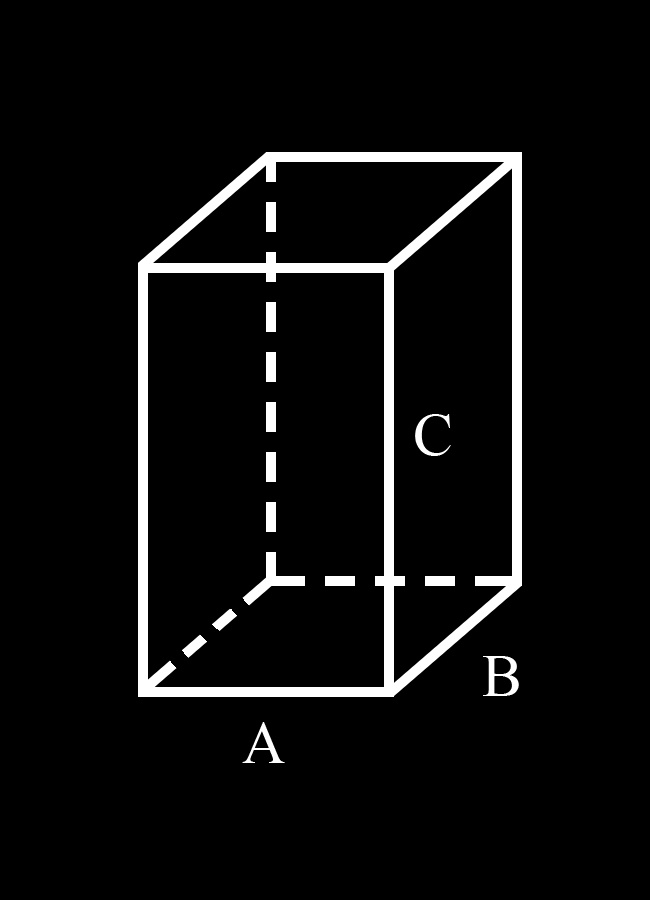
Инструкция
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.
Параллелепипед – это призма, основанием которой является параллелограмм.
Параллелепипед имеет 6 граней, и все они являются параллелограммами.
Противоположные грани равны и параллельны. Это важно.
Источники:
- сумма длин ребер прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
Как обнаружить сумму длин всех рёбер параллелепипеда
У вас появилось затруднение в решении геометрической задачи, связанной с параллелепипедом. Тезисы решения таких задач, основанные на свойствах параллелепипеда , высказаны в примитивный и доступной форме. Осознать – значит решить. Сходственные задачи огромнее не будут вызывать у вас сложностей.
Инструкция
1. Для комфорта введем обозначения:А и В стороны основания параллелепипеда ; С – его боковая грань.
2. Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что супротив стороны А лежит равная ей сторона А. От того что противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3. То же дозволено сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4. Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда ). Ребро С единовременно является стороной 2-х соседних граней параллелепипеда . От того что противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5. Таким образом, сумма всех ребер параллелепипеда : 4А+4В+4С либо 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.Таким образом, решение задачи касательно пространственного тела неизменно дозволено свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Надобно примитивно отменно усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.Параллелепипед – это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, и все они являются параллелограммами. Противоположные грани равны и параллельны. Это главно.
Given the area of three faces of the rectangular parallelepiped which has a common vertex. Our task is to find the sum of lengths of all 12 edges of this parallelepiped.
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square or as a cuboid to a rectangle. A picture of a rectangular parallelepiped is shown below.
Examples:
Input: 1 1 1
Output: 12Input: 20 10 50
Output: 68
Approach: The area given are s1, s2 and s3 . Let a, b and c be the lengths of the sides that have one common vertex. Where , , . It’s easy to find the length in terms of faces areas: , , . The answer will be the summation of all the 4 sides, there are four sides that have lengths equal to a, b and c.
In the first example the given area s1 = 1, s2 = 1 and s3 = 1. So with the above approach, the value of a, b, c will come out to be 1. So the sum of the length of all 12 edges will be 4 * 3 = 12.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double findEdges(double s1, double s2, double s3)
{
double a = sqrt(s1 * s2 / s3);
double b = sqrt(s3 * s1 / s2);
double c = sqrt(s3 * s2 / s1);
double sum = a + b + c;
return 4 * sum;
}
int main()
{
double s1, s2, s3;
s1 = 65, s2 = 156, s3 = 60;
cout << findEdges(s1, s2, s3);
return 0;
}
Java
import java.io.*;
class GFG {
static double findEdges(double s1, double s2, double s3)
{
double a = Math.sqrt(s1 * s2 / s3);
double b = Math.sqrt(s3 * s1 / s2);
double c = Math.sqrt(s3 * s2 / s1);
double sum = a + b + c;
return 4 * sum;
}
public static void main (String[] args) {
double s1, s2, s3;
s1 = 65; s2 = 156; s3 = 60;
System.out.print(findEdges(s1, s2, s3));
}
}
Python3
import math
def findEdges(s1, s2, s3):
a = math.sqrt(s1 * s2 / s3)
b = math.sqrt(s3 * s1 / s2)
c = math.sqrt(s3 * s2 / s1)
sum = a + b + c
return 4 * sum
if __name__=='__main__':
s1 = 65
s2 = 156
s3 = 60
print(int(findEdges(s1, s2, s3)))
C#
using System;
public class GFG{
static double findEdges(double s1, double s2, double s3)
{
double a = Math.Sqrt(s1 * s2 / s3);
double b = Math.Sqrt(s3 * s1 / s2);
double c = Math.Sqrt(s3 * s2 / s1);
double sum = a + b + c;
return 4 * sum;
}
static public void Main (){
double s1, s2, s3;
s1 = 65; s2 = 156; s3 = 60;
Console.WriteLine(findEdges(s1, s2, s3));
}
}
PHP
<?php
function findEdges($s1, $s2, $s3)
{
$a = sqrt($s1 * $s2 / $s3);
$b = sqrt($s3 * $s1 / $s2);
$c = sqrt($s3 * $s2 / $s1);
$sum = $a + $b + $c;
return 4 * $sum;
}
$s1; $s2; $s3;
$s1 = 65; $s2 = 156; $s3 = 60;
echo findEdges($s1, $s2, $s3);
?>
Javascript
function findEdges(s1, s2, s3) {
let a = Math.sqrt(s1 * s2 / s3);
let b = Math.sqrt(s3 * s1 / s2);
let c = Math.sqrt(s3 * s2 / s1);
let sum = a + b + c;
return 4 * sum;
}
let s1 = 65, s2 = 156, s3 = 60;
console.log(findEdges(s1, s2, s3));
Time Complexity: O(logn) because the inbuilt sqrt function is being used
Auxiliary Space: O(1)
