Как найти общую эдс источника тока

Как найти общую эдс источника тока

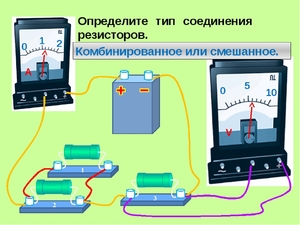
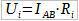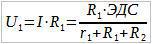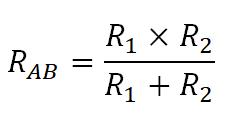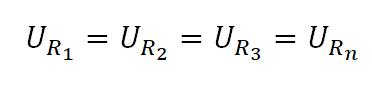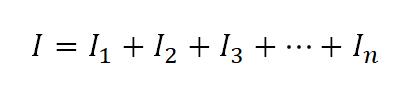§ 17. Последовательное и параллельное соединение источников

При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.

При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.

В схеме на рис. 17.1 $$ {mathcal{E}}_{1}=12$$ В, $$ {mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.

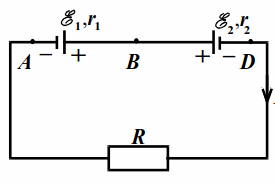Рис. 17.1

Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {varphi }_{A}-{varphi }_{B}$$ и $$ {varphi }_{B}-{varphi }_{D}$$.

ЭДС батареи последовательно соединённых источников:

$$ mathcal{E}={mathcal{E}}_{1}-{mathcal{E}}_{2}=9$$ B.

Причём, полярность батареи совпадает с полярностью источника $$ {mathcal{E}}_{1}$$ т. к. $$ {mathcal{E}}_{1}>{mathcal{E}}_{2}$$.

Ток по закону Ома для замкнутой цепи $$ I=mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:

$$ {varphi }_{A}-{varphi }_{B}+{mathcal{E}}_{1}=I{r}_{1,}$$, $$ {varphi }_{B}-{varphi }_{D}-{mathcal{E}}_{2}=I{r}_{2}$$.

Отсюда $$ {varphi }_{A}-{varphi }_{B}=I{r}_{1}-{mathcal{E}}_{1}=-11$$ B, $$ {varphi }_{B}-{varphi }_{D}=I{r}_{2}+{mathcal{E}}_{2}=5$$ B.

Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.

Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {mathcal{E}}_{1}=mathcal{E}$$, $$ {r}_{1}=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal{E}$$ и $$ {mathcal{E}}_{1}$$:

$$ {mathcal{E}}_{0}=3mathcal{E}-{mathcal{E}}_{1}=3mathcal{E}-mathcal{E}=2mathcal{E}$$,

$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.

Ток $$ I={displaystyle frac{{mathcal{E}}_{0}}{R+{r}_{0}}}={displaystyle frac{6mathcal{E}}{3R+11r}}$$.

Источник

ЭДС. Закон Ома для полной цепи

  • Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

  • Сторонняя сила

  • Закон Ома для полной цепи

  • КПД электрической цепи

  • Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

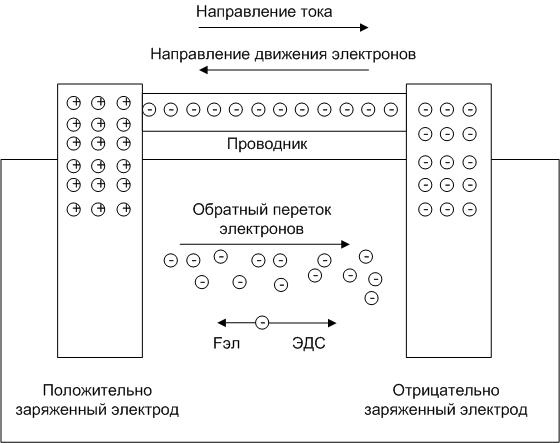
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд q:

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду q нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила vec{F_E}, направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила vec{F_{CT}} не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через A_{CT} работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы A_{CT} называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда q вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, A_{CT} — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа A_{CT} прямо пропорциональна перемещаемому заряду q. Поэтому отношение A_{CT}/q уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается mathcal E:

mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}. (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением r, которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной mathcal E, и внутренним сопротивлением r подключён к резистору R (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока I в цепи и напряжение U на резисторе R.

За время t по цепи проходит заряд q = It. Согласно формуле (1) источник тока совершает при этом работу:

A_{CT} = Eq = EIt. (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях R и r. Данное количество теплоты определяется законом Джоуля–Ленца:

Q = I^2Rt + I^2rt = I^2(R + r)t. (3)

Итак, A_{CT} = Q, и мы приравниваем правые части формул (2) и (3):

mathcal E It = I^2(R + r)t.

После сокращения на It получаем:

mathcal E = I(R + r).

Вот мы и нашли ток в цепи:

I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}. (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0), то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе R с помощью закона Ома для участка цепи:

U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}. (5)

Это напряжение является разностью потенциалов между точками a и b (рис. 2). Потенциал точки a равен потенциалу положительной клеммы источника; потенциал точки b равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет Utextless mathcal E — ведь mathcal E умножается на дробь, меньшую единицы. Но есть два случая, когда U = mathcal E.

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт U = mathcal E.

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: R = infty. Тогда величина R + r неотличима от R, и формула (5) снова даёт нам U = mathcal E.

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор R называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке R за время t, обозначим Q_{polezn}.

Если сила тока в цепи равна I, то

Q_{polezn} = I^2Rt.

Некоторое количество теплоты выделяется также на источнике тока:

Q_{ist} = I^2rt.

Полное количество теплоты, которое выделяется в цепи, равно:

Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.

КПД электрической цепи — это отношение полезного тепла к полному:

eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0).

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3  показан неоднородный участок, содержащий резистор R и источник тока. ЭДС источника равна mathcal E, его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно r, можно просто заменить резистор R на резистор R + r).

Рис. 3. ЭДС «помогает» току: varphi_a - varphi_b + mathcal E = IR

Сила тока на участке равна I, ток течёт от точки a к точке b. Этот ток не обязательно вызван одним лишь источником mathcal E. Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток I является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек a и b равны соответственно varphi_a и varphi_b. Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: U = varphi_a - varphi_b. За время t через участок проходит заряд q = It, при этом стационарное электрическое поле совершает работу:

A_{POL} = Uq = UIt.

Кроме того, положительную работу совершает источник тока (ведь заряд q прошёл сквозь него!):

A_{CT} = mathcal Eq = mathcal EIt.

Сила тока постоянна, поэтому суммарная работа по продвижению заряда q, совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: A_{POL} + A_{CT} = Q.

Подставляем сюда выражения для A_{POL}, A_{CT} и закон Джоуля–Ленца:

UIt + mathcal EIt = I^2Rt.

Сокращая на It, получаем закон Ома для неоднородного участка цепи:

U + mathcal E = IR, (6)

или, что то же самое:

varphi a - varphi b + mathcal E = IR. (7)

Обратите внимание: перед mathcal E стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд q от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки a к точке b.

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то mathcal E = 0. Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением r. Это, как мы уже упоминали, равносильно замене R на R + r:

varphi_a - varphi_b + mathcal E = I(R + r).

Теперь замкнём наш участок, соединив точки a и b. Получим рассмотренную выше полную цепь. При этом окажется, что varphi_a = varphi_b, и предыдущая формула превратится в закон Ома для полной цепи:

mathcal E = I(R + r).

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник mathcal E «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от a к b, направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току: varphi_a - varphi_b - mathcal E = IR

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против mathcal E. Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

A_{CT} = mathcal E q = mathcal EIt.

Тогда закон Ома для неоднородного участка примет вид:

varphi_a - varphi_b - mathcal E = IR, (8)

или:

U - mathcal E = IR,

где по-прежнему U = varphi_a - varphi_b — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

varphi_a - varphi_b pm mathcal E = IR.

Ток при этом течёт от точки a к точке b. Если направление тока совпадает с направлением сторонних сил, то перед mathcal E ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника  r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

  1. Сопротивление проводника тем больше, чем больше его длина.
  2. Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением:  (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На ри­сун­ке приведён гра­фик за­ви­си­мо­сти на­пря­же­ния на кон­цах же­лез­но­го про­во­да пло­ща­дью по­пе­реч­но­го се­че­ния 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

displaystyle I=frac{U}{R};

displaystyle R=frac{U}{I}.

По графику: при U=60 B, I=3 B.

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через по­пе­реч­ное се­че­ние про­вод­ни­ков за 8 с про­шло 1020 элек­тро­нов. Ка­ко­ва сила тока в про­вод­ни­ке? Ответ дайте в амперах.

Решение:

По определению силы тока:

displaystyle I=frac{q}{t}.

Заряд всех электронов: q=Ncdot e, где е — модуль заряда электрона, e=1,6cdot 10^{-19} Кл.

Тогда displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.

Ответ: 2.

Задача 3. Иде­аль­ный ам­пер­метр и три ре­зи­сто­ра общим со­про­тив­ле­ни­ем 66 Ом вклю­че­ны по­сле­до­ва­тель­но в элек­три­че­скую цепь, со­дер­жа­щую ис­точ­ник с ЭДС рав­ной 5 В, и внут­рен­ним со­про­тив­ле­ни­ем r=4 Ом. Ка­ко­вы по­ка­за­ния ам­пер­мет­ра? (Ответ дайте в ам­пе­рах, округ­лив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда displaystyle I=frac{5}{66+4}=0,07 A.

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На ри­сун­ке изоб­ра­же­на схема элек­три­че­ской цепи, со­сто­я­щей из ис­точ­ни­ка по­сто­ян­но­го на­пря­же­ния с ЭДС 5 В и пре­не­бре­жи­мо малым внут­рен­ним со­про­тив­ле­ни­ем, ключа, ре­зи­сто­ра с со­про­тив­ле­ни­ем 2 Ом и со­еди­ни­тель­ных про­во­дов. Ключ за­мы­ка­ют. Какой заряд про­те­чет через ре­зи­стор за 10 минут? Ответ дайте в ку­ло­нах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

displaystyle I=frac{q}{t}.

Отсюда q=Icdot t=2,5cdot 600=1500 Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

На чтение 9 мин Просмотров 1.8к. Опубликовано 11.09.2022 Обновлено 11.09.2022

Содержание

  1. Понятие ЭДС и единица измерения
  2. Где и как образуется электродвижущая сила
  3. Виды ЭДС
  4. Законы и формулы
  5. ЭДС аккумуляторной батареи
  6. ЭДС индукции
  7. Внутреннее сопротивление источника ЭДС
  8. Закон Ома для полной цепи
  9. Как найти мощность ЭДС

Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.

Понятие ЭДС и единица измерения

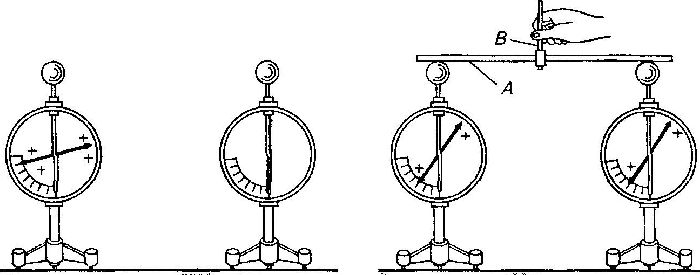
Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Опыт с двумя электроскопами

Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.

Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.

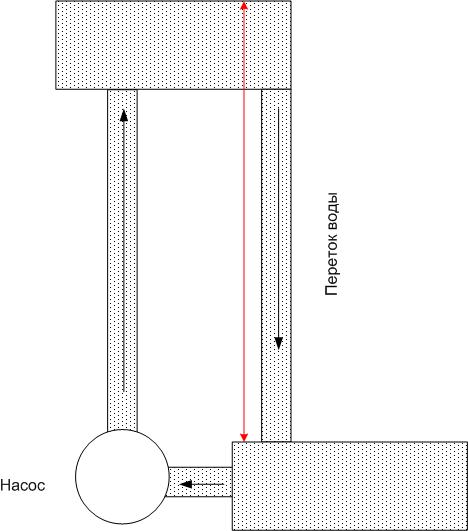
В чем суть ЭДС: единица измерения, виды и формулы для расчета

Перенос зарядов посредством ЭДС

Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Необходимость наличия ЭДС на примере перетока воды

ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.

Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.

В видео простыми словами объясняется чем отличаются ЭДС и напряжение

Где и как образуется электродвижущая сила

Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.

Виды ЭДС

Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:

  • фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
  • электрохимической природы – всем известные гальванические элементы и аккумуляторы;
  • термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
  • пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
  • ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.

В технике встречаются и некоторые другие виды ЭДС, но реже.

Законы и формулы

Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.

Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:

ε=A/q=A/(I*t)

ЭДС аккумуляторной батареи

ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:

  1. Свинцово-кислотные элементы – 2,17 вольта.
  2. Никель-кадмиевые батареи – 1,37 вольта.
  3. Никель-металлогидридные элементы – 1,37 вольта.
  4. Щелочные аккумуляторы – 1,45 вольта.
  5. Литий-ионные элементы – 4,2 вольта.

Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Последовательно соединенные элементы автомобильной батареи

ЭДС индукции

Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.

Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:

ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Ток в замкнутом контуре, вызываемый ЭДС индукции под действием внешнего магнитного поля

В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Статор автомобильного генератора – витки соединяются последовательно

Внутреннее сопротивление источника ЭДС

Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Снижение выходного напряжения аккумулятора при уменьшении сопротивления нагрузки

Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.

Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.

Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Внутреннее сопротивление в виде резистора внутри источника тока

Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.

Для наглядности рекомендуем видео-урок.

Закон Ома для полной цепи

Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).

Как найти мощность ЭДС

Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.

Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:

  • I*R=Uвнеш – напряжение на внешней нагрузке;
  • i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.

Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.

Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:

I=U/R=11,5/5=2,3 А.

Выражение для ЭДС примет вид:

ε= 2,3*5+2,3*r=11,5+2,3*r.

Для второго замера на сопротивлении 1 Ом ток составит:

I=U/R=9,86/1=9,86 ампер

Следовательно,

ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.

Левые части уравнений равны, тогда можно приравнять правые:

11,5+2,3*r=9,86 +9,86 *r

Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.

Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.

Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.

Источник

Содержание

  • 1 Как посчитать эдс?
  • 2 Где находится эдс?
  • 3 Как найти эдс источника питания?
  • 4 Как найти силу тока в цепи через эдс?
  • 5 Каким образом можно измерить эдс источника тока?
  • 6 Как определить силу тока при коротком замыкании?
  • 7 Где используется эдс?
  • 8 Где возникают сторонние силы?
  • 9 Как возникает эдс?
  • 10 Как связаны между собой эдс и напряжение?
  • 11 Как найти внутреннее сопротивление источника тока?
  • 12 Что такое эдс для чайников?
  • 13 Как найти силу тока если известна мощность и напряжение?
  • 14 Как найти силу тока через?

Как посчитать эдс?

Электродвижущая сила (ЭДС) элемента равна разности потенциалов правого и левого электродов: E = EП — EЛ. Если ЭДС элемента положительна, то реакция (так, как она записана в элементе) протекает самопроизвольно.

Где находится эдс?

— элемент контура. ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке.

Как найти эдс источника питания?

На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи.

Как найти силу тока в цепи через эдс?

Через ЭДС, внутреннее сопротивление и нагрузку R

Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры: внешнее сопротивление проводников (R); ЭДС источника питания (ε); внутреннее сопротивление источника, обладающего ЭДС (r′).

Каким образом можно измерить эдс источника тока?

Для измерения величины ЭДС и напряжения применяется прибор, называемый вольтметром. Если вольтметр подключить непосредственно к полюсам источника электрической энергии, то при разомкнутой электрической цепи он покажет ЭДС источника электрической энергии, а при замкнутой — напряжение на его зажимах: (рис.

Как определить силу тока при коротком замыкании?

Формула для измерения силы тока короткого замыкания: Iкз = E/r.
…
Сила тока при коротком замыкании участка цепи

  1. -I – величина тока (его сила);
  2. U – разность потенциалов (напряжение сети);
  3. R – электрическое сопротивление.

Где используется эдс?

Используется в холодильниках, термопарах. Индукционная. Образуется при пересечении проводником магнитного поля. Эффект используется в электродвигателях, генераторах, трансформаторах.29 мая 2018 г.

Где возникают сторонние силы?

В гальванических элементах сторонние силы возникают за счет энергии химических реакций между электродами и электролитами Гальванические элементы и аккумуляторы преобразуют химическую энергию в электрическую. В генераторе сторонние силы образуются за счет механической энергии вращения ротора генератора и т.

Как возникает эдс?

е. чем больше его индукция, тем большая ЭДС возникает в проводнике, пересекающем это поле. Итак, величина ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо пропорциональна индукции магнитного поля, длине проводника и скорости его перемещения.

Как связаны между собой эдс и напряжение?

По действием эдс в цепи протекает ток i=E/(R0+R). Напряжение на зажимах источника, то есть напряжение на внешней части, U=E-i*R0. А так как i*R0=U0 — напряжение на внутренней части цепи, то E=U0+U. Ответ: E=U0+U.

Как найти внутреннее сопротивление источника тока?

Нужно определить внутреннее сопротивление аккумулятора.

  1. По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом;
  2. Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.

Что такое эдс для чайников?

Электродвижущая сила (ЭДС) — в устройстве, осуществляющем принудительное разделение положительных и отрицательных зарядов (генераторе), величина, численно равная разности потенциалов между зажимами генератора при отсутствии тока в его цепи, измеряется в Вольтах.

Как найти силу тока если известна мощность и напряжение?

Если известна мощность и напряжение

  1. P=UI. После несложных мы получаем формулу для вычислений
  2. I=P/U. Следует отметить, что такое выражение справедливо для цепей постоянного тока. …
  3. Р1 = Р2/η …
  4. S = P1/cosφ …
  5. Iном = S/(1,73·U) …
  6. I=U/R. …
  7. P=UI. …
  8. U=IR.

Как найти силу тока через?

Силу тока можно определить и по другой формуле, которая в себе содержит напряжение и мощность. Она имеет вид: I=P/U (сила тока равна электрическая мощность деленная на напряжение). То есть, 1 ампер равен 1 ватт деленный на 1 вольт. Две других формулы, выходящие из этой, имеют такой вид: P=U*I и U=P/I.

Источник

Электрическая цепь — это совокупность элементов и устройств, предназначенных для протекания электрического тока, электромагнитные процессы в которых, могут быть описаны с помошью понятий сила тока и напряжение .

Электрическая схема — это документ, составленный в виде изображения, на котором с помощью условных обозначений показаны элементы электрической цепи и их взаимодействие.

Рассмотрим два основных элемента электрической цепи: источник ЭДС и резистор .

Резистор — это элемент электрической цепи, обладающий определенным или переменным значением омического сопротивления, предназначенный для линейного преобразования силы тока в напряжение, напряжения в силу тока, ограничения тока и поглащения электрической энергии. На электрических схемах, резистор обозначается:

Далее, рассмотрим основные характеристи и параметры реальных резистров:

20 градусов цельсия).


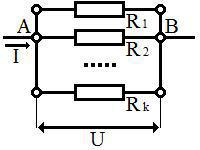
Пусть по некоторому участку цепи A-B, являющегося последовательным только соединением резисторов R1. Rk, течет электрический ток I. Необходимо определить падение напряжения на данном участке цепи и общее электрическое сопротивление данного участка.

В начале, найдем падение напряжения на участке A-B. Т.к. в цепи нет источников ЭДС, то согласно закону ома, падение напряженя на i-м участке цепи равно: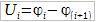

Просуммировав падение напряжения на всех участках (на всех резистрах), получим: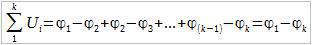

Заметим, что Ф1 = Фa, а Фk = Фb, тогда: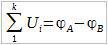

Разность потенциалов точек A и B по определению (с учетом того, что ЭДС на участке A-B равна нулю) является падением напряжения на участке A-B.
Имеем, что: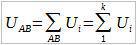

Теперь, определим суммарное сопротивление участка цепи A-B.
Запишим закон Ома для участка A-B: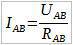

Из этой формулы выразим сопротивление Rab: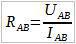

Далее, вспомним, что падение напряжения на участке A-B равно сумме падений напряжений на каждом из резисторов: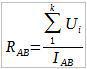

Теперь, для каждого резистра запишем закон Ома для однородного участка цепи: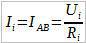

Отсюда:


Перед тем, как переходить к условию задачи, введем дополнительное определение:
Узел — участок электрической цепи в котором сходятся более двух проводников.

Пусть в узел A втекакет ток I (из закона сохранения зарядов следует, что из узла B вытекает точно такой-же по величине ток). Необходимо определить эквивалентное сопротивление участка цепи A-B.
Вспомним, что: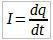

Рассмотрим достаточно малый промежуток времени, на котором ток можно считать постоянным, тогда: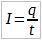

Ток через участок A-B равен отношению суммарного заряда q, прошедшего через данный участок цепи за время t к этому времени.
В узле A произойдет разделение тока на k — путей. Заряды будут перемещаться через каждый резистор. Пусть за время t через резистор R1 пройдет заряд q1, через R2 — q2, . , Rk — qk. Поскольку, выполняется закон сохранения заряда: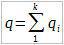

Разделим оба выражения на t, получим: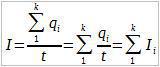

Получаем, что ток втекающий в узел равен сумме токов, вытекающих из этого узла. Более точно данное правило формулируется так: Алгебраическая сумма токов сходящихся в каждом узле любой цепи равна нулю — первое правило Кирхгофа.

Далее, применем закон Ома для однородного участка цепи: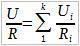

Заметим, что напряжения на всех резистрах одинаковы и равны U, т.к. Ui = Фa — Фb. Получаем: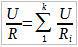

Далее разделим уравнение на U: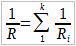

В результате, мы получили закон для поиска эквивалентного сопротивления при параллельном соединении резисторов.

Источник ЭДС (идеальный источник напряжения) — это элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока. ЭДС источника м.б. задана либо как постоянная величина, либо как функция от врмени или внешнего управления. Идеальный источник ЭДС имеет следующее графическое обозначение на электрических схемах: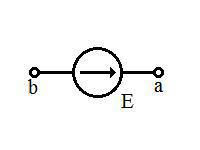

На практике, идеальных источников ЭДС не существует. Попробуем убедится в этом: Запишем закон Ома для полной цепи: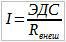

Заметим, что при уменьшении внешнего сопротивления до нуля, получим бесконечный рост силы тока, что физически невозможно. По этой причине вводят понятие реального источника напряжения
Реальный источник напряжения — это элемент электрической цепи, имеющий сопротивление r, на котором действует ЭДС. Обозначается: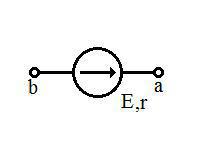

Реальный источник напряжения м.б. представлен как последовательное соединение источника ЭДС и резистра r: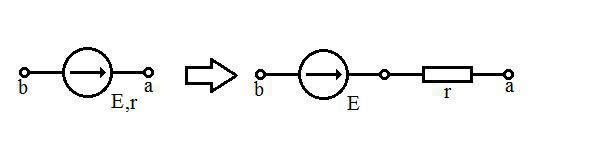

// тут нужно дописать о выборе направления ЭДС //

Делитель напряжения — это устройство входное и выходное напряжение связаны коэффиентом передачи a, 0
Рассмотрим устройство резистивного делителя напряжения:


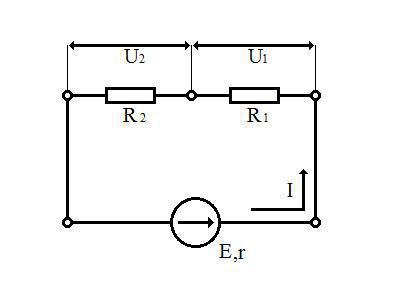
Пусть электрисеская цепь состоит из источника ЭДС (E,r) и двух резистров R1 и R2. По ней течет электрический ток, I. Необходимо найти отношение падений напряжения на резистрах и их сумму.

Запишем закон Ома для полной цепи: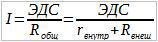

Сопротивление источника ЭДС нам известно, оно равно r. Резистры R1 и R2 образуют последовательное соединение, по этому их сопротивления складываются: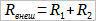

Ток I, протекающий через цепь равен: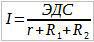

Теперь, применим закон Ома для участка цепи к R1 и R2: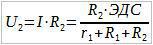


Разделим U1 на U2: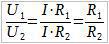

Отношение напряжений U1 к U2 равно отношению сопротивлений R1 к R2.

Далее, сложим U1 и U2. Получим U12 — падение напряжения на внешнем участке цепи: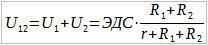

Если r достаточно мало, то падение напряжения на внешнем участке цепи практически равно ЭДС.

1) Подключите лабораторный блок питания (далее, БП) к вольтметру (рисунок ниже). С помошью ручки регулятора (располагается на блоке питания) изменяйте напряжение на вольтметре пока он не покажет значение 9 Вольт. Поскольку, внутреннее сопротивление блока питаия мало ( После установки сопротивления для каждого из вариантов А), Б), В), необходимо отключа ть мультимет р, используемый для измерения сопротивления.

4)Далее, необходимо:
Замкнуть ключ K. С помощью вольтметра измерить падение напряжения на резистре R для случаев A, Б и B. Проанализировать полученные результаты, на основании замеров сделать вывод о внутреннем сопротивлении источников питания.

5)Сфотографируйте и разместите этапы сборки.

6)Заполните таблицу падений напряжения для случаев А,Б,В.

Ход работы:
1)Соберите электрическую цепь, состоящую из источника ЭДС, двух последовательно соединенных резисторов R1, R2 и вольтметра (мультиметр в ежиме измерения напряжения) согласно схеме: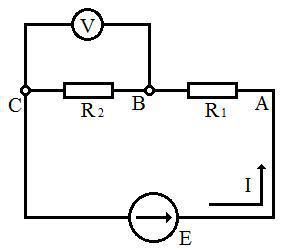

В качестве источника ЭДС возьмите лабораторный БП (установите на 15 вольт).
Используйте резистры R1 и R2 сопротивлениями:
А) 1КОм, 1КОм.
Б) 1КОм, 2КОм.
В) 1КОм, 5КОм.
Г) 1КОм, 10КОм.

2)Для всех вариантов А-Г с помощью мультиметра измерьте падение напряжения на участке С-B. Проанализируйте полученные результаты. В каких отношениях резистры делят напряжение?

3)Сфотографируйте и разместите этапы сборки.

4)Заполните таблицу падений напряжения для случаев А-Г.

При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.

При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.

Найти напряжения на зажимах источников, т. е. разность потенциалов $$ <varphi >_-<varphi >_$$ и $$ <varphi >_—<varphi >_$$.

ЭДС батареи последовательно соединённых источников:

Причём, полярность батареи совпадает с полярностью источника $$ <mathcal>_<1>$$ т. к. $$ <mathcal>_<1>><mathcal>_<2>$$.

Ток по закону Ома для замкнутой цепи $$ I=mathcal/(R+_<1>+_<2>)=1$$ A. По закону Ома для участков цепи `AB` и `BD`:

Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.

Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ <mathcal>_<1>=mathcal$$, $$ _<1>=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal$$ и $$ <mathcal>_<1>$$:

Источник

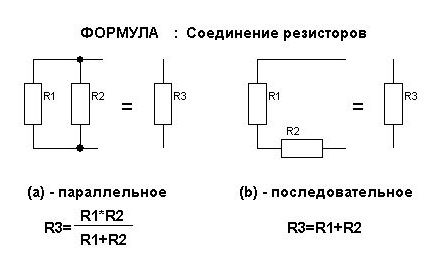
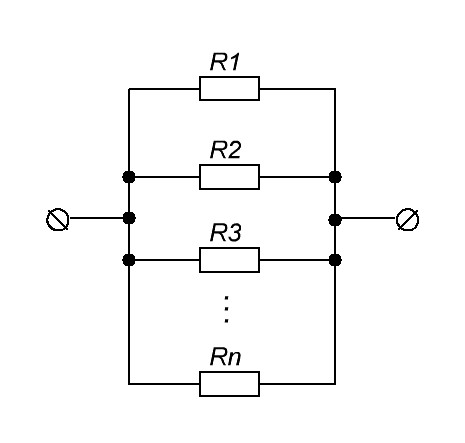
Последовательное и параллельное соединение резисторов

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

  1. С правого края – правый.
  2. С левого края – левый.

Понятие параллельного подключения резисторов

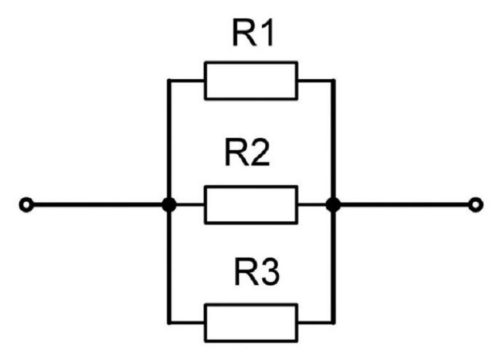
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Типы проводников


Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Последовательное и параллельное соединение резисторов

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

  1. Проводники (все металлы, ионизированный газ и электролитические растворы).
  2. Полупроводники (Si, Ge, GaAs, InP и InSb).
  3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

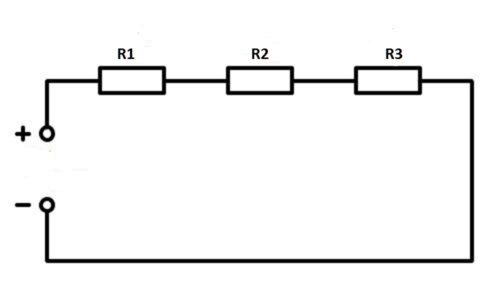
Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Теоретическая часть

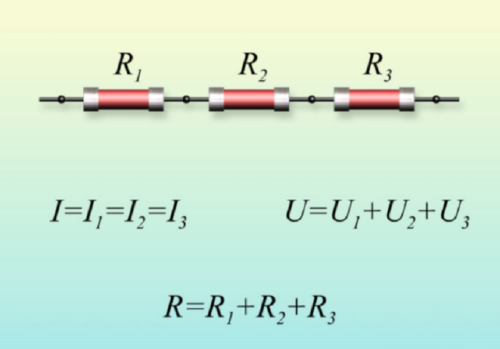
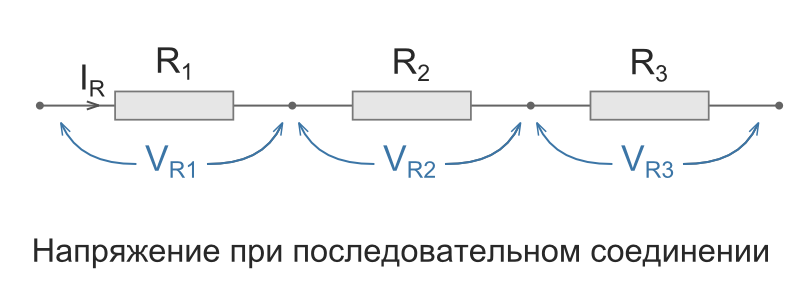
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

  • U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
  • U2 = R2 * I = 800 Ом * 2А = 1600 В.

Будет интересно➡ SMD резисторы: что это такое и для чего используются?

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Общее сопротивление Rобщ

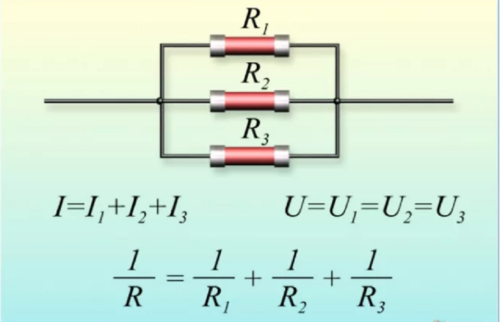
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

Схема параллельного соединения

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Урок 11. ВСЕ Способы соединения резисторов

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

  • R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
  • I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

  • R – рассчитанное нами сопротивление для определенной схемы;
  • U – падение напряжения на данном резистивном элементе.

Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.

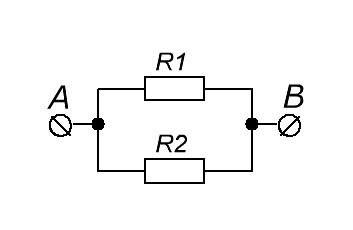
Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.


параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

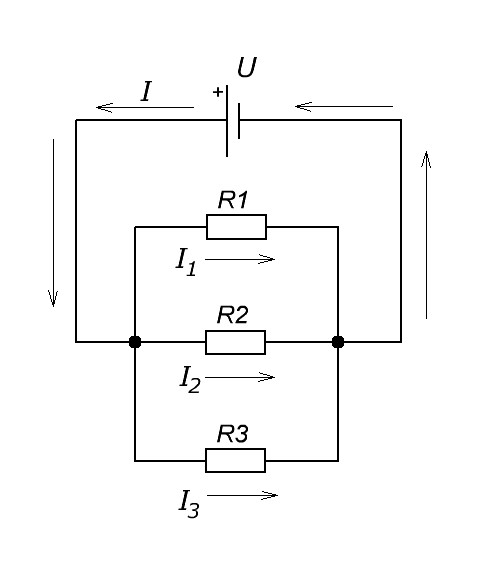
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

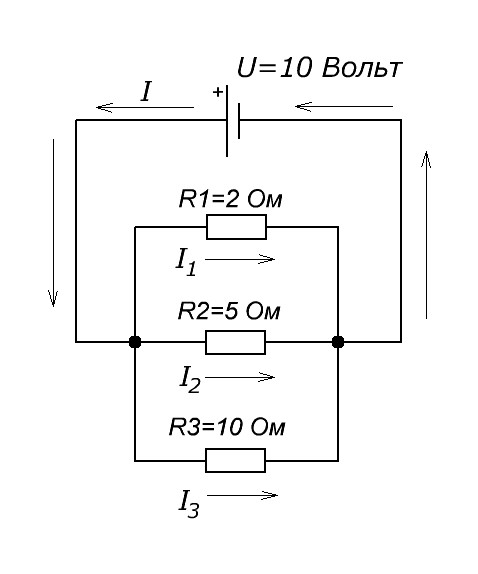
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I1 = U/R1 = 10/2=5 Ампер

I2 = U/R2 = 10/5=2 Ампера

I3 = U/R3 = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I1 + I2 + I3 = 5+2+1=8 Ампер

2-ой способ найти I

Чтобы найти Rобщее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.

I=U/Rобщее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

  1. Температура окружающей среды и материала.
  2. Электрические величины.
  3. Геометрические свойства вещества.
  4. Тип материала, из которого изготовлен проводник (полупроводник).

последовательное и параллельное соединение резисторов

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины


Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры


Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

  1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
  2. Визуально определить форму материала.
  3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.


В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Урок 11. ВСЕ Способы соединения резисторов

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a

Стандартная формула напряжения

Формула для вычисления напряжения

При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.

При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.

Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:

U = U1 = U2 = … = Uобщ.

Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.

Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.

Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.


Определение мощности на примере ламп

В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.

ЧТО ТАКОЕ ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

Отличия между двумя видами подключений

Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.


Пример подключения с предохранителем

Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.

Как рассчитать сложные схемы соединения резисторов

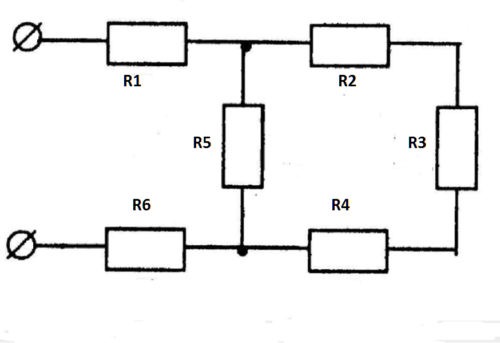
Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.

  • источник постоянного тока 12V;
  • сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.
  • основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
  • подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
  • эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
  • ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.

По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.

Расчет 1 (последовательное и параллельное соединение):

  • для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
  • эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
  • второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
  • общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
  • Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.

Расчет 2 (сложное параллельное соединение):

  • в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
  • Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
  • суммарное значение для цепи: R1 + R2 = 20 Ом;
  • по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
  • после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
  • делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.

В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).

В этом случае разница потенциалов на шестом резисторе составит:

U6 = I *R6 = 1,2 * 7,5 = 9 В.

Соответственно, изменится напряжение между контрольными точками:

Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.

Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип — U6).

Источник

Источник

Добавить комментарий