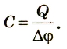Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
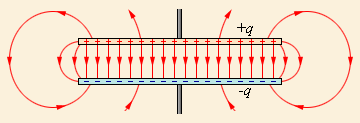
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
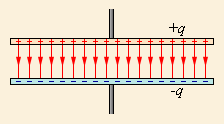
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε0.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε0.
Как рассчитать электроемкость конденсатора
Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q, а ее площадь как S, то соотношение qS даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками (d), мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.
C=q∆φ=σ·SE·d=ε0Sd.
Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
C=εε0Sd.
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Сферическим конденсатором называется система из 2-х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R1 и R2 соответственно.
Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L, а радиусы R1 и R2.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
- C=4πε0εR1R2R2-R1(сферический конденсатор),
- C=2πε0εLlnR2R1(цилиндрический конденсатор).
Как рассчитать электроемкость батареи конденсаторов
Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U1=U2 =U, а заряды можно найти по формулам q1=С1U и q2=C2U. При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C, заряд – q=q1+q2, а напряжение – U. В виде формулы это выглядит так:
С=q1+q2U или C=C1+C2
Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
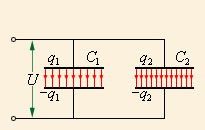
Рисунок 1.6.3. Конденсаторы, соединенные параллельно. C=C1+C2
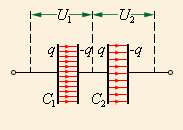
Рисунок 1.6.4. Конденсаторы, соединенные последовательно: 1C=1C1+1C2
Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q1=q2=q. Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
C=qU1+U2 или 1C=1C1+1C2
Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
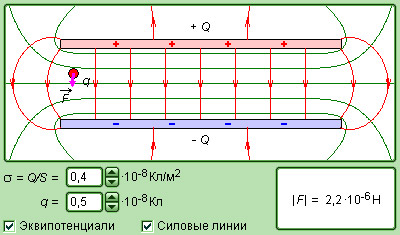
Рисунок 1.6.5. Смоделированное электрическое поле плоского конденсатора.
Элементы цепи могут быть подключены двумя способами:
- последовательно
- параллельно
Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).
- последовательное соединение конденсаторов

Рис. 1. Последовательное соединение конденсаторов
Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).
Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

Рис. 2. Последовательное соединение конденсаторов
Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — (помним, что они одинаковы), электроёмкости —
,
и соответствующие напряжения —
и
.
Учитывая определение электроёмкости:
(1)
Тогда:
(2)
(3)
(4)
Памятуя о том, что конденсаторы соединены последовательно, получаем:
(5)
Тогда:
(6)
Или в общем виде:
(7)
Для цепи из двух последовательных соединений:
(8)
- параллельное соединение конденсаторов

Рис. 3. Параллельное соединение конденсаторов
Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости
Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:
(9)
(10)
(11)
С учётом того, что , получим:
(12)
Сокращаем:
(13)
Или в общем виде:
(14)
Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:
Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
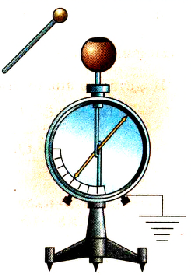
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
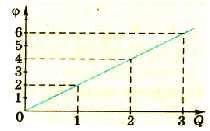
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
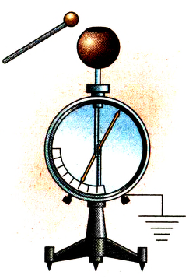
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
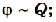
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
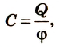
где C – электроемкость проводника; Q – заряд; φ – потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
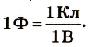
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф – довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
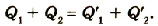
Отсюда
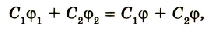
или
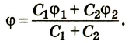
Подставив значения физических величин и произведя расчеты, получим:
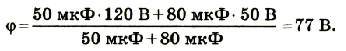
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
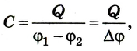
где Q – заряд одной пластины; (φl– φ2) и ∆φ – разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
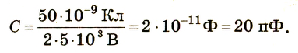
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) – голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор – лейденскую банку и провел опыты с ней. |

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
Плоским конденсатором обычно называют систему плоских проводящих пластин – обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
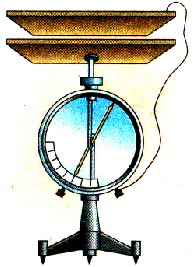
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
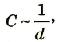
где d – расстояние между обкладками.
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
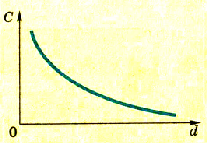
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
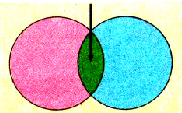
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении – наоборот.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
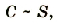
где S – площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
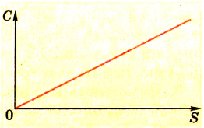
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
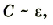
где ε – диэлектрическая проницаемость диэлектрика.
Эта зависимость изображена графиком на рисунке 1.40.
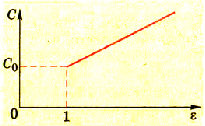
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
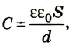
где ε – относительная диэлектрическая проницаемость диэлектрика; ε0– электрическая постоянная; d – расстояние между пластинами; S – площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
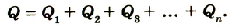
Если учесть, что 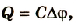 то
то
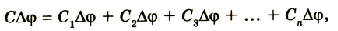
или
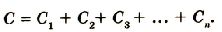
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
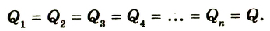
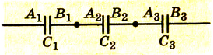
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
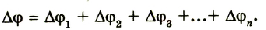
Учитывая, что 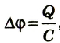 будем иметь
будем иметь
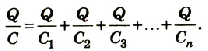
Разделим левую и правую части равенства на Q:
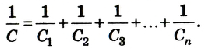
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
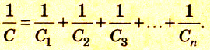
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
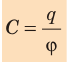
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл; 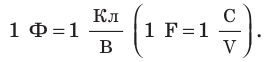
1 Ф — очень большая единица емкости, поэтому используют дольные единицы: 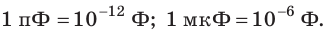
Что такое конденсатор
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).

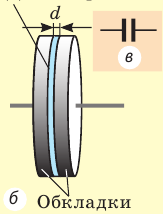
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (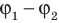 ) между его обкладками не зависит ни от значения q, ни от разности потенциалов (
) между его обкладками не зависит ни от значения q, ни от разности потенциалов (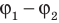 ), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
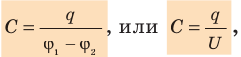
где U — напряжение между обкладками: 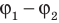 .
.
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
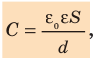
где 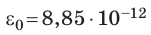 Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями 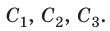
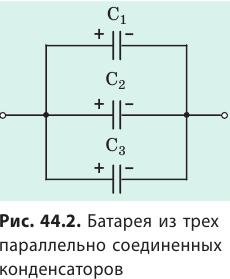
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
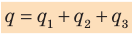
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
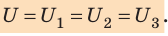
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку 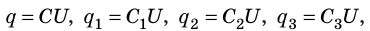 то
то 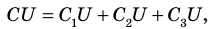 следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
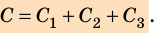
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
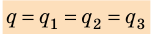
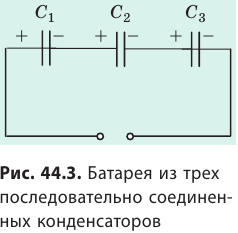
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
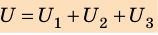
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
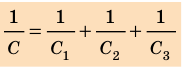
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
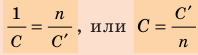
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
Вычислим энергию заряженного до напряжения 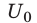 конденсатора емкостью С, на котором накоплен заряд
конденсатора емкостью С, на котором накоплен заряд 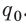 . Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
. Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 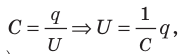 поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
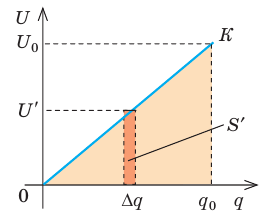
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: 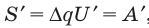 , где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда
, где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда 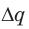 ; A′ — работа, которую совершило поле при потере конденсатором заряда
; A′ — работа, которую совершило поле при потере конденсатором заряда 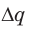 . Полная работа, которую совершило поле при уменьшении заряда конденсатора от
. Полная работа, которую совершило поле при уменьшении заряда конденсатора от 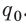 до 0, определяется площадью выделенного на рис. 44.4 треугольника.
до 0, определяется площадью выделенного на рис. 44.4 треугольника.
Следовательно,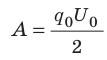 . Учитывая, что
. Учитывая, что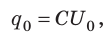 получим:
получим: 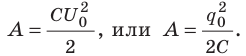 С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от
С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от 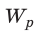 до нуля: A=
до нуля: A=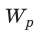 − 0 = W. Таким образом, энергия
− 0 = W. Таким образом, энергия 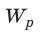 заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
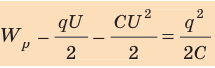
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:

- Энергию заряженного конденсатора можно вычислить по формулам:
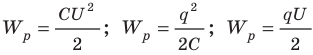
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона
Условие задачи:
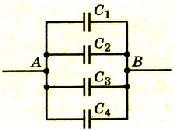
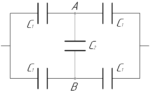 Определить электроемкость батареи конденсаторов, изображенной на рисунке, если (C_1=2) мкФ, (C_2=4) мкФ.
Определить электроемкость батареи конденсаторов, изображенной на рисунке, если (C_1=2) мкФ, (C_2=4) мкФ.
Задача №6.4.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(C_1=2) мкФ, (C_2=4) мкФ, (C-?)
Решение задачи:
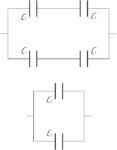 Обратите Ваше внимание на то, что схема симметричная, а это значит, что потенциалы точек A и B будет одинаковыми. Это означает, что конденсатор с электроемкостью (C_2) будет незаряжен (так как разности потенциалов между его обкладками нет), поэтому этот конденсатор можно легко исключить, и исходная схема примет следующий вид (смотрите рисунок справа).
Обратите Ваше внимание на то, что схема симметричная, а это значит, что потенциалы точек A и B будет одинаковыми. Это означает, что конденсатор с электроемкостью (C_2) будет незаряжен (так как разности потенциалов между его обкладками нет), поэтому этот конденсатор можно легко исключить, и исходная схема примет следующий вид (смотрите рисунок справа).
Полученную схему легко преобразовать в другую. Так как два конденсатора в верхней и нижней ветви соединены последовательно, то заменим их эквивалентной электроемкостью (C_3), которую можно найти таким образом:
[frac{1}{{{C_3}}} = frac{1}{{{C_1}}} + frac{1}{{{C_1}}}]
[frac{1}{{{C_3}}} = frac{2}{{{C_1}}}]
[{C_3} = frac{{{C_1}}}{2};;;;(1)]
А так как конденсаторы (C_3) соединены последовательно, то искомая электроемкость (C) равна:
[C = {C_3} + {C_3}]
Учитывая (1), получим:
[C = frac{{{C_1}}}{2} + frac{{{C_1}}}{2}]
[C = {C_1}]
[C = 2;мкФ]
Ответ: 2 мкФ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.42 Найти общую электроемкость соединенных по схеме конденсаторов, если
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B
6.4.45 Какое количество теплоты выделяется при замыкании пластин конденсатора электроемкостью
Электроемкость зависит от формы проводника! Поэтому для каждого вида существует своя формула расчета электроемкости.
Электроемкость шара
Конденсатор
Конденсатор – это система, состоящая из двух или более проводников.
Плоский конденсатор – две параллельные металлические пластины (обкладки), между которыми находится диэлектрик.
В быту можно встретить подобные конденсаторы
На схеме конденсатор обозначается следующим образом (запомнить выделенное обозначение)
Электроемкость плоского конденсатора
Используя общую формулу нахождения электроемкости, можно получить
Поле между обкладками конденсатора однородно, поэтому напряжение можно определить как
Батарея конденсаторов
Несколько конденсаторов, соединенных вместе, образуют батарею конденсаторов.
Различают последовательное, параллельное и смешанное соединение конденсаторов
Движение заряженной частицы в конденсаторе
Энергия заряженного конденсатора
Энергия определяется по формуле
Объемная плотность энергии конденсатора
Энергию конденсатора можно определить как
Объемная плотность энергии определяется как