Download Article
Download Article
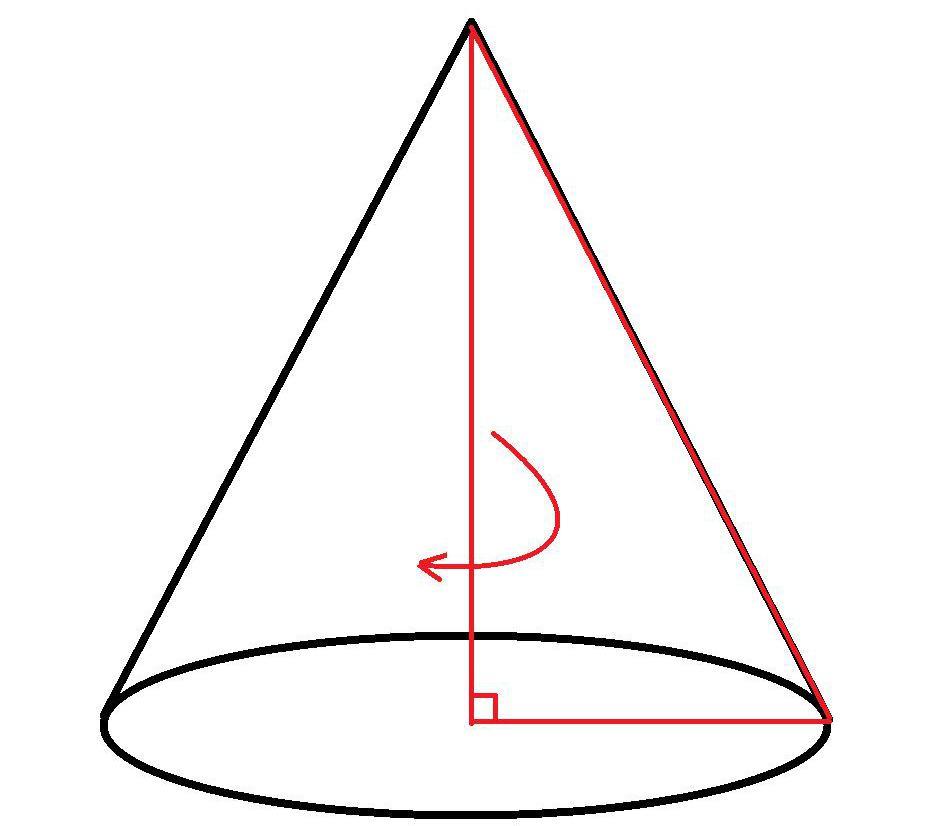
The surface area of a cone is the sum of the lateral surface area and the base surface area. If you know the radius of the base and the slant height of the cone, you can easily find the total surface area using a standard formula. Sometimes, however, you might have the radius and some other measurement, such as the height or volume of the cone. In these instances, you can use the Pythagorean Theorem and the volume formula to derive the slant height, and thus the surface area of the cone.
-

1
-

2
Plug the value of the radius into the formula. This length should be given, or you should be able to measure it. Make sure you substitute for both
variables in the formula.
- For example, if the radius of the base of a cone is 5 cm, your formula will look like this:
.
Advertisement
- For example, if the radius of the base of a cone is 5 cm, your formula will look like this:
-

3
Plug the value of the slant height into the formula. This length should be given, or you should be able to measure it.
- For example, if the slant height of a cone is 10 cm, your formula will look like this:
.
- For example, if the slant height of a cone is 10 cm, your formula will look like this:
-

4
-

5
-

6
Add the lateral surface area and the base area of the cone. This will give you the total surface area of the cone, in square units.
- For example:
So, the surface area of a cone with a radius of 5 cm and a slant height of 10 cm is 235.5 square centimeters.
- For example:
Advertisement
-

1
-

2
-

3
Square the lengths of the radius and height, then add. Remember that squaring a number means to multiply it by itself.
-

4
Take the square root of each side of the equation. This will give you the length of the hypotenuse of the right triangle, which is equal to the slant height of the cone.[9]
-

5
-

6
Plug all the known values into the formula. The radius should be given, and you already calculated the slant height. Make sure you use the slant height in the surface area formula, not the (perpendicular) height. If you are not using a calculator, use 3.14 for
- For example, for a cone with a radius of 5 cm and a slant height of 13 cm, your formula will look like this:
.
- For example, for a cone with a radius of 5 cm and a slant height of 13 cm, your formula will look like this:
-

7
Multiply to find the lateral area and the base area. Then, add these products together. The sum will give you the total surface area of the cone in square units.[11]
Advertisement
-

1
-

2
Plug the known values into the formula. You should know the volume and the length of the radius. If not, you cannot use this method. If you are not using a calculator, use 3.14 for
.
- For example, if you know a cone has a volume of 950 cubic centimeters and a radius of 6 centimeters, your formula will look like this:
.
- For example, if you know a cone has a volume of 950 cubic centimeters and a radius of 6 centimeters, your formula will look like this:
-

3
-

4
Divide each side by the
coefficient. This will give you the value of
, which is the perpendicular height of the cone. You will need this information to find the slant height of the cone, which is necessary to know when solving for the surface area.
-

5
Set up the formula for the Pythagorean Theorem. The formula is
, where
and
equal the side lengths of a right triangle, and
equals the length of the hypotenuse (the side opposite the right angle).[15]
-

6
-

7
Solve for
. This will give you the length of the right triangle’s hypotenuse, which is also the slant height of the cone.
-

8
-

9
Plug all the known values into the formula. Make sure you use the slant height in the surface area formula, not the (perpendicular) height. If you are not using a calculator, use 3.14 for
- For example, for a cone with a radius of 6 cm and a slant height of 25.91 cm, your formula will look like this:
.
- For example, for a cone with a radius of 6 cm and a slant height of 25.91 cm, your formula will look like this:
-

10
Multiply to find the lateral area and the base area. Then, add these products together. The sum will give you the total surface area of the cone in square units.[17]
Advertisement
References
Add New Question
-
Question
What is the area of the base of a cone with a volume of 36 cubic inches and height of 9 inches?

The formula for volume of a cone is 1/3 x Base Area (i.e. area of a circle) x height.
Solution:
Volume = 1/3 x BA x H
36 = 1/3 x (BA)* x 9
36 x 3 = BA x 9 (we moved the 1/3 to the other side of the equation, hence it reciprocated)
108/9 = BA
Base area of the cone is 12 inches. -
Question
How do I show that slant height is 2r?

If you’re given the radius of the base and the height of the cone, you can do the Pythagorean theorem.
-
Question
How do I find the radius of the base of a cone given its surface area of 500 pi and height of 15 cm?

Assuming you are given the lateral surface area and the slant height, divide the lateral surface area by the product of pi and the slant height. If instead of the slant height you are given the perpendicular height, use Method 2 above to find the slant height, then multiply the slant height by pi, and divide that product into the lateral surface area to get the radius of the base.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The Pythagorean theorem applies to the radius, perpendicular height, and slant height, with the slant height acting as the hypotenuse: (radius)2 + (perpendicular height)2 = (slant height)2.
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
To find the surface area of a cone if you know the length of the slant, use the formula (πrs)+πr^2. Put the value of the radius of the circle at the bottom of the cone into the formula where you see an “r” and be sure to square it where necessary. Then, insert the length of the slant into the formula for “s,” and multiply the radius, slant, and pi together. Once you have the first part of the equation, multiply pi by the radius squared. To get the total surface area, add the two values together, and be sure to record your answer in units squared! For help finding the surface area of a cone if you know the radius and the perpendicular height, or the radius and the volume, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 239,447 times.
Did this article help you?
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой – сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
Содержание
- Определение и элементы конуса
- Основные сведения
- Виды конусов
- Свойства кругового конуса
- Общая формула объёма фигуры
- Расчет объема
- Объём усечённого конуса
- Первый способ вычисления объема усеченного конуса
- Второй способ вычисления объема усеченного конуса
- Объем наклонного конуса
- Площадь поверхности фигуры
- Формула образующей конуса
- Формула площади боковой поверхности конуса
- Формула площади основания конуса
- Сечение конуса
- Площадь сечения
- Площадь усечённого конуса
- Уравнение конуса
- Составляющие конуса
- Длина образующих в прямом конусе
- Образующая в наклонном конусе
- Примеры задач
Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.
При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.
Хотелось бы рассмотреть ещё несколько понятий по этой теме:
- Под конусностью понимают отношение диаметра основания фигуры и её высоты:
![]()
Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.
- Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

- Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Основные сведения
- R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
- h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
- Точка C – вершина конуса.
- l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
- Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
- Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.
Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):
l2 = h2 + R2
Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.
- длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
- α – угол развёртки (или центральный угол);
- l – радиус сектора.
Виды конусов
- Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания.
- Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
- Усеченный конус (конический слой) – часть конуса, которая остается между его основанием и секущей плоскостью, параллельной данному основанию.
- Круговой конус – основанием фигуры является круг. Также бывают: эллиптический, параболический и гиперболический конусы.
- Равносторонний конус – прямой конус, образующая которого равняется диаметру его основания.
Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:
- Образующие кругового конуса равны друг другу.
- Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
- Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.
Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.
Общая формула объёма фигуры
Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где
- V – это объем конуса;
- h – высота;
- r – радиус;
- π — константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2- b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 — r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 — h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объём усечённого конуса
Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

Объём данного тела можно вычислить по формуле:

Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} left( Hcdot S_2 + h cdot s_1 right) ]
где:
- V – объем конуса
- h – расстояния от плоскости верхнего основания до вершины
- H – расстояния от плоскости нижнего основания до вершины
- S1 – площадь верхнего (ближнего к вершине) основания
- S2 – площадь нижнего основания
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} pi h left( R^2 + R cdot r + r^2 right) ]
где:
- V – объем конуса
- h – высота конуса
- R – радиус нижнего основания
- r – радиус верхнего основания
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Площадь поверхности фигуры
Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.

Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где
- S – это площадь сечения;
- d – диаметр основания;
- r – радиус;
- h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Площадь усечённого конуса
Для нахождения данного параметра нужно воспользоваться формулами:
- площади боковой поверхности усечённого конуса Sбок;
- полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.
Уравнение конуса
Часто требуется при решении математических задач. Записывается в следующем виде:

где x0, y0,z0- координаты по соответствующим осям.
Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
- Круга, являющегося его основанием.
- Боковой поверхности.
- Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
- Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.

Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.

То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где
- l – образующая;
- r – радиус;
- h – высота.
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.

Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 — h2
где
- r1 – это часть радиуса между осью и высотой;
- k – длина оси;
- h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где
- R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
- r – радиус основания;
- r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
![]()
Задание 2
Высота конуса равна 7 см, а его радиус – 4 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
![]()
мы называем конус геометрическое тело, также известное как круглое тело или твердое тело революции, которое он имеет круглое основание и построен из вращения треугольника.. Конус и другие геометрические тела являются объектами изучения пространственной геометрии. По своим характеристикам его можно классифицировать как:
- прямой конус;
- косой конус;
- равносторонний конус.
Там есть конкретные формулы для расчета общей площади и объема конуса.
Читайте тоже: Что такое геометрические фигуры?
Элементы значка
конус твердый геометрический известный как революция солидная. Он очень присутствует в нашей повседневной жизни и известен как революционный продукт. построен из вращения треугольник.
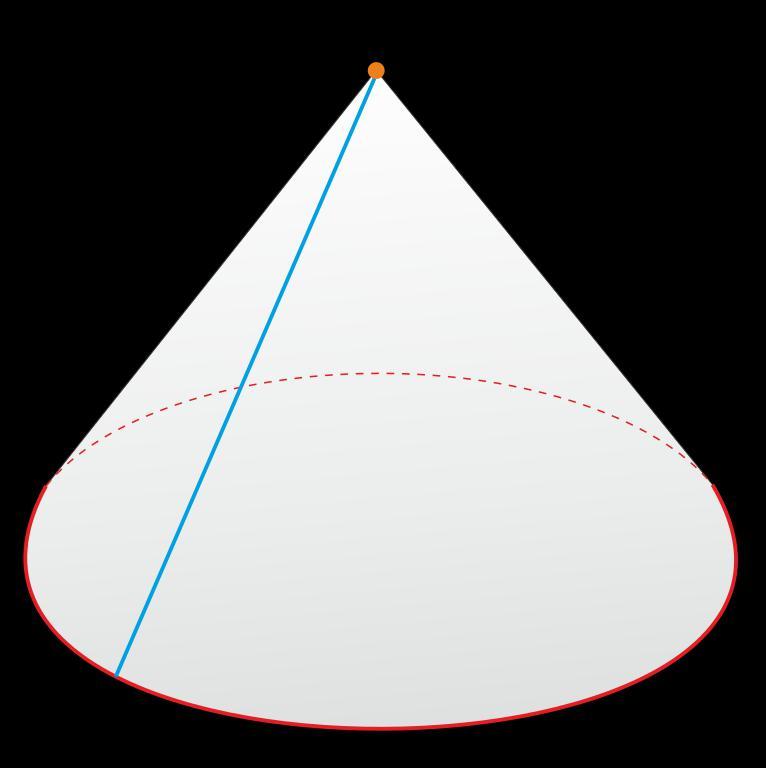
Его основа всегда круг. Помимо самой базы, еще одним важным элементом является молнияр окружности, известной как радиус основания конуса. Также есть вершина конуса (V) и высота (h), который по определению представляет собой отрезок, который выходит из вершины и перпендикулярен основанию, то есть образует угол 90º.

В дополнение к уже упомянутым элементам, в конусе есть еще один важный элемент, которым является образующая. Мы называем любой отрезок, который начинается от вершины и встречается с длина окружности от базы.
Образующая – это сегмент AV-линии на изображении. Обратите внимание, что он гипотенуза штрихового треугольника, скоро мы сможем установить отношения Пифагорейский между радиусом, высотой и образующей.
g² = r² + h²

грамм → генератор конуса
р→ базовый радиус
ЧАС→ высота
Смотрите также: Каковы приложения теоремы Пифагора?
Классификация иконок
По своим характеристикам, мы можем классифицировать конус в двух случаях: прямой или косой. Как частный случай прямого конуса, существуют равносторонние конусы.
-
косой конус
Конус называется наклонным, если отрезок, соединяющий вершину с центром ее основания, не соответствует высоте конуса.

Когда вершина не выровнена с центром основания, сегмент, который соединяет вершину с центром длина окружности это уже не высота, как в прямом конусе. Обратите внимание, что ось конуса на изображении не перпендикулярна основанию. В этом случае их образующие не все конгруэнтны, поэтому их длину невозможно найти с помощью Теорема Пифагора без конкретных формул для образующей или для объема и его площади общий.
-
прямой конус
Конус известен как прямой когда его ось совпадает с высотой конуса, то есть отрезок, соединяющий вершину с центром окружности основания, перпендикулярен плоскости, содержащей основание конуса.

-
равносторонний конус
Прямой конус называется равносторонним, если его диаметр равен его образующей.

Обратите внимание, что треугольник AVB – это равносторонний треугольник, то есть все стороны совпадают, это означает, что ее образующая конгруэнтна диаметру основания и, следовательно, длина образующей равна удвоенной длине радиуса основания.
Также доступ: Коники – фигуры, образованные пересечением плоскости и двойного конуса.
Формулы конуса
При изучении геометрических тел существует два важных вычисления для каждого из них: вычисление объема и вычисление общей площади геометрического тела. Для расчета стоимости объем конуса для каждого из них необходимо использовать определенные формулы. Помните, что эти формулы относятся к прямому конусу.
-
Формула объема конуса
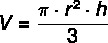
r → радиус основания
V → объем
h → высота
-
Формула общей площади конуса
Для расчета общей площади, анализируя планирование конуса, мы суммируем боковую площадь с площадью основания конуса.
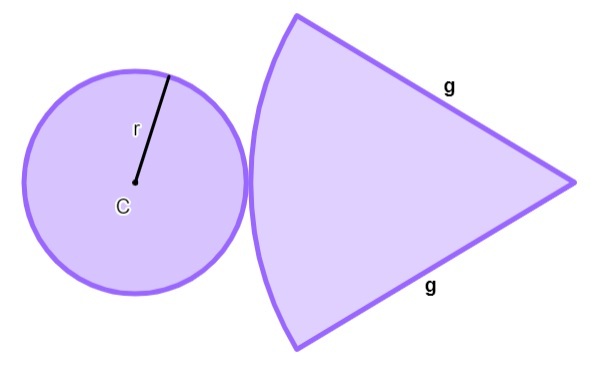
Его основание – круг, поэтому площадь рассчитывается по формуле:
ВB = π · r².
Его боковая площадь представляет собой круговой сектор, который равен:
Втам = π · r · g
Следовательно, общая площадь равна:
Вт = π · r² + π · r · g
Помещая π · r в доказательство, мы можем рассчитать общую площадь по:
Вт = π · r (r + g)
r → радиус
g → образующая
конус ствол
Когда конус пересекается плоскостью, параллельной основанию, можно создать геометрическое тело, известное как ствол конуса. О ствол конуса всегда будет две базы в форме кругов, один больше, а другой меньше.
Читайте тоже: Цилиндр – твердое тело, образованное двумя круглыми основаниями в различных и параллельных плоскостях.
решенные упражнения
Вопрос 1 – (Enem 2013) Повар, специалист по выпечке тортов, использует форму в формате, показанном на рисунке:
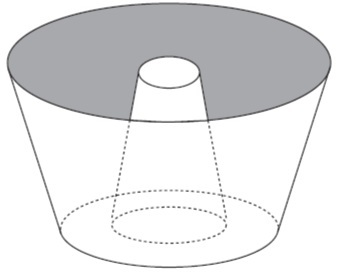
Он определяет представление двух трехмерных геометрических фигур. Вот эти цифры:
А) усеченный конус и цилиндр.
Б) конус и цилиндр.
В) ствол пирамиды и цилиндр.
Г) два конусообразных ствола.
Д) два цилиндра.
разрешение
Альтернатива D. Обратите внимание, что два твердых тела имеют большее основание и большее круглое основание, что делает их обоими усеченными конусами.
Вопрос 2 – Резервуар будет построен в форме конуса с использованием алюминия в качестве материала. Если не учитывать толщину резервуара и знать, что это прямой конус с радиусом 1,5 м и высотой 2 м, какое количество алюминия необходимо для создания этого резервуара? (используйте π = 3)
А) 10 м²
Б) 14 м²
C) 16 м²
Г) 18 м²
E) 20 м²
разрешение
Альтернатива D.
Мы хотим вычислить общую площадь конуса, которая определяется по формуле:
Вт = π · r (r + g)
Обратите внимание, что у нас нет значения g, поэтому сначала давайте вычислим значение образующей g.
g² = r² + h²
g² = 1,5² + 2²
g² = 2,25 + 4
g² = 6,25
г = √6,25
г = 2,5 м
Итак, общая площадь будет:
Вт = π · r (r + g)
Вт = 3·1,5(1,5+2,5)
Вт = 4,5·4
Вт = 18 м²
Рауль Родригес де Оливейра
Учитель математики
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
 Вам будет интересно:Площадь основания правильной шестиугольной призмы. Формулы площади правильного шестиугольника
Вам будет интересно:Площадь основания правильной шестиугольной призмы. Формулы площади правильного шестиугольника
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
 Вам будет интересно:Жить – это не только существовать
Вам будет интересно:Жить – это не только существовать
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
 Вам будет интересно:Значение выражения “угрюмый человек”
Вам будет интересно:Значение выражения “угрюмый человек”
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
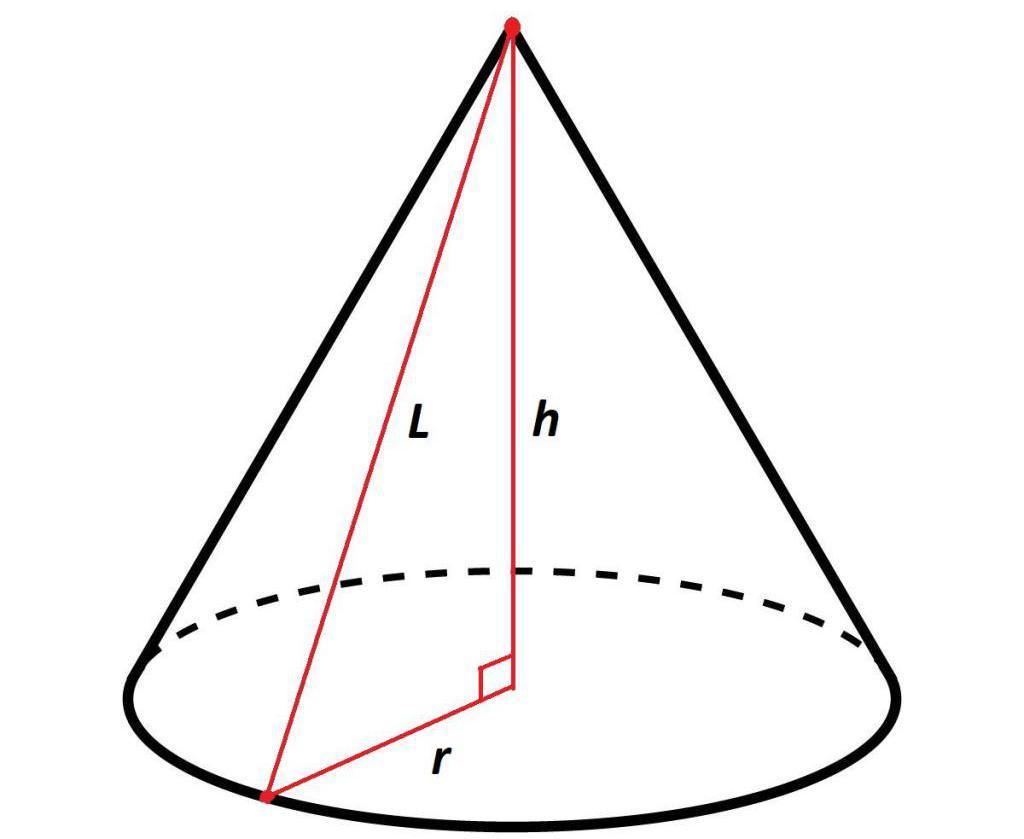
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
r – радиус;
h – высота.
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
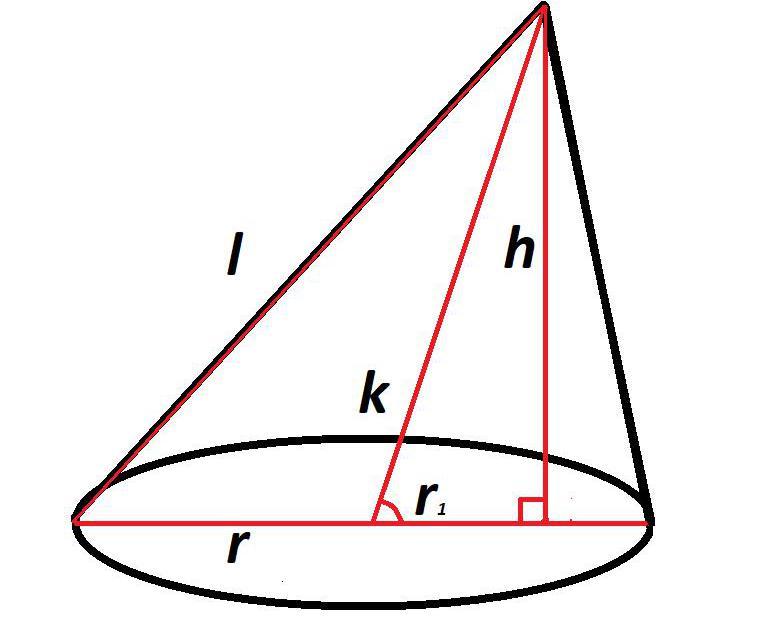
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 – h2
где r1 – это часть радиуса между осью и высотой;
k – длина оси;
h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу – использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
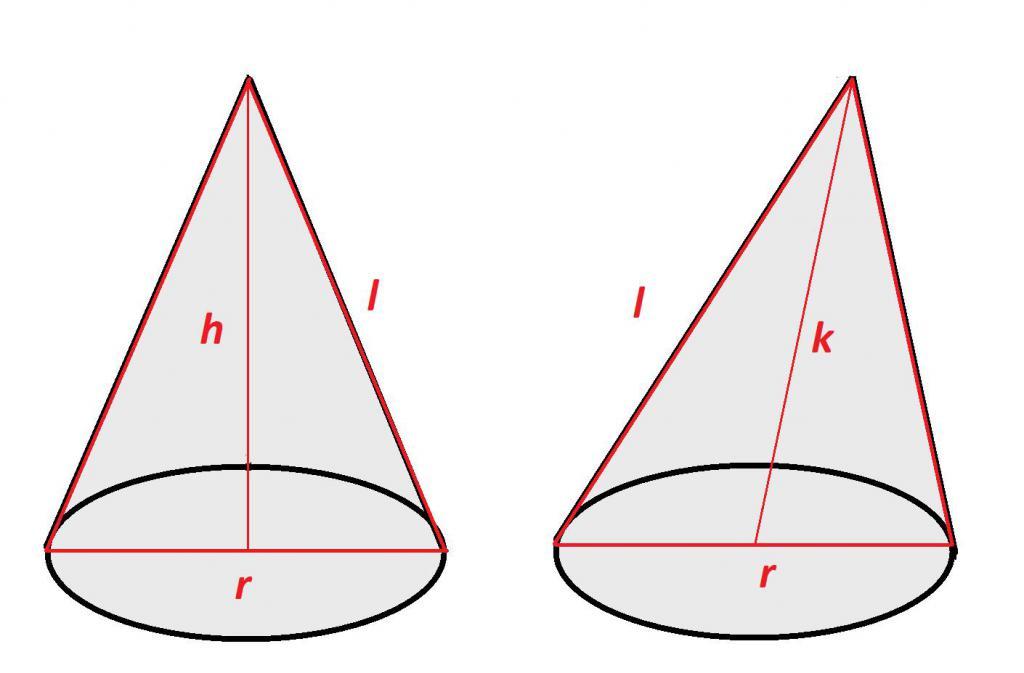
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие – оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
r – радиус;
h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
h – высота;
r – радиус;
π – константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2- b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 – r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 – h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.

