Как найти общую площадь боковых граней - Сайт, где вы сможете решить свои вопросы

Формулы для расчета приведены под калькулятором.

Площадь четырехугольной пирамиды

Угол наклона граней в градусах (α)

Точность вычисления

Знаков после запятой: 2

Четырехугольная пирамида

В формулах ниже будем использовать следующие обозначения:
a – длина первой стороны основания
b – длина второй стороны основания (для квадрата будет равна первой)
h – высота пирамиды
r – ребро пирамиды
d – диагональ основания
e – высота треугольника, образованного боковой гранью, т.е. высота, опущенная из вершины пирамиды на ее сторону
α – угол наклона грани пирамиды (угол между высотой треугольника боковой грани и плоскостью основания)

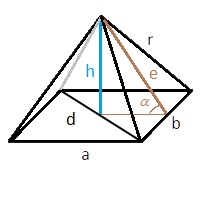
Во всех случаях площадь основания вычисляется тривиально – перемножением длин сторон основания. Ниже рассмотрим нахождение площадей боковых граней для разных случаев.

Площадь поверхности пирамиды через высоту

Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном высотой пирамиды, высотой треугольника боковой грани, и проекцией высоты треугольника на плоскость основания. Длина проекции очевидно равна половине длины противоположной стороны. Таким образом, высота треугольника, опущенная на сторону a
$e_a=sqrt{h^2+frac{b^2}{4}}$
высота треугольника, опущенная на сторону b
$e_b=sqrt{h^2+frac{a^2}{4}}$
Находим площади боковых граней, по формуле площади равнобедренного треугольника
$S_a=frac{acdot e_a}{2}\S_b=frac{bcdot e_b}{2}$
Общая площадь боковых граней

Площадь поверхности пирамиды через угол наклона

Расчет через один угол наклона возможен, только если в основании пирамиды лежит квадрат (иначе пришлось бы задавать два угла). Соответственно, сторона a равна стороне b, и все грани одинаковые.

Находим высоту треугольника, образованного боковой гранью, поделив длину проекции на плоскость основания на косинус угла наклона
$e=frac{frac{a}{2}}{cos alpha}$
Находим площадь боковой грани, по формуле площади равнобедренного треугольника
$S=frac{acdot e}{2}$
Общую площадь боковых граней получаем, умножив площадь одной грани на 4.

Площадь поверхности пирамиды через длину ребра

Здесь есть ограничение: длина ребра должна быть больше чем половина диагонали основания (иначе это не пирамида)

Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном ребром пирамиды, высотой треугольника боковой грани, и половиной стороны, на которую опущена высота. Таким образом, высота треугольника, опущенная на сторону a
$e_a=sqrt{r^2-frac{a^2}{4}}$
высота треугольника, опущенная на сторону b
$e_b=sqrt{r^2-frac{b^2}{4}}$
Находим площади боковых граней, по формуле площади равнобедренного треугольника
$S_a=frac{acdot e_a}{2}\S_b=frac{bcdot e_b}{2}$
Общая площадь боковых граней

Источник

weanculspe375

Вопрос по математике:

Найдите общую площадь боковых граней прямоугольного параллелепипеда, если его длина, ширина , высота соответственно равны: 0,8м. 0,2м. 4,5 м

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

rondong916

( 0.8 + 0.2 ) * 2 * 4.5 = 9 м² площадь боковых граней параллелепипеда

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат – это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

A rectangular pyramid is a three-dimensional object that has a rectangular base upon which are erected four triangular faces that meet at a common point called the apex. It has a total of five faces, i.e., a rectangular base, four triangular faces, five vertices, and eight edges. In a rectangular pyramid, all the triangular faces are congruent to the opposite face. A rectangular pyramid is classified into two types, i.e., a right rectangular pyramid and an oblique rectangular pyramid. A right rectangular pyramid is a rectangular pyramid that has its apex directly above the center of its base, whereas an oblique rectangular pyramid is a rectangular pyramid where the apex is not aligned right above the center of its base. The height of an oblique rectangular pyramid is the perpendicular line drawn from the apex to the base of the pyramid. In this article, we will discuss the surface area of a rectangular pyramid in detail.

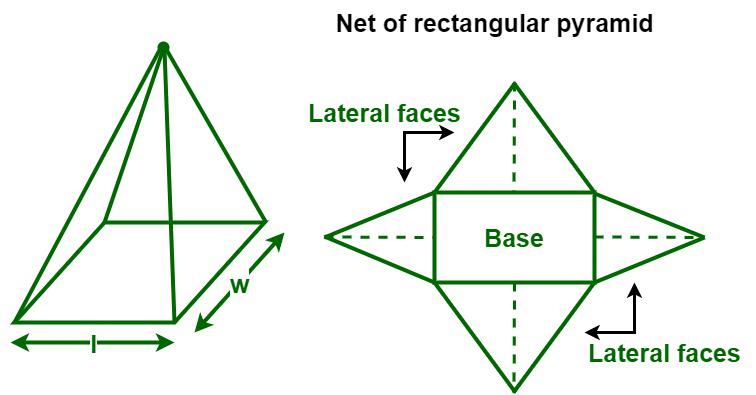
Surface Area of a Rectangular Pyramid

Surface area is defined as the total region occupied by the surfaces of a three-dimensional figure, and it is measured in terms of square units such as cm², m², in², ft², etc. A rectangular pyramid has two types of surface areas, i.e., the lateral surface area and the total surface area.

Lateral Surface Area

The lateral surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces (triangular faces). In a rectangular pyramid, the areas of the opposite triangular faces are the same. To find the surface area of a rectangular pyramid, we need to know the measures of the base length, base width, and slant height of the triangular face.

Lateral Surface Area of a Pyramid (LSA) = Sum of Areas of the lateral surfaces (triangles) of the pyramid

Slant height of length face of the pyramid = √[h² + (w/2)²]

Slant height of width face of the pyramid = √[h² + (l/2)²]

We know that,

The area of a triangle = ½ × base × height

Area of the triangle that has a length as the base = ½ × l × {√[h² + (l/2)²]}

Area of the triangle that has a width as the base = ½ × w × {√[h² + (w/2)²}

Now, LSA = ½ × l × {√[h² + (w/2)²]} + ½ × w × {√[h² + (l/2)²} + ½ × l × {√[h² + (w/2)²]} + ½ × w × {√[h² + (l/2)²}

= 2 × {½ × l ×√[h² + (w/2)²]} + 2 × {½ × w ×√[h² + (l/2)²]}

= l√[h² + (w/2)²] + w√[h² + (l/2)²]

Lateral surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²]

where,
“l” is the base length,
“w” is the base width, and
“h” is the height of the pyramid.

Total Surface Area

The total surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces (triangular faces) and the area of its rectangular base. To determine the total surface area of a rectangular pyramid, we need to find the area of its rectangular base and its lateral surface area, i.e., the sum of the areas of its four triangular faces.

Total surface area of a pyramid (TSA) = Lateral surface area of the pyramid + Area of the base

Area of rectangular base = l × w

So, TSA = l√[h² + (w/2)²] + w√[h² + (l/2)²] + l × w

TSA of a Rectangular Pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²] + l × w

where,

“l” is the base length,
“w” is the base width, and
“h” is the height of the pyramid.

How to Calculate the Surface Area of a Rectangular Pyramid?

The surface area of a rectangular pyramid is calculated by converting the 3-D shape into its 2-D net. After opening the Rectangular pyramid, we get four triangles and one rectangle. To find its surface area follow these steps.

Steps used to calculate the surface area of a rectangular pyramid is:

Step 1: Find the area of the rectangular base. The area of the rectangle is calculated using its length and breadth.

Step 2: Find an area of the triangle faces. The area of a triangle is calculated using its base and height.

Step 3: Now for finding the required surface area the area of the rectangular base and the triangular face are added accordingly.

Step 4: The area obtained in Step 3 is the required area it is measured in unit²

Solved Examples on Surface Area of Rectangular Pyramid

Problem 1. Determine the lateral surface area of a rectangular pyramid if the base length is 10 inches and the base width is 8 inches, and the height of the pyramid is 12 inches.

Solution:

Given data,

Base length (l) = 16 inches

Base width (w) = 12 inches

The height of the pyramid (h) = 15 inches

We know that,

Lateral surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²]

= 10 × √[12² + (8/2)²] + 8 × √[12² + (10/2)²]

= 10 × √(144 + 16) + 8 × √(144 + 25)

= 10 × √160 + 8 × √169

= 10 × 12.649 + 8 × 13

= 126.49 + 104 = 230.49 sq. in

Hence, the lateral surface area of the given rectangular pyramid is 230.49 sq. in.

Problem 2. Find the surface area of a rectangular pyramid if the base length is 8 cm and the base width is 6 cm, and the height of the pyramid is 10 cm.

Solution:

Given data,

Base length (l) = 8 cm

Base width (w) = 6 cm

The height of the pyramid (h) = 10 cm

We know that,

Total surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²] + l × w

= (8 × √[10² + (6/2)²] + 6 × √[10² + (8/2)²] + 8 × 6

= 8 × √(100 + 9) + 6 × √(100 + 16) + 48

= 8 × √109 + 6 × √116 + 48

= 8 × 10.440 + 6 × 10.770 + 48

= 83.522 + 64.621 + 48 = 196.143 sq. cm

Hence, the surface area of the given rectangular pyramid is 196.143 sq. cm.

Problem 3. Find the total surface area of a rectangular pyramid if the base length is 12 cm and the base width is 10 cm, and the height of the pyramid is 15 cm.

Solution:

Given data,

Base length (l) = 12 cm

Base width (w) = 10 cm

The height of the pyramid (h) = 15 cm

We know that,

Total surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²] + l × w

= (10 × √[15² + (12/2)²] + 12 × √[15² + (10/2)²] + 12 × 10

= 10 × √(225 + 36) + 12 × √(225 + 25) + 120

= 10 × √261 + 12 × √250 + 120

= 10 × 16.155 + 12 × 15.811 + 120

= 161.554 + 189.736 + 120 = 471.29 sq. cm

Hence, the surface area of the given rectangular pyramid is 471.29 sq. cm.

Problem 4. Determine the lateral surface area of a rectangular pyramid if the base length is 8 m and the base width is 4 m, and the height of the pyramid is 9 m.

Solution:

Given data,

Base length (l) = 8 m

Base width (w) = 4 m

The height of the pyramid (h) = 9 m

We know that,

Lateral surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²]

= 8 × √[9² + (4/2)²] + 4 × √[9² + (8/2)²]

= 8 × √(81 + 4) + 4 × √(81 + 16)

= 8 × √85 + 4 × √97

= 8 × 9.219 + 4 × 9.849

= 73.756 + 39.395 = 113.151 sq. m

Hence, the lateral surface area of the given rectangular pyramid is 113.151 sq. m.

Problem 5. Find the surface area of a rectangular pyramid if the base length is 20 inches and the base width is 16 inches, and the height of the pyramid is 25 inches.

Solution:

Given data,

Base length (l) = 20 inches

Base width (w) = 16 inches

The height of the pyramid (h) = 25 inches

We know that,

Total surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h²+ (l/2)²] + l × w

= (20 × √[25² + (16/2)²] + 16 × √[25² + (20/2)²] + 20 × 16

= 20 × √(625 + 36) + 16 × √(625 + 100) + 320

= 20 × √689 + 16 × √250 + 320

= 20 × 26.249 + 16 × 26.925 + 320

= 524.976 + 430.813 + 320 = 1,275.789 sq. in

Hence, the surface area of the given rectangular pyramid is 1,275.789 sq. in.

FAQs on Surface Area of Rectangular Pyramid

Question 1: What is the definition of a rectangular pyramid?

Answer:

A rectangular pyramid is a three-dimensional geometric figure that has a rectangular base and four triangular faces that meet at a common vertex called the apex.

Question 2: What are the types of rectangular pyramids?

Answer:

There are two types of rectangular pyramids, namely, a right rectangular pyramid and an oblique rectangular pyramid.

Question 3: What is the formula to find the lateral surface area of a rectangular pyramid?

Answer:

The lateral surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces (triangular faces), and the formula to calculate it is given below.

Lateral surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²]

Where “l” is the base length,

“w” is the base width, and

“h” is the height of the pyramid.

Question 4: Define surface area.

Answer:

Surface area is defined as the total region occupied by the surfaces of a three-dimensional figure.

Question 5: What is the formula to find the total surface area of a rectangular pyramid?

Answer:

The total surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces (triangular faces) and the area of its rectangular base, and the formula to calculate it is given below.

Total surface area of a rectangular pyramid = l√[h² + (w/2)²] + w√[h² + (l/2)²] + l × w

where,
“l” is the base length,
“w” is the base width,
“h” is the height of the pyramid.

Related Resources

Surface Area of Pyramid

Volume of Pyramid

Square Pyramid

Источник

Напомним,
что пирамида – это многогранник, в основании которого лежит –угольник,
а остальные граней
– треугольники с общей вершиной.

Многоугольник
называется
основанием пирамиды.

Треугольники
,
,
…, называются
боковыми гранями пирамиды.

Точка
–
вершиной пирамиды, а отрезки ,
,
…, –
её боковыми рёбрами.

Отрезок,
соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к
этой плоскости, называется высотой пирамиды.

Пирамиду
с вершиной и
основанием называют
-угольной
пирамидой и обозначают так: .

Диагональное
сечение – это сечение пирамиды плоскостью, которая проходит
через два боковых ребра, не принадлежащих одной грани.

Объединение
боковых граней называется боковой поверхностью пирамиды, а объединение
всех граней называется полной поверхностью пирамиды.

Тогда
площадью боковой поверхности пирамиды называется сумма площадей её
боковых граней.

А
площадью полной поверхности пирамиды называется сумма площадей всех её
граней.

Объём
пирамиды равен:

Пирамида,
в зависимости от того, какой многоугольник лежит в основании, имеет своё
название.

Пирамида
называется правильной, если её основанием является правильный
многоугольник, а все боковые рёбра равны.

Отрезок,
соединяющий вершину пирамиды с центром основания, является её высотой.

Высота
боковой грани правильной пирамиды, проведённая из её вершины к ребру основания,
называется апофемой.

Выше
изображена правильная пирамида. –
одна из её апофем. Все апофемы правильной пирамиды равны друг другу.

Отметим
некоторые свойства правильной -угольной
пирамиды.

1.
В правильной -угольной
пирамиде все боковые рёбра равны между собой.

2.
Боковые рёбра равно наклонены к основанию.

3.
Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.

4.
Боковые грани равно наклонены к основанию.

5.
Вершина проектируется в центр основания (основание высоты совпадает с центром
основания).

6.
Площадь боковой поверхности правильной пирамиды равна:

7.
Объём правильной четырёхугольной пирамиды со стороной основания и
высотой равен:

Параллельное
сечение пирамиды – сечение пирамиды плоскостью,
параллельной основанию.

Параллельное
сечение пирамиды обладает следующими свойствами:

1.
сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых
рёбрах пропорциональные отрезки;

2.
в сечении получается многоугольник, подобный основанию;

3.
площади сечения и основания относятся как квадраты их расстояний до вершины.

Усечённая
пирамида – это часть пирамиды, заключённая между основанием и
параллельным сечением пирамиды.

Основания
усечённой пирамиды – подобные многоугольники, лежащие в параллельных
плоскостях.

Боковые
грани усечённой пирамиды – трапеции.

Высота
усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего
основания на плоскость нижнего.

Площадь
полной поверхности усечённой пирамиды равна сумме площади
боковой поверхности и площадей двух оснований.

Объём
усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его
ещё можно вычислить по следующей формуле:

Правильная
усечённая пирамида получается из правильной пирамиды.

Апофема
– высота боковой грани правильной усечённой пирамиды.

Площадь
боковой поверхности правильной усечённой пирамиды равна:

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача
первая. Дана треугольная пирамида, боковые рёбра которой
взаимно перпендикулярны и равны см,
см
и см.
Найдите площадь боковой поверхности пирамиды.

Решение.

Задача
вторая. Дана правильная четырёхугольная пирамида со стороной
основания см
и высотой см.
Найдите площадь полной поверхности пирамиды.

Решение.

Задача
третья. Найдите высоту правильной усечённой треугольной
пирамиды ,
если стороны её оснований равны см
и см,
а боковое ребро равно см.

Решение.

Задача
четвёртая. В пирамиде боковое
ребро перпендикулярно
основанию и равно ребру .
Треугольник –
прямоугольный с катетами см
и см.
Найдите объём пирамиды.

Решение.

Задача
пятая. Найдите объём правильной треугольной пирамиды с
ребром основания, равным см,
и боковым ребром, равным см.

Решение.

Источник

Полная площадь боковой поверхности пирамиды состоит из суммы площадей его боковых граней.

В четырехугольной пирамиде различается два вида граней – четырехугольник в основании и треугольники с общей вершиной, которой образуют боковую поверхность.
Для начала потребуется рассчитать площадь боковых граней. Для этого можно использовать формулы площади треугольника, а можно также воспользоваться формулой площади поверхности четырехугольной пирамиды (только в случае, если многогранник правильный). Если пирамида правильная и в ней известна длина ребра a основания и проведенной к нему апофемы h, то:

$S_bok={1/2}ah$

Если по условиям даны длина ребра c правильной пирамиды и длина стороны основания a, то можно найти значение по следующей формуле:
$S_bok={1/2}a sqrt{c^2-{{a^2}/4}}$
Если же дана длина ребра в основании и противолежащий ей острый угол у вершины, то можно рассчитать площадь боковой поверхности по соотношению квадрата стороны a к удвоенному косинусу половины угла α:
$S_bok={a^2}/{2*cos{{alpha}/2}}$
Рассмотрим пример расчета площади поверхности четырехугольной пирамиды через боковое ребро и сторону основания.

Задача: пусть дана правильная четырехугольная пирамида. Длина ребра b = 7 см, длина стороны основания a = 4 см. Подставим заданные значения в формулу:
$S_bok={1/2}*4*sqrt{7^2-{{4^2}/4}}={1/2}*4*sqrt{49-4}=13,4{cm}^2$

Мы показали расчеты площади одной боковой грани для правильной пирамиды. Соответственно. Чтобы найти площадь всей поверхности необходимо умножить результат на количество граней, то есть на 4. Если пирамида произвольная и ее грани не равны между собой, то рассчитать площадь необходимо для каждой отдельной стороны. Если в основании лежит прямоугольник или параллелограмм, то стоит вспомнить их свойства. Стороны у этих фигур попарно параллельны, а соответственно грани пирамиды будут также попарно одинаковы.
Формула площади основания четырехугольной пирамиды напрямую зависит от того, какой четырехугольник лежит в основании. Если пирамида правильная, то площадь основания рассчитывается по формуле площади квадрата, если в основании лежит ромб, то потребуется вспомнить, как находится площадь ромба. Ели же в основании лежит прямоугольник, то найти его площадь будет довольно просто. Достаточно знать длины сторон основания. Рассмотрим пример расчета площади основания четырехугольной пирамиды.

Задача: Пусть дана пирамида, в основании которой лежит прямоугольник со сторонами a = 3 см, b = 5 см. К каждой из сторон из вершины пирамиды опущена апофема. h-a=4 см,h-b=6 см. Вершина пирамиды лежит на одной линии с точкой пересечения диагоналей. Найдите полную площадь пирамиды.
Формула площади четырехугольной пирамиды состоит из суммы площадей всех граней и площади основания. Для начала найдем площадь основания:

$S_osn=3*5=15{cm}^2$
Теперь рассмотрим грани пирамиды. Они попарно одинаковы, потому что высота пирамиды пересекает точку пересечения диагоналей. То есть, в нашей пирамиде есть два треугольника с основанием a и высотой h-a, а также два треугольника с основанием b и высотой h-b. Теперь найдем площадь треугольника по известной формуле:
$S_a={1/2}*3*4=6{cm}^2$
$S_b={1/2}*5*6=15{cm}^2$
Теперь выполним пример расчета площади четырехугольной пирамиды. В нашей пирамиде с прямоугольником в основании, формула будет выглядеть так:

$S_poln=15+2*6+2*15=15+12+30=57{cm}^2$