Площадь поверхности тетраэдра
Площадь поверхности тел
Тетраэдром является геометрическая фигура, представляющая собой простейший многогранник с четырьмя гранями. Любая грань тетраэдра является треугольником. Кроме 4-х граней у тетраэдра имеется шесть ребер и четыре вершины. В правильном тетраэдре все ребра равны. Расчет S тетраэдра необходим при решении разных проектировочных задач, т.к. он является важным конструктивным элементом в сложных строительных и других конструкциях. Площадь поверхности тетраэдра несложно вычислить с помощью онлайн калькулятора, подставив исходные данные в приведенную ниже формулу:
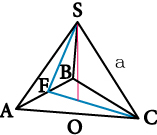
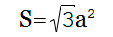
a — величина ребра тетраэдра.
Площадь тетраэдра рассчитывается как корень квадратный из произведения квадрата длины ребра на 3.
Расчет площади поверхности тетраэдра
Что такое тетраэдр: определение, виды, формулы площади и объема
В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение тетраэдра
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.
Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» – означает грань (тетраэдр – четырехгранник).
Поэтому на вопрос – “что такое тетраэдр?”, можно дать следующее определение: ” Тетраэдр это геометрическое тело из четырех граней, каждая их которых – правильный треугольник “.
Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Тетраэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 4;
- Число рёбер, примыкающих к вершине – 3;
- Общее число вершин – 4;
- Общее число рёбер – 6;
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.
Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.
Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.
Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы тетраэдра определяется по формуле:

, где a – длина стороны.

Сфера может быть вписана внутрь тетраэдра.
Радиус вписанной сферы тетраэдра определяется по формуле:



Площадь поверхности тетраэдра
Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой: 

Объем тетраэдра определяется по следующей формуле:


Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки
Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка – единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал тетраэдр с “земным” элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
– если Вы предполагаете распечатать на цветном принтере – цветная развертка
– если Вы предполагаете использовать для сборки цветной картон – развертка
Видео. Тетраэдр из набора “Волшебные грани”


Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора “Волшебные грани”.
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Популярное
Сделать новогодний праздник красивым и необычным, чтобы дети видели в нём сказку, а гости восхищались, можно только своими руками. Бумажные многогранники –.
1. Вы хотели бы увидеть, как можно преобразовать развертку обычного куба? Если да, то следующий.
Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.
В этой статье мы постараемся рассказать можно ли наборы «волшебные грани» отнести к разновидности оригами. Как одну и ту же геометрическую фигуру можно получить, используя детали из.
С приходом весны, все растения вокруг оживают, появляется листва, всё зеленеет, и распускаются цветы. Но для домашних растений лето продолжается круглый год, конечно при.
Визитная карточка Республики Беларусь – новое здание Национальной библиотеки в Минске. Проект нового здания был разработан еще в конце 80-х годов прошлого века и в 1989.
АРХИМЕД (287 – 212 до н.э.) – древнегреческий математик, физик и механик. Архимед – автор многочисленных открытий и изобретений: машины для.
Тетраэдр.
Тетраэдр – это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Типы тетраэдров.
Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр – это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
– Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
– Соразмерный тетраэдр, бивысоты у него одинаковы.
– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Формулы для определения элементов тетраэдра.
Высота тетраэдра:
где h – высота тетраэдра, a – ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
где V – объем тетраэдра, a – ребро тетраэдра.
Основные формулы для правильного тетраэдра:
Где S – Площадь поверхности правильного тетраэдра;
h – высота, опущенная на основание;
r – радиус вписанной в тетраэдр окружности;
[spoiler title=”источники:”]
http://mnogogranniki.ru/tetraedr.html
http://www.calc.ru/1535.html
[/spoiler]
Онлайн калькулятор площади тетраэдра может вычислить площадь боковой поверхности тетраэдра. Расчет возможен для правильного (равностороннего) тетраэдра и для прямоугольного тетраэдра.
Сделайте расчет на этом калькуляторе площади тетраэдра и получите ответ в развернутом виде а также детального пошаговое решение с выводом формул.
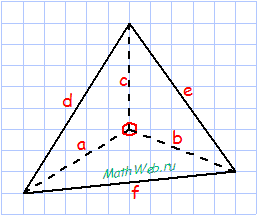
Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°
Формула площади поверхности прямоугольного тетраэдра: 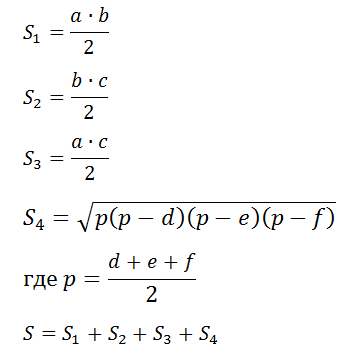
где a,b,c – стороны при угле 90°, d,e,f – стороны основания
Решение:
S1 =
=
=
= 616
S2 =
=
=
= 1144
S3 =
=
=
= 1144
p =
=
=
= 62
S4 = √p·(p-d)·(p-e)·(p-f)
= √62·(62-44)·(62-28)·(62-52)
= √62·18·34·10
= 615.987
S = S1+S2+S3+S4
= 616+1144+728+615.987
=
3103.987
Ответ: Площадь всей поверхности прямоугольного тетраэдра равна 3103.987
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.
Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
Тетраэдр – это уникальная пирамида с равносторонним треугольником в основании, которое идентично боковым граням. Таким образом, у тетраэдра всего четыре треугольные грани, которые конгруэнтны между собой – и это главное условие для правильных многогранников, ряд которых открывает тетраэдр. Площадь боковой поверхности тетраэдра будет равна трем площадям треугольников, а площадь полной поверхности тетраэдра – четырем. Для их нахождения достаточно знать всего лишь сторону треугольника:

Площадь тетраэдра вычисляется по формуле, в которой производится действие умножения квадрата длины ребра состоящей из трех треугольных плоскостей объемной геометрической фигуры на корень из 3.
Тетраэдр простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Востребованность расчета S тетраэдра возникает при решении различных проектировочных задач. В виду наличия в правильном тетраэдре равенства всех ребер конструктивный элемент представляет собой максимально надежный и экономичный по затратам используемого материала конструктивный элемент, который можно включать в более сложные строительные и иные конструкции.
Расчет площади тетраэдра может быть востребован при проектировании высокоточного оптического оборудования. Довольно часто при решении сложных технических расчетных задач кроме вычисления площади объемной фигуры требуется вписывание в тетраэдр октаэдра и описывание тетраэдра икосаэдром. Может быть востребовано вписывание тетраэдра в куб с совмещением его 4-х вершин с 4 вершинами куба. Вычисление площади и объема компактной фигуры может быть необходимо при проектировании транспортной и пользовательской тары.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

