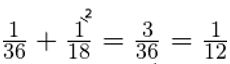Как найти общую скорость работы

Задачи на совместную работу

Рассмотрим задачи, в которых речь идёт о совместном выполнении некоторой работы. При этом всё равно, какую работу выполняют и чем эту работу измеряют — числом деталей, количеством вспаханных гектаров и т. п. Если, например, некоторая работа выполняется за  10  часов, то за  1  час, очевидно, выполняется    всей работы, а вся работа составляет десять таких частей  .  Поэтому обычно в таких задачах всю работу принято считать равной единице, объём выполненной работы выражают как часть этой единицы.

Под совместной работой можно понимать и одновременную работу двух труб при наполнении бассейна, и прохождение некоторого пути при движении навстречу друг другу и т. п. Метод решения остаётся тем же.

Математика

5 класс

Урок № 69

Задачи на совместную работу

Перечень рассматриваемых вопросов:

– введение понятий производительность, общая производительность, время работы;

– алгоритм решения задач на совместную работу арифметическим способом;

– отработка применения алгоритма при решении задач.

Тезаурус

Производительность (Р) – объём работы, выполняемый за единицу времени.

Время работы (Т) – время выполнения всей работы.

Общая производительность – объём работы, выполняемый совместно всеми работниками за единицу времени.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 классы. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

На предыдущих уроках мы научились выполнять арифметические действия с обыкновенными дробями. Сегодня мы рассмотрим, как с помощью обыкновенных дробей решать задачи на совместное выполнение некоторой работы.

Под совместной работой можно понимать абсолютно любое действие: и одновременный поток воды из двух труб при наполнении бассейна, и изготовление деталей двумя рабочими, и вспашку поля несколькими тракторами, и набор текста на компьютере.

Всю работу мы будем принимать за единицу. А объём выполненной работы выражать как часть этой единицы.

Если какая-то работа выполняется за шесть часов, то за час выполняется одна шестая часть этой работы.

Объём работы, выполненный за единицу времени, называется производительностью. Она обозначается как Р.

Рассмотрим задачу.

Первый столяр может выполнить заказ за 36 часов, а второй – за 18 часов. За сколько часов этот заказ выполнят оба столяра, работая вместе?

Вся работа – 1

1-й столяр – 36 ч

2-й столяр – 18 ч

1-й и 2-й столяр – ? ч

(первый столяр за один час, или производительность Р₁ первого столяра)

(второй столяр за один час, или производительность Р₂ второго столяра)

(оба столяра за один час, или общая производительность Р)

(время выполнения всей работы совместно)

Ответ: за 12 ч.

Рассмотрим следующую задачу.

Одна труба заполняет бассейн за 60 минут, а вторая – за 20 минут. За сколько минут заполнится бассейн при включении обеих труб?

Вся работа – 1

1-я труба – 60 минут

2-я труба – 20 минут

Обе трубы – ?

часть бассейна (наполняет первая труба за одну минуту, или производительность Р₁)

часть бассейна (наполняет вторая труба за одну минуту, или производительность Р₂)

часть бассейна (заполняют обе трубы, работая вместе, или общая производительность Р)

минут (время заполнения бассейна двумя трубами)

Ответ: за 15 минут.

Рассмотрим задачу, в которой, зная время выполнения работы совместно, надо найти время работы одного из участников.

Работая вместе, два мастера Гжели выполняют заказ за шесть дней. Первый мастер, работая один, может выполнить этот заказ за 10 дней. За сколько дней этот заказ может выполнить второй мастер?

Вся работа – 1

1-й и 2-й мастер – 6 дней

1-й мастер – 10 дней

2-й мастер – ? дней

часть заказа (первый и второй мастера за один день, или общая производительность Р)

часть заказа (первый мастер за один день, или производительность Р₁)

часть заказа (выполнит второй мастер за один день, или производительность Р₂)

дней – время выполнения заказа вторым мастером

Ответ: за 15 дней.

Алгоритм решения задач на совместную работу

Т₁ – время, за которое первый объект самостоятельно выполнит всю работу;

Т₂ – время, за которое второй объект самостоятельно выполнит всю работу.

1. Всю выполненную работа принимаем за единицу.
2. Находим часть работы, выполненную первым объектом за единицу времени (производительность Р₁ = 1 ꞉ Т₁).
3. Находим часть работы, выполненную вторым объектом за единицу времени (производительность Р₂ = 1 ꞉ Т₂).
4. Находим часть работы, выполненную двумя (или более) объектами за единицу времени (общая производительность Р = Р₁ + Р₂).
5. Находим время, затраченное на выполнение всей работы всеми объектами (Т = 1 ꞉ Р).

Тренировочные задания

№ 1. Путешественник планирует пройти маршрут за семь дней. Какую часть маршрута он пройдёт за один день? За три дня? За пять дней? Какая часть маршрута останется не пройденной за эти же промежутки времени? Используйте следующие значения ; ; ; ; .

За 1 день

Пройденная часть маршрута – ?

Осталось пройти – ?

За 3 дня

Пройденная часть маршрута – ?

Осталось пройти – ?

За 5 дней

Пройденная часть маршрута – ?

Осталось пройти – ?

Пройденная часть маршрута за день – это производительность путешественника. И находится она так же, как и другая производительность. Найдём часть маршрута, пройденную за один день:

Очевидно, что за три дня путешественник пройдет в три раза больше, чем за день. Рассчитаем эту часть пути:

Чтобы найти оставшуюся часть маршрута, надо из всего маршрута, то есть единицы, вычесть пройденную часть. Найдём, например, какую часть маршрута осталось пройти через три дня: .

Аналогично действуем и в остальных случаях.

Правильный ответ:

За 1 день

Пройденная часть маршрута –

Осталось пройти –

За 3 дня

Пройденная часть маршрута –

Осталось пройти –

За 5 дней

Пройденная часть маршрута –

Осталось пройти –

№ 2. Подберите к каждому действию правильное пояснение.

Два тракториста вспахали поле за 6 ч совместной работы. Первый тракторист мог бы один выполнить ту же работу за 10 ч. За сколько часов второй тракторист может вспахать поле?

Пояснения к действиям:

• Время выполнения всей работы вторым трактористом;
• Общая производительность обоих трактористов;
• Часть всей работы, выполняемая вторым трактористом за один час.

Действия:

Рассмотрим первое действие. Единица делится на шесть, где единица – это вся работа, а шесть – время совместной работы. Значит, этим действием мы находим общую производительность обоих тракторов.

Во втором действии из общей производительности вычитаем . Так как первый тракторист выполняет работу за 10 часов, то – это производительность первого тракториста. Значит, мы находим производительность второго тракториста, то есть объём работы, который он выполнил за один час.

В третьем действии единица (вся работа) делится на производительность второго тракториста: таким образом, мы находим время выполнения всей работы вторым трактористом.

Правильный ответ:

– это общая производительность обоих трактористов.

– это часть всей работы, выполняемая вторым трактористом за 1 ч.

ч – это время выполнения всей работы вторым трактористом.

Для решения задач на совместную работу используются уравнения и системы уравнений. Применение уравнений для решения задач в 4 классе является дискуссионым, однако часто без них никак.

Задачи на совместную работу многообразны. Это могут быть и бригады рабочих, выполняющие одну и ту же работу, и трубы, наполняющие бассейн и выводящие из него воду, землекопы, копающие траншеи и пр.

Принципы решения задач на совместную работу схожи с принципами решения задач на движение. В задачах на движение путь – это произведение скорости на время.

В задачах на совместную работу аналогом пройденного пути выступает объём сделанной работы, который вычисляется как скорость производства чего бы то ни было (скорость наполнения воды в бассейне, копания канавы и пр.), умноженная на время.

В задачах на движение скорости двух объектов, движущихся навстречу друг другу, складываются, а в случае, когда один объект догоняет другой, то скорость сближения определяется как разность скоростей двух объектов.

Аналогично в задачах на совместную работу скорости выполнения работ – если это работа в одно направлении, складываются, и вычитаются, если это работы в противоположном направлении. Например, если две трубы заполняют бассейн с определённой скоростью, то для вычисления времени, за который бассейн будет заполнен двумя трубами, надо сложить скорости заполнения каждой из труб – этот случай аналогичен движению объектов навстречу друг другу (у них одна цель, т.е. они делают одну и ту же работу).

Если же у нас из одной трубы в бассейн втекает объём воды с определённой скоростью, а из другой трубы вытекает с другой (меньшей) скоростью, то для нахождения времени заполнения бассейна нам надо из скорости первой трубы вычесть скорость второй трубы. Это аналогично случаю, когда более быстрый объект догоняет более медленный. У них разные цели – один хочет оторваться от преследования, второй хочет его догнать, и их скорости вычитаются. Точно так же у двух труб разные цели – одна хочет бассейн наполнить, а вторая опустошить.

Рассмотрим конкретные примеры.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Задача 1

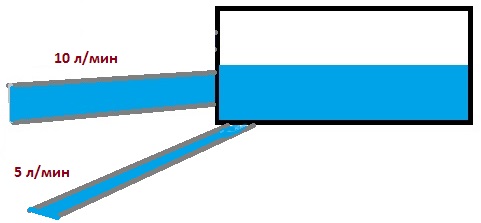
2 трубы наполняют бассейн. Одна со скоростью 5 литров в минуту, вторая со скоростью 10 литров в минуту. Объём бассейна 300 литров. За какое время две трубы наполнят бассейн?

Решение

Две трубы делают одну и ту же работу, поэтому для нахождения суммарной скорость их работы надо сложить скорость наполнения бассейна первой трубой со скоростью наполнения второй трубой.

V = 5 + 10 = 15 л/мин.

Объём бассейна нам известен – 300 л. Следовательно, для того, чтобы найти, за какое время он будет наполнен, надо объём бассейна разделить на скорость наполнения, которую мы только что нашли.

t = 300 / 15 = 20 минут.

Ответ: бассейн наполнится за 20 минут

Задача 2

В изначально пустой бассейн объёмом 400 литров поступает вода из трубы со скоростью 30 литров в минуту. Из второй трубы меньшего диаметра вода вытекает из бассейна со скоростью 20 литров в минуту. За какое время наполнится бассейн?

Решение

В данном случае трубы выполняют противоположную работу, поэтому для нахождения итоговой скорости работы надо из большей скорости вычесть меньшую скорость.

V = 30 – 20 = 10 л/мин

10 л/мин – это итоговая скорость наполнения бассейна. Если у нас за одну минуту в бассейн вылилось 30 литров воды, и за эту же минуту 20 литров вытекло из него, то осталось всего 10 литров – это и есть скорость наполнения.

Время заполнения бассейна водой мы находим аналогично первой задаче:

t = 400/10 = 40 мин.

Ответ: бассейн заполнится за 40 минут

Задача 3

Первая бригада может выполнить задание за 36 ч, а вторая бригада может выполнить то же задание за 18 ч. За сколько часов это задание выполнят две бригады при совместной работе?

Решение. 1 способ – с помощью дробей

В старших классах такая задача решается просто с помощью дробей.

Примем всю работу за единицу, тогда за 1 ч первая бригада выполняет 1/36 работы, а вторая бригада за 1 час сделает 1/18 работы. При совместной работе за 1 ч две бригады выполняют всей работы, поэтому всю работу они выполнят

всей работы. Таким образом, если за 1 час выполняется 1/12 всей работы, то вся работа целиком будет сделана за 12 часов.

Ответ: 12 часов

Решение. 2 способ – по действиям без дробей

Если первая бригада всю работу делает за 36 часов, то мы можем представить, что работа состоит из 36 частей, каждая из которых равна 1 часу.

1. Определим, какую часть работы делает за 1 час первая бригада.

Для этого разделим общее количество частей, из которых состоит работа, на то время, за которое первая бригада делает всю работу

36:36 = 1 часть

2. Определим, какую часть работы делает за 1 час вторая бригада.

Делаем как в первом действии

36:18 = 2 части.

3. Найдём, сколько частей работы делают за один час две бригады в месте

2 + 1 = 3 части

4. Найдём, за какое время обе бригады сделают всю работу.

Для этого общее количество частей (36) разделим на суммарную скорость работы двух бригад, т.е. 3 части в час.

36:3 = 12 часов.

Как видим, при решении вторым способом мы получили тот же ответ, что и при решении с помощью дробей.

Ответ: 12 часов

Одна труба может наполнить бассейн водой за 12 часов, а другая – за 20 часов. За какое время бассейн будет наполнен водой, если две трубы будут работать одновременно?

Решение

В 4-м классе дети дробей ещё не знают, поэтому задачу надо решать через части.

Итак, нам надо всю работу обозначить каким-то количеством частей, и далее, исходя из этого, определить скорость работы труб в частях.

Наиболее простой способ определения количества частей – перемножить 12 на 20 и получить 240 частей. В этом случае скорость работы первой трубы – 20 частей в час (12 – это 1/20 от 240), а скорость второй трубы – 12 частей в час (20 – это 1/12 от 240).

Суммарная скорость работы двух труб: 20+12 = 32 части в час.

Чтобы найти время, за которое наполнится бассейн, надо 240 поделить на 32. Дробных чисел дети в 4-м классе ещё не знают, поэтому поделим нацело 240 на 32 и найдём частное и остаток:

240:32 = 7 остаток 16.

16 – это половина от 32

Суммарная скорость двух труб – 32 части в час, значит 16 частей бассейна заполняются за полчаса, то есть 30 минут.

Ответ – 7 часов 30 минут.

Общее количество частей можно определить не путём перемножения времени работы первой трубы на время работы второй, а путём нахождения наименьшего общего кратного (НОК) этих двух чисел.

Для 12 и 20 НОК равен 60. 60 – наименьшее число, которое без остатка делится и на 12 и на 20.

Таким образом, если вся работа – 60 частей, то

скорость первой трубы – 60:12 = 5 частей в час

скорость второй трубы – 60:2- = 3 части в час.

Суммарная скорость двух труб: 5+3 = 8 частей в час.

Теперь для нахождения времени заполнения бассейна нам надо 60 поделить на 8.

60:8 = 7 остаток 4.

Суммарная скорость двух труб – 8 частей в час, значит 4 части бассейна заполняются за полчаса, то есть 30 минут.

Таким образом, общее время наполнения бассейна – 7 часов 30 минут. Мы получили то же самое время, что и в первом способе, когда у нас вся работа состояла из 240 частей.

Ответ: 7 часов 30 минут

Задача 5

За пять недель пират Ерёма

Способен выпить бочку рома

А у пирата, у Емели

Ушло б на это две недели.

За сколько дней прикончат ром

Пираты, действуя вдвоём?

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Решение

Эту задачу можно решить через дроби. 5 недель – это 35 дней, 2 недели – 14 дней, далее нужно 1/35 (скорость выпивания бочки в день пирата Ерёмы) сложить с 1/14 (скорость Емели), привести дроби к общему знаменателю, получить суммарную скорость в 1/10, и, соответственно, ответ в 10 дней.

Но можно решить эту задачу и без использования дробей.

Аналогично предыдущей задачи про бассейн, выразим всю работу в частях, при этом так, чтобы это число делилось без остатка и на 35 и на 14.

Наименьшее число, которое делится без остатка и на 35 и на 14 – это 70. (Если мы испытываем сложности с нахождением минимального числа, то всегда можно перемножить 35 на 14 и получить 490).

Итак, всю бочку рома мы приняли равной в 70 частей. Акцентирую ваше внимание, что мы вместо 70 могли бы взять любое другое количество частей – это не повлияло бы на логику решения задачи, но, т.к. в 4-м классе дети не умеют работать с дробными числами, то мы берём то число частей, которое без остатка делится на скорость работы всех работников, которые есть в условии задачи. В нашем случае работники – это два пирата, работа которых заключается в выпивании рома.

Таким образом, если Ерёма выпивает всю бочку за 35 дней, то его скорость это

70:35 = 2 части в день

Скорость Емели, который ту же бочку выпивает за 14 дней:

70:14 = 5 частей в день.

Суммарная скорость выпивания рома Ерёмы и Емели – 5 + 2 = 7 частей в день.

Таким образом, если весть объём рома – это 70 частей, а оба пирата за день выпивают 10 частей, то весь ром они выпьют за

70:7 = 10 дней.

Ответ: 10 дней.

Задача 6

Два оператора могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 4 ч, а второй 12 ч, то они выполнят всю работу. За какое время может набрать весь текст каждый оператор, работая отдельно?

Решение

введём обозначения

x – объём текста, который в час печатает первый оператор

y – объём текста, который в час печатает второй оператор

С одной стороны, весь объём работы можно выразить как

8x + 8y (два оператора набирают текст за 8 часов).

С другой стороны, этот же объём работы:

4x + 12y

Т.к. это одинаковые объёмы работы, то составим уравнение:

8x + 8y = 4x + 12y

8x – 4x = 12y – 8y

4x = 4y

x = y

Отсюда делаем вывод, что операторы работают с одинаковой скоростью.

Рассмотрим случай, когда первый оператор будет работать 4 ч, а второй 12 ч.

Вот схема их работы:

Первые 4 часа оба оператора работают вместе, и за это время они сделают половину всей работы (т.к. работая вместе 8 часов, они сделают всю работу).

После 4 часов работы первый оператор прекращает работать и продолжает работать второй оператор. Всего он по условию задачи работает 12 часов – то есть ещё 8 часов после того, как прошли первые 4 часа.

И если за первые 4 часа сделана половина работы, то оставшиеся 8 часов работы второго оператора – это вторая половина работы.

То есть второй оператор половину работы делает за 8 часов, и, следовательно, всю работу он сделает за 16 часов. Как мы уже выяснили ранее, скорости работы операторов равны, поэтому первый оператор также всю работу выполнит за 16 часов.

Ответ: и первый и второй оператор всю работу по отдельности выполнят за 16 часов.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Задача 7

Первая труба наполняет резервуар объемом 180 литров, а вторая труба наполняет резервуар объемом 120 литров. При этом известно, что одна из труб пропускает на 1 литр воды в минуту меньше, чем другая. Необходимо определить, сколько литров в минуту пропускает первая труба, если резервуары полностью заполняются за одинаковое время.

Решение

Как мы уже говорили в начале этого урока, принципы решения задач на совместную работу схожи с принципами решения задач на движение.

Рассматриваемая задача схожа с задачами на движение, в которых один объект догоняет другой. Напомню, что в таких задачах, если у нас известно первоначальное расстояние между двумя объектами, и скорости этих объектов, то время, за которое второй объект догонит первый, рассчитывается как первоначальное расстояние, поделённое на скорость сближения объектов, где скорость сближения – разница между скоростью догоняющего объекта и догоняемого.

В этой задаче про два резервуара известно, что они наполняются за одинаковое время, хотя их объёмы разные. То есть скорость наполнения первого, более большого резервуара, очевидно выше, чем скорость наполнения второго, меньшего по объему. Разница между скоростями наполнения известна – 1 литр в минуту.

Таким образом, если проводить аналогии с задачами на движение, где один объект догоняет второй, мы можем сказать, что скорость догона в нашем случае – это тот самый 1 литр в минуту, а первоначальное расстояние между объектами – это разница в объёмах двух резервуаров, то есть 180-120 = 60 л. И чтобы найти, за какое время один объект догонит другой – то есть в нашем случае, когда они полностью заполнятся, надо разницу в объёмах разделить на разницу в скоростях заполнения.

То есть 60/60 = 1 час.

1 час равен 60 минутам.

По условию задачи нам надо определить, сколько литров в минуту пропускает первая труба.

Для этого объём первого резервуара надо поделить на время, за которое он полностью заполняется.

То есть 180 литров /60 минут = 3 литра в минуту.

Ответ: скорость первой трубы – 3 литра в минуту.

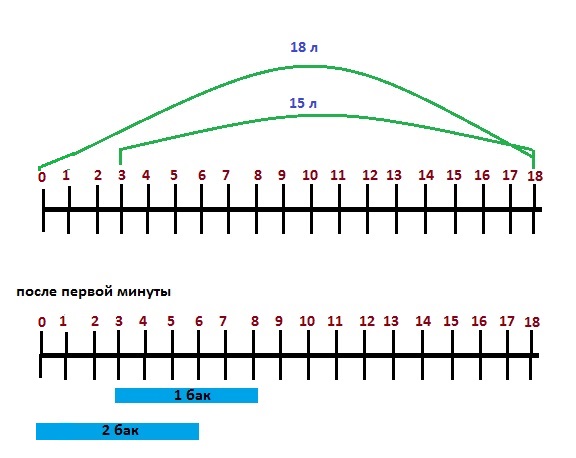
Мы понимаем, что приведённые при решении этой задачи рассуждения могут показаться неочевидными. Для того, чтобы вы могли убедиться, что данная методика является верной, проиллюстрируем её на примере с меньшими цифрами.

Пусть у нас есть два бака, один объёмом 15 литров, второй объёмом 18 литров. Первый наполняется со скоростью 5 литров в минуту, а второй – со скоростью 6 литров в минуту.

Несложно подсчитать, что время заполнения у них будет одинаковое – 3 минуты (15:5 = 3, 18:6 = 3).

Эти же три минуты можно получить по другому:

Разница в объёмах баков – 3 литра (18- 15 = 3). Разница в скоростях наполнения – 1 литр в минуту (6 – 5 = 1).

Соответственно, время, за которое второй, более объёмный бак, “догонит” первый, меньший по объёму, составляет 3:1 = 3 минуты.

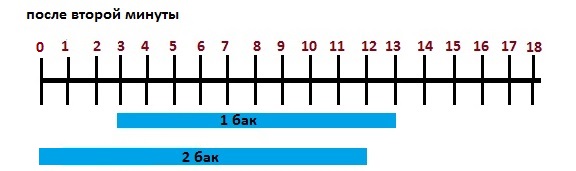
Проиллюстрируем это на рисунке.

На горизонтальной шкале отложим объём – от нуля до 18 литров.

Для первого бака, который объёмом 15 литров, отсчёт будем вести от отметки в 3 л и до 18 л. То есть как будто бы его объём тоже 18 литров, но на три литра он уже заполнен, и осталось заполнить 15 литров.

Таким образом отметка в 3 литра – это первоначальное “расстояние” между двумя баками.

После первой минуты первый бак заполнился на 5 литров, и мы рисуем синюю полоску от отметки 3 л до отметки 8 л. Второй бак заполнился на 6 литров, и мы рисуем синюю полоску от 0 до 6 л. Таким образом, за первую минуту разница в объёмах воды в двух баках (“расстояние” между ними) сократилось с первоначальных 3 литров до 2 литров.

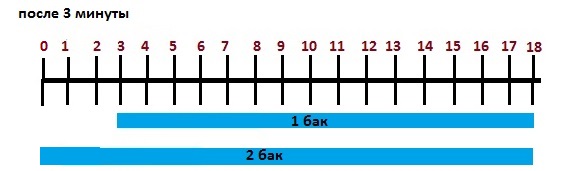
После второй минуты первый бак заполнился ещё на 5 литров (итого за 2 минуты на 10 литров), и мы рисуем синюю полоску от отметки 3 литра до отметки 13 литров. Второй бак заполнился ещё на 6 литров (итого на 12 литров за 2 минуты), и мы рисуем синюю полоску от отметки 0 до 12 литров. Разница в объёмах воды в баках сократилась с 2 литров до 1 литра.

После третьей минуты первый бак заполнился ещё на 5 литров (итого за 3 минуты на 15 литров), и мы рисуем синюю полоску от отметки 3 литра до финальной отметки 18 литров. Второй бак заполнился ещё на 6 литров (итого на 18 литров за 3 минуты), и мы рисуем синюю полоску от отметки 0 до 18 литров. Разница в объёмах воды в баках сократилась с 1 литров до нуля. Оба бака заполнились полностью.

Таким образом, из данного рисунка следует, с каждой минутой разница в объёмах воды в баках сокращается ровно на величину, равную разнице скоростей наполнения баков.

Поэтому применённая нами формула для решения этой задачи, согласно которой время наполнения – это разница в объёмах резервуаров, делённая на разницу скоростей, является рабочей.

Текстовые задачи на производительность

Задачи на производительность включают в себя задачи, в которых фигурирует какой-либо рабочий процесс и его характеристики: работа, время и производительность. Эти параметры связаны через формулу совместной работы:

(A = Pt,)

где (A) – работа, (t) – время, (P) – производительность.

Через эту формулу можно выразить производительность и время:

(P = frac{A}{t})

(t = frac{A}{P})

С помощью этих формул можно выражать одни характеристики работы через другие. Рассмотрим пример.

Пример №1:

За 5 дней работы рабочие на заводе произвели 35 деталей для автомобилей. Сколько деталей в день изготавливалось на заводе?

1. Для того, чтобы найти производительность, зная работу и время, нужно поделить работу на время:

(P = frac{A}{t} = frac{35}{5} = 7 деталей/день)

Ответ: 7.

ЗАДАЧИ НА ОБЩУЮ РАБОТУ

Часто в задачах на производительность можно увидеть вопрос на общую работу, когда нам известно время работы отдельных заводов или людей, а нужно найти совместное время, производительность или работу. В таком случае мы не сможем сложить время, т. к. при совместной работе время не увеличивается. А наоборот уменьшается за счет увеличения производительности. Рассмотрим на примере, как находить общее время работы.

Пример №2:

Для производства инструментов нужно сделать 600 деталей. Первый завод сделает эту работу за 10 дней, а второй завод за 15. За сколько дней будут готовы все детали, если их будут делать сразу два завода?

1. Мы знаем работу и время производства деталей в первом заводе. Найдем их производительность:

(P_{1} = frac{600}{10} = 60 )

(деталей в день делает первый завод)

1. Также найдем производительность для второго завода:

(P_{2} = frac{600}{15} = 40 )

(деталей в день делает второй завод)

1. Тогда за один день два завода вместе сделают:

(P_{общ} = 60 + 40 = 100 деталей в день)

Это производительность является общей для заводов.

1. С такой производительностью они сделают 600 деталей за:

(t_{общ} = frac{600}{100} = 6 дней)

Мы узнали, за какое время заводы сделаю 600 деталей, если каждый день будут работать вместе. Запишем ответ.

Ответ: 6.

ЗАДАЧИ С ДОПОЛНИТЕЛЬНЫМ УСЛОВИЕМ

Это такие задачи, где мы знаем, разницу между одной характеристикой нескольких рабочих или заводов. Тогда дополнительное условие позволяется связать нам данные и составить уравнение. Рассмотрим на примере.

Пример №3:

Заказ на 110 деталей второй рабочий выполняет на 1 час быстрее, чем первый. Сколько деталей за час изготавливает первый рабочий, если известно, что второй за час изготавливает на 1 деталь больше.

1. Составим таблицу. Вместо искомого поставим переменную 𝑥. В данном случае это производительность первого рабочего, т. к. спрашивают, сколько деталей он делает за час. Тогда производительность второго рабочего на единицу больше:

1. При этом рабочие выполняют одинаковую работу – по 110 деталей, тогда заполним колонку работы:

1. Тогда, зная производительность и работу каждого, выразим время для обоих рабочих:

(t_{1} = frac{110}{x})

(t_{2} = frac{110}{x + 1})

1. Теперь, когда мы знаем все характеристики работы рабочих, можем использовать дополнительное условие, которое заключается в том, что второй выполняет этот объем работы на час быстрее, значит, составим уравнение, которое объединяет время работы обоих рабочих:

(frac{110}{x + 1} + 1 = frac{110}{x})

1. Теперь работаем только с уравнением. Приведем обе части уравнения к одному знаменателю, в данном случае к знаменателю ((x + 1)x). Преобразуем получившееся уравнение, перенесем все в одну сторону и раскроем скобки:

(frac{110x}{(x + 1)x} + frac{(x + 1)x}{(x + 1)x} = frac{110(x + 1)}{x(x + 1)})

(frac{110x}{(x + 1)x} + frac{(x + 1)x}{(x + 1)x} – frac{110(x + 1)}{x(x + 1)} = 0)

(frac{110x + x^{2} + x – 110x – 110}{(x + 1)x} = 0)

1. Дробь будет равна нулю, если числитель равен нулю, а знаменатель его НЕ равен, т. е. (x neq –1) и (x neq 0):

(110x + x^{2} + x – 110x – 110 = 0)

(x^{2} + x – 110 = 0)

1. По т. Виета:

({x_{1} + x_{1} = –1 }{x_{1}x_{1} = –110})

Тогда:

(leftlbrack frac{x_{1} = 10}{x_{2} = –11} right. )

1. Проверим корни на адекватность. Оба решения являются корнями уравнения, но вернемся к тому, что мы искали. Мы приняли за x производительность первого рабочего, а такая реальная характеристика, как выполненная за час работа не может быть отрицательной. Таким образом ответом данной задачи будет являться первый корень уравнения. Запишем ответ.

Ответ: 10.