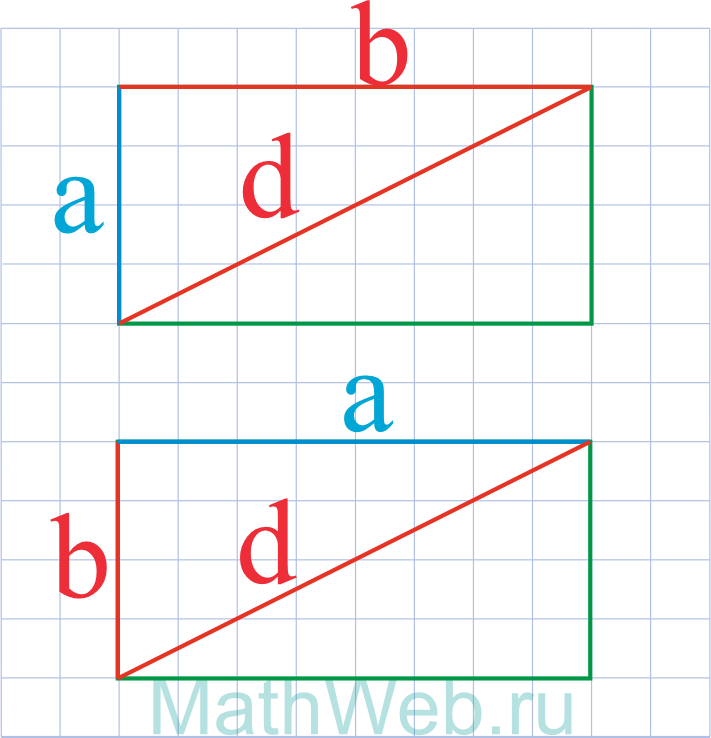
Где d – диагональ,b – сторона.
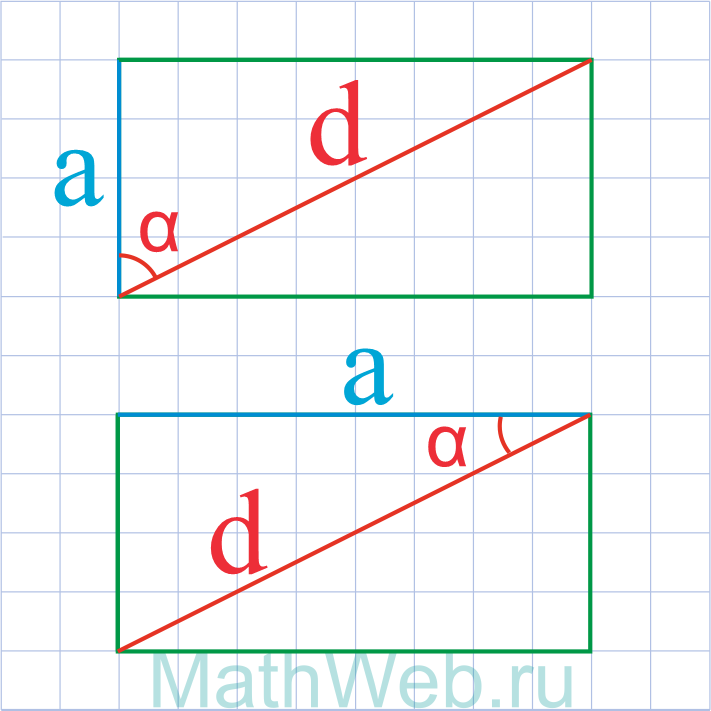
Где d – диагональ,α – угол между диагональю и искомой стороной.
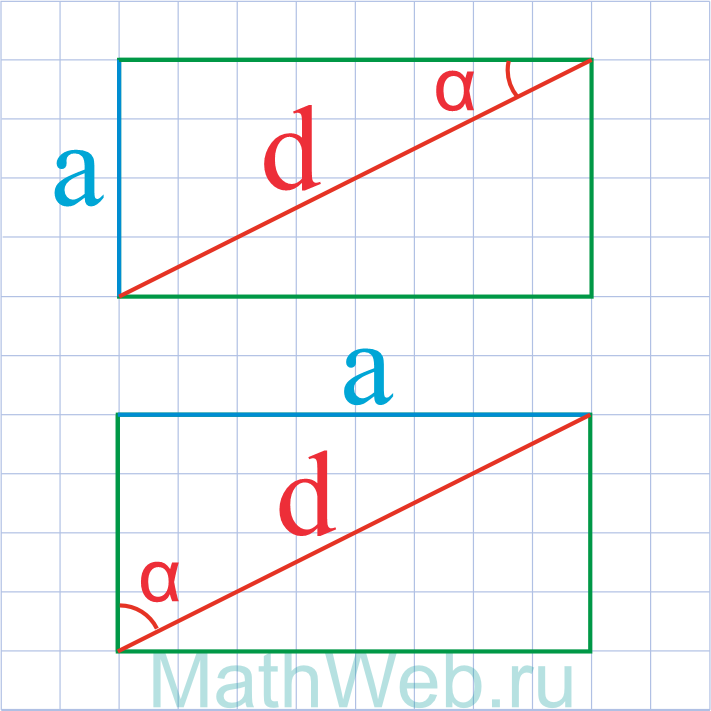
Где d – диагональ,α – угол между диагональю и другой стороной.
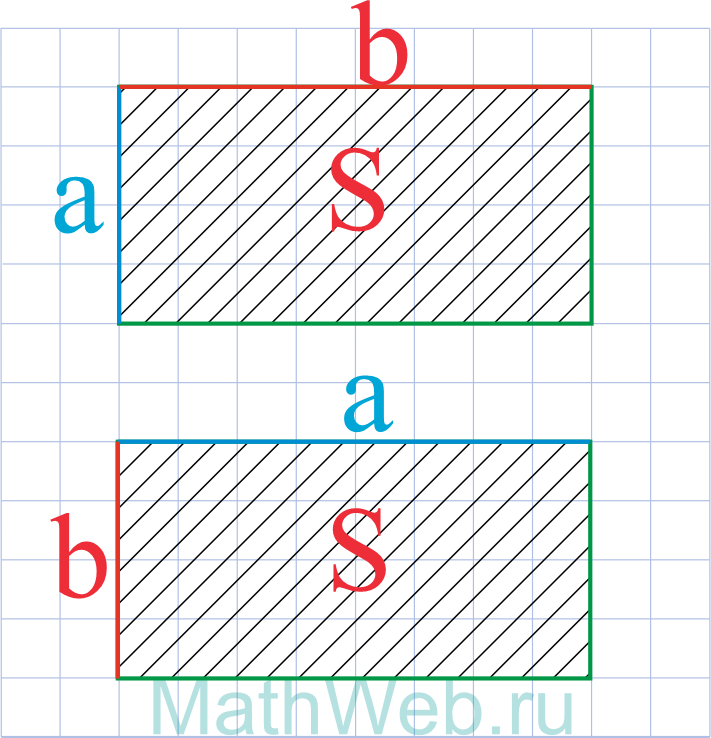
Где S – площадь, b– известная сторона.
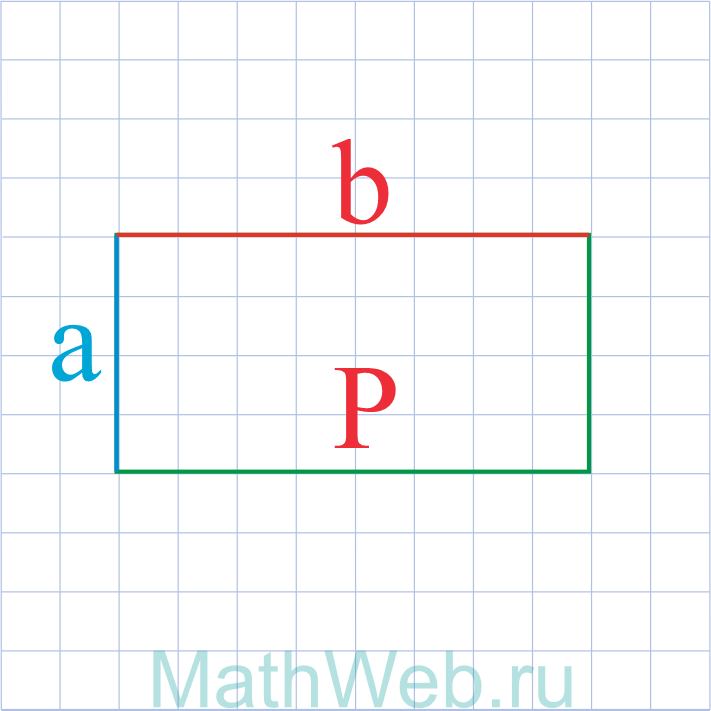
Где P – периметр, b – известная сторона.
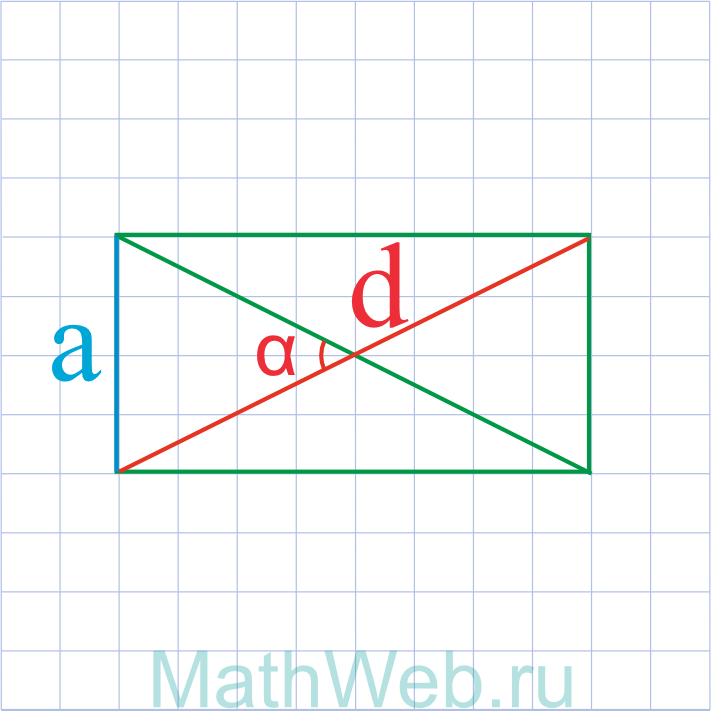
Где d – диагональ, α – угол между диагоналями.
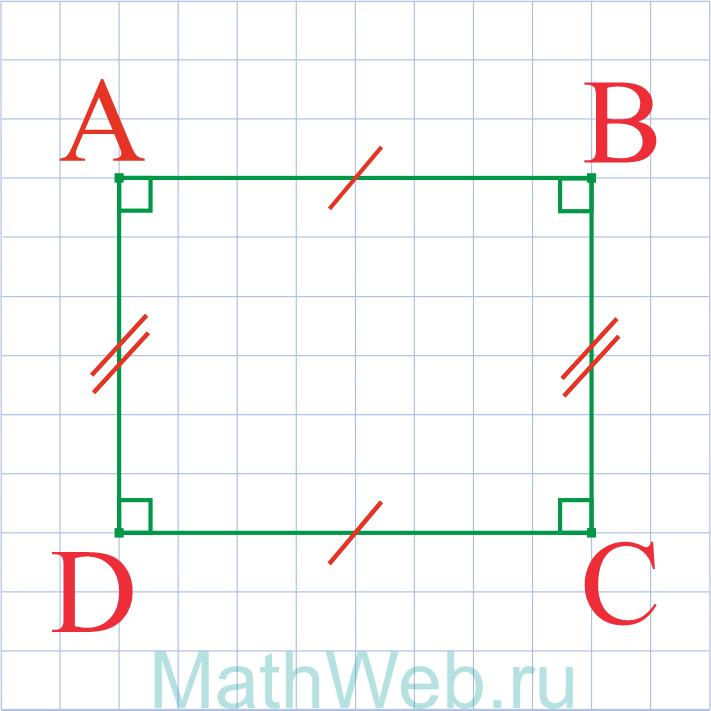
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = √d2 ― b2 |
 |
a = d·cos(α) |
 |
a = d·sin(α) |
 |
a = S b |
 |
a = P – 2b 2 |
 |
a = d·sin(0.5·α) |
Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.
- Сторона прямоугольника через диагональ и угол между
диагональю и стороной - Сторона прямоугольника через диагональ и известную
сторону - Сторона прямоугольника через площадь и другую известную
сторону - Сторона прямоугольника через периметр и другую известную
сторону - Сторона прямоугольника через диагональ и угол между
диагоналями
Через диагональ и угол между диагональю и стороной
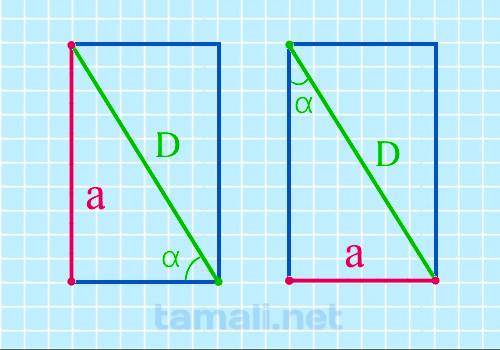
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:
a = d * sinα
где d — это диагональ, а, b — одна из сторон фигуры.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.
Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.
Через его площадь и известную сторону
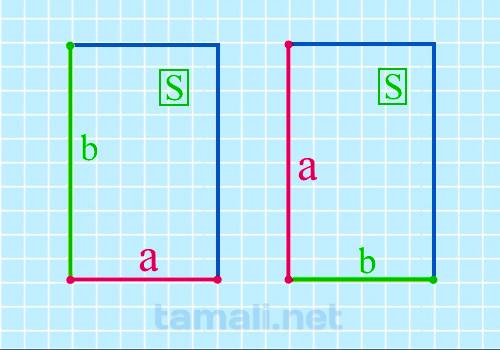
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно
a = S / b
где S — площадь прямоугольника, b — известная сторона.
Цифр после
запятой:
Результат в:
Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.
Через диагональ и известную сторону
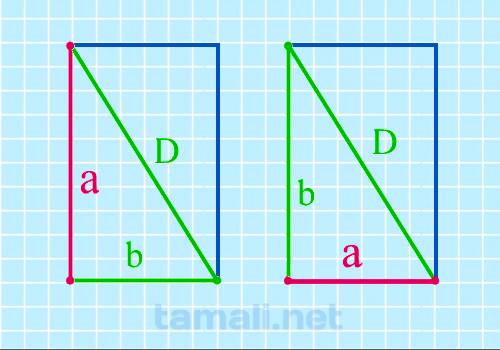
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :
a = √(d² — b²)
где d — диагональ, а, b — стороны.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.
Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
Через диагональ и угол между диагоналями
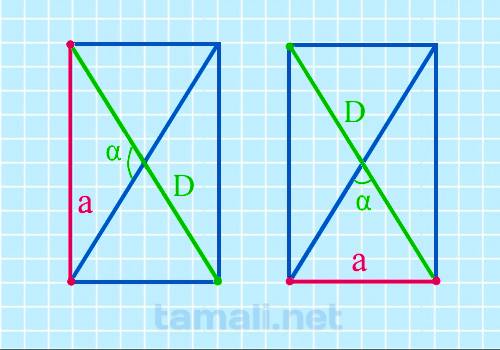
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:
a = D • sin(α/2)
где D — диагональ, α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.
Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.
Через периметр и другую известную сторону
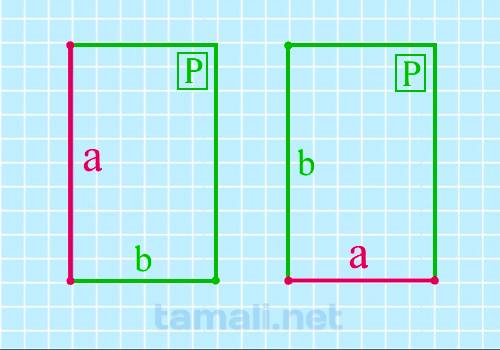
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).
a = (P — 2b) / 2
где P — периметр прямоугольника, b — другая известная сторона.
Цифр после
запятой:
Результат в:
Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.
Другие примеры по решению задач на прямоугольник с использованием длины и ширины
- Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов - Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см². - Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.
Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника являются равными и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма внутренних углов равна 360°.
- Диагонали пересекаются друг с другом.
- Длина диагоналей равна.
- Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2). - Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.
Как найти сторону прямоугольника зная Полупериметр и другую его сторону
Р = а + b, где р — полупериметр, а — длина, b — ширина. б) Чтобы найти неизвестную сторону, нужно из полупериметра вычесть известную сторону. а = р — b. b = р — а.
- Как найти другую сторону прямоугольника
- Как найти стороны прямоугольника если известен периметр и соотношение сторон
- Чему равен полупериметр в см
- Как найти стороны прямоугольника по периметру и диагонали
- Как найти сторону если известны две другие
- Как найти 3 сторону прямоугольника
- Как узнать стороны прямоугольника если знаешь периметр
- Как найти периметр прямоугольника с разными сторонами
- Как узнать длину сторон зная периметр
- Чему равен полупериметр прямоугольника
- Как узнать полупериметр прямоугольника
- Как найти площадь через полупериметр
- Как найти длину стороны прямоугольника
- Чему равна диагональ прямоугольника стороны которого 5 см и 12 см
- Как найти диагональ прямоугольника зная одну сторону
- Как можно найти прямоугольника
- Как найти одну из сторон треугольника если известен периметр
- Как определить прямоугольник
- Как найти площадь прямоугольника если известен периметр и одна из его сторон
- Как найти периметр прямоугольника с одной известной стороной
- Как найти боковую сторону периметр
- Как найти площадь прямоугольника если известно две стороны
- Как найти меньшую сторону прямоугольника
- Как найти сторону если известна сторона и площадь
Как найти другую сторону прямоугольника
А = Р/2 — в, где Р — периметр прямоугольника, а — одна сторона прямоугольника, в — вторая сторона прямоугольника; 2. Если известна площадь прямоугольника, и одна из сторон прямоугольника: а = S: b, где S — площадь прямоугольника, b — сторона прямоугольника.
Как найти стороны прямоугольника если известен периметр и соотношение сторон
Если известен периметр и одна из сторон прямоугольника, допусти В, находим из формулы сторону А: 2А = Р — 2В; А = (Р — 2В) / 2. Ответ: А = (Р — 2В) / 2.
Чему равен полупериметр в см
Полупериметр — это половина периметра, значит формула полупериметра будет выглядеть так: P1/2 = a + b. Найдем полупериметр. P1/2 = 10 + 6 = 16 см.
Как найти стороны прямоугольника по периметру и диагонали
Как найти стороны прямоугольника если известна диагональ и периметр:
- Периметр нашего прямоугольника делим на 2.
- Выражаем одну из сторон прямоугольника.
- Составляем уравнение с двумя неизвестными по теореме Пифагора, где нашу диагональ возводим в квадрат.
Как найти сторону если известны две другие
В этом случае для вычисления нужно использовать теорему косинусов. Согласно которой: a2 = b2 + c2 — 2 * b * c * cos A, где «a» неизвестная сторона, «b» и «c» известные стороны, «A» угол между сторонами «b» и «c». Также можно применить теорему Пифагора* только для прямоугольных треугольников.
Как найти 3 сторону прямоугольника
Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Как узнать стороны прямоугольника если знаешь периметр
Пояснение: Периметр равен сумме длин всех сторон. В параллельные стороны попарно равны. Записываем формулу периметра прямоугольника через буквы и выражаем, чему равна каждая сторона.
Как найти периметр прямоугольника с разными сторонами
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны. P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Как узнать длину сторон зная периметр
Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.
Чему равен полупериметр прямоугольника
А) Полупериметр прямоугольника равен сумме длины и ширины. Так же полупериметр равен половине периметра. р = а + b, где р — полупериметр, а — длина, b — ширина.
Как узнать полупериметр прямоугольника
Сумма длины и ширины называется полупериметром. Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2. Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7 + 3) · 2 = 20 (см).
Как найти площадь через полупериметр
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Как найти длину стороны прямоугольника
P = a + b + a + b = 2a + 2b. Отсюда можно выразить длину стороны а: 2а = P — 2b; а = (P — 2b): 2.
Чему равна диагональ прямоугольника стороны которого 5 см и 12 см
C = √(a^2 + b^2) = √(12^2 + 5^2) = √(144 + 25) = √169 = 13 см длина диагонали.
Как найти диагональ прямоугольника зная одну сторону
Для нахождения диагонали применим теорему Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.
Как можно найти прямоугольника
Чтобы узнать площадь прямоугольника, можно найти квадрат диагонали и любой стороны, из первого числа вычесть второе, найти корень из результата, и на полученное число умножить длину известной стороны. Вуаля! S = a × √(d2 — а2), где а — известная сторона, d — диагональ.
Как найти одну из сторон треугольника если известен периметр
Периметр равен сумме сторон геометрической фигуры. Таким образом, если известен периметр треугольника Р и две стороны треугольника а и в, то третью сторону с можно найти как разность периметра треугольника и суммы двух других его сторон: с = Р — (а + в).
Как определить прямоугольник
- Прямоугольник — четырёхугольник, у которого все углы прямые (равны 90 градусам).
- В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°.
Как найти площадь прямоугольника если известен периметр и одна из его сторон
Умножьте периметр на длину известной стороны. Найдите квадрат известной стороны и умножьте полученное число на 2.От первого произведения отнимите второе и разделите результат на 2:
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
Как найти периметр прямоугольника с одной известной стороной
Поделите площадь на длину известной стороны. Прибавьте результат к известной стороне. Умножьте полученное число на два.Умножьте полученное число на два:
- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
Как найти боковую сторону периметр
Так же нам понадобится формула для нахождения периметра. Вспомним ее. Периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны: P = a + 2b.
Как найти площадь прямоугольника если известно две стороны
Чтобы узнать площадь прямоугольника, можно найти квадрат диагонали и любой стороны, из первого числа вычесть второе, найти корень из результата, и на полученное число умножить длину известной стороны. Вуаля! S = a × √(d2 — а2), где а — известная сторона, d — диагональ.
Как найти меньшую сторону прямоугольника
Общая формула выглядит так: P = 2 * (a + b) — где, а и b — стороны прямоугольника.
Как найти сторону если известна сторона и площадь
Ответ: сторону квадрата находим путем извлечения квадратного корня из значения площади.
Оставить отзыв
Сторона прямоугольника по площади и другой стороне в м

Введите длину стороны a в м:
0.00м
S = a • b ⇒ b = S : a
S — площадь прямоугольника в м2 (квадратных метрах);
a — известная длина одной из сторон прямоугольника в м (метрах).
b — неизвестная длина другой стороны прямоугольника в м (метрах)
Например:
Площадь прямоугольника равна 192 м2, одна сторона равна 8 м. Найдите длину другой стороны прямоугольника.
Краткое решение: b = S : a = 192 : 8 = 24 м.
Площадь прямоугольника равна 144 м2, длина прямоугольника равна 18 м. Найдите его ширину.
Краткое решение: ширина прямоугольника b = S : a = 144 : 18 = 8 м.
Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне.
b=S/a
Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение
P=2(a+b)=2(a+S/a)
Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )
Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение.
α=arc tan〖b/a〗=arc tan〖S/a^2 〗
β=arc tan〖a/b=arc tan〖a^2/S〗 〗
Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2)
γ=2α
δ=2β
Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3)
R=d/2=√(a^2+S^2/a^2 )/2
