Как найти общую сумму выплат егэ - Сайт, где вы сможете решить свои вопросы

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Содержание:

Возникли проблемы с пониманием дифференцированного платежа? Записывайтесь ко мне на частные уроки!
Условие задачи
Решение задачи
- Арифметический способ решения
- Алгебраический способ решения
- Графико-аналитический способ решения
Выводы
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
Остались вопросы, недопонимание? Записывайтесь ко мне на частные уроки!

Возникли проблемы с пониманием дифференцированного платежа? Записывайтесь ко мне на частные уроки!

Привет! Меня зовут Александр Георгиевич. Я профессиональный репетитор по математике, информатике и программированию. Уже на протяжении свыше 10 лет я помогаю школьникам и студентам по всей России сдавать рубежные контроли.

Если вам предстоит сдача ЕГЭ по математике, и вы имеете колоссальные сложности в понимании того, как решаются задачи на дифференцированный платеж из экономического блока, то срочно берите в руки мобильный телефон и набирайте мой контактный номер.

Я понимаю, что вы достаточно занятой человек, ценящий свое время, но, несмотря на это, я настоятельно рекомендую потратить буквально (2) минуты и познакомиться с отзывами клиентов, прошедших подготовку под моим началом.

Условие задачи

В мае планируется взять кредит в банке на сумму (10) миллионов рублей на (5) лет.
Условия его возврата таковы:

Каждый декабрь долг возрастает на (10%) по сравнению с концом предыдущего года.
С января по март каждого года необходимо выплатить часть долга.
В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.

Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?

Решение задачи

Практически в обязательном порядке я всем своим ученикам в первую очередь предлагаю ознакомиться с теорией, ориентированной на дифференцированный платеж. Поэтому, если вы не знаете или не помните в чем смысл дифференцированного платежа, его признаков и свойств, то обязательно переходите по ссылке и потратьте несколько минут своего времени для ознакомления. Поверьте, после знакомства, вам будет гораздо проще понять решение данной задачи.

Почему данную задачу следует отнести к категории задач на дифференцированный платеж? Вся фишка в этом предложении: “В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года“. То есть тело кредита уменьшается равными долями, а это ключевой маркер дифференцированной схемы платежей.

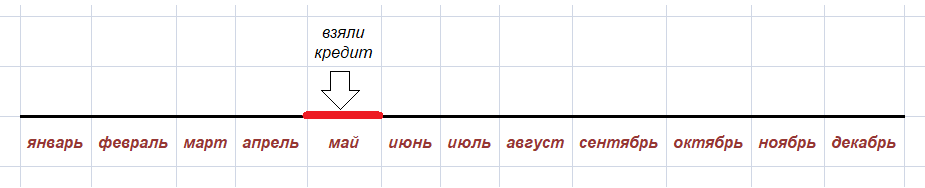
Давайте я вам покажу некоторую хронологическую линию, отражающую последовательность банковских операций.

Схема №1. Получение кредита в мае месяце

Данная схема является тривиальной, которая, по сути, отражает момент, когда заемщик получает кредит от банка. Важно просто запомнить месяц, когда это было сделано, так как именно с июня начинается полноценный процесс кредитования.

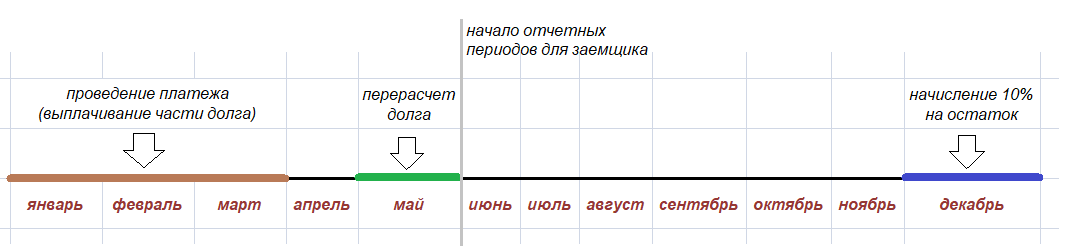
Схема №2. Последовательность банковских операций

Используя схему №2, нетрудно вывести последовательность банковских операций. Как было показано в схеме №1, отчетные периоды начинают действовать приблизительно с июня месяца. Кстати, в данной задачи можно оперировать месяцами, не вдаваясь в конкретные числа. В некоторых экономических задачах важны в том числе и точные даты конкретных месяцев!

Последовательность действий в рассматриваемой схеме дифференцированных платежей имеет вид:

В декабре происходит банковское начисление (10%) на остаток тело кредита.
В период с января по март заемщик проводит очередной платеж, то есть выплачивает какую-то часть долга, уменьшая таким образом задолженность по кредиту перед банком.
В какой-то день мая (в какой конкретно? это не имеет значения в данном случае) происходит перерасчет долга клиента перед банком по заему.

Последовательность этих действий повторяется ровно (5) раз. Почему именно (5) раз, а, например, не (8) или (17)? Потому что в формулировке задачи было сказано, что кредит берется сроком на (5) лет. То есть мы имеем дело с (5)-ю отчетными периодами.

Далее встает вопрос о способе решения поставленной задачи! Фундаментально существует (3) способа решения задач в математике: арифметический, алгебраический и графико-аналитический способ. Лично я рекомендую стремиться к алгебраическому способу решения, то есть стремиться к выводу какого-либо уравнения/неравенства или их системах. Но конкретно эту задачу можно решать и арифметическим способом, то есть поэтапным вычислением.

Поэтому я предлагаю решить поставленную задачу обоими этими способами, причем начнем с арифметического способа, как наиболее простого и быстро вычислимого. Но арифметический способ решения заданий не всегда возможен в принципе! Помните об этом и приучайтесь решать задания, прибегая к алгебре, а не к арифметике, хотя порою они так похожи…

Арифметический способ решения

Рассмотрим (1-й) отчетный период:

Размер кредита на начало периода, млн.	(10)
Размер начисленных банком процентов на остаток по кредиту, млн.	(10 * 0.1 = 1)
Размер кредита с учетом банковских процентов, млн.	(10 + 1 = 11)
Размер платежа по кредиту, млн.	(1 + frac{10}{5} = 1 + 2 = 3)
Размер кредита после проведения платежа, млн.	(11 – 3 = 8)

Краткие выводы. Схема дифференцированных платежей требует, чтобы тело кредита уменьшалось равными порциями. Так как у нас (5) отчетных периодов, то ежегодно размер кредита должен сокращаться на (2) млн. рублей.

Рассмотрим (2-й) отчетный периода:

Размер кредита на начало периода, млн.	(8)
Размер начисленных банком процентов на остаток по кредиту, млн.	(8 * 0.1 = 0.8)
Размер кредита с учетом банковских процентов, млн.	(8 + 0.8 = 8.8)
Размер платежа по кредиту, млн.	(0.8 + 2 = 2.8)
Размер кредита после проведения платежа, млн.	(8.8 – 2.8 = 6)

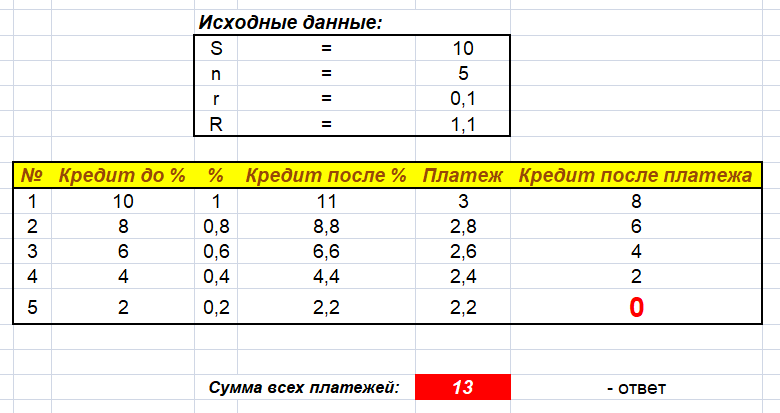
Предлагаю все последующие арифметические вычисления свести в агрегирующую/сводную таблицу. Хочу заметить, хорошо, что количество отчетных периодов равно (5), а, например, не (40). В случае (40) отчетных периодов арифметический способ решения стал бы абсолютно неэффективным, так как затребовал бы слишком много времени на все эти арифметические вычисления.

Сводая таблица, показывающая все действия по кредиту:

№ периода	Кредит до начисления %, млн.	Начисленные %, млн.	Кредит после начисления %, млн.	Платеж, млн.	Кредит после платежа, млн.
1	10	1	11	3	8
2	8	0.8	8.8	2.8	6
3	6	0.6	6.6	2.6	4
4	4	0.4	4.4	2.4	2
5	2	0.2	2.2	2.2	0

Сколько времени требуется на составление такой таблицы? Если вы хорошо понимаете смысл дифференцированного платежа, то, думаю, где-то минут (5-6), не больше! Но это еще не конец решения! Нас по условию задачи не просили составить такую таблицу, а просили выяснить общую сумму выплат по кредиту за все отчетные периоды.

Как найти эту общую сумму выплат? В принципе можно просуммировать значения, находящиеся в колонке “Платеж, млн.”. Ведь по факту сумма этих платежей и будет составлять общую сумму выплат. Повторюсь, хорошо, что количество отчетных периодов в данной задач мало, а иначе такой устный подсчет может представлять некоторую трудность и приводить к различного рода вычислительным ошибкам.

Наша задача просуммировать следующие значения: ({3, 2.8, 2.6, 2.4, 2.2}). Нетрудно заметить, что перед нами некоторый ряд, являющийся убывающей арифметической прогрессией, с шагом (-0.2). Общее количество слагаемых равно (5). Ну, тогда давайте воспользуемся известной формулой, которая позволяет найти сумму членов арифметической прогрессии:

(S_{n}) = $frac{a_{1} + a_{n}}{2} * n$, где

$a_{1}$ – 1-й член прогрессии (в нашем случае (a_{1} = 3.0));

$a_{n}$ – последний член прогрессии (в нашем случае $a_{n} = a_{5} = 2.2)$;

(n) – общее количество членов, участвующих в сумме (в нашем случае (n = 5));

(S_{n}) – рассчитываемая сумма.

Имеем конечную формулу:

$S_{5} = frac{3.0 + 2.2}{2} * 5 = frac{5.2 * 5}{2} = frac{26}{2} = 13$, млн.

А вот это полученное значение уже является официальным ответом к данной задаче. Готово! То есть нашим ответом является $13$ миллионов. На официальной сдаче ЕГЭ по математике предельно внимательно следите за тем, в каких единицах измерения нужно давать ответ. В поставленной задаче ответ нужно указать в миллионах, то есть в соответствующую ячейку бланка нужно вписать число $13$ и больше ничего.

Алгебраический способ решения

Сейчас нам предстоит вывод некой алгебраической зависимости, например, составление уравнения/неравенства или их систем. Вообще, алгебраический способ решения экономических задач хорош тем, что позволяет проводить анализ любого количества отчетных периодов. Чего нельзя сказать про арифметический способ решения!

Введем следующие обозначения:

(S) – размер первоначального кредита;

(r) – процентная ставка банка, выраженная в долях:

(R = 1 + r) – вспомогательная величина для удобства расчетов;

(n) – количество отчетных периодов;

(i) – номер текущего отчетного периода;

$p_{i}$ – платеж, проводимый за (i)-й отчетный период;

(P) – общая сумма всех платежей;

(O) – переплата по взятому кредиту;

Сведем в таблицу входные данные, которые нам известны из формулировки поставленной задачи:

(S = 10), млн.

(r = 0.1) (или (10%))

(R = 1.1)

(n = 5)

Поскольку заем берется на условиях дифференцированных выплат, то размер долга будет сокращаться после каждого $p_{i}$ – платежа ровно на $frac{S}{n} = frac{10}{5} = 2$, млн. рублей.

Давайте вспомним ключевую формулу, которая поможет нам понять, к чему стремиться в процессе расчетов:

<Общая выплата> = <Тело кредита> + <Начисленные банком проценты>

То есть, чтобы получить ответ, нам достаточно выяснить размер начисленных банком процентов, так как в формуле выше, слагаемое <Тело кредита> нам уже известно, это не что иное, как (S = 10), млн. Заметьте, нас не сильно будут интересовать размеры проводимых платежей!

№ периода	Кредит до %, млн.	Начисленные %, млн.
1	$frac{5}{5} * S$	$frac{5}{5} * S * r$
2	$frac{4}{5} * S$	$frac{4}{5} * S * r$
…	…	…
5	$frac{1}{5} * S$	$frac{1}{5} * S * r$

Давайте просуммируем значения из колонки “Начисленные %, млн.“

.$frac{5}{5} * S * r + frac{4}{5} * S * r + … + frac{1}{5} * S * r = frac{1}{5} * S * r * (5 + 4 + … + 1)$

Обратим внимание на выражение суммы, стоящей в скобках. Нетрудно заметить, что перед нами некоторый ряд, являющийся убывающей арифметической прогрессией, с шагом (-1). Общее количество слагаемых равно (5). Ну, тогда давайте воспользуемся известной формулой, которая позволяет найти сумму членов арифметической прогрессии:

(S_{n}) = $frac{a_{1} + a_{n}}{2} * n$, где

$a_{1}$ – 1-й член прогрессии (в нашем случае (a_{1} = 5));

$a_{n}$ – последний член прогрессии (в нашем случае $a_{n} = a_{5} = 1)$;

(n) – общее количество членов, участвующих в сумме (в нашем случае (n = 5));

(S_{n}) – рассчитываемая сумма.

Имеем конечную формулу:

$S_{5} = frac{5 + 1}{2} * 5 = frac{6}{2} * 5 = 3 * 5 = 15$

И теперь, с чистой совестью, можно рассчитать начисленные банком проценты за весь период кредитования:

$frac{1}{5} * S * r * (5 + 4 + … + 1) = frac{1}{5} * 10 * 0.1 * 15 = 3$, млн.

Другими словами, (3) млн. рублей – переплата клиента за пользование банковским заемом. Это именно та сумма, которую банк зарабатывает на клиенте, за предоставление последнему услугу кредитования.

Теперь мы знаем все необходимое, чтобы получить окончательный ответ.

$P = S + O = 10 + 3 = 13$, млн.

Все, что остается сделать – выписать в бланк соответствующий ответ и получить за данное решение максимальный балл при проверке.

Графико-аналитический способ решения

К сожалению, данная задача не предполагает ее решение подобным образом Какой график вы хотели бы построить? Правильно, нет такого графика, и нечего выдумывать и извращаться. Хотя, если очень сильно постараться, то наверняка можно вывести какую-то графическую модель…

Выводы

А какие выводы можно сделать? Ну, во-первых, для того, чтобы максимально успешно решать подобные задачи, вам нужно досконально понимать структуру дифференцированной модели платежей. Без должного понимания далеко не уедете, где-нибудь споткнетесь!

Во-вторых, как могли заметить в процессе выкладок, нам не раз пригождалась формула суммы арифметической прогрессии. Надо бы зазубрить ее основательно, желательно до конца жизни.

В-третьих, всегда старайтесь определиться со способом решения подобной задачи: арифметическим или алгебраическим способом. Лично я рекомендую прибегать к алгебраическому методу решения. Да, он сложнее, чем арифметический, но гораздо более действенный, когда, например, количество отчетных периодов достаточно велико.

Зачастую на своих индивидуальных уроках, когда мы решаем задачи из финансового блока, после получения окончательного ответа я провожу верификацию полученных результатов в программе “MS Excel”. Это очень удобно и наглядно, так как позволяет посмотреть операции над кредитом в динамике.

Примеры условий реальных задач, встречающихся на ЕГЭ по математике

Пример №1

В мае планируется взять кредит в банке на сумму (10) миллионов рублей на (5) лет.
Условия его возврата таковы:

Каждый декабрь долг возрастает на (10%) по сравнению с концом предыдущего года.
С января по март каждого года необходимо выплатить часть долга.
В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.

Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?

Перейти к текстовому решению

Пример №2

В июле планируется взять кредит в банке на сумму (6) миллионов рублей на некоторый срок.
Условия его возврата таковы:

Каждый январь долг возрастает на (20%) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил (1.8) миллиона рублей?

Перейти к текстовому решению

Пример №3

В июле планируется взять кредит в банке на сумму (20) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:

Каждый январь долг возрастает на (30%) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась (47) миллионов рублей?

Перейти к текстовому решению

Пример №4

В июле планируется взять кредит в банке на сумму (16) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:

Каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась (40) миллионов рублей?

Перейти к текстовому решению

Пример №5

В июле планируется взять кредит в банке на сумму (6) миллионов рублей на срок (15) лет.
Условия его возврата таковы:

Каждый январь долг возрастает на (q%) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

Найти (q), если известно, что наибольший годовой платеж по кредиту составит не более (1.9) миллиона рублей, а наименьший не менее (0.5) миллиона рублей.

Перейти к текстовому решению

Пример №6

(15) января планируется взять кредит в банке на (39) месяцев.
Условия его возврата таковы:

(1-го) числа каждого месяца долг возрастает на (q%) по сравнению с концом предыдущего месяца.
Со (2-го) по (14-е) число месяца необходимо выплатить часть долга.
(15-го) числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на (15-е) число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на (20%) больше суммы, взятой в кредит. Найдите (q).

Перейти к текстовому решению

Пример №7

Анатолий взял банковский кредит сроком на (9) лет. В конце каждого года общая сумма оставшегося долга увеличивается на (17%), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину.

Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)?

Перейти к текстовому решению

Пример №8

Анна взяла кредит в банке на срок (12) месяцев ((1) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется (q%) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга.

Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется “схемой с дифференцированными платежами”). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на (13%) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть (q).

Перейти к текстовому решению

Пример №9

В июле планируется взять кредит в банке на сумму (28) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:

Каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит (9) миллионов рублей?

Перейти к текстовому решению

Пример №10

(15) января планируется взять кредит в банке на (15) месяцев.
Условия его возврата таковы:

(1-го) числа каждого месяца долг возрастает на (1%) по сравнению с концом предыдущего месяца.
Со (2-го) по (14-е) число каждого месяца необходимо выплатить часть долга.
(15-го) числа каждого месяца долг должен быть на одну и ту же величину меньше долга на (15-е) число предыдущего месяца.

Известно, что восьмая выплата составила (108,000) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?

Перейти к текстовому решению

Остались вопросы, недопонимание? Записывайтесь ко мне на частные уроки!

Если после прочтения данной статьи у вас остались вопросы, некоторые математические выкладки вызывают затруднения, то звоните мне на сотовый телефон и записывайтесь на первый пробный урок!

Последние годы мои частные уроки проходят дистанционно. Это очень эффективный, удобный и достаточно выгодный в плане денег для вас способ подготовки к ЕГЭ по математике.

На своих занятиях основной упор делаю на практическую составляющую, то есть в процессе урока показываю обучаемому массу всевозможных примеров, а также демонстрирую грамотные методики их решения.

И не забывайте о том, что я достаточно востребованный репетитор по математике и информатике, мне постоянно поступают звонки с просьбой записаться на индивидуальную подготовку. Поэтому не откладывайте свое решение в долгий ящик, а действуйте прямо сейчас, так как завтра свободных мест уже может и не остаться.

Источник

Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.

В этой статье:

Как научиться решать «экономические» задачи. С чего начать.

Две схемы решения задач на кредиты и как их распознать.

Комбинированные задачи.

В чем основная сложность «экономической» задачи.

Задания на оптимальный выбор. В том числе — с применением производной.

Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.

Надеемся, что вы уже сейчас сможете ответить на такие вопросы:

Что принимается за 100%?
Величина х увеличилась на p%. Как это записать?
Величина y дважды уменьшилась на р%. Как это записать?

Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.

Запомним, что есть всего две схемы решения задач на кредиты

Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.

Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.

Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.

Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.

Давайте потренируемся.

1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?

Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.

Введем обозначения:

S=6902 тыс. рублей – сумма долга. Расчеты будем вести в тысячах рублей.

– процент банка,

$k=1+frac{{ p}}{100}=1+frac{125}{1000}=1+frac{1}{8}=frac{9}{8}$ – коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,

— сумма ежегодного платежа.

Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:

– сумма долга увеличивается в раз;

– Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на .

Вот что получается:

Раскроем скобки:

$S{{ k}}^4-{ X}left({{ k}}^3+{{ k}}^2+{ k}+1right)=0.$

Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как

$1+{{ k}+{{ k}}^2+{ k}}^3$ . В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.

Применим формулу суммы геометрической прогрессии:

${{ Sk}}^4={ X}cdot frac{{{ k}}^4-1}{{ k}-1}=0.$ И выразим из этой формулы .

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}.$ Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби $frac{9}{8}$ , Иначе у вас будет 12 знаков после запятой!

И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}=frac{{ S}cdot 9^4left(frac{9}{8}-1right)}{8^4cdot left(frac{9^4}{8^4}-1right)}=frac{{ S}cdot 9^4}{8cdot left(9^4-8^4right)}=frac{{ S}cdot 9^4}{8cdot left(9^2-8^2right)left(9^2+8^2right)}=frac{{ S}cdot 9^4}{8cdot left(9+8right)left(9^2+8^2right)}=$

$=frac{6902cdot {81}^2}{8cdot 17cdot 145}=frac{406cdot {81}^2}{8cdot 145}=frac{203cdot {81}^2}{4cdot 145}=frac{29cdot 7cdot {81}^2}{4cdot 29cdot 5} = 2296,35$ тыс.руб.

Ответ: 2296350 рублей.

Вот следующая задача.

2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа.

Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.

Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.

Как обычно, ${ k}=1+frac{{ p}}{100}.$

Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна $frac{1}{24}{ S}.$ После первой выплаты сумма долга равна $frac{23}{24}{ S},$ после второй $frac{22}{24}{ S}.$

Тогда первая выплата ${{ X}}_1={ kS}-frac{23}{24}{ S},$ вторая выплата ${{ X}}_2={ k}cdot frac{23}{24}{ S}-frac{22}{24}{ S}$ ,

dots

Последняя в году выплата ${{ X}}_{12}={ k}cdot frac{13}{24}{ S}-frac{12}{24}{ S}.$

Сумма всех выплат в течение первого года:

${ X}={{ X}}_1+{{ X}}_2+dots +{{ X}}_{12}={ kS}left(1+frac{23}{24}+dots frac{13}{24}right)-{ S}left(frac{23}{24}+frac{22}{24}+dots +frac{12}{24}right).$

В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой ${{ a}}_1=frac{13}{24};{{ a}}_{{ n}}=frac{24}{24}=1.$ Обозначим эту сумму ${{ S}}_1.$

${{ S}}_1=frac{{{ a}}_1+{{ a}}_{12}}{2}cdot 12=frac{13+24}{2cdot 24}cdot 12=frac{37}{4}.$

Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой ${{ b}}_1=frac{12}{24};{{ b}}_{{ n}}=frac{23}{24}.$ Эту сумму обозначим ${{ S}}_{2.}$

${{ S}}_2=frac{{{ b}}_1+{{ b}}_{12}}{2}cdot 12=frac{12+23}{2cdot 24}cdot 12=frac{35}{4}.$

Общая сумма выплат за год:

$small X= S left({ kS}_1-{{ S}}_2right)=frac{1800}{4}left({ 1,01}cdot 37-35right)=$
$=frac{1800cdot { 2,37}}{4}={ 2,37}cdot 450= 1066,5$ тыс. рублей.

Ответ: 1066500 рублей.

Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.

3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Введем переменные: ${ k}=1+frac{25}{100}=frac{5}{4},Y=625$ тысяч рублей. Рисуем схему погашения кредита:

Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой .

Это значит, что и тогда

${ S}=frac{left({ k}+1right){ Y}}{{{ k}}^2}{ X}=3cdot frac{left({ k}+1right){ Y}}{{{ k}}^2}left({ k}-1right)+2{ Y}=3{ y}left(frac{{{ k}}^2-1}{{{ k}}^2}right)+2{ Y}=$
$={ Y}left(5-frac{3}{{{ k}}^2}right)=625left(5-frac{3cdot 16}{25}right)=frac{625cdot 77}{25}=77cdot 25=1925$ тысяч рублей.

Ответ: 1925 тыс. рублей.

Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары	Себестоимость, 1 центнера	Отпускная цена, 1 центнера
стеклянная	1500 руб	2100 руб
жестяная	1100 руб	1750 руб

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.

Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% – компот в жестяных банках).

Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках – 80y центнеров в сутки.

Составим таблицу.

Вид тары	Доля в общем количестве	Производится в сутки	Прибыль за 1 центнер
стеклянная			2100 – 1500 = 600 руб
жестяная			1750 – 1100 = 650 руб

Общая прибыль завода за сутки равна

По условию, и , то есть $xge frac{2}{9}$ и $yge frac{1}{4}.$

Нужно найти наибольшее значение выражения при выполнении следующих условий:

$left{begin{matrix} x+y=1\ {{2}over{9}}leq x textless 1, \ {1over4}leq y textless 1 end{matrix}right. Leftrightarrow left{begin{matrix} y=1-x\ {2over9}leq x leq {3over4} end{matrix}right. .$

Подставим y=1-x в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при $x=frac{3}{4}.$ Тогда $y=frac{1}{4}$ и максимально возможная прибыль завода за день равна

$2000cdot left(27cdot frac{3}{4}+26cdot frac{1}{4}right)=2000cdot frac{107}{4}=53500$ руб.

Ответ: 53500 руб.

Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной – здесь:

Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная

Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.

Если вам понравился наш материал – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 15. Финансовая математика u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 266 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила сумма, уплаченная Сергеем банку сверх кредита?

Источник: Интеллект-центр. Репетиционные варианты ЕГЭ 2015.

Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

Источник: Интеллект-центр. Репетиционные варианты ЕГЭ 2015.

31 декабря 2014 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая  — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?