Спасибо за ваши закладки и рекомендации
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как $A subset B$.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
$$P(A+B)=P(A)+P(B).$$
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
$$Pleft(sum_{i=1}^{n}A_i right)=sum_{i=1}^{n} P(A_i).$$
Если случайные события $A_1, A_2, …, A_n$ образуют полную группу несовместных событий, то имеет место равенство
$P(A_1)+P(A_2)+…+P(A_n)=1.$ Такие события (гипотезы) используются при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
$$P(A+B)=P(A)+P(B)-P(Acdot B).$$
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
$$P(Acdot B)=P(A)cdot P(B).$$
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
Примеры решений задач с событиями
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика,  ;
;
 – вынули черный шар из первого ящика,
– вынули черный шар из первого ящика,  ;
;
В – белый шар из второго ящика,  ;
;
 – черный шар из второго ящика,
– черный шар из второго ящика,  .
.
Нам нужно, чтобы произошло одно из событий  или
или  . По теореме об умножении вероятностей
. По теореме об умножении вероятностей
 ,
,  .
.
Тогда искомая вероятность по теореме сложения будет
 .
.
Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка,  ;
;
В – попадание второго стрелка,  .
.
Тогда  – промах первого,
– промах первого,  ;
;
 – промах второго,
– промах второго,  .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, 
б) 
 – двойной промах,
– двойной промах,  .
.
в) А+В – хотя бы одно попадание,
 .
.
г)  – одно попадание,
– одно попадание,
 .
.
См. обучающую статью “решение задач о стрелках”
Пример. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй – 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера, б) ровно 1 станок потребует внимания мастера.
Решение.
Вводим базовые независимые события $A_i$ = (Станок $i$ потребовал внимания рабочего в течение смены), $i=1, 2, 3$. По условию выписываем вероятности: $p_1=0,4$, $p_2=0,6$, $p_3=0,3$. Тогда $q_1=0,6$, $q_2=0,4$, $q_3=0,7$.
Найдем вероятность события $X$=(Ни один станок не потребует внимания в течение смены):
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= q_1 cdot q_2 cdot q_3 =
0,6cdot 0,4 cdot 0,7 = 0,168.
$$
Найдем вероятность события $Z$= (Ровно один станок потребует внимания в течение смены):
$$
P(Z)= \ = P(A_1) cdot Pleft(overline{A_2} right) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1}right) cdot P(A_2) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1} right) cdot Pleft(overline{A_2} right) cdot P(A_3)=\
= p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3 =\ =
0,4cdot 0,4 cdot 0,7+0,6cdot 0,6 cdot 0,7+0,6cdot 0,4 cdot 0,3 = 0,436.
$$
См. обучающую статью “решение задач о станках”
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. 
2.  .
.
3. 
Вероятность наступления хотя бы одного события
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?
Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий $A_1, A_2, …, A_n$, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
$$
P(A)=1-Pleft(overline{A_1}right)cdot Pleft(overline{A_2}right)cdot … cdot Pleft(overline{A_n}right)= 1-q_1 cdot q_2 cdot … cdot q_n.
$$
Если события $A_1, A_2, …, A_n$ имеют одинаковую вероятность $p$, то формула принимает простой вид:
$$
P(A)=1-(1-p)^n=1-q^n.
$$
Примеры решений на эту тему
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия),
(попадание первого орудия),  (попадание второго орудия) и
(попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям  ,
,  и
и  (т. е. вероятности промахов), соответственно равны:
(т. е. вероятности промахов), соответственно равны:
 ,
,  ,
, 
Искомая вероятность  .
.
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События “машина работает” и “машина не работает” (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: 
Отсюда вероятность того, что машина в данный момент не работает, равна 
Искомая вероятность 
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие “при n выстрелах стрелок попадает в цель хотя бы один раз”. События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула  .
.
Приняв во внимание, что, по условию,  (следовательно,
(следовательно,  ), получим
), получим

Прологарифмируем это неравенство по основанию 10:

Итак,  , т.е. стрелок должен произвести не менее 5 выстрелов.
, т.е. стрелок должен произвести не менее 5 выстрелов.
См. обучающую статью “решение задач с хотя бы один…”
Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Теоремы сложения вероятностей
Найдем вероятность суммы событий и
(в предположении их совместности либо несовместности).
Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.
Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие
) или 45-го (событие
), или не меньше 46-го (событие
), т. е. событие
есть сумма событий
. События
,
и
несовместны. Поэтому согласно теореме о сумме вероятностей получаем
Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.
Решение. События “очередной будет продана пара обуви меньше 44-го размера” и “будет продана пара обуви размера не меньше 44-го” противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой “Electra Ltd” оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим
. Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события
являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
Зависимые и независимые события. Условная вероятность
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или не появления “герба” во втором испытании (событие
). В свою очередь, вероятность появления “герба” во втором испытании не зависит от результата первого испытания. Таким образом, события
и
независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события
, называется условной вероятностью события
и обозначается
.
Условие независимости события от события
записывают в виде
, а условие его зависимости — в виде
. Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а
— извлечение нового. Тогда
. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события зависит от того, произошло или нет событие
.
Формулы умножения вероятностей
Пусть события и
независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий
и
.
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ),
. Вероятность того, что из второго ящика взята стандартная деталь (событие
),
. Вероятность того, что из третьего ящика взята стандартная деталь (событие
),
. Так как события
,
и
независимые в совокупности, то искомая вероятность (по теореме умножения)
Пусть события и
зависимые, причем вероятности
и
известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие
, и событие
.
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие
) и при третьем — синий (событие
).
Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность
. Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный,
. Искомая вероятность
Формула полной вероятности
Теорема 2.5. Если событие наступает только при условии появления одного из событий
, образующих полную группу несовместных событий, то вероятность события
равна сумме произведений вероятностей каждого из событий
на соответствующую условную вероятность события
:
(2.1)
При этом события называются гипотезами, а вероятности
— априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим событие, означающее годность собранного узла;
,
и
— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
Искомая вероятность
Формула Байеса
Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
. Априорные (до опыта) вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
. Для гипотезы
формула Байеса выглядит так:
Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка
для второго станка
для третьего станка
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Полная вероятность и формула Байеса
- Зависимые события и условные вероятности
- Вероятность совместного появления событий
- Формула полной вероятности
- Формула Байеса
- Примеры
п.1. Зависимые события и условные вероятности
Чтобы вспомнить о сложении и умножении вероятностей и независимых событиях – см. §39 справочника для 9 класса.
Напомним, что два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Например: при бросании монеты несколько раз каждый следующий бросок совершенно не зависит от предыдущих.
Два случайных события A и B называют зависимыми, если вероятность одного из них зависит от того, произошло или нет другое событие.
Вероятность события B, определенная при условии, что событие A произошло, называется условной вероятностью и обозначается (P(B|A)) или (P_A(B)).
Для условных вероятностей справедливы формулы: $$ P(A|B)=frac{P(Awedge B)}{P(B)}, P(B|A)=frac{P(Awedge B)}{P(A)} $$ где (P(Awedge B)) – вероятность совместного появления событий A и B.
Например:
Рассмотрим урну, в которой находится 3 белых и 3 черных шара.
Мы достаем шары, смотрим на их цвет и не возвращаем их на место. События в последовательности становятся зависимыми.
Пусть событие A=”в 1й раз достаем черный шар”,
Событие B=”во 2й раз достаем белый шар”
Событие C=”во 2й раз достаем черный шар”
После того, как произошло событие A, в урне остается 3 белых и 2 черных шара.
Тогда условная вероятность для события B при условии, что событие A произошло:
(P(B|A)=frac35)
Аналогично, условная вероятность для события C:
(P(B|A)=frac25)
п.2. Вероятность совместного появления событий
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло: $$ P(Awedge B)=P(B)cdot P(A|B)=P(A)cdot P(B|A) $$ Это утверждение также называют теоремой умножения вероятностей.
Например:
Продолжая предыдущий пример, вероятность события ((Awedge B)) – 1й раз достали черный шар и 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B|A)=frac12cdot frac35=0,3 $$ Также, напомним:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: $$ P(Awedge B)=P(A)cdot P(B) $$
Например:
Пусть в урне 3 белых и 3 черных шара. Мы достаем шары, смотрим на их цвет и возвращаем их на место. В последовательности наших действий все события будут независимыми. Каждый раз, вероятность достать белый или черный шар будет равна 1/2. Поэтому, в этом случае вероятность события ((Awedge B)) – 1й раз достали черный шар, а 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B)=frac12cdotfrac12=0,25 $$
п.3. Формула полной вероятности
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
При подбрасывании монеты события A=«получить орла» и B=«получить решку» – несовместные, т.к. одновременно произойти не могут.
В то же время, эти несовместные события A и B образуют пространство элементарных событий или полную группу (Omega=left{B;Bright}), т.к. ничего другого, кроме орла или решки, получить нельзя. Сумма вероятностей (P(A)+P(B)=frac12+frac12=1), как и положено для полной группы.
Если событие A может произойти только при выполнении одного из событий (B_1,B_2,…,B_k), которые образуют полную группу событий, то вероятность события A определяется по формуле полной вероятности: $$ P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+…+P(B_k)P(A|B_k)=sum_{i=1}^k P(B_i)P(A|B_i) $$
Например:
В 11А и 11Б учится по 35 человек, а в 11В – 30 человек. Будем считать тех, у кого 4 и 5 баллов по алгебре и геометрии, «знатоками математики». Таких учеников в 11А – 10 человек, в 11Б – 7 человек, и в 11В – 3 человека.
Какова вероятность, что произвольно выбранный 11-классник окажется знатоком математики?
Пусть события A=«знаток математики», Bi=«ученик i-го класса», (i=overline{1,3})
Составим таблицу:
| i | Класс | К-во учеников |
(P(B_i)) | К-во знатоков |
(P(A|B_i)) | (P(B_i)cdot P(A|B_i)) |
| 1 | 11A | 35 | 35/100=0,35 | 10 | 10/35=2/7 | 0,1 |
| 2 | 11Б | 35 | 35/100=0,35 | 7 | 7/35=1/5 | 0,07 |
| 3 | 11В | 30 | 30/100=0,3 | 10 | 3/30=1/10 | 0,03 |
| Всего | 100 | 1 | 20 | × | 0,2 |
Получаем полную вероятность (P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,2)
В данном случае ответ можно получить и проще: 20 знатоков на 100 человек дает (P(A)=0,2).
п.4. Формула Байеса
По данному выше определению полной вероятности событие A случается, если происходит одно из событий полной группы (left{B_iright}).
Допустим, что событие A случилось. А какова вероятность, что при этом произошло конкретное событие (B_1inleft{B_iright})? Т.е., нас интересует условная вероятность (P(B_1|A)).
По теореме об умножении вероятностей: $$ P(Awedge B_1)=P(B_1)cdot P(A|B_1)=P(A)cdot P(B_1|A) $$ Откуда: $$ P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)} $$ То же самое справедливо для любого события (B_pinleft{B_iright}). Предположение о том, что случилось событие (B_p), называют гипотезой.
Если событие A может произойти только при выполнении одного из событий полной группы (left{B_iright}) и событие A случилось, то вероятность гипотезы, что при этом случилось событие (B_pinleft{B_iright}), определяется формулой Байеса: $$ P(B_p|A)=frac{P(B_p)cdot P(A|B_p)}{P(A)}=frac{P(B_p)cdot P(A|B_p)}{sum_{i=1}^k P(B_i)P(A|B_i)} $$ Вероятность (P(B_p)) называют априорной вероятностью.
Вероятность (P(B_p|A)) называют апостериорной вероятностью. Случившееся событие A может поменять априорную (предварительную) оценку вероятности события (B_p).
Например:
Продолжим задачу с 11-классниками. Какова вероятность того, что произвольно взятый знаток математики учится в 11Б?
Наши события: A=«знаток математики», B2=«ученик 11Б класса».
Событие A «случилось» – у нас имеется знаток, а событие B2 – это гипотеза про 11Б.
И ответом на поставленный вопрос является вероятность (P(B_2|A)).
Из нашей таблицы: $$ P(B_2)cdot P(A|B_2)=0,07; P(A)=0,2 $$ Получаем: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,07}{0,2}=0,35 $$ Т.е. 11Б дает 35% всех знатоков математики в этой школе.
Если сравнить апостериорную вероятность (P(B_2|A)=0,35) с априорной вероятностью (P(B_2)=0,35), они равны. Событие A не повлияло на оценку вклада 11Б в интеллектуальный багаж школы, он находится на среднем уровне.
Теперь найдем вероятность того, что произвольно взятый знаток математики учится в 11А: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{0,1}{0,2}=0,5\ P(B_1|A)gt P(B_1) end{gather*} Вклад 11А по факту (апостериорная вероятность 0,5) оказывается большим, чем ожидалось по количеству учеников (априорная вероятность 0,35). 50% знатоков всей школы – из этого класса.
Наконец, найдем вероятность того, что произвольно взятый знаток математики учится в 11В: begin{gather*} P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{0,03}{0,2}=0,15\ P(B_3|A)lt P(B_3) end{gather*} Вклад 11В по факту (апостериорная вероятность 0,15) оказывается меньшим, чем ожидалось по количеству учеников (априорная вероятность 0,3). Только 15% знатоков всей школы – из этого класса.
п.5. Примеры
Пример 1. Двигатель работает в трех режимах: нормальном (65% времени), форсированном (25% времени) и холостом. Вероятность поломки в каждом из режимов соответственно равна (p_1=0,1; p_2=0,8; p_3=0,05).
а) найдите вероятность поломки двигателя во время работы;
б) двигатель сломался. Какова вероятность, что он в этот момент работал в форсированном режиме?
а) Пусть событие A=«поломка двигателя», Bi – «работа в i-м режиме», (i=overline{1,3})
Необходимо найти полную вероятность (P(A)).
Составим таблицу:
| i | Режим | Часть времени (P(B_i)) |
Вероятность поломки (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | Нормальный | 0,65 | 0,1 | 0,065 |
| 2 | Форсированный | 0,25 | 0,8 | 0,2 |
| 3 | Холостой | 0,1 | 0,05 | 0,005 |
| Всего | 1 | × | 0,27 |
Вероятность поломки (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,27 $$
б) Событие A=«поломка двигателя» произошло. Гипотеза B2 – «работа в форсированном режиме» при фактической поломке имеет вероятность: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,2}{0,27}=frac{20}{27}approx 0,741 $$ Апостериорная вероятность (P(B_2|A)approx 0,741) больше априорной вероятности (P(B_2)=0,25).
Ответ: a) 0,27; б) (frac{20}{27}approx 0,741)
Пример 2. В состязании лучников участвуют три стрелка. Вероятность попадания в мишень для каждого из них равна 0,3; 0,5 и 0,7. Один из стрелков стреляет и не попадает. Какова вероятность, что это был:
а) первый стрелок;
б) второй стрелок;
в) третий стрелок;
Пусть событие A=«промах», Bi – «выстрел i-го стрелка», (i=overline{1,3})
Т.к. стрелять мог любой из стрелков (P(B_i)=frac13) для каждого из них.
Чтобы найти вероятность промаха, нужно от 1 отнять вероятность попадания.
Составим таблицу:
| i | (P(B_i)) | Вероятность промаха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | (frac13) | 1-0,3=0,7 | (frac13cdot 0,7=frac{7}{30}) |
| 2 | (frac13) | 1-0,5=0,5 | (frac13cdot 0,5=frac{1}{6}) |
| 3 | (frac13) | 1-0,7=0,3 | (frac13cdot 0,3=frac{1}{10}) |
| ∑ | 1 | × | 0,5 |
Полная вероятность: $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=frac{7}{30}+frac16+frac{1}{10}=0,5 $$ Промах произошел. Находим апостериорные вероятности для каждого стрелка: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{7/30}{0,5}=frac{7}{15}approx 0,467\ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{1/6}{0,5}=frac{2}{3}approx 0,333\ P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{1/10}{0,5}=frac{1}{5}=0,2\ end{gather*} С точки зрения практической, можно сказать, что «вероятнее всего», это был первый стрелок.
Ответ: a) (frac{7}{15}); б) (frac{1}{3}); в) (frac{1}{5})
Пример 3. Три фрилансера на площадке выполняют заказы в отношении по количеству 3:4:3. Доля успешно выполненных заказов для каждого из них составляет 98%, 95% и 90%.
а) найдите вероятность успешного выполнения заказа на площадке;
б) найдите вероятность неуспеха на площадке;
в) кто из фрилансеров, вероятнее всего, виноват в неуспешной работе?
Пусть событие A=«успех», Bi – «работа i-го фрилансера», (i=overline{1,3})
Составим таблицу успешной деятельности:
| i | (P(B_i)) | Вероятность успеха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | 0,3 | 0,98 | 0,294 |
| 2 | 0,4 | 0,95 | 0,38 |
| 3 | 0,3 | 0,9 | 0,27 |
| ∑ | 1 | × | 0,944 |
Вероятность успешного выполнения (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,944 $$ б) Вероятность неуспеха (противоположное событие): $$ P(overline{A})=1-P(A)=1-0,944=0,056 $$ в) Составим таблицу неуспешной деятельности:
| i | (P(B_i)) | Вероятность неуспеха (P(overline{A}|B_i)) |
(P(B_i)cdot P(overline{A}|B_i)) |
| 1 | 0,3 | 1-0,98=0,02 | 0,006 |
| 2 | 0,4 | 1-0,95=0,05 | 0,02 |
| 3 | 0,3 | 1-0,9=0,1 | 0,03 |
| ∑ | 1 | × | 0,056 |
Апостериорные вероятности для каждого из фрилансеров: begin{gather*} P(B_1|overline{A})=frac{P(B_1)cdot P(overline{A}|B_1)}{P(overline{A})}=frac{0,006}{0,056}=frac{3}{28}approx 0,107\ P(B_2|overline{A})=frac{P(B_2)cdot P(overline{A}|B_2)}{P(overline{A})}=frac{0,02}{0,056}=frac{5}{14}approx 0,357\ P(B_3|overline{A})=frac{P(B_3)cdot P(overline{A}|B_3)}{P(overline{A})}=frac{0,03}{0,056}=frac{15}{28}approx 0,536 end{gather*} Наибольшая вероятность неуспеха – у третьего фрилансера.
Ответ: а) 0,944; б) 0,056; в) третий фрилансер.
Пример 4. Докажите, что если полная вероятность события A равна $$ P(A)=sum_{i=1}^k P(B_i)cdot P(A|B_i) $$ то вероятность противоположного события равна (P(overline{A})=1-P(A)).
По условию событие A происходит только при выполнении одного из событий полной группы (left{B_iright}. i=overline{i,k}). Соответственно, противоположное событие (overline{A}) также происходит при выполнении одного из событий (B_i). При этом условная вероятность для противоположного события: $$ P(overline{A}|B_i)=1-P(A|B_i) $$ Заметим также, что для полной группы сумма вероятностей равна 1: begin{gather*} sum_{i=1}^k P(B_i)=1 end{gather*} Получаем: begin{gather*} P(overline{A})=sum_{i=1}^k P(B_i)cdot P(overline{A}|B_i)=sum_{i=1}^k P(B_i)cdot (1-P(A|B_i))=\ =sum_{i=1}^k P(B_i)-sum_{i=1}^k P(B_i)cdot P(A|B_i)=1-P(A) end{gather*} Что и требовалось доказать.
Почему в одной ситуации вероятности складываются, в другой – умножаются, а в третьей – вообще всё сложнее ?
Приветствую Вас, уважаемые Читатели! В одном из прошлых материалов, где я рассказывал про доску Гальтона – механическое устройство, которое визуализирует биномиальное распределение, я использовал три незыблемых правила манипулирования вероятностью. В этом материале хотелось бы поговорить об этом подробнее. Поехали!
Что такое событие?
Согласно словарю Ожегова событие – это “то, что произошло, то или иное значительное явление, факт общественной, личной жизни“. Глобально события можно разделить на два вида: детерминированные и вероятностные.
- Первые – это те события, исход которых можно предсказать и описать до факта его совершения. Например, если Вы бросите камень с 9-го этажа, то можете быть уверены, что он упадёт на Землю.
- Вторые – это те, которые даже при одинаковых начальных условиях могут привести к неожиданному или случайному исходу. Классическим примером случайного события является бросок монеты: до того, как монета не упадет, мы можем только предполагать, какой стороной она окажется к верху.
Однако и во втором случае есть место детерминированности. Мы на 100% уверены, что событий может быть только два: “Орёл” или “Решка”.
События “Орёл” и “Решка” образуют т.н. называемую полную группу событий. Математически это можно записать следующим образом:
Есть еще много различных классификаций “событий”, но я позволю остановиться на этом
Несовместные события
Что еще нужно сказать о событиях “Орёл” и “Решка” ? Самое главное – это то, что появление одного из них исключает выпадение другого. В теории вероятностей такие события принято называть несовместными, а в случае двух исходов, как в нашем случае, – противоположными.
Для несовместных событий действует теорема о сложении вероятностей:
- Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
В случае с подбрасыванием монетки это звучит так: вероятность получить или “Орёл” или “Решку” равно сумме вероятностей каждого исхода. Здесь ключевую роль играет союз “ИЛИ”, ведь именно он вербально задаёт несовместимость событий.
Независимые события
Казалось бы, следует перейти к понятию совместного события, однако логика требует иначе. Давайте представим, что мы параллельно подбрасываем две монеты. Зависит ли исход каждого испытания друг от друга?
Да, можно пытаться хитрить, но природу не обманешь….
Очевидно, что нет. Таким образом два события называются независимыми, если появление одного из них, не изменяет вероятность появления другого.
Правило вычисления вероятности независимых событий называется теоремой об умножении вероятностей:
Здесь уже главенствует союз “И” : вероятность наступления и того, и другого события равно произведению вероятностей наступления каждого из них по отдельности (независимые события!).
На конкретном примере вероятность выпадения двух “Орлов” или двух “Решек” при одновременном подбрасывании двух монет равняется 1/2*1/2 = 1/4.
Совместные события
Продолжим подбрасывать параллельно две монеты и попытаемся ответить на вопрос, а чему равна вероятность выпадения хотя бы одного “Орла” или “Решки” ?
- Очевидно, что, если складывать вероятности, то получим 1/2+1/2 = 1, что противоречит здравому смыслу. Ведь легко представить ситуацию, когда мы загадаем “Орла”, а две монеты выпадут “Решкой”.
- Умножение вероятностей так же не работает, ведь мы ищем вероятность хотя бы одного, а не одновременного выполнения событий.
Ответ: совместить два подхода и использовать формулу:
Таким образом, вероятность равняется 1/2+1/2 – 1/2*1/2 = 3/4.
События такого вида называются совместными – возникновение каждого из них не исключает возникновение другого. Естественно, что указанная выше формула распространяется и на произвольное количество событий, разве что будет немного посложнее.
Осталось рассмотреть еще один важный класс событий – зависимые, но это я сделаю в одном из следующих материалов. Спасибо за внимание!
- Ставьте “Нравится” и подписывайтесь на канал прямой сейчас, чтобы не пропустить следующие публикации.
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Вероятность суммы двух событий. Независимость двух событий. Вероятность произведения двух независимых событий
Содержание
![]()
Вероятность суммы двух событий
Пусть A и B – два произвольных события в случайном эксперименте с множеством элементарных исходов Ω .
Справедливо следующее утверждение.
УТВЕРЖДЕНИЕ 1. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.
Другими словами, верна формула:
|
|
(1) |
ДОКАЗАТЕЛЬСТВО. Рассмотрим диаграммы Эйлера – Венна для суммы двух событий и произведения двух событий, разместив их на одном рисунке (рис.1).
Рис.1
Проведем доказательство утверждения 1 на примере геометрического определения вероятности.
Если площадь произвольной фигуры F обозначить символом S (F) , то из рисунка 1 легко установить справедливость равенства:
|
|
(2) |
которое словами можно выразить так: «Площадь фигуры A + B равна сумме площадей фигур A и B минус площадь фигуры ![]() ».
».
Если обе части равенства (2) разделить на число S (Ω) , то мы получим равенство
В силу геометрического определения вероятности справедливы формулы
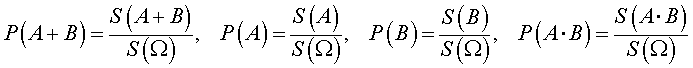
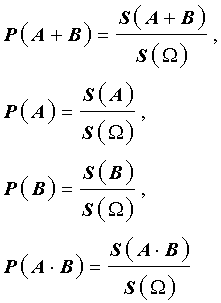
с помощью которых равенство (3) преобразуется к виду (1), что и завершает доказательство утверждения 1.
Доказательство утверждения 1 для классического определения вероятности проводится аналогичным образом, и мы оставляем его читателю в качестве полезного упражнения.
Несовместные события
ОПРЕДЕЛЕНИЕ. Два события A и B называют несовместными, если они не пересекаются.
Другими словами, события A и B несовместны, если
![]()
ЗАМЕЧАНИЕ 1. События A и B несовместны в том, и только в том случае, если событие B является подмножеством события ![]() , то есть
, то есть ![]() .
.
ЗАМЕЧАНИЕ 2. События A и B несовместны в том, и только в том случае, если событие A является подмножеством события ![]() , то есть
, то есть ![]() .
.
ЗАМЕЧАНИЕ 3. Если события A и B несовместны, то вероятность их произведения равна нулю.
Другими словами, для несовместных событий A и B верна формула
![]()
ЗАМЕЧАНИЕ 4. Если события A и B несовместны, то вероятность суммы событий A + B равна сумме вероятностей событий A и B .
Другими словами, для несовместных событий A и B верна формула
P (A + B) = P (A) + P (B)
Независимость двух событий. Вероятность произведения двух независимых событий
Два события A и B называют независимыми, если появление одного из этих событий никак не влияет на вероятность появления второго события.
ЗАМЕЧАНИЕ 5. Несовместные события и независимые события – это совершенно разные понятия, и их не следует путать.
Справедливо следующее утверждение.
УТВЕРЖДЕНИЕ 2. Вероятность произведения двух независимых событий равна произведению их вероятностей.
Другими словами, для двух независимых событий A и B верна формула
|
(4) |
Проиллюстрируем справедливость формулы (4) на примере.
ПРИМЕР 1. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 .
РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны все 36 возможных вариантов пар чисел, выпадающих при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании синей кости, а первый столбец таблицы – это числа, выпавшие при бросании красной кости. На пересечении строки и столбца указана пара чисел, выпавших на двух костях.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 1, 5 | 1, 6 |
| 2 | 2, 1 | 2, 2 | 2, 3 | 2, 4 | 2, 5 | 2, 6 |
| 3 | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 3, 5 | 3, 6 |
| 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 | 4, 5 | 4, 6 |
| 5 | 5, 1 | 5, 2 | 5, 3 | 5, 4 | 5, 5 | 5, 6 |
| 6 | 6, 1 | 6, 2 | 6, 3 | 6, 4 | 6, 5 | 6, 6 |
Благоприятным является только один исход, а именно, клетка с результатом 4, 3 , окрашенная в таблице желтым цветом. Следовательно, вероятность события, состоящего в том, что на синей игральной кости выпадает число 3 , а на красной игральной кости выпадает число 4 , равна ![]() .
.
Теперь рассмотрим случайный эксперимент, описанный в примере 1, с другой стороны. Для этого обозначим буквой A случайное событие, состоящее в том, что на синей игральной кости выпадает число 3 , а буквой B – случайное событие, состоящее в том, что на красной игральной кости выпадает число 4 . События A и B являются независимыми событиями, а их вероятности равны:
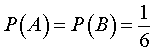
Событие ![]() состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
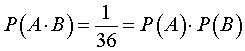
то в рассматриваемом случайном эксперименте по подбрасыванию двух игральных костей формула (4) верна.
В заключение приведем ещё одну иллюстрацию применимости формулы для вероятности суммы двух событий и формулы для вероятности произведения двух независимых событий.
ПРИМЕР 2. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью 0,9 . Второй стрелок поражает мишень с вероятностью 0,8 . Найти вероятность того, что мишень будет поражена.
РЕШЕНИЕ. Обозначим буквой A случайное событие, состоящее в том, что в мишень попадает первый стрелок, а буквой B обозначим случайное событие, состоящее в том, что в мишень попадает второй стрелок. Тогда событие A + B означает, что мишень поражена, а событие ![]() означает, что в мишень попали оба стрелка. По условию
означает, что в мишень попали оба стрелка. По условию
P (A) = 0,9 и P (B) = 0,8
а поскольку события A и B независимы, то в силу формулы (4)
![]()
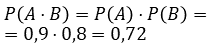
Воспользовавшись формулой (1), находим
![]()
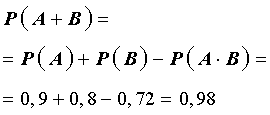
ОТВЕТ: 0,98