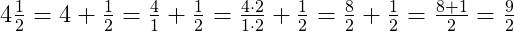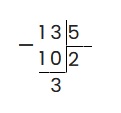Перевод неправильной дроби в смешанное число и обратно
- Главная
- /
- Математика
- /
- Арифметика
- /
- Перевод неправильной дроби в смешанное число и обратно
Если вам необходимо перевести неправильную дробь в смешанное число или наоборот воспользуйтесь нашим онлайн калькулятором:
Перевод неправильной дроби в смешанное число
Перевод смешанного числа в неправильную дробь
Просто заполните необходимые поля и получите ответ и подробное решение.
Теория
Как перевести неправильную дробь в смешанное число
Для того чтобы перевести неправильную дробь в смешанное число, то есть выделить целую часть из неправильной дроби, нужно произвести следующие действия:
- Сократить дробь, если это возможно
- Разделить в столбик числитель на знаменатель
- Полученное целое число записать в целую часть смешанного числа
- Полученный остаток записать в числитель, а знаменатель оставить прежним
Пример №1
Преобразуем 146 в смешанное число:
146=7⋅23⋅2=73
| 7 | 3 |
| 6 | 2 |
| 1 | |
73=213
Всё решение можно ещё записать так:
146=7⋅23⋅2=73=2⋅3+13=2⋅33 + 13=213
Тут мы раскладываем число 7 на 2⋅3+1 и далее путём сокращения получаем результат.
Пример №2
Преобразуем 83 в смешанное число:
83=2⋅3+23=2⋅33 + 23=223
Как перевести смешанное число в неправильную дробь
Для того чтобы перевести смешанное число (смешенную дробь) в неправильную дробь следует воспользоваться следующей формулой:
Формула
a bc=b+a⋅cc
Пример
Преобразуем 213 в неправильную дробь:
213=1+2⋅33=73
См. также
Перевод смешанного числа в неправильную дробь
- Калькулятор перевода в неправильную дробь
Любое смешанное число можно представить в виде обыкновенной (неправильной) дроби. Для этого нужно выполнить сложение целой и дробной части смешанного числа.
Для примера переведём смешанное число 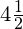
Перевод смешанного числа в неправильную дробь можно записывать в более краткой форме. Для этого нужно:
- Умножить единицы целой части на знаменатель дробной части.
- К полученному произведению прибавить числитель дробной части. Полученная сумма будет числителем неправильной дроби.
- Знаменатель оставить без изменений.
Согласно этому, перепишем пример в более краткой форме:
Перевод смешанного числа в неправильную дробь можно выразить в виде общей формулы:
Калькулятор перевода в неправильную дробь
Данный калькулятор поможет вам перевести смешанное число в неправильную дробь. Просто введите смешанное число и нажмите кнопку Перевести
.
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Если мы возьмем сумму n+ab, где значением n может быть любое натуральное число, а ab представляет из себя правильную обыкновенную дробь, то мы можем записать то же самое, не используя плюс: nab. Возьмем конкретные числа для ясности: так, 28+57 – это то же самое, что и 2857. Запись дроби рядом с целым числом принято называть смешанным числом.
Смешанное число представляет собой такое число, которое равно сумме натурального числа n с правильной обыкновенной дробью ab. В таком случае n является целой частью числа, а ab – его дробной частью.
Из определения следует, что любое смешанное число равно тому, что получится в результате сложения его целой и дробной части. Таким образом, будет выполняться равенство nab=n+ab.
Его также можно записать в виде n+ab=nab.
Какие можно привести примеры смешанных чисел? Так, к ним относится 518, при этом пятерка – это его целая часть, а одна восьмая – дробная. Еще примеры: 112, 2343453, 34000625.
Выше мы писали, что в дробной части смешанного числа должна стоять только правильная дробь. Иногда можно встретить записи вида 5223, 7572. Они не являются смешанными числами, т.к. их дробная часть неправильная. Их нужно понимать как сумму целой и дробной части. Такие числа можно привести к стандартному виду записи смешанных чисел, выделив целую часть из неправильной дроби и добавив ее к 5 и 75 в этих примерах соответственно.
Числа вида 0314также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
Возьмем целый торт и еще три четверти такого же. Согласно правилам сложения, у нас на столе находится 1+34 торта. Эту сумму можно представить в виде смешанного числа как 134 торта. Если мы возьмем целый торт и тоже разрежем его на четыре равные части, то у нас на столе будет 74 торта. Очевидно, что от разрезания количество не увеличилось, и 134=74.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Вернемся к нашим 74 торта, оставшимся на столе. Сложим из его кусочков один торт обратно (1+34). У нас опять будет 134.
Ответ: 74=134.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Например,
84=2, так как 8:4=2.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число nab как сумму целой и дробной части. Получается n+ab
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n1).
3.После этого выполняем уже знакомое действие – складываем две обыкновенные дроби n1 и ab. Получившаяся в результате неправильная дробь и будет равной смешанному числу, данному в условии.
Разберем это действие на конкретном примере.
Представьте 537 в виде неправильной дроби.
Решение
Выполняем последовательно шаги указанного выше алгоритма. Наше число 537 – это сумма целой и дробной части, то есть 5+37. Теперь пятерку запишем в виде 51. У нас получилась сумма 51+37.
Последний шаг – сложение дробей, имеющих разные знаменатели:
51+37=357+37=387
Все решение к краткой форме можно записать как 537=5+37=51+37=357+37=387.
Ответ: 537=387.
Таким образом, с помощью указанной выше цепочки действий мы можем перевести любое смешанное число nab в неправильную дробь. У нас получилась формула nab=n·b+ab, которую мы и будем брать для решения дальнейших задач.
Представьте 1525 в виде неправильной дроби.
Решение
Возьмем указанную формулу и подставим в нее нужные значения. У нас n=15, a=2, b=5, следовательно, 1525=15·5+25=775.
Ответ: 1525=775.
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Любая неправильная дробь ab –это смешанное число qrb. Здесь q представляет собой неполное частное, а r – это остаток от ab. Таким образом, целая часть смешанного числа есть неполное частное от деления ab, а дробная – это остаток.
Приведем доказательство этого утверждения.
Нам требуется пояснить, почему qrb=ab. Для этого смешанное число qrb надо представить в виде неправильной дроби, выполнив все шаги алгоритма из предыдущего пункта. Поскольку – неполное частное, а r – остаток от деления a на b, то должно выполняться равенство a=b·q+r.
Таким образом, q·b+rb=ab поэтому qrb=ab. Это и есть доказательство нашего утверждения. Подытожим:
Выделение целой части из неправильной дроби ab осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
2) Записываем результаты в виде qrb. Это и есть наше смешанное число, равное исходной неправильной дроби.
Представьте 1074 в виде смешанного числа.
Решение
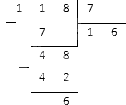
Делим 104 на 7 столбиком:
Деление числителя a=118 на знаменатель b=7 дает нам в итоге неполное частное q=16 и остаток r=6.
В итоге мы получаем, что неправильная дробь 1187 равна смешанному числу qrb=1667.
Ответ: 1187=1667.
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).
Для этого вспомним, какая связь существует между обыкновенными дробями и делением. Из этого можно вывести равенства: ab=a:b=c. Получается, что неправильную дробь ab можно заменить натуральным числом c.
Например, если в ответе получилась неправильная дробь 273, то можем записать вместо нее 9, поскольку273=27:3=9.
Ответ: 273=9.
Нередки случаи, когда при решении задач с дробями, возникает необходимость привести смешанное число в неправильную дробь или наоборот. Рассмотрим на примерах как это делается.
Как из смешанной дроби сделать неправильную?
Для перевода смешанного числа в неправильную дробь, необходимо целое число умножить на знаменатель и прибавить числитель. В общем виде это выглядит так:
Пример 1: Перевести смешанную дробь
5
2 7
в неправильную
5
2 7
=
5 × 7 + 2 7
=
37 7
Пример 2: Перевести смешанную дробь
2
3 5
в неправильную
2
3 5
=
2 × 5 + 3 5
=
13 5
Преобразование неправильной дроби в смешанное число
Из неправильной дроби сделать смешанное число можно следующим образом.
- Разделить столбиком числитель на знаменатель;
- Полученное целое число записать в целую часть смешанного числа;
- Полученный остаток записать в числитель, а знаменатель оставить прежним.
Пример 3: Перевести неправильную дробь
13 5
в смешанную
1. Разделим столбиком 13 на 5
2. Согласно вышеприведенному алгоритму: 2 — целая часть смешанной дроби, 3 — числитель, 5 — знаменатель. Таким образом:
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Оцените материал:
Загрузка…
превратить смешанную в обычную дробь
как перевести смешанную в обычную – это очень простая тема, перевод смешанной дроби в обычную. У нас есть определение смешанной дроби.
Здесь… закралась
смайлы некая формулировочная ошибка! Нельзя перевести смешанную в обычную дробь, потому, что обычная дробь – это правильная дробь!
А смешанная дробь может переводиться только в –
НЕправильную
дробь!
Далее по тексту :
“перевод смешанной дроби в
обычную
” – читай :
“перевод смешанной дроби в
неправильную
“
Пример перевода смешанной дроби в обычную
Для примера возьмем смешанную дробь – одна целая, одна-пятая :
115
Для того, чтобы данную смешанную дробь преобразовать в обычную, целое число 1 нужно представить в виде дроби, это можно представить как дробь 1/1 :
11
Теперь мы можем представить нашу смешанную дробь, как сумму двух дробей 1/1 + 1/5:
11 + 15
Далее, чтобы прибавить данные две дроби, их нужно привести к общему знаменателю – 5:
(11) * 5 + 15
Как вы знаете, что при умножении на одно число, числителя и знаменателя дроби – значение дроби не меняется!
и у нас получается две дроби 5/5 и 1/5. Прибавляем их, поскольку у нас знаменатели одинаковые, то складываем только числитель.
115 = 55 + 15 = 5 + 1 5 = 65
Результат перевода смешанной дроби в обычную
Итого у нас получается после перевода смешанной дроби – одна целая, одна-пятая :
115
В обычную, шесть-пятых :
65
Не благодарите, но ссылкой можете поделиться!
COMMENTS+
BBcode