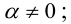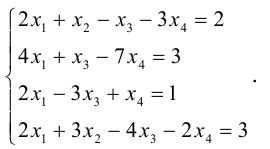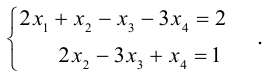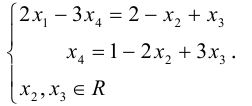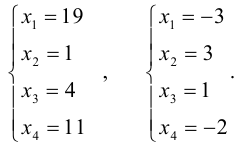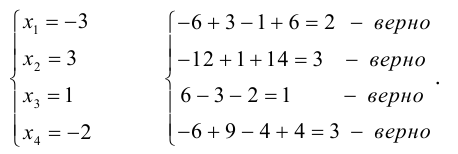Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 1001
И есть число 0,01 — это «сто в минус первой степени», 100-1
При перемножении этих двух чисел получится единица:
1001 × 100-1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А-1 × А × Х = А-1 × В
Добавляем единичную матрицу и упрощаем запись:
А-1 × А = E — единичная матрица
E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А-1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.
Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.
Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.
Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Этого котика не существует, а матрицы — существуют.
Решение матричных уравнений
Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
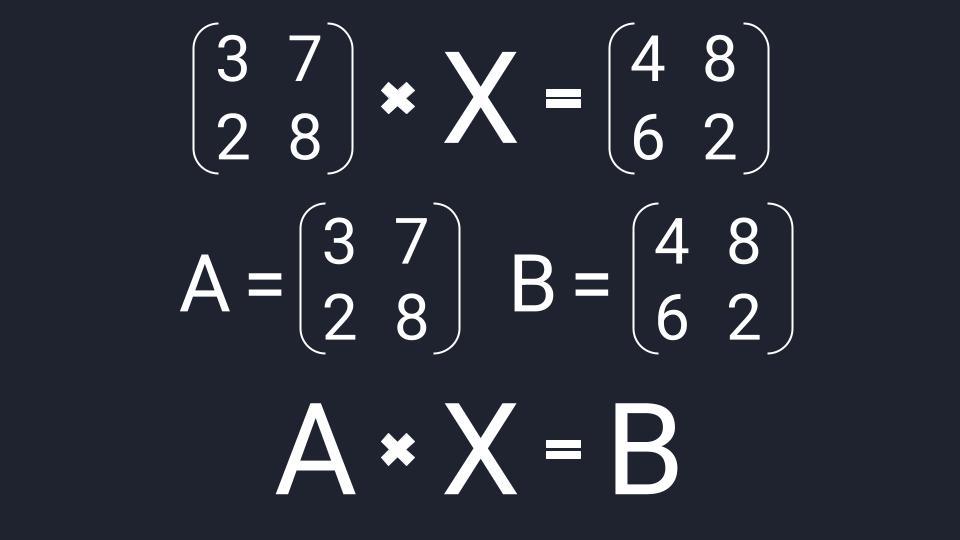
Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Решение матричных уравнений: теория и примеры
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x – неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы – это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B – известные матрицы, X – неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E – единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :
.
Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
.
Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :
.
Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :
.
Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :
.
Находим матрицу, обратную матрице B :
.
Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n – матрица системы.
X = x 1 x 2 ⋮ x n – столбец неизвестных,
B = b 1 b 2 ⋮ b n – столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A – 1 :
A – 1 × A × X = A – 1 × B .
Так как А – 1 × А = Е , то Е × X = А – 1 × В или X = А – 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 – 4 x 2 + 3 x 3 = 1 x 1 – 2 x 2 + 4 x 3 = 3 3 x 1 – x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 – 4 3 1 – 2 4 3 – 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 – 4 3 1 – 2 4 3 – 1 5 = 2 × ( – 2 ) × 5 + 3 × ( – 4 ) × 4 + 3 × ( – 1 ) × 1 – 3 × ( – 2 ) × 3 – – 1 × ( – 4 ) × 5 – 2 × 4 – ( – 1 ) = – 20 – 48 – 3 + 18 + 20 + 8 = – 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А – 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( – 1 ) ( 1 + 1 ) – 2 4 – 1 5 = – 10 + 4 = – 6 ,
А 12 = ( – 1 ) 1 + 2 1 4 3 5 = – ( 5 – 12 ) = 7 ,
А 13 = ( – 1 ) 1 + 3 1 – 2 3 – 1 = – 1 + 6 = 5 ,
А 21 = ( – 1 ) 2 + 1 – 4 3 – 1 5 = – ( – 20 + 3 ) = 17 ,
А 22 = ( – 1 ) 2 + 2 2 3 3 5 – 10 – 9 = 1 ,
А 23 = ( – 1 ) 2 + 3 2 – 4 3 – 1 = – ( – 2 + 12 ) = – 10 ,
А 31 = ( – 1 ) 3 + 1 – 4 3 – 2 4 = – 16 + 6 = – 10 ,
А 32 = ( – 1 ) 3 + 2 2 3 1 4 = – ( 8 – 3 ) = – 5 ,
А 33 = ( – 1 ) 3 + 3 2 – 4 1 – 2 = – 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = – 6 7 5 17 1 – 10 – 10 – 5 0
- Записываем обратную матрицу согласно формуле:
A – 1 = 1 d e t A ( A * ) T : А – 1 = – 1 25 – 6 17 – 10 7 1 – 5 5 – 10 0 ,
- Умножаем обратную матрицу А – 1 на столбец свободных членов В и получаем решение системы:
X = A – 1 × B = – 1 25 – 6 17 – 10 7 1 – 5 5 – 10 0 1 3 2 = – 1 25 – 6 + 51 – 20 7 + 3 – 10 5 – 30 + 0 = – 1 0 1
Ответ: x 1 = – 1 ; x 2 = 0 ; x 3 = 1
[spoiler title=”источники:”]
http://function-x.ru/matrix_equations.html
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/matrichnyj-metod-reshenija-slau/
[/spoiler]
Если вы перешли к изучению данной темы, то уже знаете, что такое матрица и определитель матрицы, умеете находить определители второго, третьего и высших порядков, а также обратные матрицы. Если какая-то из этих тем вам незнакома, то следует изучить сначала ее.
Приступим к рассмотрению понятия матричного уравнения.
Матричные уравнения
Матричные уравнения устроены практически также как и числовые, только вместо чисел в них содержатся числовые матрицы. Как правило, типовое матричное уравнение состоит из нескольких матриц и некоторой неизвестной матрицы XX, которую и требуется найти.
Рассмотрим примеры наиболее простых матричных уравнений и их решения.
Пример 1
Решить матричное уравнение
(1234)+x=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+x=begin{pmatrix}1&1\0&1end{pmatrix}.
Перенесем матрицу из левой части в правую:
x=(1101)−(1234)x=begin{pmatrix}1&1\0&1end{pmatrix}-begin{pmatrix}1&2\3&4end{pmatrix}.
Найдем разность матриц в правой части уравнения:
x=(1−11−20−31−4)x=begin{pmatrix}1-1&1-2\0-3&1-4end{pmatrix}.
Значит, x=(0−1−3−3)x=begin{pmatrix}0&-1\-3&-3end{pmatrix}.
Можно провести проверку:
(1234)+(0−1−3−3)=(1+02−13−34−3)=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+begin{pmatrix}0&-1\-3&-3end{pmatrix}=begin{pmatrix}1+0&2-1\3-3&4-3end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix},
(1101)=(1101)begin{pmatrix}1&1\0&1end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix}.
Пример 2
Решить матричное уравнение (58−469−5)−12x=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.
Перенесем матрицу из левой части в правую:
−12x=(341212)−(58−469−5)-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}-begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}.
Найдем разность матриц в правой части уравнения:
−12x=(3−54−81−(−4)2−61−92−(−5))-frac{1}{2}x=begin{pmatrix}3-5&4-8&1-(-4)\2-6&1-9&2-(-5)end{pmatrix},
−12x=(−2−45−4−87)-frac{1}{2}x=begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix}.
Умножим обе части уравнения на -2:
x=−2(−2−45−4−87)x=-2begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix},
x=(48−10816−14)x=begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}.
Можно провести проверку:
(58−469−5)−12(48−10816−14)=(58−469−5)−(24−548−7)=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}=begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-begin{pmatrix}2&4&-5\4&8&-7end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix},
(341212)=(341212)begin{pmatrix}3&4&1\2&1&2end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.
Такие уравнения элементарны, поэтому они довольно редко встречаются на практике.
Простейшие матричные уравнения
Обычно решение матричных уравнений сводится к одному из двух видов:
- A⋅X=BAcdot X=B;
- X⋅A=BXcdot A=B.
Рассмотрим, как решается каждое из этих уравнений.
| Уравнение вида A⋅X=BAcdot X=B | Уравнение вида X⋅A=BXcdot A=B |
|---|---|
| Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} слева: A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B.
Так как A−1⋅A=EA^{-1}cdot A=E, то E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица. Так как E⋅X=XEcdot X=X, то X=A−1⋅BX=A^{-1}cdot B. |
Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} справа: X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1}.
Так как A⋅A−1=EAcdot A^{-1}=E, то X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица. Так как X⋅E=XXcdot E=X, то X=B⋅A−1X=Bcdot A^{-1}. |
Рассмотрим примеры решения простейших матричных уравнений вида A⋅X=BAcdot X=B.
Пример 1
Решить матричное уравнение (3728)⋅X=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdot X=begin{pmatrix}4&8\6&2end{pmatrix}. Выполнить проверку.
Уравнение имеет вид A⋅X=BAcdot X=B, где A=(3728)A=begin{pmatrix}3&7\2&8end{pmatrix}, B=(4862)B=begin{pmatrix}4&8\6&2end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} слева:
A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,
E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,
X=A−1⋅BX=A^{-1}cdot B.
Найдем матрицу A−1A^{-1}.
∣3728∣=3⋅8−2⋅7=24−14=10≠0begin{vmatrix}3&7\2&8end{vmatrix}=3cdot8-2cdot7=24-14=10neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(3728∣1001)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Вычтем из строки №1 строку №2:
(3728∣1001)∼(1−128∣1−101)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1−128∣1−101)∼(1−1010∣1−1−23)begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}.
Умножим строку №1 на 10:
(1−1010∣1−1−23)∼(10−10010∣10−10−23)begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 1:
(10−10010∣10−10−23)∼(100010∣8−7−23)begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}.
Умножим строку №1 и №2 на 110frac{1}{10}:
(100010∣8−7−23)∼(1001∣810−710−210310)begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{matrix}end{pmatrix}.
Значит, A−1=(810−710−210310)=110(8−7−23)A^{-1}=begin{pmatrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{pmatrix}=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}.
A−1⋅B=110(8−7−23)⋅(4862)=110(−105010−10)=(−151−1)=XA^{-1}cdot B=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}cdotbegin{pmatrix}4&8\6&2end{pmatrix}=frac{1}{10}begin{pmatrix}-10&50\10&-10end{pmatrix}=begin{pmatrix}-1&5\1&-1end{pmatrix}=X.
Проверка:
(3728)⋅(−151−1)=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdotbegin{pmatrix}-1&5\1&-1end{pmatrix}=begin{pmatrix}4&8\6&2end{pmatrix}. — Верно.
Ответ: X=(−151−1)X=begin{pmatrix}-1&5\1&-1end{pmatrix}.
Пример 2
Решить матричное уравнение (0230)⋅X=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdot X=begin{pmatrix}2&4\3&-6end{pmatrix}. Выполнить проверку.
Уравнение имеет вид A⋅X=BAcdot X=B, где A=(0230)A=begin{pmatrix}0&2\3&0end{pmatrix}, B=(243−6)B=begin{pmatrix}2&4\3&-6end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} слева:
A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,
E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,
X=A−1⋅BX=A^{-1}cdot B.
Найдем матрицу A−1A^{-1}.
∣0230∣=0⋅0−3⋅2=0−6=−6≠0begin{vmatrix}0&2\3&0end{vmatrix}=0cdot0-3cdot2=0-6=-6neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(0230∣1001)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Поменяем местами строки №1 и №2:
(0230∣1001)∼(3002∣0110)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.
Умножим строку №1 на 13frac{1}{3}, а строку №2 на 12frac{1}{2}:
(3002∣0110)∼(1001∣013120)begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}0&frac{1}{3}\frac{1}{2}&0end{matrix}end{pmatrix}.
Значит, A−1=(013120)=16(0230)A^{-1}=begin{pmatrix}0&frac{1}{3}\frac{1}{2}&0end{pmatrix}=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}.
A−1⋅B=16(0230)⋅(243−6)=16(6−12612)=(1−212)=XA^{-1}cdot B=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}cdot begin{pmatrix}2&4\3&-6end{pmatrix}=frac{1}{6}begin{pmatrix}6&-12\6&12end{pmatrix}=begin{pmatrix}1&-2\1&2end{pmatrix}=X.
Проверка:
(0230)⋅(1−212)=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdotbegin{pmatrix}1&-2\1&2end{pmatrix}=begin{pmatrix}2&4\3&-6end{pmatrix}. — Верно.
Ответ: X=(1−212)X=begin{pmatrix}1&-2\1&2end{pmatrix}.
Рассмотрим примеры решения простейших матричных уравнений вида X⋅A=BXcdot A=B.
Пример 3
Решить матричное уравнение
X⋅(9711)=(201812)Xcdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. Выполнить проверку.
Уравнение имеет вид X⋅A=BXcdot A=B, где A=(9711)A=begin{pmatrix}9&7\1&1end{pmatrix}, B=(201812)B=begin{pmatrix}2&0\18&12end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} справа:
X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},
X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,
X=B⋅A−1X=Bcdot A^{-1}.
Найдем матрицу A−1A^{-1}.
∣9711∣=9⋅1−1⋅7=9−7=2≠0begin{vmatrix}9&7\1&1end{vmatrix}=9cdot1-1cdot7=9-7=2neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(9711∣1001)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Поменяем строки №1 и №2 местами:
(9711∣1001)∼(1197∣0110)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -9:
(1197∣0110)∼(110−2∣011−9)begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}.
Умножим строку №2 на −12-frac{1}{2}:
(110−2∣011−9)∼(1101∣01−1292)begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на -1:
(1101∣01−1292)∼(1001∣12−72−1292)begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.
Значит, A−1=(12−72−1292)=12(1−7−19)A^{-1}=begin{pmatrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{pmatrix}=frac{1}{2}begin{pmatrix}1&-7\-1&9end{pmatrix}.
B⋅A−1=(201812)⋅12⋅(1−7−19)=12(201812)⋅(1−7−19)=12(2−146−18)=(1−73−9)=XBcdot A^{-1}=begin{pmatrix}2&0\18&12end{pmatrix}cdot frac{1}{2}cdot begin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&0\18&12end{pmatrix}cdotbegin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&-14\6&-18end{pmatrix}=begin{pmatrix}1&-7\3&-9end{pmatrix}=X.
Проверка: (1−73−9)⋅(9711)=(201812).begin{pmatrix}1&-7\3&-9end{pmatrix}cdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. — Верно.
Ответ: X=(1−73−9)X=begin{pmatrix}1&-7\3&-9end{pmatrix}.
Пример 4
Решить матричное уравнение X⋅(1325)=(4−132)Xcdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. Выполнить проверку.
Уравнение имеет вид X⋅A=BXcdot A=B, где A=(1325)A=begin{pmatrix}1&3\2&5end{pmatrix}, B=(4−132)B=begin{pmatrix}4&-1\3&2end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} справа:
X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},
X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,
X=B⋅A−1X=Bcdot A^{-1}.
Найдем матрицу A−1A^{-1}.
∣1325∣=1⋅5−2⋅3=5−6=−1≠0begin{vmatrix}1&3\2&5end{vmatrix}=1cdot5-2cdot3=5-6=-1neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(1325∣1001)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1325∣1001)∼(130−1∣10−21)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 3:
(130−1∣10−21)∼(100−1∣−53−21)begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}.
Умножим строку №2 на -1:
(100−1∣−53−21)∼(1001∣−532−1)begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}-5&3\2&-1end{matrix}end{pmatrix}.
Значит, A−1=(−532−1)A^{-1}=begin{pmatrix}-5&3\2&-1end{pmatrix}.
B⋅A−1=(4−132)⋅(−532−1)=(−2213−117)=XBcdot A^{-1}=begin{pmatrix}4&-1\3&2end{pmatrix}cdotbegin{pmatrix}-5&3\2&-1end{pmatrix}=begin{pmatrix}-22&13\-11&7end{pmatrix}=X.
Проверка:
(−2213−117)⋅(1325)=(4−132)begin{pmatrix}-22&13\-11&7end{pmatrix}cdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. — Верно.
Ответ: X=(−2213−117).X=begin{pmatrix}-22&13\-11&7end{pmatrix}.
Существует третий вид матричных уравнений: A⋅X⋅B=CAcdot Xcdot B=C, но в действительности он встречается редко.
Обе части уравнения умножим на A−1A^{-1} слева: A−1⋅A⋅X⋅B=A−1⋅CA^{-1}cdot Acdot Xcdot B=A^{-1}cdot C.
Зная, что A−1⋅A=EA^{-1}cdot A=E, получим: E⋅X⋅B=A−1⋅CEcdot Xcdot B=A^{-1}cdot C.
Поскольку E⋅X=XEcdot X=X, то X⋅B=A−1⋅CXcdot B=A^{-1}cdot C.
Обе части уравнения умножим на B−1B^{-1} справа: X⋅B⋅B−1=A−1⋅C⋅B−1Xcdot Bcdot B^{-1}=A^{-1}cdot Ccdot B^{-1}.
Зная, что B⋅B−1=EBcdot B^{-1}=E, получим: X⋅E=A−1⋅C⋅B−1Xcdot E=A^{-1}cdot Ccdot B^{-1}.
Поскольку X⋅E=XXcdot E=X, то X=A−1⋅C⋅B−1X=A^{-1}cdot Ccdot B^{-1}.
Калужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Московский
государственный технический университет
имени Н.Э. Баумана»
(КФ
МГТУ им. Н.Э. Баумана)
Влайков
Н.Д.
Решение
матричных уравнений
Методические
указания для проведения упражнений
по
курсу аналитической геометрии
Калуга
2011г.
Содержание.
Цели
занятия
стр.4
План
занятия
стр.4
Необходимые
теоретические сведения
стр.5
Практическая
часть
стр.6
Контроль
освоения пройденного материала
стр.10
Домашнее
задание
стр.11
Количество
часов: 2
Цели
занятия:
-
Систематизировать
полученные теоретические знания о
видах матричных уравнений и способах
их решения. -
Применить
на практике методы решения матричных
уравнений.
План
занятия:
-
Кратко
изложить теоретический материал. -
Решить
матричное уравнение вида
методом с использованием обратной
матрицы. -
Решить
матричное уравнение видаметодом,
основанным на элементарных преобразованиях
строк матрицы. -
Сравнить
использованные методы. -
Решить
матричное уравнение вида
методом с использованием обратной
матрицы. -
Решить
матричное уравнение вида
методом с использованием обратной
матрицы. -
Проверить
выполнение текущего домашнего задания. -
Провести
проверочную работу. -
Представить
тему следующего семинарского занятия. -
Выдать
текущее домашнее задание.
Необходимые
теоретические сведения.
Рассмотрим
два вида матричных уравнений относительно
неизвестной матрицы
:
и
,
где матрицы
и
– известны, причем
– квадратная и невырожденная.
Опр.
Некоторую матрицу называют решением
матричного уравнения относительно
неизвестной матрицы
,
если при ее подстановке вместо
матричное уравнение превращается в
тождество.
Рассмотрим
уравнение
.
Первый
метод предполагает
вычисление обратной матрицы
и дает запись решения матричного
уравнения в виде
.
Причем данное решение единственно.
Второй
метод
основан на элементарных преобразованиях
строк блочной матрицы
и имеет своей целью преобразование ее
к виду
,
в котором вместо матрицы
стоит единичная матрица
.
Тогда матрица
и будет решением уравнения.
Проверка
ответа
выполняется подстановкой найденного
решения в исходное уравнение.
Матричное
уравнение
так же можно решить двумя способами.
Если известна матрица
,
то умножаем справа на
матричное уравнение
и после очевидных преобразований
получаем ответ в виде произведения двух
матриц
.
Другой метод решения матричного уравнения
состоит
в транспонировании его левой и правой
частей
,
.
После введения новой неизвестной матрицы
получаем уравнение вида
,
которое решается методом элементарных
преобразований.
Практическая
часть.
Пример
1. Решить
матричное уравнение:
,
где
;
.
Решение.
1-ый
способ.
Найдем решение, используя обратную
матрицу:
Решение
ищем в виде
;
Найдем
матрицу
(например, при помощи присоединенной
матрицы)
.
Таким
образом, получим:
.
2-ой
способ. Найдем
решение методом элементарных
преобразований:
Запишем
матрицу
и выполним элементарные преобразования
ее строк с целью привести ее к виду
.
.
Следовательно,
.
Проверка
осуществляется подстановкой в исходное
уравнение:
–
Верно.
Пример
2. Решить
матричное уравнение:
,
где
;
;
.
Решение.
Если
для матриц
и
существуют обратные матрицы
и
соответственно, умножим обе части
уравнения слева на
,
справа на
.
В результате получим:
.
Учитывая, что
,
(–
единичная матрица) можно записать:
.
Так как
–
единичная матрица, окончательно имеем
уравнение:
где
матрица
– решение уравнения.
Если
же хотя бы одна из матриц
или
не имеет обратную, уравнение не имеет
решения.
Для
матрицы
найдем
или
докажем, что она не существует.
а)
обратная
матрица существует.
б)
.
в)
Найдем алгебраические дополнения для
матрицы
и
составим из них присоединенную матрицу
:
.
г)
Известно, что
;
тогда
.
Для
матрицы
найдем
или докажем, что она не существует.
а)
обратная
матрица существует.
б)
.
в)
Найдем алгебраические дополнения для
матрицы
и
составим из них присоединенную матрицу
:
.
г)
По формуле
;
.
Найдем
неизвестную матрицу
.
.
Ответ:.
Решить
матричные уравнения:
№2.121(2.39)
.
Отв.:
№2.122(2.40)
.
Отв.:
№2.123(2.41)
.
Отв.:
№2.124(2.42)

Отв.:
№2.125(2.43)
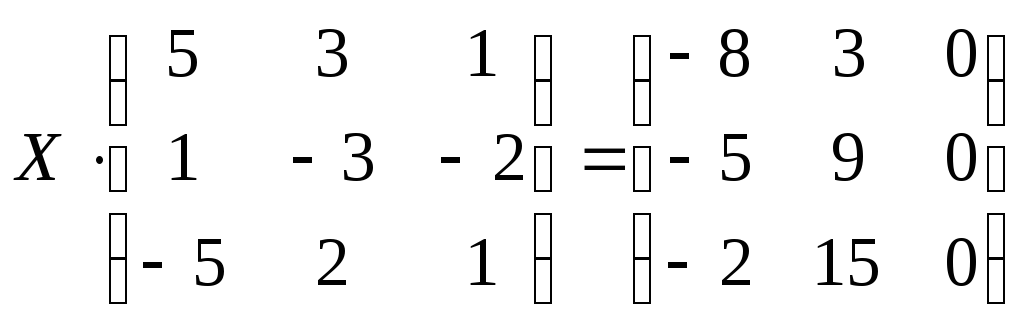
Отв.:
Представление
темы следующего семинара.
Решение
систем линейных однородных уравнений.
Контроль
освоения пройденного материала.
Проверочная
работа 5 минут. Участвует 4 студента с
четными номерами по журналу, начиная с
№10
Задание:
|
Вар№1 Выполнить |
Вар№2 Выполнить |
|
Вар№3 Найти
|
Вар№4 Найти |
Ответы:
|
Вар№1 Выполнить
|
Вар№2 Выполнить |
|
Вар№3 Найти
|
Вар№4 Найти |
Домашнее
задание.
1.Решить
матричное уравнение
:
1)


2)


2.Решить
матричное уравнение
:
1)
;
;
.
2)
;
;
.
3.Проработка
лекций на темы:
Системы
линейных алгебраических уравнений
(СЛАУ). Координатная, матричная и
векторная формы записи. Критерий
Кронекера — Капелли совместности СЛАУ.
Однородные СЛАУ. Критерий существования
ненулевого решения однородной СЛАУ.
Свойства решений однородной СЛАУ.
Фундаментальная система решений
однородной СЛАУ, теорема о ее существовании.
Нормальная фундаментальная система
решений. Теорема о структуре общего
решения однородной СЛАУ.
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Линейная алгебра
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.
Матрицы и операции над ними
Основные определения:
В математике и ее приложениях наряду с числами часто бывает удобным использовать числовые таблицы, которые называются матрицами. Аппарат теории матриц эффективно применяется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.
Определение: Матрицей размерности m х n называется прямоугольная таблица действительных чисел, состоящая из m строк и n столбцов.
Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам матрицы используются два индекса: первый указывает на номер строки, второй – на номер столбца, на пересечении которых расположен данный элемент.
Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:
Более компактно с указанием элементов матрица записывается в виде:
Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.
Рассмотрим некоторые специальные виды матриц.
Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.
Числа 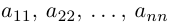
Квадратная матрица, диагональные элементы которой равны единице, а все остальные – нулю, называется единичной матрицей и обозначается через 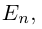
Таким образом,
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица
Матрица называется трапециевидной, если она представляет собой следующую таблицу:
Операции над матрицами
Введем сначала линейные операции над матрицами.
Произведением действительного числа 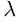
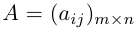
Суммой двух матриц 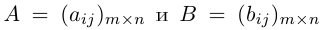
Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.
Разность матриц А и B можно определить как А – В = А + (-1)В.
Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.
Пример №1
Даны матрицы
Найти матрицу -2А +3В.
Решение.
Тогда
Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.
Произведением этих строки и столбца называется число1
Рассмотрим так называемые согласованные матрицы 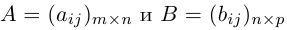
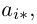
Произведением данных согласованных матриц А и B называется матрица
Часто для суммы n чисел 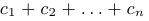
размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.
Пример №2
Найти произведение согласованных матриц
Решение. Найдем произведение строк матрицы А на столбцы матрицы В.
Осталось записать искомое произведение матриц:
Отметим некоторые свойства произведения матриц1.
Первые три сразу следуют из определения произведения матриц. Докажем последнее свойство. Пусть заданы три матрицы 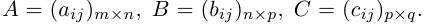
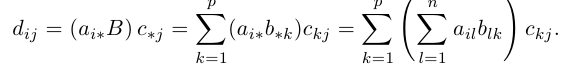
что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.
Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не перестановочны). Приведем соответствующий
Контрпример. Доказать, что матрицы
не коммутируют.
Действительно,
Таким образом, для этих матриц
Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.
Мы предполагаем, что все матрицы в свойствах согласованы.
Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.
Определитель матрицы и его свойства
Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Введем предварительно понятие перестановки и изучим некоторые ее свойства.
Перестановки
Перестановкой n натуральных чисел 1, 2, ….., n называется строка
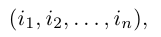
содержащая все эти числа.
Первым элементом перестановки может быть любое из чисел 1, 2, …., n, вторым – любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно 
Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через
В связи с этим перестановка (1) называется четной, если в ней число 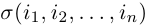
Отметим два свойства перестановок, которые мы будем использовать ниже.
Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.
Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или настолько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем переставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четности исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.
Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных перестановок, мы получим p нечетных и, следовательно, 
Лемма 2. Пусть
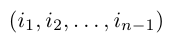
– перестановка чисел 1, 2, …, n – 1. Зафиксируем число j из множества {1, 2, … , n} и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, … , n – 1 и увеличив на единицу все не меньшие, чем j элементы этой перестановки. В результате получим перестановку
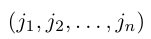
чисел 1, 2, …. , n. Четности перестановок (2) и (3) связаны равенством
Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 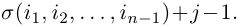
Определитель и его вычисление для матриц второго и третьего порядков
Рассмотрим квадратную матрицу порядка n :
Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:
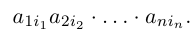
Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, … , n.
Определение: Число, равное сумме всех n! произведений
называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как
Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.
Так как 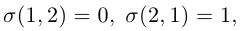
Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :
Тогда
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком ” + ” следует брать произведения по схеме
а со знаком ” – ” – по схеме
Пример №3
Вычислить определитель
Решение. Воспользуемся правилом треугольников: 
Свойства определителя
1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.
2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.
3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указанной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.
Эти свойства напрямую следуют из определения определителя.
4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.
Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.
5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.
В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесения за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.
6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) добавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.
Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополнения к элементу матрицы.
Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число
где 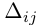
7) Разложение определителя по элементам строки (столбца).
Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столбца) на соответствующие алгебраические дополнения. Таким образом,
или
Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение
содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.
Рассмотрим произвольное произведение
Каждое слагаемое определителя 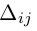
чисел 1, 2, … , n — 1. Умножив данное произведение на число 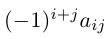
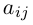
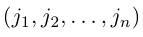
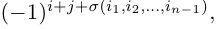
Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.
Пример №4
Вычислить определитель.
Решение. Разложим этот определитель по элементам второй строки:
Пример №5
Вычислить определитель треугольной матрицы
Разлагая этот и следующие определители по первому столбцу, получим:
таким образом, определитель треугольной матрицы равен произведению диагональных элементов.
8) Сумма произведений n действительных чисел на алгебраические дополнения к элементам какой-нибудь строки (столбца) равна определителю, в котором в указанной строке (столбце) расположены данные числа, а все остальные элементы совпадают с соответствующими элементами исходного определителя.
Это свойство является прямым следствием предыдущего.
9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.
Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.
10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.
Достаточно громоздкое доказательство этого свойства мы приводить не будем.
Обратная матрица
Определение: Обратной к квадратной матрице 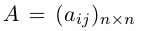
Из этого определения следует, что матрица А-1 также является квадратной той же размерности, что и матрица А.
Отметим некоторые свойства обратной матрицы, следующие из ее определения.
а) У матрицы не может существовать больше одной обратной.
Действительно, пусть для матрицы А имеются две обратные 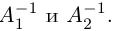
Умножив обе части первого равенства слева на матрицу 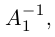
b) (A-1)-1 = A.
c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем
Выясним условия, при которых обратная матрица существует.
Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.
Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А 
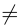
Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:
Действительно, если
откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:
т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.
В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.
Пример №6
Найти обратную к матрице
Решение. Найдем сначала определитель матрицы: 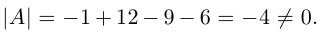
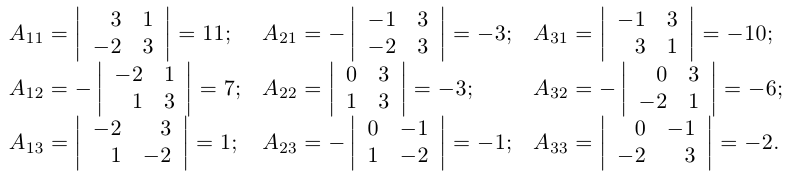
Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение
AX = B
с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:
Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а решением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.
Ранг матрицы и его вычисление
Рассмотрим произвольную матрицу
Минором порядка k матрицы A называется определитель, стоящий на пересечении выбранных k строк и k столбцов данной матрицы.
Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.
Естественно считать, что rang O = 0. Очевидно также, что
Пример №7
Найти ранг матрицы
Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:
Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.
Как видно из определения, вычисление ранга матрицы через миноры является весьма трудоемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.
Элементарными преобразованиями матрицы называются следующие операции над ее строками или столбцами:
- перестановка двух строк (столбцов) матрицы;
- умножение строки (столбца) на ненулевое действительное число;
- добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.
Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как
Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.
Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число 
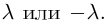
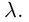
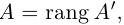
Из этой теоремы следует, что для вычисления ранга матрицы достаточно привести ее с помощью элементарных преобразований к более простой – трапециевидной, ранг которой легко находится. Изложим соответствующий алгоритм, который мы будем использовать ниже при решении систем линейных алгебраических уравнений.
Итак, рассмотрим матрицу
Если А = О, то rang A = 0. Пусть теперь 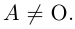
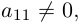
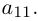
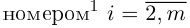
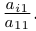
Повторяя теперь все рассуждения из предыдущего абзаца применительно к полученной матрице с вычеркнутыми из нее первой строкой и первым столбцом и всем последующим матрицам, после конечного числа шагов, не превышающего m — 1, мы придем к трапециевидной матрице
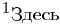
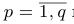
с r ненулевыми диагональными элементами a11, b22, . . . , crr. Ранг матрицы 
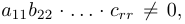
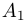
элементарных преобразований, то
Замечание. При практическом использовании приведенного алгоритма матрицу бывает
иногда удобно приводить к форме, которая отличается от трапециевидной порядком следования столбцов.
Пример №8
Найти ранг матрицы
Решение.
Приведем матрицу к трапециевидной с помощью элементарных преобразований:
Здесь вторая матрица получена из исходной вычитанием в ней из второй и третьей строк первой, умноженной на 4 и 3 соответственно, а затем вторая матрица преобразована в третью вычитанием из последней строки, умноженной на 5, второй строки. Перегнав в последней матрице четвертый столбец на первое место, получим трапециевидную матрицу с тремя ненулевыми элементами на диагонали. Следовательно, rang
Системы линейных алгебраических уравнений
Основные определения:
Определение: Системой m линейных алгебраических уравнений с n неизвестными (или, короче, линейной системой) называется система вида
где действительные числа 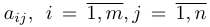
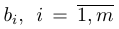
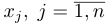
Числа 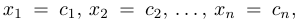
Для этого введем следующие обозначения:

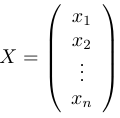
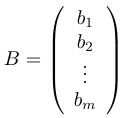
В этих обозначениях данная линейная система принимает вид:
AX = B.
Линейная система с нулевыми правыми частями, т.е. система АХ = О, называется однородной.
Решение невырожденных линейных систем
Рассмотрим линейную систему n уравнений с n неизвестными и невырожденной основной матрицей. Такая система называется невырожденной.
Рассмотрим два метода решения невырожденных систем.
Метод обратной матрицы
Так как определитель основной матрицы невырожденной системы линейных уравнений отличен от Iгуля. то решение этой системы мы можем найти как решение матричного линейного уравнения (§3)
по формуле
Полученное таким образом решение является единственным. Действительно, пусть 
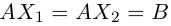
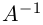
Пример №9
Решить систему линейных уравнений:
Решение.
Здесь
В §3 был вычислен определитель матрицы данной системы 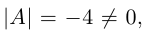
Тогда
Таким образом, 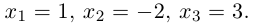
Формулы Крамера
Воспользовавшись представлением обратной матрицы через алгебраические дополнения, получим:
следовательно,
По свойству 8) определителя выражение в скобках равно
т. е. определителю, который может быть получен из определителя 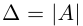
Пример №10
Решить систему линейных уравнений:
Решение. Для этой системы 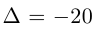
Тогда по формулам Крамера
Решение произвольных систем линейных уравнений. Метод исключения неизвестных (метод Гаусса)
Рассмотрим линейную систему общего вида:
Определим, как и для матриц, элементарные преобразования над уравнениями линейной системы. Таковыми являются:
- перестановка двух уравнений системы;
- умножение обеих частей уравнения на отличное от. нуля действительное число:
- добавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на действительное число.
Все эти преобразования, очевидно, обратимы и поэтому их результатом является система, эквивалентная исходной, т. е. система, множество решений которой, совпадает с множеством решений данной системы.
Упростим теперь систему, последовательно исключая неизвестные из ее уравнений с помощью элементарных преобразований. Для этого, расширенную матрицу системы
с помощью элементарных преобразований над ее строками приведем к трапециевидной форме с помощью алгоритма, изложенного в §4. В результате получим матрицу
где диагональные элементы 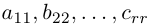
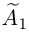
Очевидно, последняя система получена из исходной с помощью тех же элементарных преобразований, какими матрица 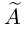
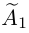
Рассмотрим два случая, которые здесь возможны.
a) 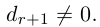
b)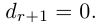
Здесь, в свою очередь, представляются две возможности.
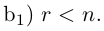
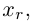
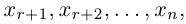
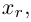
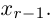
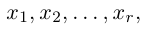
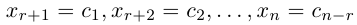
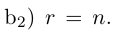
Приведенный алгоритм метода исключения неизвестных позволяет сформулировать критерий совместности линейной системы.
Теорема Кронекера. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы.
Доказательство немедленно следует из вида матрицы 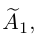
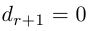
Из теоремы Кронекера следует, что если 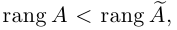
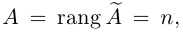
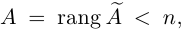
Пример №11
Решить систему линейных уравнений:
Решение. Приведем расширенную матрицу этой системы к трапециевидной с помощью элементарных преобразований над ее строками:
Вторая матрица получена из первой вычитанием из третьей строки второй и добавлением ко второй строке, умноженной на 2, первой строки. С точностью до перестановки столбцов, мы получили трапециевидную матрицу. Здесь, очевидно, rang 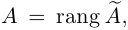
Придавая свободным неизвестным 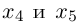
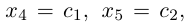
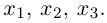
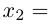
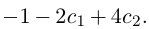
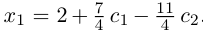
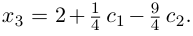
где 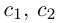
Замечание. Однородная система линейных уравнений всегда совместна, так как она имеет нулевое решение. Если rang A = n, то однородная система имеет единственное (нулевое) решение. а если 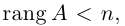
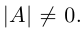
Обращение невырожденной матрицы с помощью элементарных преобразований
Рассмотрим невырожденную квадратную матрицу 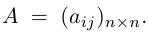
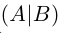
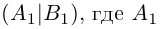
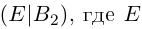
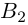
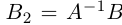
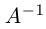
Таким образом, для того, чтобы найти матрицу, обратную к данной невырожденной матрице А, достаточно в расширенной матрице 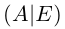
Пример №12
Найти обратную к матрице
Решение. Воспользуемся изложенным выше алгоритмом.
Следовательно,
Изложенный выше алгоритм нахождения обратной матрицы является более экономичным по сравнению с изложенным в §3, так как он требует гораздо меньшего объема вычислений. Заметим также, что программирование этого метода также не представляет трудностей.
Справочный материал по линейной алгебра
Этот раздел математики возник в связи с необходимостью решать системы линейных уравнений.
Рассмотрим систему линейных уравнений:
Чтобы решить ее, можно, например, выразить одну из переменных из первого уравнения, подставить во второе, после чего найти неизвестные x и y .
Однако можно найти решение быстрее: легко убедиться, что
Способ получения этого результата станет ясным, если рассмотреть таблицы, составленные из коэффициентов системы:
Такие таблицы называются матрицами второго порядка (так как в них две строки и два столбца), а соответствующие числа – определителями. Матрицы и определители играют важную роль при решении более сложных систем линейных уравнений, поэтому начнем изучение линейной алгебры с матриц.
Матрицы и действия над ними
Определение: Числовой матрицей размера 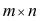
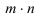
столбцов.
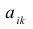
Определение: Если 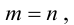
Элементы 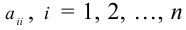
Матрица размера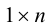
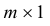
Пример №13
Определение: Две матрицы называются равными, если они имеют
одинаковый размер и равны их элементы, стоящие на одинаковых местах.
Пример №14
Определение: Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть
На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой E .
Пример №15
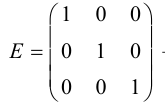
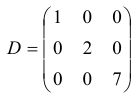
Определение: Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.
Пример №16
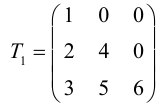
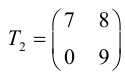
Линейные операции над матрицами
К числу линейных относятся операции сложения и умножения на число.
Определение: Пусть 
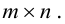
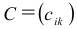
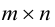
Пример №17
Определение: Произведением матрицы 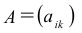
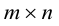
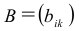
Пример №18
Определение: Нулевой матрицей O называется матрица, все элементы которой равны нулю.
Определение: Матрица (-1) * A называется противоположной для A и обозначается -A.
Очевидно, что 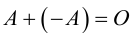
Определение: Разностью матриц A и B одного размера называется сумма 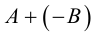
Определение: Результат конечного числа линейных операций над матрицами называется их линейной комбинацией.
Пример №19
Пусть
Матрица 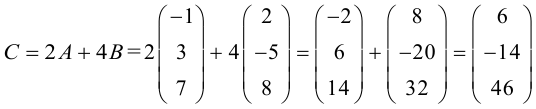
Свойства линейных операций
Если A , B , и C – матрицы одного размера, 
1. 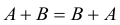
2. 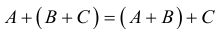
3. 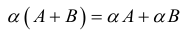
4. 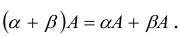
5.
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
Определение: Транспонированной матрицей 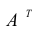
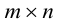
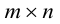
То есть, если
Пример №20
Определение: Если 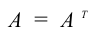
Все диагональные матрицы симметрические, так как равны их элементы,
симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
Определение: Пусть 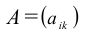
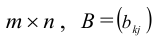
матрица размера 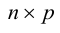
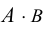
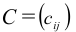
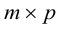
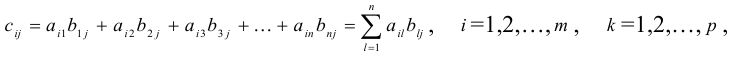
Пример №21
Произведение 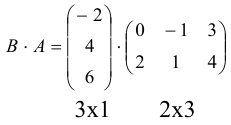
Свойства операции умножения матриц
1. 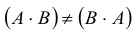
Пример №22
Определение: Матрицы A и B называются перестановочными, если 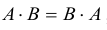
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
Пример №23
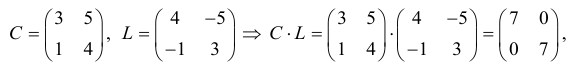
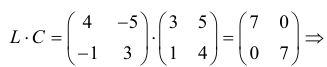
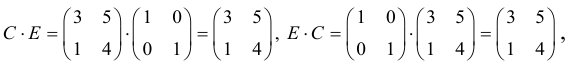
Вообще единичная матрица перестановочная с любой квадратной матрицей того же порядка, и для любой матрицы 
чисел таким свойством обладает число 1.
Если соответствующие произведения определены, то:
Пример №24
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
Пример №25
Определители и их свойства
Каждой квадратной матрице можно по определенным правилам поста-
вить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим квадратную матрицу второго порядка:
Её определителем называется число, которое записывается и вычисляется так:
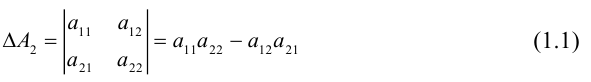
Такой определитель называется определителем второго порядка и может
обозначаться по-другому:
Определителем третьего порядка называется число, соответствующее квадратной матрице 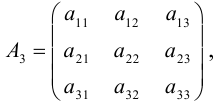
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:

Пример №26
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
То есть при вычислении определителя третьего порядка используются
определители второго порядка, причем 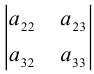
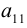
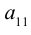
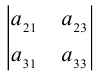
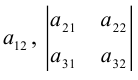
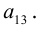
Определение: Дополнительным минором 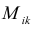
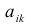
Пример №27
и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
Определение: Алгебраическим дополнением элемента aik квадратной
матрицы A называется число
Пример №28
Для матрицы A2 :
Для матрицы A3: 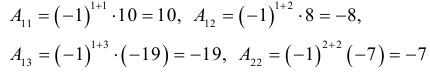
Итак, с учетом сформулированных определений (1.3) можно переписать в
виде: 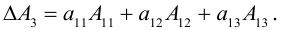
Перейдем теперь к общему случаю.
Определение: Определителем квадратной матрицы 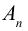
Равенство (1.4) называется разложением определителя по элементам первой строки. В этой формуле алгебраические дополнения вычисляются как определители 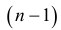
Пример №29
Рассмотрим (без доказательства) свойства определителей:
1. Определитель можно разложить по элементам первого столбца:
Пример №30
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
2. При транспонировании матрицы величина ее определителя не меняется:
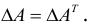
Отсюда следует, что строки и столбцы определителя равноправны.
3. Если в определителе поменять местами две строки (два столбца), то
определитель изменит свой знак, не изменившись по абсолютной вели-
чине.
4. Определитель, имеющий две равные строки (столбца), равен нулю.
5. Если все элементы некоторой строки (столбца) определителя умножить на число 
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
6. Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
7. Определитель можно разложить по элементам любой строки (любого
столбца):
или
Равенство (1.6) называется разложением определителя по элементам i -й строки.
Равенство (1.7) называется разложением определителя по элементам k -го столбца.
8. Сумма произведений всех элементов некоторой строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю, то есть при
9. Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца),умноженных на одно и то же число.
10. Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: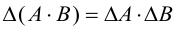
Пример №31
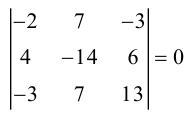
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
Пример №32
Определение обратной матрицы
Определение: Матрица 
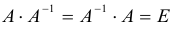
Из определения следует, что A и 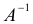
Определение: Квадратная матрица A называется невырожденной, если 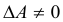
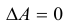
Пример №33
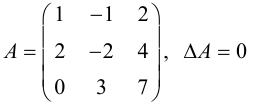
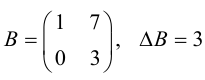
Теорема: Всякая невырожденная матрица имеет обратную, причем одну.
Доказательство: Рассмотрим для определенности квадратную матрицу A третьего порядка:
Покажем, что матрица вида 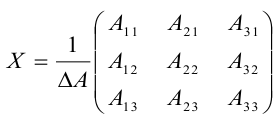
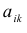
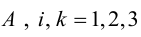
По условию A – невырожденная, т.е. 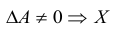
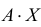
Аналогично доказывается, что 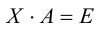
Следовательно, по определению матрица X является обратной для A .
Докажем единственность обратной матрицы.
Пусть невырожденная матрица A имеет две обратные: 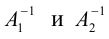
Умножим (1.8) слева на
Используя свойство 2 умножения матриц и равенство (1.9), получим:
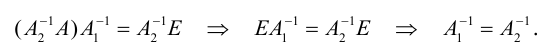
Таким образом, обратная матрица единственна, что и требовалось доказать.
Обратная матрица для матрицы A n – го порядка имеет вид:
Пример №34
Найти матрицу, обратную для
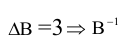
Проверка:
Пример №35
Найти матрицу, обратную для 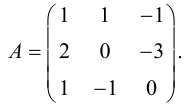
существует.
Проверка:
Аналогично проверяется, что
Крамеровские системы уравнений
Рассмотрим систему n линейных уравнений с n неизвестными:
Матрица, составленная из коэффициентов системы (1.10)
называется основной матрицей системы (1.10), 
Определение: Система линейных уравнений называется Крамеровской, если
1) число уравнений равно числу неизвестных;
2) основной определитель не равен нулю.
Рассмотрим матрицы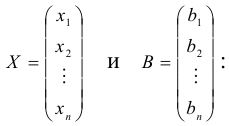
В – столбец правых частей. Очевидно, что система (1.10) может быть записана
в виде матричного уравнения
Определение: Совокупность n чисел 
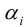
Теорема: Всякая Крамеровская система имеет решение, причем одно.
Доказательство: По условию 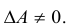
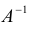
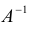
По формуле (1.12) определяется каждое из неизвестных 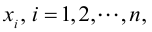
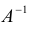
ЗАМЕЧАНИЕ. Способ решения системы (1.10) по формуле (1.12) называется матричным способом решения системы линейных уравнений.
Пример №36
Решить систему уравнений матричным способом:
В предыдущем примере было показано, что 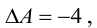
Таким образом, 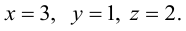
ЗАМЕЧАНИЕ. Матричный способ удобен, когда надо решить несколько Крамеровских систем, которые отличаются только правыми частями.
Вернемся к равенству (1.12). Из него следует, что
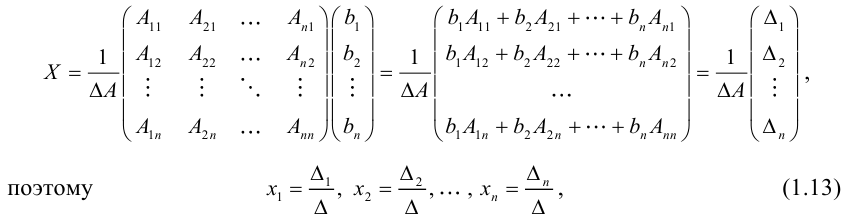
где 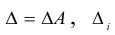
Ранг матрицы и элементарные преобразования
Определение: Минором порядка k матрицы А называется определитель k -го порядка, составленный из элементов матрицы А, стоящих на пересечении произвольно выбранных k строк и k столбцов без изменения порядка их следования.
Пример №37
Рассмотрим матрицу
Миноры первого порядка – каждый элемент матрицы A .
Миноры второго порядка: 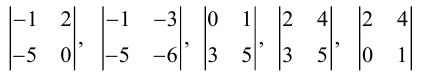
Матрица A имеет всего 18 миноров второго порядка.
Миноры третьего порядка:
Миноров четвертого порядка у этой матрицы нет.
Теорема: Если все миноры k -го порядка матрица А равны нулю, то равны нулю и все миноры старших порядков, если они существуют.
Доказательство: Рассмотрим минор порядка (k+1) . Это определитель (k-1) -го порядка, который ( по свойству 7 ) можно разложить по элементам некоторой строки (столбца ). В разложении будут алгебраические дополнения, которые с точностью до знака совпадают с минорами k – го порядка и по условию равны нулю. Поэтому равен нулю и рассматриваемый минор порядка k( 1 ). Аналогично равны нулю и миноры старших порядков 
Определение:. Рангом матрицы А называется такое целое число r ,
что среди ее миноров r -го порядка есть хотя бы один ненулевой, а все миноры
порядка (r+1) равны нулю.
Из доказанной теоремы следует, что, другими словами, ранг матрицы – это наивысший порядок отличного от нуля минора.
Будем обозначать 
Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны
нулю, то есть если матрица нулевая.
Пример №38
Матрица F , очевидно, имеет ненулевой минор второго порядка, например,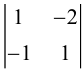
поэтому 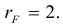
Определение: Элементарными преобразованиями матрицы называются следующие действия:
- умножение любой строки на число
;
- перемена местами двух строк;
- прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число
;
- отбрасывание нулевой строки;
- отбрасывание одной из двух пропорциональных строк;
- те же преобразования со столбцами.
Теорема: Элементарные преобразования не изменяют ранга матрицы.
С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства).
Покажем теперь, что ранг матрицы F из последнего примера равен 2.
При переходе от F к 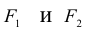
Вычислить 
Исследование произвольных систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными.
Матрица 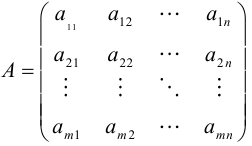
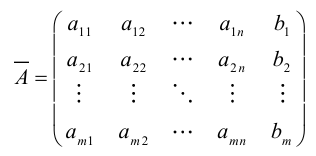
Определение: Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Определение: Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.
Пример №39
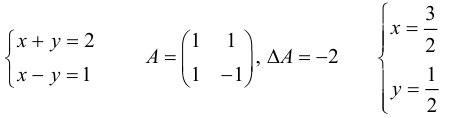
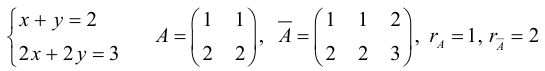
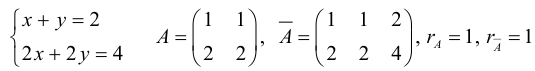
Теорема: (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства).
Теорема: (о числе решений). Пусть выполнены условия совместности системы линейных уравнений. Тогда, если 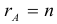
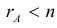
Однородные системы линейных уравнений
Система линейных уравнений вида
называется однородной.
Однородная система всегда совместна, так как 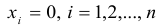
Теорема: Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы r был меньше числа неизвестных n .
Доказательство:
- Достаточность:
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
- Необходимость: (1.15) имеет нетривиальное решение
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.
Доказательство:
- Достаточность:
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
- Необходимость: система имеет нетривиальное решение
Если
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
Метод Гаусса
Этим методом можно решить любую систему линейных уравнений (1.14) или доказать, что она несовместна. Он состоит в последовательном исключении неизвестных системы (1.14) по следующей схеме: выписывается расширенная матрица системы 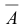
- перемена местами двух строк (уравнений);
- умножение любой строки (уравнения) на число
- отбрасывание одной из двух равных или пропорциональных строк (уравнений) ;
- прибавление к любой строке (уравнению) другой строки (уравнения), умноженной на число
После выполнения преобразований возможны три случая:
а)
б) 
в) 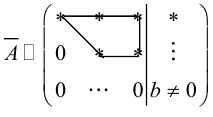
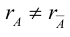
Пример №40
Решить систему линейных уравнений:
Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:
Очевидно, что 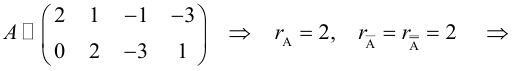
Кронекера-Капелли система совместна.
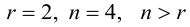
Выпишем систему, соответствующую матрице 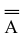
Перенесем в правую часть переменные 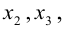
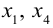
Теперь подставим 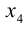
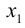
Определение: Общим решением системы (1.14) называется решение, содержащее информацию обо всех неизвестных, в котором зависимые переменные выражаются как функции свободных.
Решение, полученное из общего при конкретных значениях свободных переменных, называется частным решением.
Например, частными решениями этой системы являются:
Сделаем проверку частного решения (для всех уравнений исходной системы!):
Лекции по предметам:
- Математика
- Алгебра
- Векторная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
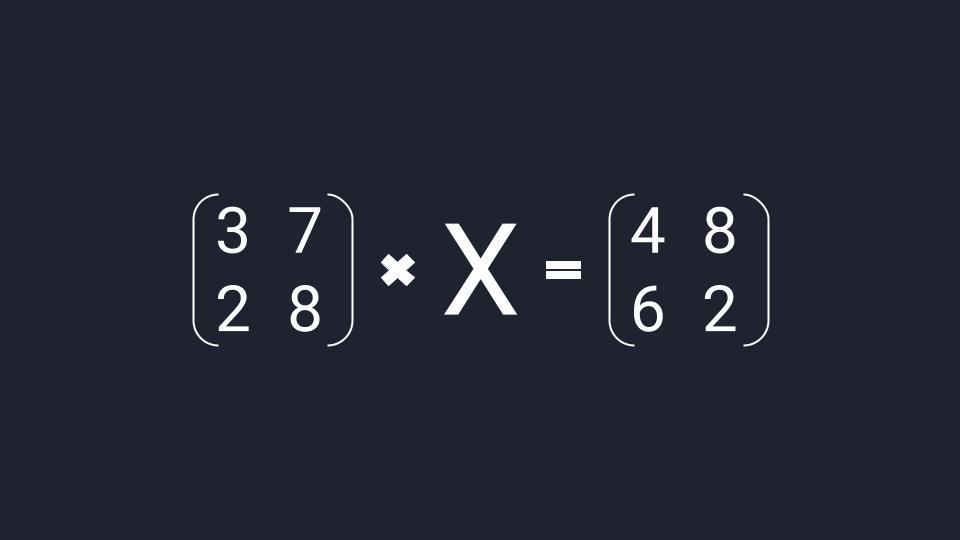
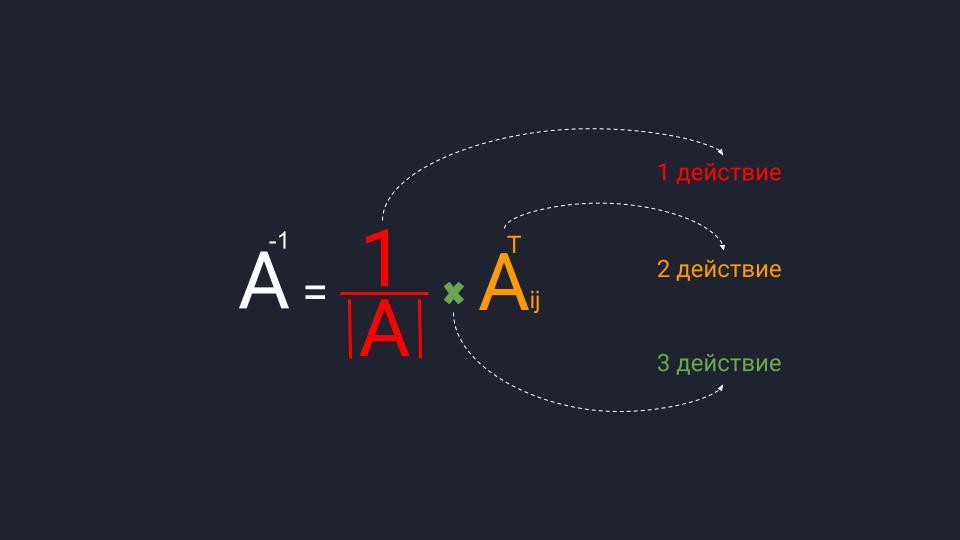

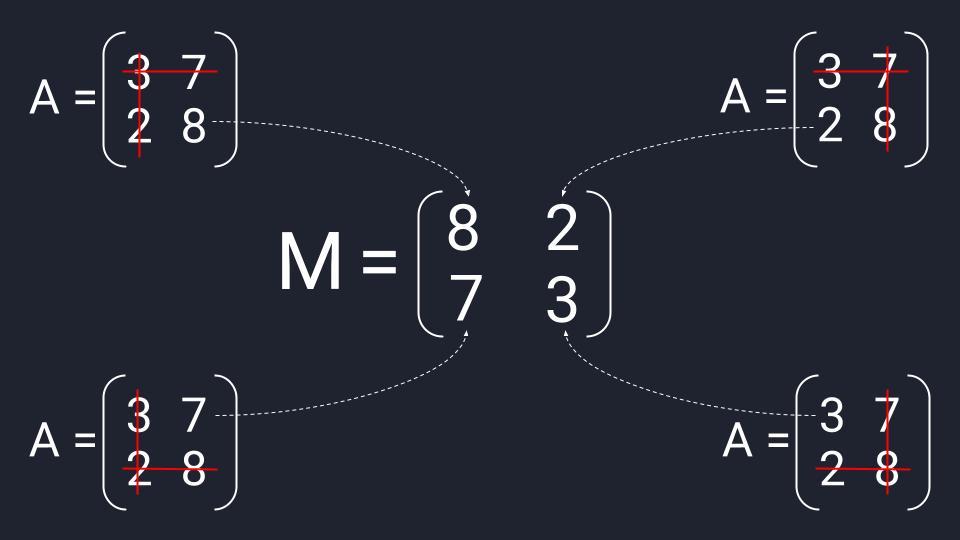











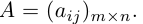
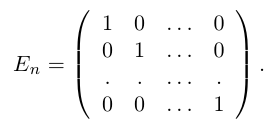

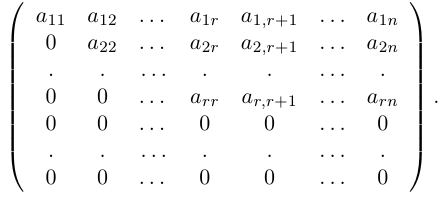
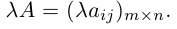
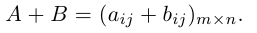
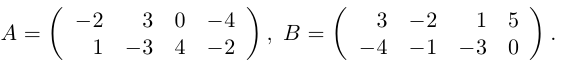
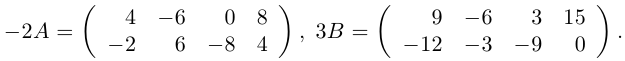
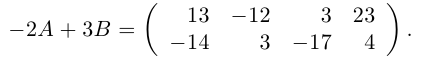
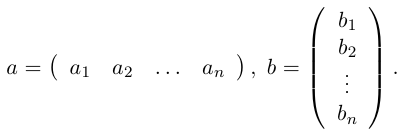
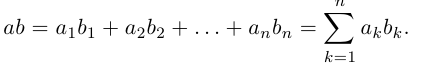
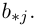
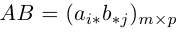
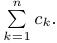
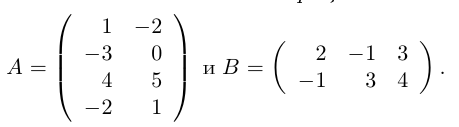
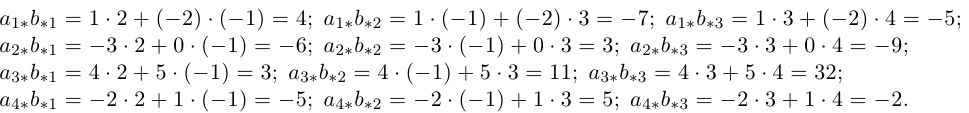
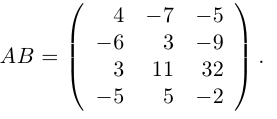
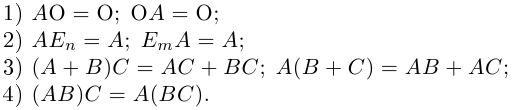
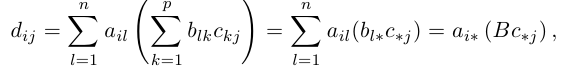
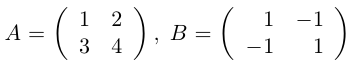
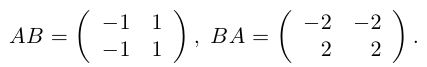
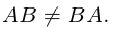
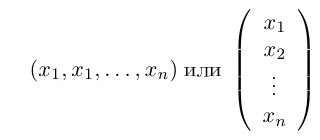
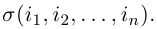
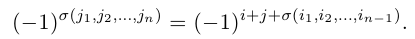
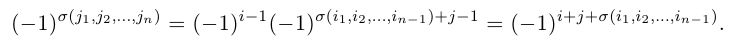

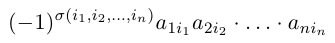

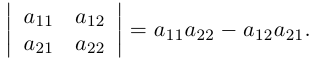
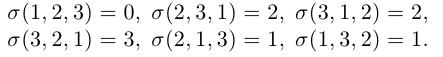
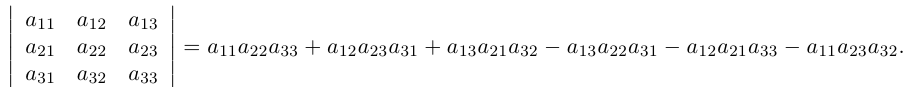
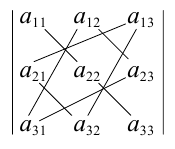
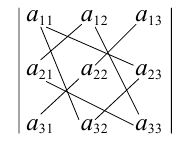

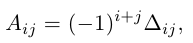
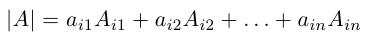
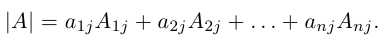
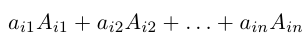
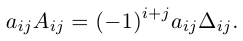

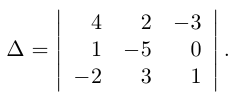
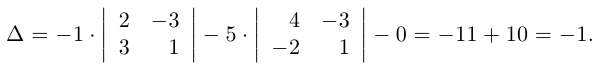

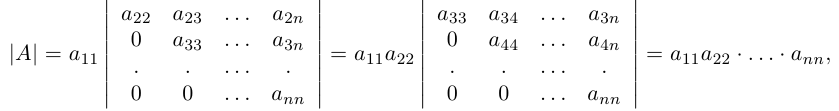
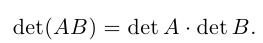
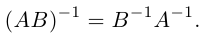
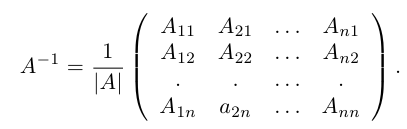
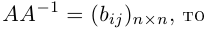
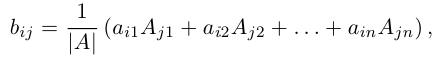
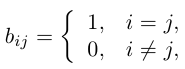
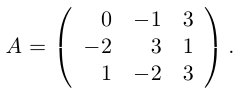
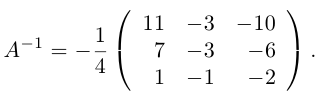
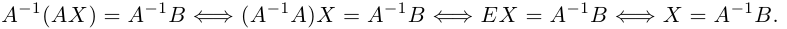
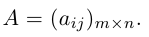
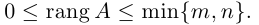
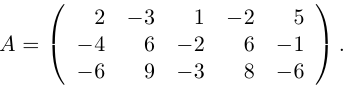
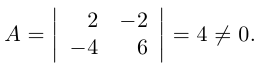

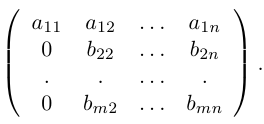
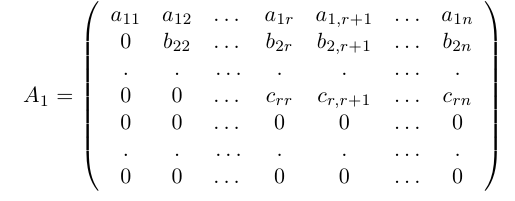
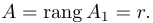
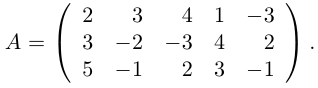
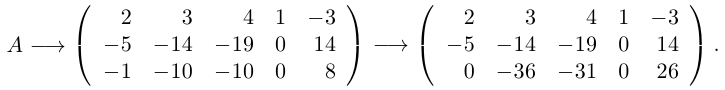
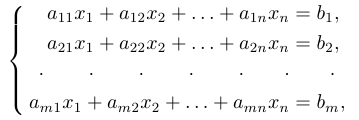
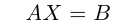
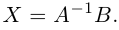
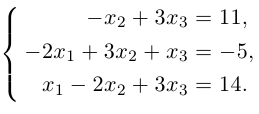
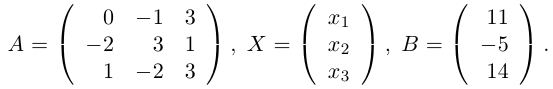
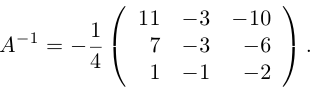
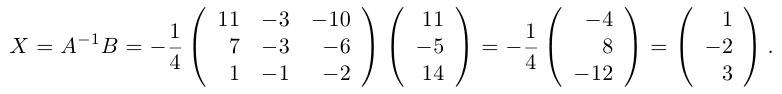

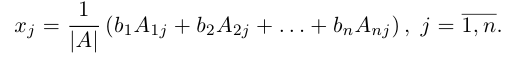
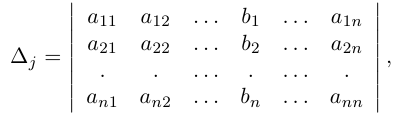
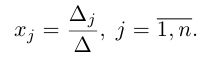
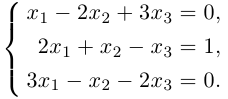
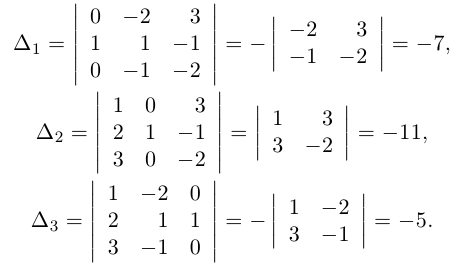
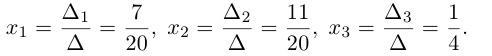
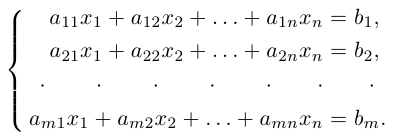
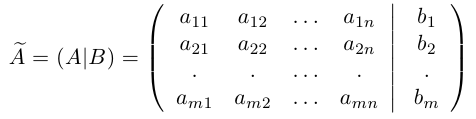
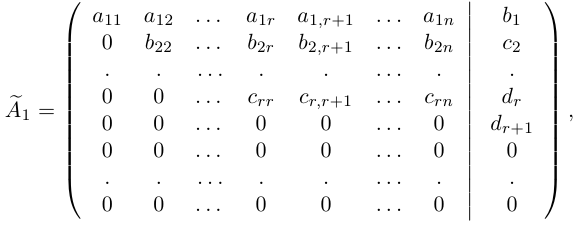
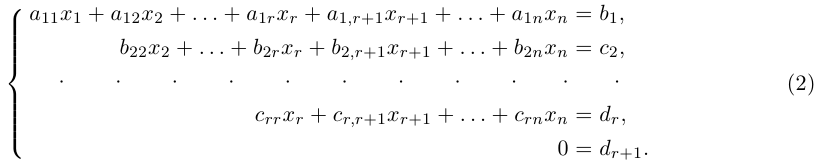
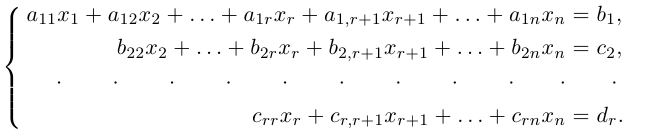
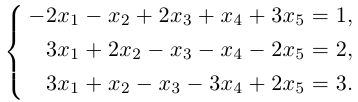

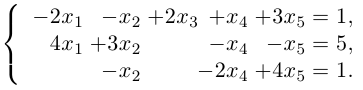
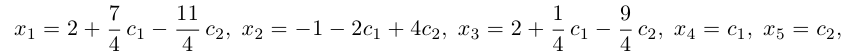
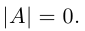
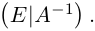
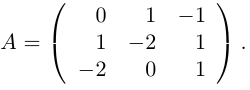

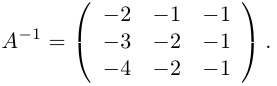
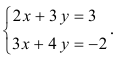
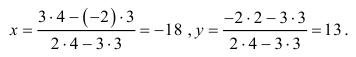
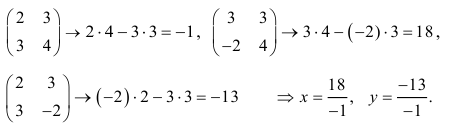
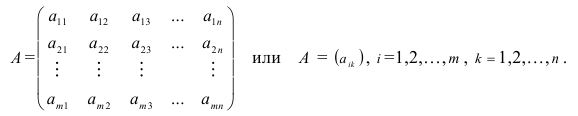
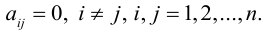
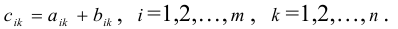
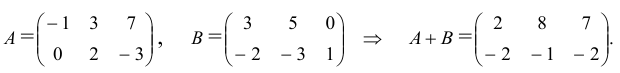
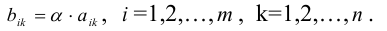

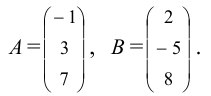
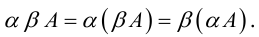
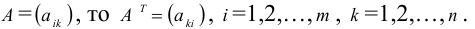
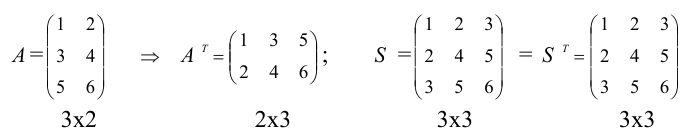
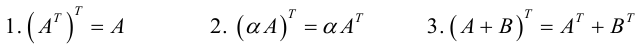
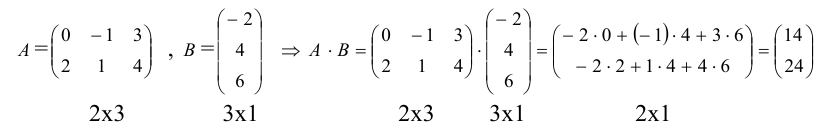
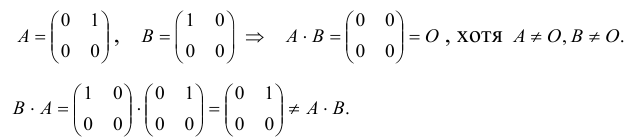
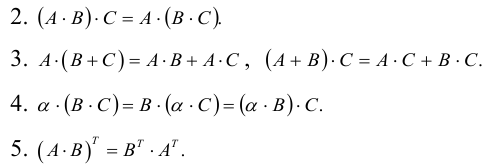
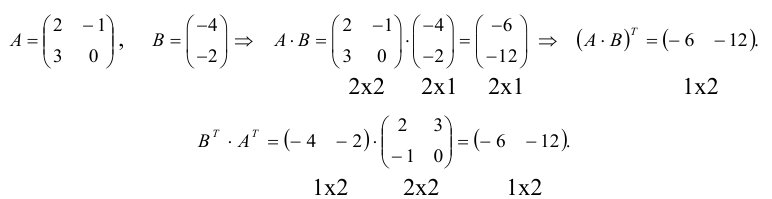
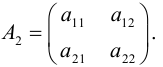
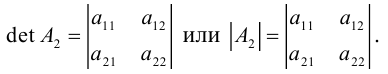
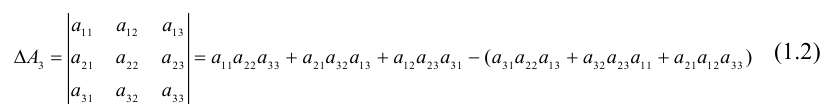
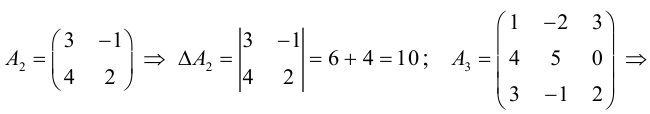
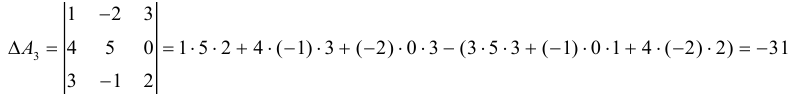
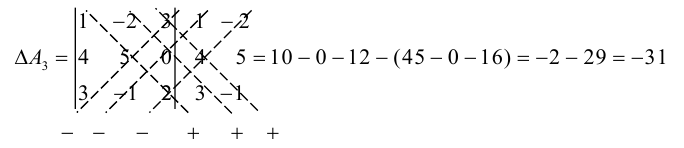
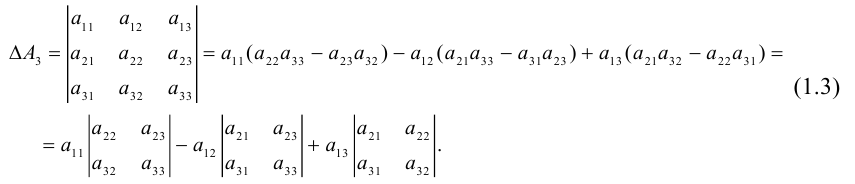
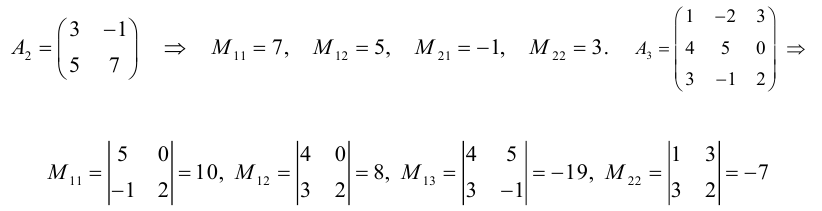
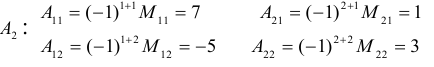
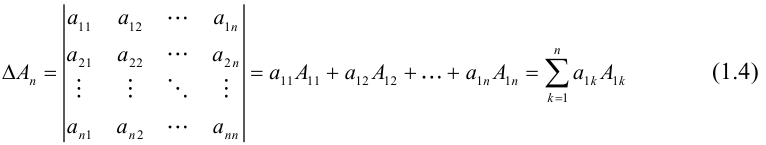
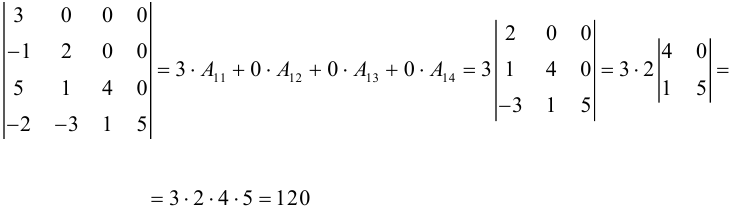
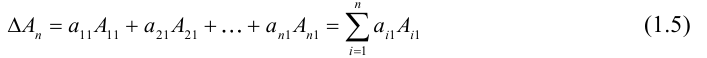
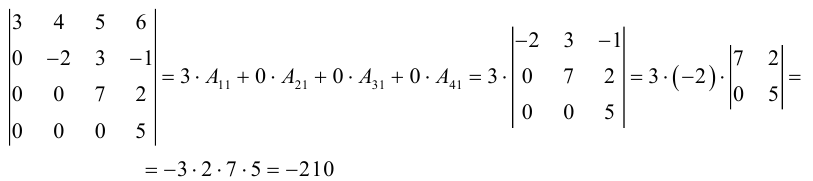
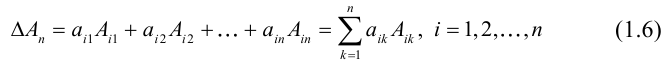
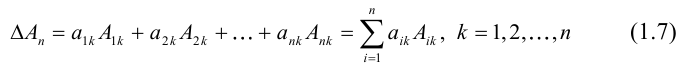

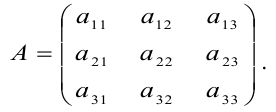
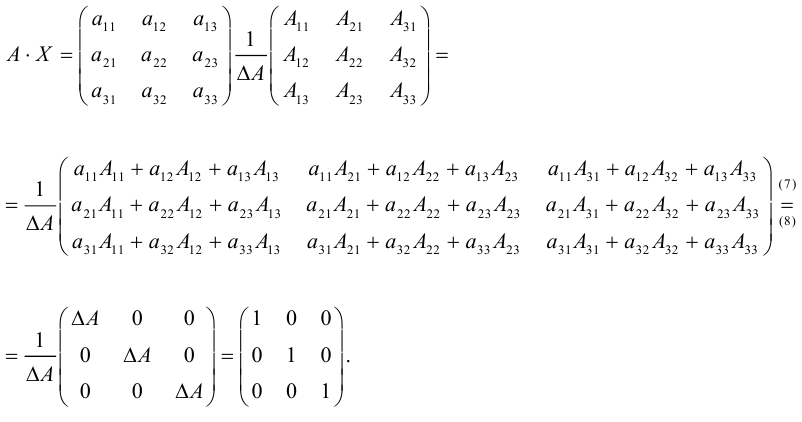

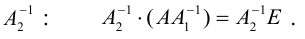

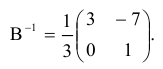
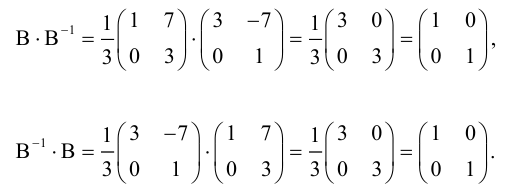
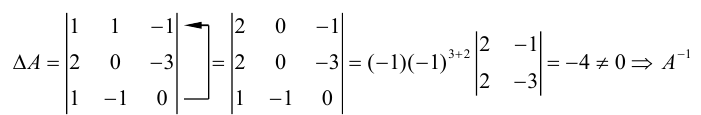
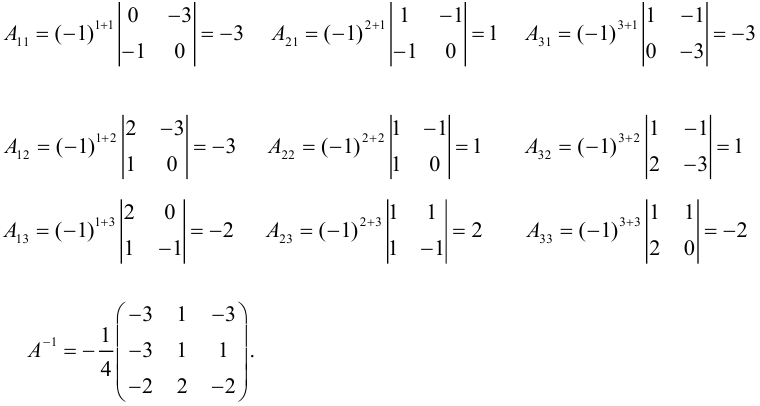
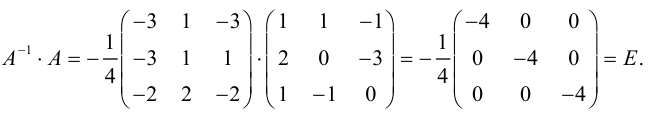
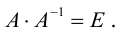
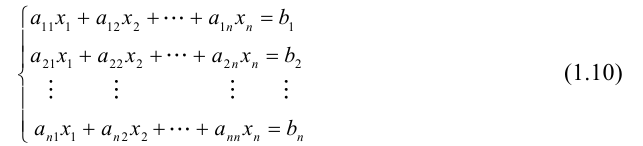
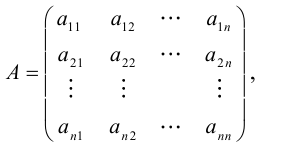

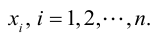
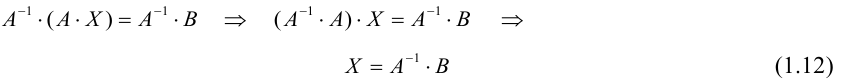
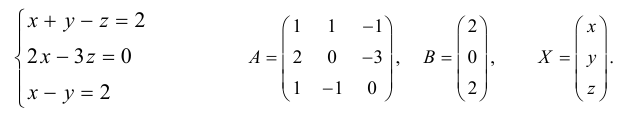
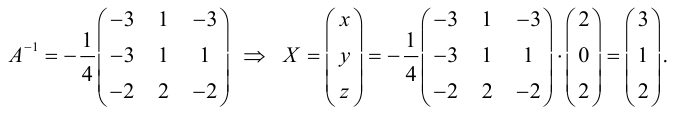
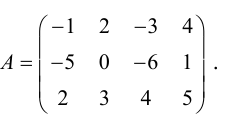
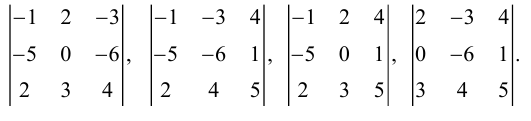
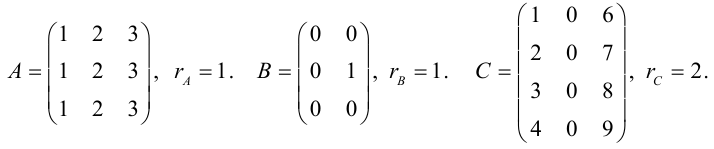
 ;
;  ;
; 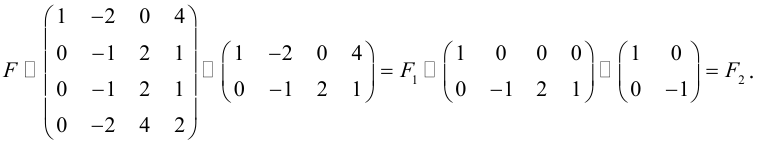
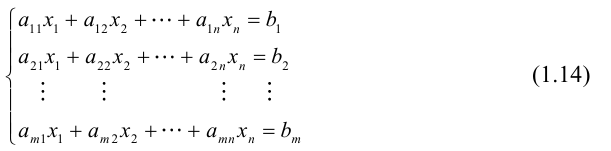
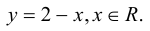
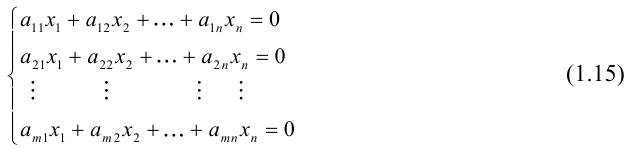
 (1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.  Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.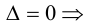 система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует. 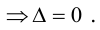 Если
Если 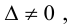 то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.