Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2021 года; проверки требуют 7 правок.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются[источник не указан 1062 дня] и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Прикладное описание понятия[править | править код]
Плотность распределения одномерной непрерывной случайной величины 





![{displaystyle [x_{1},x_{1}+Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd3360df1299dc75d795101fbbe129ae7f39d82b)
![{displaystyle [x_{2},x_{2}+Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f0f296084fe77cda39c76d8a28a502c9f8b3081)
Плотность распределения неотрицательна при любом 
При стремлении 




Если в конкретной ситуации известно выражение для 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
-
.
Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум 
Также с помощью плотности вероятности находится среднее значение случайной величины:
и среднее значение измеримой функции 
-
.
Чтобы перейти к плотности распределения 

-
,
где 

Значение плотности распределения 




Интеграл
называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция 


Самым простым распределением является равномерное распределение на отрезке ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как
-
,
где 


-
и
,
и максвелловское (
-
и
.
В двух последних примерах множитель 



Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции 




Спадающий при стремлении аргумента к 



Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность 
Определение плотности вероятности в теории меры[править | править код]
Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве 
Пусть 






Вероятность 

Если вероятность 

,
где использовано общепринятое сокращение 
В более общем виде, пусть 





то такую функцию называют плотностью меры 



.
Плотность случайной величины[править | править код]
Пусть определено произвольное вероятностное пространство 





Если распределение 



Таким образом для абсолютно непрерывной случайной величины имеем:
.
Замечания[править | править код]
- Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.
- Функция распределения абсолютно непрерывной случайной величины
непрерывна и может быть выражена через плотность следующим образом:
.
В одномерном случае:
.
Если 

.
В одномерном случае:
.
- Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:
,
где 
![mathbb{E}[g(X)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb253635a926d6c62d417eb547d9efbe4141ff70)
Плотность преобразования случайной величины[править | править код]
Пусть 






.
В одномерном случае:
.
Свойства плотности вероятности[править | править код]
- Интеграл от плотности по всему пространству равен единице:
.
Обратно, если 




- Замена меры в интеграле Лебега:
,
где 

Примеры абсолютно непрерывных распределений[править | править код]
- Бета-распределение
- Гамма-распределение
- Гиперэкспоненциальное распределение
- Двумерное нормальное распределение
- Логнормальное распределение
- Многомерное нормальное распределение
- Непрерывное равномерное распределение
- Нормальное распределение
- Обобщённое гиперболическое распределение
- Полукруговой закон Вигнера
- Распределение variance-gamma
- Распределение Вейбулла
- Распределение Гомпертца
- Распределение Колмогорова
- Распределение копулы
- Распределение Коши
- Распределение Лапласа
- Распределение Накагами
- Распределение Парето
- Распределение Пирсона
- Распределение Райса
- Распределение Рэлея
- Распределение Стьюдента
- Распределение Трейси — Видома
- Распределение Фишера
- Распределение хи-квадрат
- Частотное распределение
- Экспоненциальное распределение
См. также[править | править код]
- Распределение вероятностей
- Сингулярное распределение
- Функция вероятности
Литература[править | править код]
- Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
На практике очень
часто приходится рассматривать системы
более чем двух случайных величин. Функция
распределения системы нескольких (более
двух) случайных величин вводится как
обобщение функции распределения системы
двух случайных величин. Так, функцией
распределения системы
случайных величин
называется функция
аргументов
,
равная вероятности совместного выполнения
неравенств
,
то есть:
.
Эта функция является
неубывающей функцией каждой переменной
при фиксированных значениях других
переменных. Если хотя бы одна из переменных
стремится к
,
то функция распределения стремится к
нулю. Если все переменные стремятся к
,
то функция распределения стремится к
единице. Функция распределения каждой
из величин, входящих в систему, получится,
если в функции распределения системы
все остальные аргументы положить равными
,
например,
.
Аналогично
одномерному случаю можно вывести
формулу, связывающую функцию распределения
и плотность вероятности
:
,
или, что то же
самое,
.
Плотность
распределения системы не может быть
отрицательной:
.
Вероятность
попадания случайной точки с координатами
в
– мерную область
выражается
интегралом
.
Используя свойства
функции распределения, получаем
.
Плотность
распределения каждой из величин, входящих
в систему, получится, если плотность
распределения системы проинтегрировать
в бесконечных пределах по всем остальным
аргументам. Например,
.
10. Числовые характеристики произвольного числа случайных величин
Основными числовыми
характеристиками, с помощью которых
может быть охарактеризована система
случайных величин
,
являются следующие:
-
математические
ожидания
случайных величин, входящих в систему
,
которые в совокупности
определяют математическое ожидание
–мерного
случайного вектора;
-
дисперсии
случайных величин,
входящих в систему;
-
корреляционные
моменты
каждой пары из
случайных величин
,
характеризующие
попарно корреляцию всех случайных
величин, входящих в систему.
Зная корреляционные
моменты, можно найти коэффициенты
корреляции

которые характеризуют
степень связи между каждой парой
случайных величин.
Так как дисперсия
каждой из случайных величин системы
есть не что иное, как частный случай
корреляционного момента, а именно:
корреляционный момент величины
и той же величины
,
то все корреляционные
моменты и дисперсии располагают в виде
прямоугольной таблицы (матрицы)

которая называется
корреляционной
матрицей
системы
случайных величин.
Из определения
корреляционного момента следует, что
.
Это означает, что элементы корреляционной
матрицы, расположенные симметрично по
отношению к главной диагонали, равны.
В этой связи часто для простоты в
корреляционной матрице заполняют только
её половину (правый верхний треугольник):

Если случайные
величины системы некоррелированы, имеем
при
.
Следовательно, корреляционная матрица
системы некоррелированных случайных
величин имеет вид:
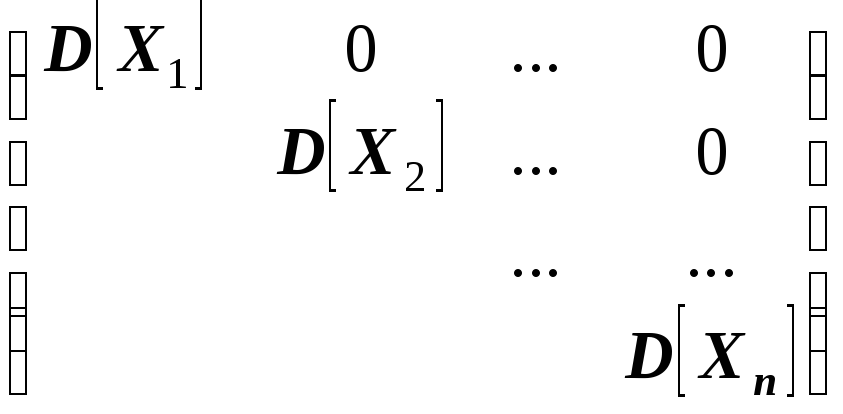
Такая матрица,
как вам известно, называется диагональной.
Вместо корреляционной матрицы часто
используют нормированную корреляционную
матрицу. Матрица, элементами которой
являются коэффициенты корреляции,
называется
нормированной корреляционной матрицей.
Все элементы главной диагонали
нормированной корреляционной матрицы
равны единице. Нормированная корреляционная
матрица имеет вид:

ЗАДАЧИ
(рассмотреть
самостоятельно)
Задача 1.
Закон распределения двумерной дискретной
случайной величины
задан таблицей
|
Y X |
– 4 |
– 2 |
0 |
|
0 |
0,1 |
0,1 |
0,2 |
|
1 |
0,1 |
0,2 |
0,1 |
|
4 |
0 |
0,1 |
0,1 |
Найти:
-
собственные законы
распределения случайных величин
и
;
-
математические
ожидания
;
-
дисперсии
;
-
корреляционный
момент
;
-
коэффициент
корреляции
;
-
закон распределения
случайной величины
при условии, что случайная величина
принимает своё наименьшее значение.
Решение.
Складывая вероятности по строкам,
получим закон распределения случайной
величины
в виде ряда распределения
|
|
0 |
1 |
4 |
|
|
|
0,4 |
0,4 |
0,2 |
|
Складывая
вероятности по столбцам, получим закон
распределения случайной величины
в виде ряда распределения
|
|
– 4 |
– 2 |
0 |
|
|
|
0,2 |
0,4 |
0,4 |
|
Найдём математические
ожидания и дисперсии составляющих:
Найдём корреляционный
момент
и коэффициент корреляции
:
Найдём закон
распределения случайной величины
при условии, что случайная величина
принимает своё наименьшее значение, то
есть при условии, что
.
Искомый закон распределения, как ранее
отмечалось, определяется совокупностью
условных вероятностей
,
где
Следовательно,
искомый закон распределения имеет вид:
|
|
0 |
1 |
4 |
|
|
0,5 |
0,5 |
0 |
Задача 2.
Вне области
плотность распределения двумерной
случайной величины
равна 0; в области
плотность распределения
.
Найти:
-
коэффициент
;
-
вероятность
,
где
;
-
одномерные
плотности распределения
;
-
математические
ожидания
;
-
дисперсии
;
-
корреляционный
момент
;
-
коэффициент
корреляции
.
Решение.
Для нахождения параметра А
воспользуемся
формулой
.
Тогда
Получим:
Найдём теперь вероятность
попадания двумерной случайной величины
в плоскую область G:
Далее, найдём
одномерные плотности распределения:
Итак:
Найдём математические
ожидания и дисперсии составляющих
1:
Далее
Тогда
Так как
,
то нетрудно вычислить

1
Предлагаем все дальнейшие вычисления
сделать самостоятельно.
11
Соседние файлы в папке Теор.вер. (лекции)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одномерные случайные величины
Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения вероятностей и ее свойства. Плотность распределения вероятности и ее свойства. Числовые характеристики случайных величин: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода и медиана; начальные и центральные моменты, асимметрия и эксцесс. Числовые характеристики среднего арифметического n независимых случайных величин.
Понятие случайной величины
Случайной называется величина, которая в результате испытаний принимает то или иное (но при этом только одно) возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. В отличие от случайного события, являющегося качественной характеристикой случайного результата испытания, случайная величина характеризует результат испытания количественно. Примерами случайной величины могут служить размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Среди случайных величин, с которыми приходится встречаться на практике, можно выделить два основных типа: дискретные и непрерывные.
Дискретной называется случайная величина, принимающая конечное или бесконечное счетное множество значений. Например: частота попаданий при трех выстрелах; число бракованных изделий в партии из штук; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов прибора за определенный промежуток времени при испытании его на надежность; число выстрелов до первого попадания в цель и т. д.
Непрерывной называется случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Очевидно, что число возможных значений непрерывной случайной величины бесконечно. Например: ошибка при измерении дальности радиолокатора; время безотказной работы микросхемы; погрешность изготовления деталей; концентрация соли в морской воде и т. д.
Случайные величины обычно обозначают буквами и т. д., а их возможные значения —
и т. д. Для задания случайной величины недостаточно перечислить все ее возможные значения. Необходимо также знать, как часто могут появиться те или иные ее значения в результате испытаний при одних и тех же условиях, т. е. нужно задать вероятности их появления. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
Законы распределения случайной величины
Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.
Закон распределения случайной величины может быть задан в виде таблицы, функции распределения либо плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины.
Табличное задание закона распределения можно использовать только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.
Для наглядности ряд распределения представляют графически. При графическом изображении в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат — соответствующие вероятности. Точки , соединенные прямолинейными отрезками, называют многоугольником распределения (рис. 5). Следует помнить, что соединение точек
выполняется только с целью наглядности, так как в промежутках между
и
,
и
и т. д. не существует значений, которые может принимать случайная величина
, поэтому вероятности её появления в этих промежутках равны нулю.
Многоугольник распределения, как и ряд распределения, является одной из форм задания закона распределения дискретной случайной величины. Они могут иметь различную форму, однако все обладают одним общим свойством: сумма ординат вершин многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Это свойство следует из того, что все возможные значения случайной величины образуют полную группу несовместных событий, сумма вероятностей которых равна единице.
Функция распределения вероятностей и ее свойства
Функция распределения является наиболее общей формой задания закона распределения. Она используется для задания как дискретных, так и непрерывных случайных величин. Обычно ее обозначают . Функция распределения определяет вероятность того, что случайная величина
принимает значения, меньшие фиксированного действительного числа
, т. е.
. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения. Ее еще называют интегральной функцией распределения.
Геометрическая интерпретация функции распределения очень проста. Если случайную величину рассматривать как случайную точку оси
(рис. 6), которая в результате испытания может занять то или иное положение на оси, то функция распределения
— это вероятность того, что случайная точка
в результате испытания попадет левее точки
.
Для дискретной случайной величины , которая может принимать значения
, функция распределения имеет вид
где неравенство означает, что суммирование распространяется на все значения
, меньше
. Из этой формулы следует, что функция распределения дискретной случайной величины представляет собой ступенчатую ломаную линию (рис. 7). При каждом новом значении случайной величины ступень поднимается выше на величину, равную вероятности этого значения. Сумма всех скачков функции распределения равна единице.
Непрерывная случайная величина имеет непрерывную функцию распределения, график этой функции имеет форму плавной кривой (рис. 8 ).
Рассмотрим общие свойства функций распределения.
Свойство 1. Функция распределения — неотрицательная, функция, заключенная между нулем и единицей:
Справедливость этого свойства вытекает из того, что функция распределения определена как вероятность случайного события, состоящего в том, что
.
Свойство 2. Вероятность попадания случайной величины в интервал равна разности значений функции распределения на концах этого интервала, т. е.
Отсюда следует, что вероятность любого отдельного значения непрерывной случайной величины равна нулю.
Свойство 3. Функция распределения случайной величины есть неубывающая функция, т. е. .
Свойство 4. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности — единице, т. е. и
.
Пример 1. Функция распределения непрерывной случайной величины задана выражением
Найти коэффициент и построить график
. Определить вероятность того, что случайная величина
в результате опыта примет значение на интервале
.
Решение. Так как функция распределения непрерывной случайной величины непрерывна, то при
получим
. Отсюда
. График функции
изображен на рис. 9.
Исходя из второго свойства функции распределения, имеем
Плотность распределения вероятности и ее свойства
Функция распределения непрерывной случайной величины является ее вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения случайной величины в небольшой окрестности той или другой точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины дает функция, которая называется плотностью распределения вероятности, или дифференциальной функцией распределения случайной величины.
Плотность распределения равна производной от функции распределения
, т. е.
Смысл плотности распределения состоит в том, что она указывает на то, как часто случайная величина
появляется в некоторой окрестности точки
при повторении опытов. Кривая, изображающая плотность распределения
случайной величины, называется кривой распределения.
Рассмотрим свойства плотности распределения.
Свойство 1. Плотность распределения неотрицательна, т. е.
Свойство 2. Функция распределения случайной величины равна интегралу от плотности в интервале от до
, т. е.
Свойство 3. Вероятность попадания непрерывной случайной величины на участок
равна интегралу от плотности распределения, взятому по этому участку, т. е.
Свойство 4. Интеграл в бесконечных пределах от плотности распределения равен единице:
Пример 2. Случайная величина подчинена закону распределения с плотностью
Определить коэффициент а; построить график плотности распределения; найти вероятность попадания случайной величины на участок от до
определить функцию распределения и построить ее график.
Решение. Площадь, ограниченная кривой распределения, численно равна
Учитывая свойство 4 плотности распределения, находим . Следовательно, плотность распределения можно выразить так:
График плотности распределения на рис. 10. По свойству 3, имеем
Для определения функции распределения воспользуемся свойством 2:
Таким образом, имеем
График функции распределения изображен на рис. 11
Числовые характеристики случайных величин
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются математическое ожидание, дисперсия, моменты различных порядков, мода и медиана.
Математическое ожидание иногда называют средним значением случайной величины. Рассмотрим дискретную случайную величину , принимающую значения
с вероятностями соответственно
Определим среднюю арифметическую значений случайной величины, взвешенных по вероятностям их появлений. Таким образом, вычислим среднее значение случайной величины, или ее математическое ожидание
:
Учитывая, что получаем
Итак, математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.
Для непрерывной случайной величины математическое ожидание
Математическое ожидание непрерывной случайной величины , возможные значения которой принадлежат отрезку
,
Используя функцию распределения вероятностей , математическое ожидание случайной величины можно выразить так:
Свойства математического ожидания
Свойство 1. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
Свойство 2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
Свойство 3. Математическое ожидание постоянной величины равно самой постоянной:
Свойство 4. Постоянный множитель случайной величины можно вынести за знак математического ожидания:
Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример 3. Найти математическое ожидание количества бракованных изделий в выборке из пяти изделий, если случайная величина (количество бракованных изделий) задана рядом распределения.
Решение. По формуле (4.1) находим
Модой дискретной случайной величины называется наиболее вероятное ее значение.
Модой непрерывной случайной величины называется такое ее значение, которому соответствует наибольшее значение плотности распределения. Геометрически моду интерпретируют как абсциссу точки глобального максимума кривой распределения (рис. 12).
Медианой случайной величины называется такое ее значение, для которого справедливо равенство
С геометрической точки зрения медиана — это абсцисса точки, в которой площадь фигуры, ограниченной кривой распределения вероятностей и осью абсцисс, делится пополам (рис. 12). Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, то функция распределения в точке, соответствующей медиане, равна 0,5, т. е.
С помощью дисперсии и среднеквадратического отклонения можно судить о рассеивании случайной величины вокруг математического ожидания. В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины и обозначают
:
Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующие вероятности:
Для непрерывной случайной величины, закон распределения которой задан плотностью распределения вероятности , дисперсия
Размерность дисперсии равна квадрату размерности случайной величины и поэтому ее нельзя интерпретировать геометрически. Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое вычисляется по формуле
Свойства дисперсии случайных величин
Свойство 1. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Свойство 2. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
Свойство 3. Дисперсия постоянной величины равна нулю:
Свойство 4. Постоянный множитель случайной величины, можно выносить за знак дисперсии, предварительно возведя его в квадрат:
Свойство 5. Дисперсия произведения двух независимых случайных величин и
определяется по формуле
Пример 4. Вычислить дисперсию количества бракованных изделий для распределения примера 3.
Решение. По определению дисперсии
Обобщением основных числовых характеристик случайной величины является понятие моментов случайной величины.
Начальным моментом q-го порядка случайной величины называют математическое ожидание величины :
Начальный момент дискретной случайной величины
начальный момент непрерывной случайной величины
Центральным моментом q-го порядка случайной величины называют математическое ожидание величины :
Центральный момент дискретной случайной величины
центральный момент непрерывной случайной величины
Начальный момент первого порядка представляет собой математическое ожидание, а центральный момент второго порядка — дисперсию случайной величины.
Нормированный центральный момент третьего порядка служит характеристикой скошенности или асимметрии распределения (коэффициент асимметрии):
Нормированный центральный момент четвертого порядка служит характеристикой островершинности или плосковершинности распределения (эксцесс):
Пример 5. Случайная величина задана плотностью распределения вероятностей
Найти коэффициент , математическое ожидание, дисперсию, асимметрию и эксцесс.
Решение. Площадь, ограниченная кривой распределения, численно равна
Учитывая, что эта площадь должна быть равна единице, находим . По формуле (4.2) найдем математическое ожидание:
Дисперсию определим по формуле (4.3). Для этого найдем сначала математическое ожидание квадрата случайной величины:
Таким образом,
Используя начальные моменты, вычисляем центральные моменты третьего и четвертого порядка:
Числовые характеристики среднего арифметического n независимых случайных величин
Пусть — значения случайной величины
, полученные при
независимых испытаниях. Математическое ожидание случайной величины равно
, а ее дисперсия
. Эти значения можно рассматривать как независимые случайные величины
с одинаковыми математическими ожиданиями и дисперсиями:
Средняя арифметическая этих случайных величин
Используя свойства математического ожидания и дисперсии случайной величины, можно записать:
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Geometric visualisation of the mode, median and mean of an arbitrary unimodal probability density function.[1]
In probability theory, a probability density function (PDF), or density of an absolutely continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample.[2][3] Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.
In a more precise sense, the PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on any one value. This probability is given by the integral of this variable’s PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and the area under the entire curve is equal to 1.
The terms probability distribution function and probability function have also sometimes been used to denote the probability density function. However, this use is not standard among probabilists and statisticians. In other sources, “probability distribution function” may be used when the probability distribution is defined as a function over general sets of values or it may refer to the cumulative distribution function, or it may be a probability mass function (PMF) rather than the density. “Density function” itself is also used for the probability mass function, leading to further confusion.[4] In general though, the PMF is used in the context of discrete random variables (random variables that take values on a countable set), while the PDF is used in the context of continuous random variables.
Example[edit]
Suppose bacteria of a certain species typically live 4 to 6 hours. The probability that a bacterium lives exactly 5 hours is equal to zero. A lot of bacteria live for approximately 5 hours, but there is no chance that any given bacterium dies at exactly 5.00… hours. However, the probability that the bacterium dies between 5 hours and 5.01 hours is quantifiable. Suppose the answer is 0.02 (i.e., 2%). Then, the probability that the bacterium dies between 5 hours and 5.001 hours should be about 0.002, since this time interval is one-tenth as long as the previous. The probability that the bacterium dies between 5 hours and 5.0001 hours should be about 0.0002, and so on.
In this example, the ratio (probability of dying during an interval) / (duration of the interval) is approximately constant, and equal to 2 per hour (or 2 hour−1). For example, there is 0.02 probability of dying in the 0.01-hour interval between 5 and 5.01 hours, and (0.02 probability / 0.01 hours) = 2 hour−1. This quantity 2 hour−1 is called the probability density for dying at around 5 hours. Therefore, the probability that the bacterium dies at 5 hours can be written as (2 hour−1) dt. This is the probability that the bacterium dies within an infinitesimal window of time around 5 hours, where dt is the duration of this window. For example, the probability that it lives longer than 5 hours, but shorter than (5 hours + 1 nanosecond), is (2 hour−1)×(1 nanosecond) ≈ 6×10−13 (using the unit conversion 3.6×1012 nanoseconds = 1 hour).
There is a probability density function f with f(5 hours) = 2 hour−1. The integral of f over any window of time (not only infinitesimal windows but also large windows) is the probability that the bacterium dies in that window.
Absolutely continuous univariate distributions[edit]
A probability density function is most commonly associated with absolutely continuous univariate distributions. A random variable 


Hence, if 

and (if 

Intuitively, one can think of 

![[x,x+dx]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f07271dbe3f8967834a2eaf143decd7e41c61d7a)
Formal definition[edit]
(This definition may be extended to any probability distribution using the measure-theoretic definition of probability.)
A random variable 






That is, f is any measurable function with the property that:
for any measurable set
Discussion[edit]
In the continuous univariate case above, the reference measure is the Lebesgue measure. The probability mass function of a discrete random variable is the density with respect to the counting measure over the sample space (usually the set of integers, or some subset thereof).
It is not possible to define a density with reference to an arbitrary measure (e.g. one can’t choose the counting measure as a reference for a continuous random variable). Furthermore, when it does exist, the density is almost unique, meaning that any two such densities coincide almost everywhere.
Further details[edit]
Unlike a probability, a probability density function can take on values greater than one; for example, the uniform distribution on the interval [0, 1/2] has probability density f(x) = 2 for 0 ≤ x ≤ 1/2 and f(x) = 0 elsewhere.
The standard normal distribution has probability density
If a random variable X is given and its distribution admits a probability density function f, then the expected value of X (if the expected value exists) can be calculated as
Not every probability distribution has a density function: the distributions of discrete random variables do not; nor does the Cantor distribution, even though it has no discrete component, i.e., does not assign positive probability to any individual point.
A distribution has a density function if and only if its cumulative distribution function F(x) is absolutely continuous. In this case: F is almost everywhere differentiable, and its derivative can be used as probability density:
If a probability distribution admits a density, then the probability of every one-point set {a} is zero; the same holds for finite and countable sets.
Two probability densities f and g represent the same probability distribution precisely if they differ only on a set of Lebesgue measure zero.
In the field of statistical physics, a non-formal reformulation of the relation above between the derivative of the cumulative distribution function and the probability density function is generally used as the definition of the probability density function. This alternate definition is the following:
If dt is an infinitely small number, the probability that X is included within the interval (t, t + dt) is equal to f(t) dt, or:
Link between discrete and continuous distributions[edit]
It is possible to represent certain discrete random variables as well as random variables involving both a continuous and a discrete part with a generalized probability density function using the Dirac delta function. (This is not possible with a probability density function in the sense defined above, it may be done with a distribution.) For example, consider a binary discrete random variable having the Rademacher distribution—that is, taking −1 or 1 for values, with probability 1⁄2 each. The density of probability associated with this variable is:
More generally, if a discrete variable can take n different values among real numbers, then the associated probability density function is:
where 

This substantially unifies the treatment of discrete and continuous probability distributions. The above expression allows for determining statistical characteristics of such a discrete variable (such as the mean, variance, and kurtosis), starting from the formulas given for a continuous distribution of the probability.
Families of densities[edit]
It is common for probability density functions (and probability mass functions) to be parametrized—that is, to be characterized by unspecified parameters. For example, the normal distribution is parametrized in terms of the mean and the variance, denoted by 

Different values of the parameters describe different distributions of different random variables on the same sample space (the same set of all possible values of the variable); this sample space is the domain of the family of random variables that this family of distributions describes. A given set of parameters describes a single distribution within the family sharing the functional form of the density. From the perspective of a given distribution, the parameters are constants, and terms in a density function that contain only parameters, but not variables, are part of the normalization factor of a distribution (the multiplicative factor that ensures that the area under the density—the probability of something in the domain occurring— equals 1). This normalization factor is outside the kernel of the distribution.
Since the parameters are constants, reparametrizing a density in terms of different parameters to give a characterization of a different random variable in the family, means simply substituting the new parameter values into the formula in place of the old ones.
Densities associated with multiple variables[edit]
For continuous random variables X1, …, Xn, it is also possible to define a probability density function associated to the set as a whole, often called joint probability density function. This density function is defined as a function of the n variables, such that, for any domain D in the n-dimensional space of the values of the variables X1, …, Xn, the probability that a realisation of the set variables falls inside the domain D is
If F(x1, …, xn) = Pr(X1 ≤ x1, …, Xn ≤ xn) is the cumulative distribution function of the vector (X1, …, Xn), then the joint probability density function can be computed as a partial derivative
Marginal densities[edit]
For i = 1, 2, …, n, let fXi(xi) be the probability density function associated with variable Xi alone. This is called the marginal density function, and can be deduced from the probability density associated with the random variables X1, …, Xn by integrating over all values of the other n − 1 variables:
Independence[edit]
Continuous random variables X1, …, Xn admitting a joint density are all independent from each other if and only if
Corollary[edit]
If the joint probability density function of a vector of n random variables can be factored into a product of n functions of one variable
(where each fi is not necessarily a density) then the n variables in the set are all independent from each other, and the marginal probability density function of each of them is given by
Example[edit]
This elementary example illustrates the above definition of multidimensional probability density functions in the simple case of a function of a set of two variables. Let us call 

Function of random variables and change of variables in the probability density function[edit]
If the probability density function of a random variable (or vector) X is given as fX(x), it is possible (but often not necessary; see below) to calculate the probability density function of some variable Y = g(X). This is also called a “change of variable” and is in practice used to generate a random variable of arbitrary shape fg(X) = fY using a known (for instance, uniform) random number generator.
It is tempting to think that in order to find the expected value E(g(X)), one must first find the probability density fg(X) of the new random variable Y = g(X). However, rather than computing
one may find instead
The values of the two integrals are the same in all cases in which both X and g(X) actually have probability density functions. It is not necessary that g be a one-to-one function. In some cases the latter integral is computed much more easily than the former. See Law of the unconscious statistician.
Scalar to scalar[edit]
Let 
Here g−1 denotes the inverse function.
This follows from the fact that the probability contained in a differential area must be invariant under change of variables. That is,
or
For functions that are not monotonic, the probability density function for y is
where n(y) is the number of solutions in x for the equation 

Vector to vector[edit]
Suppose x is an n-dimensional random variable with joint density f. If y = H(x), where H is a bijective, differentiable function, then y has density g:
with the differential regarded as the Jacobian of the inverse of H(⋅), evaluated at y.[5]
For example, in the 2-dimensional case x = (x1, x2), suppose the transform H is given as y1 = H1(x1, x2), y2 = H2(x1, x2) with inverses x1 = H1−1(y1, y2), x2 = H2−1(y1, y2). The joint distribution for y = (y1, y2) has density[6]
Vector to scalar[edit]
Let 







This result leads to the law of the unconscious statistician:
Proof:
Let 



It is clear that 

which is an upper triangular matrix with ones on the main diagonal, therefore its determinant is 1. Applying the change of variable theorem from the previous section we obtain that
which if marginalized over 
Sums of independent random variables[edit]
The probability density function of the sum of two independent random variables U and V, each of which has a probability density function, is the convolution of their separate density functions:
It is possible to generalize the previous relation to a sum of N independent random variables, with densities U1, …, UN:
This can be derived from a two-way change of variables involving Y = U + V and Z = V, similarly to the example below for the quotient of independent random variables.
Products and quotients of independent random variables[edit]
Given two independent random variables U and V, each of which has a probability density function, the density of the product Y = UV and quotient Y = U/V can be computed by a change of variables.
Example: Quotient distribution[edit]
To compute the quotient Y = U/V of two independent random variables U and V, define the following transformation:
Then, the joint density p(y,z) can be computed by a change of variables from U,V to Y,Z, and Y can be derived by marginalizing out Z from the joint density.
The inverse transformation is
The absolute value of the Jacobian matrix determinant 
Thus:
And the distribution of Y can be computed by marginalizing out Z:
This method crucially requires that the transformation from U,V to Y,Z be bijective. The above transformation meets this because Z can be mapped directly back to V, and for a given V the quotient U/V is monotonic. This is similarly the case for the sum U + V, difference U − V and product UV.
Exactly the same method can be used to compute the distribution of other functions of multiple independent random variables.
Example: Quotient of two standard normals[edit]
Given two standard normal variables U and V, the quotient can be computed as follows. First, the variables have the following density functions:
We transform as described above:
This leads to:
This is the density of a standard Cauchy distribution.
See also[edit]
- Density estimation
- Kernel density estimation
- Likelihood function
- List of probability distributions
- Probability amplitude
- Probability mass function
- Secondary measure
- Uses as position probability density:
- Atomic orbital
- Home range
References[edit]
- ^ “AP Statistics Review – Density Curves and the Normal Distributions”. Archived from the original on 2 April 2015. Retrieved 16 March 2015.
- ^ Grinstead, Charles M.; Snell, J. Laurie (2009). “Conditional Probability – Discrete Conditional” (PDF). Grinstead & Snell’s Introduction to Probability. Orange Grove Texts. ISBN 978-1616100469. Archived (PDF) from the original on 2003-04-25. Retrieved 2019-07-25.
- ^ “probability – Is a uniformly random number over the real line a valid distribution?”. Cross Validated. Retrieved 2021-10-06.
- ^ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (for example, Table 5.1 and Example 5.4)
- ^ Devore, Jay L.; Berk, Kenneth N. (2007). Modern Mathematical Statistics with Applications. Cengage. p. 263. ISBN 978-0-534-40473-4.
- ^ David, Stirzaker (2007-01-01). Elementary Probability. Cambridge University Press. ISBN 978-0521534284. OCLC 851313783.
Further reading[edit]
- Billingsley, Patrick (1979). Probability and Measure. New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
- Casella, George; Berger, Roger L. (2002). Statistical Inference (Second ed.). Thomson Learning. pp. 34–37. ISBN 0-534-24312-6.
- Stirzaker, David (2003). Elementary Probability. ISBN 0-521-42028-8. Chapters 7 to 9 are about continuous variables.
External links[edit]
- Ushakov, N.G. (2001) [1994], “Density of a probability distribution”, Encyclopedia of Mathematics, EMS Press
- Weisstein, Eric W. “Probability density function”. MathWorld.
Плотность распределения вероятностей непрерывной случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).
Плотностью распределения вероятностей непрерывной случайной величины
называют функцию
– первую производную от функции распределения
:
Из этого определения следует, что
функция распределения является первообразной для плотности распределения.
Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.
Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина
примет
значение, принадлежащее интервалу
равна
определенному интегралу от плотности распределения, взятому в пределах от
до
:
Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу
, равна площади криволинейной трапеции, ограниченной
осью
, кривой распределения
и прямыми
и
.
В частности, если
– четная
функция и концы интервала симметричны относительно начала координат, то:
Зная плотность распределения
можно найти
функцию распределения
по формуле:
Свойства плотности распределения
Свойство 1.
Плотность
распределения – неотрицательная функция:
Свойство 2.
Несобственный
интеграл от плотности распределения в пределах от
до
равен единице:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Интегральная функция распределения вероятностей
Примеры решения задач
Пример 1
Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики F(x) и f(x);
4) найти
математическое ожидание и дисперсию X;
5) найти
вероятность того, что X примет значение из
интервала (α,β):
α=1; β=1.7
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда
принадлежит
интервалу
.
Получаем:
3) Построим графики
и
:
График плотности распределения
График функции распределения
4)
Математическое ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
5)
Вероятность того, что случайная величина примет значение из интервала
:
Пример 2
Плотность
распределения вероятности непрерывной случайной величины равна
, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).
Решение
Нормировочный множитель
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
Пример 3
Непрерывная
случайная величина
имеет плотность распределения:
Найти
величину a, вероятность P(X<0) и математическое
ожидание X.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Постоянный
параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности имеет вид:
Вероятность:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Задачи контрольных и самостоятельных работ
Задача 1
Плотность
распределения непрерывной случайной величины X имеет вид:
Найти:
а)
параметр a;
б)
функцию распределения F(x);
в)
вероятность попадания случайной величины X в интервал (6.5; 11);
г)
математическое ожидание M(X) и дисперсию D(X);
Построить
график функций f(x) и F(x).
Задача 2
Задана
функция распределения непрерывной случайной величины:
Найти и
построить график функции плотности распределения вероятностей.
Задача 3
Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).
Задача 4
Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).
α=1,β=2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 5
Непрерывная
случайная величина
задана плотностью распределения вероятностей.
Требуется
найти:
– функцию
распределения вероятностей;
–
математическое ожидание;
–
дисперсию;
– среднее
квадратическое отклонение;
– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;
–
построить графики функции распределения и плотности распределения вероятностей.
Задача 6
Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).
Задача 7
Случайная
величина X~N(a,σ)
a=25;
σ=4; α=13; β=30; δ=0.1.
Требуется:
–
составить функцию плотности распределения и построить ее график;
– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);
– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.
Задача 8
Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:
Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Случайная
величина X задана функцией распределения вероятностей F(x).
Требуется:
1. Найти
функцию плотности распределения f(x).
2. Найти M(X).
3. Найти
вероятность P(α<X<β)
4.
Построить графики f(x) и F(x).
α=2, β=4.5
Задача 10
Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).
M(X)=-1; D(X)=8
Задача 11
Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:
а) найти
параметр C;
б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);
в)
построить графики функций F(x) и f(x);
г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);
д)
вычислить вероятность попадания в интервал P(a≤x≤b)
е)
определить, квантилем какого порядка является точка xp;
ж)
вычислить квантиль порядка p
a=π/4; b=π/3; xp=π/2; p=0.75
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ


![{displaystyle P(xi in [a,b])=int _{a}^{b}f(x),{mbox{d}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f5d450b65bc2c713a3cd16d466e686244cd45e9)





![{displaystyle f(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565bc74e74e3f0519d2d586641f56b5fa710c651)

![{displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma }}exp left[-{frac {(x-mu )^{2}}{2sigma ^{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3778189b53134af9f4d6d92d6566660fe3e55d)
![{displaystyle f(x)=Aexp left[-lambda ,xright],,(xgeq 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83655fcbe56b69c48f4efc7b587e3aafbd650351)

![{displaystyle f(x)=Ax^{2}exp left[-alpha x^{2}right],,(xgeq 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8572c117d42337da967269cff21493a2009b45a)





![F_X(x_1,ldots, x_n) = mathbb{P}left(X in prodlimits_{i=1}^n (-infty,x_i]right) = intlimits_{-infty}^{x_n} !! ldots !! intlimits_{-infty}^{x_1} f_X(x'_1,ldots, x'_n), dx'_1ldots dx'_n](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a7b60ccb54e84544d3be234eec312f5ce76b20e)



![mathbb{E}[g(X)] = intlimits_{mathbb{R}^n} g(x) , mathbb{P}^X(dx) = intlimits_{mathbb{R}^n} g(x), f_X(x), dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbf21213a347e4cba3843602fcd32b9e939b0197)








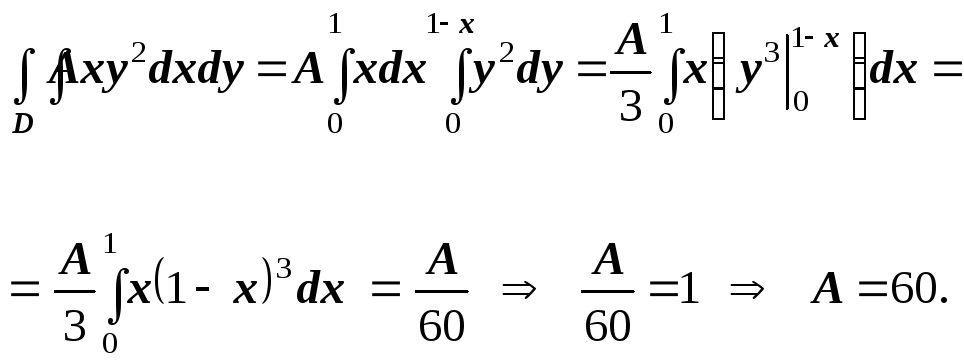





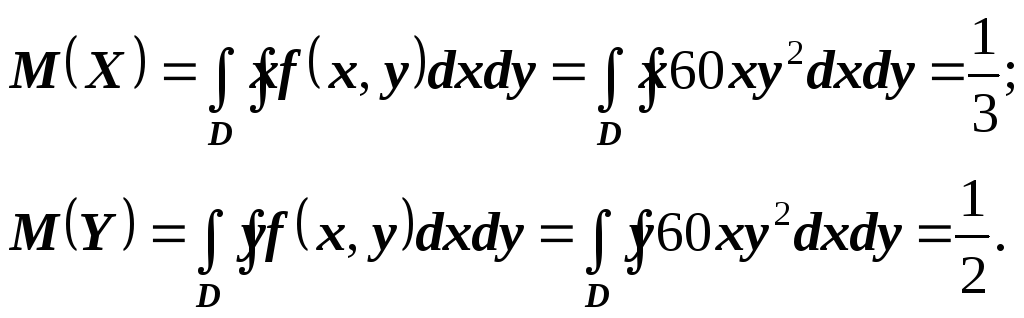



![{displaystyle Pr[aleq Xleq b]=int _{a}^{b}f_{X}(x),dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fd7691b5fbd323f64834d8e5b8d4f54c73a6f8)



![{displaystyle Pr[Xin A]=int _{X^{-1}A},dP=int _{A}f,dmu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/591b4a96fefea18b28fe8eb36d3469ad6b33a9db)


![{displaystyle operatorname {E} [X]=int _{-infty }^{infty }x,f(x),dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00ce7a00fac378eafc98afb88de88d619e15e996)


















![{displaystyle g(mathbf {y} )=f{Bigl (}H^{-1}(mathbf {y} ){Bigr )}left|det left[left.{frac {dH^{-1}(mathbf {z} )}{dmathbf {z} }}right|_{mathbf {z} =mathbf {y} }right]right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732bd3920089d7177a63016ab1717b6e0a56b654)


![{displaystyle operatorname {E} _{Y}[Y]=int _{mathbb {R} }yf_{Y}(y),dy=int _{mathbb {R} }yint _{mathbb {R} ^{n}}f_{X}(mathbf {x} )delta {big (}y-V(mathbf {x} ){big )},dmathbf {x} ,dy=int _{{mathbb {R} }^{n}}int _{mathbb {R} }yf_{X}(mathbf {x} )delta {big (}y-V(mathbf {x} ){big )},dy,dmathbf {x} =int _{mathbb {R} ^{n}}V(mathbf {x} )f_{X}(mathbf {x} ),dmathbf {x} =operatorname {E} _{X}[V(X)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad5325e96f2d76c533cb1a21d2095e8cf16e6fc7)














![{displaystyle {begin{aligned}p(y)&=int _{-infty }^{infty }p_{U}(yz),p_{V}(z),|z|,dz\[5pt]&=int _{-infty }^{infty }{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}y^{2}z^{2}}{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}z^{2}}|z|,dz\[5pt]&=int _{-infty }^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}left(y^{2}+1right)z^{2}}|z|,dz\[5pt]&=2int _{0}^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}left(y^{2}+1right)z^{2}}z,dz\[5pt]&=int _{0}^{infty }{frac {1}{pi }}e^{-left(y^{2}+1right)u},du&&u={tfrac {1}{2}}z^{2}\[5pt]&=left.-{frac {1}{pi left(y^{2}+1right)}}e^{-left(y^{2}+1right)u}right|_{u=0}^{infty }\[5pt]&={frac {1}{pi left(y^{2}+1right)}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63983efb2501c35f094487a9c6473a30e9405551)
