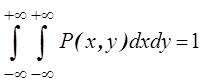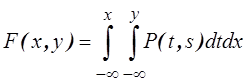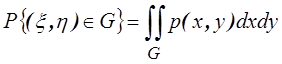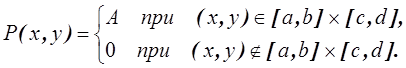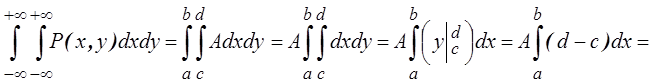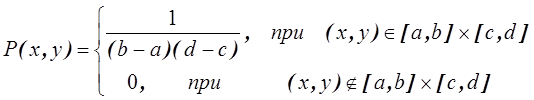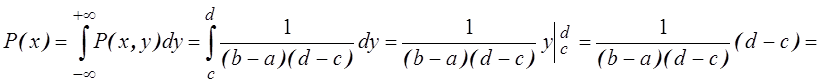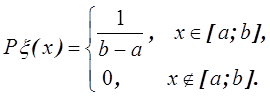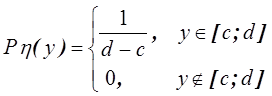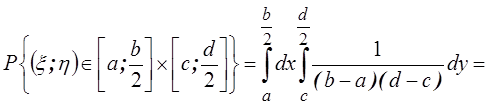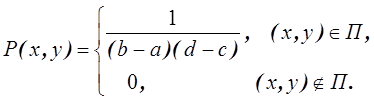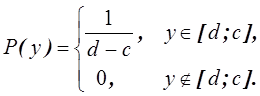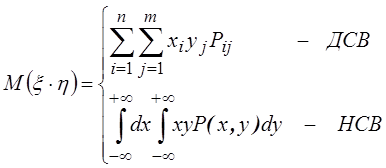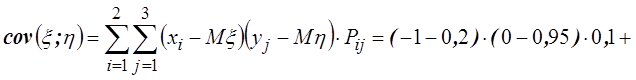Как найти одномерные законы

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

 и

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

 на плоскости

 либо как случайный вектор

.

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

 получим вероятность

.

Пусть
составляющие

 и

 дискретны и имеют соответственно следующие
возможные значения:

; 

.

Условным распределением составляющей

 при

 (j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

.

Условные
вероятности составляющих

 и

 вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

.

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

 и

 называют коррелированными, если их коэффициент
корреляции отличен от нуля.

 и

 называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

 и

 – зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

 в виде линейной функции величины

:

где

 и

 – параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

 на

 имеет вид:

Коэффициент

называют
коэффициентом регрессии

 на

, а прямую

называют
прямой среднеквадратической регрессии

 на

.

Аналогично
можно получить прямую среднеквадратической регрессии

 на

:

Смежные темы решебника:

• Двумерная непрерывная случайная величина
• Линейный выборочный коэффициент корреляции
• Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

–
определить одномерные законы распределения случайных величин X и Y;

– найти
условные плотности распределения вероятностей величин;

–
вычислить математические ожидания m_x и m_y;

–
вычислить дисперсии σ_x и σ_y;

–
вычислить ковариацию μ_xy;

–
вычислить коэффициент корреляции r_xy.

xy	3	5	8	10	12
-1	0.04	0.04	0.03	0.03	0.01
1	0.04	0.07	0.06	0.05	0.03
3	0.05	0.08	0.09	0.08	0.05
6	0.03	0.04	0.04	0.06	0.08

---

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X;  в) построить регрессию случайной величины X на Y;  г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Y	X
1	2	3	4	5
30	0.05	0.03	0.02	0.01	0.01
40	0.03	0.02	0.02	0.04	0.01
50	0.05	0.03	0.02	0.02	0.01
70	0.1	0.03	0.04	0.03	0.01
90	0.1	0.04	0.01	0.07	0.2

---

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

x y	1	2	3
1.5	0.03	0.02	0.02
2.9	0.06	0.13	0.03
4.1	0.4	0.07	0.02
5.6	0.15	0.06	0.01

---

Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

XY	1	2
-3	0,1	0,2
0	0,2	0,3
-3	0	0,2

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

---

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

---

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

	ξ=-1	ξ=0	ξ=2
η=1	0,1	0,1	0,1
η=2	0,1	0,2	0,1
η=3	0,1	0,1	0,1

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ  и D_γ.

---

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

XY	1	2	4
-2	0,25	0	0,25
1	0	0,25	0
3	0	0,25	0

---

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

YX	-1	1
-1	0,4	0,1
1	0,2	0,3

---

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

	X=-3	X=0	X=1
Y=-2	0,3	?	0,1
Y=1	0,1	0,1	0,2

---

Задача 10

Совместный
закон распределения пары

 задан таблицей:

xh	-1	0	1
-1	1/12	1/4	1/6
1	1/4	1/12	1/6

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

---

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

X	20	25	30	35
P	0.1	0.1	0.4	0.4

и

---

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

XY	0	1	2
-1	?	0,1	0,2
1	0,1	0,2	0,3

---

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

ξη	-1	1	2
0	1/7	2/7	1/7
1	1/7	1/7	1/7

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

---

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

XY	2,3	2,9	3,1	3,4
0,2	0,15	0,15	0	0
2,8	0	0,25	0,05	0,01
3,3	0	0,09	0,2	0,1

---

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

xy	1	4
-10	0,1	0,2
0	0,3	0,1
20	0,2	0,1

---

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

XY	-1	0	1	2
-1	0	1/6	0	1/12
0	1/18	1/9	1/12	1/9
2	1/6	0	1/9	1/9

---

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

XY	0	1	3
0	0,15	0,05	0,3
-1	0	0,15	0,1
-2	0,15	0	0,1

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

---

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.

	5	20	35
100	—	—	0.05
115	—	0.2	0.15
130	0.15	0.35	—
145	0.1	—	—-

Одномерные случайные величины

Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения вероятностей и ее свойства. Плотность распределения вероятности и ее свойства. Числовые характеристики случайных величин: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода и медиана; начальные и центральные моменты, асимметрия и эксцесс. Числовые характеристики среднего арифметического n независимых случайных величин.

Понятие случайной величины

Случайной называется величина, которая в результате испытаний принимает то или иное (но при этом только одно) возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. В отличие от случайного события, являющегося качественной характеристикой случайного результата испытания, случайная величина характеризует результат испытания количественно. Примерами случайной величины могут служить размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Среди случайных величин, с которыми приходится встречаться на практике, можно выделить два основных типа: дискретные и непрерывные.

Дискретной называется случайная величина, принимающая конечное или бесконечное счетное множество значений. Например: частота попаданий при трех выстрелах; число бракованных изделий в партии из штук; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов прибора за определенный промежуток времени при испытании его на надежность; число выстрелов до первого попадания в цель и т. д.

Непрерывной называется случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Очевидно, что число возможных значений непрерывной случайной величины бесконечно. Например: ошибка при измерении дальности радиолокатора; время безотказной работы микросхемы; погрешность изготовления деталей; концентрация соли в морской воде и т. д.

Случайные величины обычно обозначают буквами и т. д., а их возможные значения — и т. д. Для задания случайной величины недостаточно перечислить все ее возможные значения. Необходимо также знать, как часто могут появиться те или иные ее значения в результате испытаний при одних и тех же условиях, т. е. нужно задать вероятности их появления. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.

---

Законы распределения случайной величины

Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Закон распределения случайной величины может быть задан в виде таблицы, функции распределения либо плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины.

Табличное задание закона распределения можно использовать только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.

Для наглядности ряд распределения представляют графически. При графическом изображении в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат — соответствующие вероятности. Точки , соединенные прямолинейными отрезками, называют многоугольником распределения (рис. 5). Следует помнить, что соединение точек выполняется только с целью наглядности, так как в промежутках между и , и и т. д. не существует значений, которые может принимать случайная величина , поэтому вероятности её появления в этих промежутках равны нулю.

Многоугольник распределения, как и ряд распределения, является одной из форм задания закона распределения дискретной случайной величины. Они могут иметь различную форму, однако все обладают одним общим свойством: сумма ординат вершин многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Это свойство следует из того, что все возможные значения случайной величины образуют полную группу несовместных событий, сумма вероятностей которых равна единице.

---

Функция распределения вероятностей и ее свойства

Функция распределения является наиболее общей формой задания закона распределения. Она используется для задания как дискретных, так и непрерывных случайных величин. Обычно ее обозначают . Функция распределения определяет вероятность того, что случайная величина принимает значения, меньшие фиксированного действительного числа , т. е. . Функция распределения полностью характеризует случайную величину с вероятностной точки зрения. Ее еще называют интегральной функцией распределения.

Геометрическая интерпретация функции распределения очень проста. Если случайную величину рассматривать как случайную точку оси (рис. 6), которая в результате испытания может занять то или иное положение на оси, то функция распределения — это вероятность того, что случайная точка в результате испытания попадет левее точки .

Для дискретной случайной величины , которая может принимать значения , функция распределения имеет вид

где неравенство означает, что суммирование распространяется на все значения , меньше . Из этой формулы следует, что функция распределения дискретной случайной величины представляет собой ступенчатую ломаную линию (рис. 7). При каждом новом значении случайной величины ступень поднимается выше на величину, равную вероятности этого значения. Сумма всех скачков функции распределения равна единице.

Непрерывная случайная величина имеет непрерывную функцию распределения, график этой функции имеет форму плавной кривой (рис. 8 ).

---

Рассмотрим общие свойства функций распределения.

Свойство 1. Функция распределения — неотрицательная, функция, заключенная между нулем и единицей:

Справедливость этого свойства вытекает из того, что функция распределения определена как вероятность случайного события, состоящего в том, что .

Свойство 2. Вероятность попадания случайной величины в интервал равна разности значений функции распределения на концах этого интервала, т. е.

Отсюда следует, что вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Свойство 3. Функция распределения случайной величины есть неубывающая функция, т. е. .

Свойство 4. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности — единице, т. е. и .

---

Пример 1. Функция распределения непрерывной случайной величины задана выражением

Найти коэффициент и построить график . Определить вероятность того, что случайная величина в результате опыта примет значение на интервале .

Решение. Так как функция распределения непрерывной случайной величины непрерывна, то при получим . Отсюда . График функции изображен на рис. 9.

Исходя из второго свойства функции распределения, имеем

---

Плотность распределения вероятности и ее свойства

Функция распределения непрерывной случайной величины является ее вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения случайной величины в небольшой окрестности той или другой точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины дает функция, которая называется плотностью распределения вероятности, или дифференциальной функцией распределения случайной величины.

Плотность распределения равна производной от функции распределения , т. е.

Смысл плотности распределения состоит в том, что она указывает на то, как часто случайная величина появляется в некоторой окрестности точки при повторении опытов. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.

Рассмотрим свойства плотности распределения.

Свойство 1. Плотность распределения неотрицательна, т. е.

Свойство 2. Функция распределения случайной величины равна интегралу от плотности в интервале от до , т. е.

Свойство 3. Вероятность попадания непрерывной случайной величины на участок равна интегралу от плотности распределения, взятому по этому участку, т. е.

Свойство 4. Интеграл в бесконечных пределах от плотности распределения равен единице:

---

Пример 2. Случайная величина подчинена закону распределения с плотностью

Определить коэффициент а; построить график плотности распределения; найти вероятность попадания случайной величины на участок от до определить функцию распределения и построить ее график.

Решение. Площадь, ограниченная кривой распределения, численно равна

Учитывая свойство 4 плотности распределения, находим . Следовательно, плотность распределения можно выразить так:

График плотности распределения на рис. 10. По свойству 3, имеем

Для определения функции распределения воспользуемся свойством 2:

Таким образом, имеем

График функции распределения изображен на рис. 11

---

Числовые характеристики случайных величин

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются математическое ожидание, дисперсия, моменты различных порядков, мода и медиана.

Математическое ожидание иногда называют средним значением случайной величины. Рассмотрим дискретную случайную величину , принимающую значения с вероятностями соответственно Определим среднюю арифметическую значений случайной величины, взвешенных по вероятностям их появлений. Таким образом, вычислим среднее значение случайной величины, или ее математическое ожидание :

Учитывая, что получаем

Итак, математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.

Для непрерывной случайной величины математическое ожидание

Математическое ожидание непрерывной случайной величины , возможные значения которой принадлежат отрезку ,

Используя функцию распределения вероятностей , математическое ожидание случайной величины можно выразить так:

---

Свойства математического ожидания

Свойство 1. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

Свойство 2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

Свойство 3. Математическое ожидание постоянной величины равно самой постоянной:

Свойство 4. Постоянный множитель случайной величины можно вынести за знак математического ожидания:

Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

---

Пример 3. Найти математическое ожидание количества бракованных изделий в выборке из пяти изделий, если случайная величина (количество бракованных изделий) задана рядом распределения.

Решение. По формуле (4.1) находим

---

Модой дискретной случайной величины называется наиболее вероятное ее значение.

Модой непрерывной случайной величины называется такое ее значение, которому соответствует наибольшее значение плотности распределения. Геометрически моду интерпретируют как абсциссу точки глобального максимума кривой распределения (рис. 12).

Медианой случайной величины называется такое ее значение, для которого справедливо равенство

С геометрической точки зрения медиана — это абсцисса точки, в которой площадь фигуры, ограниченной кривой распределения вероятностей и осью абсцисс, делится пополам (рис. 12). Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, то функция распределения в точке, соответствующей медиане, равна 0,5, т. е.

С помощью дисперсии и среднеквадратического отклонения можно судить о рассеивании случайной величины вокруг математического ожидания. В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины и обозначают :

Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующие вероятности:

Для непрерывной случайной величины, закон распределения которой задан плотностью распределения вероятности , дисперсия

Размерность дисперсии равна квадрату размерности случайной величины и поэтому ее нельзя интерпретировать геометрически. Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое вычисляется по формуле

---

Свойства дисперсии случайных величин

Свойство 1. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

Свойство 2. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

Свойство 3. Дисперсия постоянной величины равна нулю:

Свойство 4. Постоянный множитель случайной величины, можно выносить за знак дисперсии, предварительно возведя его в квадрат:

Свойство 5. Дисперсия произведения двух независимых случайных величин и определяется по формуле

---

Пример 4. Вычислить дисперсию количества бракованных изделий для распределения примера 3.

Решение. По определению дисперсии

---

Обобщением основных числовых характеристик случайной величины является понятие моментов случайной величины.

Начальным моментом q-го порядка случайной величины называют математическое ожидание величины :

Начальный момент дискретной случайной величины

начальный момент непрерывной случайной величины

Центральным моментом q-го порядка случайной величины называют математическое ожидание величины :

Центральный момент дискретной случайной величины

центральный момент непрерывной случайной величины

Начальный момент первого порядка представляет собой математическое ожидание, а центральный момент второго порядка — дисперсию случайной величины.

Нормированный центральный момент третьего порядка служит характеристикой скошенности или асимметрии распределения (коэффициент асимметрии):

Нормированный центральный момент четвертого порядка служит характеристикой островершинности или плосковершинности распределения (эксцесс):

---

Пример 5. Случайная величина задана плотностью распределения вероятностей

Найти коэффициент , математическое ожидание, дисперсию, асимметрию и эксцесс.

Решение. Площадь, ограниченная кривой распределения, численно равна

Учитывая, что эта площадь должна быть равна единице, находим . По формуле (4.2) найдем математическое ожидание:

Дисперсию определим по формуле (4.3). Для этого найдем сначала математическое ожидание квадрата случайной величины:

Таким образом,

Используя начальные моменты, вычисляем центральные моменты третьего и четвертого порядка:

---

Числовые характеристики среднего арифметического n независимых случайных величин

Пусть — значения случайной величины , полученные при независимых испытаниях. Математическое ожидание случайной величины равно , а ее дисперсия . Эти значения можно рассматривать как независимые случайные величины с одинаковыми математическими ожиданиями и дисперсиями:

Средняя арифметическая этих случайных величин

Используя свойства математического ожидания и дисперсии случайной величины, можно записать:

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1. Закон распределения системы дискретных
случайных величин может быть задан
таблично ():

		. . .		. . .
	. . .	. . .	. . .	. . .
		. . .		. . .
	. . .	. . .	. . .	. . .

Законы распределения составляющих
системы находятся суммированием
вероятностей по строкам и столбцам
таблицы соответственно.

2. Преобразование функции и плотности
распределения системы выполняется в
соответствии с формулами (1.44) – (1.51).

Пример1.14. Физические параметры
человека, такие как рост и вес, могут
быть описаны двумерной случайной
величиной(Х , У), гдеХрост;Увес. На основании исследования
экспериментальных данных получен
двумерный закон распределения системы(Х,У), который представлен табл.1.7.

Таблица 1.7.
Распределение вероятности соотношения
роста и веса

	x1=160	x2=170	x3=180
y1=70
y2=80

В этой таблице
показывает вероятность того, что человек,
обладающий ростом,будет
иметь вес.

Требуется найти одномерные законы
распределения каждой из случайных
величин системы (Х,У).

Решение. Сложив вероятности по
столбцам, получим вероятности возможных
значений весаY:

Закон распределения составляющей Хзапишется так (табл.1.8):

Таблица 1.8.
Распределение
вероятности роста

	0,26	0,38	0,36

Контроль:
.

Сложив вероятности по строкам, получим
закон распределения составляющей У(табл.1.9).

Таблица 1.9.
Распределение
вероятности веса

	0,56	0,44

Контроль:

Пример
1.15. Система случайных величин (Х,
У) описывает
рост и вес человека в отклонениях от
средних значений (рост –

= 170 см;вес –
=66 кг) и имеет функцию
распределения

Найти плотность распределения вероятностей
системы случайных величин f(x, y).

Решение. Согласно формуле (3.2) находим

Отсюда

Полученное выражение позволяет определить
вероятность встречи человека с заданным
соотношением веса и роста.

Пример1.16. Ошибка позиционирования
пера графопостроителя может быть описана
системой двух случайных величин(Х,У)(координатных осей). Система двух
случайных величин подчинена равномерной
плотности распределения внутри круга
радиусомr. Написать выражение для
плотности распределения системы и
отдельных СВ.

Решение. Плотность распределения
системы(Х, У),равномерно
распределенной внутри круга, выражается
формулой

Пользуясь формулами (3.7), найдем плотность
распределения вероятностей отдельных
величин:

Аналогично

.

Задания для самостоятельной работы

1.Число рабочих циклов двигателя Хи пробег автомобиляУвзаимосвязаны.
Найдите законы распределения составляющих(Х, У),заданных двумерной таблицей
распределения вероятностей (табл.1.10).

Таблица 1.10.
Распределение вероятности системы
двух СВ

		= 0,062	= 0,082
	= 0,116	= 0,16	= 0,07
	= 0,111	= 0,111	=0,182

2. Координаты радиостанции, полученные
в результате пеленга, представляют
собой систему двух случайных величин
(Х, У),подчиненную равномерному
закону распределения в треугольнике,
определенном прямымиХ = 0, У = 0, Х + У
= а, гдеа 
0. Определите:

а) функцию распределения системы (Х,
У); б) законы распределения одномерных
случайных величин.

3. Положение точки на экране навигационного
прибора имеет погрешность по осям
координат, которая задана независимыми
СВ ХиУ, подчиняющимися законам
равномерной плотности распределения
вероятностей в интервалах (–1; 1) и (0; 2)
соответственно. Определите плотность
распределения вероятностей и функцию
распределения системы(Х, У).

4.
Составьте и решите задачу описания
законов распределения системы случайных
величин.

Соседние файлы в папке Тер вер и мат стат

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

            Если функция распределения  непрерывна и имеет непрерывную смешанную
производную второго порядка 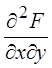, то – непрерывная СВ с двумерной плотностью
распределения

.

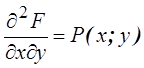
Свойства плотности
распределения:

1. 

2. 

3. 

4.

5. ,  .

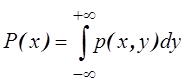
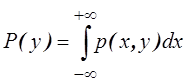
         Пример. Известна
плотность вероятности двумерной СВ

Найти 1) константу , 2) , 3) .

Решение.

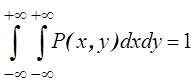
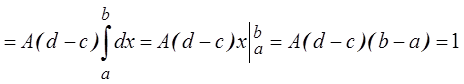
1) Из условия нормировки  имеем

.

Отсюда  .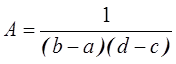

Тогда

2) Находим плотности
распределения одномерных случайных величин

.

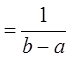
Отсюда 

Аналогично

3)

.

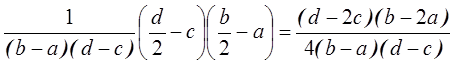
5.5.
Независимость случайных величин

            Определение 5.3. Двумерная случайная величина  называются независимыми,
если для любых действительных чисел x и y справедливо равенство

.

Из определения следует, что если
 дискретная СВ, то .

Если  непрерывная
СВ, то .

         Пример. Двумерная случайная величина  задана
плотностью вероятности

Проверить, являются ли случайные величины  и  независимыми.

Решение.
Плотности вероятностей одномерных случайных величин имеют вид

 и

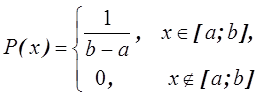
 Очевидно, что  и –
независимы.

Пример. Двумерная дискретная случайная
величина задана законом распределения

	5	6
1	0,1	0,4
2	0,2	0,3

Проверить, являются ли случайные величины  и  независимыми.

Решение. Одномерные законы
распределения случайных величин  и  имеют
вид

	1	2
	0,5	0,5

	5	6
	0,3	0,7

С одной стороны . С другой стороны ,
. Отсюда заключаем, что  и  зависимыми.

5.6. Ковариация. Коэффициент
корреляции.

            Определение
5.4. Ковариацией случайных величин   и  называется число

.

            Данная формула для дискретных СВ имеет вид:

,

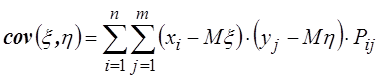
для непрерывных СВ:

.

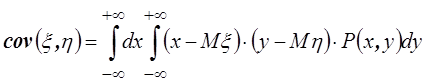
            Ковариация характеризует рассеивание СВ  и , а
также их взаимное влияние. Поэтому ее иногда называют моментом связи или
корреляционным моментом.

Свойства ковариации.

1. .

2.  где

3. Если СВ  и
 независимы,
то .

Обратное неверно.

            Определение 5.5. Коэффициентом
корреляции называется число

,

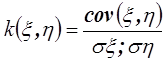
где
,  .

            Если ,  , то коэффициент корреляции  не
существует.

Свойства коэффициента
корреляции.

1.  .

2.  Если  и  линейно
зависимы, т. е. , где ,  – числа, то .

           Определение 5.6 
Случайные величины  и  называются некоррелируемыми, если .
Случайные величины  и  называются
коррелируемыми, если .

           Коэффициент
корреляции определяет степень линейной вероятностной зависимости между
случайными величинами  и . Это проявляется в том, что при возрастании
одной СВ другая тоже возрастает; при убывании – другая тоже убывает.

            Пример. Найти коэффициент корреляции СВ.

Решение. Находим одномерные законы
распределения и их числовые характеристики.:

, , .

, , .

Тогда

.

Тогда 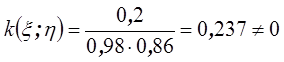. Отсюда следует, что случайные величины  и
 коррелируемы, т.е. взаимосвязаны.

КОНТРОЛЬНЫЕ
ВОПРОСЫ

1. Приведите примеры
   количественных характеристик событий.
2. Дайте определение двумерной
   дискретной случайной величины. Как получить законы одномерные законы
   распределения из двумерного закона распределения?
3. Дайте определение функции
   распределения двумерной случайной величины и перечислите ее свойства.
4. Дайте определение
   непрерывной двумерной случайной величины и перечислите ее свойства.
5. Какие случайные величины
   называются независимыми?
6. Дайте определение
   ковариации и перечислите ее свойства. Что называется коэффициентом
   корреляции и что он характеризует?

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

1