Задача по статистике. Определение однородности совокупности. Правило «трех сигм». Показатели цента распределения
- Пользуясь базой данных официального сайта www.gks.ru, сформировать массив значений признака Y (Уровень экономической активности, %) ПО ВСЕМ СУБЪЕКТАМ РФ за последний год, оценить однородность совокупности с помощью коэффициента вариации и сделать проверку на нормальность распределения с помощью правила «трёх сигм». В случае наличия резко выделяющихся значений, исключить эти субъекты из массива для проведения более объективного дальнейшего исследования.
| Область | Уровень экономической активности, Y млн. руб. | (Y-Ycp)^2 |
| Белгоpодская область | 66,2 | 5,01 |
| Бpянская область | 66,7 | 3,02 |
| Владимиpская область | 70,3 | 3,46 |
| Воpонежская область | 64,6 | 14,73 |
| Ивановская область | 68,5 | 0,00 |
| Калужская область | 70,4 | 3,85 |
| Костpомская область | 70 | 2,44 |
| Курская область | 65,8 | 6,96 |
| Липецкая область | 70,7 | 5,11 |
| Московская область | 72,8 | 19,02 |
| Оpловская область | 65,1 | 11,15 |
| Рязанская область | 63,5 | 24,39 |
| Смоленская область | 71,3 | 8,19 |
| Тамбовская область | 64,1 | 18,82 |
| Твеpская область | 70,5 | 4,25 |
| Тульская область | 67,6 | 0,70 |
| Яpославская область | 68,8 | 0,13 |
| г. Москва | 72,2 | 14,15 |
| Республика Каpелия | 66,9 | 2,37 |
| Республика Коми | 70,8 | 5,58 |
| Аpхангельская область | 68 | 0,19 |
| в том числе Ненецкий автономный округ | 71,7 | 10,64 |
| Вологодская область | 69,9 | 2,14 |
| Калинингpадская область | 70,7 | 5,11 |
| Ленингpадская область | 71,6 | 9,99 |
| Муpманская область | 74,9 | 41,75 |
| Новгоpодская область | 69,3 | 0,74 |
| Псковская область | 68,5 | 0,00 |
| г. Санкт-Петеpбуpг | 73,6 | 26,64 |
| Республика Адыгея | 61,5 | 48,14 |
| Республика Калмыкия | 67,3 | 1,30 |
| Кpаснодаpский кpай | 65,2 | 10,49 |
| Астpаханская область | 67 | 2,07 |
| Волгогpадская область | 66,8 | 2,68 |
| Ростовская область | 65,5 | 8,64 |
| Республика Дагестан | 63,6 | 23,41 |
| Республика Ингушетия | 69,1 | 0,44 |
| Кабаpдино-Балкаpская Республика | 59,7 | 76,36 |
| Каpачаево-Чеpкесская Республика | 67,4 | 1,08 |
| Республика Севеpная Осетия — Алания | 67,2 | 1,53 |
| Чеченская Республика | 70,7 | 5,11 |
| Ставpопольский кpай | 65,1 | 11,15 |
| Республика Башкоpтостан | 66,7 | 3,02 |
| Республика Маpий Эл | 68,5 | 0,00 |
| Республика Моpдовия | 70,7 | 5,11 |
| Республика Татаpстан | 70,4 | 3,85 |
| Удмуpтская Республика | 71,7 | 10,64 |
| Чувашская Республика | 68,7 | 0,07 |
| Пеpмский край | 67,7 | 0,55 |
| Киpовская область | 67,6 | 0,70 |
| Нижегоpодская область | 71,4 | 8,77 |
| Оpенбуpгская область | 67,6 | 0,70 |
| Пензенская область | 65,5 | 8,64 |
| Самаpская область | 69,3 | 0,74 |
| Саpатовская область | 65,8 | 6,96 |
| Ульяновская область | 67,7 | 0,55 |
| Куpганская область | 64,3 | 17,13 |
| Свеpдловская область | 69,2 | 0,58 |
| Тюменская область | 72,3 | 14,91 |
| в том числе: Ханты-Мансийский автономный округ — Югра | 74,5 | 36,74 |
| Ямало-Ненецкий автономный округ | 79 | 111,54 |
| Челябинская область | 70,5 | 4,25 |
| Республика Алтай | 67,3 | 1,30 |
| Республика Буpятия | 63,9 | 20,60 |
| Республика Тыва | 56,5 | 142,53 |
| Республика Хакасия | 64,7 | 13,98 |
| Алтайский кpай | 65 | 11,82 |
| Забайкальский край | 64,4 | 16,31 |
| Красноярский край | 68,6 | 0,03 |
| Иpкутская область | 67,7 | 0,55 |
| Кемеpовская область | 66,7 | 3,02 |
| Новосибиpская область | 69 | 0,32 |
| Омская область | 68,8 | 0,13 |
| Томская область | 60 | 71,21 |
| Республика Саха (Якутия) | 69,8 | 1,85 |
| Камчатский край | 72,9 | 19,90 |
| Пpимоpский кpай | 68,3 | 0,02 |
| Хабаpовский кpай | 69,9 | 2,14 |
| Амуpская область | 67,3 | 1,30 |
| Магаданская область | 79,1 | 113,67 |
| Сахалинская область | 72,4 | 15,69 |
| Евpейская автономная область | 65,4 | 9,23 |
| Чукотский автономный окpуг | 82,50 | 197,72 |
| Сумма | 5680,4 | 1321,72 |
Определение однородности совокупности
Определим средний Уровень экономической активности по формуле средней арифметической простой:

Дисперсия определяется по формуле:

Среднее квадратическое отклонение:
![]()
Коэффициент вариации составит:

Совокупность однородна, т.к. коэффициент вариации менее 0,33
Правило «трех сигм»
Исключение из массива первичной информации всех резко выделяющихся единиц по уровню факторного признака производится по правилу «трех сигм»: исключаются все единицы, у которых уровень признака-фактора не попадает в интервал:

В интервал
![]()
56,47 <x< 80,41 попадают не все значения, поэтому по данному правилу нужно исключить одно значение по Чукотскому автономному округу. 82,5%
Группировка данных по формуле Стерджесса
2. По оставшимся данным произвести группировку субъектов РФ, образовав группы с равными интервалами.
На начальном этапе проведения группировки необходимо определить целесообразное число групп и величину интервала. Необходимо самостоятельно выбрать порядок образования интервалов (для этого можно воспользоваться рекомендательной формулой Стерджесса).
Формируя группы, нужно помнить, что распределение единиц совокупности внутри групп должно быть как можно более равномерным (в каждую группу должно входить не менее 2-3-х значений), кроме того, распределение должно иметь только один модальный интервал (имеющий максимальную частоту).
Для соответствия этим критериям, фактическая величина интервала и число групп могут иногда отличаться от расчётных значений. Для удобства восприятия и анализа группировки рекомендуется брать величину интервала, кратную пяти, десяти, ста, и т.д. в зависимости от величины и степени вариации признака.
Определяем число групп по формуле Стерджесса:
n = 1 + 3,322lgN = 1 + 3,322lg82 = 7,36
принимаем n =7
Определяем шаг интервала:

xmax, xmin — максимальное и минимальное значение
n – число групп
Произведем группировку с равными интервалами
| Интервалы | Диапазон по уровню ВРП | Число регионов, f |
| 1 | 56,5 — 59,7 | 2 |
| 2 | 59,7 — 63 | 2 |
| 3 | 63 – 66,2 | 17 |
| 4 | 66,2 – 69,4 | 32 |
| 5 | 69,4 — 72,6 | 22 |
| 6 | 72,6 — 75,9 | 5 |
| 7 | 75,9 — 79,1 | 2 |
В 1,2 и 7 интервалы попадает менее 3 субъектов. При сокращении интервалов на 1 в последний попадет 2 субъекта. Сократим число интервалов и примем n = 5
h = (79,1-56,5)/5 = 4,5%
| Интервалы | Диапазон по уровню экономической активности | Число регионов, f | накопленная частота | доля |
| 1 | 56,5 — 61 | 3 | 3 | 3,7% |
| 2 | 61 – 65,5 | 16 | 19 | 19,5% |
| 3 | 65,5 – 70,1 | 38 | 57 | 46,3% |
| 4 | 70,1 – 74,6 | 22 | 79 | 26,8% |
| 5 | 74,6 – 79,1 | 3 | 82 | 3,7% |
3. Проанализировать полученный в п.2 ряд распределения значений признака Y. Для этого построить таблицу, содержащую интервальные группы, число субъектов в каждой группе и частоты групп (f), по сгруппированным данным рассчитать статистические показатели, характеризующие
- центр распределения,
- абсолютную и относительную вариацию,
- степень дифференциации
Дополнить расчеты описательными выводами и способами графического представления рядов распределения.
Показатели цента распределения
Определим средний уровень экономической активности по формуле средней арифметической взвешенной :

X’ — середина интервала
Дисперсия определяется по формуле

Составим расчетную таблицу


Совокупность можно считать однородной, т.к. коэффициент вариации менее 33%
Расчет моды и медианы
Интервал, имеющий наибольшую частоту, будет являться модальным, а конкретное (дискретное) значение моды будет находиться внутри него. Рассчитать конкретное, значение моды в интервальном ряду можно по следующей формуле:

где: ХМо — нижняя граница модального интервала,
i — длина модального интервала,
fMo — частота модального интервала,
fMo-1 — частота, соответствующая предшествующему интервалу,
fMo+1 — частота, соответствующая последующему интервалу.
Самая большая частота — 38, соответствует варианту 65,5 – 70,1. Этот интервал является модальным.
![]()
Медиана применяется для количественной характеристики структуры и равна такому варианту, который делит ранжированную совокупность на две равные части. У одной половины совокупности признаки не больше медианы (меньше или равны), у второй — не меньше медианы (больше или равны).
Если рассматриваемый ряд интервальный, то накопленные частоты покажут нам медианный интервал. Конкретное значение медианы рассчитывается по формуле:

i — длина медианного интервала,
fMe’ — накопленная частота в интервале, предшествующем медианному,
fMe — частота медианного интервала.
Для нахождения медианного интервала нужно знать половину частот, то есть 82 : 2 = 41. Во 2-м интервале частот накопилось менее половины, модальным является 3-й интервал 65,5 – 70,1
![]()
Размах вариации составит: R = xmax — xmin = 79.1-56.5=22.6% (абсолютная вариация)
Построим график распределения

Получаем примерное равенство моды, медианы и средней, т.е. распределение близко к нормальному
Показатели степени дифференциации
Децильный коэффициент дифференциации
Децильный коэффициент дифференциации рассчитывается так:

Д9 – дециль №9;
Д1 – дециль №1.
дециль №1 (10%) находится в интервале 61 – 65,5, где удельный вес субъектов с уровнем экономической активности

хн – нижняя граница децильного интервала
hд — шаг интервала
Fд-1 — сумма накопленных удельных весов до децильного интервала
fд — удельный вес децильного интервала

дециль №9 (90%) находится в интервале 70,1 – 74,6

![]()
Вывод: Значение децильного коэффициента менее 1,2, то можно говорить о слабой дифференциации по уровню экономической активности.
Статистика
позволяет выявить и измерить закономерности
развития социально-экономических
явлений и процессов,
взаимосвязи между ними. Познание
закономерностей возможно
только в том случае, если изучаются не
отдельные явления,
а совокупности
явлений
— ведь закономерности общественной
жизни проявляются в полной мере лишь в
массе явлений.
Объекты
конкретного статистического исследования
образуют статистической совокупностью.
Статистическая
совокупность
— это множество единиц (объектов,
явлений) общественной жизни, объединенных
единой закономерностью (общей связью),
но отличающихся друг от друга отдельными
признаками.
Таковы, например,
совокупность домохозяйств, совокупность
семей, совокупность предприятий, фирм,
объединений и т. п.
Статистическая
совокупность состоит из единиц
совокупности.
Под единицей
совокупности
понимается первичный неделимый элемент,
являющийся носителем признаков,
подлежащих изучению.
Совокупности
могут быть однородными и разнородными.
Совокупность называется однородной,
если все её
единицы обладают изучаемыми существенными
признаками.
Совокупность
оказывается однородной именно с точки
зрения этих признаков. Однородность
совокупности устанавливается в каждом
конкретном статистическом исследовании
в соответствии с его целями.
Выделение однородных
совокупностей необходимо для расчета
обобщающих показателей, статистического
изучения вариации, связей между
признаками.
Совокупность, в
которую входят явления разного типа,
считается разнородной.
Совокупность
может быть однородна в одном отношении
и разнородна — в другом. В каждом
отдельном случае однородность совокупности
устанавливается путем проведения
качественного анализа, выяснения
содержания изучаемого общественного
явления.
Единицы
совокупности обладают определенными
свойствами,
качествами.
Эти свойства принято называть признаками.
Признак
—
качественная особенность единицы
совокупности, характеризующая его
некоторые свойства.
Например, признаки
человека: возраст, образование, занятие,
рост, вес, семейное положение и т.д.;
признаки предприятия:
форма собственности, специализация
(отрасль), численность
работников, величина уставного фонда,
экономическая
эффективность его деятельности и т.д.
Значение каждого
признака отдельных единиц совокупности
называет его вариантой.
Вариация –
различия в
значениях того или иного признака у
отдельных единиц, входящих в данную
совокупность.
Различия в значениях
признака одной и той же совокупности
возникают в результате того, что
индивидуальные значения подвержены
различным случайным факторам, которые
действуют на него в разнообразных
сочетаниях.
Статистика
изучает явления через их признаки: чем
более однородна
совокупность, тем больше общих признаков
имеют ее
единицы и тем меньше варьируются их
значения.
Признаки
различаются способами их измерения и
другими
особенностями, влияющими на приемы
статистического изучения.
Это дает основание для классификации
признаков.
Классификация
признаков в статистике
|
Основы классификации |
||||
|
По характеру |
По способу |
По отношению к |
По характеру |
По отношению ко |
|
Описательные Количественные |
Первичные
Вторичные |
Прямые Косвенные |
Альтернативные Дискретные Непрерывные |
Моментные Интервальные |
Описательные
признаки
выражаются словесно: национальность
человека, разновидность почв, материал
стен здания.
Описательные признаки подразделяются
на номинальные
и
порядковые.
Эти
термины взяты из теории измерений.
Отличия между ними в том, что номинальные
— это описательные
признаки, по которым нельзя ранжировать
(упорядочивать)
данные, а порядковые — это признаки, по
которым можно
ранжировать данные. Например, пользуясь
оценками экспертов,
ранжируют фигуристов по технике и
артистичности
исполнения программы или работников —
по мастерству, студентов
— по успеваемости и т.д.
Количественные
признаки
выражаются числами. Они играют
главенствующую роль в статистике. Таковы
возраст человека,
площадь пашни, заработная плата рабочих,
население города,
доход кооператива и т.д.
Первичные
признаки
характеризуют единицу совокупности в
целом. Это абсолютные величины. Они
могут быть измерены, сосчитаны,
взвешены и существуют сами по себе
независимо от
их статистического изучения. Например,
площадь пашни, мощность
двигателей на предприятии, численность
населения города,
число автомобилей, произведенных в
стране.
Вторичные,
или
расчетные,
признаки
не измеряются непосредственно,
а рассчитываются. Они являются продуктами
человеческого
сознания, результатом познания изучаемого
объекта.
Например, себестоимость единицы
продукции, производительность
труда, рентабельность, урожайность и
т.п. Вторичные
признаки представляют собой соотношения
первичных
признаков: деление объема выпущенной
продукции на
численность работников дает показатель
производительности
труда; деление суммы затрат на произведенную
продукцию на число
единиц данной продукции дает себестоимость
т.д. Прямые
(непосредственные) признаки
— это свойства, непосредственно
присущие тому объекту, который ими
характеризуется. Таковы возраст человека,
поголовье коров на ферме,
объем продукции завода, численность
его рабочих.
Косвенные
признаки
являются свойствами, присущими не самому
объекту, а другим совокупностям,
относящимся к объекту,
входящим в него.
Практически
деление признаков на прямые и косвенные
совпадает
с их делением на первичные и вторичные.
Признаки
различаются в статистике и по характеру
их вариации,
т.е. по различиям их значений у разных
единиц совокупности.
Выделяются альтернативные
признаки,
которые могут
принимать только два значения. Таковыми
являются признаки
обладания или не обладания чем-то.
Например, все садовые
участки по признаку наличия посадок
вишни можно разделить на имеющие посадки
вишни и не имеющие их. Альтернативным
признаком являются пол человека, место
проживания
(город, село), ходовая система трактора
(гусеничный
или колесный).
К
дискретным
относятся
количественные признаки, которые
могут принимать только целочисленные
значения, без промежуточных
значений между ними. Это число членов
семьи,
количество этажей здания, комнат в
квартире.
Непрерывные,
точнее
непрерывно варьирующиеся, признаки
способны принимать любые значения,
конечно, в определенных
границах. К непрерывным относятся
расчетные вторичные признаки. Ведь их
значения — результат деления, а
оно может приводить к любым числам —
целым, дробным, иррациональным.
На практике нередко значения непрерывных
признаков округляют с конечной степенью
точности, так что
они становятся квазидискретными. С
другой стороны, дискретные
по существу признаки, например число
работников
предприятия на 1 января, поголовье коров
на ту же дату, имеют такое громадное
число возможных значений, что на практике
статистика вынуждена обращаться с ними,
как с квазидискретным.
Моментные
признаки
характеризуют изучаемый объект в
какой-то
момент времени, установленный планом
статистического
исследования. Они существуют на любой
момент и характеризуют
наличие чего-либо: численность населения,
стоимость
фондов, количество скота, размеры жилой
площади.
К
интервальным
относятся
признаки, характеризующие результаты
процессов. Поэтому их значения могут
возникать только
за интервал времени: год, месяц, сутки,
но не на момент
времени. Таковы число родившихся,
умерших, объем промышленной
продукции, надой молока, сумма полученной
прибыли.
Моментные признаки — характеристики
состояния,
а
интервальные — характеристики процесса.
Различие
между
моментными и интервальными признаками
существенно при
изучении динамики. Единицы измерения
моментных признаков относятся только
к характеризуемым ими свойствам объектов,
а единицы измерения интервальных
признаков содержат еще и указание того
отрезка времени, за который определено
значение признака. Так, стоимость
основных производственных
фондов предприятия на 1 января выражается
в миллионах рублей, а объем продукции
за январь — в тысячах
или миллионах рублей за месяц.
Особенностью
статистического исследования является
то, что в
нем изучаются только варьирующие
признаки,
т. е. признаки, принимающие
различные значения.
Если же изменения изучаемого явления
происходят в разные периоды времени и
при этом носят характер
закономерности, то говорят уже не о
вариации признака, а о его динамике.
Признаки,
характеризующие статистическую
совокупность взаимосвязаны между собой,
выделяются факторные признаки и
результативные признаки.
Факторные признаки
– это
независимые признаки, оказывающие
влияние на другие связанные с ними
признаки.
Результативные
признаки –
зависимые признаки, значения которых
изменяются под влиянием факторных
признаков.
Квалификация, стаж
работы – факторные признаки,
производительность труда – результативный
признак.
Задача статистики
– установить общие свойства единиц
совокупности, изучить имеющиеся
взаимосвязи и закономерности
функционирования процесса. Достигается
это с помощью расчета статистических
показателей и их анализа.
Статистический
показатель —
это, количественно, качественная
характеристика какого – то свойства
группы единиц совокупности или
совокупности в целом.
Этим он отличается
от индивидуальных значений, которые
называются признаками.
Объем продукции
предприятия
за месяц –
показатель, производительность труда
рабочего за месяц – признак.
Статистические
показатели рассматриваются как обобщающие
значения признака.
Статистические
показатели определяются
путем суммирования абсолютных значений
признака (численность населения,
безработных, трудовых ресурсов),
вычисления средних значений признаков
(средняя заработная плата, средний доход
на душу населения), относительных величин
(индекс себестоимости, темпы прироста).
Статистические
показатели
могут быть плановыми,
отчетными и прогностическими (т. е.
выступать в качестве прогнозных оценок).
Статистические
показатели следует отличать от
статистических данных.
Статистические
данные — это
конкретные численные значения
статистических показателей. Они всегда
определены не только качественно, но и
количественно и зависят от конкретных
условий места и времени.
Статистические
показатели делятся на первичные,
вторичные.
Первичные
характеризуют:
общее число единиц совокупности, сумму
значений какого – либо признака.
Вторичные
выражаются
средними и относительными величинами
Задачи статистики:
-
правильно
определить содержание статистического
показателя (валового
национального продукта, национального
дохода, производительности труда и т.
п.); -
разработать
методологию подсчета и расчета
статистического показателя.
Так как отдельные
свойства совокупности связанны между
собой, то и статистические показатели,
характеризующие эти свойства, не являются
обособленными и образуют определенную
систему показателей.
Система
статистических показателей —
совокупность статистических
показателей, отражающая взаимосвязи,
которые объективно
существуют между явлениями.
Для
каждой общественно-экономической
формации характерна определенная
система взаимосвязи
общественных явлений, что обусловливает
статистические
показатели. Система статистических
показателей охватывает все
стороны жизни общества на различных
уровнях: страны и региона (макроуровень),
предприятий, фирм, объединений, семей
и домохозяйств и т. д. (микроуровень).
Системы статистических
показателей имеют следующие особенности:
-
они
носят исторический характер: меняются
условия жизни населения,
общества — меняются и системы
статистических показателей; -
методология
расчета статистических показателей
непрерывно совершенствуется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Понятие и показатели вариации, оценка однородности совокупности.
- однородная совокупность
- Тематики
- Смотреть что такое «однородная совокупность» в других словарях:
- СОВОКУПНОСТЬ, ОДНОРОДНАЯ
- Смотреть что такое «СОВОКУПНОСТЬ, ОДНОРОДНАЯ» в других словарях:
- Статистическая совокупность
- Оценка однородности совокупности
Понятие и показатели вариации, оценка однородности совокупности.
Поможем написать любую работу на аналогичную тему
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период времени.
– Если значения признака у отдельных единиц совокупности значительно отличаются между собой и значительно отличаются от средней, то совокупность является неоднородной.
– Если значения признака у отдельных единиц совокупности не значительно отличаются между собой и не значительно отличаются от средней, то совокупность является однородной.
1. Размах вариации – это разность между наибольшим (xmax) и наименьшим (xmin) значениями вариантов.
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
2. Дисперсия (или средний квадрат отклонений значения от средней величины)

3. Среднее квадратическое отклонение

Среднее квадратическое отклонение характеризует абсолютное отклонение конкретных значений признака от их среднего значения.
4. Коэффициент вариации (V)

Коэффициент вариации характеризует степень отклонения значений признака от средней величины и показывает степень однородности совокупности.
Если коэффициент вариации меньше или равен 33% (V ≤ 33 %), то совокупность считается однородной:
Источник
однородная совокупность
однородная совокупность
(напр. ядерных энергетических установок)
[А.С.Гольдберг. Англо-русский энергетический словарь. 2006 г.]
Тематики
Справочник технического переводчика. – Интент . 2009-2013 .
Смотреть что такое «однородная совокупность» в других словарях:
Совокупность Однородная — статистическая совокупность, для которой характерны принадлежность составных ее элементов к одному и тому же типу явления и сходство между элементами по существенным для данного исследования признакам. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
Совокупность статистическая — совокупность объектов или явлений общественной жизни, объединённых общей связью, но различающихся по ряду варьирующих признаков. Эти объекты или явления представляют собой элементы (единицы) С. с. Так, С. с. будет население, элементами… … Большая советская энциклопедия
СОВОКУПНОСТЬ, ОДНОРОДНАЯ — статистическая совокупность, для которой характерно принадлежность составных ее элементов к одному и тому же типу явления и сходство между элементами по существенным для данного исследования признакам. Статистическая совокупность может быть по… … Большой экономический словарь
статистическая совокупность — относительно однородная группа объектов или явлений, характеризующаяся наличием некоторых общих признаков и подвергающаяся изучению путем сбора количественных данных, их обработки и анализа … Большой медицинский словарь
множество — ▲ , совокупность ↑ однородный множество совокупность объектов, имеющих к л. общую характеристику; однородная совокупность; совокупность видов; неупорядоченная совокупность однородных попарно различных элементов; оно включает все такие элементы;… … Идеографический словарь русского языка
КОМПЛЕКС — Совокупность однородных предметов, образующих целое. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КОМПЛЕКС однородная совокупность, рассматриваемая как одно целое. Полный словарь иностранных слов, вошедших в… … Словарь иностранных слов русского языка
Сорт растений — (франц. sorte, от лат. sors разновидность, вид) культивар, совокупность растений, созданная в результате селекции и обладающая определёнными, передающимися по наследству морфологическими, физиологическими, хозяйственными признаками и… … Большая советская энциклопедия
Линия — В Викисловаре есть статья «линия» Линия (от лат. linea «льняная нить, шнур; линия») протяжённый и тонкий п … Википедия
Линии — Линия или кривая математическое понятие. Линия (единица длины) внесистемная единица измерения длины. Линия провод или пучок проводов, по которому идет сигнал. Линия (улица) название типа улицы. Линия (метро) синоним «ветка метро» Линия… … Википедия
типы национальной психики человека — а) условное отнесение людей к группам представителей конкретных наций, народностей, объединенных общностью черт национальной психики; б) относительно устойчивая форма проявления национально психологических особенностей в поведении конкретных… … Этнопсихологический словарь
Источник
СОВОКУПНОСТЬ, ОДНОРОДНАЯ
Большой экономический словарь. — М.: Институт новой экономики . А.Н. Азрилиян . 1997 .
Смотреть что такое «СОВОКУПНОСТЬ, ОДНОРОДНАЯ» в других словарях:
Совокупность Однородная — статистическая совокупность, для которой характерны принадлежность составных ее элементов к одному и тому же типу явления и сходство между элементами по существенным для данного исследования признакам. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
Совокупность статистическая — совокупность объектов или явлений общественной жизни, объединённых общей связью, но различающихся по ряду варьирующих признаков. Эти объекты или явления представляют собой элементы (единицы) С. с. Так, С. с. будет население, элементами… … Большая советская энциклопедия
однородная совокупность — (напр. ядерных энергетических установок) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN homogeneous population … Справочник технического переводчика
статистическая совокупность — относительно однородная группа объектов или явлений, характеризующаяся наличием некоторых общих признаков и подвергающаяся изучению путем сбора количественных данных, их обработки и анализа … Большой медицинский словарь
множество — ▲ , совокупность ↑ однородный множество совокупность объектов, имеющих к л. общую характеристику; однородная совокупность; совокупность видов; неупорядоченная совокупность однородных попарно различных элементов; оно включает все такие элементы;… … Идеографический словарь русского языка
БИОТИП — совокупность особей данного вида, однородная генетически и экологически … Словарь ботанических терминов
функция управляющего объекта — Совокупность действий управляющего объекта, относительно однородная по некоторому признаку, направленная на достижение частной цели, подчиненной общей цели управления … Политехнический терминологический толковый словарь
группа — 1.3.2 группа : Лампы с одинаковыми электрическими параметрами и характеристиками катода, физическими размерами и методом зажигания. Источник: ГОСТ Р МЭК 61195 99: Лампы люминесцентные двухцокольные. Требования безопасности … Словарь-справочник терминов нормативно-технической документации
ГОСТ 7.74-96: Система стандартов по информации, библиотечному и издательскому делу. Информационно-поисковые языки. Термины и определения — Терминология ГОСТ 7.74 96: Система стандартов по информации, библиотечному и издательскому делу. Информационно поисковые языки. Термины и определения оригинал документа: 7.8 автоматизированное индексирование : Индексирование, технология которого… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 22515-77: Связь телеграфная. Термины и определения — Терминология ГОСТ 22515 77: Связь телеграфная. Термины и определения оригинал документа: 4. Абонентский комплект Устройство, предназначенное для сопряжения коммутационного оборудования с каналом связи, соединяющим оконечную установку с… … Словарь-справочник терминов нормативно-технической документации
Источник
Статистическая совокупность



Статистическая совокупность – множество социально-экономических объектов или явлений общественной жизни, объединенных некой качественной основой, общей связью, но отличающихся друг от друга отдельными признаками.
Пример: совокупность домохозяйств, семей, предприятий, фирм, городов области и т.д.
Совокупности могут быть однородными и разнородными.
Совокупность однородная, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Например, мужской пол, возраст 18-25 лет, малые предприятия, предприятия торговли и т.д.
Совокупность разнородная, если в нее входят явления разного типа. Совокупность может быть однородна в одном отношении и разнородна в другом: например, торговые предприятия любого размера (малые, средние, крупные).
Единица совокупности – отдельная, первичная, неделимая часть совокупности, обладающая признаками, подлежащими регистрации, и основой ведущегося при обследовании счета.
Признак совокупности – качественная особенность единицы совокупности. Например, признаки человека: возраст, пол, образование и т.д.; признаки предприятия: форма собственности, отрасль, численность занятых, эффективность и т.д.
1) по характеру выражения
а) альтернативные (принимают только два значения),
б) дискретные (принимают только целочисленные значения),
в) непрерывные (принимают любые значения),
2) по способу измерения
— первичные (измеряются, считаются, взвешиваются…),
3) по отношению к характеризуемому объекту
— прямые (непосредственно присущи объекту),
— косвенные (опосредованно присущи объекту),
4) по отношению ко времени
— моментные (характеризуют объект в один момент времени),
— интервальные (характеризуют результаты процессов за период времени)
Важной чертой любой статистической совокупности является наличие вариации – изменение величины либо значения признака при переходе от одной единицы совокупности к другой.
Если изменения изучаемого явления происходят в разные периоды времени и носят характер закономерности, то говорят о динамике признака.
Статистические закономерности устанавливаются с помощью закона больших чисел: при определенных условиях (наличие вероятностных процессов, независимость, большое число факторов) совместное действие большого числа случайных факторов приводит к результатам практически независящим от случая.
Источник
Оценка однородности совокупности



априорный анализ статистический совокупность распределение
Для оценки однородности совокупности используют различные методы, такие как: группировка, расчет показателей вариации (дисперсия, коэффициент вариации), анализ аномальных наблюдений на основе l- и q-статистик.
На основе группировки и ее графического изображения (рис.1.1 – рис.1.9) можно предположить, что ряды распределения по трем признакам не являются однородными. Но вместе с тем, следует иметь виду, что при незначительном объеме выборки (n
Причины появления в совокупности аномальных наблюдений могут быть:
1) внешние, возникающие в результате технических ошибок;
2) внутренние, объективно существующие.
Для дальнейшего анализа формы распределения используют показатели вариации. Показатели вариации делятся на абсолютные и относительные. К абсолютным относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и квартильное отклонение. Коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации и относительный показатель квартильной вариации – относительные показатели.
В данной курсовой работе для характеристики однородности совокупности рассчитывались такие показатели, как дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Дисперсия – это средний квадрат отклонений индивидуальных значений признака от средней величины. Дисперсия не только является основной мерой колеблемости признака, но также используется для построения показателей тесноты корреляционной связи, при оценке результатов выборочных наблюдений и т.д.
Для сгруппированных данных она вычисляется по формуле (1.3):
 ,
,
где xi – i-ый вариант осредняемого признака;
 – выборочная средняя величина или средняя агрегатная;
– выборочная средняя величина или средняя агрегатная;
ni – частота, то есть число, показывающее сколько раз встречаются варианты из данного интервала, или вес i-го варианта;
n – число объектов совокупности.
Для оценки влияния различных факторов, обуславливающих вариацию признака, рассчитывается дисперсия по каждому из показателей. Для этого строятся расчетные таблицы:
Расчетная таблица для вычисления дисперсии по величине выручки от продажи товаров, продукции, работ, услуг
xi — 
(xi —  ) 2 ni
) 2 ni
Источник
Adblock
detector
| Группы предприятий по выручке от продажи, тыс. руб. | Число предприятий ni | Середина интервала xi |
From Wikipedia, the free encyclopedia
In statistics, homogeneity and its opposite, heterogeneity, arise in describing the properties of a dataset, or several datasets. They relate to the validity of the often convenient assumption that the statistical properties of any one part of an overall dataset are the same as any other part. In meta-analysis, which combines the data from several studies, homogeneity measures the differences or similarities between the several studies (see also Study heterogeneity).
Homogeneity can be studied to several degrees of complexity. For example, considerations of homoscedasticity examine how much the variability of data-values changes throughout a dataset. However, questions of homogeneity apply to all aspects of the statistical distributions, including the location parameter. Thus, a more detailed study would examine changes to the whole of the marginal distribution. An intermediate-level study might move from looking at the variability to studying changes in the skewness. In addition to these, questions of homogeneity apply also to the joint distributions.
The concept of homogeneity can be applied in many different ways and, for certain types of statistical analysis, it is used to look for further properties that might need to be treated as varying within a dataset once some initial types of non-homogeneity have been dealt with.
Of variance[edit]

Plot with random data showing homoscedasticity: at each value of x, the y-value of the dots has about the same variance.
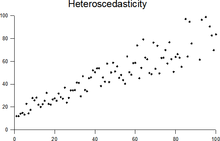
Plot with random data showing heteroscedasticity: The variance of the y-values of the dots increase with increasing values of x.
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings homoskedasticity and heteroskedasticity are also frequently used.[1][2][3]
Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient.
The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and inference based on the assumption of homoskedasticity is misleading. In that case, generalized least squares (GLS) was frequently used in the past.[4][5] Nowadays, standard practice in econometrics is to include Heteroskedasticity-consistent standard errors instead of using GLS, as GLS can exhibit strong bias in small samples if the actual Skedastic function is unknown.[6]
Because heteroscedasticity concerns expectations of the second moment of the errors, its presence is referred to as misspecification of the second order.[7]
The econometrician Robert Engle was awarded the 2003 Nobel Memorial Prize for Economics for his studies on regression analysis in the presence of heteroscedasticity, which led to his formulation of the autoregressive conditional heteroscedasticity (ARCH) modeling technique.[8]
Examples[edit]
Regression[edit]
Differences in the typical values across the dataset might initially be dealt with by constructing a regression model using certain explanatory variables to relate variations in the typical value to known quantities. There should then be a later stage of analysis to examine whether the errors in the predictions from the regression behave in the same way across the dataset. Thus the question becomes one of the homogeneity of the distribution of the residuals, as the explanatory variables change. See regression analysis.
Time series[edit]
The initial stages in the analysis of a time series may involve plotting values against time to examine homogeneity of the series in various ways: stability across time as opposed to a trend; stability of local fluctuations over time.
Combining information across sites[edit]
In hydrology, data-series across a number of sites composed of annual values of the within-year annual maximum river-flow are analysed. A common model is that the distributions of these values are the same for all sites apart from a simple scaling factor, so that the location and scale are linked in a simple way. There can then be questions of examining the homogeneity across sites of the distribution of the scaled values.
Combining information sources[edit]
In meteorology, weather datasets are acquired over many years of record and, as part of this, measurements at certain stations may cease occasionally while, at around the same time, measurements may start at nearby locations. There are then questions as to whether, if the records are combined to form a single longer set of records, those records can be considered homogeneous over time. An example of homogeneity testing of wind speed and direction data can be found in Romanić et al., 2015.[9]
Homogeneity within populations[edit]
Simple populations surveys may start from the idea that responses will be homogeneous across the whole of a population. Assessing the homogeneity of the population would involve looking to see whether the responses of certain identifiable subpopulations differ from those of others. For example, car-owners may differ from non-car-owners, or there may be differences between different age-groups.
Tests[edit]
A test for homogeneity, in the sense of exact equivalence of statistical distributions, can be based on an E-statistic. A location test tests the simpler hypothesis that distributions have the same location parameter.
See also[edit]
- Consistency (statistics)
- Reliability (statistics)
References[edit]
- ^ For the Greek etymology of the term, see McCulloch, J. Huston (1985). “On Heteros*edasticity”. Econometrica. 53 (2): 483. JSTOR 1911250.
- ^
White, Halbert (1980). “A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity”. Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934. - ^
Gujarati, D. N.; Porter, D. C. (2009). Basic Econometrics (Fifth ed.). Boston: McGraw-Hill Irwin. p. 400. ISBN 9780073375779. - ^ Goldberger, Arthur S. (1964). Econometric Theory. New York: John Wiley & Sons. pp. 238–243. ISBN 9780471311010.
- ^ Johnston, J. (1972). Econometric Methods. New York: McGraw-Hill. pp. 214–221.
- ^ Angrist, Joshua D.; Pischke, Jörn-Steffen (2009-12-31). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press. doi:10.1515/9781400829828. ISBN 978-1-4008-2982-8.
- ^ Long, J. Scott; Trivedi, Pravin K. (1993). “Some Specification Tests for the Linear Regression Model”. In Bollen, Kenneth A.; Long, J. Scott (eds.). Testing Structural Equation Models. London: Sage. pp. 66–110. ISBN 978-0-8039-4506-7.
- ^ Engle, Robert F. (July 1982). “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation”. Econometrica. 50 (4): 987–1007. doi:10.2307/1912773. ISSN 0012-9682. JSTOR 1912773.
- ^ Romanić D. Ćurić M- Jovičić I. Lompar M. 2015. Long-term trends of the ‘Koshava’ wind during the period 1949–2010. International Journal of Climatology 35(2):288-302. DOI:10.1002/joc.3981.
Further reading[edit]
- Hall, M.J. (2003) The interpretation of non-homogeneous hydrometeorological time series a case study. Meteorological Applications, 10, 61–67. doi:10.1017/S1350482703005061
- Krus, D.J., & Blackman, H.S. (1988).Test reliability and homogeneity from perspective of the ordinal test theory. Applied Measurement in Education, 1, 79–88 (Request reprint).
- Loevinger, J. (1948). The technic of homogeneous tests compared with some aspects of scale analysis and factor analysis. Psychological Bulletin, 45, 507–529.



