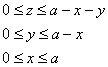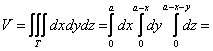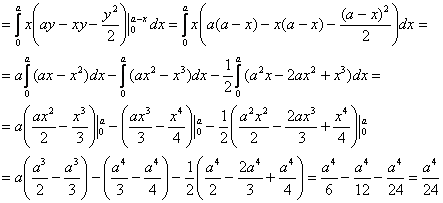Как найти однородные координаты центра масс

Сущность понятия «центр масс»

Понятие “центр масс” широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.

Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке “15 см”. Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.

На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.

Нахождение координат центра масс

Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.

Расстояние между точечными телами равно:

$Delta x = x_2 – x_1$

Пропорция между массами и расстояниями, согласно определению:

$frac{l_1}{l_2} = frac{m_2}{m_1}$,

«Как найти координаты центра масс» 👇

где $l_1$, $l_2$ – расстояния от соответствующих тел до центра масс.

Выразив, длины через координаты

$l_1 = x_c – x_1; l_2 = x_2 – x_c$,

центр масс можно определить как

$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.

где $x_c$ – координата центра тяжести.

Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):

$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$

В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.

Приложения кратных интегралов в механике

Краткая теория

---

Масса и статистические моменты пластики

Если

 – область плоскости

, занятая пластинкой, и

 – поверхностная плотность пластики в точке

, то масса

 пластинки и ее статистические моменты

 и

 относительно осей

 и

 выражаются двойными интегралами:

Если
пластика однородна, то

Координаты центра тяжести пластики

Если

 – центр тяжести пластики, то

где

 – масса пластинки и

 – ее статистические моменты относительно осей
координат.

Моменты инерции пластики

Моменты
инерции пластинки относительно осей

 и

 соответственно равны:

Момент инерции пластики относительно
начала координат:

Полагая

, получаем геометрические моменты инерции плоской
фигуры.

Масса тела, занимающего область
 и статистические моменты тела относительно
координатных плоскостей

где

 – плоскость тела в точке

Координаты центра тяжести

Если тело
однородно, то формулах для координат центра тяжести можно положить

.

Моменты инерции относительно
осей координат

Полагая в
этих формулах

, получаем геометрические
моменты инерции тела.

Примеры решения задач

---

Задача 1

Вычислить
массу материальной пластины, занимающей область

 плоскости

, если поверхностная
плотность

 и границы области

 заданы уравнениями.

Решение

Сделаем
чертеж области

:

Искомая
масса материальной пластины:

Ответ:

---

Задача 2

Найти
статистический момент фигуры, ограниченной линиями

 и

 относительно оси абсцисс.

Решение

Сделаем
чертеж:

Статистический
момент относительно оси

:

Ответ:

---

Задача 3

Вычислить
координаты центра масс однородной

 материальной пластины

, ограниченной данными
линиями:

Решение

Сделаем
чертеж:

Масса
пластинки:

Статистические
моменты:

Искомые
координаты центра масс:

Ответ:

.

---

Задача 4

Вычислить массу тела

, ограниченного заданными поверхностями

 -плотность в
точке

.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Изобразим
тело на рисунке:

С боков
тело будет ограничено цилиндром

 и плоскостями

. Сверху плоскостью

Проекция на плоскость

:

           

Ответ:

---

Задача 5

Найти
момент инерции однородного шара

 с массой

 относительно оси

.

Решение

Момент
инерции относительно оси

 можно найти по формуле:

Шар
однородный, поэтому плотность:

Перейдем
к сферическим координатам:

Получаем:

Ответ:



2.6.2. Центр тяжести тела

Подобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с

помощью двойного интеграла, задача об отыскании центра тяжести тела

решается аналогичным способом – с помощью тройного интеграла.

Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести,

то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени это не

реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил

дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.

Центр тяжести  неоднородного тела  рассчитывается по формулам:
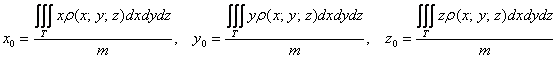
, где  – функция плотности тела, а  – масса тела.

Если же тело однородно (стеклянное, оловянное, пластмассовое и т.д.), то формулы упрощаются. Так как плотность  постоянна, и масса –  есть произведение плотности на объём, получаем:
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла .

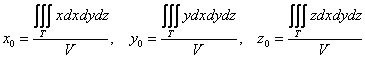
Для центра тяжести однородного тела справедливы следующие утверждения:

– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);

– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;

– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.

Как видите, практически полная аналогия с центром тяжести плоской фигуры.

Ну и, само собой, не могу не порадовать вас тематической задачей:

Пример 42

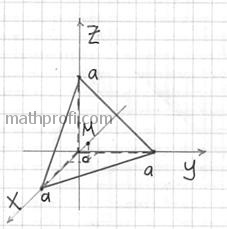
Найти центр тяжести однородного тела, ограниченного поверхностями , . Выполнить чертежи данного тела и его проекции на плоскость .

Решение: искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в

отрезках: . Выберем «а» за единицу

масштаба и выполним трёхмерный чертёж:

На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.
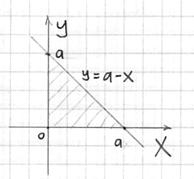
Проекция тела на плоскость  очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие

простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости  нужно решить систему, составленную из их уравнений:
 
Подставляем значение  в 1-е

уравнение системы:  и получаем

уравнение  «плоской» прямой:

Для взятия грядущих интегралов выберем «классический» порядок обхода тела:

Координаты  центра тяжести  тела  вычислим по формулам:
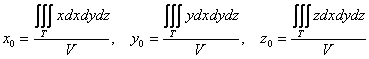
, где  – объём данного тела. И понеслась песня:

1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме

тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем

случае параллелепипед представляет собой куб с ребром «а», а посему: .
Осталось аккуратно провести штатные вычисления:

В примерах с громоздкими преобразованиями рекомендую записывать решение «столбиком» – меньше шансов запутаться:
 (да, так можно – сразу снести

 в средний интеграл)

, и дело за тремя тройными

интегралами:

2) Вычислим «иксовый» интеграл, …и местечка у меня тут не хватает, поэтому решение в столбик отменяется:

Таким образом, «иксовая» координата центра тяжести: 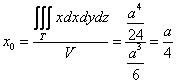, ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь» тела.

Учитывая симметрию тела, две другие координаты должны получиться такими же. Теперь ошибочный финал практически исключён! И

я вам предлагаю рассчитать  самостоятельно, после чего можно записать красивый ответ.

…А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)

3. Криволинейные интегралы

2.6. Физические приложения тройного интеграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Содержание:

1. Центр масс
2. Центр параллельных сил
3. Центр тяжести
4. Центры тяжести некоторых плоских однородных фигур
5. Центр тяжести дуги окружности
6. Центр тяжести кругового сектора
7. Центр тяжести кругового сегмента
8. Центр тяжести треугольника
9. Центр тяжести трапеции
10. Примеры решения задач на тему: Центр масс
11. Способы определения координат центра тяжести тела
12. Метод симметрии
13. Метод разбиения
14. Метод дополнения
15. Экспериментальные способы
16. Центры тяжести некоторых однородных тел
17. Центр тяжести дуги окружности
18. Центр тяжести треугольника
19. Центр тяжести сектора

Центр масс – это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Центр масс

Центр масс – это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.

Центр параллельных сил

Если на тело действует система параллельных сил , ,…, , то точка , через которую проходит равнодействующая этой системы сил, называется центром параллельных сил (рис.9.1).

Координаты центра параллельных сил определяются по зависимостям:

где  – координаты точек приложения сил .

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.

Центр тяжести

Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести­ , которая направлена к центру Земли. Поскольку размеры тела небольшие по сравнению с размерами Земли, то образованную систему сил можно рассматривать как параллельную. Равнодействующая этой параллельной системе сил , которая равна их сумме, называется тяжестью тела, а центр этой системы – точка называется центром тяжести тела (рис.9.2).

Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:

где  – сила тяжести элементарной частицы тела;

 – тяжесть тела;

 – координаты центра тяжести;

 – координаты элементарной частицы тела.

Если тело однородное, то есть удельный вес не меняется по объему , то:

где  – объем тела;

 – объем элементарной частицы.

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:

Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.

Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами  и и зависит от формы площади фигуры:

где  – площадь элементарной части плоской фигуры;

 – площадь плоской фигуры.

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.

Если выбранный элементарный объем  (площадь элементарной площадки в плоском случае) направить к нулю, то формулы для вычисления координат центра тяжести приобретут интегральный вид:

а) для однородного твердого тела:

где  – объем тела, интегрирование выполняется по всему объему тела;

б) для однородной поверхности:

где  – площадь поверхности, интегрирование выполняется по всей поверхности тела;

в) для однородной плоской фигуры, лежащей в плоскости xy:

г) для однородной линии:

где  – длина линии, интегрирование выполняется по всей длине линии.

Центры тяжести некоторых плоских однородных фигур

Для упрощения определения центра тяжести используются следующие вспомогательные правилами:

1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.

Центр тяжести дуги окружности

Центр тяжести дуги окружности  (рис.9.3) лежит на ее оси симметрии и на расстоянии от центра окружности:

где  – радиус окружности;

 – половина центрального угла, опирающегося на дугу .

Центр тяжести кругового сектора

Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сектора.

Центр тяжести кругового сегмента

Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сегмента.

Центр тяжести треугольника

Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан – на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.

Центр тяжести трапеции

Центр тяжести трапеции (рис.9.7) с основаниями  и  и высотой лежит на прямой , которая соединяет середины основ.

Расстояния  и центра тяжести площади трапеции от ее основ определяются по формулам:

Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.

Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, можно определить.

Координаты центра тяжести фигуры определяются по формулам:

где  – координаты центра тяжести первой части плоской фигуры;

 – площадь первой части и т.п.

Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).

В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть .

Координаты центра тяжести фигуры равны:

где  – координаты центра тяжести сплошной фигуры 1, площадь которой равна ;

 – координаты центра тяжести вырезанной части 2, площадь которой равна – .

Первый из этих методов имеет название “метод разбиения”, второй – “метод дополнения”, или “метод отрицательных масс”. В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:

где  – площадь всей фигуры.

Примеры решения задач на тему: Центр масс

Задача № 1

Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.

Решение. Поскольку форма сечения имеет ось симметрии, ось направим вдоль оси симметрии, а ось перпендикулярно ей.

В силу симметричности профиля относительно оси центр тяжести будет лежать на этой оси, то есть

Линиями и поделим профиль на три прямоугольника 1, 2 и 3.

Запишем уравнение для определения абсциссы центра тяжести площади:

где  – абсциссы центров тяжести прямоугольников 1, 2, 3;

 – площади этих прямоугольников.

Поскольку центры тяжести прямоугольников и лежат на пересечении их диагоналей, то (рис.9.10):

Площади этих прямоугольников соответственно равны:

Тогда: 

Таким образом, центр тяжести фигуры лежит в точке с координатами: 

Ответ: 

Задача № 2

Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину  и толщину

Решение. Разделим пересечение линией на два прямоугольника и , центры тяжести которых лежат на пересечении соответствующих диагоналей.

Запишем формулы для координат  и  центра тяжести пересечения:

где  и  – координаты центров тяжести прямоугольников 1 и 2;

,  – площади прямоугольников 1 и 2.

С рис.9.11 видим, что

Тогда: 

Ответ: 

Задача № 3

Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью  радиуса и двумя прямыми равной длины и , причем

Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось . Поскольку центр тяжести площади лежит на оси симметрии, то

Разделим площадь линией на две части: полуокружность и равнобедренный треугольник .

Абсцисса центра тяжести площади будет равняться:

где  – координата центра тяжести половины круга ;

 – координата центра тяжести треугольника ;

,  – площади половины круга и треугольника.

Для определения воспользуемся приведенными в разделе 9.3.2 координатами центра тяжести кругового сектора

В случае половины круга 

Площадь половины круга равна:

Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник равнобедрен, то линия  будет его медианой и расстояние будет равняться третьей части от :

Площадь треугольника равна:

Подставив найденные значения , ,  и  в уравнение для , получим:

Ответ: 

Задача № 4

Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса (рис.9.13), если

Решение. Осью симметрии рассматриваемой фигуры будет диагональ прямоугольника

Поэтому направим ось вдоль этой линии, а ось – перпендикулярно (рис.9.13).

Центр тяжести пластины будет лежать на оси , то есть

Площадь фигуры можно представить как разницу площадей квадрата (положительная площадь) и сектора (отрицательная площадь).

Абсцисса центра тяжести фигуры будет равняться:

где  – абсцисса центра тяжести квадрата ;

 – абсцисса центра тяжести сектора ;

 и  – площади квадрата и сектора.

Для квадрата получим:

Как следует из рис. 9.13, равняется

где  – расстояние от точки к центру тяжести кругового сектора .

Для кругового сектора (раздел 9.3.2) получим:

Поскольку  и , то 

Таким образом, абсцисса равняется:

Площадь кругового сектора :

Подставив значение , ,  и  в формулу для , получим:

Ответ:  

Задача № 5

Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы , осью  и прямой

Решение. На расстоянии  от оси выделяем элементарную площадку шириной (заштрихованная область).

Площадь выделенной элементарной площадки будет равняться:

Площадь фигуры, что ограничена заданными линиями:

Поскольку точка представляет собой пересечение параболы и прямой , то 

Отсюда: 

Тогда:

Абсцисса центра тяжести

Для определения координаты выделим элементарную площадку шириной на расстоянии  от оси .

Площадь выделенной площадки:

Ордината центра тяжести:

Тогда: 

Ответ: 

Способы определения координат центра тяжести тела

Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.

Рассмотрим последовательно эти способы.

Метод симметрии

Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.

Метод разбиения

Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.

Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.

Пример:

Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64

Решение.

Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c₁, c₂ и c₃ соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c₁ (–1,1), c₂ (1,5), c₃ (5,9). Площади каждого тела соответственно равны: I — s₁ = 4 см²; II — s₂ = 20 см²; III — s₃ = 12 см². Площадь всей пластины равна: S = s₁ + s₂ + s₃ = 36 см².

Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим

По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.

Метод дополнения

Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.

Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C₁C₂ = a.

Решение.

Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C₁ и C₂. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату x_C, поскольку вторая координата y_C равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x₁ = 0; x₂ = C₁C₂ = a. Площади тел равны: Общая площадь всего тела будет равна физической разницы между площадями первого и второго тел, а именно
Для определения неизвестной координаты центра тяжести
заданной пластины используем первое уравнение выражения.

Подставив значения всех известных величин в это уравнение, получим

Таким образом, значение координаты x_C отрицательное, а потому, поскольку вторая координата 0 y_C = 0, то центр тяжести пластины C размещен на оси x слева от точки C₁.

Экспериментальные способы

Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.

При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.

Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.

Пример.

Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).

Решение.

Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию . Аналогично определяем вес переднего моста, или реакцию . Вполне понятно, что сумма этих реакций равна общему весу трактора, а именно:

Q = R_A + R_B.

Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна

Откуда определяем продольную координату центра тяжести:

x_C = .

Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.

Центры тяжести некоторых однородных тел

Определим далее координаты центров тяжести некоторых простых однородных тел.

Центр тяжести дуги окружности

Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (y_C = 0). Остается только вычислить координату x_C.

Используем для вычисления этой координаты первое уравнение выражения, а именно

Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M₁ длиной dl, равной:

dl = R · dφ.

Если φ — угол, определяющий положение элемента M M₁ на дуге AB, то координата x элемента M M₁ будет равна:

x = Rcosφ.

Общая длина дуги AB равна:

L = 2α · R.

Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:

Таким образом, координата x_C будет равняться

x_C = .

Центр тяжести треугольника

Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A₁ (x₁, y₁), A₂ (x₂, y₂), A₃ (x₃, y₃) (рис. 1.68). Если провести прямые, которые будут параллельны основе A₁A₃ и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.

Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

где x₁, x₂, …, y₃  — координаты вершин треугольника.

Полезно также знать, что

Центр тяжести сектора

Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.

Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии  от центра сектора. Таким образом, центры тяжести всех треугольников расположены на дуге A´B´. Итак, если 0 ∆φ → 0, то центры тяжести образуют дугу AB, тогда необходимо найти центр тяжести дуги A´B´. Используем формулу, по которой определяется центр тяжести дуги окружности радиусом r:

Тогда учитывая, что

Будем иметь

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2022 года; проверки требуют 3 правки.

Центр масс (тж. центр ине́рции) — геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого^[1]. Радиус-вектор данной точки задаётся формулой

где — зависящая от координат плотность, а интегрирование осуществляется по объёму тела. Центр масс может оказаться как внутри, так и вне тела.

Использование понятия центра масс, а также системы координат, связанной с центром масс, удобно во многих приложениях механики и упрощает расчёты. Если на механическую систему не действуют внешние силы, то её центр масс движется с постоянной по величине и направлению скоростью.

Джованни Чева применял рассмотрение центров масс к решению геометрических задач, в результате были сформулированы теоремы Менелая и теоремы Чевы^[2].

В случае систем материальных точек и тел в однородном гравитационном поле центр масс совпадает с центром тяжести, хотя в общем случае это разные понятия.

Центр масс в классической механике[править | править код]

Определение[править | править код]

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом^[3]:

где  — радиус-вектор центра масс,  — радиус-вектор i-й точки системы,  — масса i-й точки.

Для случая непрерывного распределения масс:

где  — суммарная масса системы,  — объём,  — плотность.
Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Если система состоит не из материальных точек, а из протяжённых тел с массами , то радиус-вектор центра масс такой системы связан с радиус-векторами центров масс тел соотношением^[4]:

Действительно, пусть даны несколько систем материальных точек с массами Радиус-вектор -ной системы:

При переходе к протяженным телам с непрерывным распределением плотности в формулах будут интегралы вместо сумм, что даст тот же результат.

Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.

Примеры[править | править код]

Центры масс плоских однородных фигур

• У отрезка — середина.
• У многоугольников :
  • У параллелограмма — точка пересечения диагоналей.
  • У треугольника — точка пересечения медиан (центроид).
• У правильного многоугольника — центр поворотной симметрии.
• У полукруга — точка, делящая перпендикулярный радиус в отношении от центра круга.

Координаты центра масс однородной плоской фигуры можно вычислить по формулам (следствие из теорем Паппа — Гульдина):

и , где — объём тела, полученного вращением фигуры вокруг соответствующей оси, — площадь фигуры.

Центры масс периметров однородных фигур

• Центр масс сторон треугольника находится в центре вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Это означает то, что если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с центром вписанной окружности дополнительного треугольника или с центром Шпикера.

Использование[править | править код]

Понятие центра масс широко используется в физике, в частности, в механике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

Центр масс в релятивистской механике[править | править код]

В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:

где  — радиус-вектор центра масс,  — радиус-вектор i-й частицы системы,  — полная энергия i-й частицы.

Данное определение относится только к системам невзаимодействующих частиц. В случае взаимодействующих частиц в определении должны в явном виде учитываться импульс и энергия поля, создаваемого частицами^[5].

Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лифшица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (англ. center-of-mass): оба термина эквивалентны.

Скорость центра масс в релятивистской механике можно найти по формуле:

Смежные понятия[править | править код]

Центр масс vs. барицентр[править | править код]

Термин «центр масс» синонимичен одному из значений понятия барицентр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр), однако последнее применяется преимущественно в задачах астрофизики и небесной механики. Под барицентром подразумевается общий для нескольких небесных тел центр масс, вокруг которого эти тела движутся. Примером может выступить совместное движение планеты и звезды (см. рис.) или компонент двойных звёзд. Центр масс (барицентр) в таком случае находится на отрезке длины , соединяющем тела массами и , на удалении от тела .

Другое значение слова барицентр относится, скорее, к геометрии, нежели к физике; в этом значении выражение для координаты барицентра отличается от формулы для центра масс отсутствием плотности (как если бы всегда было const).

Центр масс vs. центр тяжести[править | править код]

Центр масс тела не следует путать с центром тяжести.

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести (действующих на систему) равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

В однородном гравитационном поле центр тяжести всегда совпадает с центром масс. В некосмических задачах гравитационное поле обычно может считаться постоянным в пределах объёма тела, поэтому на практике эти два центра почти совпадают.

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (поскольку реального гравитационного поля нет, то и учёт его неоднородности не имеет смысла). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.

См. также[править | править код]

• Классическая механика
• Теоретическая механика
• Теорема о движении центра масс системы
• Неваляшка
• Барицентр
• Центроид треугольника

Примечания[править | править код]

Литература[править | править код]

• Бобылёв Д. К. Центр, в физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Журавлёв В. Ф.  Основы теоретической механики. 2-е изд. — М.: Физматлит, 2001. — 320 с. — ISBN 5-94052-041-3..