Левой производной функции f(x) в точке х называется левый предел отношения приращения функции $Delta $y к приращению аргумента $Delta $х, когда $Delta $х$to $0:
[f’_{-} (x)=mathop{lim }limits_{Delta xto 0-0} frac{Delta y}{Delta x} ]
Для того, чтобы функция f(x) имела производную в точке х, необходимо и достаточно, чтобы в этой точке функция была непрерывна, и существовали односторонние производные f`-(x) и f`+(x), равные между собой.
Если
[f’_{-} (x)ne f’_{+} (x)]
то в точке x производной не существует, и график функции имеет излом (рис. 1).
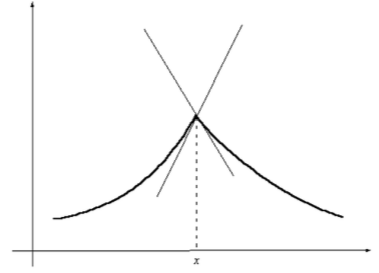
Рисунок 1. Излом функции
Пример 1
Найти левую и правую производные в точке $x_0 = 0$ функции:
y = $| Delta x|$
Решение.
[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{Delta y}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{f(0+Delta x)-f(0)}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{left|Delta xright|-0}{Delta x} =frac{left|Delta xright|}{Delta x} ]
Так как $Delta $х$to $0-, то $Delta $х является маленькой отрицательной величиной, а тогда по определению модуля $|Delta х|$ = -$Delta $х. Отсюда
[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|Delta xright|}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{-left|Delta xright|}{Delta x} =-1]
Аналогично найдем правую производную
[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{Delta y}{Delta x} =mathop{lim }limits_{Delta xto 0+} frac{f(0+Delta x)-f(0)}{Delta x} =mathop{lim }limits_{Delta xto 0+} frac{left|Delta xright|-0}{Delta x} =frac{left|Delta xright|}{Delta x} ]
[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{left|Delta xright|}{Delta x} =mathop{lim }limits_{Delta xto 0-} frac{+left|Delta xright|}{Delta x} =1]
Графически это означает, что функция имеет излом в точке = 0
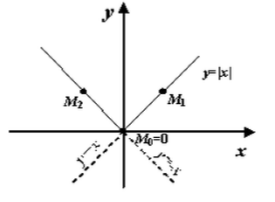
Рисунок 2. Излом функции
[y=left|xright|=left{begin{array}{c} {-x,begin{array}{cc} при & {x
Пример 2
Вычислить производные функции:
[y=left|x^{2} -1right|]
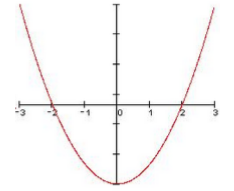
Рисунок 3. График функции
Решение.
Из графика функции видно, что производная не существует в точках -2 и 2. Найдем односторонние производные.
а) Левая производная
[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|(2+Delta x)^{2} -4right|-left|2^{2} -4right|}{Delta x} =-4]
[f’_{-} (0)=mathop{lim }limits_{Delta xto 0-} frac{left|(-2+Delta x)^{2} -4right|-left|left(-2right)^{2} -4right|}{Delta x} =-4]
б) Правая производная
[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{left|(2+Delta x)^{2} -4right|-left|2^{2} -4right|}{Delta x} =4]
[f’_{+} (0)=mathop{lim }limits_{Delta xto 0+} frac{left|(2+Delta x)^{2} -4right|-left|2^{2} -4right|}{Delta x} =4]
Вывод: Правая производная при 2 и -2 существует и равна 4. Левая производная при 2 и -2 существует и равна -4.
Найдем производные при х=1.
[mathop{lim }limits_{Delta xto 0} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]
[mathop{lim }limits_{Delta xto 0-} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]
[mathop{lim }limits_{Delta xto 0+} frac{left|(1+Delta x)^{2} -4right|-left|1^{2} -4right|}{Delta x} =-2]
Значит, производная в точке 1 существует и равна -2
I.
Пусть функция
![]()
определена в точке х0
и в некоторой правосторонней окрестности
u+(x0)
этой точки. В этом случае для вычисления
предела отношения

приходится ограничиться приближением
![]()
к нулю лишь справа (![]() ;
;
![]()
стремится к нулю, оставаясь больше
нуля).
Если существует
конечный или бесконечный (определенного
знака) предел
 ,
,
то этот предел называется соответственно
конечной или бесконечной правосторонней
производной
функции
![]()
в точке x0
и обозначается
![]() .
.
II.
Пусть функция
![]()
определена в точке x0
и в некоторой левосторонней окрестности
u–(x0)
этой точки. В этом случае при вычислении
предела отношения

приходится ограничиться приближением
![]()
к нулю лишь слева (![]() ;
;
![]()
стремится к нулю, оставаясь меньше
нуля).
Если существует
конечный или бесконечный (определенного
знака) предел
 ,
,
то этот предел называется соответственно
конечной или бесконечной левосторонней
производной
функции
![]()
в точке х0
и обозначается
![]() .
.
Замечание.
Об односторонних производных функции
![]()
в точке х0
можно говорить и в случае, когда эта
функция определена в точке х0
и в некоторой окрестности u(x0)
точки x0
(т. е.
![]()
определена одновременно и в u+(x0)
и в u–(x0)).
Для функции
![]() ,
,
определенной в u(x0),
справедливы утверждения:
-
Если у функции

в точке x0
существует конечная или бесконечная
(определенного знака) обычная (т. е.
двусторонняя) производная
 ,
,
то у этой функции в точке x0
существуют одновременно

и
 ,
,
причем
 .
. -
Если у функции

в точке x0
существуют одновременно конечные или
бесконечные (определенного знака)

и

и если
 ,
,
то у этой функции в точке х0
существует соответственно конечная
или
бесконечная (определенного знака)
обычная (т. е. двусторонняя) производная ,
,
равная общему значению односторонних
производных.
Отметим, что бывают
случаи, когда у функции
![]()
в точке х0
существуют одновременно
![]()
и
![]() ,
,
но
![]() .
.
В этих случаях обычной (т. е. двусторонней)
производной у функции
![]()
в точке х0
нет.
В качестве примера
рассмотрим функцию
![]() .
.
Найдем правостороннюю и левостороннюю
производные этой функции в точке
![]() .
.
Имеем
![]() .
.
Если
![]() ,
,
то
![]()
и, следовательно,
![]() .
.
Если
![]() ,
,
то
![]()
и, следовательно,
 .
.
Видим, что
![]() .
.
Значит, производная функции
![]()
в точке
![]()
в обычном смысле (т. е. двусторонняя) не
существует.
В качестве еще
одного примера рассмотрим функцию
![]() .
.
Найдем правостороннюю и левостороннюю
производные этой функции в точке
![]() .
.
Имеем
![]() .
.
Следовательно,
 ;
;
 .
.
Видим, что и в этом
примере
![]() .
.
Значит, у функции
![]()
в точке
![]()
не существует обычной (т. е. двусторонней)
производной.
Графики функций
![]()
и
![]()
имеют вид, схематически изображенный
на рис. 4.7 и 4.8 соответственно.
|
|
|
|
Рис.
|
Рис.
|
§2. Понятие дифференцируемости функции
1. Понятие
дифференцируемости функции в данной
точке. Пусть
функция
![]()
определена в некотором промежутке X,
и пусть точка
![]() .
.
Дадим значению х0
аргумента приращение
![]()
— любое, но такое, что
![]()
и точка
![]() .
.
Пусть
![]() ,
,
т.е.
![]()
есть приращение функции
![]()
в точке х0,
соответствующее приращению
![]()
аргумента.
Определение.
Функция
![]()
называется дифференцируемой в точке
х0,
если приращение
![]()
этой функции в точке х0
может быть представлено в виде
![]() ,
,
(1)
где А
— некоторое число, не зависящее от
![]() ,
,
а
![]()
— функция аргумента
![]()
такая, что
![]()
при
![]() .
.
Заметим, что функция
![]()
в точке
![]()
может принимать любое значение (при
этом в точке х0
представление (1) остается справедливым).
Ради определенности можно положить,
например,
![]() .
.
(Тогда частное значение функции
![]()
в точке
![]()
будет совпадать с ее предельным значением
в этой точке.)
Теорема.
Для того, чтобы функция
![]()
была дифференцируемой в точке х0,
необходимо и достаточно, чтобы она имела
в этой точке конечную производную.
Необходимость.
Дано: функция
![]()
дифференцируема в точке х0.
Требуется доказать, что существует
конечная производная
![]() .
.
► По условию
функция
![]()
дифференцируема в точке х0.
Но тогда приращение
![]()
этой функции в точке х0,
соответствующее приращению аргумента
![]() ,
,
представимо в виде
![]() ,
,
где
![]()
при
![]() .
.
Предположив, что
![]()
и поделив обе части последнего равенства
на
![]() ,
,
получим
![]() .
.
Переходя здесь к
пределу при
![]() ,
,
находим
![]() .
.
А это означает, что
![]()
существует конечная, причем
![]() .
.
◄
Достаточность.
Дано: функция
![]()
имеет в точке х0
конечную производную
![]() .
.
Требуется доказать, что функция
![]()
дифференцируема в точке х0.
► По условию
![]()
— существует конечная. Но тогда, как мы
знаем, разность
![]()
есть бесконечно малая функция при
![]() .
.
Значит, если положить
![]() ,
,
то
![]() .
.
Имеем, следовательно,
![]() ,
,
откуда
![]()
причем
![]()
при
![]() .
.
Видим, что полученное представление
![]()
совпадает с представлением (1), если
обозначить через А
не зависящее от
![]()
число
![]() .
.
Тем самым доказано, что функция
![]()
дифференцируема в точке х0.
◄
Замечание.
Из доказанной теоремы следует, что
дифференцируемость функции
![]()
в точке х0
равносильна существованию в этой точке
конечной производной
![]() .
.
2. Связь между
понятиями дифференцируемости и
непрерывности функции.
Имеет место следующее утверждение.
Теорема.
Если функция
![]()
дифференцируема в точке х0,
то она непрерывна в точке х0.
► Так как функция
![]()
дифференцируема в точке х0,
то ее приращение
![]()
в этой точке представимо в виде
![]() ,
,
где А —
постоянное число, не зависящее от
![]() ,
,
а
![]()
при
![]() .
.
Из последнего равенства следует, что
![]() ,
,
т. е. что бесконечно малому приращению
аргумента отвечает бесконечно малое
приращение функции. А это означает, что
функция
![]()
непрерывна в точке х0.
◄
Замечание.
Доказанная теорема необратима: из
непрерывности функции
![]()
в точке х0
не вытекает дифференцируемость этой
функции в точке х0.
Существуют функции, непрерывные в
некоторой точке, но не являющиеся в этой
точке дифференцируемыми. Примером такой
функции может служить функция
![]() .
.
Эта функция непрерывна в точке
![]() ,
,
но она не является дифференцируемой в
этой точке, ибо у нее в точке
![]()
не существует производная (это показано
в предыдущем § 1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Главная
- Справочник
- Односторонние производные
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Односторонние производные
Определение
Правой производной $y_{+}^{prime}$ функции
$y=f(x)$ в данной точке
$x_0$ называется величина:
$$y_{+}^{prime}=f^{prime}left(x_{0}+0right)=lim _{Delta x rightarrow 0_{+}} frac{Delta y}{Delta x}$$
а левой производной – величина:
$$y_{-}^{prime}=f^{prime}left(x_{0}-0right)=lim _{Delta x rightarrow 0_{-}} frac{Delta y}{Delta x}$$
если эти пределы существуют.
Теорема
Для того чтобы в точке $x$ существовала
производная $f^{prime}(x)$, необходимо и достаточно,
чтобы в точке $x$ функция
$y=f(x)$ имела правую и левую производные, и эти
производные были равны между собой: $y^{prime}(x)=y_{+}^{prime}(x)=y_{-}^{prime}(x)$ .
Читать дальше: дифференциал функции.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
Производной функции y=f(x)y = f(x) в точке x0x_0 называется предел отношения приращения функции в этой точке к приращению аргумента ΔxDelta x при Δx→0Delta x→0 (при условии существования данного предела).
Онлайн-калькулятор
Пусть задана функция y=f(x)y = f(x). Выберем любую точку x0x_0 из области определения DD этой функции. Приращение аргумента функции в точке x0x_0:
ΔxDelta x такое, что x0+Δx∈Dx_0 + Delta xin D.
Тогда Δy=f(x0+Δx)−f(x0)Delta y =f (x_0 + Delta x) – f(x_0).
Пусть f(x)=x3f(x) = x^3, x0=5x_0=5, Δx=1Delta x =1.
Вычислим ΔyDelta y:
Δy=f(x0+Δx)−f(x0)=(5+1)3−53=216−125=91Delta y = f(x_0 + Delta x) – f(x_0) = (5+1)^3 – 5^3 = 216 – 125 = 91
Обозначение производной функции
Производная функции в точке x=x0x=x_0 обозначается как f′(x0)f'(x_0):
f′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δxf'(x_0) = displaystylelim_{Delta x→0} frac{Delta y}{Delta x} = displaystylelim_{Delta x→0} frac{f (x_0 + Delta x) – f(x_0)}{Delta x}
Пусть для некоторого x0:f′(x0)=limΔx→0ΔyΔx=±∞x_0:f'(x_0) = displaystylelim_{Delta x→0}frac{Delta y}{Delta x} = ±∞.
В этом случае f(x)f(x) имеет в точке x0x_0 бесконечную производную.
Вычислим производную f(x)=x2f(x) = x^2 в точке x=x0x = x_0.
Снабдим аргумент xx в точке x0x_0 приращением ΔxDelta x:
Δy=f(x0+Δx)−f(x0)=(x0+Δx)2−x02=x02+2×0Δx+(Δx)2−x02=Delta y= f(x_0 + Delta x) – f(x_0) =(x_0 + Delta x)^2 – x_0^2 = x_0^2 +2x_0Delta x + (Delta x)^2 – x_0^2 =
=2×0Δx+(Δx)2=2x_0Delta x + (Delta x)^2
Отсюда:
ΔyΔx=2×0Δx+(Δx)2Δx=Δx(2×0+Δx)Δx=2×0+Δxfrac{Delta y}{Delta x} =frac{2x_0Delta x + (Delta x)^2}{Delta x} =frac{Delta x(2x_0 + Delta x)}{Delta x} =2x_0 + Delta x
Найдем предел этого отношения, устремив ΔxDelta x к нулю:
limΔx→0ΔyΔx=2×0+0=2x0displaystylelim_{Delta x→0}frac{Delta y}{Delta x} = 2x_0 + 0 = 2x_0
f′(x0)=2x0f'(x_0) = 2x_0
Односторонние производные
Правой производной функции f(x)f(x) в точке x0x_0 называется предельное значение отношения ΔyDelta y к ΔxDelta x при Δx→0+Delta x→0+, если данный предел существует.
Левой производной называется предельное значение того же отошения при Δx→0−Delta x→0-
Обозначается как f+′(x0)f’_+(x_0) и f−′(x0)f’_- (x_0).
f+′(x0)=limΔx→0+ΔyΔx=limΔx→0+f(x0+Δx)−f(x0)Δxf’_+(x_0) = displaystylelim_{Delta x→0+}frac{Delta y}{Delta x} = displaystylelim_{Delta x→0+}frac{f(x_0 + Delta x) – f(x_0)}{Delta x}
f−′(x0)=limΔx→0−ΔyΔx=limΔx→0−f(x0+Δx)−f(x0)Δxf’_-(x_0) = displaystylelim_{Delta x→0-}frac{Delta y}{Delta x} = displaystylelim_{Delta x→0-}frac{f(x_0 + Delta x) – f(x_0)}{Delta x}
Напомним, что Δx→0+Delta x→0+ и Δx→0−Delta x→0- обозначают соответственно: Δx→0Delta x→0, Δx>0Delta x>0 и Δx→0Delta x→0, Δx<0Delta x<0
Правую и левую производные называют односторонними.
Из того, что f(x)f(x) имеет производную в точке x0x_0, следует: f(x)f(x) имеет в этой точке равные правую и левую производные. Из существования односторонних производных в точке не следует, что в ней имеется производная.
Рассмотрим функцию f(x)=∣x∣f(x) = |x|. Возьмем x0=0x_0 = 0 Тогда f+′(0)=1f’_+(0) = 1, f−′(0)=−1f’_- (0) = -1. Правая и левая производные существуют в точке x0=0x_0=0, но их значения не одинаковы, поэтому производной в x0x_0 = 0 не существует.


