Как найти односторонние углы при параллельных прямых - Сайт, где вы сможете решить свои вопросы

Внутренние односторонние углы — теория, правило и свойства

Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.

Углы по определению

Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.

Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.

Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.

Доказательство теоремы

Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.

Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.

Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.

Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.

Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.

Следствие из свойства прямых

На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.

Далее можно провести через С1 линию с, перпендикулярную а.

Затем через точку А нужно начертить АС2, которая параллельна с.

После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.

Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.

Построение параллелограмма

Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.

Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.

Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:

По построению AB=BD=AD.

Следовательно, AB=CD.

Точки C и D равноудалены от A и B.

Отрезки AB и CD параллельны.

Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.

Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.

Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.

Углы при пересечении двух прямых

Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.

При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.

На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).

Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:

Углы при пересечении параллельных прямых

Если секущая пересекает две параллельные прямые линии, то:

внутренние накрест лежащие углы равны;
сумма внутренних односторонних углов равна 180°;
соответственные углы равны;
внешние накрест лежащие углы равны;
сумма внешних односторонних углов равна 180°.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

[spoiler title=”источники:”]

http://izamorfix.ru/matematika/planimetriya/ugly_dvuh_pryam.html

http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/

[/spoiler]

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Параллельные прямые
Теорема об односторонних углах

Советуем посмотреть:

Параллельные прямые

Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Параллельные прямые

Правило встречается в следующих упражнениях:

7 класс

Задание 208,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 376,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 387,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 388,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 399,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 710,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 731,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 891,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1030,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1233,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы при параллельных прямых и секущей

Пусть прямая пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна $180^{circ}$ .

Углы 3 и 5 (а также 1 и 7, 2 и 8, 4 и 6) — накрест лежащие.

Накрест лежащие углы равны.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна $180^{circ}$ , то есть

$angle 1+angle 6=180^{circ}$ ,

$angle 4+angle 7=180^{circ}$ .

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.

Соответственные углы равны, то есть

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач по геометрии, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть две параллельных прямые и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это – один из шагов, из которых и состоит решение.

В этой статье – полезные теоремы и примеры решения задач ЕГЭ и ОГЭ по теме «Углы при параллельных прямых и секущей».

Этот материал можно использовать для проектов по геометрии, в работе на уроке и самостоятельно.

Теорема 1.

Углы с соответственно параллельными сторонами равны, если они оба острые или тупые.

Доказательство:

Дано два острых угла: и Известно, что их стороны параллельны: и

Докажем, что

Пусть

Тогда как соответственные углы при параллельных прямых CA и NF и секущей CB.

как соответственные углы при параллельных прямых CB и NM и секущей NF.

Отсюда следует, что что и требовалось доказать.

Аналогично и для тупых углов.

Теорема 2.

Углы с соответственно параллельными сторонами в сумме составляют $180{}^circ ,$ если один из них острый, а другой тупой.

Доказательство:

Дано: – острый, а – тупой. Известно, что их стороны параллельны: и

Докажем, что сумма углов и равна $180{}^circ .$

Пусть Продолжим луч NM за точку N и получим прямую MK.

Получили два острых угла, и с параллельными сторонами. Согласно теореме 1, они равны, т. е.

$angle MNF+angle FNK=180{}^circ$ как смежные. Значит, $angle MNF+angle ACB=180{}^circ.$

Теорема доказана.

Теорема 3.

Если накрест лежащие углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей AB накрест лежащие углы равны:

Докажем, что Если углы 1 и 2 прямые, то прямые и перпендикулярны к прямой AB и, следовательно, параллельны.

Рассмотрим случай, когда углы 1 и 2 не прямые.

Из середины О отрезка АВ проведем перпендикуляр OH к прямой

На прямой от точки В отложим отрезок ${BH}_1$ равный отрезку AH

по двум сторонам и углу между ними, поэтому и Из равенства следует, что точка H_1 лежит на продолжении луча OH, т. е. точки H, O и H_1 лежат на одной прямой, а из равенства следует, что угол 6 – прямой (так как угол 5 – прямой). Итак, прямые и перпендикулярны к прямой HH_1, поэтому они параллельны. Теорема доказана.

Теорема 4.

Если соответственные углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей соответственные углы равны, например

Так как углы 2 и 3 – вертикальные, то Из этих двух равенств следует, что . Но углы 1 и 3 – накрест лежащие, поэтому прямые и параллельны. Теорема доказана.

Теорема 5.

Если сумма односторонних углов равна 180 градусов, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей сумма односторонних углов равна $180{}^circ ,$ например $angle 1+angle 4=180{}^circ.$

Так как углы 3 и 4 – смежные, то Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые и параллельны. Теорема доказана

И самое главное. Подборка примеров заданий ОГЭ и ЕГЭ по темам: углы при параллельных прямых и секущей, внешние накрест лежащие и внутренние накрест лежащие углы, односторонние углы.

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задача 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.

Решение:

Стороны BC и AD параллелограмма параллельны, АК – секущая. Углы и равны как накрест лежащие.

– равнобедренный треугольник.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

AB=BK=5.

$P_{ABCD}=left(AB+BCright)cdot 2;$

$P_{ABCD}=left(5+19right)cdot 2=48.$

Ответ: 48.

Задача 2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.

Найдите AB, если AF=24, BF=10.

Решение:

Основания трапеции АD и ВС параллельны, поэтому углы BAD и АВС – односторонние при параллельных прямых АD и ВС и секущей АВ. Сумма односторонних углов равна

Сумма углов, прилежащих к боковой стороне трапеции, равна $180{}^circ .$

Мы получили, что

AF – биссектриса угла А,

BF – биссектриса угла В, поэтому

$angle FAB=frac{1}{2}angle BAD;; angle ABF=frac{1}{2}angle ABC,$ тогда

Из треугольника AFB получим, что $AFB=90{}^circ .$

Мы доказали теорему:

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AFB – прямоугольный.

По теореме Пифагора, ${AB}^2={AF}^2+{BF}^2Rightarrow AB=sqrt{{24}^2+{10}^2}=sqrt{676}=26.$

Ответ: 26.

Задача 3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.

Решение:

Пусть М – середина АВ, N – середина ВС. Тогда MN – средняя линия треугольника АВС,

Значит, как односторонние углы при параллельных прямых и и секущей АВ.

по двум углам.

Отсюда $displaystyle frac{AB}{BM}=displaystyle frac{AC}{MN}Rightarrow BM=displaystyle frac{ABcdot MN}{AC}$ ;

$BM=displaystyle frac{28cdot 12}{16}=21.$

Ответ: 21.

Задача 4. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108 ${}^circ.$ Найдите угол B этой трапеции. Ответ дайте в градусах.

Решение:

ABCD – трапеция, – основания, AB – секущая.

Значит, angle A и angle B – внутренние односторонне углы.

Отсюда $angle B=180{}^circ -108{}^circ =72{}^circ.$

Ответ: 72.

Задача 5. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Сумма углов, прилежащих к боковой стороне параллелограмма, равна $180{}^circ .$

Это значит, что $angle BAD +angle ABC = 180{}^circ.$

AК – биссектриса угла А,

BК – биссектриса угла В, поэтому

$angle KAB=frac{1}{2}angle BAD; ; angle ABK=frac{1}{2}angle ABC,$ тогда

$angle KAB+angle ABK= 90{}^circ .$

Из треугольника AKB получим, что $angle ABK= 90{}^circ .$

Мы доказали теорему:

Биссектрисы углов параллелограмма, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AKB – прямоугольный.

Расстояние от точки K до стороны AB – это длина перпендикуляра, проведенного из точки на прямую АВ, т.е. KH=4.

по гипотенузе и острому углу

Аналогично, по гипотенузе и острому углу

Получили:

Тогда $S_{ABCD}=ADcdot MN$ ; $S_{ABCD}=8cdot 7=56.$

Ответ: 56.

Задача 6. На плоскости даны четыре прямые. Известно, что $angle 1=120{}^circ ,$ $angle 2=60{}^circ ,$ $angle 3=55{}^circ .$ Найдите Ответ дайте в градусах.

Решение:

angle 1 и angle 2 – это внутренние односторонние углы,

$angle 1+angle 2=120{}^circ +60{}^circ =180{}^circ.$

Отсюда следует, что прямые параллельны, т.е.

Рассмотрим углы при параллельных прямых и секущей d.

angle 3 и angle 4 – это односторонние углы, а значит, они равны: $angle 3=angle 4=55{}^circ.$

Ответ: 55.

Задача 7. Прямые m и n параллельны. Найдите если $angle 1=22{}^circ ,$ $angle 2=72{}^circ .$ Ответ дайте в градусах.

Решение:

$mparallel nRightarrow angle 1=angle 4=22{}^circ$ как односторонние углы.

Сумма углов треугольника равна $180{}^circ .$

Для треугольника на рисунке:

$angle 2+angle 3+angle 4=180{}^circ Rightarrow angle 3=180{}^circ -72{}^circ -22{}^circ =86{}^circ .$

Ответ: 86.

Задача 8. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30 ${}^circ$ и 45 ${}^circ.$ Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение:
$angle A=angle BAC+angle CAD=30{}^circ +45{}^circ =75{}^circ ,$

angle A и angle B – это внутренние односторонние углы при параллельных прямых.

и секущей АВ, их сумма равна $180{}^circ .$

Тогда $angle B=180{}^circ -angle A=180{}^circ -75{}^circ =105{}^circ .$

Это и есть наибольший угол параллелограмма.

Ответ: 105.

Задача 9. Найдите величину тупого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15 ${}^circ.$ Ответ дайте в градусах.

Решение:

AK – биссектриса угла А параллелограмма ABCD, $angle A=30{}^circ.$

angle A и angle B – внутренние односторонние углы при параллельных прямых.

и секущей АВ. Их сумма равна $180{}^circ ,$ значит, $angle B=180{}^circ -30{}^circ =150{}^circ.$

Ответ: 150.

Задача 10. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=169{}^circ .$ Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение: тогда – равнобедренный, в нем OC= CD. Значит, $angle COD=angle CDO=displaystyle frac{180{}^circ -169{}^circ }{2}=5,5{}^circ .$

Ответ: 5,5.

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Задача 1, ЕГЭ. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Пусть BM – биссектриса тупого угла B. По условию, отрезки MD и AB равны 3x и 4x соответственно.

Рассмотрим углы CBM и BMA. Поскольку AD и BC параллельны, BM – секущая, углы CBM и BMA являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник ABM – равнобедренный, следовательно, AB = AM = 4x.

Периметр параллелограмма – это сумма всех его сторон, то есть

7x+7x+4x+4x=88.

Отсюда x=4, 7x=28.

Ответ: 28.

Задача 2, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на рисунок. По условию, $alpha -beta =50{}^circ ,$ то есть $alpha =beta +50{}^circ .$

Углы alpha и beta – односторонние при параллельных прямых и секущей, следовательно,

$alpha +beta =180{}^circ ,$ по свойству односторонних углов.

Итак, $2beta +50{}^circ =180{}^circ.$

$beta =65{}^circ ,$ тогда $alpha =115{}^circ .$

Ответ: 115.

Задача 3, ЕГЭ. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение:

angle B и angle C – внутренние односторонние углы и при параллельных прямых

и и секущей BC; их сумма равна $180{}^circ .$

BE – биссектриса угла В, значит как накрест лежащие углы при и секущей BE. Тогда – равнобедренный,

Аналогично, CE – биссектриса угла С, значит как накрест лежащие углы при и секущей CE. Тогда – равнобедренный и

Значит

Ответ : 10.

Задача 4, ЕГЭ. В ромбе ABCD угол ABC равен 122 ${}^circ.$ Найдите угол ACD. Ответ дайте в градусах.

Решение:

angle B и angle C – это внутренние односторонние углы при параллельных прямых.

и секущей BC, их сумма равна $180{}^circ .$

Значит, $angle C=180{}^circ -angle B=180{}^circ -122{}^circ =58{}^circ .$

ABCD – ромб, диагонали ромба делят его углы пополам.

Тогда $angle ACD=58div 2=29{}^circ .$

Ответ: 29.

Задача 5, ЕГЭ. Угол между стороной и диагональю ромба равен $54{}^circ .$ Найдите острый угол ромба.

Решение:

Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба. Поэтому один из углов ромба равен градусов, и это тупой угол ромба. Тогда острый угол ромба равен $180{}^circ -108{}^circ =72{}^circ .$

Ответ: 72.

Задача 6, ЕГЭ. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 ${}^circ.$ Найдите площадь трапеции.

Решение:

Пусть $angle D=150{}^circ ; AB=18; DC=6; AD=7.$

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними при и секущей BC. Их сумма равна $180{}^circ .$

Тогда $angle A=30{}^circ .$ Построим высоту из вершины Получим прямоугольный треугольник с острым углом в 30 ${}^circ .$

Высота трапеции DH – это катет, лежащий напротив угла в $30{}^circ$ и равный половине гипотенузы, т. е.

Отсюда $S_{ABCD}=displaystyle frac{DC+AB}{2}cdot h;$ $S_{ABCD}=displaystyle frac{6+18}{2}cdot 3.5=12cdot 3.5=42.$

Ответ: 42.

Задача 7, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

У равнобедренной трапеции углы при основании равны т.е.

По условию, $angle D-angle B=50{}^circ Rightarrow angle C-angle B=50{}^circ ;$

angle C и прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых
и и секущей BC. Их сумма равна $180{}^circ .$

$angle C+angle B=180{}^circ.$

Получили:

$left{ begin{array}{c}angle C-angle B=50{}^circ \angle C+angle B=180{}^circ end{array}right. .$

Сложив два уравнения, получим: $2angle C=230{}^circ ,$ тогда $angle C=115{}^circ.$

Ответ: 115.

Задания ЕГЭ Базового уровня, геометрия. Свойства углов при параллельных прямых и секущей.

Задание 1. Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол $150{}^circ .$ Найдите площадь трапеции.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных основаниях трапеции и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол трапеции равен 30 ${}^circ .$ Построив высоту, мы увидим, что она лежит против прямого угла в прямоугольном треугольнике. Значит, высота равна половине боковой стороны, т.е. h=4.

Отсюда

Ответ: 60.

Задание 2. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен $135{}^circ .$ Найдите меньшую боковую сторону.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $45{}^circ .$

Вторая высота отсекает равнобедренный прямоугольный треугольник с катетом, равным разности оснований. Значит, высота равна: 7–4=3.

Отсюда

Ответ: 16,5.

Задание 3. В трапеции ABCD известно, что AB = CD, $angle BDA=40{}^circ$ и $angle BDC=30{}^circ .$ Найдите угол ABD. Ответ дайте в градусах.

Решение:

$angle D=angle BDA+angle BDC=40{}^circ +30{}^circ =70{}^circ .$ Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $110{}^circ .$

Нам дана трапеция, в которой AB=CD. Очевидно, что это боковые стороны, и трапеция равнобедренная с основаниями и .

и параллельны, BD секущая, тогда $angle ADB=angle DBC=40{}^circ .$

$angle ABD=angle ABC-angle DBC=110{}^circ -40{}^circ =70{}^circ.$

Ответ: 70.

Задание 4. В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке K. Найдите KC, если AB = 4, а периметр параллелограмма равен 20.

Решение:

ABCD – параллелограмм, тогда AB = DC = 4.

AK – биссектриса угла А, значит,

как накрест лежащие углы при параллельных прямых и и секущей AK.

Получили, что – равнобедренный и

$P_{ABCD}=left(AB+ADright)cdot 2=20,$ значит

Ответ: 2.

Задание 5. Прямые m и n параллельны (см. рисунок). Найдите если $angle 1=117{}^circ ,$ $angle 2=24{}^circ .$ Ответ дайте в градусах.

Решение:

$angle 2=angle 4=24{}^circ$ (как накрест лежащие углы).

$angle 1+angle 4+angle 3=180{}^circ$ (развернутый угол).

Тогда $angle 3=180{}^circ -left(angle 1+angle 4right)=180{}^circ -left(117{}^circ +24{}^circ right)=39{}^circ .$

Ответ: 39.

Задание 6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=104{}^circ .$ Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение:

Пусть диагонали пересекаются в точке О, т.е.

$AC=2ABRightarrow AB=displaystyle frac{1}{2}cdot ACRightarrow AB=AO=OC=CD.$

и параллельны, АС – секущая, $Rightarrow angle BAC=angle ACD=104{}^circ .$

– равнобедренный, отсюда угол между диагоналями равен:

$angle BOA=displaystyle frac{180{}^circ -104{}^circ }{2}=38{}^circ .$

Ответ: 38.

Если вам понравился наш материал на тему “Углы при параллельных прямых и секущей” – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

На этой странице вы узнаете:

Какими бывают углы?
По каким признакам можно сказать, что треугольники равны?
Что такое коэффициент подобия?
Какие бывают многоугольники?
Какими формулами пользоваться, чтобы найти площадь фигуры?
Что такое окружность и из чего она состоит?
Когда можно вписать окружность в многоугольник, а когда около него можно её описать?

Прямая, отрезок, луч, углы

Квадрат, круг, треугольник. Несомненно, вы знаете о таких геометрических фигурах, эти фигуры относятся к разделу геометрии, который называется планиметрия. Планиметрия – это наука о изучении геометрических фигур на плоскости. Точки, прямые, отрезки, лучи и углы являются основой этого раздела геометрии. Давайте их и рассмотрим.

Прямая – это линия, не имеющая ни начала, ни конца, такая линия может быть бесконечной.

Отрезок – это часть прямой, ограниченная с обеих сторон.

Луч – это отрезок, ограниченный только с одной стороны.

Угол – это фигура, образованная двумя лучами, исходящими из одной точки, измеряется в градусах.

Рассмотрим части угла:

Углы бывают четырёх видов:

Смежные и вертикальные углы

Смежные углы – это углы, имеющие одну общую сторону, а две другие стороны этих углов лежат на одной прямой.

Смежные углы в сумме дают 180°.

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого угла.

Рассмотрим углы при параллельных прямых

Накрест лежащие углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по разные стороны от секущей между параллельным прямыми. Такие углы всегда равны.

Внутренние односторонние углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей между параллельным прямыми. Сумма этих углов 1800.

Соответственные углы — это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей так, что один угол находится между двумя прямыми относительно одной прямой, а другой угол прилегает к другой прямой с внешней стороны. Эти углы равны.

Пусть a || b, а с – секущая

Тогда 3 и 6, 4 и 5 накрест лежащие; 3 и 5, 4 и 6 внутренние односторонние; 1 и 5, 2 и 6, 3 и 7, 4 и 8 соответственные

Треугольники, их виды и признаки их равенства

Сумма углов любого треугольника равна 180°

Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон

Элементы треугольника:

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)

Биссектриса – это отрезок, делящий угол на два равных угла. Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)

Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)

Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.

Виды треугольников:

У равностороннего треугольника все стороны равны и углы по 600.

У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой.

У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы

Признаки равенства треугольников:

Треугольники равны по двум сторонам и углу между ними

АВ = А₁В₁

АС = А₁С₁

Угол ВАС = угол В₁А₁С₁

Треугольники равны по стороне и двум прилежащим к ней углам

АВ = А₁В₁

Угол ВАС = угол В₁А₁С₁

Угол АВС = угол А₁В₁С₁

Треугольники равны по трём сторонам

АВ = А₁В₁

АС = А₁С₁

ВС = В₁С₁

Давайте теперь разберёмся, что значит подобие:

Если треугольники похожие, но отличаются только размером, тогда поможет подобие треугольников

Коэффициент подобия – это число, в которое отличаются стороны треугольников

Если АВС подобен А1В1С1, тогда верно равенство, где к – коэффициент подобия

Если треугольники подобны, тогда отношение их площадей равно квадрату коэффициента подобия

Признаки подобия треугольников:

По двум сторонам и углу между ними

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны

По двум углам

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны

По трём сторонам

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны

Площадь треугольника

Площадь треугольника, если известна высота и основание, к которому она проведена

Площадь треугольника с двумя известными сторонами и углом между ними

Площадь прямоугольного треугольника с известными катетами

Площадь правильного треугольника, если известна только сторона

Формула Герона позволяет вычислить площадь треугольника, если известны его стороны

Площадь треугольника, когда известен полупериметр и радиус вписанной окружности

Площадь треугольника, когда известны стороны и радиус описанной окружности

Многоугольник

Многоугольник – это часть плоскости, ограниченная замкнутой ломаной линией

Многоугольники бывают выпуклые и невыпуклые

Многоугольник является выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону

Для нахождения площади любого выпуклого четырёхугольника существует формула:

Виды многоугольников:

Параллелограмм – это четырёхугольник, у которого стороны попарно параллельны

Свойства параллелограмма:

Противоположные стороны равны
Противоположные углы равны
Диагонали делятся точкой пересечения пополам

Формулы площади

Прямоугольник – это четырехугольник, у которого все углы прямые

Свойства прямоугольника:

Диагонали равны
Противоположные стороны параллельны и равны
Угол между сторонами прямой
Сумма углов 360 градусов

Формула площади

Квадрат – это частный случай прямоугольника

Свойства квадрата:

Диагонали взаимно перпендикулярны и равны
Диагонали делят углы квадрата пополам
Все стороны равны
Угол между сторонами прямой
Сумма углов 360 градусов

Формулы площади

Трапеция – это четырёхугольник с двумя параллельными сторонами (основаниями), а две другие стороны у него не параллельны

Трапеция может быть произвольной, равнобедренной или прямоугольной.

Общие свойства трапеции:

Сумма углов, прилежащих к боковой стороне, равна 180 градусов
Средняя линия равна полусумме оснований
Отрезок, соединяющий середины диагоналей, равен полуразности её оснований

Свойства равнобедренной трапеции:

Углы при основании равны
Диагонали равны

Формулы площади

Ромб – это параллелограмм, у которого все стороны равны

Свойства ромба:

Противоположные углы равны
Все стороны равны
Диагонали делятся точкой пересечения пополам
Диагонали перпендикулярны друг другу
Диагонали являются биссектрисами углов

Формулы площади

Окружность

Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)

Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности

В окружности можно провести радиус, диаметр и хорду

Радиус – расстояние от центра до окружности

Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности

Хорда – прямая, соединяющая две любых точки окружности

Также в окружности есть два вида углов

Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается

Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается

Окружность, вписанная в четырёхугольник

Чтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны

a + c = b + d

Окружность, вписанная в прямоугольный треугольник

У вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r

Окружность, описанная около четырёхугольника

Чтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:

Сумма противоположных углов треугольника равна 180 градусов
Вписанные углы, опирающиеся на одну хорду, равны

Окружность, описанная около прямоугольного треугольника

Диаметр окружности равен гипотенузе вписанного треугольника
Радиус описанной окружности равен половине гипотенузы

R=c/2, где c-диаметр

Теорема синусов:

Отношения длин сторон треугольника к синусам противолежащих углов равны между собой, а также равны двум радиусам описанной окружности

Фактчек

Равенство треугольников можно определить по одному из трёх признаков равенства треугольников (по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам).

Признаки подобия немного отличаются от признаков равенства треугольников (по двум сторонам и углу между ними, по двум углам, по трём сторонам), по ним определяется отношение соответственных сторон одного треугольника к сторонам другого.

Для нахождения площади выпуклого четырёхугольника есть универсальная формула
S = ½* d1* d2 *sin α , где d 1, d 2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.

Окружность можно вписать в четырёхугольник, если суммы его противоположных сторон равны, а описать окружность около четырёхугольника можно, если пара противоположных углов в сумме даёт 180 градусов.

Так же стоит помнить, что в теореме синусов равны не только отношения противолежащих сторон к синусам углов, но и каждое такое отношение равно двум радиусам описанной окружности.

Проверь себя

Задание 1.
Чему равен отрезок соединяющий середины диагоналей в трапеции с основаниями а и b?

1. (a + b) / 2
2. (a — b) / 2
3. a-b
4. a+b

Задание 2.
В прямоугольном треугольнике один из катетов равен половине гипотенузы, чему равен угол напротив этого катета?

1. 90°
2. 60°
3. 30°
4. 20°

Задание 3.
Чему равен вписанный угол, опирающийся на хорду равную 84 градусам?

1. 42°
2. 21°
3. 84°
4. 90°

Задание 4.
Чему равен радиус описанного прямоугольного треугольника с катетами 3 и 4?

1. 5
2. 1,5
3. 2,5
4. 2

Задание 5.
Из каких длин сторон треугольника нельзя получить треугольник?

1. 4 16 12
2. 5 6 9
3. 3. 41 18 24
4. 17 14 28

Ответы: 1. — 2; 2. — 2; 3. — 1; 4. — 3; 5. — 1.

Источник

Пересечение двух параллельных прямых секущей

Параллельными называются пара прямых, которые при продолжении не пересекаются.

Когда две паралелльные прямые $a$ и $b$ пересекаются секущей $c$ , то образуется много разнообразных углов.

Некоторые пары углов имеют свои имена – названия:

пара     накрест лежащие углы   :   ∠3   и   ∠5,         ∠4   и    ∠6;
пара     односторонние углы   :       ∠4    и   ∠5,         ∠3   и   ∠6;
пара     соответственные углы :      ∠1   и   ∠5,         ∠4   и   ∠8,      ∠2   и   ∠6,      ∠3   и   ∠7.

Свойства:

накрест лежащие углы равны: 3 = 5, 4 = 6.
соответственные углы равны: 1 = 5, 4 = 8, 2 = 6, 3 = 7.
сумма односторонних углов равна 180 градусов: 3 + 6 = 180 градусов, 4 + 5 = 180 градусов.

_____________________________________________________________________________________

Теорема    Если две параллельные линии пересекаются третьей (Секущей), тогда выполняется следующее:
ТеоремаТеорема    *      накрест лежащие углы равны   ;
ТеоремаТеорема    *      соответственные углы равны ;
ТеоремаТеорема    *      сумма односторонних углов 180 град. ;
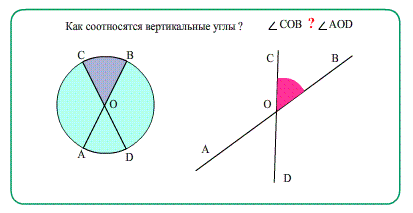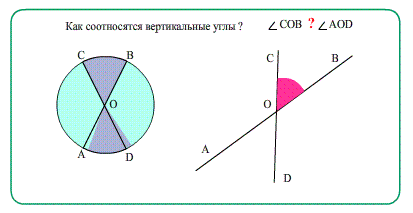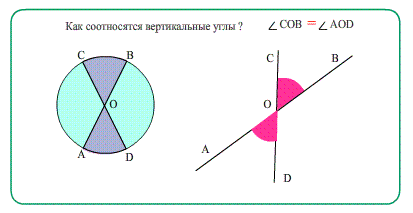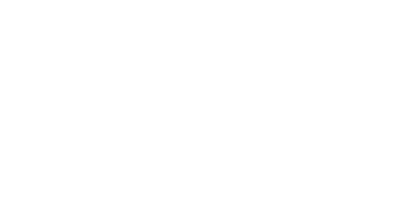
ТеоремаТеорема    *      вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .

_____________________________________________________________________________________

Теорема Если две прямые перпендикулярны (обе одновременно) к третьей, то они параллельны друг другу.

_____________________________________________________________________________________

Теорема Если две прямые не параллельны друг другу, то равенства для сумм углов не выполняются: 3 + 6 < 180 ; 4 + 5 > 180 .

_____________________________________________________________________________________

Теорема Если одна прямая параллельна второй, а вторая параллельна третьей, то первая прямая так же параллельна третьей.

_____________________________________________________________________________________

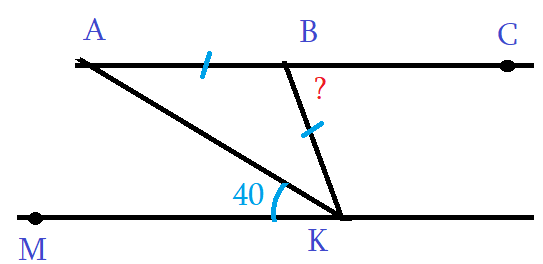
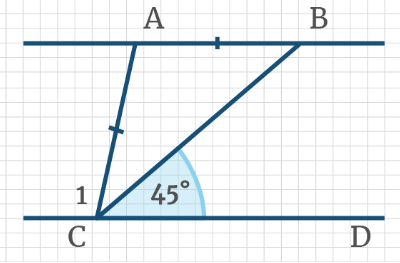
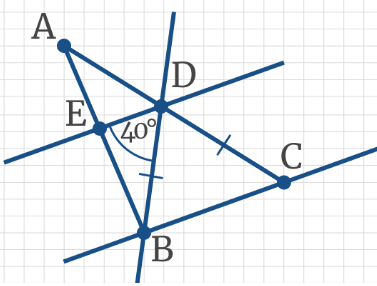
Задача 1: На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.

Решение: АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠АКМ и ∠КАВ накрест лежащие, $Rightarrow$ ∠КАВ = 40°.
∆АВК – равнобедренный, АВ = ВК $Rightarrow$ углы у основания ∠КАВ = ∠АКВ значит, $Rightarrow$ ∠АКВ = 40°.
Значит, углы ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность, ∠МКВ = ∠АКВ + ∠АКМ = 80°.
АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠ВКМ и ∠КВС накрест лежащие, $Rightarrow$ Ответ: ∠КВС = 80°.

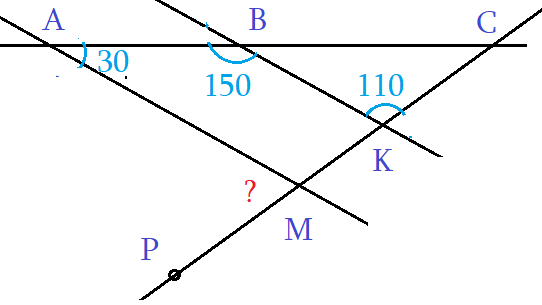
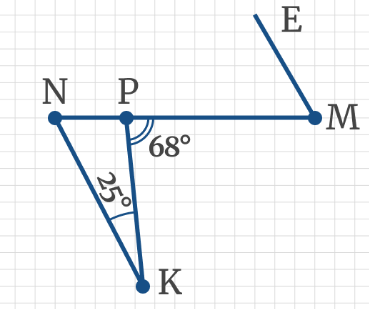
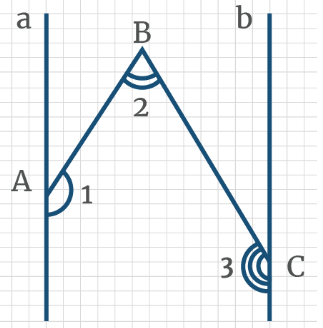
Задача 2: На рисунке, даны углы ∠ВАМ = 30°, ∠АВК = 150°, ∠ВКС = 110°. Найти ∠АМР.

Решение: Углы ∠ВАМ и ∠АВК – односторонные от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
Сумма односторонных 180°? … по теореме “о параллельных”, прямые АМ и ВК должны быть параллельными. АМ ║ ВК.
Теперь: АМ ║ ВК, СР – секущая. Односторонные углы равные, ∠ВКС = ∠АМК. Значит, ∠АМК = 110°.
Наконец, углы ∠АМК и ∠АМР – смежные. Значит, ∠АМК + ∠АМР = 180°. $Rightarrow$ ∠АМР = 180° – ∠АМК = 70°.
Ответ: ∠АМР = 70°. Замечание: “надо видеть все секущие к параллельным, и углы к ним”.

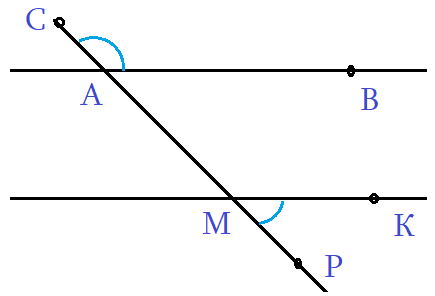
Задача 3: На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.

Решение: Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим: ∠САВ = 3∠РМК
Как связаны искомые углы по рисунку? ∠САВ и ∠МАВ – смежные, значит ∠МАВ = 180° – ∠САВ.
Углы ∠МАВ и ∠РМК односторонные углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
Из двух равенств получаем ∠РМК = 180° – ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим: ∠РМК = 180° – 3∠РМК
∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°. Ответ: 45°, 135°

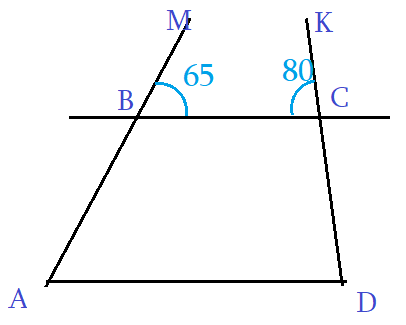
Задача 4: На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти четырехугольника АВСD.

Трапеция АВСD: Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
Решение: Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° – ∠МВС = 115°.
Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° – ∠ВСК = 100°.
АМ секущая к АD ║ ВС $Rightarrow$ ∠ВАD и ∠МВС соответственные, значит равные ∠ВАD = ∠МВС = 65°.
Аналогично, КD секущая к АD ║ ВС $Rightarrow$ ∠АDС и ∠ВСК соответственные, значит равные ∠АDС = ∠ВСК = 80°.
Ответ: Углы трапеции ∠ВАD = 65° ∠АВС = 115° ∠ВСD = 100° ∠АDС= 80°

Задача 4, продолжение, “углы в трапеции”: Пусть углы любые: ∠МВС = х, ∠ВСК = у.

Такими же рассуждениями о смежных и односторонных, получим: ∠А = х ∠В = 180° – х ∠С = 180° – у ∠D = у
Видно: ∠А + ∠В = 180° ∠С + ∠D = 180°. Сумма углов при боковой стороне трапеции 180° . Односторонные!
Видно: ∠А + ∠В + ∠С + ∠D = 180°. Сумма всех углов трапеции равна 360°. . Как у четырехугольника?

Факты, Следствия из теорем о углах при параллельных и секущей к ним:

В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
В паралеллограмме сумма углов у одной стороны равен 180 град. – внутренные односторонные. Что секущая?
В трапеции сумма углов у боковых сторон равен 180 град. – внутренные односторонные. Что секущая?
Еще о углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!

Интерактивные Упражнения:

Задачи из сайта https://resh.edu.ru :

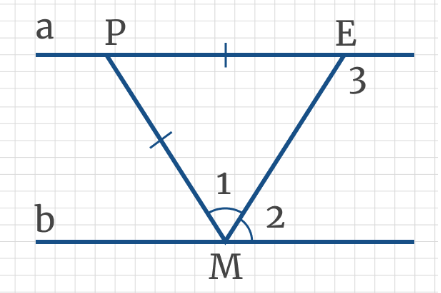
Задача 1: Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.

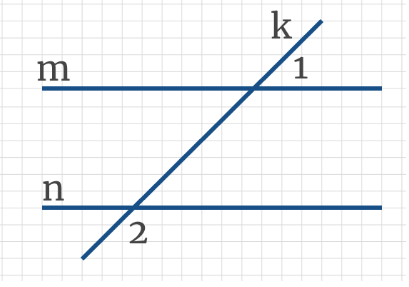
Задача 2: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.

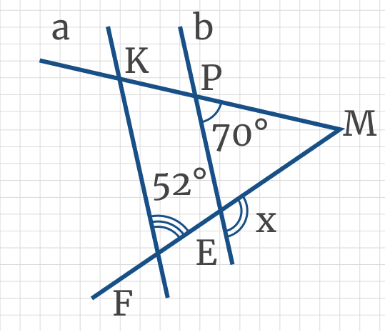
Задача 3: По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.

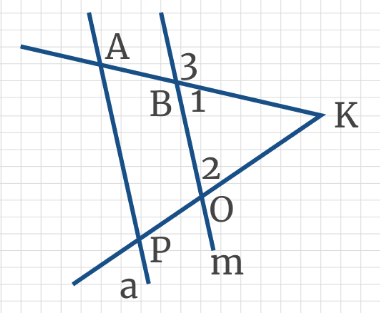
Задача 4: Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?

Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2

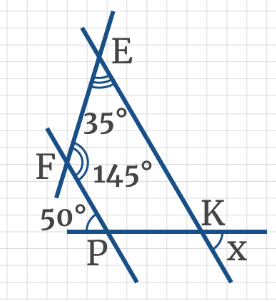
Задача 6: Прямые FP и EK параллельны, чему равна градусная мера угла x?

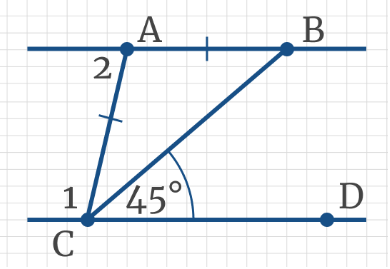
Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.

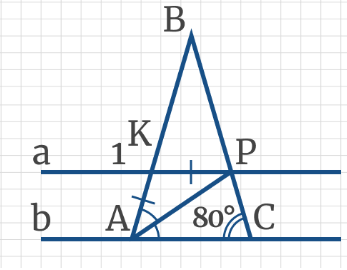
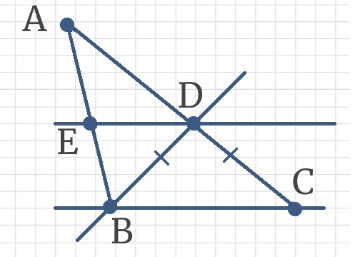
Задача 8: В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?

Задача 9: Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.

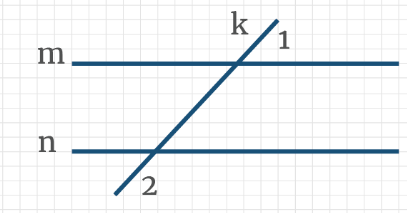
Задача 10: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.

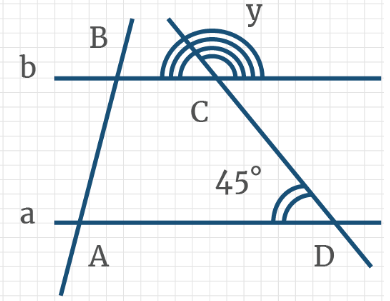
Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.

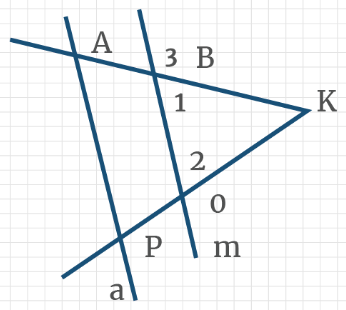
Задача 12: ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?

Задача 13: На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.

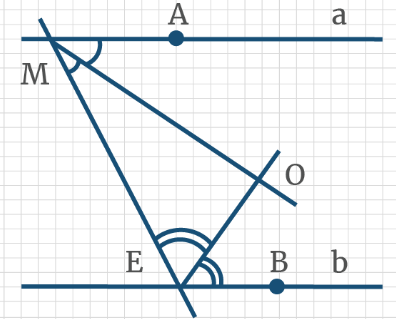
Задача 14: На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?

Задача 15: Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?

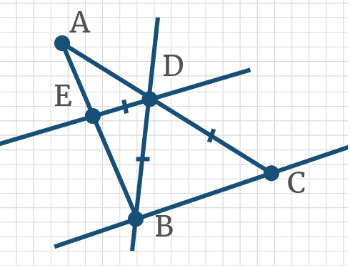
Задача 16: Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?

Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?

Задача 18: Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.

Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.

Задача 20: “углы в параллелограмме и трапеции”:

один из углов параллелограмма 40. найти остальные
найти углы параллелограмма, если известно, что сумма двух 80. (100, 160)
найти углы параллелограмма, если известно, что разность двух 70. (110, 130)
Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма
Углы параллелограмма относятся как 2:3 найти все углы
Чему равны углы равнобедренной трапеции, если разность противолежащих 40

Источник

Внутренние односторонние углы — теория, правило и свойства

Углы по определению

Доказательство теоремы

Следствие из свойства прямых

Построение параллелограмма

Углы при пересечении двух прямых

Углы при пересечении параллельных прямых

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы при параллельных прямых и секущей

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

На этой странице вы узнаете:

Прямая, отрезок, луч, углы

Рассмотрим углы при параллельных прямых

Треугольники, их виды и признаки их равенства

Элементы треугольника:

Виды треугольников:

Признаки равенства треугольников:

Признаки подобия треугольников:

Площадь треугольника

Многоугольник

Виды многоугольников:

Свойства параллелограмма:

Формулы площади

Свойства прямоугольника:

Формула площади

Свойства квадрата:

Формулы площади

Общие свойства трапеции:

Свойства равнобедренной трапеции:

Формулы площади

Свойства ромба:

Формулы площади

Окружность

Окружность, вписанная в четырёхугольник

Окружность, вписанная в прямоугольный треугольник

Окружность, описанная около четырёхугольника

Окружность, описанная около прямоугольного треугольника

Теорема синусов:

Фактчек

Проверь себя

Вам также может понравиться

Как найти работу на ледоколе

Как найти сайт туту ру

Как найти объем кота

Добавить комментарий Отменить ответ