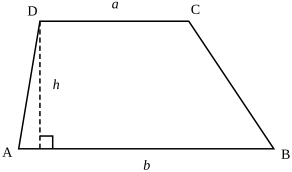
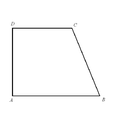
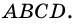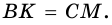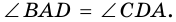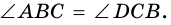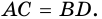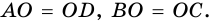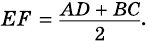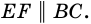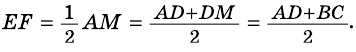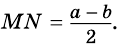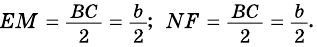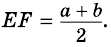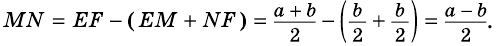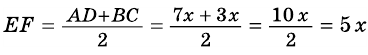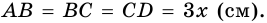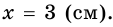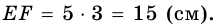Какими могут быть углы трапеции?
рисунок 1
Как и все другие четырехугольники и многоугольники, которые изучаются в школьном курсе, трапеция — выпуклый четырехугольник. Поэтому сумма углов трапеции равна 360º (речь идет о внутренних углах).
То есть для трапеции ABCD ∠A+∠B+∠C+∠D=360º.
Поскольку основания трапеции лежат на параллельных прямых, сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусам.
Для трапеции ABCD (рисунок 1)
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),
∠C+∠D=180º (как внутренние односторонние при AD ∥ BC и секущей CD).
Следовательно, если один из углов, прилежащих к одной боковой стороне, острый, то другой — тупой. Если один из этих углов прямой, другой — тоже прямой.
Суммы углов, прилежащих к боковым сторонам трапеции, равны:
∠A+∠B=∠C+∠D
Могут ли углы трапеции, взятые в последовательном порядке, относиться как
1) 7:3:5:2?
Нет, поскольку 7k+3k≠5k+2k и 7K+2k≠3k+5k.
2) 5:4:6:3?
5k+4k=6k+3k, следовательно, углы трапеции могут быть пропорциональны этим числам.
На рисунке 1 углы прилежащие к основанию AD, оба острые, углы, прилежащие к основанию BC, оба тупые. В паре противолежащих углов ∠A и ∠С, ∠B и ∠D один — острый, другой — тупой.
Существует ли трапеция, у которой два противолежащих угла обо тупые или оба острые?
рисунок 2
Да, такая трапеция существует.
Например, трапеция, изображенная на рисунке 2.
Существует ли трапеция, у которой два противоположных угла оба прямые? Противоположные углы равны?
Нет, такой трапеции не существует (противоположные углы равны у параллелограмма).
Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Содержание:
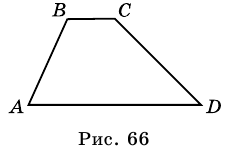
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 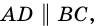
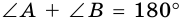
2. Трапеция является выпуклым четырехугольником.
Поскольку 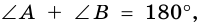
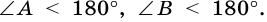
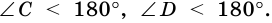
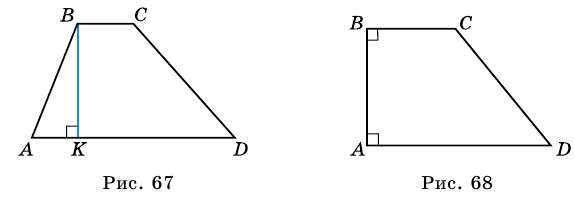
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 – прямоугольная трапеция 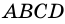
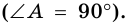
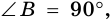
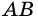
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 – равнобокая трапеция
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 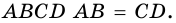
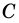
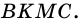
2) 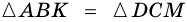
3) Также 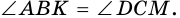
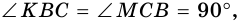
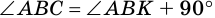
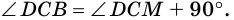
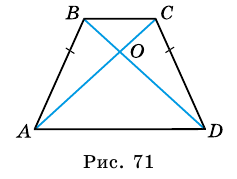
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 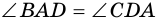
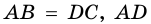
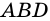
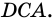
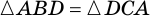
Пример:
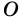
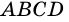
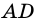
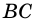
Доказательство:
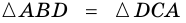
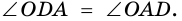
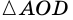
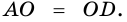
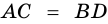
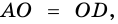
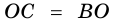
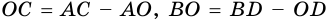
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 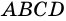
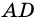
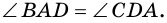
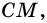
2) Тогда 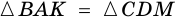
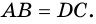
А еще раньше…
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» – однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие – не параллельны.
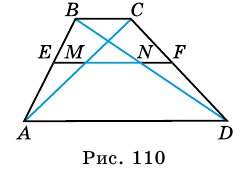
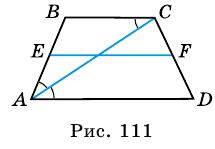
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 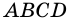
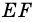
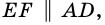
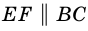
1) Проведем луч 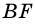
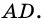
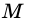
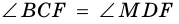
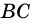
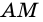
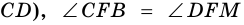
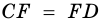
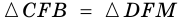
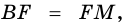
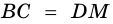
2) Поскольку 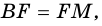
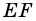
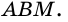
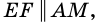
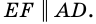
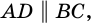
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 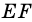
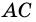
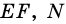
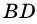
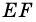
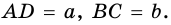
1) Так как 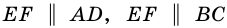
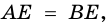
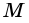
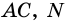
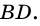
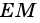
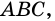
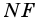
Тогда
2) 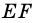
3)
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции – 48 см.
Решение:
Пусть 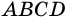
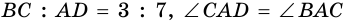
1) Обозначим 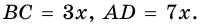
2) 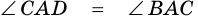
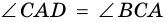
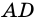
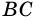
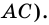
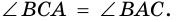
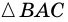
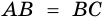
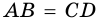
3) Учитывая, что 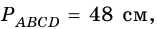
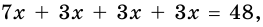
4) Тогда
Ответ. 15 см.
А еще раньше…
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2022 года; проверки требуют 27 правок.
Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны[1]. Часто в определении трапеции опускают последнее условие (см. ниже). Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.
Варианты определения
Существует и другое определение трапеции.
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны[2][3]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.
Связанные определения
Элементы трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Параллельные противоположные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Углом при основании трапеции называется её внутренний угол, образованный основанием с боковой стороной.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой[4] или равнобочной[5] трапецией).
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
-
Равнобедренная трапеция
-
Прямоугольная трапеция
Свойства
Основной источник: [6]
- Сумма углов, прилежащих к боковой стороне трапеции, равна
(как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
- Средняя линия трапеции параллельна основаниям и равна их полусумме.[7]
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен
среднему гармоническому длин оснований трапеции.
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
- Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
- Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими [имеют одинаковую площадь].
- Если отношение оснований равно
, то отношение площадей треугольников, прилежащих к основаниям, равно
.
- Высота трапеции определяется формулой:
-
- где
— большее основание,
— меньшее основание,
и
— боковые стороны.
-
- Их можно выразить в явном виде:
- Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:
- а при известных основаниях и диагоналях боковые стороны следующие:
- Если же известна высота
, то
- Прямая Ньютона для трапеции совпадает с её средней линией.
Неравенства для отрезков в трапеции
Теорема о четырёх точках трапеции
Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
Равнобедренная трапеция
Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:
- прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции)[8];
- высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
- углы при любом основании равны;
- сумма противоположных углов равна 180°;
- длины диагоналей равны;
- диагонали трапеции образовывали с одним и тем же основание равные углы;
- из каждой вершины одного основания другое основание было видно под одним и тем же углом[9];
- вокруг этой трапеции можно описать окружность;
- вершинами этой трапеции также являются вершины некоторого антипараллелограмма.
Кроме того
- если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Если 




Вписанная и описанная окружность
- Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
- В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
- Если трапецию можно вписать в окружность — то она равнобедренная.
- Радиус описанной окружности равнобедренной трапеции:[источник не указан 2875 дней]
-
- где
— боковая сторона,
— бо́льшее основание,
— меньшее основание,
— диагонали равнобедренной трапеции.
- Если
, то в равнобедренную трапецию можно вписать окружность радиуса
Площадь
- Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:
-
- или
- Средняя линия
разбивает фигуру на две трапеции, площади которых соотносятся как[11]
- Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Формулы площади равнобедренной трапеции
- Площадь равнобедренной трапеции:
-
- где
— боковая сторона,
— бо́льшее основание,
— меньшее основание,
— угол между бо́льшим основанием и боковой стороной[12].
- Площадь равнобедренной трапеции через её стороны
- Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:
В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. 
История
Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).
Примечания
- ↑ Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 587.
- ↑ Вся элементарная математика. Дата обращения: 6 июля 2015. Архивировано 9 июля 2015 года.
- ↑ Wolfram MathWorld. Дата обращения: 6 июля 2015. Архивировано 19 апреля 2015 года.
- ↑ Коллектив авторов. Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022.
- ↑ М. И. Сканави. Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489.
- ↑ Четырёхугольники. Архивная копия от 16 сентября 2015 на Wayback Machine
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 99.
- ↑ Эквивалентная формулировка: отрезки, соединяющие середины противоположных сторон трапеции, были взаимно перпендикулярны.
- ↑ Следствие. В случае перпендикулярности диагоналей боковым сторонам трапеция является равнобедренной.
- ↑ Комарова В. В. Экзаменационные вопросы и ответы. Геометрия: 9 и 11 выпускные классы. — М.: АСТ-ПРЕСС, 2000. — 448 с. — ISBN 5-7805-0416-4.
- ↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. 2-е изд., перераб. и доп. — М.: Наука, 1974. — 592 с.
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов 1986. С. 184
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).
Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).
И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Снова порассуждаем об углах:
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
( displaystyle angle 1=angle 2)
( displaystyle angle 3=angle 4)
Что из этого может следовать?
Очень важный факт:
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).