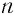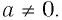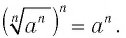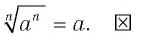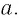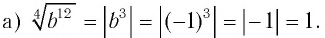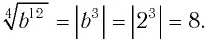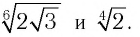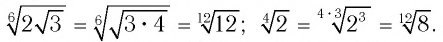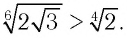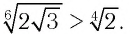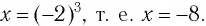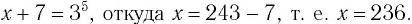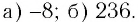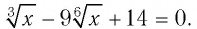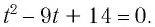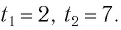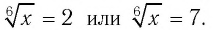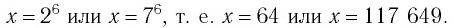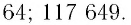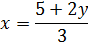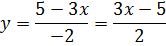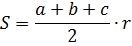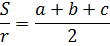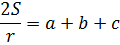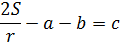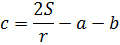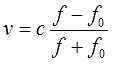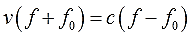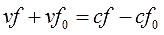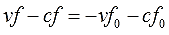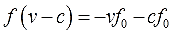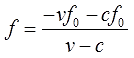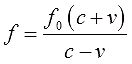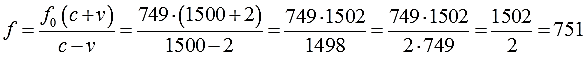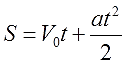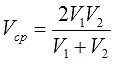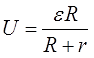Преподаватель который помогает студентам и школьникам в учёбе.
Тождества с корнями, содержащие одну переменную с примерами решения
Содержание:
Корни
Теорема:
Пусть 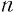
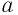
Доказательство:
Равенства (1) и (2), как и другие равенства в теоремах этого пункта, очевидно, верны при 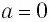
Рассмотрим равенство (1). Возведя его левую и правую части в 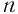
Согласно тождеству (1) из п. 1.2 это верное числовое равенство при любом значении 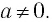
Равенство (2) доказывается аналогично: устанавливается, что 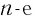
Аналогичными рассуждениями можно обосновать и остальные равенства в теоремах этого пункта.
Заметим, что каждое из этих равенств является тождеством, поскольку оно обращается в верное числовое равенство при любом значении переменной, при котором входящие в это равенство выражения имеют смысл.
Теорема:
Пусть 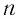
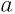
Теорема 3. Пусть 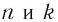
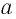
Заметим, что, когда оба числа 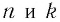
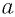
Равенство (5) означает, что при извлечении корня, из корня подкоренное выражение остается прежним, а показатели корней перемножаются.
Теорема:
Пусть 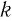
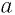
Примеры с решением
Пример №1
Найти значение 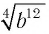
Решение:
б)
Ответ:
Пример №2
Сравнить числа
Решение:
Поскольку верно неравенство 12 > 8, то будет верным и неравенство 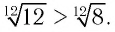
Ответ:
Пример №3
Решить уравнение:
Решение:
а) По определению корня 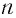
б)
Ответ:
- Заказать решение задач по высшей математике
Пример №4
Решить уравнение
Решение:
Обозначим 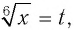
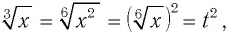
Корни этого уравнения
Таким образом, имеем:
Решив эти уравнения, найдем:
Ответ:
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Логарифмические уравнения и неравенства
- Степенная функция – определение и вычисление
- Степень с целым показателем
- Корень n-й степени
Этот урок — полезное дополнение к предыдущей теме “Тождественные преобразования уравнений”.
Умение делать такие вещи — штука не просто полезная, она — необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях — как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула — это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и тождественные преобразования уравнений. Вот и применяем их в удобном нам порядке и — готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка — для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3x – 2y = 5
Здесь две переменные — икс и игрек.
Допустим, нас просят выразить x через y.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа — что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3x – 2y = 5
Здесь нам мешаются тройка перед иксом и –2y. Начнём с –2у, это попроще будет.
Перекидываем –2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3x = 5 + 2y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек. Слева — чистый икс, а справа — что уж получилось в результате “очищения” икса.
Можно было бы сначала поделить обе части на тройку, а затем — переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное — не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
3x – 2y = 5
выразить y через x?
А почему — нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:
–2y = 5 — 3x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула — тоже уравнение.
Например, такое задание:
Из формулы
выразить переменную с.
Формула — тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа — что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби — нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с — скорость звука в воде,
f0 — частота испускаемых импульсов (в МГц),
f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
“Многа букафф”, да… Но буквы — это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там — видно будет. Для этого применяем второе преобразование — умножаем обе части на знаменатель.
Получим:
А вот тут — очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с. Что и выражается скобками в правой части.)
А вот теперь скобки и раскрыть можно:
Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f — справа. Займёмся переносом:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем. Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v–c) и — дело в шляпе!
В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно “причесать” полученное выражение — вынести f0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь – не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас – примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S=300, V0=20, t=10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V1 и V2 — средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с-1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы — это как-нибудь сами…)
Начнем разговор о тождествах, дадим определение понятия, введем обозначения, рассмотрим примеры тождеств.
Что представляет собой тождество
Начнем с определения понятия тождества.
Тождество представляет собой равенство, которое верно при любых значениях переменных. Фактически, тождеством является любое числовое равенство.
По мере разбора темы мы можем уточнять и дополнять данное определение. Например, если вспомнить понятия допустимых значений переменных и ОДЗ, то определение тождества можно дать следующим образом.
Тождество – это верное числовое равенство, а также равенство, которое будет верным при всех допустимых значениях переменных, которые входят в его состав.
Про любые значения переменных при определении тождества речь идет в пособиях и учебниках по математике для 7 класса, так как школьная программа для семиклассников предполагает проведение действий исключительно с целыми выражениями (одно- и многочленами). Они имеют смысл при любых значениях переменных, которые входят в их состав.
Программа 8 класса расширяется за счет рассмотрения выражений, которые имеют смысл только для значений переменных из ОДЗ. В связи с этим и определение тождества меняется. Фактически, тождество становится частным случаем равенства, так как не каждое равенство является тождеством.
Знак тождества
Запись равенства предполагает наличие знака равенства «=», от которого справа и слева располагаются некоторые числа или выражения. Знак тождества имеет вид трех параллельных линий «≡». Он также носит название знака тождественного равенства.
Обычно запись тождества ничем не отличается от записи обыкновенного равенства. Знак тождества может быть применен для того, чтобы подчеркнуть, что перед нами не простое равенство, а тождество.
Примеры тождеств
Обратимся к примерам.
Числовые равенства 2≡2 и -3≡-3 это примеры тождеств. Согласно определению, данному выше, любое верное числовое равенство по определению является тождеством, а приведенные равенства верные. Их также можно записать следующим образом 2≡2 и -3≡-3.
Равенства 2+3=5 и 7−1=2·3 также можно считать тождествами, так как они являются вернными. Здесь также допустима запись 2+3≡5 и 7−1≡2·3.
Тождества могут содержать не только числа, но также и переменные.
Возьмем равенство 3·(x+1)=3·x+3. Это равенство является верным при любом значении переменной x. Подтверждает сей факт распределительное свойство умножения относительно сложения. Это значит, что приведенное равенство является тождеством.
Возьмем тождество y·(x−1)≡(x−1)·x:x·y2:y. Рассмотрим область допустимых значений переменных x и y. Это любые числа, кроме нуля.
Возьмем равенства x+1=x−1, a+2·b=b+2·а и |x|=x. Существует ряд значений переменных, при которых эти равенства неверны. Например, при при x=2 равенство x+1=x−1 обращается в неверное равенство 2+1=2−1. Да и вообще, равенство x+1=x−1 не достигается ни при каких значениях переменной x.
Во втором случае равенство a+2·b=b+2·a неверно в любых случаях, когда переменные a и b имеют различные значения. Возьмем a=0 и b=1 и получим неверное равенство 0+2·1=1+2·0.
Равенство, в котором |x| – модуль переменной x, также не является тождеством, так как оно неверно для отрицательных значений x.
Это значит, что приведенные равенства не являются тождествами.
Если вспомнить тригонометрию и логарифмы, то здесь мы также можем найти примеры тождеств. Это основное логарифмическое тождество alogab=b и основное тригонометрическое тождество вида sin2α+cos2α=1.
В математике мы постоянно имеем дело с тождествами. Делая записи действий, производимых с числами, мы работаем с тождествами. Тождествами являются записи свойств степеней, свойств корней и прочие.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
доказать тождество:
2t−(17−(t−7))=3(t−8)
.
Решение:
выпишем отдельно левую часть равенства и преобразуем, т. е. попытаемся доказать, что она равна правой части.
При раскрытии скобок (обеих) знаки поменяем, т. к. перед скобками стоит знак минус.
2t−(17−(t−7))=2t−17+(t−7)==2t¯−17+t¯−7=3t−24=3(t−8).
.
Получили, что левая часть исходного равенства равна правой.
Значит, исходное равенство — тождество.
Тождественные преобразования
Что такое тождественные преобразования
Тождество — это равенство, выполняемое на всем множестве значений переменных, которые в него включены.
К примеру, тождествами являются, в том числе, квадратные выражения:
a 2 − b 2 = ( a + b ) ( a − b )
( a + b ) 2 = a 2 + 2 a b + b 2
В рассмотренных выражениях любые значения a и b обращают их в верные равенства, что полезно знать при решении примеров.
Тождественно равными выражениями называют такие два выражения, которые обладают равными значениями при всех значениях переменных.
Данное равенство существует только в том случае, когда:
Рассматриваемое равенство не является тождеством, а представляет собой уравнение. Для обозначения тождественного равенства принято использовать символ тройного равенства: ≡ .
Разница между тождеством и уравнением заключается в том, что тождество является верным при любом из значений переменных. Уравнение же верно лишь в том случае, когда имеется одно или несколько значений переменных.
Это уравнение верное только, когда ответ соответствует х = 10 .
В этом случае тождество не включает в себя переменные.
Замена чисел и выражений тождественно равными им выражениями
Тождественное преобразование выражения (преобразование выражения) представляет собой замену одних выражений на другие, которые тождественно равны между собой.
Данное объяснение преобразований позволяет значительно упростить решение задач. К примеру, для этого используют законы сокращенного умножения, арифметические свойства и другие тождества.
Рассмотрим конкретный пример:
Выполним работу по тождественным преобразованиям этой дроби:
x 3 – x x 2 – x = x ( x 2 – 1 ) x – 1 = x ( x – 1 ) ( x + 1 ) x ( x – 1 ) = x + 1
x 3 – x x 2 – x = x + 1
В результате получили тождество, которое существует, если х ≠ 0 и х ≠ 1 . То есть необходимо исключить недопустимые значения, так как знаменатель слева не должен принимать нулевые значения:
Доказательство тождеств
В процессе доказательства тождества необходимо выполнить ряд действий:
- тождественно преобразовать обе или только одну часть равенства;
- получить в обеих частях идентичные алгебраические выражения.
В качестве самостоятельного примера для тренировки докажем следующее тождество:
x 3 – x x 2 – x = x 2 + x x
В первую очередь избавимся от х , записав его за скобками:
x ( x 2 – 1 ) x ( x – 1 ) = x ( x + 1 ) x
Заметим, что можно сократить х :
x 2 – 1 x – 1 = x + 1
( x – 1 ) ( x + 1 ) x – 1 = x + 1
Выполним сокращение на х – 1 :
Заключим, что рассмотренное равенство является тождеством, если х ≠ 0 и х ≠ 1
Когда требуется доказать, что равенство не относится к тождеству, следует определить одно допустимое значение переменной, при котором полученные числовые выражения обращаются в неравные друг другу. К примеру:
x 2 – x x = x 2 + x x → x ≠ 0
Упростим вычисления с помощью сокращения х :
Выполним подстановку какого-то числа вместо х , например, числа 5:
Данное равенство не является тождеством.
Примеры тождеств
Изучить тождества на практике можно с помощью решения задач на различные тождественные преобразования алгебраических выражений. Ключевой целью таких действий является замена начального выражения на выражение, которое ему тождественно равно.
От перестановки местами слагаемых сумма не меняется:
От перестановки местами сомножителей произведение не меняется:
Согласно данным правилам, можно записать примеры тождественных выражений:
128 × 32 = 32 × 128
При наличии в сумме более двух слагаемых допускается группировать их путем заключения в скобки. Также можно предварительно переставлять эти слагаемые местами:
a + b + c + d = ( a + c ) + ( b + d )
Аналогичным способом группируют сомножители в произведении:
a × b × c × d = ( a × d ) × ( b × c )
Приведем примеры таких тождественных преобразований:
15 + 6 + 5 + 4 = ( 15 + 5 ) + ( 6 + 4 )
6 × 8 × 11 × 4 = ( 6 × 4 × 8 ) × 11
При увеличении или уменьшении обеих частей тождества на одинаковое число, данное тождество остается верным:
( a + b ) ± e = ( c + d ) ± e
Равенство сохраняется также при умножении или делении обеих частей этого равенства на одно и то же число:
( a + b ) × e = ( c + d ) × e
( a + b ) ÷ e = ( c + d ) ÷ e
Запишем несколько примеров:
35 + 10 = 9 + 16 + 20 ⇒ ( 35 + 10 ) + 4 = ( 9 + 16 + 20 ) + 4
42 + 14 = 7 × 8 ⇒ ( 42 + 14 ) × 12 = ( 7 × 8 ) × 12
Какую-либо разность допускается записывать, как сумму слагаемых:
Аналогичным способом можно выполнить замену частного на произведение:
Рассмотрим примеры тождественных преобразований:
76 – 15 – 29 = 76 + ( – 15 ) + ( – 29 )
42 ÷ 3 = 42 × 3 – 1
Заменить математическое выражение на более простое можно с помощью арифметических действий:
Преобразования следует выполнять с соблюдением алгоритма:
- В первую очередь выполняют возведение в степень, извлекают корни, вычисляют логарифмы, тригонометрические и прочие функции.
- Далее можно приступать к действиям с выражениями, заключенными в скобки.
- На последнем этапе, начиная с левой стороны, двигаясь вправо, выполняют действия, которые остались. При этом умножение и деление являются приоритетными, выполняются в первую очередь. Затем можно приступить к сложению и вычитанию. Данное правило распространяется и на выражения, записанные в скобках.
Пример 7
14 + 6 × ( 35 – 16 × 2 ) + 11 × 3 = 14 + 18 + 33 = 65
20 ÷ 4 + 2 × ( 25 × 3 – 15 ) – 9 + 2 × 8 = 5 + 120 – 9 + 16 = 132
В арифметических выражениях можно избавляться от скобок при необходимости. Исходя из знаков в выражении, определяются правила, согласно которым раскрывают скобки.
Рассмотрим несколько примеров преобразований с помощью раскрытия скобок:
117 + ( 90 – 74 – 38 ) = 117 + 90 – 74 – 38
1040 – ( – 218 – 409 + 192 ) = 1040 + 218 + 409 – 192
22 × ( 8 + 14 ) = 22 × 8 + 22 × 14
18 ÷ ( 4 – 6 ) = 18 ÷ 4 – 18 ÷ 6
Другим распространенным действием при упрощении выражений, содержащих скобки, является вынесение за них общего множителя. В результате в скобках остаются слагаемые, поделенные на вынесенный множитель. Данный способ преобразования можно применять в выражениях, которые содержат буквенные переменные.
3 × 5 + 5 × 6 = 5 × ( 3 + 6 )
28 + 56 – 77 = 7 × ( 4 + 8 – 11 )
31 x + 50 x = x × ( 31 + 50 )
В процессе тождественных преобразований часто применяют формулы для сокращенного выражения.
Примеры тождественных преобразований:
( 31 + 4 ) 2 = 31 2 + 2 ⋅ 31 ⋅ 4 + 4 2 = 1225
Решение тождественных уравнений примеры решений
Пример 5. Решите уравнение 3у + у 2 = у.
Решение:
3у + у 2 = у – неполное квадратное уравнение; у 2 + 3у – у = 0;
у 2 + 2у =0; у∙(у + 2) = 0.
x 2 – 5х = – 6 или х 2 – 5х = 36;
х 2 – 5х + 6 = 0 или х 2 – 5х – 36 =0.
По теореме Виета:
х1 = 2, х2 = 3, х3 = – 4, х4 =9.
Ответ: – 4, 2, 3, 9.
Тождество
Тема урока: § 4. Тождество.
Тождественные выражения
Сравним значения выражений ( 2x+3x^<2>) и ( 5x^<3>) при некоторых значениях переменной ( x.) При ( x=2) значение первого выражения ( 16,) а второго ( 40.) Числа ( 16) и ( 40) — соответственные значения выражений: ( 2x+3x^<2>) и ( 5x^<3>.) Некоторые пары соответственных значений этих выражений показаны в таблице:
| $$textcolor<#ed5fa6>$$ | $$-0,4$$ | $$-0,1$$ | $$ 0 $$ | $$0,1$$ | $$ 1 $$ |
| $$2x+3x^<2>$$ | $$-0,32$$ | $$-0,17$$ | $$0$$ | $$0,23$$ | $$5$$ |
| $$5x^<3>$$ | $$-0,32$$ | $$-0,005$$ | $$0$$ | $$0,005$$ | $$5$$ |
Легко заметить, что не при всех значениях переменной ( x) значения выражений ( 2x+3x^<2>) и ( 5x^<3>) равны, а значит нельзя сказать, что выражения тождественно равны.
Что такое тождество?
Выражения ( x+5) и ( 5+x) тождественно равны, поэтому равенство ( x+5=5+x) верно при любых значениях ( x.) Такое равенство называют тождеством.
Определение:
Тождеством называется такое равенство двух выражений, которое верно при любых значениях переменных.
Примеры тождеств
Верное числовое равенство также называют тождеством.
Тождественные преобразования выражений
Рассмотрим выражения ( x(y+7)) и ( xy+7x.) Вычислим их значения при ( x=9) и ( y=-2)
Мы видим что при ( x=9) и ( y=-2) соответственные значения выражений ( x(y+7)) и ( xy+7x) равны. Из распределительного и переместительного свойств умножения следует, что соответственные значения этих выражений равны при любых значениях переменных. О таких выражениях говорят, что они тождественно равны.
При решении уравнений, вычислении значений выражений и ряде других случаев одни выражения заменяют другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами. Мы уже встречались с тождественными преобразованиями выражений. К ним относятся, например, приведение подобных слагаемых, раскрытие скобок.
Пример 1. Приведем подобные слагаемые в сумме (5x+2x-3x.)
Чтобы привести подобные слагаемые, надо, как известно, сложить их коэффициенты и результат умножить на общую буквенную часть.
Имеем: $$5x+2x-3x=(5+2-3)x=4x$$ Выполненное преобразование основано на распределительном свойстве умножения.
Пример 2. Раскроем скобки выражения (2a+(b-3c).)
Воспользуемся правилом раскрытия скобок, перед которыми стоит знак “плюс”: если перед скобками стоит знак “плюс”, то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки.
Получим: $$2a+(b-3c)=2a+b-3c$$ Проведенное преобразование основано на сочетательном свойстве сложения.
Пример 3. Раскроем скобки в выражении (a-(4b-c).)
Применим правило раскрытия скобок, перед которыми стоит знак “минус”: если перед скобками стоит знак “минус”, то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки.
Выполненное преобразование также основано на свойствах действий над числами. Действительно, представим данное выражение в виде суммы: $$a-(4b-c)=a+(-1)cdot(4b-c)$$ Применим распределительное и сочетательное свойства умножения:
Доказательство тождеств
Если в выражении (textcolor<#ed5fa6><5(b-c)-3c>) раскрыть скобки, а затем привести подобные слагаемые, то получится тождественно равное ему выражение (textcolor<#ed5fa6><5b-8c.>)
верно при любых значениях переменных. Такие равенства называют тождественными.
Свойства действий над числами также являются тождествами, приведем некоторые из них:
Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений.
Докажем, например, тождество $$tag <1>7(2+b)-(14-b)=8b$$ Преобразуем левую часть равенства ((1):)
[smallbegin <2>7(2+b)-(14-b)= \ 14+7b-14+b= \ 8b end] В результате тождественных преобразований мы получили правую часть равенства ((1).) Значит, это равенство есть тождество.
Для доказательства тождества иногда преобразуют каждую его часть. Докажем, например, тождество $$tag <2>d(c-a)+ab=a(b-d)+cd$$ Выполним преобразования: [smallbegin <2>d(c-a)+ab=cd-ad+ab, \ a(b-d)+cd= \ ab-ad+cd= \ cd-ad+ab end]
Левая и правая части равенства ((2)) тождественно равны одному и тому же выражению. Поэтому они тождественно равны между собой. Значит, равенство ((2)) — тождество.
Не всякое равенство есть тождество. Так, равенство (x+2=2x) не является тождеством. Действительно, если бы это равенство было тождеством, то оно было бы верным при всех значениях (x.) Однако, например, при (x=1) это равенство не является верным. Значит, оно не является тождеством.
Задачи для самостоятельного решения
№1. Являются ли выражения тождественно равными:
Первые два выражения тождественно равны. Т.е. равны при любых значениях переменной (footnotesize c. )
Вторая пара является тождеством, можно понять с помощью сочетательного закона сложения: $$a+(b+c)=(a+b)+c$$
Тождество, т.к. (footnotesize -2a+2a=2a-2a=0 )
Тождество, т.к. (footnotesize (x-x)a=0cdot a=0 )
Пятая пара выражений не будет являться тождеством. Предположим обратное:
Видно что равенство верно при (footnotesize x=y,) но если (footnotesize x) и (footnotesize y) отличны друг от друга, то равенства достигаться не будет.
Тождество. Рассмотрим первое выражение
Видно, что первое выражение в точности является вторым.
№2. Упростите выражение, используя переместительное и сочетательное
свойства умножения:
[spoiler title=”источники:”]
http://www.sites.google.com/a/ssga.ru/ssga4school/matematika/tema-3
http://reshu.su/algebra/04/
[/spoiler]