Как найти треть окружности
Деление круга на равные части
Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, ребята. Меня зовут Игрек, я самый умный фиксик.
На уроке вы узнаете новые математические понятия.
Приготовьте тетрадь, ручку, простой карандаш, линейку, циркуль.
Понятие доли
Вы когда-нибудь заглядывали в тетради к старшеклассникам? Смотрите, какой у меня пример.
Видите сложение, вычитание, умножение? Знаки этих действий известны: плюс, минус, точка. Деление же в примере обозначено горизонтальной чертой.На рисунке она выделена красным цветом. Я расскажу, когда в математике используют черту.
Мы умеем делить несколько предметов, но часто деление нужно, чтобы раздробить одно число на равные части — доли от целой величины.
Один разделить на два — это одна вторая. Что же это такое?
В жизни вы часто так делали. Например, один апельсин делили с другом: брали нож и разрезали его пополам.
Каждый из вас получал половину или одну долю.
На лесной полянке собралось девять друзей, апельсин делили на всех. Рассмотрите рисунок. Как называется каждая часть фрукта?
Совершенно верно, это долька. Апельсин поделили на 9 одинаковых долек.Каждая 1 долька апельсина — это одна из девяти равных долей целого фрукта.
Вы теперь поняли, ребята, что в жизни человеку приходится не только пересчитывать предметы, но и делить (дробить) целое на части, вот так появилось в математике понятие доли и дроби.
Знак доли (дроби) обозначают дробной горизонтальной или наклонной чертой. Например, так — 1/9 (одна девятая). Запись придумали арабы в 16 веке.
Доли называют по количеству частей раздробленного одного предмета:
- Разделите, например, яблоко на две равные части, у вас получится название доли «половина» или 1/2 (одна вторая)
- Разрежьте яблоко на три части. Один кусок — это «треть» — 1/3 (одна третья)
- Разломите на четыре доли — «четверть» — 1/4 (одна четвертая)
Знание о долях помогает решить задачи.
Запомните правило по математике нахождения доли.Чтобы найти долю от числа надо число разделить на эту долю. В дроби число, на которое делят, записано под чертой и называется знаменателем. То число, которое надо разделить, пишут над чертой. Это числитель.
Задание 1
Найдите пятую долю от числа 25. Это значит, что надо выполнить действие деления.
Привычный пример 25 : 5 можно записать вот таким образом:
Или так — 25/5. 25 – это числитель, а 5 — знаменатель.
Ответ: одна пятая доля от числа 25 равна пяти.
Задание 2
Чему равна 1/4 доля от полоски длинной 16 см?
Полоску согните пополам, ещё раз пополам. Разверните. На сколько долей линией сгиба разделили полоску? Правильно, на 4.
Закрасьте одну такую долю.
Какую долю вы закрасили? (одну четвёртую)
Ответ: длина одной четвертой доли полоски составляет 4 см.
Задание 3
Решите задачи на понятие доли. Рассмотрите рисунки. Какая доля каждой фигуры закрашена серым цветом?
Рассуждаем так.
На рисунке 1 отрезок разделили на 7 частей.Значит, закрашена одна седьмая (1/7) доля фигуры.
Проверьте:
На следующих рисунках заштрихована 1/16 доля квадрата, 1/6 доля шестиугольника, 1/5 доля круга.
Чтобы разобрать понятие массовой доли, представьте себе килограмм яблок (1000 г), который мама купила своим трем детям.
Из этого килограмма самому младшему ребенку досталась половина всех яблок (несправедливо, конечно!). Старшему — лишь 200 г, а среднему — 300 г.
Значит, массовая доля яблок у младшего ребенка составит половину, или одну вторую (1/2) массовую долю.
У старшего ребенка будет:
1000 : 200 = 5 — одна пятая (1/5) массовая доля
Далее рассуждаем так:
Младшему ребенку дали половину яблок.
Яблоки разделили между детьми по 500г, 200г и 300г. Вы знаете, что 500 — это 5 сотен, 200 — 2 сотни, 300 — 3 сотни.
На сколько сотен разделили все яблоки?
5 сотен + 2 сотни + 3 сотни = 10 сотен.
Сколько граммов будет в одной десятой доле?
1000 : 10 = 100 (г) в одной десятой доле
У среднего ребенка 300 г. Во сколько раз больше, чем 100 г?
В три раза. Значит, у среднего ребенка будет не одна, а три десятых массовых долей 3/10.
Ребята, вы молодцы. Верное решение.
Окружность. Круг
А сейчас познакомимся с самой совершенной фигурой, как считал древнегреческий математик Пифагор. Ответьте на вопрос: «Какие известные вам геометрические плоские фигуры не содержат углов?»
Правильно, круги, а еще окружности.
Совершенная форма этой геометрической фигуры привлекает внимание художников, дизайнеров, архитекторов. Они используют её в своих изделиях для украшения.
Ограда на набережной реки Невы в Санкт-Петербурге
Назовите предметы из обычной жизни, которые по форме похожи на эти фигуры.Правильно, круглые очки. Вы очень внимательные ребята.
Посмотрите на рисунок. Назовите окружности и круги.
Проверьте себя:
Но как начертить такие ровные окружности? Приглашаю на помощь лучшего друга.
Знакомьтесь, ребята, к нам пришел новый житель страны Геометрии – чертежный инструмент. Он поможет разобраться, как изобразить круг.
Привет, я циркуль. Мое имя произошло от старинного латинского слова «циркулюс», что означает круг.
Давайте потренируемся чертить циркулем:
- В тетради или альбоме поставьте точку карандашом. Это центр окружности.
- Аккуратно раздвиньте «ножки» циркуля, например, на 30 мм. Измерьте расстояние между грифелем и иголкой по линейке.
- Крепко воткните иголку циркуля в центр, а другой «ножкой», вращая головку циркуля большим, указательным и средним пальцем, начертите грифелем замкнутую линию.
Линию, нарисованную грифелем циркуля, называют окружностью.
Точки на окружности А и В расположены от центра на равном расстоянии. Их соединяет отрезки ОА и ОВ – называются радиусами окружности.
Продлите по линейке отрезок ВО поперек всей окружности. Вы начертили диаметр окружности— отрезок ВС. Он прошел через центр и соединил 2 точки на окружности В и С.
Как вы думаете, сколько диаметров можно провести в одной окружности?
Совершенно верно — сколько угодно, как говорят математики — бесконечное число.
Посмотрите на колесо от велосипеда.
Втулка — это центр, а спицы напоминают радиусы и диаметры.
Если величину диаметра умножить на 3, мы получим примерную длину окружности. Точную формулу вычисления вы узнаете в 7 классе на уроках геометрии, а также, что такое вписанная и описанная окружности.
А сейчас возьмите альбомный лист, начертите окружность и по этой границе аккуратно вырежьте фигуру. Её можно закрасить любым цветом, например, синим, как на рисунке. Это круг — часть плоскости, ограниченная окружностью.
У круга есть площадь. Окружность вырезать невозможно, потому что это просто замкнутая кривая линия вокруг круга — его граница.
Решите задачу
На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь закрашенной части фигуры.
Рассуждайте так: на рисунке закрашена четвертая доля фигуры. Значит надо выполнить деление.
Ответ: площадь равна 10
Диаметр круга
Нарисуйте две окружности с радиусом 3 см. Фигуру справа закрасьте желтым карандашом. Получится круг.В обеих фигурах проведите диаметры и радиусы.
Измерьте диаметр окружности и диаметр круга. Сколько у вас получилось?
Правильно, 6 см. Радиус круга равен 3 см. Он два раза помещается в диаметре, значит это половина или одна вторая доля от целого.
Радиус круга равен половине или 1/2 диаметра.
Путем несложных математических вычислений можно понять, что диаметр в 2 раза больше радиуса.
Решите задачу
Третьеклассник вырезал круг радиусом 50 мм. Сколько сантиметров в его диаметре?
Решение:
Ответ: диаметр круга равен 10 см.
Вы хорошо справились.
Нам пора провести зарядку для глаз, чтобы сберечь зрение.
Физкультминутка
- Зажмурьтесь, потом откройте глаза шире. Лоб остается гладким без морщин. Повторите упражнение три раза.
- Теперь подойдите к окну, посмотрите вдаль. Внимательно вглядитесь, потом попытайтесь увидеть кончик носа. Получилось? Тогда повторяйте упражнение четыре раза. Не спешите.
- Медленно делайте круговые движения снизу вверх, направо, вниз, влево глазами, как будто вращаете большое колесо, 2 раза в одну сторону. Теперь обратно. Не двигайте головой, следите только глазами.
- Найдите взглядом верхний правый угол комнаты, хлопните в ладоши, опустите взор на кончик носа.Смотрите вверхний левый угол, далее на кончик носа. Повторите пять раз.
- Прикройте глаза, 10 секунд постойте спокойно, ровно неглубоко подышите.
Ребята, я тоже люблю укреплять здоровье. Вчера пошел на хоккейную площадку. Но вместо игры попросили начертить круги больших диаметров, чтобы обновить разметку поля.
Задача 1
Как начертить без циркуля круг для вбрасывания шайбы диаметром 300 мм?
Решение:
Радиус круга равен половине диаметра.
Возьмите гвоздь, карандаш, нитку длиной 15 см. Начертите окружность как показано на рисунке.
Задача 2
Из центра поля нужно нарисовать круг синей краской диаметром 9 метров.
Рассуждаем: диаметр круга 9 м, значит радиус — половина.
900 : 2 = 450 (см) = 4 м 50 см.
На центральную точку встает друг Гвоздик, крепко держит конец веревки, а к другому концу нужно закрепить кисть с краской. Фиксик Игрек на коньках едет вокруг Гвоздика, рисует линию окружности. Главное — туго натягивать веревку, чтобы радиус в 450 см не уменьшался. Вот такая разметка получается в центре хоккейной площадки:
После работы пора поиграть в хоккей.
Похожим способом можно начертить 7 окружностей больших диаметров на картоне для новогодней елки. Посмотрите на рисунок, какая красавица получается.
Поделку делайте вместе с родителями. Для больших кругов возьмите карандаш, гвоздик и нитку. Маленькие — нарисуйте циркулем. Понадобится начертить всего 11 окружностей для десяти обручей елки.
Задача 3
Диаметр первого нижнего круга елки равен 80 см, а каждого следующего уменьшается на 8 см. Найдите, чему равны диаметры следующих кругов.
Какой диаметр маленького круга наверху у елки?
Для решения задачи вспомните таблицу умножения на 8.
Обратный отсчет диаметров круга по таблице 80, 72, 64, 56, 48, 40, 32, 24, 16, 8.
Диаметр маленького круга 8 см.
Вы отлично выполнили вычисления.
Теперь отгадайте новую загадку. Что идет, не двигаясь с места? (Правильно, это время.)
Единицы времени
Каждый человек хочет понять время. Оно нам нужно, потому что мы живем по режиму, а магазины, библиотеки, вокзалы — по расписанию. Определенное количество дел намечаем сделать в единицу времени.
Давайте познакомимся с единицами измерения времени.
Земля обращается вокруг Солнца за 365 суток. Это год. Один раз в 4 года он увеличивается на сутки, и называется високосным.
С глубокой древности круг считается символом годовых сезонных циклов: зимы, весны, лета и осени. Рассмотрите рисунок годового круга: он поделен на 4 доли — четыре времени года.
Единица величины каждого времени года делится на 3 месяца.
В году 3 ∙ 4 = 12 месяцев. Месяц — единица времени, за которую Луна обходит планету Земля вокруг.
В каждом месяце 30 или 31, а в феврале 28 или 29 суток.
Исторически основной единицей для времени были сутки (часто говорят «день»). За одни сутки Земля поворачивается вокруг своей оси.
В результате деления суток на меньшие временные интервалы возникли часы, минуты и секунды. Сутки – единица времени, равная 24 часам. Один час — это 60 минут. Минута состоит из 60 секунд.
Выполните задания
1. Выразите время в указанных единицах измерения
8 ч 25 мин. = … мин.
95 мин. = … ч … мин.
2 мин. 14 сек. = … сек.
187 сек. = … мин. … сек.
Решение:
1 час = 60 мин. Значит, в восьми часах будет в 8 раз больше. Нужно выполнить умножение.
В 8 часах — 480 минут да еще 25 мин. Действие сложения.
480 + 25 = 505 (мин.)
Ответ: 8 ч 25 мин. = 505 мин.
Дальше решайте аналогично:
2 мин. 14 сек. = 60 ∙ 2 + 14 = 134 сек.
95 мин. = 1 ч 35 мин.
187 сек. = 3 ч. 7 сек.
2. Выберите единицы времени, которые расположены в порядке возрастания
а) час, минута, секунда
б) секунда, минута, час
в) минута, час, секунда
Проверьте себя.
Правильный ответ — б.
3. Автомобиль до Москвы едет 2 суток, а обратно 48 часов. Почему такая разница?
Проверьте себя.
2 сут. = 48 ч. Разницы нет.
Наш урок подходит к концу. Я надеюсь, что вы будете ценить свое время, не будете терять его зря.
Я с вами прощаюсь, а вы проверьте свои знания.
В материалах урока использованы кадры из м/с «Фиксики», 2010
Деление окружности на любое число равных частей
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.
Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на 4 и 8 одинаковых частей
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Деление окружности на 5 и 10 равных частей
Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Нахождение центра дуги окружности
Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
Что такое треть круга?
Как называется третий?
одна из трех равных частей делимого целого. синонимы: третий, ярус.
Как найти площадь одной трети круга?
Площадь круга равна Pi π умножить на радиус r в квадрате. Подставляем значение радиуса r = 13 r = 1 3 в формулу для площади круга. Pi π примерно равно 3,14.
Какая треть на круговой диаграмме?
Поскольку ваш числитель равен 1, ваша дробь означает “1 часть из 3 частей. “Если бы на приведенном выше графике был изображен настоящий пирог, а затемненные части были съедены, можно было бы сказать, что 1 /3 пирога нет.
Какая третья из 30?
Калькулятор процентов: что составляет 3 процента от 30? знак равно 0.9.
Какая третья из 12?
Треть из 12 – это 4.
Какая третья часть от 100%?
Ответ: 1/3 из 100 – это 100/3 или 33⅓.
Деление окружности на любое число равных частей
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.
Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на 4 и 8 одинаковых частей
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Деление окружности на 5 и 10 равных частей
Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки “а” в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке “b”. Радиусом R3 из точки “1” проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние “b-О” даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки “1” окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Нахождение центра дуги окружности
Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
[spoiler title=”источники:”]
http://borismarkin.ru/chto-takoe-tret-kruga
http://v3c.ru/arifmetika/delenie-okruzhnosti-na-ravnye-chasti
[/spoiler]
Содержание
- – Как называется третий?
- – Как найти площадь одной трети круга?
- – Какая треть на круговой диаграмме?
- – Какая третья из 30?
- – Какая третья из 12?
- – Какая третья часть от 100%?
- – Что такое 1/3 в процентах?
Трина. аспект 120 ° (одна треть круга).
Как называется третий?
одна из трех равных частей делимого целого. синонимы: третий, ярус.
Как найти площадь одной трети круга?
Площадь круга равна Pi π умножить на радиус r в квадрате. Подставляем значение радиуса r = 13 r = 1 3 в формулу для площади круга. Pi π примерно равно 3,14.
Какая треть на круговой диаграмме?
Поскольку ваш числитель равен 1, ваша дробь означает “1 часть из 3 частей. “Если бы на приведенном выше графике был изображен настоящий пирог, а затемненные части были съедены, можно было бы сказать, что 1/3 пирога нет.
Какая третья из 30?
Калькулятор процентов: что составляет 3 процента от 30? знак равно 0.9.
Какая третья из 12?
Треть из 12 – это 4.
Какая третья часть от 100%?
Ответ: 1/3 из 100 – это 100/3 или 33⅓.
Что такое 1/3 в процентах?
Примеры значений
| Процентов | Десятичный | Дробная часть |
|---|---|---|
| 331/3% | 0.333… | 1/3 |
| 50% | 0.5 | 1/2 |
| 75% | 0.75 | 3/4 |
| 80% | 0.8 | 4/5 |
Интересные материалы:
Как предотвратить протекание металлического резервуара для воды?
Как предотвратить протекание пластикового резервуара для воды?
Как предотвратить провисание бельевой веревки?
Как предотвратить раскачивание абажура?
Как предотвратить разбиение слов на страницы?
Как предотвратить разряд аккумулятора в холодную погоду?
Как предотвратить ротацию фотографий на Facebook?
Как предотвратить скрип дерева?
Как предотвратить смазывание моего лазерного принтера?
Как предотвратить утечку чернил в картридже?
Хоть деление круга на несколько равных частей входит в школьную программу, но со временем основы забываются. А строителям, сантехникам, жестянщикам и другим представителям рабочих специальностей эти знания необходимы. Рассмотрим, как разделить круг на 3, 6 и 12 частей.
Диаметр круга не имеет значения. Если нужен очень большой размер – вместо циркуля используют веревку и карандаш.
Деление на 3 части
Шаг 1 из 7
Чертим произвольный круг.

Шаг 2 из 7
Радиус окружности делит ее на 6 равных частей. Поэтому выбираем любую позицию на периметре круга, устанавливаем острие циркуля и находим с двух сторон от нее точки, расстояние до которых равно радиусу.

Шаг 3 из 7
Затем грифель оставляем на одной из этих точек, а острие перемещаем на такую же длину.

Шаг 4 из 7
С этой позиции определяем следующую точку.

Шаг 5 из 7
На окружности получится 3 засечки.

Шаг 6 из 7
Соединяем засечки с центральной точкой фигуры.

Шаг 7 из 7
Каждая из трех частей имеет внутренний угол 120°.
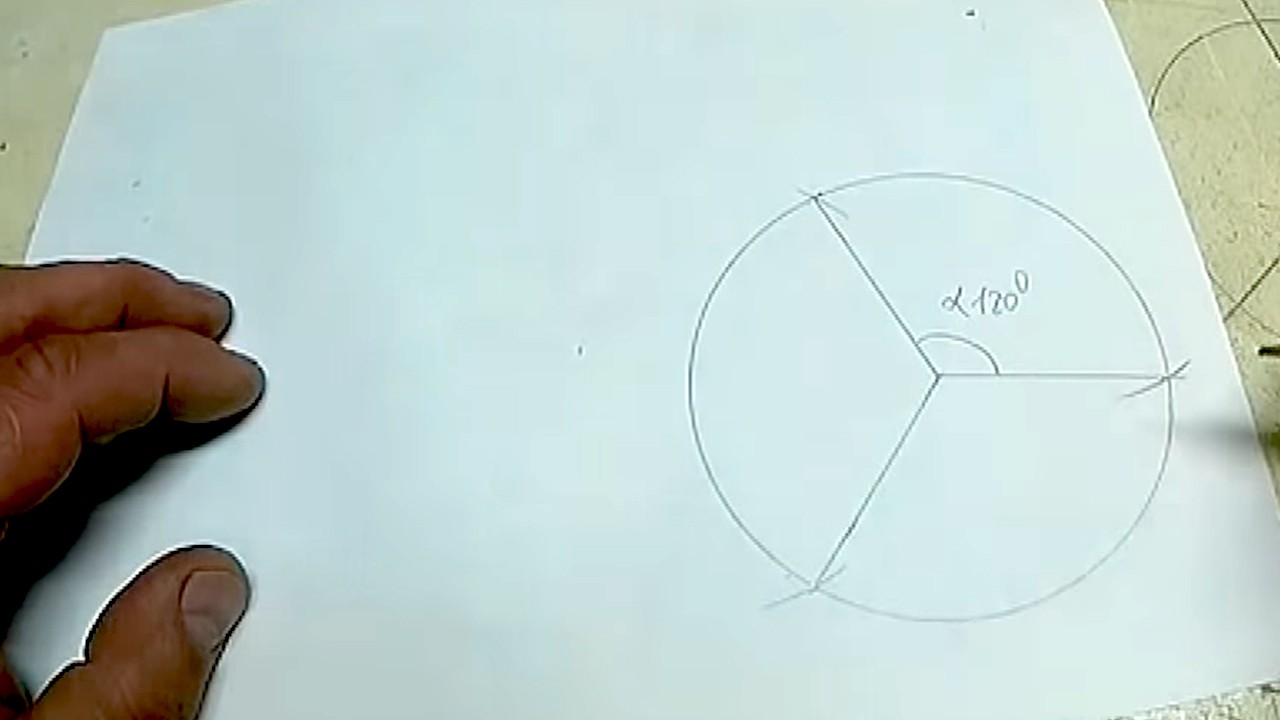
Деление на 6 частей
Шаг 1 из 3
Для деления на 6 частей делаем засечки на окружности, не через одну позицию, а последовательно.

Шаг 2 из 3
Получаем 6 точек на окружности.
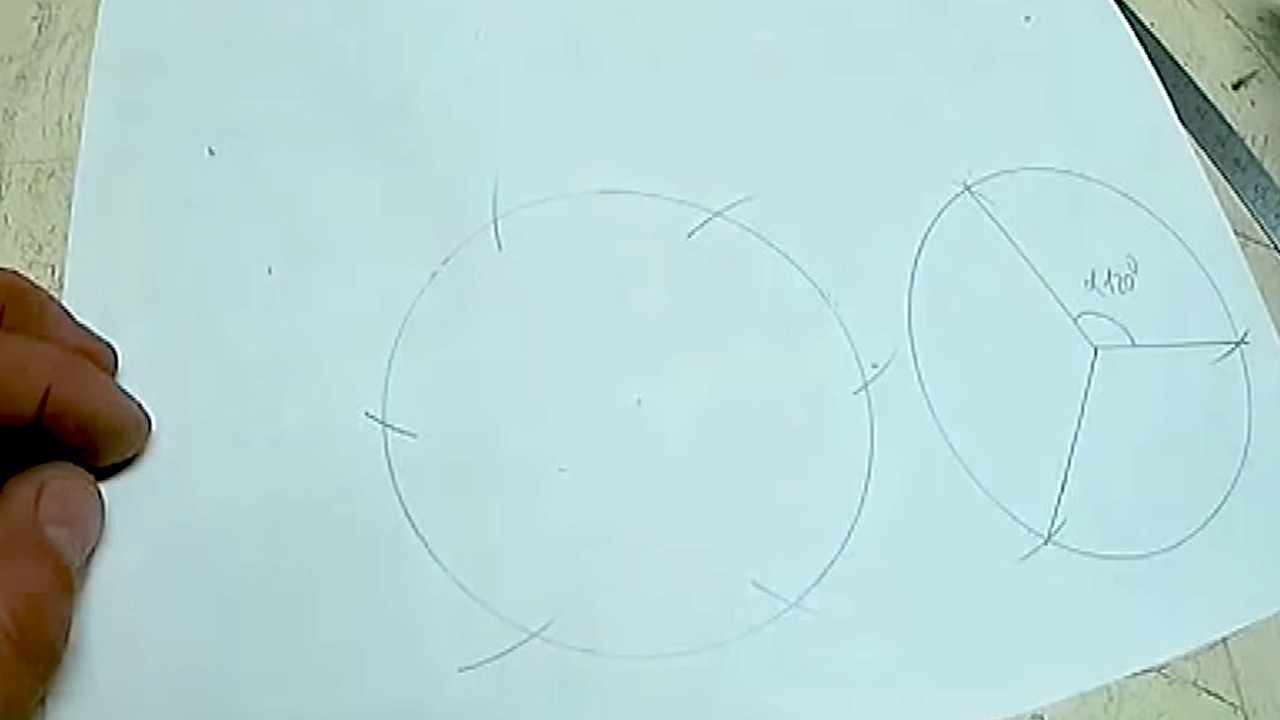
Шаг 3 из 3
Соединяем точки с центром и параллельной засечкой и получаем 6 частей.


Деление на 12 частей: 1 способ
Шаг 1 из 6
Чтобы разбить на 12 есть, как минимум, 2 способа. Первый способ – расчеты проводятся из круга, деленного на 6 частей.
Для этого из двух ближайших точек окружности проводим 2 дуги за пределы фигуры, навстречу друг другу.
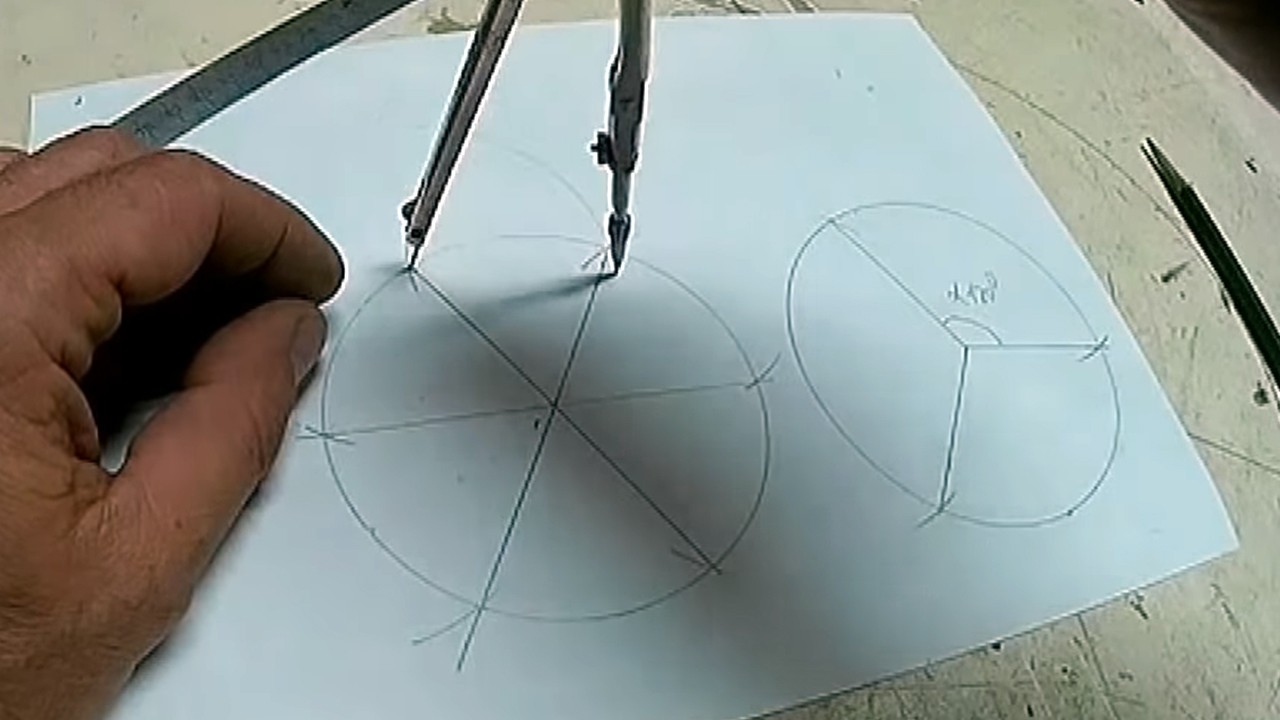
Шаг 2 из 6
Точку пересечения дуг соединяем с центральной точкой окружности.

Шаг 3 из 6
Так мы делим 1/6 на 2 части.
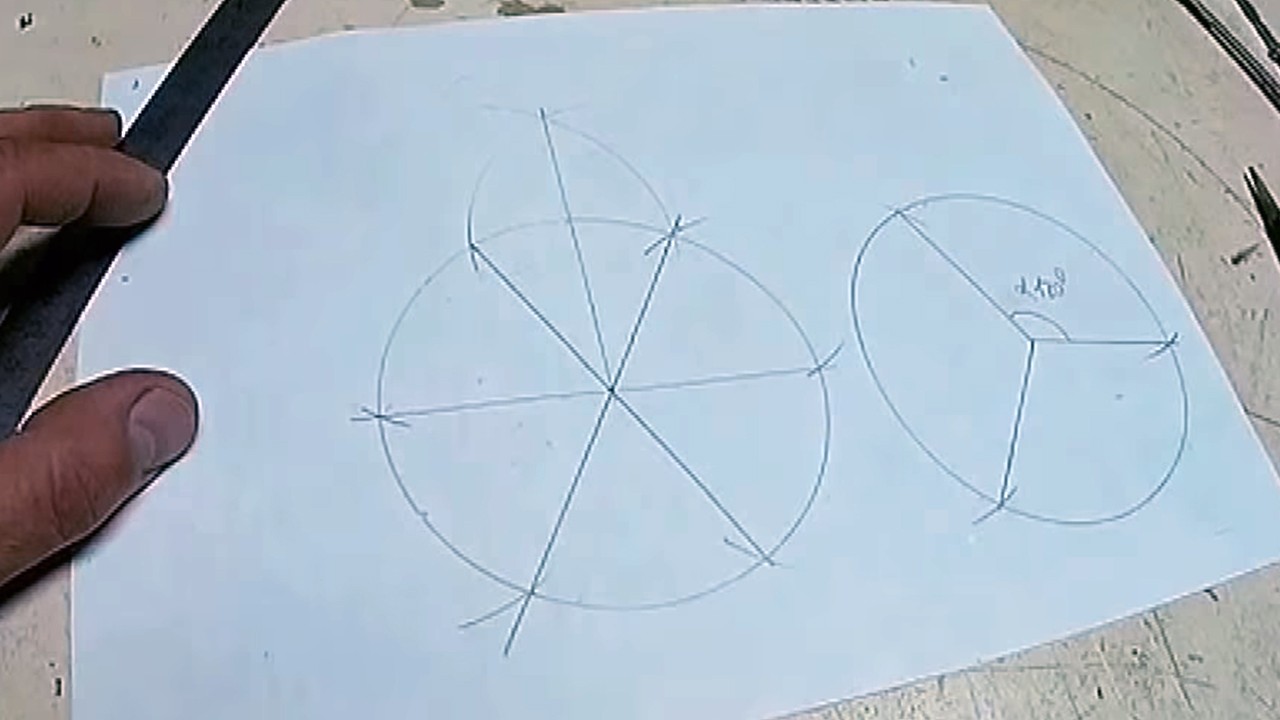
Шаг 4 из 6
Циркулем измеряем длину получившегося сегмента.

Шаг 5 из 6
Эту длину откладываем на других частях.

Шаг 6 из 6
Затем новые засечки соединяем прямыми с центром, получаем деление на 12 частей.

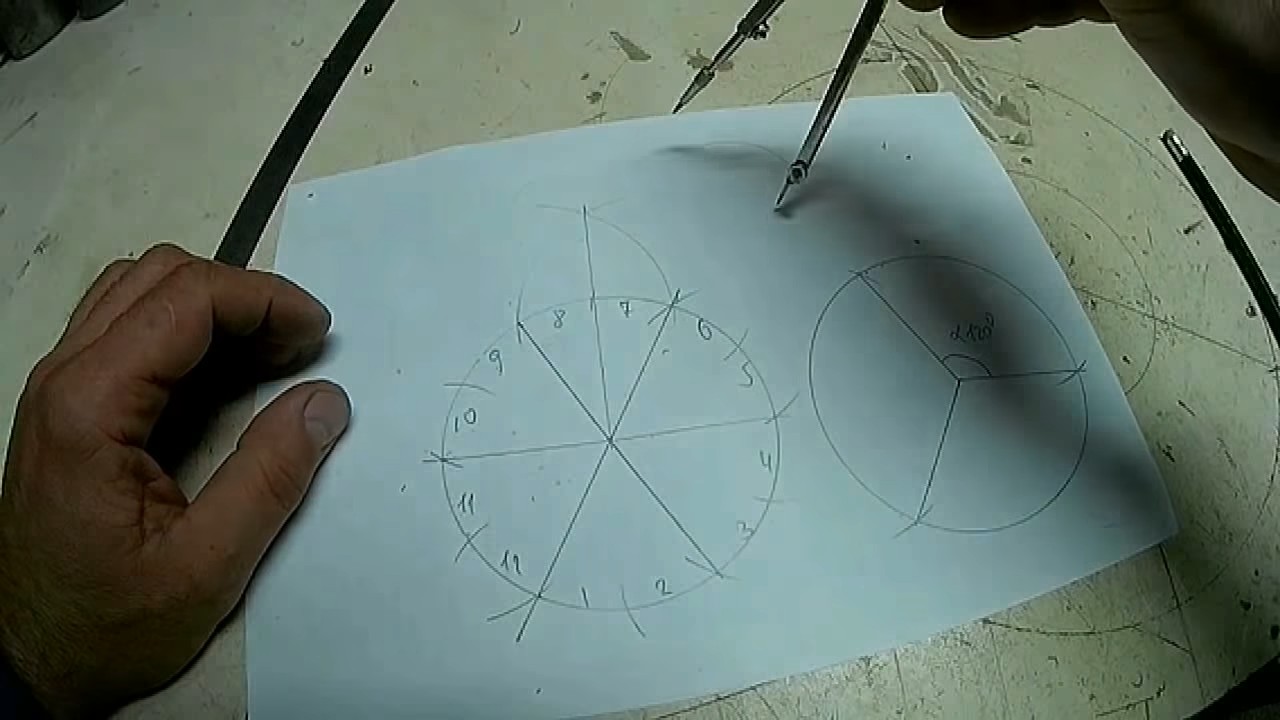
Деление на 12 частей: 2 способ
Шаг 1 из 2
Второй способ – рисуем 2 перпендикулярные прямые через центр окружности, тем самым делим ее на 4 сегмента.

Шаг 2 из 2
От каждой точки пересечения прямой и окружности в 2 стороны отмеряем расстояние, равное радиусу, намечаем. Так мы получаем снова 12 частей.
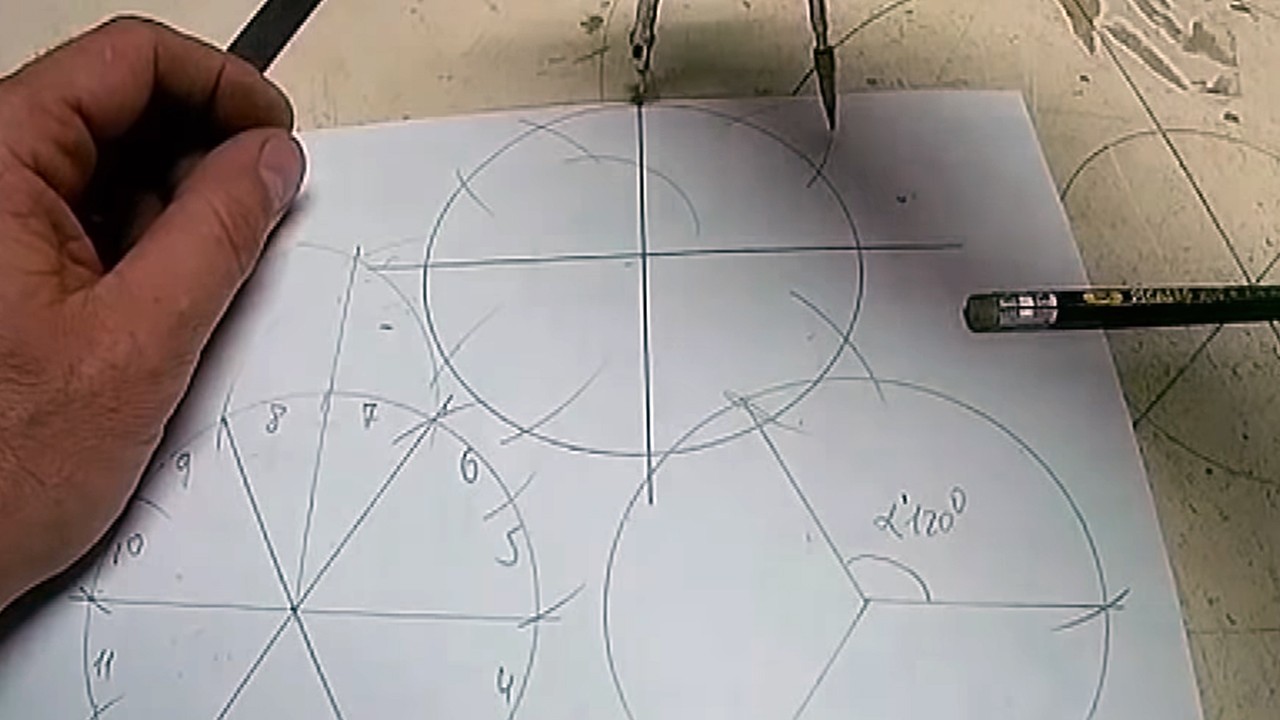
|
Это смотря что измерять если взять третью часть от полного угла, то это будет угол 120 градусов, одна треть от развернутого угла равна углу 60 градусов, а 1/3 прямого угла равна углу 30 градусов. Если отмерять время, то здесь полезно знать, что треть месяца называется декадой и она равна 10 дням, а треть часа равна 20 минутам, треть минуты 20 секундам. Если пройденный путь это треть от всего пути, то он всегда в два раза меньше того пути, который осталось еще пройти. Если в десятичной системе, то треть равна 0,33(3), а если треть записать в виде правильной дроби. то она будет равна 1/3 = 2/6 = 3/9 = 4/12 и т.д. модератор выбрал этот ответ лучшим
olelena84 9 лет назад Третья часть – это одна часть из равных трех частей. Чтобы вычислить в процентах, необходимо проделать следующие действия: 100*1=100/3=33,33333%, для вычисления в числовом значении: 1/3=0,33333. Например, берем торт и делим на три одинаковых куска, один кусок – это одна третья всего торта.
Афанасий44 8 лет назад
Если в классе, к примеру, 30 человек учится, то третья часть от всего количества составит 10 человек. Если человеку нужно пройти 3 километра, то треть пути будет ровно один километр. Третья часть от килограмма – это 333,333 грамма. Ну и так далее. Яна 2015 8 лет назад Это если всё имеющееся количество разделить на 3 части, а потом взять одну из этих частей. Если говорить о числах или количестве чего-то, что можно посчитать по штукам – нужно просто число/ количество штук разделить на три. Если речь идет о чем-то, что штуками не измерить – например, “треть стакана – это сколько?” (“1/3 стакана – это сколько?”)- то просто разделите на глаз и возьмите одну из частей. Так же можно посчитать 2/3 стакана: разделите стакан на глаз на три части и насыпьте/ налейте 2 из них. Третья часть – это одна третья. Третью часть ещё называют одна третья или треть. Если записать математически, то это 1/3 или 0.3333333…. А если пытаться понять, то тогда: Попробуйте взять что-нибудь, что можно разрезать, например пирог. Разрежьте пирог на три равные между собой части. Возьмите в руку одну из отрезанных частей пирога. Вы держите в руке одну третью часть пирога.
Sveta S 8 лет назад Третья часть или 1/3. Если взять число и разделить его на три, это уже и будет третья часть. Например, есть число 12. Третья часть от 12 (12 : 3 = 4) – это 4. Если нас интересует третья часть не числа, а какого-нибудь вещества, например, муки в стакане, надо условно разделить стакан муки на три части и взять из них одну часть. Это и будет третья часть стакана муки.
Андрей0817 8 лет назад Третья часть – это одна часть одного целого, если это одно целое разделить на три равные части. Если кусок теста разделить на 3 равные части, то одна такая часть – это третья часть. Если разделить одно целое на 2, 4, 5, 6 частей, то получатся одна вторая, одна четвёртая (четверть), одна пятая и т.д.
Про100 й 8 лет назад Третью часть легко определить от числа делящегося на три например число 9: Число 9 делим на три и получаем три- это и будет третья часть. В круге 360 градусов и если поделить на три каждая часть будет составлять 120 градусов – это количество тоже является третью частью круга.
Артём Денисов 8 лет назад Смотря третья часть чего именно. Третья часть – это какой-то предмет/вещь/цифра и т.д. деленная на три части и одна из этих частей как раз и будет третьей. Можно еще сказать, что это 33.33% чего-либо – так вроде немного понятнее становится.
Ксюшенька 8 лет назад Простите, а чего третья часть? Или опять нас поймать хотите?) Я возьму ту величину, что мне ближе всего и скажу сколько будет. Например, сто килограммов. Третья часть будет примерно, тридцать три килограмма.
Cveto4ek 8 лет назад Если в процентном соотношении, то третья часть – это 33,33 % от общего количества чего-то. Другими словами, целое нужно поделить на три равных части, одна из которых и будет называться третья часть. Sergey78 9 лет назад Это один кусок из трёх одинаковых кусков. Знаете ответ? |
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала – традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним – нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
![]()
Деление круга на равные по площади части радиусами
Точность вычисления
Знаков после запятой: 2
![]()
Деление круга на равные по площади части параллельными хордами
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга – по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё – мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
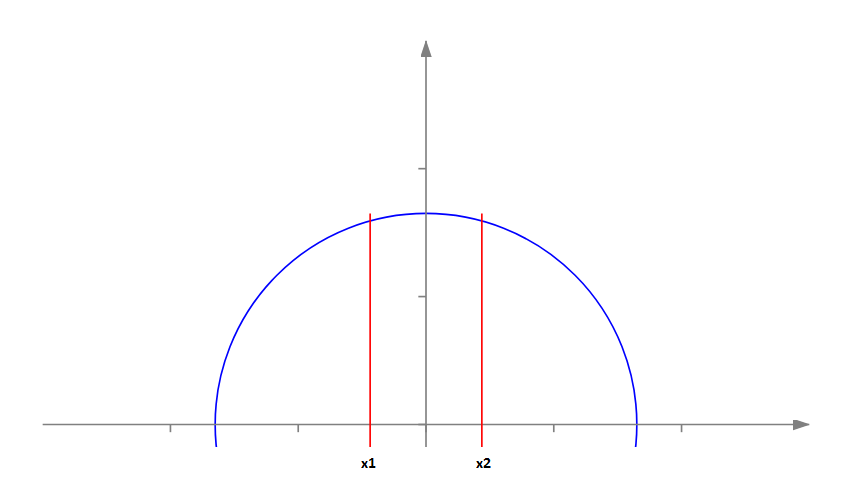
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x – это координата вдоль оси абсцисс, а y – это функция, численно равная y координате соответствующей точки верхней полуокружности.
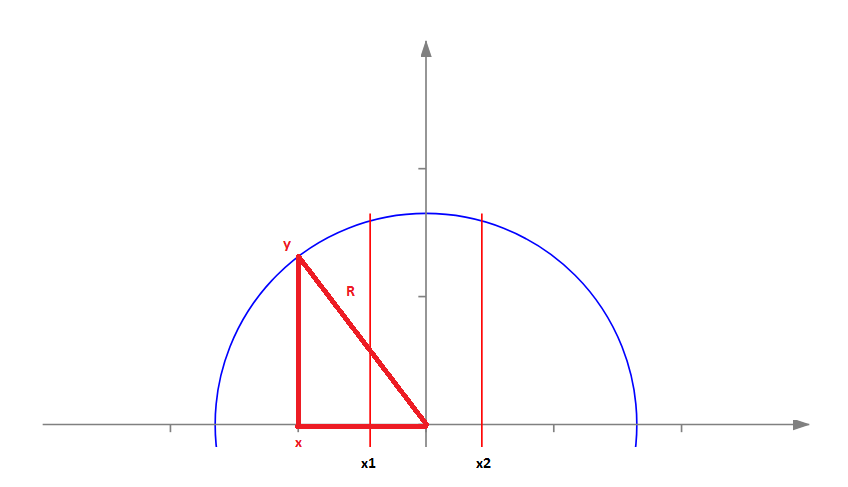
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
, откуда
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей
и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.


