Сколько см составляет одна вторая отрезка.
Вы находитесь на странице вопроса Сколько см составляет одна вторая отрезка? из категории Математика.
Уровень сложности вопроса рассчитан на учащихся 1 – 4 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
Эта информация доступна зарегистрированным пользователям
Начнем знакомство с одним из разделов математики, который называется геометрия.
Слово геометрия древнегреческого происхождения, оно означает «землемерие» («гео» – земля, «метрео» – измерять).
Геометрия – древняя наука, возникла в результате практической деятельности человека: строительства зданий и дорог, установления земельных наделов и определения их размеров.
Становление данной науки происходило тысячелетиями.
В настоящее время геометрия – наука, занимающаяся изучением геометрических фигур, их свойствами, размерами и преобразованиями.
Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.
Эта информация доступна зарегистрированным пользователям
Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.
Научимся сравнивать, находить длины отрезков.
Познакомимся с различными единицами измерения отрезков.
Рассмотрим свойства измерения длин отрезков.
Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).
Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.
Одной такой элементарной фигурой является точка.
Точка – это неделимая фигура, не имеет частей и размеров (высоты, радиуса, длины и т.д.), направления и других характеристик.
В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.
Эта информация доступна зарегистрированным пользователям
Слово «точка» с латинского языка означает мгновенное касание, укол.
Точку принято рассматривать как некоторое место в пространстве или на плоскости.
Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).
Две точки на плоскости можно соединить бесконечным множеством линий.
Эта информация доступна зарегистрированным пользователям
Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.
Кратчайшая линия между двумя точками называется отрезком.
Любые две точки можно соединить только одним отрезком.
Эта информация доступна зарегистрированным пользователям
Отрезок – это часть прямой линии, ограниченной двумя точками.
Точки, ограничивающие отрезок, называются концами отрезка.
Отрезок обозначают указанием имен его концов.
Рассмотрим пример:
Через точки А и В с помощью линейки провели прямую.
Эта информация доступна зарегистрированным пользователям
А и В – концы отрезка.
Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.
Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».
В названии отрезка не важно в каком порядке указываются его концы.
Отрезок АВ и ВА – это один и тот же отрезок.
Отрезок можно построить с помощью линейки.
Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.
Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:
Между точками А и В отметить точку С.
Эта информация доступна зарегистрированным пользователям
Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.
Эта информация доступна зарегистрированным пользователям
Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.
Эта информация доступна зарегистрированным пользователям
Каждый отрезок имеет определенную длину, значение которой является числом.
Длина в геометрии – это величина, которая характеризует протяженность.
Длина отрезка – это расстояние между концами отрезка.
Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.
Существует несколько способов сравнения отрезков.
1. Приблизительный способ сравнения.
Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.
Пример: Даны два отрезка АВ и ЕР
Эта информация доступна зарегистрированным пользователям
Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР
2. Совмещение отрезков – более точный способ сравнения отрезков.
Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.
По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.
Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).
Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).
Пример: Даны два отрезка АВ и ОЕ
Эта информация доступна зарегистрированным пользователям
Сравним данные отрезки методом совмещения отрезков.
Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.
Эта информация доступна зарегистрированным пользователям
Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.
Значит, отрезок ОЕ короче отрезка АВ.
Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.
3. Сравнение отрезков с помощью измерителя.
Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.
В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.
Эта информация доступна зарегистрированным пользователям
Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.
Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.
- Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
- Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
- Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.
Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.
В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.
Пример:
Пусть даны три отрезка СD, АЕ, BG
Эта информация доступна зарегистрированным пользователям
Сравним эти отрезки с помощью циркуля.
Соединим ножки циркуля с концами С и D отрезка СD.
Приложим циркуль с заданным раствором к отрезку АЕ.
Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).
Приложим циркуль с заданным раствором к отрезку BG.
Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).
Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.
4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.
Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.
Большим будет являться тот отрезок, длина которого больше.
Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.
Эта информация доступна зарегистрированным пользователям
Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.
Отрезки (звенья) ломаной линии называют сторонами многоугольника.
Общие точки двух отрезков (сторон) многоугольника называют его вершинами.
Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.
Количество сторон и количество углов в многоугольнике совпадают.
Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.
Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.
Рассмотрим пример:
На рисунке изображен многоугольник АBCDEF.
Эта информация доступна зарегистрированным пользователям
Вершины многоугольника АBCDEF: А, B, C, D, Е, F.
Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.
Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.
Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.
Периметр многоугольника – это сумма длин всех сторон.
Периметр многоугольника принято обозначать заглавной латинской буквой Р
Найдем периметр многоугольника АBCDEF (изображенного на рисунке):
РАВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.
Существует огромное множество различных видов многоугольников.
Обычно многоугольники различают по числу сторон и углов.
Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник – 6 углов и 6 сторон.
Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.
Треугольник – плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.
Рассмотрим пример:
Эта информация доступна зарегистрированным пользователям
На рисунке изображен треугольник АBC (Δ АBC).
А, В, С – вершины треугольника АBC.
Отрезки AB, BC, АC– стороны треугольника АBC.
Периметр треугольника- это сумма длин трех его сторон.
Найдем периметр треугольника АBC (изображенного на рисунке):
РАВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.
Эта информация доступна зарегистрированным пользователям
В действительности часто приходится иметь дело с различными реальными объектами, а не с отрезками.
Говоря о ширине, высоте, толщине и т.д., мы имеем в виду длину какого-либо отрезка.
Давайте разберемся, что значит найти длину отрезка.
Измерить отрезок – значит найти его длину, т.е. определить расстояние между концами этого отрезка.
Для измерения длины отрезков применяют различные измерительные инструменты, сантиметровая линейка является простейшим из них.
По краю такой линейки нанесены деления (шкала), обозначающие сантиметры и их десятые части- миллиметры, что позволяет количественно оценить длину.
Чтобы измерить длину отрезка, необходимо:
- Приложить край линейки к отрезку
- Нулевую отметку шкалы делений линейки совместить с левым концом отрезка
- Результат измерения определить по шкале линейки: деление, которое совпадет с правым концом отрезка, будет означать длину отрезка
Рассмотрим пример:
Дан отрезок АВ.
Измерим его длину сантиметровой линейкой.
Эта информация доступна зарегистрированным пользователям
Нулевую точку шкалы линейки совместим с концом А отрезка АВ.
При этом конец В совпадет с делением шкалы линейки 4 см, значит, длина отрезка АВ равна 4 см. (АВ = 4 см.)
Этот способ измерение длины отрезка основан на сравнении этого отрезка с отрезком, длина которого принимается равной единице (единичным отрезком).
Измерить отрезок – это значит подсчитать сколько единичных отрезков содержится в нем.
Если за единичный отрезок, например, принять сантиметр, то для определения длины заданного отрезка необходимо узнать, сколько раз в данном отрезке помещается сантиметров.
Рассмотрим пример:
Эта информация доступна зарегистрированным пользователям
На рисунке изображены три отрезка.
Отрезок ОЕ– единичный отрезок = 1 см.
В отрезке АВ единичный отрезок ОЕ помещается 3 раза, в отрезке CD– 5 раз.
Это значит, что длина отрезка АВ = 3 единичных отрезка = 3 см. (говорят: «Отрезок АВ равен 3 см»).
Длина отрезка СD = 5 единичных отрезков = 5 см. (говорят: «Отрезок СD равен 5 см»).
Конечно, возможна ситуация, когда отрезок, принятый за единицу измерения, укладывается нецелое число раз в измеряемом отрезке, т.е. получается остаток.
В таком случае единичный отрезок (сантиметр в нашем случае) делят на десять равных частей (миллиметры) и определяют сколько в остатке измеряемого отрезка укладывается этих маленьких делений- миллиметров.
Эта информация доступна зарегистрированным пользователям
Разберемся, что называют суммой и разностью отрезков.
Задача 1
Пусть даны два отрезка СD = 5 см и АВ = 3 см.
Эта информация доступна зарегистрированным пользователям
Найдите сумму СD+АВ = ?
Решение:
Чтобы найти сумму отрезков СD и АВ, нужно расположить данные отрезки последовательно друг за другом, длина полученного отрезка будет являться суммой двух данных.
Эта информация доступна зарегистрированным пользователям
СD+ АВ = 5 см + 3 см = 8(см) сумма отрезков АВ и СD
Ответ: 8 (см)
Вывод: чтобы найти сумму отрезков, нужно сложить их длины.
Задача 2
Пусть даны два отрезка АВ = 5 см и СD = 3 см.
Эта информация доступна зарегистрированным пользователям
Найдите разность АВ – СD = ?
Решение:
Чтобы найти разность отрезков АВ и СD, нужно от левого конца большего отрезка отложить длину меньшего отрезка.
Длина отрезка, расположенного между правыми концами первого и второго отрезка, будет разностью двух исходных отрезков.
Эта информация доступна зарегистрированным пользователям
АВ – СD = 5 см – 3 см = 2(см) разность отрезков АВ и СD
Ответ: 2 (см)
Вывод: чтобы найти разность двух отрезков, нужно из длины большего отрезка вычесть длину меньшего.
Задача 3
Точка С– середина отрезка АВ.
Отрезок АВ равен 1 м 42 см.
Найдите длину отрезка АС и выразите ее в сантиметрах.
Точка С принадлежит отрезку AB и делит его на равные части, значит:
АС = СВ
1м = 100 см
АВ = 1 м 42 см = 142 см
Чтобы найти середину отрезка, нужно его длину разделить на два.
АС = СВ = АВ ÷ 2 = 142 ÷ 2 = 71 (см) длина отрезка АС
Ответ: 71 (см).
Эта информация доступна зарегистрированным пользователям
Геометрические иллюзии и обман зрения
Иллюзией называют неправильное, искаженное восприятие реальной картины мира.
Существуют различные иллюзии: слуховые, осязательные, иллюзии движения, иллюзии-перевертыши и т.д.
Геометрическая иллюзия- это оптический обман нашего мозга, который выражается в том, что видимые отношения элементов фигур не совпадают с фактическими.
Рассмотрим некоторые иллюзии связанны с искажением зрительного восприятия: иллюзии размера и контраста.
1. Иллюзия Болдуина.
Предмет кажется больше его реальной величины благодаря соседству с крупными объектами.
Эта информация доступна зарегистрированным пользователям
Отрезки №1 и №2 абсолютно равны.
2. Иллюзия Франца Мюллера-Лайера.
Стрелки и окружности на концах отрезков создают иллюзию искажения длины.
Происходит перенесения свойств целой фигуры на ее отдельные части.
Эта информация доступна зарегистрированным пользователям
Равные по длине отрезки воспринимаются неодинаковыми.
3. Иллюзия железнодорожных путей.
Верхний голубой отрезок кажется длиннее, но на самом деле оба отрезка имеют равную длину.
Эта информация доступна зарегистрированным пользователям
4. Отрезки АВ и СD равны
Эта информация доступна зарегистрированным пользователям
5. Иллюзия кинескопа.
Окна на картинке одинакового размера
Эта информация доступна зарегистрированным пользователям
6. Вертикально-горизонтальная иллюзия.
Эта информация доступна зарегистрированным пользователям
Линия №1 воспринимается длиннее линии №2.
Читайте также
Деление отрезка в заданном соотношении: координаты точки
Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.
Определение координат точки, делящей отрезок в заданном отношении, на плоскости
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .
Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:
В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .
Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .
Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .
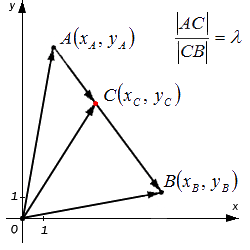
Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .
Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.
Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → – O C →
По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .
Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .
Преобразуем выражение, подставив в него : C B → = O B → – O C → .
A C → = λ · ( O B → – O C → ) .
Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → – O C → ) .
Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .
Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .
Выполним необходимые действия над векторами O A → и O B → .
O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .
Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .
Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .
Определение координат точки, делящей отрезок в заданном отношении, в пространстве
Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .
Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .
Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:
O C → = 1 1 + λ · ( O A → + λ · O B → )
Векторы и являются радиус-векторами точек А и В , а значит:
O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно
O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )
Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )
Рассмотрим теорию на конкретных примерах.
Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( – 9 , 2 , – 4 ) .
Решение
По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:
x A + λ · x B 1 + λ = 11 + 5 3 · ( – 9 ) 1 + 5 3 = – 3 2
y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8
z A + λ · z B 1 + λ = 0 + 5 3 · ( – 4 ) 1 + 5 3 = – 5 2
Ответ: C ( – 3 2 , 13 8 , – 5 2 )
Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .
Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , – 2 ) , C ( – 5 , – 4 , 8 )
Решение
Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.
Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .
Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:
x D = x B + x C 2 = 4 + ( – 5 ) 2 = – 1 2 y D = y B + y C 2 = 1 + ( – 4 ) 2 = – 3 2 z D = z B + z C 2 = – 2 + 8 2 = 3
Вычислим координаты точки М :
x M = x A + λ · x D 1 + λ = 2 + 2 · ( – 1 2 ) 1 + 2 = 1 3
y M = y A + λ · y D 1 + λ = 3 + 2 · ( – 3 2 ) 1 + 2 = 0
z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3
Деление векторов в данном соотношении
Пусть вектор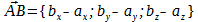 
задан координатами своего начала A(ax; ay; az) и конца B(bx; by; bz) и пусть точка C(cx; cy; cz) расположена между точка A и B
пусть при этом известно соотношение длин векторов
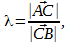
тогда координаты точки C(cx; cy; cz) находятся по формулам
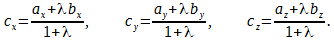
Примеры решения заданий по делению векторов и отрезков
Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.
Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении
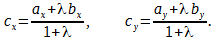
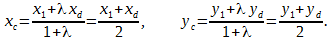
Подставим в последнее равенство координаты xc, yc, xd, yd:
3 = (x1 + 5)/2, 4 = (y1 + 6)/2,
откуда находим, x1 = 1, y1 = 2. Точка A имеет координаты A(1, 2).
Поскольку точка D есть середина отрезка CB, то xd = (xc + x2)/2, или 5 = (3 + x2)/2, отсюда x2 = 7.
отсюда y2 = 8. Получили B(7, 8).
О т в е т: A(1, 2), B(7, 8).
Даны вершины треугольника A(2, -4), B(4, -5) и C(-4, 7). Определить середины его сторон.
Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:
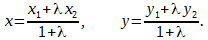
Поскольку отрезки делятся на равные части, то
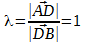
Тогда формула приобретает вид:
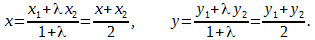
Координата x для отрезка AB равна (2+4)/2 = 3, координата y для отрезка AB равна (-4-5)/2 = -4,5.
Координата x для отрезка AC равна (2-4)/2 = -1, координата y для отрезка AC равна (-4+7)/2 = 1,5.
Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.
О т в е т: искомые точки имеют координаты (3; -4,5), (-1; 1,5) и (0; 1).
Даны три вершины параллелограмма A(2, -4), B(4, -2), C(-2, 4). Определить четвёртую вершину D, противоположную B.
Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.
Назовём точку пересечения диагоналей точкой E.
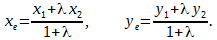
Поскольку этой точкой диагонали делятся на два равных отрезка
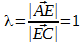
то формула приобретает вид:
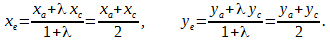
Найдём середину отрезка AC:
Итак, точка E имеет координаты (0, 0).
Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда
подставим известные значения:
Теперь найдём вторую координату:
подставим известные значения:
Даны вершины треугольника A(2, 3); B(4, -10); C(-4, 1), определить длину его медианы, проведённой из вершины B.
Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:
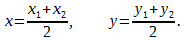
Точка D имеет координаты (-1, 2).
Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:
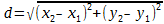
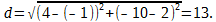
О т в е т: Длина медианы, проведённой из вершины B, равна 13.
Декартова прямоугольная система координат. Деление отрезка в данном отношении.
Декартова прямоугольная система координат
Определение 1. Осью называется прямая, на которой:
1) выбрана начальная точка (“начало” – точка О);
2) указано (стрелкой) положительное направление отсчета;
3) выбран масштаб.
Определение 2. Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY – осью ординат (третья ось OZ – осью аппликат).
Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел – координат данной точки.
Определение 3. Уравнением линии на плоскостиназывается уравнение с двумя переменными, такое, что только координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению.
Расстояние между двумя точками на плоскости
Y
Из треугольника ABC:
.
Деление отрезка в данном отношении
Пусть даны две точки M1 (x1, y1) и M2 (x2, y2). Найдем на отрезке M1M2 точку N, которая делила бы данный отрезок в отношении 
: 
.
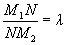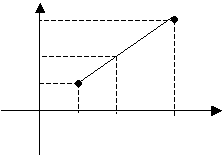B2 M2
По теореме о пропорциональности отрезков прямых, пересеченных рядом параллельных прямых, получим
,
,
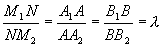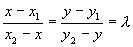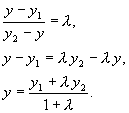
Координаты точки, делящей отрезок в данном отношении, находятся по этим формулам.
Если l = 1 , то деление отрезка производится пополам:
, 
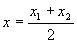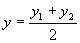– формулы для нахождения координат середины отрезка.
Скалярное произведение векторов; скалярное произведение векторов, заданных координатами.
Скалярное произведение векторов.
Скалярным произведением вект. А и В называется число, равное произведению длин этих векторов, умноженному на косинус угла между ними
Свойства. 1) (a,b)=(b,a) (коммутативность). 2) (λa,b) =(a, λb) = λ (a,b) (ассоциативность). 3) дистрибутивно относительно сумсуммы (а+b,с)=(а,b)+(а,с) 4) Скалярное произведение двух векторов равно нулю тогда и только тогда когда хотя бы один из вект. нулевой либо они перпендикулярны (a • b = 0, если a ┴ b).
Скалярным квадратом называется скалярное произведение вектора на себя => равен квадрату длины вектора.
(a,b)= 
*|b|*Cos(a^b); прab=(a,b)/ 
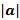(проекция a на b). Длина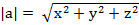 
Скалярное произведение в коорд форме.Коорд орты i,j,k имеют длины, равные единицы i 2 =j 2 =k 2 =1, их взаимное произведение равно 0 . (a,b) =ax*bx+ay*by+az*bz. Cos и ПР находятся с помощью координат.
Векторное произведение векторов.
Векторным произведением вектора а на вектор b называется вектор с, который: 1) Перпендикулярен векторам a и b, т. е. с^а и с^b; 2) Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах, т. е.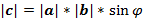 
. 3.Векторы a, b и с образуют правую тройку.
Свойства: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. [а,b] =[b,a]; 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. [а,b] = [а,b] = [b,a]; 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b [а,b] =0. 4.распределительное свойство:[a+b,с]=[а,с]+[b,с].
[spoiler title=”источники:”]
http://poisk-ru.ru/s5934t1.html
[/spoiler]
В тетради по клеточкам,так как 2 клетки равны 1см.Рисуешь отрезок размером 8 см(16 клеток)
1/2=половине отрезка,значит8:2=4 см. отмечаешь на отрезке точку 4см или (8клеток)
1/4= четвертая часть,значит 8:4= 2 см (4 клетки)
Отмена
Захар Угшенов
Отвечено 30 сентября 2019
-
Комментариев (0)
Добавить
Отмена
|
-1 / 0 / 0 Регистрация: 19.10.2012 Сообщений: 19 |
|
|
1 |
|
Как найти координаты конца отрезка11.08.2013, 02:32. Показов 34456. Ответов 9
Как можно найти координаты конца отрезка, если известны координаты начала(х0, У0) и его длина(Z). Подскажите формулу пожалуйста, нигде ничего не могу найти.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
11.08.2013, 02:32 |
|
Ответы с готовыми решениями:
Найти координаты точек отрезка если известны координаты концов отрезка Найти координаты точки отрезка 9 |
Найти координаты точек начала и конца отрезка|
2662 / 1726 / 175 Регистрация: 05.06.2011 Сообщений: 4,955 |
|
|
11.08.2013, 05:42 |
2 |
|
Собственно, никак. Конец такого отрезка будет лежать на окружности в центром в начале и радиусом, равным длине — и это всё, что можно узнать из условий.
0 |
|
2 / 0 / 0 Регистрация: 10.08.2013 Сообщений: 19 |
|
|
11.08.2013, 06:26 |
3 |
|
Действительно, если не определено как лежит данный отрезок параллельно оси абсцисс, ординат . то конец может быть в любой точке лежащей на окружности радиус которой равен длине данного отрезка.
0 |
|
Модератор
35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
11.08.2013, 10:06 |
4 |
|
Координаты конца зависят от одного параметра вот так:
где α меняется от 0 до 2π
1 |
|
670 / 163 / 22 Регистрация: 27.01.2012 Сообщений: 372 |
|
|
12.08.2013, 23:58 |
5 |
|
Конец отрезка будет круг на плоскости описывать.
0 |
|
-1 / 0 / 0 Регистрация: 19.10.2012 Сообщений: 19 |
|
|
13.08.2013, 01:30 [ТС] |
6 |
|
Спасибо, формулы мне очень помогли, я уже все сделал.
0 |
|
5561 / 1367 / 150 Регистрация: 08.02.2009 Сообщений: 4,107 Записей в блоге: 30 |
|
|
15.08.2013, 18:15 |
7 |
|
Конец отрезка будет круг на плоскости описывать. Окружность, если приглядеться.
Можно формулу этого круга вывести Вдохновили (а то думаю: чи можно, чи не можно): (x – y0) ² + (y – y0) ² = Z², где точка (x; y) и есть искомый конец.
0 |
|
74 / 4 / 2 Регистрация: 21.03.2012 Сообщений: 187 |
|
|
04.11.2014, 16:28 |
8 |
|
Catstail, а если дано: координаты начала отрезка, длина отрезка, уровнение отрезка (отсюда и угол tg fi) и найти координаты конца?
0 |
|
Модератор
35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
04.11.2014, 17:46 |
9 |
|
Если дано урАвнение отрезка (т.е. угол с осью абсцисс fi), то координаты конца считаются так: x=x0+d*cos(fi)
0 |
|
74 / 4 / 2 Регистрация: 21.03.2012 Сообщений: 187 |
|
|
04.11.2014, 19:05 |
10 |
|
Catstail, спасибо за ответ
0 |
