Операции с векторами
Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
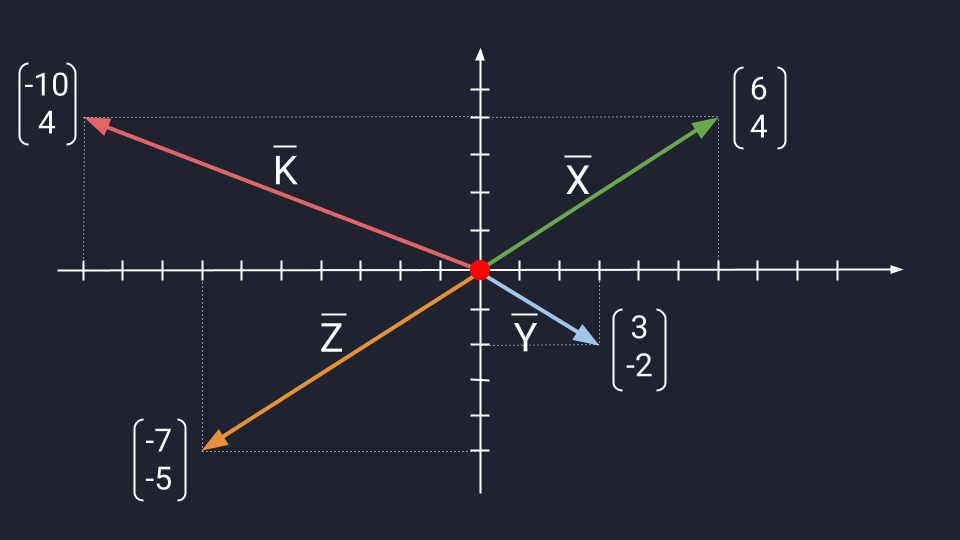 Векторы X, Y, Z, K в двухмерном пространстве
Векторы X, Y, Z, K в двухмерном пространстве
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
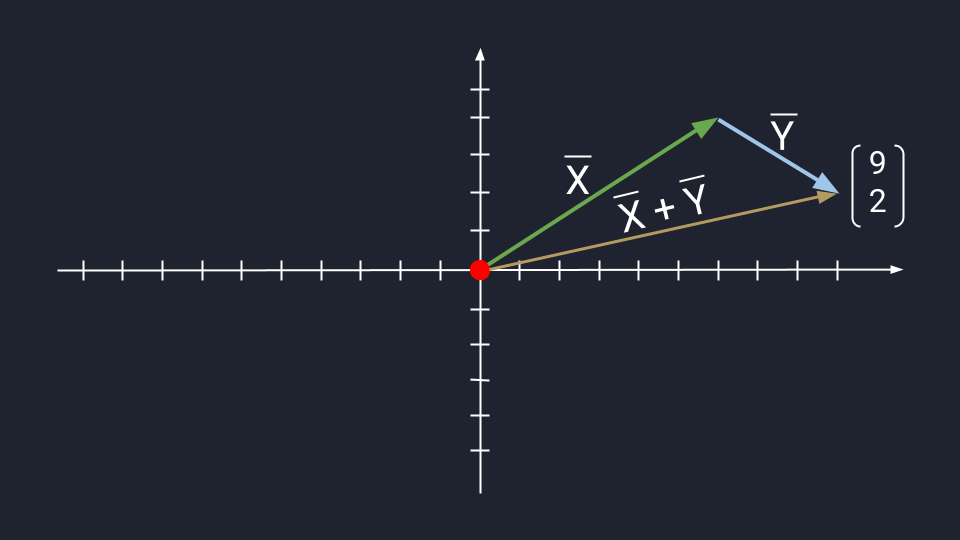 Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)
Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
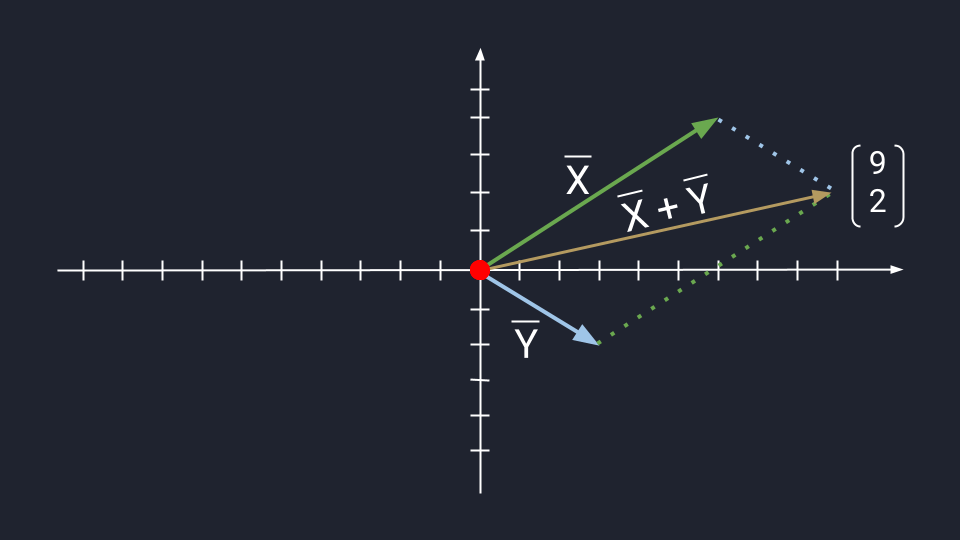 Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)
Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)
Вычитание
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
- У нас есть X = (6, 4) и Y = (3, −2).
- Превращаем формулу Х − Y в формулу Х + (−Y).
- Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
- Считаем: X + (−Y) = (3, 6).
Теперь посмотрим, как выглядит вычитание векторов на графике:
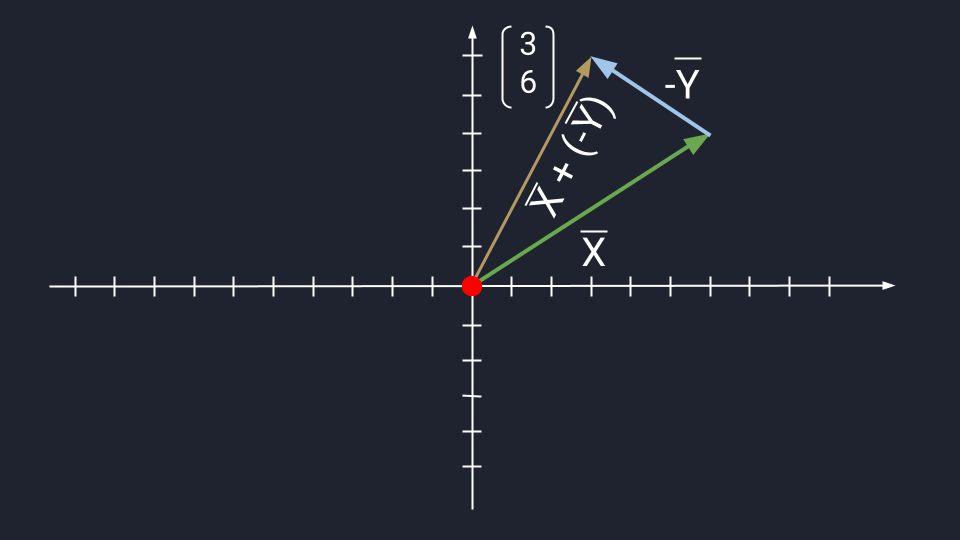 Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)
Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) 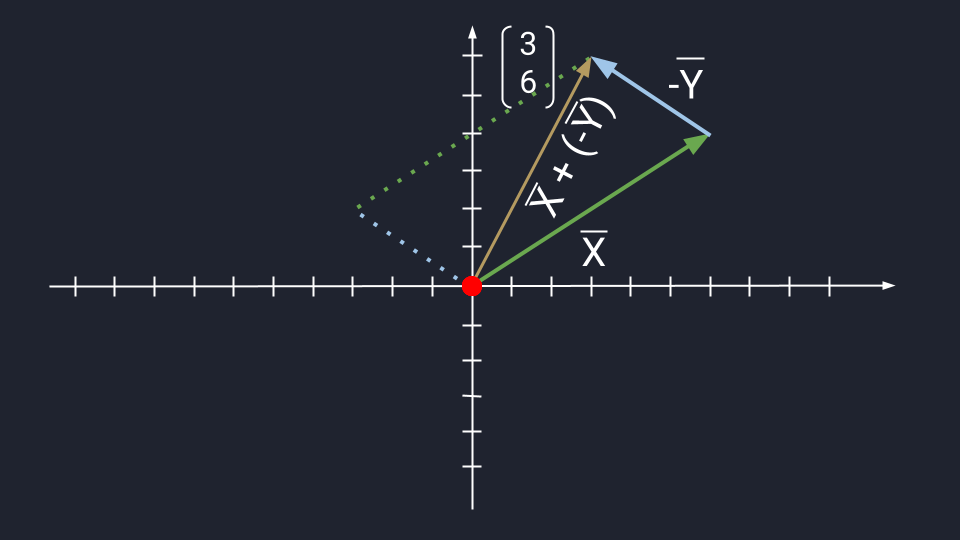 Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)
Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 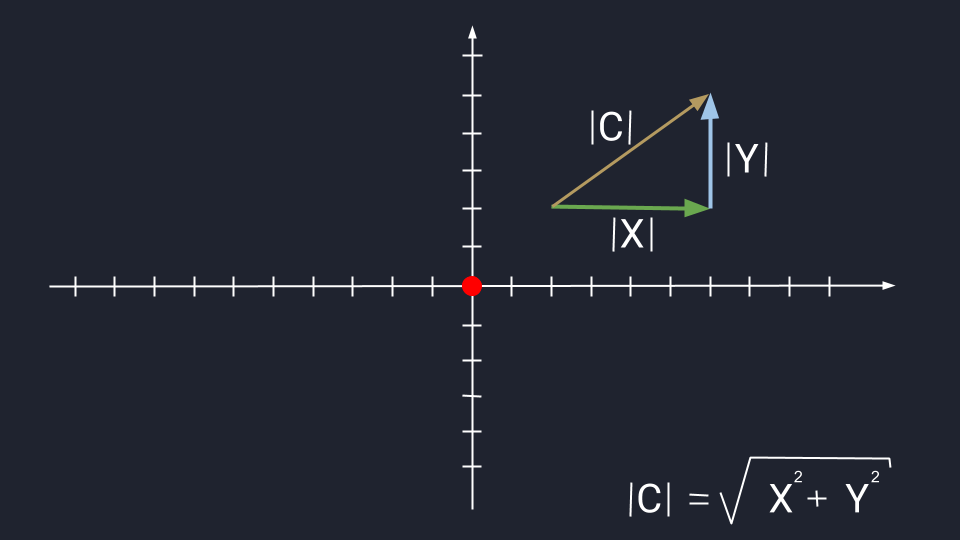 Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат
Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
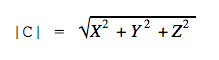
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
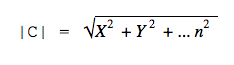
Умножение и деление вектора на число
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
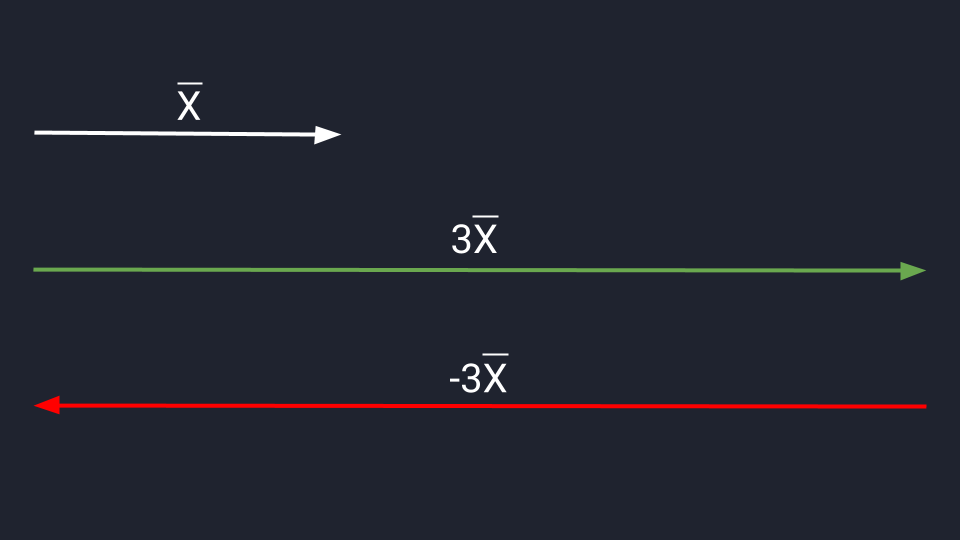 Умножение вектора на число
Умножение вектора на число
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
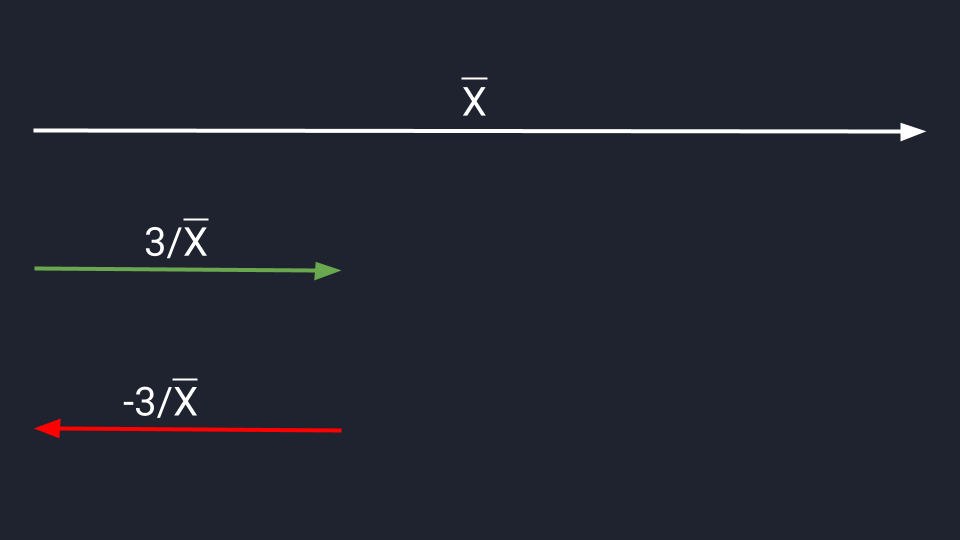 Деление вектора на число
Деление вектора на число
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
- векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
- если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
- а перемножение матриц — это и есть машинное обучение.
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения  направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор  .
.

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается:  или
или 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами: 
Здесь в скобках записаны координаты вектора  – по x и по y .
– по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы  и
и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов
, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов  и
и  .
.

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы  и
и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов
. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов  и
и  .
.

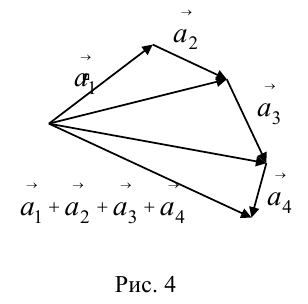
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов  и
и  получаем:
получаем:


Вычитание векторов
Вектор  направлен противоположно вектору
направлен противоположно вектору  . Длины векторов
. Длины векторов  и
и  равны.
равны.

Теперь понятно, что такое вычитание векторов. Разность векторов  и
и  – это сумма вектора
– это сумма вектора  и вектора
и вектора  .
.

Умножение вектора на число
При умножении вектора  на число k получается вектор, длина которого в k раз отличается от длины
на число k получается вектор, длина которого в k раз отличается от длины  . Он сонаправлен с вектором
. Он сонаправлен с вектором  , если k больше нуля, и направлен противоположно
, если k больше нуля, и направлен противоположно  , если k меньше нуля.
, если k меньше нуля.

Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
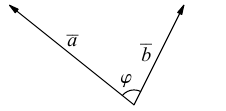
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов  и
и  :
:

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Векторное произведение векторов

О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-na-ege-po-matematike-v-zadache-v6-dejstviya-nad-vektorami/
http://skysmart.ru/articles/mathematic/vektornoe-proizvedenie-vektorov
[/spoiler]
Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
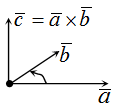
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Содержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Задание. Найти векторное произведение векторов
$bar{a}=(1 ; 0 ; 0)$ и $bar{b}=(0 ; 1 ; 0)$
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{lll}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|$$
Раскладываем определитель по первой строке:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|=$$
$$=bar{i} cdotleft|begin{array}{cc}0 & 0 \ 1 & 0end{array}right|-bar{j} cdotleft|begin{array}{cc}1 & 0 \ 0 & 0end{array}right|+bar{k} cdotleft|begin{array}{cc}1 & 0 \ 0 & 1end{array}right|=$$
$$=0 cdot bar{i}-0 cdot bar{j}+1 cdot k$$
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[bar{a}, bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[bar{a}, bar{b}]=(0 ; 0 ; 1)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы
$bar{a}=(5 ; 3 ;-4)$ и $bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения
$[bar{a}, bar{b}]$
Решение. Координаты векторного произведения
$[bar{a}, bar{b}]$ вычисляются по формуле
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 5 & 3 & -4 \ 6 & 7 & -8end{array}right|$$
Раскладываем полученный определитель по первой строке:
$$=bar{i} cdotleft|begin{array}{cc}3 & -4 \ 7 & -8end{array}right|-bar{j} cdotleft|begin{array}{cc}5 & -4 \ 6 & -8end{array}right|+bar{k} cdotleft|begin{array}{cc}5 & 3 \ 6 & 7end{array}right|=$$
$$=[3 cdot(-8)-7 cdot(-4)] cdot bar{i}-[5 cdot(-8)-6 cdot(-4)] cdot bar{j}+$$
$$+[5 cdot 7-6 cdot 3] cdot bar{k}=(-24+28) bar{i}-(-40+24) bar{j}+(35-18) bar{k}=$$
$$=4 cdot bar{i}+16 cdot bar{j}+17 cdot bar{k}$$
Тогда
$$[bar{a}, bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[bar{a}, bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами 
Длина отрезка, изображающего вектор называется его длиной и обозначается через
называется его длиной и обозначается через  Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение
Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение 
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
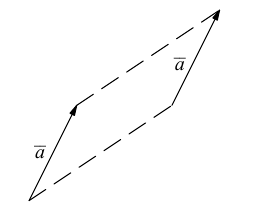
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора  называются коллинеарными (обозначение
называются коллинеарными (обозначение 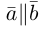 ), если отрезки их изображающие параллельны.
), если отрезки их изображающие параллельны.
Аналогично, векторы а и b называются ортогональными (обозначение 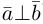 ), если соответствующие отрезки перпендикулярны.
), если соответствующие отрезки перпендикулярны.
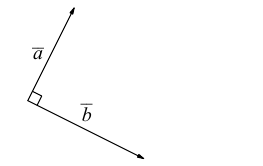
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
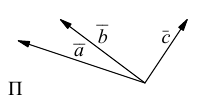
Углом между векторами  приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами
приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами 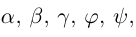 … или через
… или через 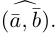
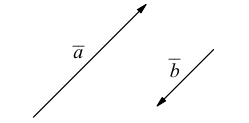
Два ненулевых вектора 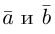 мы будем считать одинаково направленными, если
мы будем считать одинаково направленными, если 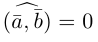 и противоположно направленными, если
и противоположно направленными, если 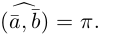
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа  на вектор
на вектор называется вектор
называется вектор 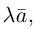 длина которого равна
длина которого равна 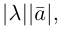 а направление его совпадает с направлением вектора
а направление его совпадает с направлением вектора 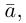 если
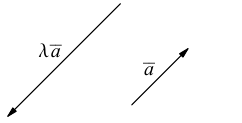
если 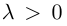 и имеет противоположное с ним направление, если
и имеет противоположное с ним направление, если 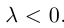 Если
Если 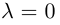 или
или 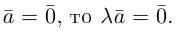
В частности, вектор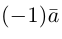 обозначается через
обозначается через 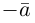 и называется вектором, противоположным вектору
и называется вектором, противоположным вектору 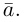
Если 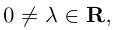 то произведение
то произведение 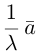 мы будем иногда записывать в виде
мы будем иногда записывать в виде 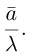
Из приведенного определения сразу же следует, что коллинеарные векторы  линейно связаны, т. е. существует константа
линейно связаны, т. е. существует константа  такая,что
такая,что 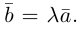 В качестве такой константы следует
В качестве такой константы следует
взять число 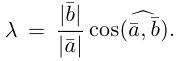 Если
Если 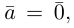 то
то 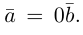 В частности, если
В частности, если 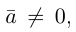 то вектором единичной длины с направлением данного вектора является вектор
то вектором единичной длины с направлением данного вектора является вектор 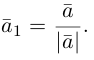
b) Сложение векторов.
Суммой двух векторов 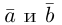 называется вектор
называется вектор 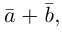 который находится по правилу треугольника
который находится по правилу треугольника
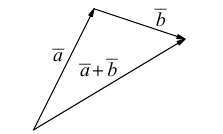
или по равносильному ему правилу параллелограмма
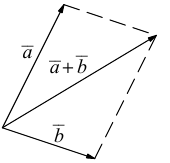
Вектор 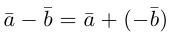 называется разностью векторов
называется разностью векторов 
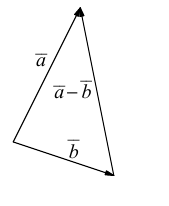
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора  на вектор
на вектор  называется число
называется число
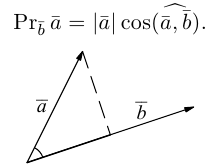
Геометрически очевидны следующие свойства проекции:
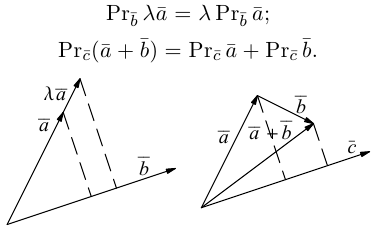
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
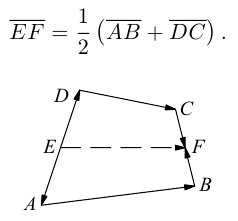
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
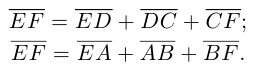
Сложив данные равенства и учитывая, что 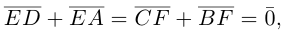 будем иметь:
будем иметь:
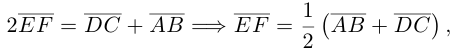
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 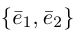 — базис на плоскости,
— базис на плоскости, 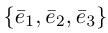 — базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора
— базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора 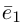 к вектору
к вектору 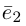 совершается против часовой стрелки, если наблюдение ведется со стороны вектора
совершается против часовой стрелки, если наблюдение ведется со стороны вектора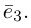 Сформулируем теперь фундаментальное свойство базиса.
Сформулируем теперь фундаментальное свойство базиса.
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 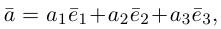 где действительные числа
где действительные числа 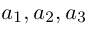 – координаты вектора
– координаты вектора 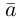 в базисе
в базисе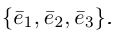
Приведем геометрическое доказательство этого утверждения.
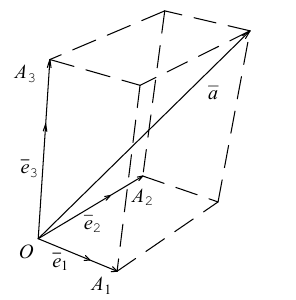
Вектор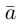 можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов
можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов 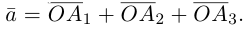 В виду коллинеарности векторов
В виду коллинеарности векторов 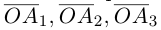 соответствующим базисным векторам, мы можем записать, что
соответствующим базисным векторам, мы можем записать, что 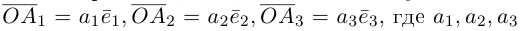 — некоторые действительные числа. Отсюда и следует искомое разложение.
— некоторые действительные числа. Отсюда и следует искомое разложение.
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 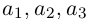 коротко записывается как
коротко записывается как 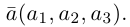
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 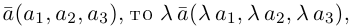 если
если 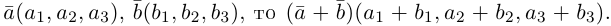 Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
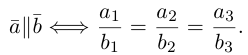
Рассмотрим теперь ортонормированный базис 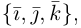 т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе
т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе 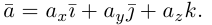
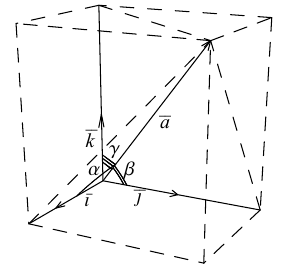
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
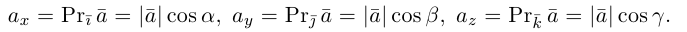
Величины 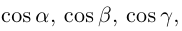 т. е. косинусы углов, которые образует данный вектор с ортами
т. е. косинусы углов, которые образует данный вектор с ортами 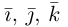 к соответственно, называются направляющими косинусами вектора
к соответственно, называются направляющими косинусами вектора 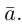 Единичный вектор
Единичный вектор 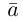 имеет координаты
имеет координаты 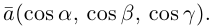
Очевидно также, что
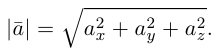
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 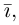 ось
ось  (ординат) — вдоль орта
(ординат) — вдоль орта 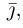 наконец, ось
наконец, ось 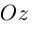 (аппликат) направим вдоль орта
(аппликат) направим вдоль орта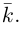

В выбранной системе координат координаты радиуса-вектора 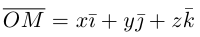 мы будем называть координатами точки М и записывать
мы будем называть координатами точки М и записывать 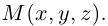
Если известны координаты начальной 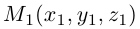 и конечной
и конечной 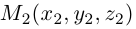 точек вектора, то из равенства
точек вектора, то из равенства 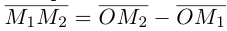 слезет, что его координаты равны
слезет, что его координаты равны
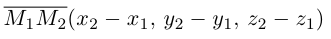 и, значит, расстояние между точками
и, значит, расстояние между точками 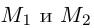 вычисляется по формуле
вычисляется по формуле
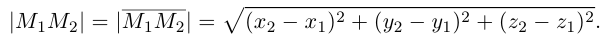
Найдем теперь координаты точки М, делящей отрезок с концами в точках 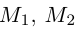 в данном
в данном
отношении 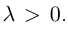 Так как
Так как 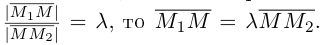 Отсюда, переходя к координатам получим:
Отсюда, переходя к координатам получим:
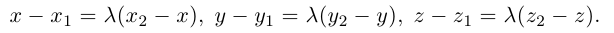
Следовательно, координаты искомой точки вычисляются по формулам:
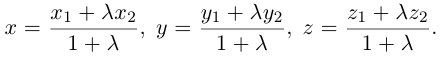
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
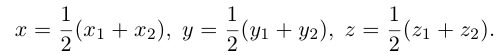
Пример №2
Треугольник задан координатами своих вершин 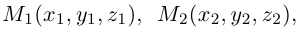
 Найти координаты точки пересечения его медиан. Решение.
Найти координаты точки пересечения его медиан. Решение.
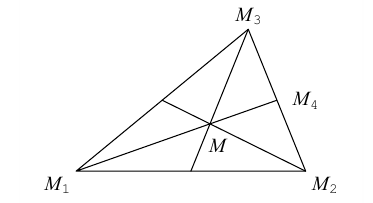
Пусть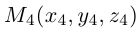 – середина отрезка
– середина отрезка 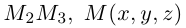 – точка пересечения медиан. Тогда
– точка пересечения медиан. Тогда
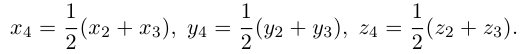
По известному свойству точки пересечения медиан 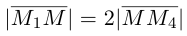 и потому
и потому
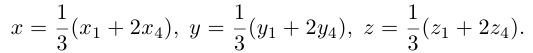
Подставив сюда найденные координаты точки 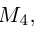 ползучим:
ползучим:
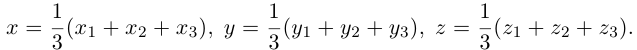
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 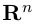 называется упорядоченная совокупность n векторов
называется упорядоченная совокупность n векторов

обладающая тем свойством, что любой вектор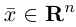 единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа
единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа 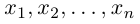 (координаты вектора
(координаты вектора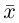 в базисе (1)) такие, что
в базисе (1)) такие, что

В качестве базиса в 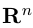 мы можем взять, например, векторы
мы можем взять, например, векторы
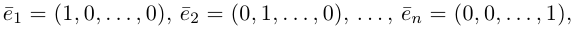
так как, очевидно, любой вектор 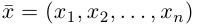 однозначно представляется в виде (2).
однозначно представляется в виде (2).
Скалярное произведение векторов
Определение: Скалярным произведением векторов  называется число
называется число
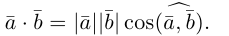
Из этого определения сразу же следует, что
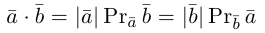
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
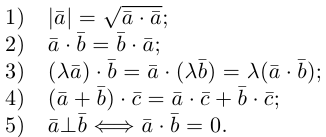
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе  векторы
векторы  имеют координаты
имеют координаты 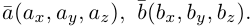 Заметив, что по свойствам 1) и 5) скалярного произведения
Заметив, что по свойствам 1) и 5) скалярного произведения
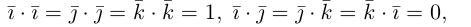
перемножим векторы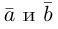 скалярно, используя свойства 2) – 4):
скалярно, используя свойства 2) – 4):
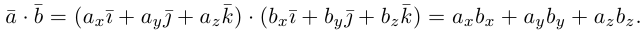
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 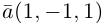 на две ортогональные составляющие, одна из которых коллинеарна вектору
на две ортогональные составляющие, одна из которых коллинеарна вектору 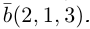
Решение.
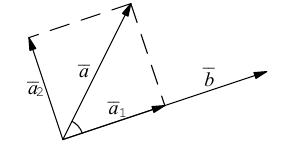
Из чертежа следует, что 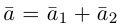 – искомое разложение. Найдем векторы
– искомое разложение. Найдем векторы 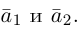 Составляющая
Составляющая 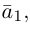 коллинеарная вектору
коллинеарная вектору 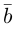 равна, очевидно, вектору проекции
равна, очевидно, вектору проекции 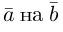 и, следовательно,
и, следовательно,
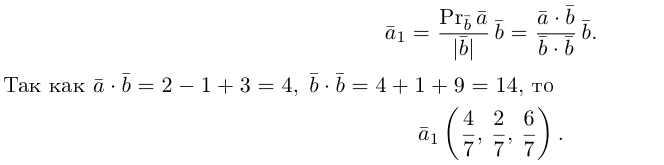
Тогда вторая ортогональная составляющая вектора 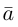 равна
равна
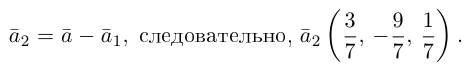
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 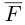 материальная тотп<а переместилась по прямой из положения В в положение С.
материальная тотп<а переместилась по прямой из положения В в положение С.
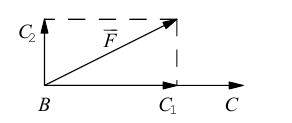
Найдем работу этой силы. Для этого разложим вектор силы 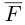 на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения
на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения 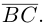 Тогда
Тогда
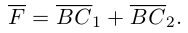
Составляющая 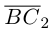 работы не совершает, следовательно, работа силы
работы не совершает, следовательно, работа силы 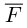 равна работе составляющей
равна работе составляющей 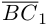 и, таким образом,
и, таким образом,
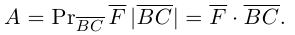
Окончательно, работа силы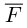 , под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
, под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
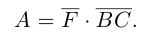
Замечание. Скалярным произведением векторов 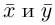 n-мерного пространства
n-мерного пространства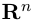 называется число
называется число 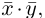 равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
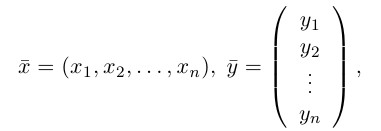
то
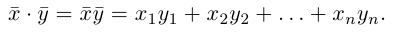
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 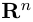 обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
Длиной вектора 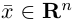 называется число
называется число
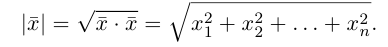
Векторы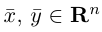 называются ортогональными, если
называются ортогональными, если 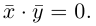 Векторы
Векторы
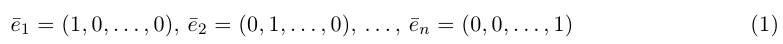
составляют ортонормированный базис пространства 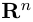 , так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
, так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
Любой вектор  мы можем рассматривать как точку
мы можем рассматривать как точку
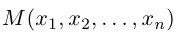
n-мерного пространства с координатами 
Взяв еще одну точку 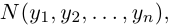 соответствующую вектору
соответствующую вектору 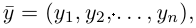 мы под расстоянием между точками М и N будем понимать длину вектора
мы под расстоянием между точками М и N будем понимать длину вектора 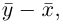 т. е. число
т. е. число
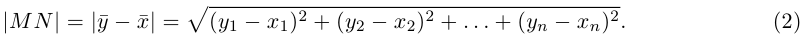
Таким образом переопределенное пространство  с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
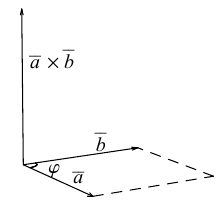
Определение: Векторным произведением некоялинеарных векторов 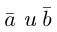 называется вектор
называется вектор  такой, что
такой, что
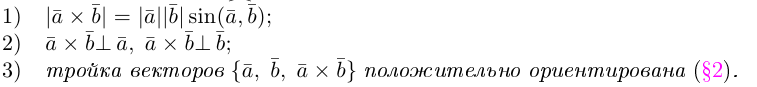
Из этого определения следует, что площадь параллелограмма, построенного на векторах 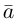 и
и 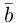 равна длине векторного произведения
равна длине векторного произведения  , т. е.
, т. е.
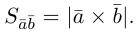
Сформулируем основные свойства векторного произведения.
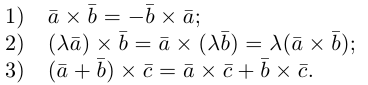
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 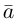 и
и 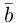 в ортонормированном базисе
в ортонормированном базисе 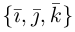 имеют координаты
имеют координаты 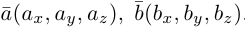 Учитывая, tito по определению векторного произведения
Учитывая, tito по определению векторного произведения
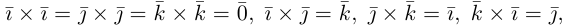
раскроем скобки в векторном произведении 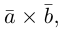 принимая во внимание свойства 1) – 3):
принимая во внимание свойства 1) – 3): 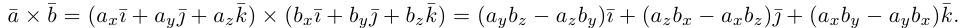
Полученный вектор мы можем записать в виде следующего символического определителя.
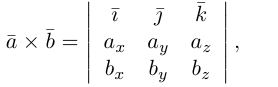
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 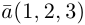 , ортогональную плоскости векторов
, ортогональную плоскости векторов 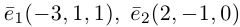 .
.
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 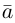 на векторное произведение
на векторное произведение и, следовательно.
и, следовательно.
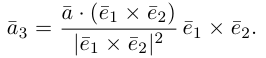
Переходим к вычислениям:
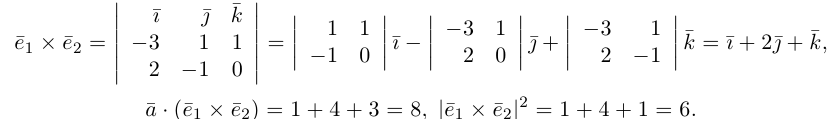
Тогда 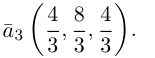
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
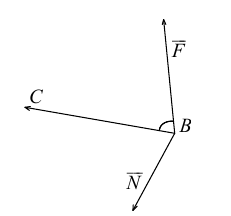
Итак, пусть сила 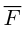 приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
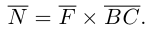
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 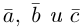 называется число
называется число
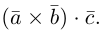
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
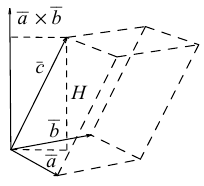
По определению смешанного произведения
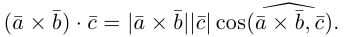
Поскольку 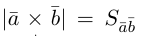 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах  (§4)
(§4)
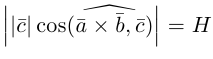 -высота параллелепипеда построенного на векторах
-высота параллелепипеда построенного на векторах 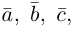 то
то
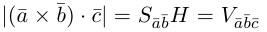
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе  , т.е.
, т.е. 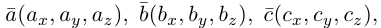 то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
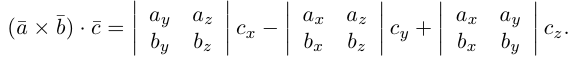
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
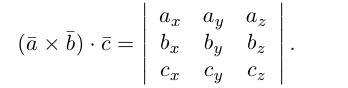
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
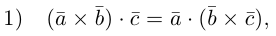
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 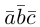 . которым мы и будем пользоваться в дальнейшем.
. которым мы и будем пользоваться в дальнейшем.
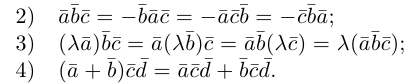
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 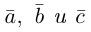 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 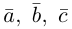 компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение
компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение 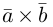 ортогонально вектору с и, следовательно,
ортогонально вектору с и, следовательно, 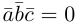 . Аналогично проверяется достаточность условия теоремы.
. Аналогично проверяется достаточность условия теоремы.
Следствие. Три вектора 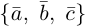 образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
Заметим, кроме того, что, если 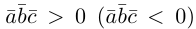 , то угол между векторами
, то угол между векторами 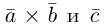 -острый (тупой) и, следовательно, базис
-острый (тупой) и, следовательно, базис 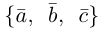 является положительно (отрицательно) ориентированным.
является положительно (отрицательно) ориентированным.
Пример №5
Доказать, что пять точек
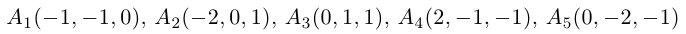
расположены в одной плоскости.
Решение. Рассмотрим векторы 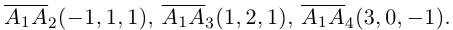 Так как
Так как
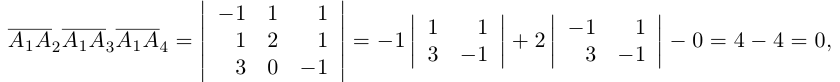
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки  находятся в одной плоскости
находятся в одной плоскости  Аналогично покажем, что и точки
Аналогично покажем, что и точки  также принадлежат одной плоскости
также принадлежат одной плоскости 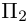 . Действительно,
. Действительно, 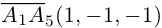
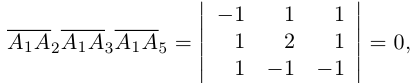
так как первая и третья строки в определителе пропорциональны. Плоскости  имеют три общие точки
имеют три общие точки  , следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
, следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
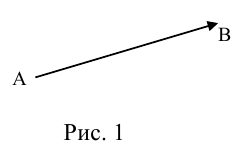 А – начало, В – конец вектора
А – начало, В – конец вектора 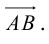
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 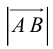 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
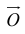 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина  .
.
Определение: Векторы  называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 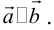
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 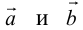 совмещаются в одной точке, и
совмещаются в одной точке, и 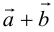 – диагональ параллелограмма, построенного на
– диагональ параллелограмма, построенного на 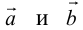 .
.
б) Правило треугольника (рис. 3): начало 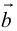 совмещается с концом
совмещается с концом 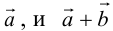 направлен от начала
направлен от начала 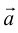 к концу
к концу  .
.
в) Правило сложения нескольких векторов (рис. 4).
Вектор 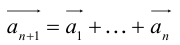 замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и
замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и 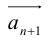 направлен от начала
направлен от начала 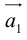 к концу
к концу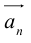 .
.
Умножение на число
Определение: Произведением вектора  на число
на число  называется вектор
называется вектор 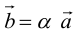 , aудовлетворяющий условиям:
, aудовлетворяющий условиям:
а) 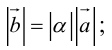
б) 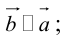
в)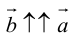 , если
, если 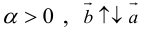 ,a если
,a если 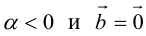 , если
, если 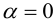 .
.
Произведение 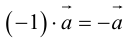 называется вектором, противоположным вектору
называется вектором, противоположным вектору . Очевидно,
. Очевидно, 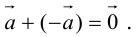 .
.
Определение: Разностью 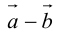 называется сумма вектора
называется сумма вектора 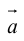 и вектора, противоположного
и вектора, противоположного 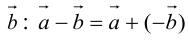 (рис. 5).
(рис. 5).

Начала 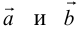 совмещаются в одной точке, и
совмещаются в одной точке, и 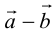 направлен от конца
направлен от конца  к концу
к концу  .
.
Свойства линейных операций
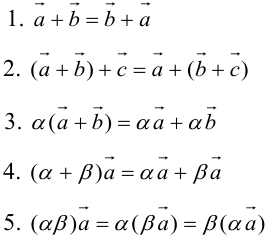
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: – линейная комбинация векторов
– линейная комбинация векторов  с коэффициентами
с коэффициентами 
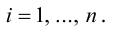
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 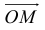 как линейную комбинацию
как линейную комбинацию
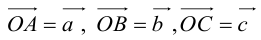 (рис. 6).
(рис. 6).
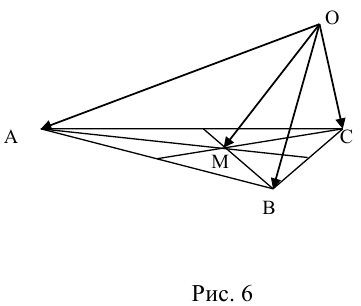
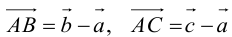 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 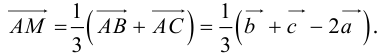
По правилу треугольника 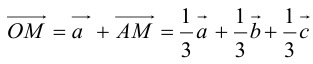 , то есть
, то есть 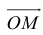 – линейная комбинация
– линейная комбинация 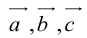 с коэффициентами
с коэффициентами 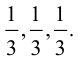
Теорема: Пусть  – неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
– неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
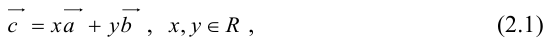
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 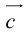 в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Доказательство:
- Пусть среди
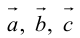 есть два коллинеарных, например:
есть два коллинеарных, например: 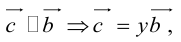
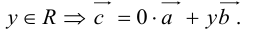
- Пусть среди
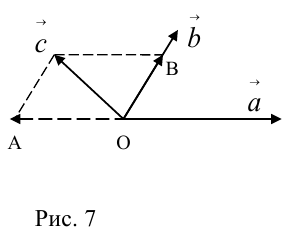
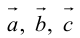 коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с 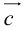 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 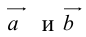 (рис. 7).
(рис. 7).
Тогда c 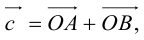 но
но 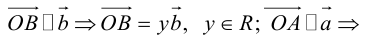
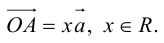 Поэтому
Поэтому 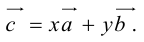
Докажем единственность разложения. Предположим, что 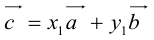 и
и 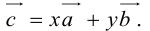 Тогда, вычитая одно равенство из другого, получим:
Тогда, вычитая одно равенство из другого, получим: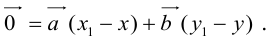
Если 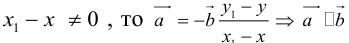 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Теорема: Пусть 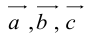 – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор 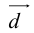 может быть представлен в виде
может быть представлен в виде
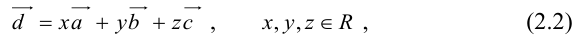
причем единственным образом.
Представление вектора 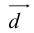 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 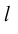 называется единичный вектор
называется единичный вектор 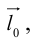
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 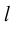 называется основание
называется основание  перпендикуляра, опущенного из М на
перпендикуляра, опущенного из М на 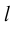 .
.
Определение: Ортогональной проекцией вектора 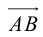 на ось
на ось 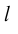 называется длина отрезка
называется длина отрезка 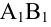 этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора 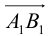 совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
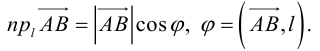
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
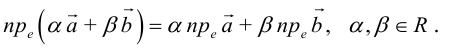
В частности, проекция суммы векторов равна сумме их проекций:
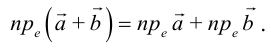
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим  – орт оси ОХ,
– орт оси ОХ, 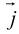 – орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).

Аналогично в пространственной системе OXYZ 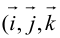 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
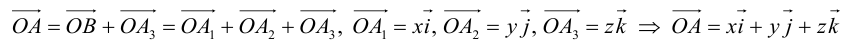
– разложение 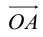 по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
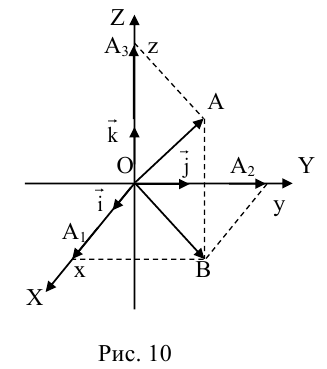
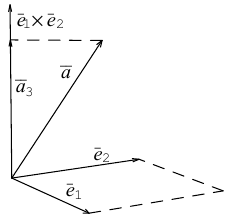
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 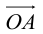 можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение: Координатами вектора 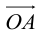 в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если  и наоборот, если
и наоборот, если
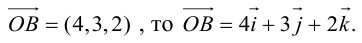
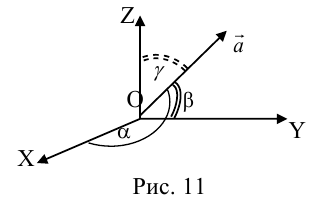
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
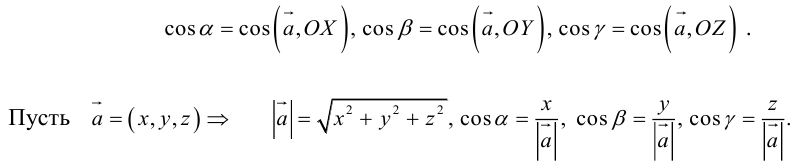
Из этих формул очевидно следует основное свойство направляющих косинусов:
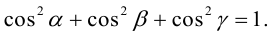
Если известны длина 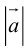 и направляющие косинусы вектора, то его координаты вычисляются по формулам:
и направляющие косинусы вектора, то его координаты вычисляются по формулам:
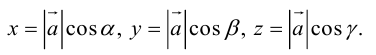
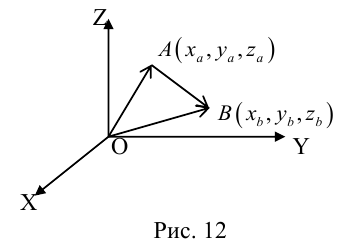
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
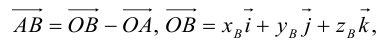
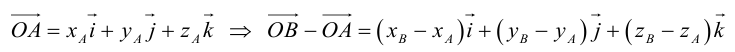 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,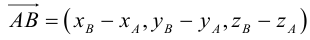 , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
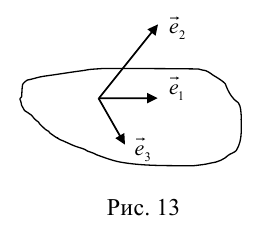
Если 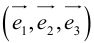 – базис, то
– базис, то 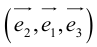 – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 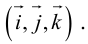
Из теоремы 2 следует, что всякий вектор 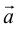 может быть разложен по базису
может быть разложен по базису 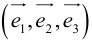 , то есть представлен в виде:
, то есть представлен в виде: 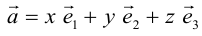 . Числа x,y,z называются координатами
. Числа x,y,z называются координатами 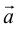 в базисе
в базисе 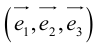 .
.
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 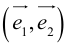 – базис, то представление вектора в виде
– базис, то представление вектора в виде  называется разложением
называется разложением 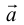 по базису
по базису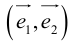 и x, y – координаты
и x, y – координаты 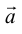 в этом базисе.
в этом базисе.
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 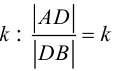 (рис. 14).
(рис. 14).
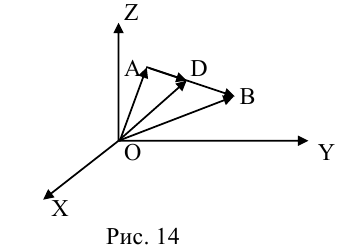
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
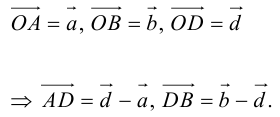
Так как 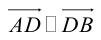 (лежат на одной прямой) и
(лежат на одной прямой) и 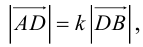 то
то
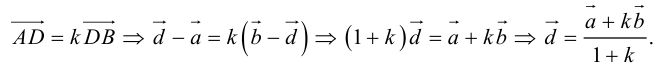
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
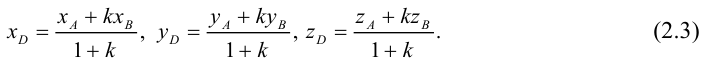
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
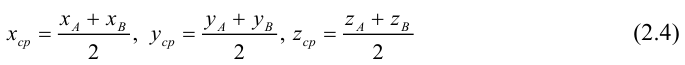
ЗАМЕЧАНИЕ 2. Если k < 0, 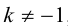 , то точка D лежит за пределами AB : так как
, то точка D лежит за пределами AB : так как 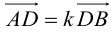 , то при
, то при 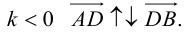
В этом случае 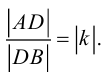
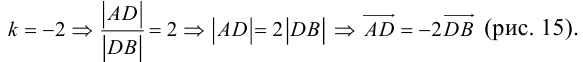
Скалярное произведение векторов
Определение: Скалярным произведением векторов 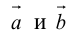 называется скаляр (число), равный
называется скаляр (число), равный 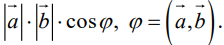
Скалярное произведение обозначается так: 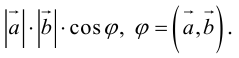 или
или 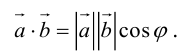
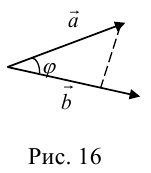
Так как 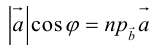 (рис. 16) или
(рис. 16) или 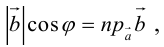 то
то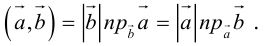
Свойства скалярного произведения
1.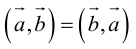 – очевидно из определения.
– очевидно из определения.
2.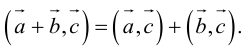
Доказательство:
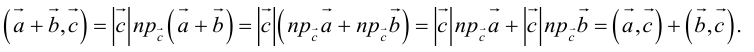
3.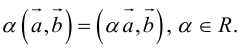
Доказательство:
а) 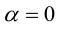 – очевидно.
– очевидно.
б) 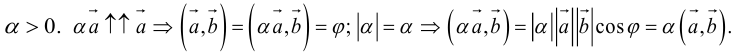
в) 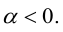 В этом случае
В этом случае
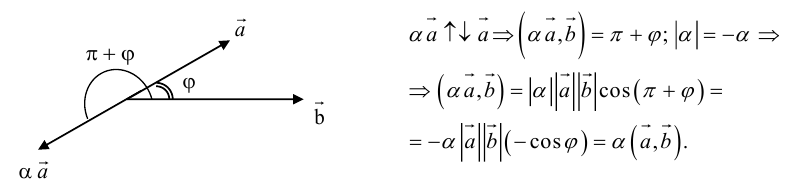
4.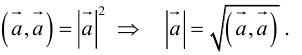
Отсюда следует, что 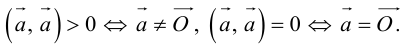
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.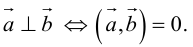
Доказательство:
а) пусть 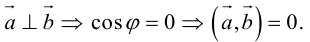
б) пусть 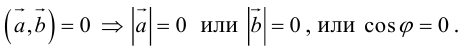
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 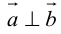 . В третьем случае
. В третьем случае 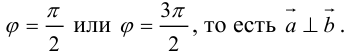
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов 
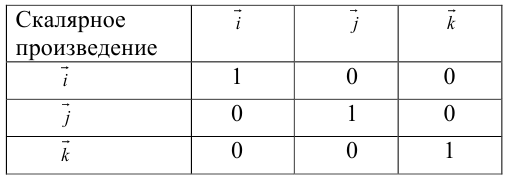
Пусть в некоторой пдск 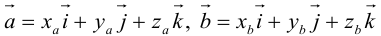 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов:
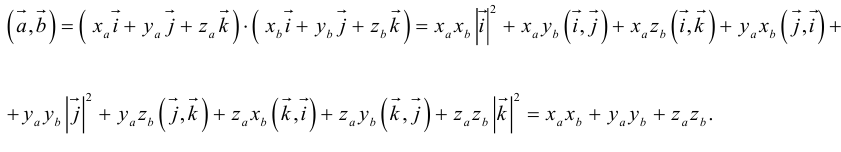
Таким образом, 
Пример №8
Найти, при каком значении x векторы 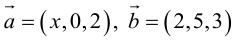 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 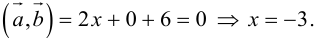
Пример №9
Найти угол между биссектрисой AD и медианой  если
если 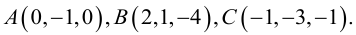
Так как 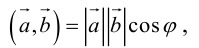
то 
Найдем координаты векторов 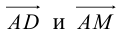 . Точка M – середина BC , поэтому по формулам (2.4)
. Точка M – середина BC , поэтому по формулам (2.4)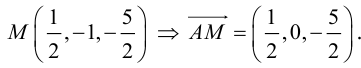
По теореме о биссектрисе внутреннего угла треугольника 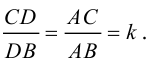
Чтобы найти k , вычислим длины AC и AB :
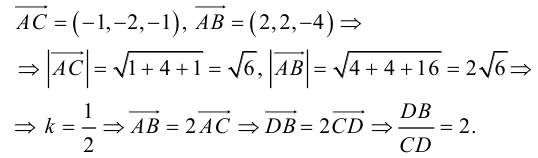
Разделим отрезок CB в данном отношении по формулам (2.3):
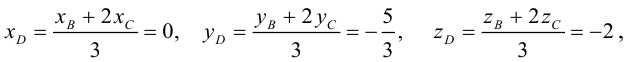
отсюда 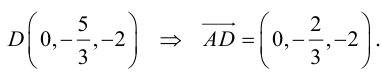
Заметим, что 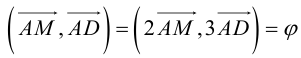 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
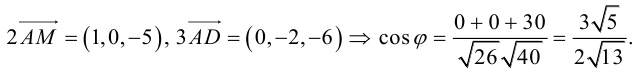
Пример №10
Найти 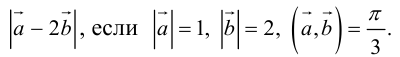
Воспользуемся свойствами 1–4 скалярного произведения:
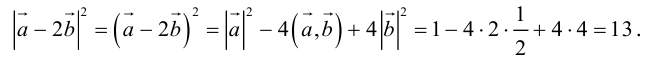
Отсюда 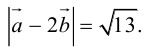
ЗАМЕЧАНИЕ. Так как работа силы 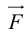 по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора 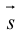 вычисляется по формуле
вычисляется по формуле 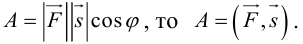
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 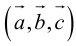 , имеющих общее начало, называется правой (левой), если
, имеющих общее начало, называется правой (левой), если  конца третьего вектора c вращение первого вектора
конца третьего вектора c вращение первого вектора  ко второму вектору
ко второму вектору 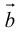 по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
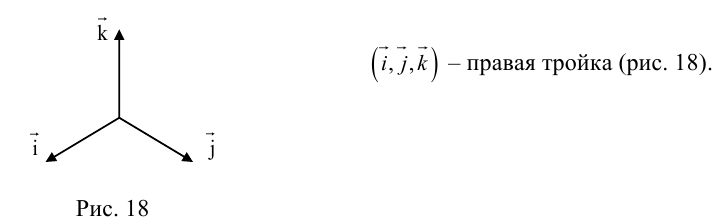
Определение: Векторным произведением вектора  на вектор
на вектор 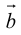 называется вектор
называется вектор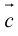 , удовлетворяющий условиям:
, удовлетворяющий условиям:
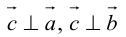 (
(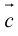 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 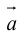 и
и 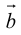 ).
). - Направление
 таково, что тройка
таково, что тройка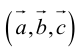 – правая.
– правая. 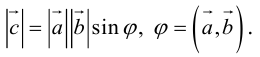
Векторное произведение обозначается так: 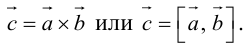
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
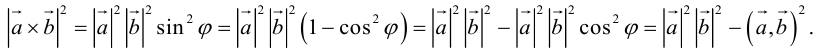
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
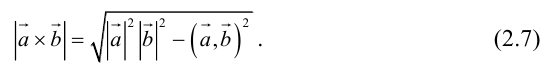
Пример №11
Найти площадь параллелограмма, построенного на векторах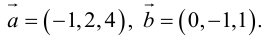
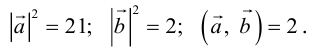
По формуле (2.7): 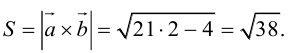
ЗАМЕЧАНИЕ 2. Направление вектора 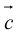 можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора 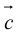 совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора 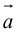 ко второму вектору
ко второму вектору 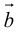 по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
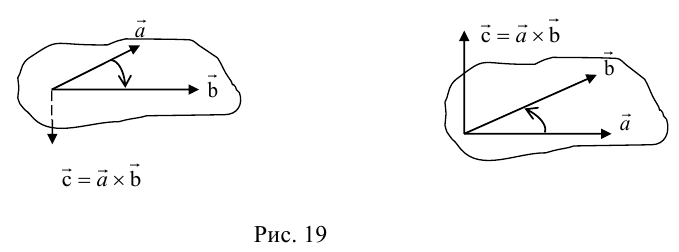
Свойства векторного произведения
1.
Доказательство:
а)пусть  или
или  . В первом и втором случаях один из сомножителей – нулевой вектор.
. В первом и втором случаях один из сомножителей – нулевой вектор.
Его направление не определено, поэтому можно считать, что 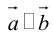 . Если
. Если 
б)пусть 
2. 
Доказательство: По определению направления векторов 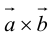 и
и 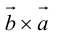 противоположны, а модули равны, значит, векторы отличаются лишь знаком.
противоположны, а модули равны, значит, векторы отличаются лишь знаком.
3.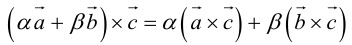 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 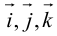 : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
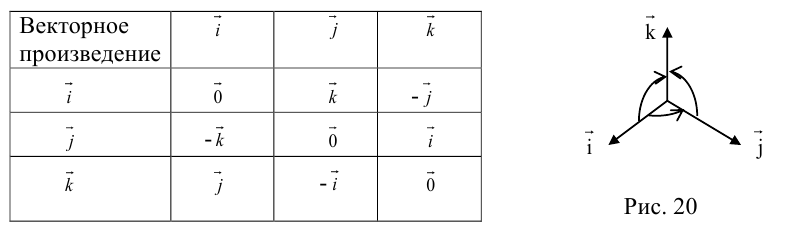
Пусть в некоторой пдск 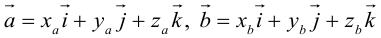 . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
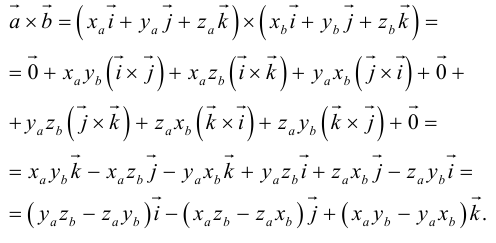
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
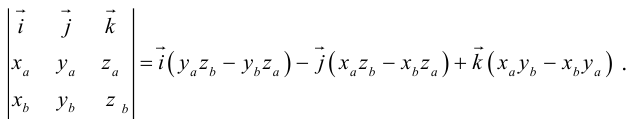
Таким образом,
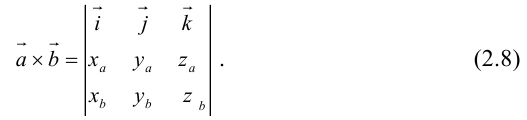
Пример №12
Вычислить векторное произведение векторов 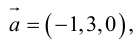
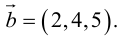
По формуле (2.8): 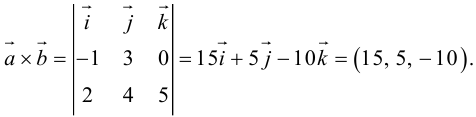
Заметим, что площадь треугольника, построенного на векторах 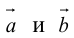 , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 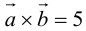
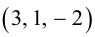
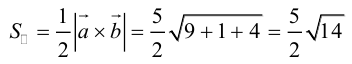
или
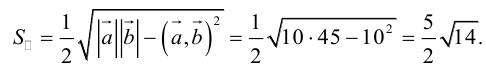
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 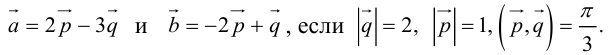
Так как 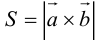 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: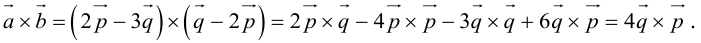
Отсюда 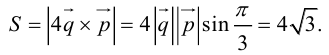
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов  называется число
называется число  – скалярное произведение a на векторное произведение
– скалярное произведение a на векторное произведение 
Смешанное произведение обозначается так: 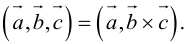
Пусть в некоторой пдск 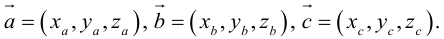
Обозначим
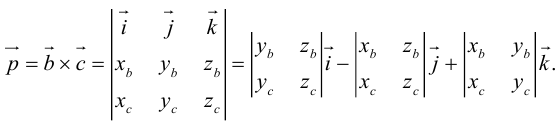
Тогда
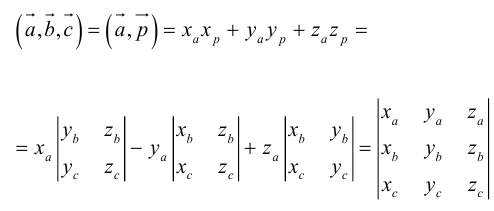
по 7 свойству определителей.
Таким образом,
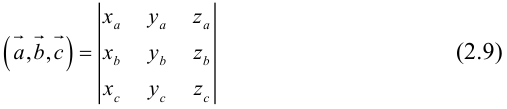
По определению скалярного произведения 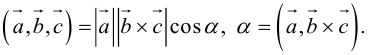
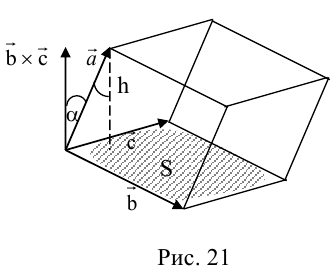
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
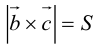 – площадь параллелограмма,
– площадь параллелограмма,
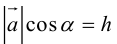 – высота параллелепипеда,
– высота параллелепипеда,
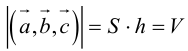 – объем параллелепипеда.
– объем параллелепипеда.
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 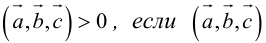 – правая тройка, и
– правая тройка, и 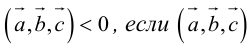 – левая тройка.
– левая тройка.
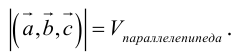
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 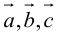 компланарны
компланарны
Доказательство: а) 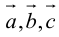 компланарны
компланарны 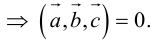
Если 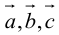 компланарны, то на них нельзя построить параллелепипед, а потому
компланарны, то на них нельзя построить параллелепипед, а потому 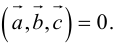
б)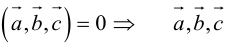 компланарны.
компланарны.
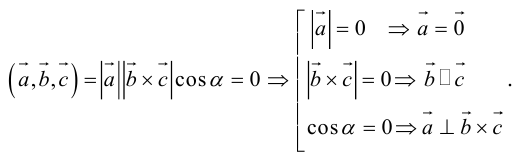
Во всех трех случаях 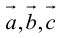 компланарны: в частности, если
компланарны: в частности, если 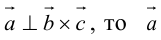 параллелен плоскости векторов
параллелен плоскости векторов 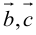 , что означает их компланарность.
, что означает их компланарность.
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
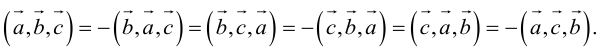
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 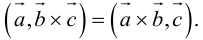
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим: 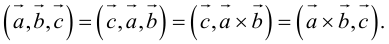
4. Смешанное произведение линейно по каждому из трех сомножителей.
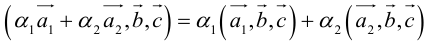 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
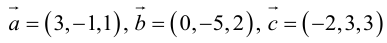 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов 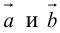 .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 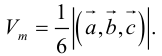
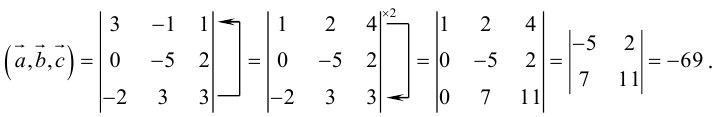
Отсюда 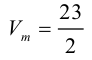 (заметим, что
(заметим, что 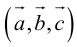 – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
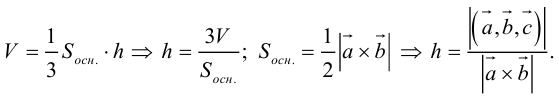
По формуле (2.7) 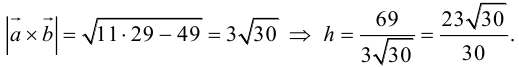
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
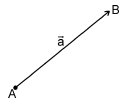
Вектором называется направленный отрезок. Вектор обозначается либо символом 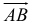 (
( — точка начала,
— точка начала,  — точка конца вектора), либо
— точка конца вектора), либо  . В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
. В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
2. Длиной (модулем) вектора 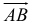 называется длина отрезка
называется длина отрезка 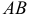 . Модуль вектора обозначается
. Модуль вектора обозначается 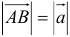 .
.
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 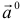 направления вектора
направления вектора  называется ортом вектора
называется ортом вектора  и определяется по формуле
и определяется по формуле 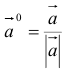 .
.
4. Вектор называется нулевым, если его начало и конец совпадают 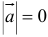 ; любое направление можно считать направлением нулевого вектора.
; любое направление можно считать направлением нулевого вектора.
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 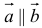 . Необходимым и достаточным условием коллинеарности векторов
. Необходимым и достаточным условием коллинеарности векторов  и
и  является существование такого числа
является существование такого числа 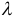 , что
, что 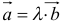 .
.
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор  называется противоположным вектору
называется противоположным вектору  , если модули их равны, а направления противоположны.
, если модули их равны, а направления противоположны.
8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
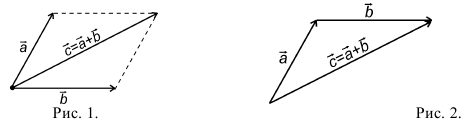
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
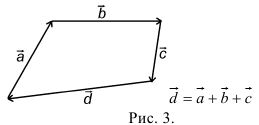
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).

10. Действие вычитания двух векторов связано с действием сложения (рис.5).
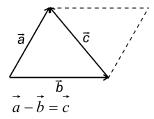
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
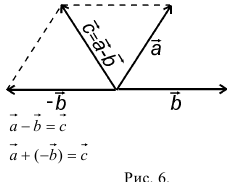
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора  на число
на число  называется вектор
называется вектор 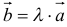 , который имеет :
, который имеет :
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
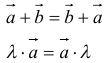
- сочетательный:
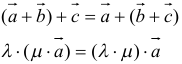
- распределительный:
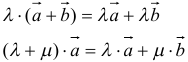

Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки 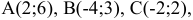
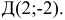
1) Найти координаты векторов
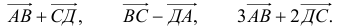
2) Написать разложение этих векторов по базису 
3) Найти длины этих векторов
4) Найти скалярное произведение 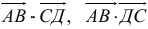
5) Найти угол между векторами  и
и 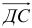 .
.
6) Найти разложение вектора 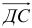 по базису
по базису  и
и 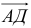
Решение:
1) Вычислим координаты векторов  и
и 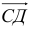 (нужно из координат точки его конца вычесть координаты его начала):
(нужно из координат точки его конца вычесть координаты его начала):
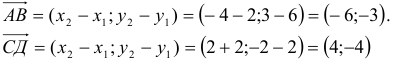
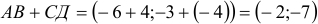 , аналогично,
, аналогично, 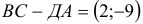
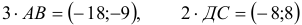 и
и 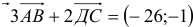
2) 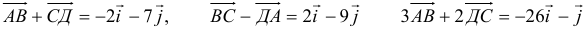
3)
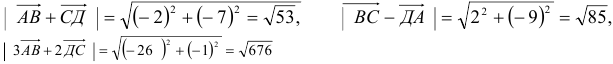
4) Для вычисления угла между векторами воспользуемся формулой:
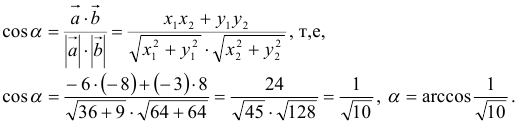
5) Разложить вектор  по векторам
по векторам  и
и  — это значит представить вектор
— это значит представить вектор  в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и 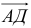 , т. е.
, т. е.
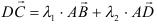 , где
, где 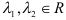 . Имеем
. Имеем 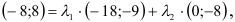
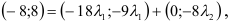
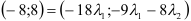 , но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем
, но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем 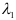 и
и 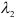 .
.
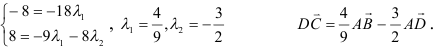
Задача:
а). Даны векторы 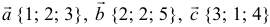 и
и 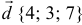 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 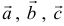 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 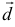 в этом базисе.
в этом базисе.
Решение:
Три вектора образуют базис, если 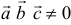 .
.
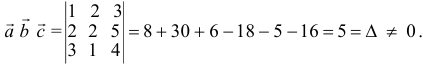
Найдем координаты вектора 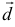 в базисе
в базисе 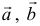 и
и 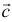 .
.
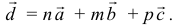
Два вектора равны, если их соответствующие координаты равны.
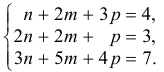
Решим систему методом Крамера:
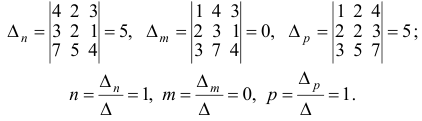
Ответ: 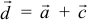 .
.
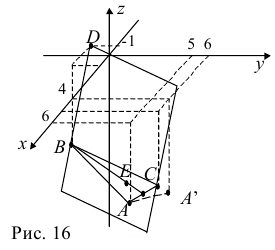
Задача:
Даны координаты вершин тетраэдра 
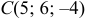 и
и 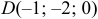 . Найти: 1) координаты точки пересечения медиан треугольника
. Найти: 1) координаты точки пересечения медиан треугольника  ; 2) уравнение прямой, проходящей через вершину
; 2) уравнение прямой, проходящей через вершину  параллельно медиане, проведенной из вершины
параллельно медиане, проведенной из вершины  треугольника
треугольника 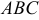 ; 3) координаты точки, симметричной точке
; 3) координаты точки, симметричной точке  относительно плоскости
относительно плоскости  . Сделать чертёж.
. Сделать чертёж.
Решение:
1) Найдем координаты т.  середины отрезка
середины отрезка 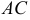 (рис. 16):
(рис. 16): 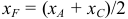
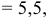
Точка  пересечения медиан треугольника делит медиану
пересечения медиан треугольника делит медиану  в отношении
в отношении 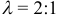 , считая от вершины
, считая от вершины  . Найдем координаты точки
. Найдем координаты точки  :
:
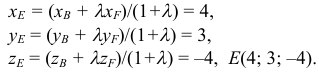
2) Найдем направляющий вектор прямой 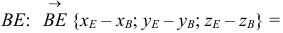
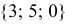 . Уравнение прямой, проходящей через вершину
. Уравнение прямой, проходящей через вершину  параллельно прямой
параллельно прямой  :
:
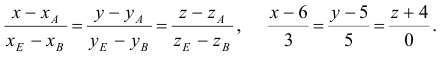
3) Найдем уравнение плоскости  :
:
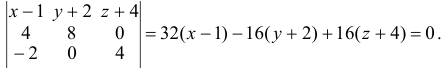
Найдем каноническое уравнение прямой, перпендикулярной плоскости  и проходящей через т.
и проходящей через т.  :
: 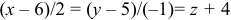 . Запишем каноническое уравнение прямой в параметрическом виде:
. Запишем каноническое уравнение прямой в параметрическом виде: 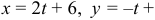
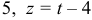 .
.
Найдем координаты точки 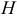 пересечения плоскости
пересечения плоскости  и найденной прямой:
и найденной прямой: 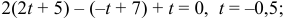
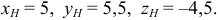
Координаты точки  симметричной точке
симметричной точке  относительно плоскости
относительно плоскости  —
— 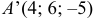 .
.
Ответ: 1) координаты точки пересечения медиан 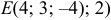 уравнение прямой
уравнение прямой 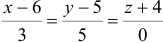 ; 3) координаты симметричном точки
; 3) координаты симметричном точки 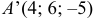 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 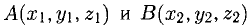 пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается
пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается 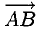 или
или  Длина вектора, обозначаемая
Длина вектора, обозначаемая  , АВ или
, АВ или 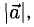 а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала:
а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала: 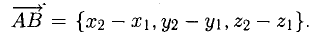 Тогда длина вектора найдется так:
Тогда длина вектора найдется так:
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора  называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут
называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут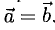 Равные векторы имеют равные координаты.
Равные векторы имеют равные координаты.
Векторы 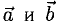 называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления:
называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления: 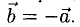
Вектор называется нулевым, если его модуль равен нулю, и обозначается 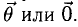
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало  совмещено с концом
совмещено с концом 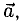 то начало
то начало 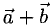 совпадает с началом
совпадает с началом 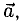 а конец — с концом
а конец — с концом 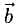 (рис. 3.1).
(рис. 3.1).
2.Если начала векторов 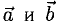 совмещены, то начало
совмещены, то начало  совпадает с концом
совпадает с концом 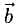 , а конец
, а конец  совпадает с концом
совпадает с концом 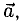 (рис. 3.2).
(рис. 3.2).
3.При умножении вектора на число (скаляр)
на число (скаляр) 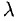 длина вектора умножается на
длина вектора умножается на 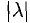 , а направление сохраняется, если
, а направление сохраняется, если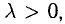 и изменяется на противоположное, если
и изменяется на противоположное, если 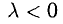 (рис. 3.3).
(рис. 3.3).
Вектор 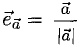 называется ортом, или единичным вектором вектора
называется ортом, или единичным вектором вектора 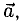 его длина равна единице:
его длина равна единице: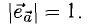
3°. Запись ci — 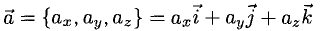 означает, что вектор
означает, что вектор  имеет координаты
имеет координаты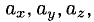 или
или  разложен по базису
разложен по базису 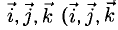 — орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
— орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
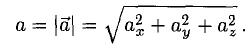
4°. Числа 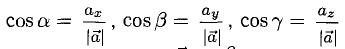 называются направляющими косинусами вектора
называются направляющими косинусами вектора  — углы между вектором
— углы между вектором  и координатными осями Ох, Оу, Oz соответственно. Единичный вектор
и координатными осями Ох, Оу, Oz соответственно. Единичный вектор 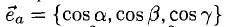 — орт вектора
— орт вектора  . Для любого вектора справедливо:
. Для любого вектора справедливо: 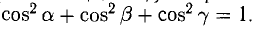
5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 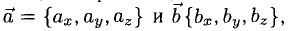 тогда
тогда
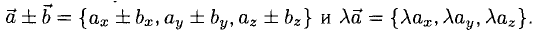
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 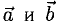 , устанавливаемое равенством
, устанавливаемое равенством 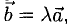 может быть записано соотношениями
может быть записано соотношениями 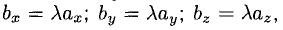 из которых следует пропорциональность их координат:
из которых следует пропорциональность их координат: 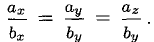
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 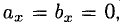 то векторы
то векторы 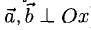 ).
).
7°. Система векторов 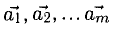 называется линейно независимой, если равенство
называется линейно независимой, если равенство
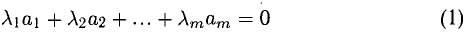
(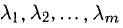 — действительные числа) возможно только при
— действительные числа) возможно только при  Если же равенство (1) возможно при некотором нетривиальном наборе
Если же равенство (1) возможно при некотором нетривиальном наборе 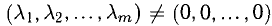 то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 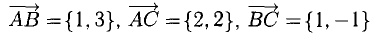 (рис. 3.4).
(рис. 3.4).
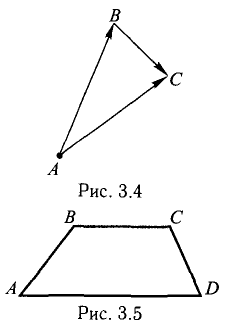
Найдем длины сторон: 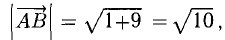
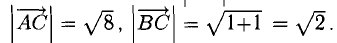
Нетрудно видеть, что 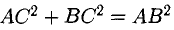 Следовательно, треугольник ABC прямоугольный с гипотенузой
Следовательно, треугольник ABC прямоугольный с гипотенузой 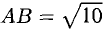 и катетами
и катетами 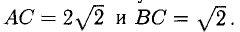
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
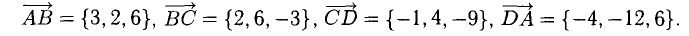
Имеем 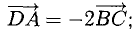 значит, ABCD — трапеция.
значит, ABCD — трапеция.
Пример:
Найти орт и направляющие косинусы вектора 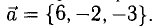
Решение:
Имеем 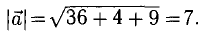 В соответствии с п. 3°, 4°
В соответствии с п. 3°, 4°
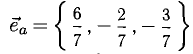 и направляющие косинусы вектора
и направляющие косинусы вектора 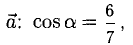
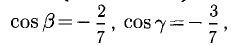 причем
причем 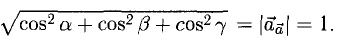
Пример:
Определить точку В, которая является концом вектора 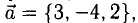 , если его начало совпадает с точкой
, если его начало совпадает с точкой
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
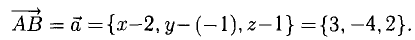
Следовательно, 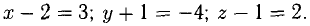 Ответ. В(5, -5,3).
Ответ. В(5, -5,3).
Пример:
Вектор 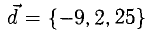 разложить по векторам
разложить по векторам
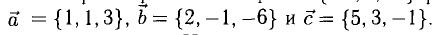
Решение:
Необходимо найти такие числа х, у, z, что 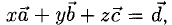 т.е.
т.е.
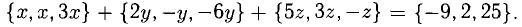
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
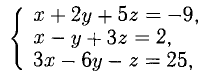
из которой
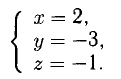
Ответ. 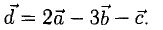
Пример:
Показать, что система векторов 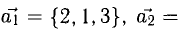
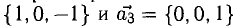 линейно независима.
линейно независима.
Решение:
В данном случае равенство (1) имеет вид 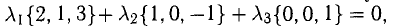 , или
, или 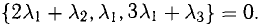 Отсюда получаем систему уравнений
Отсюда получаем систему уравнений
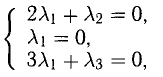
из которой следует, что 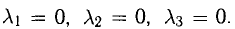 Это подтверждает линейную независимость данных векторов.
Это подтверждает линейную независимость данных векторов.
Пример:
Показать, что система векторов 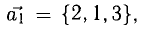
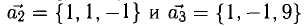 линейно зависима.
линейно зависима.
Решение:
Равенство (1) равносильно системе уравнений
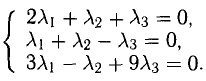
Она имеет ненулевое решение, например, 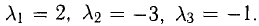 Таким образом,
Таким образом, 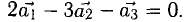 Отсюда видно, что
Отсюда видно, что 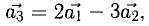 т.е. вектор
т.е. вектор 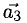 линейно выражается через
линейно выражается через 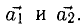 Очевидно, что
Очевидно, что 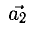 можно выразить через
можно выразить через 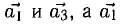 — через
— через 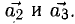
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 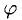 между ними:
между ними:
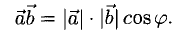
Из  (рис. 3.7) имеем
(рис. 3.7) имеем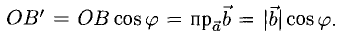 (
(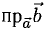 — проекция вектора
— проекция вектора на направление вектора
на направление вектора  ).
).
Итак, 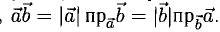
2°. Если
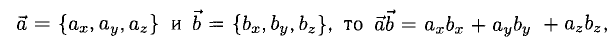
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 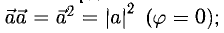 если же
если же  , т. е.
, т. е. 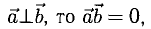 поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
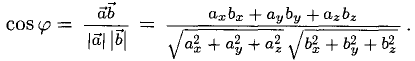
Примеры с решениями
Пример:
Перпендикулярны ли векторы  если
если 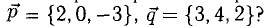
Решение:
Условие перпендикулярности векторов (п. 2°) 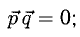 в нашем случае
в нашем случае
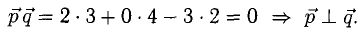
Ответ. Да.
Пример:
Найти проекцию вектора 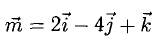 на направление вектора
на направление вектора 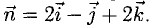
Решение:
Имеем 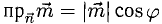 (п. 1°). Подставив сюда выражение для
(п. 1°). Подставив сюда выражение для 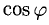 из п. 3°, получим
из п. 3°, получим
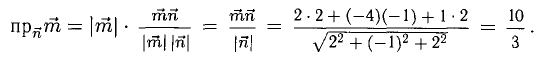
Ответ 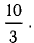
Пример:
Зная векторы, совпадающие с двумя сторонами:  и
и 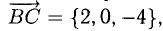 найти внутренние углы треугольника ABC.
найти внутренние углы треугольника ABC.
Решение:
Имеем (рис. 3.8)
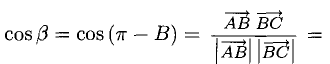
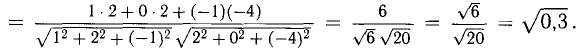
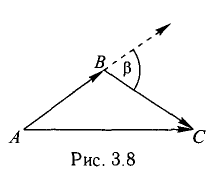
При помощи таблиц находим 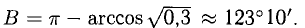 Для нахождения других углов нам понадобится вектор
Для нахождения других углов нам понадобится вектор 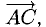 который является суммой
который является суммой 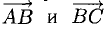 :
: 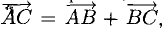 поэтому
поэтому 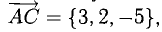
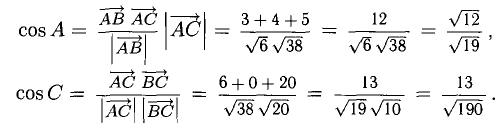
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
Найти координаты вектора 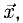 если
если 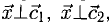 где
где 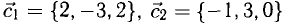 и
и 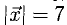
Решение:
На рис. 3.9 имеем 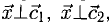 Из условий перпендикулярности векторов (п. 2°) имеем
Из условий перпендикулярности векторов (п. 2°) имеем 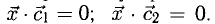 Положим
Положим 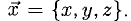 Условие задачи перепишем в виде Рис. 3.9 системы
Условие задачи перепишем в виде Рис. 3.9 системы
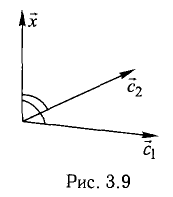
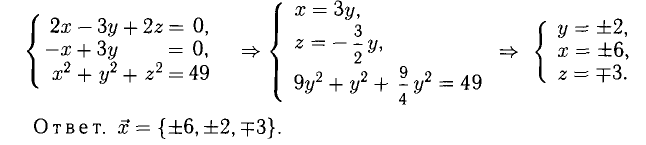
Векторное произведение векторов
1°. Векторы  приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора
приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора 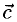 на плоскость векторов
на плоскость векторов  то кратчайший поворот от
то кратчайший поворот от  совершается против (по) часовой стрелки (рис. 3.10).
совершается против (по) часовой стрелки (рис. 3.10).
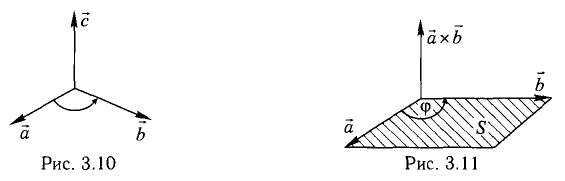
2°. Векторным произведением ненулевых векторов 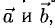 называется вектор
называется вектор 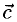 , обозначаемый
, обозначаемый 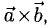 удовлетворяющий следующим трем условиям.
удовлетворяющий следующим трем условиям.
1)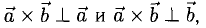 вектор
вектор 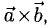 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 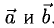
2) Вектор 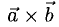 направлен так, что векторы
направлен так, что векторы  образуют правую тройку.
образуют правую тройку.
3) 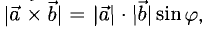 т.е. его длина численно равна площади параллелограмма, построенного на векторах
т.е. его длина численно равна площади параллелограмма, построенного на векторах 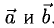 (рис. 3.11), таким образом,
(рис. 3.11), таким образом, 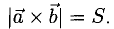
Если векторы 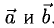 коллинеарны, то под
коллинеарны, то под 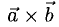 понимается нулевой вектор:
понимается нулевой вектор: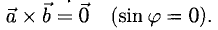
3°. Если известны координаты векторов-сомножителей 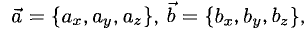 то для отыскания координат векторного произведения служит формула
то для отыскания координат векторного произведения служит формула
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В{3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов  Определим координаты векторного произведения
Определим координаты векторного произведения 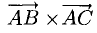 (рис. 3.12):
(рис. 3.12):
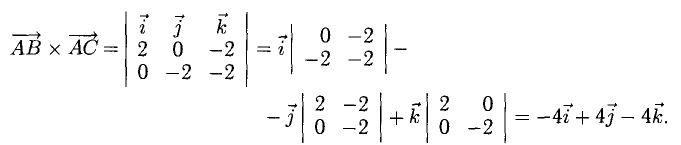
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 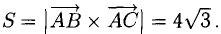 Площадь треугольника
Площадь треугольника 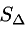 равна
равна 
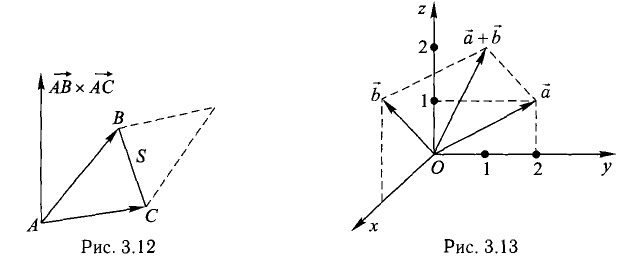
Пример:
Построить параллелограмм на векторах 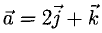 и
и 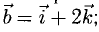 вычислить его площадь и высоту, опущенную на
вычислить его площадь и высоту, опущенную на  .
.
Сделаем чертеж (рис. 3.13). Имеем 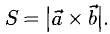 Отдельно вычисляем векторное произведение:
Отдельно вычисляем векторное произведение:
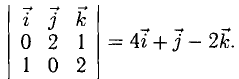
Следовательно,
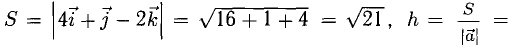
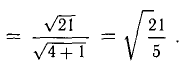
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов  называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение
называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение 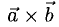 , а другой — вектор
, а другой — вектор  . Обозначение:
. Обозначение: 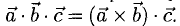 Если
Если  образуют правую тройку, то
образуют правую тройку, то 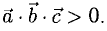 Если
Если образуют левую тройку, то
образуют левую тройку, то 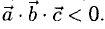
Модуль смешанного произведения векторов равен объему параллелепипеда (рис. 3.14), построенного на этих векторах,
равен объему параллелепипеда (рис. 3.14), построенного на этих векторах,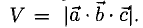 Условие
Условие 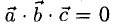 равносильно тому, что векторы
равносильно тому, что векторы  расположены в одной плоскости, т.е. компланарны. Имеет место равенство
расположены в одной плоскости, т.е. компланарны. Имеет место равенство
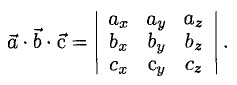
Объем тетраэдра с вершинами в точках 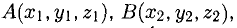
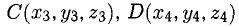 можно вычислить по формуле
можно вычислить по формуле 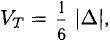 где
где
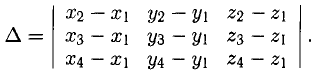
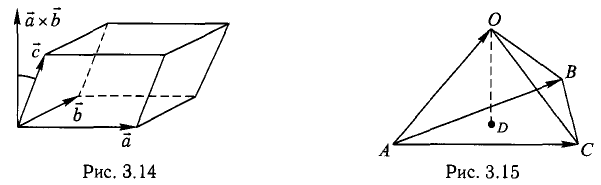
2°. Условие 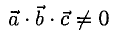 равносильно условию линейной независимости
равносильно условию линейной независимости  , а тогда любой вектор
, а тогда любой вектор 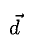 линейно выражается через них, т. е.
линейно выражается через них, т. е. 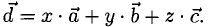 Для определения х, у, z следует решить соответствующую систему линейных уравнений
Для определения х, у, z следует решить соответствующую систему линейных уравнений
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах 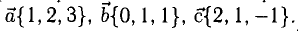
Решение:
Искомый объем 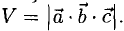 Поскольку
Поскольку
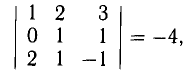
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 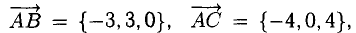
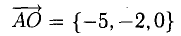 .Объем пирамиды ОАВС (тетраэда) равен
.Объем пирамиды ОАВС (тетраэда) равен
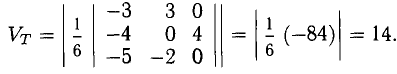
3) Площадь грани ABC
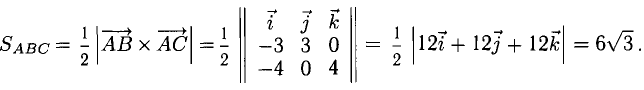
4) Объем пирамиды 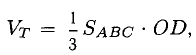 отсюда
отсюда 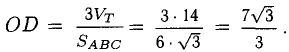
Ответ. 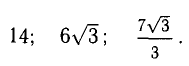
Основные понятия векторной алгебры




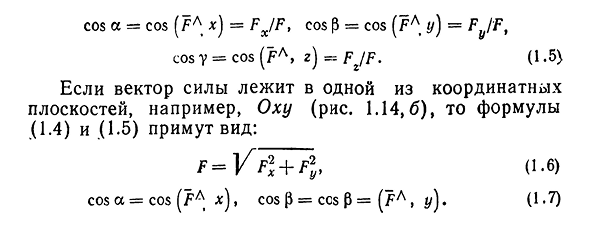
Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси  некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
Пусть М — произвольная точка оси  . Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).
. Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).

Оnределение:
Ось  с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
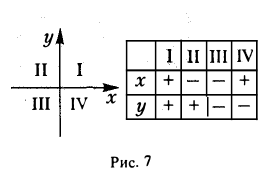
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
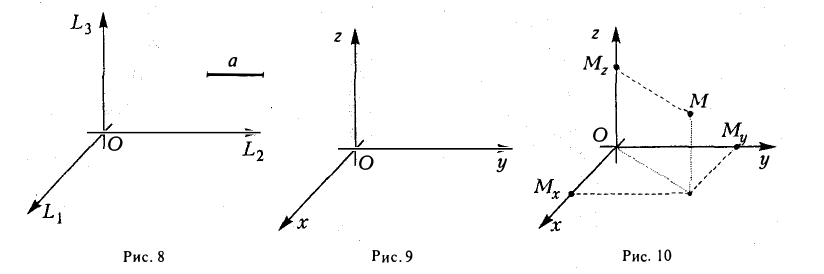
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:

Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
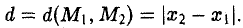
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
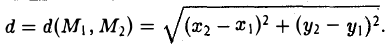
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
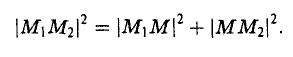
Так как расстояние d между точками M 1 и M 2 равно длине отрезка M1M2 а |M1M| = |x 2 — x 1|, |MM2| = |y 2 — y 1|, то отсюда получаем, что
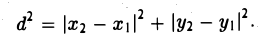
Замечая, что
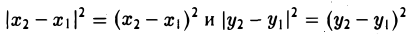
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками  в пространстве вычисляется по следующей формуле
в пространстве вычисляется по следующей формуле
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
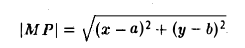
и возведем обе части полученного равенства в квадрат:
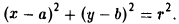
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
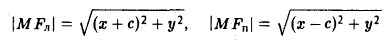
(рис. 13). Отсюда
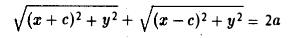
Перенесем второй корень в правую часть
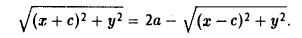
Возводя обе части в квадрат, после простых преобразований получим
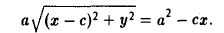
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
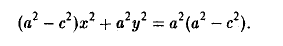
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b2 , nолучаем уравнение эллипса
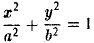
(см. главу 111) .
Деление отрезка в данном отношении:
Пусть М1 (х1 , y1) и М2 (х2 , y2) — различные точки плоскости. Пусть, далее, точка М(х, у) лежит на отрезке М1М2 и делит его в отношении λ 1 : λ 2 , т. е.
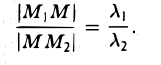
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
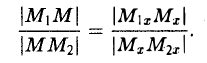
Так как
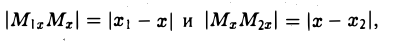
то из последних двух соотношений получаем, что
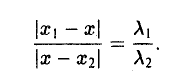
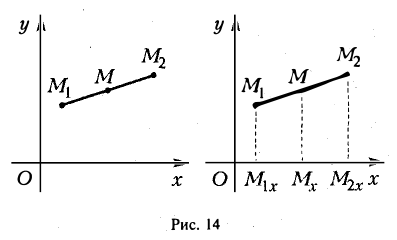
Точка М лежит между точками М1 и М2 , поэтому либо х 1 < х < х 2 , либо х 1 > х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
Отсюда

В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
доказывается аналогичным рассуждением .
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
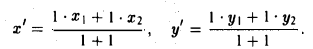
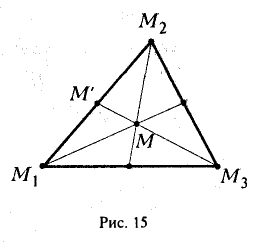
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
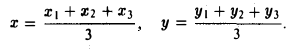
Замечание:
Если точка М(х,у,z ) делит отрезок с концами М1( х1, у1, z1) и М2( х2, у2, z2) в отношении λ1 : λ2, то ее координаты вычисляются по формулам
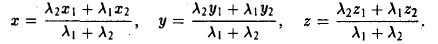
Полярные координаты
Предположим, что задана точка О, ось  .содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
.содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси  и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
Точка О называется полюсом,  — полярной осью.
— полярной осью.
Ясно, что Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный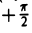 . Тогда
. Тогда
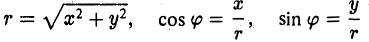
(рис.18). В свою очередь 
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г, <р) которых удовлетворяют равенству
r = R,
является окружностью радиуса R с центром в полюсе (рис. 19)
Определители 2-го и 3-го порядков
Пусть имеем четыре числа а11, а12, а21, а22 (читается — «а-один-один», «а-один-два», «а-два-один», «а-два-два»).
Определителем второго порядка называется число
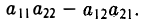
Обозначение:
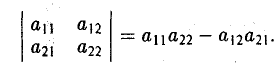
Числа а11, а12, а21, а22 называются элементами определителя; пары элементов а11, а12 и а21, а22 образуют строки определителя, а пары элементов а11, а21 и а12, а22 — его столбцы; пара элементов а11, а22 образует главную диагональ определителя, а пара а12, а21 — побочную диагональ.
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
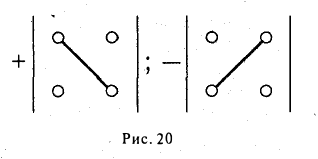
Пример:
Вычислить определитель
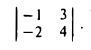
По правилу (1) имеем
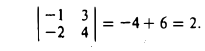
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
Решая эту систему методом исключения неизвестных при условии, что
находим
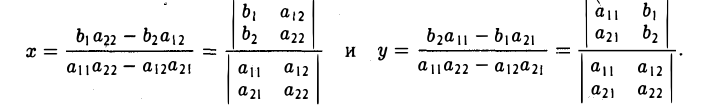
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом

и вычисляемое по следующему правилу:
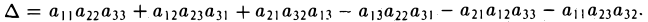
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
Элементы а11, а22, а33 образуют главную диагональ определителя ∆, элементы а13, а22, а31 — побочную диагональ, элементы а13, а22, а31 — побочную диагональ.
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Вычислить определитель

Применяя правило треугольника, находим
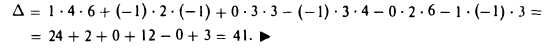
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
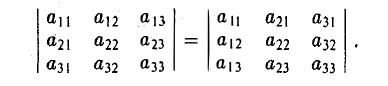
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
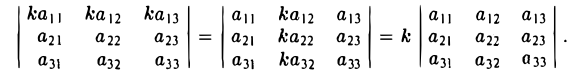
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка

Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
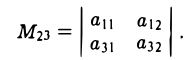
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
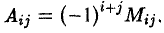
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
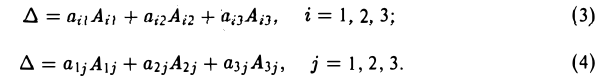
Покажем, например, что
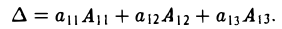
Пользуясь формулой (2), получаем, что
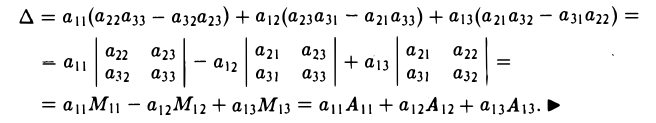
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Вычислить определитель
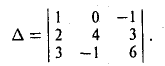
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
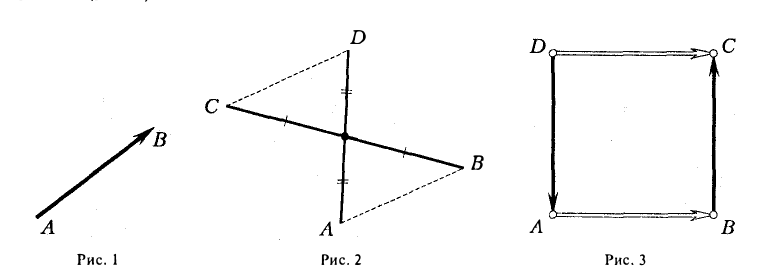
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
А В = CD.
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор  однозначно определяется заданием связанного вектора АВ.
однозначно определяется заданием связанного вектора АВ.
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
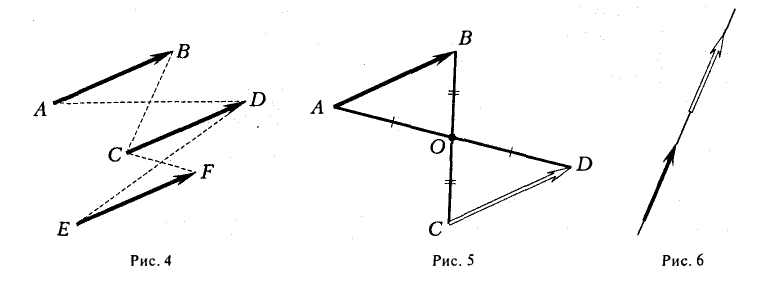
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой
 = а
= а
(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
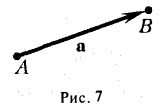
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 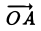 = а. От полученной точки А отложим вектор b:
= а. От полученной точки А отложим вектор b:  = b. Полученный в результате вектор
= b. Полученный в результате вектор называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
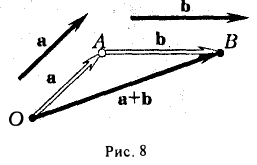
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор  , идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
, идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
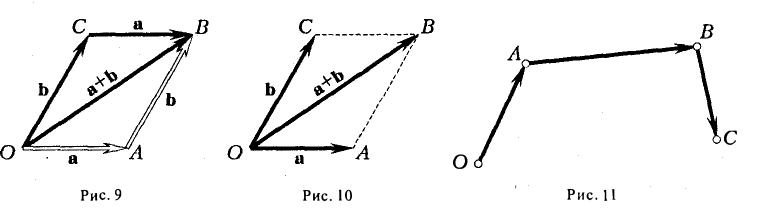
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 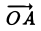 = а; от полученной точки А отложим вектор b:
= а; от полученной точки А отложим вектор b:  = b; отточки В — вектор с:
= b; отточки В — вектор с:  = с (рис. 11). По определению суммы
= с (рис. 11). По определению суммы  — а + b и
— а + b и  = (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
= (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
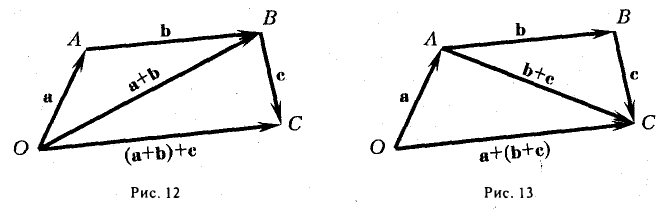
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
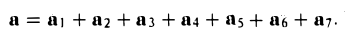
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
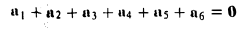
(рис. 15).
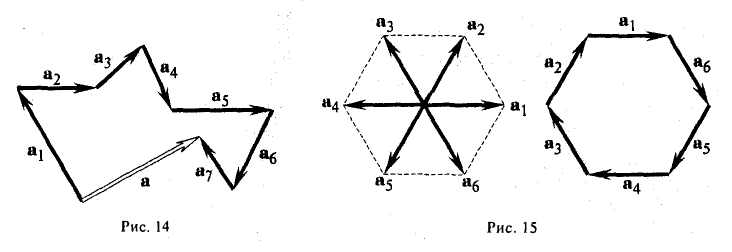
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 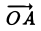 = n,
= n,  = Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
= Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
- |Ь| = |λ| • |а|;
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ < 0).
Обозначение: b = λа.
При λ = 0 положим λа = 0.
Таким образом, векторы а и Ь = λа коллинеарны по определению. Верной обратное: если векторы а(а ≠ 0) и Ь коллинеарны, то можно найти число А такое, что h = λа.
Укажем основные свойства этой операции умножения вектора на число:
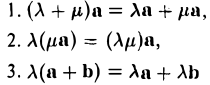
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
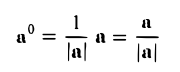
есть единичный вектор (орт) направления вектора а (рис. 18).
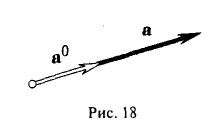
Координаты и компоненты вектора
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что

Векторы  коллинеарны соответственно единичным векторам i, j, k,
коллинеарны соответственно единичным векторам i, j, k,
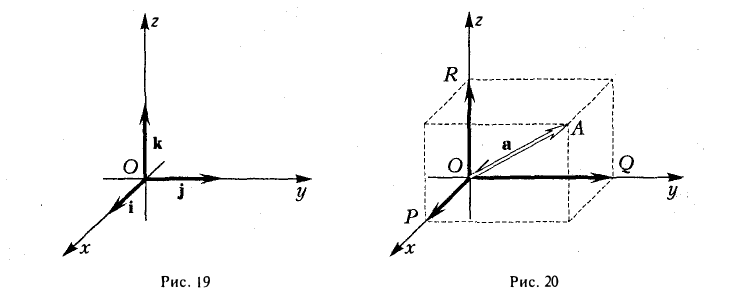
поэтому найдутся числа х, у, z такие, что
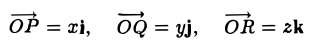
и, следовательно,
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = {х, y,z}.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
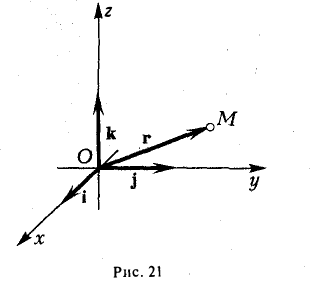
Из вышеизложенного следует, что два вектора а = { х1, у1, z1 } и b = {х2, у2, z2} равны тогда и только тогда, когда соответственно равны их координаты, т. е.
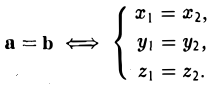
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
Пусть имеем два вектора а = { х1, у1, z1} и b = { х2, у2, z2 },так что а = х1i, у1j+ z1k. b = х2i+ у2j+z2k. На основании правила сложения векторов имеем
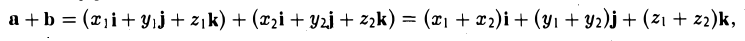
или, что то же,
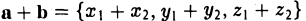
— при сложении векторов их координаты попарно складываются. Аналогично получаем
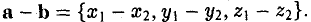
Далее,
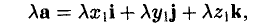
или, что то же,
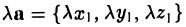
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 } — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
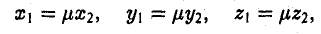
или (3)
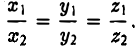
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
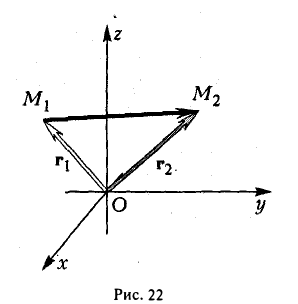
Пример:
Найти координаты вектора 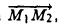 начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
Из рис. 22 видно, что 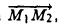 = r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
= r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
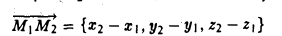
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор  , определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
, определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
Определение:
Проекцией вектора  на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
Обозначение: 
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
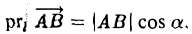
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Например,
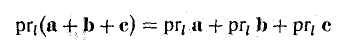
(рис. 26).
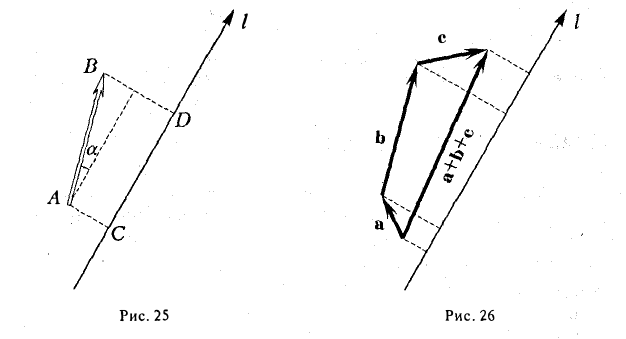
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
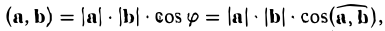
(1)
где φ, или в иной записи (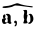 ), есть угол между векторами а и b (рис. 27 а).
), есть угол между векторами а и b (рис. 27 а).
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
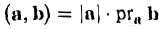
(рис. 27 б) и, аналогично,’ (2)
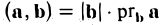
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
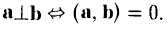
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
Действительно,
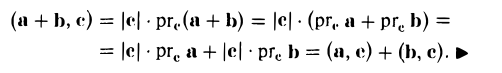
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
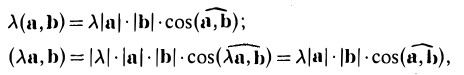
поскольку при λ > 0 углы ( ) и (λ
) и (λ ) равны (рис.28).
) равны (рис.28).
Аналогично рассматривается случай λ < 0. При λ = 0 свойство 4 очевидно.
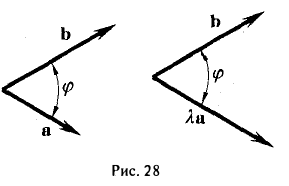
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
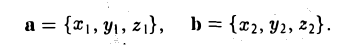
Рассмотрим скалярное произведение векторов а и b:
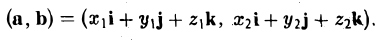
Пользуясь распределительным свойством скалярного произведения, находим
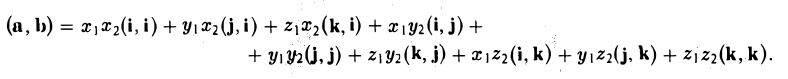
Учитывая, что
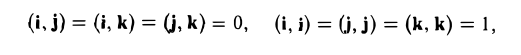
получаем (4)
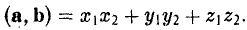
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а2.
Применяя формулу (4) при b = а, найдем (5)
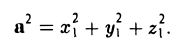
С другой стороны,
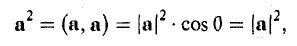
так что из (5) следует, что (6)
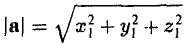
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
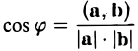
(предполагается, что векторы а и b — ненулевые).
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 }. Тогда формула (7) примет следующий вид
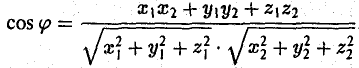
Пример:
Найти угол между векторами a = {2, -4,4,} и d = {-3,2,6}. Пользуясь формулой (8), находим
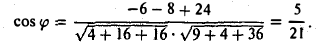
Пусть b = i, T.e. b = {1,0,0}. Тогда для всякого вектора а = { х1, у1, z1} ≠ 0 имеем
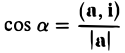
или, в координатной записи, (9)
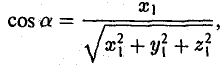
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
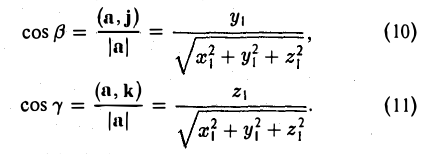
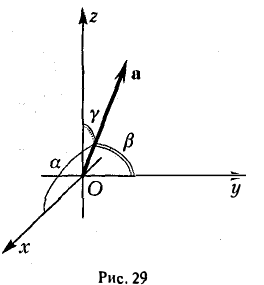
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
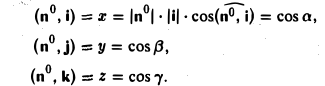
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
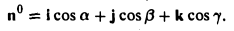
Отсюда получаем
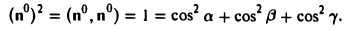
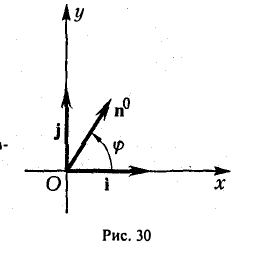
Пример:
Пусть единичный вектор n° ортогонален оси z:
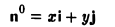
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Тем самым,
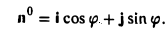
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
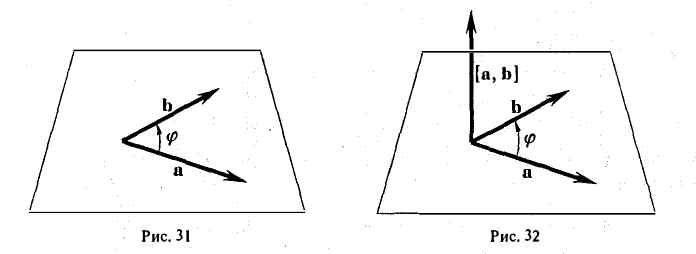
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
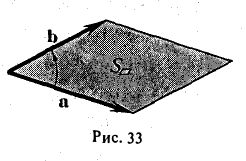
По определению длина векторного произведения (1)
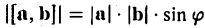
численно равна площади 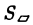 параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
|[a, b]| = 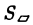 .
.
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
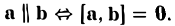
2. Векторное произведение антикоммутативно, т. е. всегда (2)
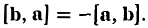
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
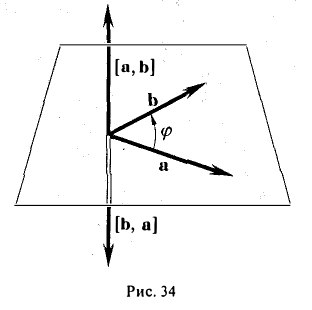
3. Векторное произведение обладает распределительным свойством по отношению к сложению
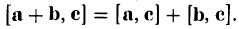
4. Числовой множитель λ можно выносить за знак векторного произведения
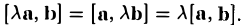
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = { х1, у1, z1}, b = { х2, у2, z2 }. Пользуясь распределительным свойством векторного произведения, находим (3)
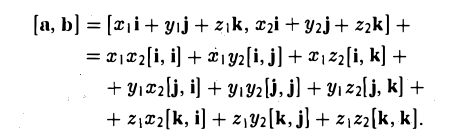
Выпишем векторные произведения координатных ортов (рис. 35):
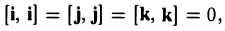
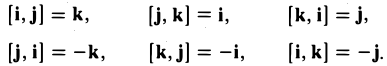
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
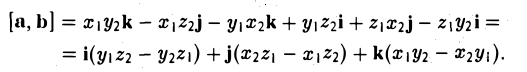
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
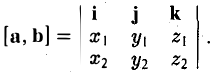
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь  = |[а, b]. Поэтому находим
= |[а, b]. Поэтому находим
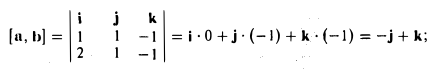
откуда
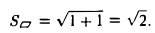
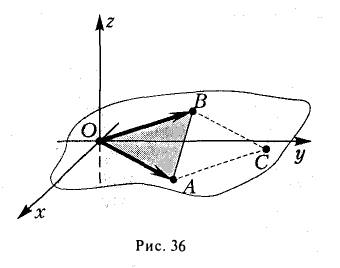
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= и b =
и b =  , получаем
, получаем
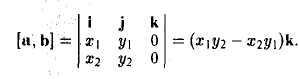
Отсюда
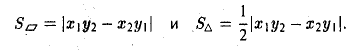
Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
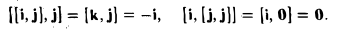
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
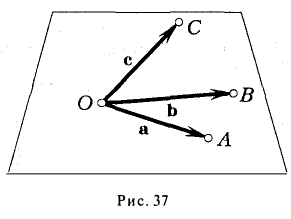
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 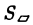 — площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
— площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
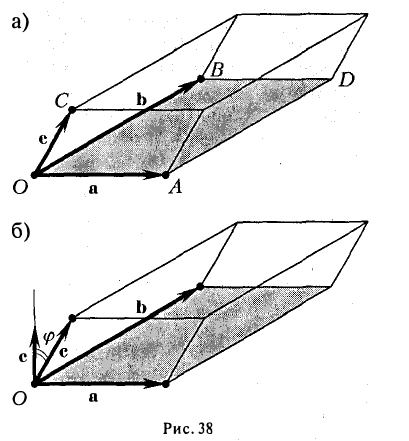
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
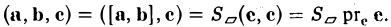
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
{а, b, с компланарны} <=> (а, b, с) = 0.
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
Найдем выражение для их смешанного произведения (а, b, с). Имеем
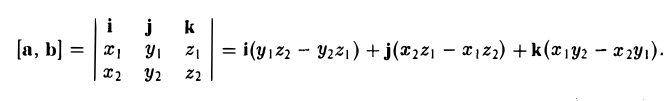
Откуда
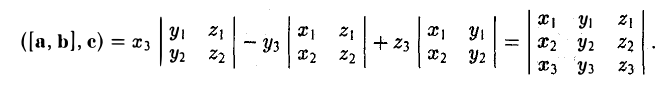
Итак,
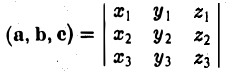
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Необходимое и достаточное условие компланарности векторов а = { х1, у1, z1}, b = { х2, у2, z2 }, c = { х3, у3, z3} запишется в следующем виде
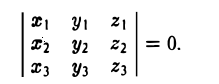
Пример:
Проверить, компланарны ли векторы
a = {7, 4,-6}, b = {2, 1,1}, с ={19, 11,17}.
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
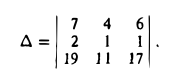
Разлагая его по элементам первой строки, получим
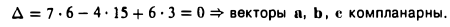
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

