Любое выражение с переменной в алгебре (математике) имеет свою область допустимых значений (или ОДЗ), где оно существует. ОДЗ – это то, что необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как найти ОДЗ (ОДЗ логарифма, ОДЗ корня), использовать на примерах
(без необходимости искать готовые решения онлайн). Также будет рассмотрена важность указания ОДЗ при решении домашних заданий, гдз и прочих случаях.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1:а, если а=0, тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут подробно ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда можно уже определять более полно
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Для примера рассмотрим выражение вида 1x-y+z, где имеются три переменные. Иначе можно записать, как x=0, y=1, z=2, другая же запись имеет вид (0,1,2). Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 10-1+2=11=1. Отсюда видим, что (1,1,2) недопустимы. Подстановка дает в результате деление на ноль, то есть 11-2+1=10.
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Если имеем выражение вида 5z-3, тогда ОДЗ имеет вид (−∞, 3)∪(3, +∞). Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида zx-y, тогда видно, что x≠y, z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f(x).
Как найти ОДЗ? Примеры, решения
Поиск определенного ОДЗ означает поиск всех допустимых значений, подходящих для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Как находить ОДЗ? Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Как решать ОДЗ? Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π2+π·k, k∈Z и котангенса π·k, k∈Z;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [-1; 1].
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x3+2·x·y−4.
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Найти ОДЗ выражения 13-x+10.
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅.
Найти ОДЗ заданного выражения x+2·y+3-5·x.
Решение
Наличие квадратного корня (квадрат корня) говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x+2·y+3≥0. То есть это и есть искомая область допустимых значений.
Ответ: множество x и y, где x+2·y+3≥0.
Определить ОДЗ выражения вида 1x+1-1+logx+8(x2+3).
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x+1-1≠0 . Выражение под корнем всегда имеет смысл, когда больше или равно нулю, то есть x+1≥0. Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x2+3>0. Основание логарифма также должно иметь положительное значение и отличное от 1, тогда добавляем еще условия x+8>0 и x+8≠1. Отсюда следует, что искомое ОДЗ примет вид:
x+1-1≠0,x+1≥0,x2+3>0,x+8>0,x+8≠1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [−1, 0)∪(0, +∞).
Ответ: [−1, 0)∪(0, +∞)
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Тождественные преобразования:
- могут не влиять на ОДЗ;
- могут привести к расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Если имеем выражение вида x2+x+3·x, тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Если взять пример выражения x+3x−3x, то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (−∞, 0)∪(0, +∞). Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Если имеется x-1·x-3, тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства (x−1)·(x−3)≥0. Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (−∞, 1]∪[3, +∞). После преобразования x-1·x-3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x-1≥0,x-3≥0. При ее решении получаем, что [3, +∞). Значит, ОДЗ полностью записывается так: (−∞, 1]∪[3, +∞).
Нужно избегать преобразований, которые сужают ОДЗ.
Рассмотрим пример выражения x-1·x-3, когда х=-1. При подстановке получим, что -1-1·-1-3=8=22. Если это выражение преобразовать и привести к виду x-1·x-3, тогда при вычислении получим, что 2-1·2-3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Рассмотрим на примере дроби вида xx3+x. Если сократить на x, тогда получаем, что 1×2+1. Тогда ОДЗ расширяется и становится (−∞ 0)∪(0, +∞). Причем при вычислении уже работаем со второй упрощенной дробью.
В случае нахождения ОДЗ для логарифмов дело обстоит немного иначе. Вот пример нахождения ОДЗ для логарифма.
Если имеется выражение вида ln x+ln(x+3), его заменяют на ln(x·(x+3)), опираясь на свойство логарифма. Отсюда видно, что ОДЗ с (0, +∞) до (−∞, −3)∪(0, +∞). Поэтому для определения ОДЗ ln(x·(x+3)) необходимо производить вычисления на ОДЗ, то есть (0, +∞) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Что такое иррациональные уравнения?
Не секрет же, что большинство чисел можно представить в виде обыкновенной дроби с натуральными числами в числителе и знаменателе?
Например, число 7 – это (frac{21}{3})
Иррациональные числа не такие. Их невозможно представить в виде дроби. Они странные.
Гиппас создал античным математикам множество проблем: их теории о том, что все в мире соизмеримо целым числам, рушились одна за другой. И они боялись.
Но мы будем смелыми 🙂
Сначала разберемся, что такое рациональные уравнения, а потом научимся находить решение иррациональных уравнений.
Итак, что из себя представляют рациональные уравнения, а что – иррациональные:
- ( 3cdot (x+1)=x) – как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
- ( 3cdot (x+1)=sqrt{x}) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
- ( 3cdot (x+1)=frac{1}{x}) – а это – рациональное;
- ( 3cdot (x+1)={{x}^{2}}) – тут вот степень, но она с целым показателем степени (( 2)– целое число) – значит, это тоже рациональное уравнение;
- ( 3cdot (x+1)={{x}^{-1}}) – даже уравнение с отрицательным показателем степени тоже является рациональным, ведь, по сути, ( {{x}^{-1}}) – это ( frac{1}{x});
- ( 3cdot (x+1)={{x}^{0}}) – тоже рациональное, т.к. ( {{x}^{0}}=1);
- ( 3cdot (x+1)={{x}^{frac{1}{2}}}) – а с ним поосторожнее, степень-то дробная, а по свойству корней ( {{x}^{frac{1}{2}}}=sqrt{x}), как ты помнишь, корня в рациональных уравнениях не бывает.
Надеюсь, теперь ты сможешь различить, к какому виду относится то или иное уравнение.
Дадим oпределение:
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень.
А вот как это выглядит: ( sqrt{x}); ( {{x}^{frac{1}{3}}}).
Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?
Так избавься от них, вот и все дела!
Если еще не догадался, как, то я подскажу: просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение.
Но проверяй все корни! Позже ты поймешь, почему делать это необходимо.
Как рациональные уравнения решать помнишь? Если забыл, то советую почитать «Рациональные уравнения».
Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего алгоритма:
Пример №3
( sqrt{12-x}=x)
После возведения обеих частей в квадрат имеем:
( 12-x={{x}^{2}}), упрощаем и решаем квадратное уравнение по теореме Виета
( {{x}^{2}}+{x}-12=0)
( left[ begin{array}{l}{{x}_{1}}=3\{{x}_{2}}=-4end{array} right.)
У нас два корня, пробуем их подставить в исходное для проверки.
Подставляем ( 3), ( sqrt{9}=3), ( 3=3) – подходит.
Подставим ( -4), получим ( sqrt{16}=-4)…
Но ведь ( 4ne -4)! Что же получается, ( -4) – посторонний корень.
Заговор какой-то!
Думаю, интрига затянулась, настало время объяснить, почему получаются какие-то посторонние корни.
Опять объяснять буду на примере:
( -2ne 2), но если мы возведем в квадрат обе части, ( {{(-2)}^{2}}={{(2)}^{2}}), ( 4=4).
Ну как тебе фокус? 🙂
То же самое получается и в нашем примере с иррациональным уравнением, в результате преобразования мы можем найти все корни, но могут примешаться и посторонние.
Их надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.
А если взять не вторую, а третью степень:
( {{(-2)}^{3}}ne {{(2)}^{3}})
( -8ne 8)
Пример №4 (метод уединения радикала)
( sqrt{2x+1}+sqrt{x}=1)
В этом примере есть два подкоренных выражения и число ( 1).
Чтобы избавиться от корня, нужно обе части возвести в квадрат, но, прежде чем сделать это, перенесем ( sqrt{x}) в правую часть.
( sqrt{2x+1}=1-sqrt{x})
«Зачем?» – спросишь ты.
Дело в том, что, если возводить в квадрат в таком виде, упрощать придется дольше, не веришь – попробуй сам, а я, пожалуй, избавлю себя от расписывания этого 🙂
Теперь возводим в квадрат обе части и упрощаем.
( sqrt{2x+1}=1-sqrt{x})
( 2x+1=1-2sqrt{x}+x)
( x=-2sqrt{x})
Понял, в чем сложность?
Этот метод решения математики называют «метод уединения радикала».
Радикал (выражение с корнем) надо уединить в одной стороне уравнения. Но уединять и возводить в степень придется не один раз.
Чтобы избавиться от корней и получить нормальное (рациональное 🙂 ) уравнение, придется выполнять множество замысловатых махинаций, которые заключаются в уединении и возведении в степень.
С другой стороны, можно заметить, что на определенной стадии решения становится без дальнейших упрощений понятно, что в уравнении, например, нет решений.
Например…
Корни степени больше 2
Ты спросишь: а что всё про квадратные корни? Как же быть с остальными степенями?
Спрошу в ответ: а чем они отличаются?
Отличие, на самом деле, есть. Но важна не конкретная степень корня, а четность этой степени.
Корни четной степени
Корни ( displaystyle 2), ( displaystyle 4), ( displaystyle 6), и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):
( displaystyle sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})
Например:
( displaystyle sqrt[4]{A}=Btext{ }Leftrightarrow text{ }left{ begin{array}{l}A={{B}^{4}}\Bge 0end{array} right.)
Корни нечетной степени
С нечетными степенями (( displaystyle 3), ( displaystyle 5), …) все намного проще!
Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)
Что это значит?
Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:
( displaystyle begin{array}{l}sqrt[3]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{3}}\sqrt[5]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{5}}end{array})
Примеры:
- ( displaystyle sqrt[5]{2-x}=-2)
- ( displaystyle sqrt[4]{3+2{x}-{{x}^{2}}+{{x}^{4}}}=x)
- ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}=x)
- ( displaystyle sqrt[3]{6+{{x}^{2}}-{{x}^{3}}}=1-x)
Ответы:
Область допустимых значений (ОДЗ) – это все значения переменной, при которых не нарушаются правила математики.
Например:
– если в выражении (frac{x}{x-1}) значение переменной будет равно 1, нарушается правило: на ноль делить нельзя. Поэтому здесь (x) не может быть единицей и ОДЗ записывается так: (xneq1);
– если в выражении (sqrt{x-2}) значение переменной равно (0), нарушается правило: подкоренное выражение не должно быть отрицательно. Значит, здесь (x) не может быть (0), а также (1, -3, -52,7) и т.д. То есть, икс должен быть больше или равен 2 и ОДЗ будет: (xgeq2);
– а вот в выражение (4x+1) мы можем подставить любое число вместо икса, и никакие правила нарушены не будут. Поэтому область допустимых значений здесь – вся числовая ось. В таких случаях ОДЗ не записывают, потому что оно не несет в себе полезной информации.
Как найти ОДЗ?
Если переменная (икс) в уравнении или неравенстве стоит в знаменателе, логарифме, под корнем, в тангенсе или котангенсе ОДЗ записать нужно.

В квадратных и линейных уравнениях
(неравенствах) ОДЗ писать не нужно. В иррациональных, дробно-рациональных, логарифмических, а также тригонометрических
с тангенсом
и котангенсом
– ОДЗ обязательно. В уравнениях с синусом и косинусом – если нет знаменателей или других «отягощающих» функций – ОДЗ не записывают.
Чтобы осознать важность ОДЗ, давайте сравним два решения уравнения: с ОДЗ и без ОДЗ.
Пример: Решить уравнение (frac{x^2-x}{x+3}=frac{12}{x+3})
Решение:
| Без ОДЗ: | С ОДЗ: | |
| (frac{x^2-x}{x+3}=frac{12}{x+3}) | (frac{x^2-x}{x+3}=frac{12}{x+3}) | |
|
ОДЗ: (x+3≠0) (⇔) (x≠-3) |
||
| (x^2-x=12) | (x^2-x=12) | |
| (x^2-x-12=0) | (x^2-x-12=0) | |
| (D=(-1)^2-4·1·(-12)=49) | (D=(-1)^2-4·1·(-12)=49) | |
| (x_1=)(frac{-(-1) + sqrt{49}}{2·1})(=4) | (x_2=)(frac{-(-1) + sqrt{49}}{2·1}) (=4) | |
| (x_1=)(frac{-(-1) – sqrt{49}}{2·1})(=-3) | (x_2=)(frac{-(-1) – sqrt{49}}{2·1})(=-3) – не подходит под ОДЗ | |
| Ответ: (4; -3) | Ответ: (4) |
Видите разницу? В первом решении у нас в ответе появился неверный, лишний корень! Почему неверный? А давайте попробуем подставить его в исходное уравнение.
(frac{(-3)^2-(-3)}{(-3)+3})(=)(frac{12}{(-3)+3})
(frac{12}{0})(=)(frac{12}{0})
Видите, у нас получились и слева, и справа невычислимые, бессмысленные выражения (ведь на ноль делить нельзя). И то, что они одинаковы уже не играет роли, поскольку эти значения – не существуют. Таким образом, “(-3)” – неподходящий, посторонний корень, а область допустимых значений оберегает нас от таких серьезных ошибок.
Именно поэтому за первое решение вы получите двойку, а за второе – пятерку. И это не занудные придирки учителя, ведь неучет одз – не мелочь, а вполне конкретная ошибка, такая же как потерянный знак или применение не той формулы. В конце концов, итоговый ответ-то неверен!
Нахождение области допустимых значений часто приводит к необходимости решать системы неравенств или уравнений, поэтому вы должны уметь это делать хорошо.
Пример: Найдите область определения выражения (sqrt{5-2x}+)(frac{1}{sqrt{14+5x-x^{2}}})
Решение: В выражении два корня, один из которых в знаменателе. Кто не помнит ограничения, накладывающиеся в этом случае, тот смотрит таблицу. Кто помнит, записывает, что выражение под первым корнем больше или равно нулю, а под вторым – больше нуля. Понимаете, почему ограничения именно такие?
| (begin{cases}5-2xgeq0\14+5x-x^{2} > 0end{cases}) |
Дело за малым, нужно решить систему неравенств. |
| (begin{cases}-2xgeq-5\x^{2}-5x-14 < 0end{cases}) |
Поделим первое неравенство на (-2). |
| (begin{cases}xleq2,5\(x-7)(x+2) < 0end{cases}) |
Отметим все корни первого неравенства на числовой оси. |

|
Запишем общий ответ для системы – это и есть допустимые значения для икса. |
Ответ: ((-2;2,5])
Скачать статью
Уравнения с радикалами. О.Д.З.
Простейшие уравнения с радикалами
Правило возведения в квадрат обеих частей уравнения::
если $A=B$ , тогда $A^2=B^2$ , но не наоборот: ($A^2=B^2$ не $Leftrightarrow$ $A=B$ ) .
$A^2=B^2$ $Rightarrow $ $A=B$ при условии: $A$ и $B$ одного и того же знака.
$sqrt{X}=C$ $Rightarrow $ $X=C^2$ при условии: $Cge0$ , $C$ – неотрицательна.
Пример 1: Решить уравнение $sqrt{frac{3+12x}{2x-1}}=3$
- Вопрос к уравнению: каким числом должно быть неизвестное $x$ , чтобы стать корнем уравнения ,
- т.е. чтобы уравнять собой левую и правую части ? не знаем каким числом в будущем окажется $x$ ,
- но сейчас , очевидно , дробь $frac{3+12x}{2x-1}$ должна равняться $9$ . а как иначе левое станет $3$? никак.
- вывод: чтобы сравнялись части, нужно, чтобы сравнялись их квадраты . $A=B$ $Rightarrow$ $A^2=B^2$ .
- метод решения – избавление от радикала – возведение обеих частей в квадрат: формула $left(sqrt{A}right)^2=A$ – .
- применим этот метод и возведем обе части в квадрат $left(sqrt{frac{3+12x}{2x-1}}right)^2=left(3right)^2$ $Leftrightarrow$ – так избавимся от радикала
- $frac{3+12x}{2x-1}=9$ и получим “простое” без радикалов уравнение $3+12x=9cdotleft(2x-1right)$ $Leftrightarrow$ $12=18x-12x$ ,
- наконец-то найдем то самое число , каким должно быть неизвестное ответ: $x=2$
Пример 2: Решить уравнение $sqrt{6-4x-x^2}=-3-2x $
- В начале уточним некоторые детали. не знаем каким станет выравнивающий обе части $x$ , но в любом случае:
- под радикалом должно быть неотрицательное значение. иначе получится “ложь” – бессмыслица.
- надо указать ОДЗ – ограничение $6-4x-x^2ge0$ : (допустимо!) все, что под радикалом $ge0$.
- избавимся от радикала одновременным возведением обеих частей в квадрат.
- но это не гарантирует “уравнивания до возведения” . (Может было 4 = -4 , стало 16 = 16)
- бывает такое: после возведения в квадрат части уравниваются, хотя до операции они были не равны .
- например: $left(-3right)^2=left(3right)^2$ , но ведь $-3ne3$ .
- нам нужны гарантии , что равные после возведения в квадрат части $A^2=B^2$ , были бы равными и до
- такое возможно только при условии : обе части уравнения до возведения $A$ и $B$ должны быть одного знака.
- $left(sqrt{6-4x-x^2}right)^2=left(-3-2xright)^2$ при условии $-3-2xge0$ (правая часть до возведения должна быть $ge0$ )
- оговорка при условии гарантирует одинаковость знаков частей “до” операции возведения в квадрат :
- левая часть – это радикал , он неотрицателен $Rightarrow$ значит правая часть уравнения неотрицательна.
- используем формулы: $left(sqrt{a}right)^2=a$ ; $left(a+bright)^2=a^2+2ab+b^2$ получим $6-4x-x^2=9+12x+4x^2$
- решим квадратное уравнение $5x^2+16x+3=0$. два корня $x=-3$ , $x=-0.2$ .
- внимание: корни должны пройти ОДЗ и при условии. Если какой-то не проходят, значит этот корень ложный.
- проверка: $x=-3$ 1) ОДЗ – да!. 2) “при” $-3-2xge0$ – да! $Rightarrow$ истинное решение.
- проверка: $x=-0.2$ $Rightarrow$ 1) ОДЗ – да!. 2) “при” $-3-2xge0$ – нет! $Rightarrow$ ложное решение.
- ответ: $x=-3$ в ответе перечисляем только истинные, уравнивающие решения.
Область Допустимых Значений – ОДЗ – ОДЗ выражения, ОДЗ уравнения
- те числовые значения переменной, при которых выражения имеют смысл … вычисляются.
- но не те числа, при которых выражение невозможно вычислить
- ОДЗ уравнения – те числовые значения неизвестного, при которых выполняется ОДЗ каждого выражения.
- У выражения с квадратным радикалом ОДЗ условие: под радикальное выражение неотрицательно.
- Если в уравнении есть радикалы, то условия ОДЗ: Каждое подрадикальное $ge0$. (под корнем минусовое нельзя)
- Если есть дробь, то условия ОДЗ: каждый знаменатель $ne0$. (делить на 0 нельзя!)
 белы
белы 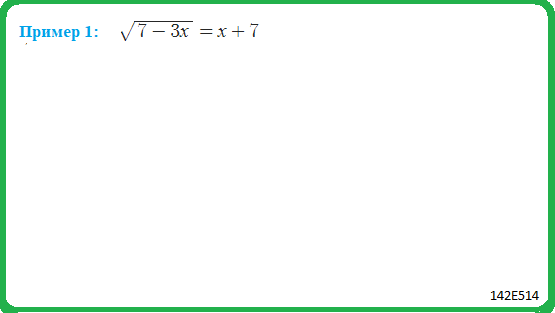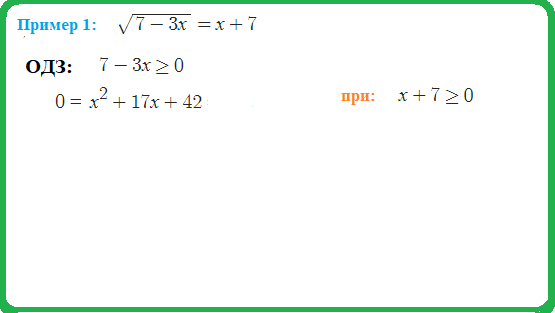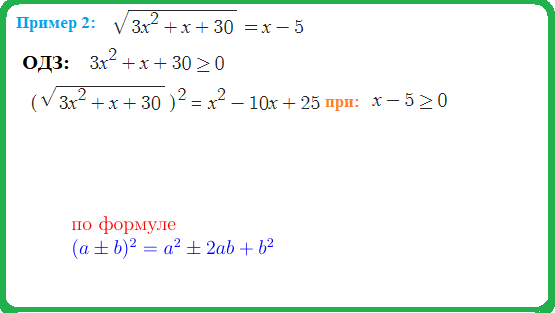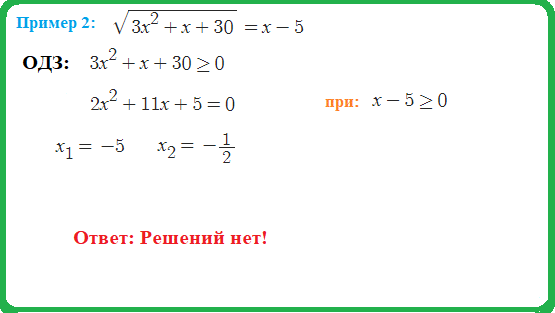
Один радикал в уравнении
Напоминание: Избавиться от радикала в уравнении $sqrt{A}=B$ можно путем возведения его в квадрат $left(sqrt{ }right)^2$ , для этого радикал должен быть уединенным в одной из частей уравнения $sqrt{A}$. “При условии” относится к противоположной от радикала части уравнения – выражению $B$ и накладывается до возведения в квадрат, но пишется при возведении $left(Bright)^2$
Пример 3: Решить уравнение $sqrt{5-x^2}-2x=3-x$
- вопросы: как нам из этого уравнения получить такое, какое мы уже научились решать? как нам прийти к виду “радикал равняется не радикальному выражению” ?
- NB: “правильно поставленный вопрос уже полдела. все открытия начинаются от хорошего вопроса. ставьте вопросы! “
- ОДЗ $5-x^2ge0$ $Leftrightarrow $ условие ОДЗ гарантирует “не ложность” решения. перенесем все нерадикальные
- слагаемые на противоположную от радикала сторону $ sqrt{5-x^2}=2x+3-x$ – так мы уединяем радикал.
- возведение обеих частей в квадрат и “при условии” : $left(sqrt{5-x^2}right)^2=left(x+3right)^2$ при $x+3ge0$
- далее, $5-x^2=x^2+6x+9$ $Leftrightarrow$ $2x^2+6x+4=0$ $Leftrightarrow$ $x^2+3x+2=0$ $Rightarrow$ корни $x=-1$ , $x=-2$
- ответ: $x=-1$ , $x=-2$ оба корня истинные, т.к. проходят ОДЗ и “при условии”.
Равенство радикалов
Пример 4: Решить уравнение $sqrt{2-x+x^2}-sqrt{6-2x}=0$
- ОДЗ: $2-x+x^2ge0$ ; $6-2xge0$ – условие допустимости к решению : определяем когда радикалы существуют.
- перенесем один из радикалов направо, тем самым сравняем радикалы и подготовим возведение в квадрат обеих частей,
- $sqrt{2-x+x^2}=sqrt{6-2x}$ . “при условии” писать не будем , ведь обе части уже $ge0$ из-за радикалов, см. ОДЗ.
дальнейшая стратегия:
1. избавимся от радикалов: возведем обе части в квадрат. условия не нужны, радикалы одного знака.
2. решим полученное нерадикальное уравнение.
3. Проверим решения на выполнимость всех ОДЗ ограничений. забракуем ложные корни.
 белы
белы 
