Как найти огибающую сигнала

Содержание

Общие сведения
Огибающая, мгновенная фаза и мгновенная частота сигнала
Узкополосные сигналы

Общие сведения

Пусть имеется гармоническое колебание

где Sm, ω0, φ — соответственно амплитуда, частота и начальная фаза сигнала; ψ(t) — текущая фаза сигнала.

Этот же сигнал можно представить в виде

где — сопряженный сигнал, полученный из исходного сигнала поворотом его фазы на −π/2.

На комплексной плоскости такой сигнал S изображается в виде вектора, как показано на рис. 2.14.

Негармонические сигналы подобно сигналу (2.24) можно представить в виде процесса с изменяющейся амплитудой (огибающей) Sm(t) и полной фазой ψ(t), т.е. S(t) = Sm(t) cosψ(t). Однако такое представление в общем случае является неоднозначным.

Действительно, пусть задан сигнал S(t). Выбрав для него произвольную функцию S1(t) и считая (Формула), а (Формула), получим (Формула).

Выбрав затем другую функцию S2(t), можно получить другой набор «амплитуд» и фаз: (Формула) и т.д..

Аналитические сигналы: огибающая, мгновенная фаза и мгновенная частота сигнала

Рис. 2.14. Геометрическое представление комплексного сигнала

Для того чтобы представление было однозначным, как в случае гармонического сигнала, сопряженный сигнал должен быть получен из исходного сигнала посредством поворота всех его гармонических составляющих на −π/2.

Рассмотрим теперь сигнал без постоянной составляющей, представленный в виде ряда
Определим для него сопряженный сигнал из исходного сигнала посредством поворота всех его составляющих на −π/2:

Тогда комплексный сигнал будет иметь вид
(25)

а его реальная часть
Отметим, что сопряженный сигнал (Формула) можно получить из исходного, не прибегая к спектральным представлениям, а используя интегральное преобразование Гильберта:

(26)

Исходный сигнал S(t) получим из сопряженного сигнала с помощью обратного преобразования Гильберта:
Функция, называемая ядром преобразования Гильберта, имеет разрыв при t = τ, поэтому интегралы следует понимать в смысле их главного значения, например:

Часто применяется символическая запись преобразований Гильберта:

Нетрудно увидеть, что прямое преобразование Гильберта эквивалентно прохождению сигнала S(t) через фильтр с импульсной характеристикой (Формула), а обратное преобразование Гильберта эквивалентно прохождению сопряженного сигнала (Формула) через фильтр, импульсная характеристика которого (Формула).

Действительно, можно записать
(Формула).

Подставив в это выражение импульсную характеристику вида (Формула), получим формулу (2.26).

Дадим теперь определение рассмотренного сигнала.

Комплексный сигнал, полученный на основе преобразования Гильберта, называется «аналитическим» и записывается в виде выражения (2.25), где исходный сигнал есть реальная часть аналитического сигнала. Заметим, что выражение (2.25), в котором S(t) и (Формула) связаны между собой преобразованиями Гильберта, во-первых, позволяет получить однозначное представление вида (2.24), а во-вторых, обусловливает ряд важных свойств сигнала (Формула), из-за которых он получил название «аналитический».

Приведем (без доказательства) лишь важнейшие свойства аналитического сигнала, используемые в теории связи.

Преобразования Гильберта являются линейными. Так, для прямого преобразования Гильберта это свойство можно записать в виде
причем при любых постоянных a1 и a2. Справедливость этого свойства следует непосредственно из выражений (2.26) и (2.27).
Преобразования Гильберта от постоянной величины тождественно равны нулю, т.е.Это свойство следует из того факта, что ядро преобразования Гильберта есть нечетная функция аргумента τ относительно точки t = τ, следовательно, интеграл от нечетной функции (Формула) в пределах (−∞, ∞) равен нулю.
Если при каком-нибудь t = τ исходный сигнал достигает экстремума (максимума или минимума), то в окрестности этой точки сопряженный сигнал проходит через нуль. Сказанное иллюстрирует рис. 2.15, где совмещены графики S(τ) (рис. 2.15, а) и ядра преобразования (Формула) (рис. 2.15, б) в точке t, где функция имеет максимум. Результат преобразования Гильберта (Формула) показан на рис. 2.15, в.

Нетрудно увидеть, что функция (Формула) является нечетной функцией аргумента τ, а значит, интеграл от нее в симметричных пределах (−∞, ∞) будет равен нулю.

4. Преобразование Гильберта от гармонических сигналов имеет вид
где.

Очевидно, что для положительных частот
H[cosωt] = sinωt;
H[sinωt] = −cosωt.

Доказательство каждого из указанных свойств следует из анализа сведений, приведенных в данном подразделе.

5. Сдвиг фаз всех составляющих действительного сигнала на угол φ соответствует умножению аналитического сигнала на (Формула), т.е. аналитический сигнал после поворота фаз, откуда легко вычислить и действительный сигнал:

Аналитические сигналы: огибающая, мгновенная фаза и мгновенная частота сигнала

Рис. 2.15. Пояснение свойств преобразований Гильберта:
а — исходный сигнал; б — ядро преобразования; в — сопряженный сигнал

Использование понятия аналитического сигнала для определения формы действительного сигнала после поворота фаз всех его спектральных составляющих на один и тот же угол φ существенно облегчает задачу нахождения действительного сигнала. В противном случае для этого было бы необходимо с помощью преобразования Фурье найти комплексную спектральную плотность, произвести смещение фаз и затем проделать обратное преобразование Фурье.

6. Сдвиг частот всех составляющих сигнала на некоторую величину f0 при f > 0 или f < 0 (преобразование частоты сигнала, причем само изменение частоты f0 может быть как положительным, так и отрицательным) соответствует умножению аналитического сигнала (Формула) на множитель (Формула), т.е.
откуда легко найти и действительный сигнал:

Без использования понятия аналитического сигнала решить эту задачу также было бы весьма сложно.

7. В спектре аналитического сигнала содержатся только положительные частоты. Спектр, полученный посредством преобразования Фурье, имеет вид

Аналогично в спектре комплексно-сопряженного аналитического сигнала

содержатся только отрицательные частоты:

Данные соотношения вытекают из формулы Эйлера.

8. Произведение аналитического сигнала (Формула) и сопряженного с ним аналитического сигнала (Формула) равно квадрату огибающей исходного действительного сигнала S(t):
Таким образом, модуль аналитического сигнала (Формула) равен огибающей сигнала, т.е. (Формула).

Огибающая, мгновенная фаза и мгновенная частота сигнала

Комплексный сигнал, как известно, можно представить в экспоненциальной форме:
откуда следует, что

Решая два последних уравнения относительно Sm(t) и ψ(t), найдем

Величина Sm(t) в этих выражениях называется мгновенной амплитудой, или огибающей, сигнала, а величина ψ(t) — мгновенной фазой сигнала. Производная от мгновенной фазы во времени (если она существует), называется мгновенной круговой частотой сигнала:

Из формулы (2.31) следует, что Sm(t) ≥ S(t), причем равенство имеет место при тех значениях t, для которых S(t) > 0. Легко убедиться, что в этих точках производная огибающей совпадает с производной сигнала, т.е. Sm(t) = S(t) (откуда и название — огибающая сигнала).

Узкополосные сигналы

В радиотехнике и ТЭС широко применяются так называемые узкополосные сигналы, которые являются полосовыми со спектром, показанным на рис. 2.16, но ширина их спектра значительно меньше средней частоты, т.е. (Формула), где (Формула), а (Формула)— соответственно средняя, максимальная и минимальная частоты спектра сигнала.

Аналитические сигналы: огибающая, мгновенная фаза и мгновенная частота сигнала

Рис. 2.16. Спектр полосового сигнала

Для узкополосных сигналов (и помех) представления (2.28) и (2.29) особенно удобны, так как в этом случае огибающая и мгновенная частота оказываются медленно изменяющимися функциями по сравнению с cosψ(t) и, следовательно, по сравнению с самим сигналом S(t). При этом формулу (2.29) удобно записать следующим образом:
причем

Возможно и преобразование соотношения (2.28) вида

Здесь
представляет собой функцию времени, называемую комплексной огибающей сигнала S(t). Модуль этой функции является обычной огибающей, а аргумент — мгновенной начальной фазой θ(t).

Комплексную огибающую можно также представить в виде

Здесь действительные функции времени (Формула) и (Формула) являются квадратурными составляющими комплексной огибающей или низкочастотными квадратурными составляющими. С их помощью сигнал можно представить в виде суммы:
что следует из выражений (2.34) и (2.37).

Учитывая «медленность» изменения функций (Формула) и (Формула) по сравнению с (Формула) и (Формула) из выражений (2.38) можно получить сопряженный сигнал:

Подставив выражения (2.38) и (2.39) в формулу (2.31), нетрудно убедиться, что Sm(t) — огибающая сигнала.

Схема, изображенная на рис. 2.17, иллюстрирует процесс формирования низкочастотных квадратурных составляющих сигнала.

Обратим особое внимание на следующее: нельзя путать понятия спектральных составляющих и мгновенной частоты, так как в первом случае частоты, входящие в спектр, не зависят от времени, а во втором — мгновенная частота есть функция времени, которая определяет скорость изменения фазы. Спектр сигнала можно измерить с помощью прибора — спектроанализатора, который выполняет приближенное преобразование Фурье. Мгновенная частота измеряется частотным детектором, работа которого будет рассмотрена далее, но по существу он реализует выражение (2.33).

Аналитические сигналы: огибающая, мгновенная фаза и мгновенная частота сигнала

Рис. 2.17. Схема формирования квадратурных составляющих узкополосного сигнала

Источник

Комплексный
сигнал можно представить в форме [6]:

(6.20)

где
называют
огибающей сигнала, (6.21)

а
мгновенной
фазой сигнала.

Здесь
s(t)
= A(t)∙cos
φ(t);
s*(t)
= A(t)∙
sin φ(t)

Функция
φ(t)
называется мгновенной фазой сигнала.

Производная
от мгновенной фазы сигнала по времени
называется мгновенной частотой сигнала:

(6.22)

Например,
для гармонического сигнала [6]:

В
общем случае мгновенная частота
изменяется во времени.

Из
(6.21) следует, что A(t)
≥ s(t),
причем равенство достигается в моменты
времени, когда s*(t)
= 0. В этих точках производная A(t)
совпадает с производной сигнала s(t):

(6.23)

Следовательно,
при s*(t)
= 0, огибающая A(t)
касается сигнала s(t).

Функция
cos(φ(t))
называется высокочастотным заполнением
сигнала.

Процесс
формирования сигнала на основе огибающей
A(t)
и фазы φ(t)
показан на рис. 6.6.

Рис.
6.6. Временное представление огибающей
и высокочастотного заполнения

Если
мгновенная частота колеблется вокруг
среднего значения ω_ср,
то можно записать:

(6.24)

где
Θ(t)
– называется мгновенной начальной
фазой сигнала.

Выражение
(6.24) удобно для описания узкополосных
сигналов. В этом случае основная часть
спектра амплитуд сосредоточена в
относительно узкой, по сравнению с A(t)
и φ(t),
полосе частот. При этом A(t)
и φ(t)
изменяются медленно по сравнению с
cos(ω_ср∙t).
Такие сигналы называются квазигармоническими.
У случайных сигналов и помех A(t),
φ(t),
ω(t),
ω_ср(t)
и Θ(t)
являются случайными функциями времени.

7. Корреляционная функция детерминированных сигналов

7.1. Автокорреляция вещественного сигнала

Греческое
слово «корреляция» обозначает связь
между различными процессами и явлениями.
Автокорреляцией называется согласование
сигнала s(t)
с собственной запаздывающей версией
s(t–τ).
Автокорреляционная функция (АКФ)
действительного вещественного сигнала
s(t)
конечной длительности определяется
следующим образом:

(7.1.)

Автокорреляционная
функция B_S(τ)
дает меру похожести сигнала с собственной
копией, смещенной на τ
единиц времени. Переменная τ
играет роль параметра сканирования или
поиска.

Если
сигнал s(t)
является периодическим с периодом Т₀,
то автокорреляционную функцию следует
выражать следующим образом:

(7.2)

Таким
образом, значение автокорреляционной
функции в нуле периодического сигнала
равно средней мощности сигнала.

Разделив
B_S(τ)
на B_S(0),
получим нормированную корреляционную
функцию, которая имеет обозначение
R_S(τ).

В
системах связи для передачи сигналов
широко используются видеоимпульсы
прямоугольной формы. Для таких сигналов
АКФ имеет вид

.
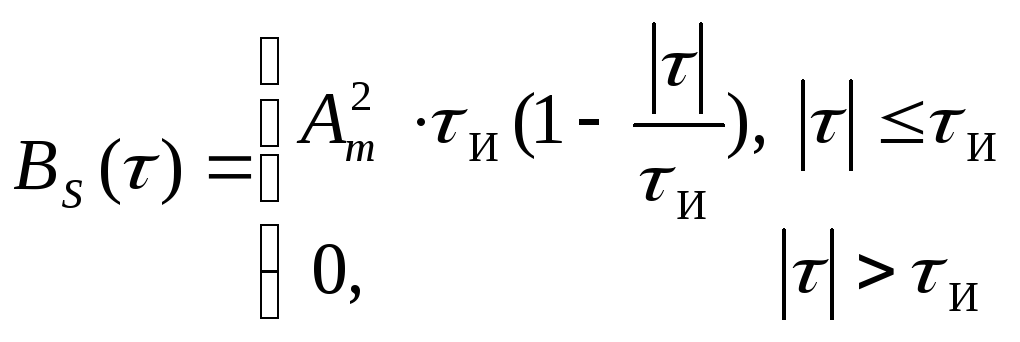(7.3)

Энергия
такого видеоимпульса равна

E_S=
A_m²
_И
(7.4)

Важным
параметром сигнала s(t)
является длительность его АКФ, называемая
интервалом корреляции τ_k.
Он определяется как отношение площади,
ограниченной АКФ сигнала s(t),
к энергии сигнала

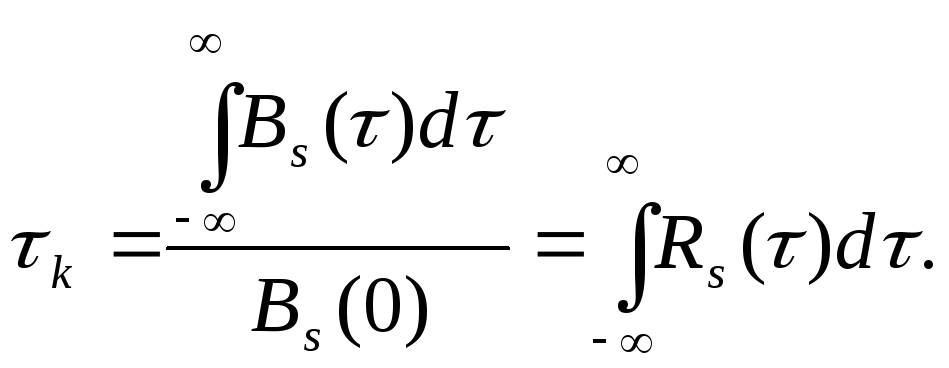
Свойства автокорреляционной функции вещественного сигнала:

1.
B_S(τ)
– четная; B_S(τ)
= B_S
(-τ)
(симметрия по τ
относительно 0);

2.
B_S(0)
– max;
,
т.е. в нуле равно энергии сигнала;

3.
B_S(τ)
≤ B_S(0),
корреляционная функция является
убывающей функцией модуля τ,
т. е.

4.– интервал корреляции случайного
процесса, характеризует ширину графика
функции корреляции:

||

_k
– то значения коррелированны,

||
> _k
– то значения не коррелированны.

R()
= В()
/ В(0)
– коэффициент корреляции, R()

1.

Процедура
нахождения АКФ представлена на рис.
7.1., где видно, что АКФ прямоугольного
видеосигнала является равнобедренным
треугольником, и ее длительность равна
удвоенной длительности импульса.

Если
же сигнал s(t)
задается в виде пачки n
импульсов, сдвинутых один относительно
другого на время Т,
то максимальное значение B_S(τ)
при τ
= 0 равно произведению энергии одного
импульса на количество импульсов (см.
рис. 7.2).

Рис.
7.1. Нахождение АКФ прямоугольного
видеоимпульса

Для
оценки степени связи между двумя
различными сигналами s₁(t)
и s₂(t)
используется взаимная корреляционная
функция (ВКФ) В₁₂(τ)

(7.5)

Рассмотренная
выше автокорреляционная функция B_S(τ)
является частным случаем функции В₁₂(τ),
когда s₁(t)
= s₂(t)
= s(t).

Необходимо
также отметить, что В₁₂(τ)
является асимметричной функцией
относительно оси ординат и не всегда
достигает максимума при τ
= 0.

Рис.
7.2. Автокорреляционная функция пачки
импульсов

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

To DRUID3:

А просто модуль отсчетов нельзя? Я так понял сигнал то real…

Про модуль отсчетов ничего не знаю:( Фильтр что ли? Но переделывать, если честно не хотелось бы, разве что, если действительно на много быстрее. Да и FFT использую заточенное под процеccор. Описание метода нашел тут: http://www.mathworks.com/products/demos/sh…ml?product=DS#2. Там описан еще один метод: возведение в квадрат и пропускание через НЧ фильтр, но он дает худший результат.

Уточните, у Вас научное или техническое задание? Т.е. строго найти огибающую или сделать приемлемый АМ детектор?

Это ТЗ, причем, кроме названия Envelope Analysis, в нем, по сути, ничего нет. Я это проинтерпретировал именно как выделение огибающей. Сигнал real.

У Вас довольно низкое отношение несущей(частоты заполнения) и максимальной частоты спектра огибающей, потому то метод так и “сбоит”…

Повысил частоту заполняющего сигнала, и действительно, метод начал давать хорошие результаты. Но все же, интересно, как бороться с неровностями по краям? Если решения не найдется, то прийдется юзать другой метод 🙁

To alex_os:

Не понял заклинание

Заклинание это смесь латеха с с++, вырвалось само собой) Там мнимая часть от неполного обратного преобразования Фурье с 1 по N/2 элемент (если положить, что все действительное БПФ лежит в массиве с индексами 0..N), удвоенная и деленная на частоту дискретизации.

Глюки и выбросы по краям неизбежны, ибо такова суть вещей. Посмотрите на формулу оригинального преобразования Гильберта там интеграл от минус бесконечности до плюс бесконечности….

Я тоже так подумал, но проблема в том, что увеличение размера преобразования не особо то повышает качество работы алгоритма.

Изменено 30 октября, 2008 пользователем iggylike

Источник

Современное состояние радиотехники характеризуется непрерывным совершенствованием способов передачи информации. Изыскиваются новые виды сигналов и новые способы их обработки.

Рассмотренные в предыдущих параграфах модулированные колебания являются лишь простейшими видами радиосигналов. Часто приходится иметь дело с радиосигналами, получаемыми в результате одновременной модуляции амплитуды и частоты (или фазы) колебания по очень сложному закону.

В любом случае предполагается, что заданный сигнал а представляет собой узкополосный процесс. Это означает, что все спектральные составляющие сигнала группируются в относительно узкой по сравнению с некоторой центральной частотой полосе.

При представлении подобных сигналов в форме

возникает неоднозначность в выборе функций , так как при любой функции всегда можно удовлетворить уравнению (3.57) надлежащим выбором функции

Так, простейшее (гармоническое) колебание

можно представить в форме

где

В выражении (3.58) огибающая в отличие от является функцией времени, которую можно определить из условия сохранения заданной функции

откуда

Из этого примера видно, что при нерациональном выборе вместо очень усложнилось выражение для , причем эта новая функция по существу не является «огибающей» в общепринятом смысле, так как она может пересекать кривую (вместо касания в точках, где имеет максимальное значение). Оперирование подобной «огибающей» не имеет смысла, а в некоторых случаях и недопустимо, так как может привести к ошибочным практическим выводам (например, при рассмотрении работы амплитудного детектора).

Неопределенности можно избежать при представлении и с помощью следующих соотношений:

где — новая функция, связанная с исходной соотношениями

Эти соотношения называются преобразованиями Гильберта, а функция — функцией, сопряженной (по Гильберту) исходной функции a(t).

Для выяснения смысла выражений (3.60), (3.61), а также требования, чтобы являлась функцией, сопряженной по Гильберту исходной функции , рассмотрим сначала некоторые свойства , вытекающие непосредственно из выражения (3.60) и справедливые при любой функции

Прежде всего мы видим, что в точках, где функция равна нулю, имеет место равенство .

Дифференцируя (3.60), получаем

Отсюда видно, что при когда , имеет место дополнительное равенство

Следовательно, в точках, в которых кривые имеют общие касательные.

Этих условий, однако, еще недостаточно для того, чтобы можно было рассматривать как «простейшую» огибающую быстро осциллирующей функции . Необходимо потребовать, чтобы кривая касалась кривой а в точках, в которых последняя имеет амплитудное или достаточно близкое к нему значение. Иными словами, в точках, где обращается в нуль, функция а должна принимать значения, близкие к амплитудным. Это условие как раз и обеспечивается, если функция является сопряженной по Гильберту функции . Это свойство преобразований Гильберта нагляднее всего иллюстрируется на примере гармонического сигнала.

Пусть . Найдем сопряженную функцию . Применяя общее выражение (3.62) и переходя к новой переменной находим

Известно, что

(в смысле главного значения) и

Следовательно, функции соответствует сопряженная функция которая проходит через нуль в моменты, когда исходная функция проходит через максимум. Аналогичным образом нетрудно убедиться, что функции соответствует сопряженная функция .

Подставляя в выражение (3.60), получаем для огибающей гармонического колебания общепринятое выражение

Аналогичный результат получается и для

Как видим, выражение (3.60) определяет огибающую в виде линии, касательной к исходной функции в точках ее максимума и в случае гармонического колебания соединяющей два соседних максимума кратчайшим путем. Таким образом, выражение (3.60) определяет «простейшую» огибающую. Это свойство выражения (3.60) сохраняется и для сложного сигнала, если выполняется условие медленности изменения огибающей, т. е. если речь идет об узкополосном сигнале [см. (3.2), (3.3)].

Если исходный сигнал представляет собой сумму спектральных составляющих

то сопряженная функция

Ряд (3.65) называется рядом, сопряженным ряду (3.64).

Если сигнал a(t) представлен не рядом (3.64), а интегралом Фурье

то функция может быть представлена в виде интеграла

сопряженного интегралу (3.66).

Нетрудно установить связь между спектрами функций Так как при преобразовании гармонического колебания по Гильберту его амплитуда остается неизменной, то очевидно, что по модулю спектральная плотность сопряженной функции не может отличаться от спектральной плотности исходной функции . Фазовая же характеристика спектра отличается от ФЧХ спектра . Из сопоставления выражений (3.66) и (3.67) непосредственно вытекает, что спектральные составляющие функции отстают по фазе на 90° от соответствующих составляющих функции . Следовательно, при спектральные плотности связаны соотношением

В области отрицательных частот соответственно получается

Вследствие изменения ФЧХ сопряженная функция по своей форме может сильно отличаться от исходной функции a(t).

После того как найдена сопряженная функция можно с помощью выражений (3.60), (3.61) найти огибающую , полную фазу и мгновенную частоту узкополосного сигнала

Выделив в найденной таким образом частоте постоянную часть можно написать выражение

в котором не содержит слагаемого, линейно зависящего от времени.

Тем самым устраняется произвол в выборе «средней частоты» сигнала и соответственно функции

В заключение следует отметить, что в некоторых случаях выражения (3.60)-(3.69) используют также и для широкополосных сигналов, когда понятие «огибающая амплитуд» теряет свой обычный смысл. При этом отказываются от требования, чтобы огибающая касалась кривой а вблизи точек, в которых имеет амплитудное значение.

Поясним применение преобразования Гильберта для определения огибающей, фазы и мгновенной частоты сигнала на следующем примере.

Пусть задан сигнал в виде суммы двух гармонических колебаний с близкими частотами

и требуется представить в форме

Расстройка полагается настолько малой по сравнению с что колебание можно считать узкополосным.

Что следует в данном случае подразумевать под и . Непосредственно из выражения (3.72) трудно выявить структуру огибающей и фазы результирующего колебания а(t). Используем поэтому выражения (3.60), (3.61). Сопряженная функция

Применяя формулу (3.60), находим огибающую сигнала

где причем для определенности считается, что .

Полную фазу суммарного колебания находим по формуле (3.61):

(3.75)

Применяя дадее формулу (3.70), после несложных алгебраических и тригонометрических преобразований приходим к следующему выражению для мгновенной частоты:

Так как постоянная составляющая функции равна нулю, то входящие в выражение (3.71) средняя частота и функция будут

(3.79)

Итак; на основании (3.74), (3.76) и (3.78), (3.79) выражение (3.73) приводится к

где определяется выражением (3.77).

При этом исключаются произвол и неопределенность в выборе огибающей и фазы суммарного колебания.

Графики функции характеризующие изменение частоты, приведены на рис. 3.24 для некоторых значений

Рис. 3.24. Мгновенная частота колебания, являющегося суммой двух гармонических колебаний

Рис. 3.25. Сумма двух гармонических колебаний с близкими частотами при одинаковых амплитудах

При при наложении слабого колебания сильное выражения (3.74)-(3.77) значительно упрощаются:

В этом случае огибающая, частота и фаза суммарного колебания изменяются по гармоническому закону с частотой относительно своих средних значений соответственно

При k = 1 функция в соответствии с (3.77) принимает постоянное значение

на всей оси времени, кроме точек , где . Эти выбросы соответствуют производным скачкообразно изменяющейся фазы при переходах огибающей биения через нуль.

Таким образом, в интервалах между указанными моментами частота суммарного колебания .

К этому результату можно прийти непосредственно из выражения (3.72), которое при подстановкой легко приводится к виду

График колебания при представлен на рис. 3.25.

Период функции равен причем в точках перехода через нуль эта функция, как отмечалось выше, меняет свой знак. Если не учитывать перемену знака, т. е. определять огибающую амплитуд функцией то период биений будет вдвое короче, как показано на рис. 3.25.

Поэтому частота биений равна .

Формулы (3.74)-(3.82) имеют большое прикладное значение, так как в физике и технике часто приходится иметь дело с биениями двух гармонических колебаний.

Источник

5. Узкополосные сигналы

5.1 Комплексная огибающая

В измерительных информационных системах и в различных системах передачи информации часто используются сигналы, спектр которых сосредоточен в узком диапазоне частот , ширина которого намного меньше среднего значения частоты (рис. 5.1). Сигнал, спектр которого соответствует рис. 5.1, расположен в полосе частот примерно от 1000 до 1400 Гц. Полоса частот, занимаемая сигналом, равна 400 Гц, среднее значение частоты составляет 1200 Гц

Подобные сигналы, имеющие форму почти гармонического колебания, у которого амплитуда и фаза изменяются во времени, и называются узкополосными сигналами (рис. 5.2). В каждый момент времени t значение такого сигнала x(t) можно рассматривать как значение некоторой придуманной для этого момента времени косинусоиды , амплитуда и начальная фаза которой различны для каждого момента времени t, а частота равна среднему значению из частотного диапазона сигнала. Такого рода узкополосный сигнал можно представить в виде выражения:

Переменная во времени амплитуда А(t) называется в этом случае амплитудной огибающей сигнала, начальная фаза φ(t) – фазовой функцией сигнала x(t), а весь аргумент косинуса – полной фазой сигнала:

Амплитудную огибающую А(t) в первом приближении можно представить себе в виде кривой, скользящей по вершинам сигнала. Фазовая функция не допускает такой простой интерпретации. По графику сигнала довольно просто восстановить форму амплитудной огибающей, но построить алгоритм выполнения этой процедуры достаточно сложно. В дальнейшем нашей задачей и будет построение алгоритма определения амплитудной огибающей и фазовой функции сигнала. Практически эта операция реализуется устройствами, которые называются амплитудными демодуляторами.

Представим узкополосное колебание в виде вещественной части комплексной экспоненты: