Данный калькулятор позволяет решать пределы любых функций онлайн.
Число b называется пределом функции f(x) при x→∞, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к b. Обозначается lim f(x)=b (x→∞).
|f(x)−b|<ε
Чтобы получить решение пределов, необходимо ввести, во первых, функцию, во вторых, число, к которому стремится x. В ответе показывается значение предела функции и график.
Калькулятор поможет найти пределы любых функций онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида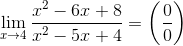 
(см. пример).
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида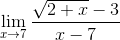 
5. Нахождение пределов, используя свойства первого замечательного предела 
, 
6. Нахождение пределов, используя свойства второго замечательного предела 
, 
, 
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число “пи” (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел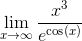 
запишем как x^3/exp(cos(x)). В качестве предела указываем infinity.
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 
= 
.
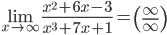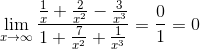2. 
= 
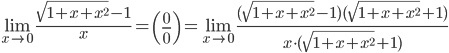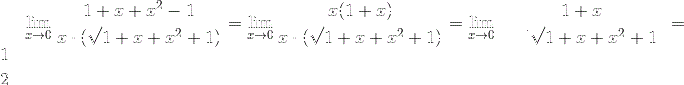
3. 
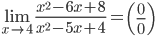. Так как числитель и знаменатель обратились в нуль при x=4, то 4 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-4). Получаем
.
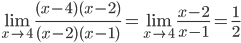4. 
.
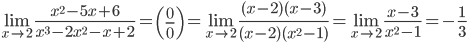5. 
= 
= 
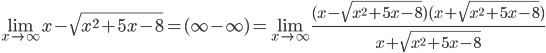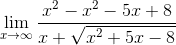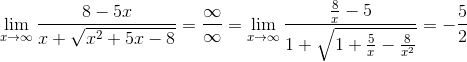
6. 
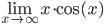– не существует, так как -1<cos(x)<1.
7. 
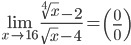. Обозначим 
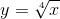, причем заметим, что при x→16, y→2. Получим:
.
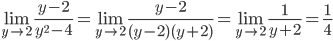8. 
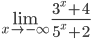. (Ответ получается непосредственно подстановкой (-∞) вместо x.)
9. 
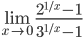. Здесь следует рассмотреть односторонние пределы:
; 
.
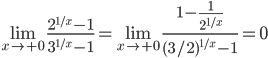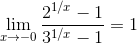Следовательно,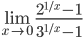 
– не существует (так как у функции разные односторонние пределы).
Найти пределы функции, не применяя правило Лопиталя.
а)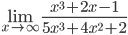
= 
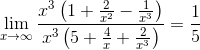
Ответ: 1/5
б)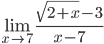 
= 
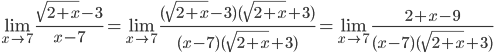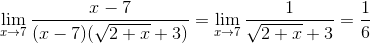
Ответ: 1/6
в)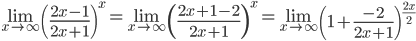 
= e-2/2 = e-1
Ответ: 1/e
г)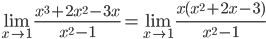 
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
, 
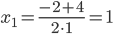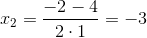
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
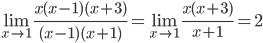
Ответ: 2
д)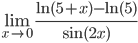 
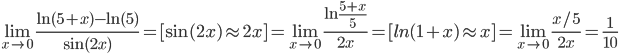
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Калькулятор симплекс-метода
Количество переменных:
Количество ограничений:
Очистить
Решить
В двойственную
Выполнено действий:
Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку “Решить”
Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 – 6·x2 – 8·x3 + x5 = -160
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Пример 2
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 – 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + 2·x5 = 30
Для ограничения с неравенством добавляем дополнительную переменную x6.
Перепишем ограничения в каноническом виде:
x1 – 2·x2 + 2·x3 + x6 = 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + 2·x5 = 30
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5, предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 |
1 2 |
-2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Пример 3
4·x1 + 5·x2 + 4·x3 → max
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 ≤ 200
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Перепишем ограничения в каноническом виде:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 + x5 = 200
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 |
1 2 |
1 | 0 | 0 | 40 |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | … | cn | 0 | 0 | … | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+k | b |
| xe1 | a11 | a12 | … | a1n | a1n+1 | a1n+2 | … | a1n+k | b1 |
| xe2 | a21 | a22 | … | a2n | a2n+1 | a2n+2 | … | a2n+k | b2 |
| … | … | … | … | … | … | … | … | … | … |
| xem | am1 | am2 | … | amn | amn+1 | amn+2 | … | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Пример 4
20·x1 + 20·x2 + 10·x3 → min
4·x1 + 3·x2 + 2·x3 ≥ 33
3·x1 + 2·x2 + x3 ≥ 23
x1 + x2 + 2·x3 ≥ 12
Меняем знаки у ограничений с ≥, путём умножения на -1:
-4·x1 – 3·x2 – 2·x3 ≤ -33
– 3·x1 – 2·x2 – x3 ≤ -23
– x1 – x2 – 2·x3 ≤ -12
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
– 4·x1 – 3·x2 – 2·x3 + x4 = -33
– 3·x1 – 2·x2 – x3 + x5 = -23
– x1 – x2 – 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Начальная симплекс-таблица
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x4 | -4 | -3 | -2 | 1 | 0 | 0 | -33 |
| x5 | -3 | -2 | -1 | 0 | 1 | 0 | -23 |
| x6 | -1 | -1 | -2 | 0 | 0 | 1 | -12 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-33| находится в первой строке.
Максимальный по модулю элемент в первой строке = -4 находится в первом столбце.
В качестве базисной переменной x4 берём x1.
Делим первую строку на -4. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в первом столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
3 4 |
1 2 |
–
1 4 |
0 | 0 |
33 4 |
| x5 | 0 |
1 4 |
1 2 |
–
3 4 |
1 | 0 |
7 4 |
| x6 | 0 | –
1 4 |
–
3 2 |
–
1 4 |
0 | 1 | –
15 4 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-
| находится в третьей строке.
Максимальный по модулю элемент в третьей строке = –
находится в третьем столбце.
В качестве базисной переменной x6 берём x3.
Делим третью строку на –
. Из первой и второй строк вычитаем третью, умноженную на соответствующий элемент в третьем столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
2 3 |
0 | –
1 3 |
0 |
1 3 |
7 |
| x5 | 0 |
1 6 |
0 | –
5 6 |
1 |
1 3 |
1 2 |
| x3 | 0 |
1 6 |
1 |
1 6 |
0 | –
2 3 |
5 2 |
Расчёт дельт
Дельты — это параметры, на основании которых проверяется оптимальность текущего решения и улучшается функция. Они рассчитываются для каждой из переменных ограничений и записываются последней строкой таблицы.
Для расчёта дельт используется следующая формула: Δi = ce1·a1i + ce2·a2i + … + cem·ami – ci. Проще говоря, чтобы вычислить дельту по заданной i-ой переменной, нужно перемножить коэффициенты условий в i-ом столбце на коэффициенты целевой функции при соответствующих базисных переменных, сложить эти произведения и вычесть из полученной суммы коэффициент целевой функции столбца i.
Пример 5
Таблица:
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | –
4 5 |
36 5 |
Вычисляем дельты: Δi = C2·a1i + C4·a2i + C5·a3i – Ci
Симплекс-таблица с дельтами
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | –
4 5 |
36 5 |
| Δ | -3 | 0 | -2 | 0 | 0 | 6 | 0 |
Проверка плана на оптимальность
После того как дельты рассчитаны, необходимо проверить оптимальность текущего плана. Критерий оптимальности формулируется следующим образом:
При максимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют отрицательные дельты.
При минимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют положительные дельты.
Пример 6
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 – 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + x5 = 30
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Критерий оптимальности: план оптимален, если в таблице отсутствуют отрицательные дельты.
План не оптимален, так как ищется максимум функции, а Δ1 = -2 отрицательна.
Если текущий план оптимален, то алгоритм завершает свою работу. Значениям переменных соответствуют значения столбца свободных коэффициентов b. Если свободной переменной нет в базисе, то её значение считается нулевым. Значение целевой функции, принимаемой на данном наборе, находится в строке с дельтами в том же столбце. Если какое-либо из значений столбца b отрицательно, то решения задачи не существует.
Переход к более оптимальному решению
Если текущий план оказался не оптимальным, то алгоритм ищет столбец с наименьшей (с наибольшей, если ищется минимум) дельтой. После чего вычисляются симплекс-отношения Q. Для этого значения свободных коэффициентов делятся на ненулевые коэффициенты из найденного столбца. Если результат деления получается отрицательным, то такие отношение игнорируются.
Среди найденных симплекс-отношений ищется строка, в которой находится симплекс-отношение с наименьшим значением. Если таких отношений нет, то алгоритм останавливает свою работу, так как целевая функция не ограничена и решения не существует.
Пример 7
Симплекс-таблица с дельтами
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Проверяем план на оптимальность: план не оптимален, так как ищется минимум функции, а Δ2 = 1 положительна.
Определяем разрешающий столбец – столбец, в котором находится максимальная дельта: 2, Δ2: 1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 | – |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 | – |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 | – |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Все значения второго столбца отрицательны. Функция не ограничена. Оптимальное решение отсутствует.
В противном случае строка с наименьшим отношением считается разрешающей и, аналогично избавлению от отрицательных свободных коэффициентов, делится на разрешающий элемент, расположенный в найденных столбце и строке, и из остальных строк вычитается найденная строка, разделённая на значения, стоящие в этом же столбце соответствующей строки. Переменная, стоящая в разрешающем столбце заменяет базисную переменную, находящуюся в найденной строке.
После этого вычисляются новые дельты и проверяется новый план. Так продолжается до тех пор пока не будет выполнен критерий оптимальности плана или не будет установлено, что решение не существует.
Пример 8
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -2 отрицательна.
Итерация 1
Определяем разрешающий столбец – столбец, в котором находится минимальная дельта: 3, Δ3: -9
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения третьего столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 3, строка 1.
На пересечении найденных строки и столбца находится разрешающий элемент: 2
В качестве базисной переменной x6 берём x3.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 | 1 | -2 | 2 | 0 | 0 | 1 | 6 | 6 / 2 = 3 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 | 24 / 1 = 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 | – |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Делим первую строку на 2. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в третьем столбце.
Вычисляем новые дельты: Δi = C3·a1i + C4·a2i + C5·a3i – Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | 3 |
| x4 |
1 2 |
3 | 0 | 1 | 0 | –
1 2 |
21 | 24 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | – |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Текущий план X: [ 0, 0, 3, 21, 42, 0 ]
Целевая функция F: 9·0 + 5·0 + 4·3 + 3·21 + 2·42 + 0·0 = 159
Проверяем план на оптимальность: план не оптимален, так как Δ2 = -6 отрицательна.
Итерация 2
Определяем разрешающий столбец – столбец, в котором находится минимальная дельта: 2, Δ2: -6
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 7, строка 2.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x4 берём x2.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | – |
| x2 |
1 2 |
3 | 0 | 1 | 0 | –
1 2 |
21 | 21 / 3 = 7 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | – |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Делим вторую строку на 3. Из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент во втором столбце.
Вычисляем новые дельты: Δi = C3·a1i + C2·a2i + C5·a3i – Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
2 3 |
0 | 1 |
1 3 |
0 |
1 3 |
10 | – |
| x2 |
1 6 |
1 | 0 |
1 3 |
0 | –
1 6 |
7 | 7 |
| x5 |
9 2 |
0 | 0 | 1 | 1 |
3 2 |
63 | – |
| Δ |
7 2 |
0 | 0 | 2 | 0 |
7 2 |
201 |
Текущий план X: [ 0, 7, 10, 0, 63, 0 ]
Целевая функция F: 9·0 + 5·7 + 4·10 + 3·0 + 2·63 + 0·0 = 201
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.
Ответ: x1 = 0, x2 = 7, x3 = 10, x4 = 0, x5 = 63, F = 201
Метод искусственного базиса
Очень часто при решении задачи линейной оптимизации бывает довольно сложно выполнять алгебраические преобразования над коэффициентами ограничений для поиска начального базиса. Для упрощения вычислений существует альтернативный метод решения, называемый методом искусственного базиса. Его суть заключается в том, что вместо того, чтобы искать базис среди имеющихся основных и дополнительных переменных, ввести так называемые искусственные переменные, которые сформируют начальный базис. Возможно, звучит сложно и непонятно, но сейчас мы всё объясним.
Подготовительный этап
Аналогично базовому симплекс-методу для всех ограничений с неравентством вводятся дополнительные переменные, причём для ограничений с ≥ они берутся с коэффициентом -1, а для ограничений с ≤ с коэффициентом 1. Ограничения с равенством остаются без изменений. Если свободный коэффициент какого-либо из ограничений меньше нуля, то такое ограничение умножается на -1 (знак неравенства при этом меняется на противоположный). После этого приступают к поиску базиса.
Пример 9
3·x1 + 2·x2 + 3·x3 → min
-2·x1 – x2 – x3 ≥ -2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Меняем знаки у ограничений с отрицательными свободными коэффициентами, путём умножения на -1:
2·x1 + x2 + x3 ≤ 2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство с ≥. Базисная переменная для этого ограничения будет определена позднее.
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 3 | 2 | 3 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 2 |
| ?1 | 3 | 8 | 2 | 0 | -1 | 8 |
| ?2 | 2 | 0 | 1 | 0 | 0 | 1 |
Формирование начального базиса
Для того, чтобы сформировать начальный базис в первую очередь можно поискать столбец, у которого одно значение равно единице, а все значения остальные значения равны нулю, и сделать соответствующую переменную базисной для этой строки. Однако такое случается довольно редко, поэтому проще сразу перейти к следующему пункту. Для всех ограничений, не имеющих базисной переменной, добавляем искусственную переменную с коэффициентом 1. В целевую функцию добавляем эту же переменную с коэффициентов -M, если ищется максимум или с коэффициентом M, если ищется минимум. M всего лишь является очень большим числом.
Пример 10
x1 – x2 → min
2·x1 + x2 = 1
x1 – 3·x2 + x3 = 3
x1 + 11·x2 = 11
Ограничение 1 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Столбец 3 является частью единичной матрицы. Переменная x3 входит в начальный базис
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 1 | -1 | 0 | 0 |
| базис | x1 | x2 | x3 | b |
|---|---|---|---|---|
| ?1 | 2 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 3 |
| ?3 | 1 | 11 | 0 | 11 |
Для ограничения 1 добавляем искусственную переменную u1 и делаем её базисной.
Для ограничения 3 добавляем искусственную переменную u2 и делаем её базисной.
В целевую функцию добавляем искусственные пременные с коэффициентом M, где M — очень большое число.
Таблица с искусственными переменными
| C | 1 | -1 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | u1 | u2 | b |
|---|---|---|---|---|---|---|
| u1 | 2 | 1 | 0 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 0 | 0 | 3 |
| u2 | 1 | 11 | 0 | 0 | 1 | 11 |
Перепишем условие задачи с учётом добавленных искусственных переменных:
F = 1x1 -1x2 + Mu1 + Mu2 → min
2·x1 + x2 + u1 = 1
x1 – 3·x2 + x3 = 3
x1 + 11·x2 + u2 = 11
Расчёт дельт и проверка плана на оптимальность
После того, как начальный базис сформирован необходимо вычислить дельты. Дельты вычисляются полностью аналогично базовому методу: Δi = ce1·a1i + ce2·a2i + … + cem·ami – ci. Единственным отличием будет тот факт, что результат может содержать значения с M. Когда дельты будут получены необходимо проверить текущий опорный план на оптимальность (см. проверку плана на оптимальность в базовом симплекс-методе). Если план оптимален, то алгоритм завершает свою работу, иначе формирует более оптимальное решение и повторяет процесс.
Пример 11
Таблица с искусственными переменными
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
Вычисляем дельты: Δi = C4·a1i + C7·a2i + C8·a3i – Ci
Δ1 = C4·a11 + C7·a21 + C8·a31 – C1 = 0·2 + M·3 + M·0 – 3 = -3 + 3M
Δ2 = C4·a12 + C7·a22 + C8·a32 – C2 = 0·1 + M·0 + M·0 – 2 = -2
Δ3 = C4·a13 + C7·a23 + C8·a33 – C3 = 0·1 + M·2 + M·1 – 3 = -3 + 3M
Δ4 = C4·a14 + C7·a24 + C8·a34 – C4 = 0·1 + M·0 + M·0 – 0 = 0
Δ5 = C4·a15 + C7·a25 + C8·a35 – C5 = 0·0 + M·(-1) + M·0 – 0 = -M
Δ6 = C4·a16 + C7·a26 + C8·a36 – C6 = 0·0 + M·0 + M·(-1) – 0 = -M
Δ7 = C4·a17 + C7·a27 + C8·a37 – C7 = 0·0 + M·1 + M·0 – M = 0
Δ8 = C4·a18 + C7·a28 + C8·a38 – C8 = 0·0 + M·0 + M·1 – M = 0
Δb = C4·b1 + C7·b2 + C8·b3 – C9 = 0·2 + M·3 + M·1 – 0 = 4M
Симплекс-таблица с дельтами
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| Δ | -3 + 3M | -2 | -3 + 3M | 0 | -M | -M | 0 | 0 | 4M |
Текущий план X: [ 0, 0, 0, 2, 0, 0, 3, 1 ]
Целевая функция F: 3·0 + 2·0 + 3·0 + 0·2 + 0·0 + 0·0 + M·3 + M·1 = 4M
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 + 3M положительна.
Предел функции при ( x to x_0 )
Пусть функция ( f(x) ) определена на некотором множестве (X) и пусть точка ( x_0 in X ) или ( x_0 notin X )
Возьмем из (X) последовательность точек, отличных от (x_0) :
(x_1 ;, ; x_2 ;, ; x_3 ;, …, ; x_n ; , ; … tag{1} )
сходящуюся к (x^*).
Значения функции в точках этой последовательности также образуют числовую последовательность
( f(x_1) ;, ; f(x_2) ;, ; f(x_3) ;, …, ; f(x_n) ; , ; … tag{2} )
и можно ставить вопрос о существовании ее предела.
Определение. Число (A) называется пределом функции (f(x)) в точке ( x = x_0 ) (или при ( x to x_0 ) ), если для
любой сходящейся к (x_0) последовательности (1) значений аргумента (x), отличных от (x_0) соответствующая
последовательность (2) значений функции сходится к числу (A).
Символически это записывается так:
$$ lim_{xto x_0}{ f(x)} = A $$
Функция (f(x)) может иметь в точке (x_0) только один предел. Это следует из того, что последовательность ( left{ f(x_n) right} )
имеет только один предел.
Существует другое определение предела функции.
Определение Число (A) называется пределом функции (f(x)) в точке (x_0), если для любого числа ( varepsilon > 0 )
существует число ( delta > 0 ) такое, что для всех ( x in X, ; x neq x_0 ), удовлетворяющих неравенству ( |x-x_0| < delta ),
выполняется неравенство ( |f(x)-A| < varepsilon )
Используя логические символы, это определение можно записать в виде
( (forall varepsilon > 0) (exists delta > 0) (forall x in X, ; x neq x_0, ; |x-x_0| < delta): |f(x)-A| < varepsilon )
Отметим, что неравенства ( x neq x_0, ; |x-x_0| < delta ) можно записать в виде ( 0 < |x-x_0| < delta )
<>Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением
«на языке последовательностей».
Второе определение называют определением «на языке ( varepsilon – delta )».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более
удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне,
а определение предела функции «на языке ( varepsilon – delta )» — определением предела функции по Коши.
Предел функции при ( x to x_{0-} ) и при ( x to x_{0+} )
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение Число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любой сходящейся
к (x_0) последовательности (1), элементы (x_n) которой больше (меньше) (x_0), соответствующая
последовательность (2) сходится к (A).
Символически это записывается так:
$$ lim_{x to x_{0+}} f(x) = A ; left( lim_{x to x_{0-}} f(x) = A right) $$
Можно дать равносильное определение односторонних пределов функции «на языке ( varepsilon – delta )»:
Определение число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любого
( varepsilon > 0 ) существует ( delta > 0 ) такое, что для всех (x), удовлетворяющих неравенствам
( x_0 < x < x_0 + delta ; (x_0 -delta < x < x_0 ) ) , выполняется неравенство ( |f(x)-A| < varepsilon ).
Символические записи:
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 < x < x_0 + delta ): |f(x)-A| < varepsilon )
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 -delta < x < x_0 ): |f(x)-A| < varepsilon )
Связь между односторонними пределами и пределом функции устанавливает следующая теорема.
Теорема
Функция (f(x)) имеет в точке (x_0) предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы,
и они равны. В этом случае предел функции равен односторонним пределам.
Предел функции при ( x to infty ), при ( x to -infty ) и при ( x to +infty )
Кроме рассмотренных понятий предела функции при ( x to x_0 ) и односторонних пределов существует также понятие предела функции
при стремлении аргумента к бесконечности.
Определение. Число (A) называется пределом функции (f(x)) при ( x to infty ), если для любой бесконечно большой
последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к (A).
Символическая запись:
$$ lim_{x to infty} f(x) = A $$
Определение. Число (A) называется пределом функции (f(x)) при ( x to +infty ; (x to -infty) ) , если для любой бесконечно
большой последовательности значений аргумента, элементы (x_n) которой положительны (отрицательны), соответствующая
последовательность значений функции сходится к (A).
Символическая запись:
$$ lim_{x to +infty} f(x) = A ; left( lim_{x to -infty} f(x) = A right) $$
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах
последовательностей на функции. Покажем это на примере двух теорем.
Теорема. Пусть функции (f(x)) и (g(x)) имеют в точке (x_0) пределы (B) и (C). Тогда функции ( f(x) pm g(x) ; , ; f(x) cdot g(x) ) и
( frac{f(x)}{g(x)} ) (при ( C neq 0 ) ) имеют в точке (x_0) пределы, равные соответственно ( B pm C ; , ; B cdot C ), и ( frac{B}{C} ).
Теорема. Пусть функции ( f(x) ; , ; g(x) ) и ( h(x) ) определены в некоторой окрестности точки (x_0), за исключением, быть
может, самой точки (x_0), и функции ( f(x) ; , ; h(x) ) имеют в точке (x_0) предел, равный (A), т.е.
$$ lim_{x to x_0} f(x) = lim_{x to x_0} h(x) = A $$
Пусть, кроме того, выполняются неравенства ( f(x) leqslant g(x) leqslant h(x) ).
Тогда $$ lim_{x to x_0} g(x) = A $$
Теорема Лопиталя. Если $$ lim_{x to x_0} f(x) = lim_{x to x_0} g(x) = 0 $$ или (infty ), (f(x)) и (g(x))
дифференцируемы в окрестности (x_0) , и ( g'(x) neq 0 ) в окрестности (x_0) ,
и существует $$ lim_{x to x_0} frac{f'(x)}{g'(x)} $$ то существует $$ lim_{x to x_0} frac{f(x)}{g(x)} = lim_{x to x_0} frac{f'(x)}{g'(x)} $$
Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида ( frac{0}{0} ) и ( frac{infty}{infty} ).
Первый замечательный предел
$$ lim_{x to 0} frac{sin x}{x} = 1 $$
Второй замечательный предел
$$ lim_{x to infty} left( 1+ frac{1}{x} right)^x = e $$
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
lim_{xto 3}(frac{5x^2-8x-13}{x^2-5})
-
lim_{xto 2}(frac{x^2-4}{x-2})
-
lim_{xto infty}(2x^4-x^2-8x)
-
lim _{xto :0}(frac{sin (x)}{x})
-
lim_{xto 0}(xln(x))
-
lim _{xto infty :}(frac{sin (x)}{x})
-
lim_{(x,y)to (3,3)}(frac{x-y}{sqrt{x}-sqrt{y}})
-
lim_{(x,y)to (0,0)}(frac{3x^{3}y}{x^{4}+y^{4}})
- Показать больше
Описание
Поэтапное вычисление пределов
limit-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Limits Calculator, Infinite limits
In the previous post we covered substitution, where the limit is simply the function value at the point. But what…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
