Пусть
a и b—дейсвительнее числа,причем a<b.
Числовыми
промежутками (интервалами)
называют подмножества всех действительных
чисел, имеющих следующий вид:
[a;
b] = {х : α ≤ х ≤ b} — отрезок (сегмент,
замкнутый промежуток);
(a; ) = {х : а <
х < b} — интервал (открытый промежуток);
[a;b)
= {х : а ≤ х < b};
(a; b] = {х : а < х ≤ b} —
полуоткрытые интервалы (или полуоткрытые
отрезки);
(-∞; b] = {х : х ≤
b};
[α, +∞) = {х : х ≥ α};
(-∞; b) = {х : х
<b};
(а, +∞) = {х : х > а};
(-∞, ∞) = {х : -∞<х<+∞}
= R — бесконечные интервалы (промежутки).
Числа
a и b называются соответственно левым и
правым концами этих промежутков. Символы
-∞ и +∞ не числа, это символическое
обозначение процесса неограниченного
удаления точек числовой оси от начала
0 влево и вправо.
Пусть
хо—любое
действительное число (точка на числовой
прямой). Окрестностью точки хо называется
любой интервал (a; b), содержащий точку
x0. В частности, интервал (хо-ε,хо+ε),
где ε >0, называется ε-окрестностью
точки хо.
Число хо называется
центром.

Если
хÎ(х0-ε;
х0 +ε),
то выполняется неравенство x0-ε<х<х 0+ε,
или, что то же, |х-х о|<ε.
Выполнение последнего неравенства
означает попадание точки х в ε -окрестность
точки хо (см.
рис. 97).
§ 14. Функция
14.1. Понятие функции.
Одним
из основных математических понятий
является понятие функции. Понятие
функции связано с установлением
зависимости (связи) между элементами
двух множеств.
Пусть
даны два непустых множества X и Y.
Соответствие ƒ, которое каждому элементу
хÎ X сопоставляет один и только один
элемент уÎ Y, называется функцией и
записывается у=ƒ(х), хÎ X или ƒ: X→Y.
Говорят еще, что функция ƒ отображает
множество X на множество Y.

Например,
соответствия ƒ и g, изображенные на
рисунке 98 а и б, являются функциями, а
на рисунке 98 в и г — нет. В случае в — не
каждому элементу хÎX соответствует
элемент уÎY. В случае г не соблюдается
условие однозначности.
Множество
X называется областью определения
функции ƒ и обозначается D(f). Множество
всех уÎY называется множеством значений
функции ƒ и обозначается Е(ƒ).
14.2 Числовые функции. График функции. Способы задания функций
Пусть
задана функция ƒ : X→Y.
Если
элементами множеств X и Y являются
действительные числа (т. е. XÌ R и YÌ R),
то функцию ƒ называют числовой функцией.
В дальнейшем будем изучать (как правило)
числовые функции, для краткости будем
именовать их просто функциями и записывать
у=ƒ(х).
Переменная
х называется при этом аргументом или
независимой переменной, а у — функцией
или зависимой переменной (от х).
Относительно самих величин х и у говорят,
что они находятся в функциональной
зависимости. Иногда функциональную
зависимость у от х пишут в виде у=у(х),
не вводя новой буквы (ƒ) для обозначения
зависимости.
Частное
значение функции
ƒ(х) при х=a записывают так: ƒ(a). Например,
если ƒ(х)=2х2-3,
то ƒ(0)=-3, ƒ(2)=5.
Графиком
функции у=(х)
называется множество всех точек плоскости
Оху, для каждой на которых х является
значением аргумента, а у — соответствующим
значением функции.
Например,
графиком функции у=√(1-х2) является
верхняя полуокружность радиуса R=1 с
центром в О(0;0) (см. рис. 99).

Чтобы
задать функцию у=ƒ(х), необходимо указать
правило, позволяющее, зная х, находить
соответствующее значение у.
Наиболее
часто встречаются три способа задания
функции: аналитический, табличный,
графический.
Аналитический
способ:
функция задается в виде одной или
нескольких формул или уравнений.

Если
область определения функции у = ƒ(х) не
указана, то предполагается, что она
совпадает с множеством всех значений
аргумента, при которых соответствующая
формула имеет смысл.Так, областью
определения функции у= √(1-х2) является
отрезок [-1; 1].
Аналитический
способ задания функции является наиболее
совершенным, так как к нему приложены
методы математического анализа,
позволяющие полностью исследовать
функцию у=ƒ(х).
Графический
способ: задается график функции.
Часто
графики вычерчиваются автоматически
самопишущими приборами или изображаются
на экране дисплея. Значения функции у,
соответствующие тем или иным значениям
аргумента х, непосредственно находятся
из этого графика.
Преимуществом
графического задания является его
наглядность, недостатком — его неточность.
Табличный
способ: функция задается таблицей ряда
значений аргумента и соответствующих
значений функции. Например, известные
таблицы значений тригонометрических
функций, логарифмические таблицы.
На
практике часто приходится пользоваться
таблицами значений функций, полученных
опытным путем или в результате наблюдений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обновлено: 23.05.2023
В предыдущей главе мы обсудили, как устроены особые точки линейных систем на плоскости. Но что мы будем делать, если нам встретится нелинейное уравнение?
11.1 Линеаризация особой точки
Пусть точка z ∗ = ( x ∗ , y ∗ ) является положением равновесия, то есть особой точкой нашей системы. В этом случае f ( x ∗ , y ∗ ) = 0 и g ( x ∗ , y ∗ ) = 0 . Чтобы не писать каждый раз две переменные, введём векторные обозначения: z = ( x , y ) и F ( z ) = ( f ( z ) , g ( z ) ) . Система принимает вид
Мы предполагаем, что функции f и g по крайней мере C 1 -гладкие (то есть имеют непрерывные частные производные) и значит отображение F является дифференцируемым. Из определения производной для функции нескольких переменных следует, что
Здесь ∂ F ∂ z — матрица Якоби для отображения F , то есть матрица, составленная из частных производных функций f и g . Обозначим эту матрицу через A :
Сделаем замену переменных: w = ( u , v ) = z − z ∗ = ( x − x ∗ , y − y ∗ ) . Таким образом мы перенесли особую точку в начало координат. Соотношение (11.3) принимает вид
Как связаны решения нелинейной системы с решениями её линеаризации в окрестности особой точки? Отброшенное при переходе к линеаризации слагаемое является очень маленьким, и чем ближе мы к особой точке, тем оно меньше. Можем ли мы им пренебречь, если нас интересует поведение системы вблизи особой точки, по крайней мере, на каком-то качественном уровне? Оказывается, ответ зависит от типа получившейся линейной особой точки.
11.2 Свойства нелинейных особых точек
Говорят, что нелинейная особая точка является, например, центром по линейным членам, если её линеаризация является центром. Аналогично с другими типами особых точек.
11.2.1 Невырожденный узел
Фазовые портреты линейных узлов выглядят по-разному в зависимости от типа узла. Если узел невырожденный, то есть собственные значения различны и существуют два разных собственных вектора, то почти все траектории стремятся к особой точке (в прямом или обратном времени), касаясь того собственного вектора, чьё собственное значение меньше по модулю. Фазовые кривые похожи на ветви парабол. Исключение составляют траектории с начальными условиями, лежащими на том собственном векторе, у которого собственное значение больше по модулю.
Например, у системы
собственные векторы — ( 1 , 0 ) с собственным значением 1 и ( 0 , 1 ) с собственным значением 2. Решением является вектор-функция, задаваемая компонентами x ( t ) = x 0 e t , y ( t ) = y 0 e 2 t . При x 0 ≠ 0 траектория лежит на параболе
и стремится к началу координат в обратном времени (при t → − ∞ ), касаясь горизонтального направления (то есть направления собственного вектора с меньшим по модулю собственным значением). Исключением являются траектории с x 0 = 0 : они стремятся к нулю вдоль вертикального направления (то есть вдоль собственного вектора с большим собственным значением).
Теорема 1. Вблизи нелинейной особой точки, являющейся невырожденным узлом по линейным членам, почти все фазовые кривые стремятся к особой точке, касаясь собственного вектора с меньшим по модулю собственным значением. Исключением является сама особая точка и ещё две специальные траектории, касающиеся другого собственного вектора.
Эту и следующие теоремы можно было бы вывести из так называемой теории нормальных форм, но это выходит за рамки нашего курса. Поэтому мы ограничимся примерами.
вблизи особой точки ( 0 , 0 ) . Её линеаризация в этой точке имеет матрицу из примера 1 предыдущей главы.
Собственные значения 1 и 5 , собственные векторы ( − 3 , 1 ) и ( 1 , 1 ) . На рис. 11.1 видно, что почти все отмеченные траектории касаются вектора ( − 3 , 1 ) .
Рис. 11.1: Фазовые портреты нелинейного узла (слева) и его линеаризации (справа) в малой окрестности особой точки ( 0 , 0 ) .
Заметим, что фазовые портреты похожи только в небольшой окрестности особой точки. Если мы удаляемся от особой точки, то нелинейные слагаемые начинают играть всё большую роль, и фазовые портреты сильно различаются, см. рис. 11.2 .
Рис. 11.2: Фазовые портреты нелинейной системы (справа) и её линеаризации (слева) в большой окрестности начала координат
11.2.2 Дикритический узел: скалярная матрица
Если собственные значения совпадают и матрица линеаризации является скалярной (то есть тождественной умноженной на число), то все фазовые траектории (кроме особой точки) — лучи прямых, каждая стремится к особой точке под собственным углом. Для соответствующей нелинейной системы траектории не обязаны быть лучами прямых, но характеристическое свойство — стремиться к особой точке под своим собственным углом — у них сохраняется.
Теорема 2. Вблизи нелинейной особой точки, являющейся дикритическим узлом по линейным членам, все траектории (кроме самой особой точки) стремятся к особой точке, каждая под своим собственным углом. Для всякого ненулевого вектора, приложенного к началу координат, существует единственная траектория, касающееся этого вектора при t → + ∞ или t → − ∞ .
11.2.3 Вырожденный узел: жорданова клетка
Если собственные значения совпадают, но матрица не является скалярной, то она в некотором базисе является жордановой клеткой. У неё есть единственный собственный вектор и все траектории такой системы, кроме особой точки, стремятся к особой точке, касаясь этого собственного вектора.
Теорема 3. Вблизи нелинейной особой точки, являющейся вырожденным узлом по линейным членам, все траектории (кроме самой особой точки) стремятся к особой точке, касаясь единственного собственного вектора матрицы линеаризации.
Рис. 11.4: Нелинейный вырожденный узел (слева) и его линеаризация (справа) в малой окрестности особой точки.
11.2.4 Фокус
В отличие от узлов, траектории фокусов стремятся к особой точке, не касаясь какого-то направления, а совершая бесконечное число оборотов вокруг особой точки. Аналогичное утверждение справедливо и для соответствующих нелинейных систем.
Теорема 4. Вблизи нелинейной особой точки, являющейся фокусом по линейным членам, все траектории (кроме самой особой точки) являются спиралями, совершающими бесконечное число оборотов при при t → + ∞ или t → − ∞ .
11.2.5 Седло
У сёдел есть два вещественных собственных значения разных знаков и, соответственно, два собственных вектора. Их фазовые кривые — ветви гипербол, кроме самой особой точки и четырёх прямолинейных лучей, называющихся сепаратрисами. Две сепаратрисы стремятся к седлу при t → + ∞ вдоль собственного вектора с отрицательным собственным значениям (такие сепаратрисы называются входящими), две другие сепаратрисы стремятся к седлу при t → − ∞ вдоль собственного вектора с положительным собственным значением (это исходящие сепаратрисы).
Например, для простейшего случая
входящие сепаратрисы — лучи x = 0 , y > 0 и x = 0 , y 0 , а исходящие — лучи x > 0 , y = 0 и x 0 , y = 0 .
У соответствующей нелинейной особой точки также существуют сепаратрисы. Они не обязаны быть прямыми, но обязаны касаться собственных векторов.
Теорема 5. Вблизи нелинейной особой точки, являющейся седлом по линейным членам, существуют две траектории, стремящиеся к особой точке при t → + ∞ , касаясь собственного вектора с отрицательным собственным значением, и ещё две траектории, стремящиеся к особой точке при t → − ∞ , касаясь собственного вектора с положительным собственным значением. Эти траектории называются сепаратрисами нелинейного седла.
Это — знаменитая теорема Адамара — Перрона, первый результат так называемой гиперболической динамики.
Рис. 11.5: Фазовый портрет нелинейного седла (слева) и его линеаризации (справа). Зелёным выделены входящие сепаратрисы, красным исходящие.
11.2.6 Центр
Чтобы построить фазовый портрет системы, перейдём в полярные координаты. Нам будет проще работать не с полярным радиусом, а с его квадратом: ρ = x 2 + y 2 . Вычислим производную функции ρ вдоль векторного поля, заданного системой (11.7) :
˙ ρ = 2 x ˙ x + 2 y ˙ y = 2 x ( y − ( x 2 + y 2 ) x ) + 2 y ( − x − ( x 2 − y 2 ) y ) = − ( x 2 + y 2 ) 2 = ρ 2 .
Решение этого уравнения можно найти явно, но нам достаточно того факта, что правая часть всегда отрицательна (кроме точки ρ = 0 ) и следовательно ρ будет монотонно убывать. То есть траектория будет приближаться к началу координат.
Можно также найти уравнение на полярный угол θ = arctan ( y / x ) . Напоминим, что ( arctan z ) ′ = 1 / ( 1 + z 2 ) . Значит по теореме о производной сложной функции: ˙ θ = ˙ y x − ˙ x y x 2 ⋅ 1 1 + y 2 x 2 = = ( − x − ( x 2 + y 2 ) y ) x − ( y − ( x 2 + y 2 ) x ) y x 2 + y 2 = − x 2 − y 2 x 2 + y 2 = − 1 Уравнение на θ имеет вид
Таким образом, двигаясь по траектории, точка приближается к началу координат, при этом её полярный угол равномерно уменьшается. Значит, эта траектория — спираль, наматывающаяся на особую точку, см. рис. 11.6 .
Такая особая точка похожа на фокус, хотя её линеаризация является центром. Она называется медленным фокусом.
11.3 Пример исследования нелинейной особой точки
Из первого уравнения мгновенно следует, что x = ± 2 . Подставляя эти значения для x во второе уравнение находим y и видим, что у системы есть две особые точки: ( 2 , − 3 ) и ( − 2 , 1 ) . Матрица Якоби имеет вид:
Эта матрица нижнетреугольная и значит её собственные значения стоят на диагонали. Они равны 1 / 3 и 1 . Следовательно соответствующая особая точка является неустойчивым узлом.
Собственные векторы равны ( − 2 , 3 ) и ( 0 , 1 ) . Первый из них имеет меньшее собственное значение, поэтому почти все траектории будут его касаться, стремясь к особой точке в обратном времени.
Неверный ответ. А вот и нет
Неверный ответ. Нет, не фокус
Неверный ответ. Нет.
Верный ответ. Да! Собственные значения − 1 / 3 и 1 . А фазовый портрет в целом выглядит вот так.
Замечание 1. Представленный способ анализа нелинейных особых точек работает только в том случае, когда линаризация имеет невырожденную матрицу. Особые точки, матрица линеаризации которых вырождена, то есть имеет нулевые собственные значения, могут иметь более сложные фазовые портреты. Существуют математические методы, которые позволяют исследовать и их тоже, но обсуждение этих методов выходит за рамки нашего курса.
Пример 3. В качестве примера приведём фазовые портреты двух систем с нулевой линеаризацией, см. рис. 11.8 . ˙ x = x 2 − y 2 , ˙ y = − 2 x y ; ˙ x = x 2 − y 2 , ˙ y = 2 x y . (11.11) (11.12)
Упражнение 1. Вы можете найти уравнения фазовых кривых для этих систем с помощью перехода к неавтономному уравнению (как обсуждалось в разделе 4.4 ) и замены z = y / x .
Замечание 2. С помощью линеаризации можно понять, как выглядит фазовый портрет вблизи каждой из особых точек, но получить надежную информацию о том, что происходит между ними, как ведут себя траектории, выходя из этих окрестностей, и как выглядит глобальная картинка мы не можем. В общем случае точное построение фазового портрета нелинейной системы является исследовательской задачей, не имеющей универсального решения. Однако на практике можно получить приближенные решения и слелать какие-то выводы с помощью численных методов.
11.4 Выводы
Фазовые портреты нелинейных систем на плоскости можно исследовать, переходя к линеаризации. Для этого надо вычислить матрицу Якоби правой части системы в особой точке — она и будет матрицей линеаризованной системы. Если линеаризация имеет особую точку типа узел, фокус или седло, фазовый портрет исходной (нелинейной) системы в окрестности особой точки похож на фазовый портрет линеаризации. Для центров это неверно: центры по линейным членам могут выглядеть как фокусы. К особым точкам с вырожденной матрицей линеаризации этот метод неприменим.
Дифференциальные уравнения на плоскости изучены относительно неплохо: хотя нахождение точных решенений конкретного уравнения может составлять сложную (или даже нерешенную) проблему, в целом человечество понимает, какие эффекты в этом мире встречаются и чего от таких уравнений можно ждать. Переход к пространствам больших размерностей принципиально усложняет динамику: мы далеки от полного понимания нелинейных уравнений уже с трёхмерным фазовым пространством. Однако линейные системы в любой размерности анализируются сравнительно несложно. Ими мы и займёмся в следующей главе.
Рассмотрим некоторую поверхность [плоскую кривую определяемую в заданной декартовой прямоугольной системе координат уравнением Относительно функции предположим, что она имеет непрерывные частные производные первого порядка по всем аргументам всюду в некоторой окрестности любой точки поверхности [кривой Будем называть данную точку поверхности [кривой ] особой, если в этой точке обращаются в нуль все частные производные первого порядка функции ]. В окрестности особой точки нельзя применить к уравнению теорему 13.1, т. е. нельзя утверждать, что это уравнение разрешимо хотя бы относительно, одной из переменных Таким образом, участок поверхности [кривой ], прилегающей к особой точке, может не допускать однозначного проектирования ни на одну из координатных плоскостей [ни на одну из осей координат]. Структура поверхности [кривой в окрестности особой точки
может быть сложной и требует дополнительного исследования.
Точки поверхности [кривой ], не являющиеся особыми, принято называть обыкновенными. В окрестности обыкновенной точки действует теорема 13.1, так что прилегающий к обыкновенной точке участок поверхности [кривой ] допускает однозначное проектирование хотя бы на одну из координатных плоскостей [хотя бы на одну из осей координат], что существенно облегчает – исследование этого участка.
Примеры. 1) Найти особые точки кругового конуса
Единственной особой точкой является начало координат. Хорошо известно, что в окрестности этой точки поверхность конуса не может быть однозначно спроектирована ни на одну из координатных плоскостей (рис. 13.3).
2) Найдем особые точки плоской кривой Так как то обе частные обращаются в нуль в двух точках (0,0) и Из этих двух точек только первая принадлежит рассматриваемой кривой, т. е. является особой. Построив кривую в окрестности точки (0, 0), мы убедимся в том, что эта точка является точкой самопересечения графика (рис. 13.4). Ясно, что в окрестности этой точки кривую нельзя однозначно спроектировать ни на ось ни на ось

Если буквально следовать определению, то для построения графика некоторой функции нужно найти в с е пары соответствующих значений аргумента и функции и построить все точки с этими координатами. В большинстве случаев это сделать практически невозможно, так как таких точек бесконечно много. Поэтому обычно исследуют функцию, что даёт возможность найти область определения и область изменения функции, области её убывания или возрастания, асимптоты, интервалы знакопостоянства и т. д.; находят несколько точек, принадлежащих графику, и соединяют их плавной кривой. Однако при построении графиков многих функций часто можно избежать проведение подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика. Изложению именно таких методов и посвящается эта статья, которая может служить практическим руководством при построении графиков многих функций.
1.1. Перенос (сдвиг) вдоль оси ординат
Пусть требуется построить график функции y=f(x)+b. Нетрудно заметить, что ординаты этого графика для всех значений аргумента на b единиц больше соответствующих ординат графика y=f(x) при b>0 и на b единиц меньше при b 0 или вниз при b 0 и на b единиц вверх, если b 0 или вправо на a единиц при a 0 или на a единиц влево при a 0 исходная функция имеет вид y=. График функции y= в области отрицательных значений x получаем отражением относительно оси ординат (рис.11).
Для нечётной функции y=f(x) в области всех значений аргумента справедливо равенство f(-x)= — f(x). Таким образом, в области отрицательных значений аргумента ординаты графика нечётной функции равны по величине, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях x. График нечётной функции симметричен относительно начала координат.
Для построения графика нечётной функции y=f(x) следует строить ветвь графика этой функции только в области положительных значений аргумента (x).
График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений x относительно оси абсцисс.
Пример 9. Построить график функции y=x.
Р е ш е н и е: Исходная функция является нечётной, поэтому строим её в области положительных значений аргумента (x), где она имеет вид y=x2. График функции y=x в области отрицательных значений аргумента получаем отражением построенной ветви относительно начала координат (рис.12).
Пример 10. Построить график функции y= .
Р е ш е н и е: Данная функция является нечётной, поэтому строим её график лишь в области x>0 (точка x=0 не входит в область определения функции), где она имеет вид y=1. Ветвь графика данной функции при x 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в A раз больше ординат графика функции y=f(x) при A>1 или в раз меньше ординат графика функции y=f(x) при A 1 (произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в раз при A 0. Рассмотрим функцию y=f(x), которая в произвольной точке x=x1 принимает значение y1=f(x1).
Очевидно, что функция y=f(wx) принимает такое же значение в точке x=x2, координата
которой определяется равенством x1=wx2, или x2=, причём это равенство справедливо для совокупности всех значений x из области определения функции. Следовательно, график функции y=f(wx) оказывается сжатым (при w>1) или растянутым (при w 1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в раз при w
Построение графиков функций
Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она. мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Темы для повторения:
1. Построим график функции
Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.
Упростим формулу функции:
График функции — прямая с выколотой точкой

2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.
3. Построим график функции
Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции
Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:
Действуем по порядку:
1) График функции y=sinx сдвинем на влево;
2) сожмем в 2 раза по горизонтали,
3) растянем в 3 раза по вертикали,
4) сдвинем на 1 вверх

5. Построим график функции
Область определения функции:
Промежутки знакопостоянства функции определим с помощью метода интервалов.

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.
Раскроем скобки в формуле функции:
Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции
Это дробно-рациональная функция.
Область определения функции
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.
Вот эскиз графика:

Еще один интересный прием — сложение графиков.
7. Построим график функции
Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте
Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!
8. Построим график функции
Область определения этой функции — положительные числа, поскольку только для положительных x определен
Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при
При значение cos x равно единице. Значение функции в этих точках будет равно при

9. Построим график функции
Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.
Нули функции — в точках, где то есть при при
Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
10. Построим график функции
Область определения функции — все действительные числа, поскольку
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.
Если x стремится к бесконечности, то стремится к нулю.
Найдем производную функции
По формуле производной частного,
Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1. Область определения функции
2. Область значений функции
3. Четность — нечетность (если есть)
4. Периодичность (если есть)
5. Нули функции (точки, в которых график пересекает оси координат)
6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).
7. Асимптоты (если есть).
8. Поведение функции в бесконечности
9. Производная функции
10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.
1. Построение графиков функций
Теория:
Построение графиков любых функций выполняется по точкам. Однако не всегда заранее мы знаем как выглядит график. В этих случаях выделяют особо значимые точки графика, которые и задают его вид.
К особо значимым точкам графика функции y = f ( x ) относят:
— стационарные и критические точки;
— точки пересечения графика с осью (x) (нули функции) и с осью (y);
— точки разрыва функции.
Таким образом, для построения сложной функции сначала нужно исследовать свойства этой функции, найти важные её точки и уже потом по этим точкам строить график.
Существует чёткий план исследования свойств функции, позволяющий определить поведение функции на области определения и построить её график.
1) Когда функция y = f ( x ) непрерывна на всей числовой прямой, тогда определяют точки пересечения графика с осями координат, стационарные и критические точки, точки экстремума, промежутки монотонности и несколько контрольных точек, если это необходимо.
2) Когда функция y = f ( x ) определена не на всей числовой прямой, тогда в первую очередь находят область определения функции и точки разрыва.
3) Проверяют функцию на чётность, т. к. график чётной функции симметричен относительно оси (y) и график нечётной функций симметричен относительно начала координат. Значит, можно построить только ветвь графика при (x>0), а затем симметрично её отобразить.
4) Если lim x → ∞ f ( x ) = b , то, прямая (y=b) является горизонтальной асимптотой графика функции y = f ( x ) .
5) Прямая (x=a) является вертикальной асимптотой графика функции y = f ( x ) , если y → ∞ при x → a .
построить график функции y = x 2 + 4 x 2 − 4 .
Решение 1. Обозначим: f ( x ) = x 2 + 4 x 2 − 4 . Область определения этой функции: D ( f ) = ( − ∞ ; − 2 ) ∪ ( − 2 ; 2 ) ∪ ( 2 ; + ∞ ) , так как x ≠ 2, x ≠ − 2 .
2. Проведём исследование функции на чётность/нечётность:
f ( − x ) = − x 2 + 4 − x 2 − 4 = x 2 + 4 x 2 − 4 = f ( x ) .
Функция чётная. Следовательно, можно построить ветви графика функции для x ≥ 0 и отобразить их симметрично относительно оси ординат.
3. Определим асимптоты. Вертикальная асимптота: прямая (x=1), т. к. при (x=1) знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем lim x → ∞ f ( x ) :
lim x → ∞ x 2 + 4 x 2 − 4 = lim x → ∞ x 2 x 2 + 4 x 2 x 2 x 2 − 4 x 2 = lim x → ∞ 1 + 4 x 2 1 − 4 x 2 = 1 .
Следовательно, (y=1) — горизонтальная асимптота.
4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y ′ = x 2 + 4 x 2 − 4 ′ = ( x 2 + 4 ) ′ ⋅ ( x 2 − 4 ) − ( x 2 + 4 ) ⋅ ( x 2 − 4 ) ′ x 2 − 4 2 = 2 x ⋅ ( x 2 − 4 ) − ( x 2 + 4 ) ⋅ 2 x x 2 − 4 2 = 2 x 3 − 8 x − 2 x 3 − 8 x x 2 − 4 2 = = − 16x x 2 − 4 2 .
Производная существует на всей области определения функции, следовательно, критических точек у функции нет.
Стационарные точки определим из уравнения y ′ = 0 . Получаем: (-16x=0) — откуда получаем, что (x=0). При (x y ′ > 0 ; при (x>0) имеем: y ′ 0 . Таким образом, в точке (x=0) функция имеет максимум, причём y max = f ( 0 ) = 0 2 + 4 0 2 − 4 = − 1 .
При (x>0) имеем: y ′ 0 . Учитывая точку разрыва (x=2), делаем вывод: функция убывает на промежутках 0 ; 2 ) и ( 2 ; + ∞ ) .
5. Найдём несколько точек, принадлежащих графику функции f ( x ) = x 2 + 4 x 2 − 4 при x ≥ 0 :
Напомним определение. Точка называется особой точкой аналитической функции , если в ней аналитичность ее нарушается.
Определение 2. Точка называется изолированной особой точкой функции , если существует окрестность этой точки с исключенной точкой , в которой аналитична, кроме самой точки .
Существует три типа изолированных особых точек. Приведем их определения.
Определение 3. Точка называется устранимой особой точкой , если разложение ее в ряд Лорана в окрестности этой точки не содержит главной части.
Определение 4. Точка называется полюсом кратности N функции, если в разложении ее в ряд Лорана в окрестности точки главная часть содержит конечное число членов, причем младшим отличным от нуля коэффициентом является .
Определение 5. Точка называется существенно особой точкой функции , если главная часть ее разложения в ряд Лорана в окрестности этой точки содержит бесконечное число членов.
Приведем критерии типа изолированных особых точек.
1) для того, чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы .
2) для того, чтобы точка была полюсом кратности N функции, необходимо и достаточно, чтобы , .
3) для того, чтобы точка была существенно особой точкой функции , необходимо и достаточно, чтобы .
Полезна следующая теорема. Для того, чтобы точка была полюсом порядка N функции, нужно, чтобы она была нулем N – го порядка функции (связь между нулями и полюсами).
Пример 1. Для функции особой точкой является . Имеем – есть устранимая особая точка.
Пример 2. Для функции является особой точкой. Так как – это полюс. Так как для функции т. является нулем пятого порядка, то – полюс пятого порядка функции .
Пример 3. Для функции является особой точкой. Разложение в ряд Лорана: в главной части содержит бесконечное число членов: это существенно особая точка.
Пример 4. Найти все особые точки функции и определить их характер.
Решение. Особыми точками являются точка и точки, в которых знаменатель обращается в нуль. Имеем , откуда , причем эти точки являются нулями первого порядка. Следовательно, в точках , функция имеет простые полюса. Точка не является изолированной особой точкой, так как она является пределом полюсов: : это означает, что любая окрестность точки содержит бесконечное число особых точек .
Задачи для самостоятельного решения
У нижеследующих функций найти нули и определить их порядки:
132. . 133. . 134. . 135. . 136. .
Найти порядок нуля для следующих функций:
138. . 139. . 140. .
Определить характер особой точки для следующих функций:
142. . 143. . 144. .
Найти особые точки и определить их характер у следующих функций:
145. . 146. . 147. . 148. . 149. .
Читайте также:
- История возникновения и развития экологического права реферат
- Смағұл сәдуақасовтың өмірі мен қоғамдық саяси қызметі реферат
- Реферат особенности строительного производства
- Что такое современность реферат
- Реферат на тему афроамериканцы
Без важнейшего понятия «окрестность точки» понять отличие интервала от отрезка не получится. А, для того, чтобы уяснить смысл «окрестности», необходимо прояснить, что из себя представляет привычная наша с вами ось вещественных чисел. Для многих (в том числе, и математиков), вещественная ось – это «палка». В такой примитивной интерпретации и отрезок, и интервал будут лишь частью «палки» с той лишь разницей, что у отрезка его точки-концы принадлежат отрезку, а у интервала – нет. Т.е. в такой примитивной интерпретации и отрезок и интервал – суть одно и то же (часть «палки»), разница лишь в принадлежности или не принадлежности концов.
В «палочной» интерпретации и само понятие «окрестности точки» совершенно не имеет необходимости. Да и сама точка у позитивистов (они позитивненько смотрят на мир) воспринимается примитивно, как некая «зарубка» на «палке». Необходимости в «окрестности» для такой вот «зарубки» совершенно нет. Смысл «окрестности» тогда вообще не понятен.
Всему виной латинское богословие, впитав которое, все представители западной науки потеряли способность видеть НЕВИДИМОЕ в видимом. Латинство в своих глубинных основаниях осталось языческим, дуальным. Великая схизма 11 века в том и состояла, что «троичное» Православие осталось стоять в прежней Апостольской Истине, а «двоичное» латинство пошло уже своей языческой дорогой.
В научном «горизонте» западного человека это язычество сформировало научный метод объективации. Так выкристаллизовывалось «шариковое» (“палочное”) объектное сознание западного человека. Тем самым сформировалось понятие РЕАЛЬНОСТИ. Реальным стало лишь то, что «я вижу и ощущаю». Всё невидимое выкидывается в запредельную область абстракции, объявляется умозрительным, и уж точно, реально не существующим. Это всё «игра человеческого ума».
Понятия «внешнее» и «внутреннее» для представителя западной науки не существует, ибо, «внутреннее» тогда перестаёт быть объективированным (становится не реальным). Нет, у них конечно же есть представление о внутренних органах (например, человека (сердце, там, лёгкие, мозг)), но всё это, так сказать, «внешние» внутренние органы, которые можно объективно ощутить. А, вот, понятия неощутимой души, как внутреннего явления, западная наука не признаёт.
Так вот, «окрестность точки» – это, если хотите, есть «душа» этой точки. Это то «внутреннее», что содержит собой «внешнее». Понимаете, сознание западного человека таким вот «шариковым» объективированием становится разорванным. По причине отсутствия связности в нём самом, это сознание и в устройстве Мира, да и в любом физическом явлении видит всё предельно разорванным. Связи «ВСЕГО СО ВСЕМ» такое сознание не допускает.
Поэтому и в вопросе «окрестности» точки такое западное сознание видит лишь некий малюсенький интервал вокруг неё – этакий «хоровод» таких же точно точек, непонятно для чего группирующихся вокруг точки-ядра (из-за такой непонятности, этот «хоровод» считается условным, невсамделишным).
В своё время, у меня уже была публикация на тему «Что есть точка?». Я там показывал, что точку стоит воспринимать совокупно во всех пространственных измерениях. В этом смысле и наша ось вещественных чисел это не «палка», она имеет троичный статус. Эту ось формируют три РЕАЛЬНО существующие пространства – вещественное, действительное и мнимое. Причём, латинствующее западное сознание вещественное и действительное не различает между собой, отождествляя их (для них это – синонимы).
Представить эти три пространства в единстве оси вещественных чисел не так-то и просто. Весьма условно их можно представить как «косичку», сплетённую из разных «нитей» – «красная нить» вещественная, «синяя» действительная, и «зелёная» мнимая. Кстати, так же условно представлены и цветовые заряды кварков в нуклоне. Я бы конечно предпочёл другую, хотя так же условную их интерпретацию: вещественное – это «внешнее пространство, а два других пространства подразделяются на «внутренние»: действительное пространство будет тогда «внутренним внешним», а мнимое – «внутренним внутренним». Такая вот «загогулина, понимаешь».
Только с введением этих пространств, понятие «окрестности» точки приобретает смысл. Причём этот самый смысл есть – «ВСЁ ВО ВСЁМ». Т.е. точка, имея такую «душу», незримо, через свою окрестность «живёт» во всём сущем, а всё сущее, в свою очередь, такой «окрестностью» формирует эту самую точку. Т.е. посредством своей «окрестности» точка присутствует сразу во всех этих трёх пространствах – в вещественном геометрическом, в действительном топологическом и в мнимом антиподном.
В вещественном геометрическом пространстве (в метрическом мире) мы, собственно, эту самую «окрестность» и не замечаем (как не замечаем мы человеческую душу, хотя, все наши действия обусловлены именно ей). «Окрестность» начинает проявляться лишь в действительном топологическом мире ультраметрики. Именно в этом ультраметрическом пространстве проявляется такое понятие, как «интервал», как «внутренний отрезок». Отличие «интервала» от «отрезка» в том, что «отрезок» задаётся в вещественном метрическом (и, соответственно, геометрическом) мире, а «интервал» – в топологическом действительном ультраметрическом мире.
В ультраметрике аддитивные (свойство складываемости) «отрезки» (с внешними точками), подчиняющиеся аксиоме Архимеда-Евдокса, становятся «интервалами» (с внутренними точками), называемых математиками «ШАРАМИ» (это условное название). У «интервалов-шаров» свойство аддитивности теряется (они уже не складываются друг с другом, но содержатся друг в друге). Не зря ведь, любимой русской игрушкой является матрёшка (только в ультраметрической матрёшке меньшее содержит большее).
Выверни ультраспиново (ультраспин (180˚+180˚=360˚) переводит действительное пространство в вещественное) внешний «отрезок», получишь внутренний «интервал». Почему в геометрии всё изменчиво, а в топологии – неизменно? Неизменность топологии во вложенности «шаров» друг в друге. И ещё, эти самые «шары не пересекаются друг с другом. Центр такого «шара» ВЕЗДЕ, а граница НИГДЕ. Именно поэтому такими «шарами-интервалами» формируются открытые множества, а «отрезками» – закрытые.
А что же мнимое пространство? Без него такие «выверты-переходы» были бы не возможны, как невозможным было бы само существование, как действительного, так и вещественного пространства. Единственное, что указывает на присутствие мнимого мира – это «выколотость» концов «интервала». Такая выколотая точка – это, если хотите, «портал» в мнимый мир.
И, вот, смотрите, наличие всех трёх миров формируется таким математическим понятием, как проектирование (проецирование), или – отображение, когда одно прецируется в другое через третье. Так, протон «смотрится» в электрон, и видит себя нейтроном. А нейтрон, знает, что он – электрон, но через протон. Таинство Триединства – оно велико.
Именно для такого вот проектирования и необходимо такое понятие, как «окрестность», когда внутренность «интервала» проецируется во внешность «отрезка». Каждая точка окрестности «интервала» будет иметь свой образ на «отрезке». Без «интервала» «отрезка» не существует, и, наоборот. И, их обоих не существует без «окрестности».
PS. Действительная окрестность формирует от орбитали электрона (четырёхмерная сфера), до сферического скопления звёздной галактики.
Мнимая же окрестность придаёт форму спиральным галактикам, эклиптикам звёздных систем, копирующих собой мнимую псевдосферу.
Каждая точка нашего организма имеет свою “окрестность”, а, значит, Вселенная всегда с нами на связи. Так, что, про «окрестность» – это всё серьёзно.
Всего Вам доброго.
Содержание:
Критерий монотонности функции:
Прежде всего, сформулируем определение монотонной функции:
- Функция f называется неубывающей (невозрастающей) на интервале (а,b), если для любых двух точек
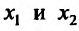
- Функция f называется возрастающей (убывающей) на интервале (а,b), если для любых двух точек
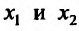 из интервала (а, b), удовлетворяющих условию
из интервала (а, b), удовлетворяющих условию 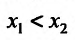 справедливо неравенство
справедливо неравенство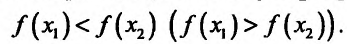 Неубывающие и невозрастающие функции называют монотонными функциями.
Неубывающие и невозрастающие функции называют монотонными функциями.
Монотонные функции
Возрастающие и убывающие функции называются строго монотонными функциями.
Например, функция у = х- возрастающая (строго монотонная) на всей числовой оси; функция 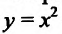 -возрастает на полуоси х > О и убывает при
-возрастает на полуоси х > О и убывает при 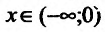 ; функция у = signx – неубывающая на всей числовой оси;
; функция у = signx – неубывающая на всей числовой оси; 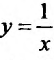 убывает при
убывает при 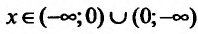 .
.
Теорема 14.1.1. (Критерий монотонности) Пусть функция 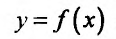 определена и дифференцируема на интервале (а,b). Для того, чтобы f не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы производная этой функции была неотрицательной (неположительной)
определена и дифференцируема на интервале (а,b). Для того, чтобы f не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы производная этой функции была неотрицательной (неположительной)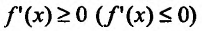 всюду на этом интервале. Для того чтобы функция / возрастала (убывала) на интервале (а, b), достаточно чтобы производная
всюду на этом интервале. Для того чтобы функция / возрастала (убывала) на интервале (а, b), достаточно чтобы производная 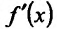 была положительной (отрицательной) на этом интервале.
была положительной (отрицательной) на этом интервале.
Доказательство: Пусть 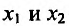 – любые две точки из интервала (а, b), удовлетворяющие условию
– любые две точки из интервала (а, b), удовлетворяющие условию 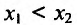 Поскольку функция f(x) дифференцируема, а стало быть и непрерывна на (а, b), то она непрерывна и дифференцируема на отрезке
Поскольку функция f(x) дифференцируема, а стало быть и непрерывна на (а, b), то она непрерывна и дифференцируема на отрезке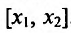 . Поэтому к функции
. Поэтому к функции 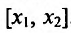 можно применить теорему Лагранжа:
можно применить теорему Лагранжа:
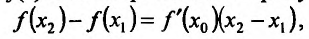 (14.1.1)
(14.1.1)
где 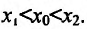 .
.
Необходимость. Пусть функция f дифференцируема на интервале (а, b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что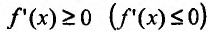 на этом интервале. Рассмотрим равенство (14.1.1). Левая часть равенства
на этом интервале. Рассмотрим равенство (14.1.1). Левая часть равенства 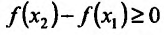
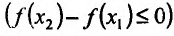 поскольку функция f не убывает (не возрастает) и
поскольку функция f не убывает (не возрастает) и 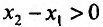 по условию, тогда и
по условию, тогда и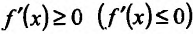 на интервале
на интервале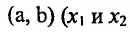 – любые две точки из интервала (а,b)).
– любые две точки из интервала (а,b)).
Достаточность. Пусть теперь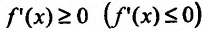 на интервале (а,b). Тогда из (14.1.1) следует, что
на интервале (а,b). Тогда из (14.1.1) следует, что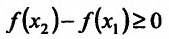
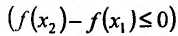 ,т.е.
,т.е.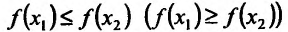 так
так 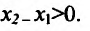
Поскольку 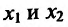 – любые две точки из интервала, то функция f не убывает (не возрастает ) на интервале (а, b).
– любые две точки из интервала, то функция f не убывает (не возрастает ) на интервале (а, b).
Аналогично теорема доказывается и для возрастающей (убывающей) функции.
Из доказанной теоремы следует, что для определения интервалов монотонности функции нужно:
- Найти область определения функции.
- Вычислить ее производную.
- Приравнять производную к нулю; полученные нули производной разобьют область определения на интервалы, в которых производная сохраняет знак.
- Определить знак производной в каждом интервале при помощи “пробной” точки и сделать вывод.
Пример:
Найти интервалы монотонности функции 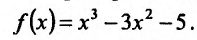
Решение:
Область определения заданной функции – вся числовая ось 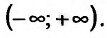 Производная
Производная 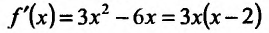 этой функции обращается в нуль в точках:
этой функции обращается в нуль в точках: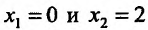 .
.
Составим схему изменения знаков производной:
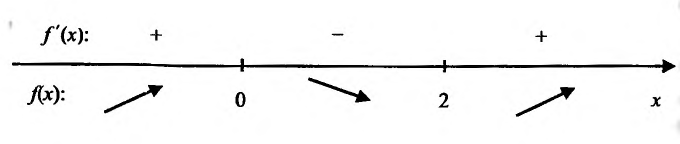
Согласно теореме’ 14.1.1, данная функция возрастает при 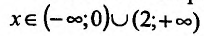 и убывает при
и убывает при 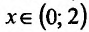 .
.
Функция 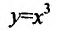 не убывает в области определения (при
не убывает в области определения (при 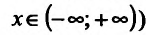 поскольку
поскольку 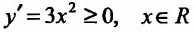 ;
;
Функция 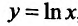 , определенная при
, определенная при 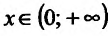 , возрастает, поскольку
, возрастает, поскольку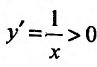
Экстремумы функций
Определение 14.2.1. Пусть функция f определена в некоторой окрестности точки 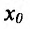 – Точка
– Точка 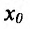 называется точкой максимума (минимума) функции f, если существует такая окрестность точки
называется точкой максимума (минимума) функции f, если существует такая окрестность точки 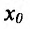 , что
, что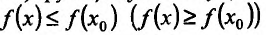 для всехx из этой окрестности.
для всехx из этой окрестности.
Если выполняются строгие неравенства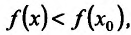
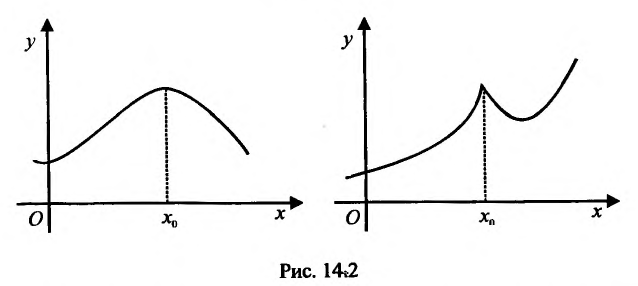
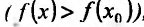 , то точка
, то точка 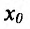 называется точкой строгого максимума (строгого минимума).
называется точкой строгого максимума (строгого минимума).
Точки максимума и минимума (строгого максимума и минимума) называются точками экстремума (строгого экстремума). 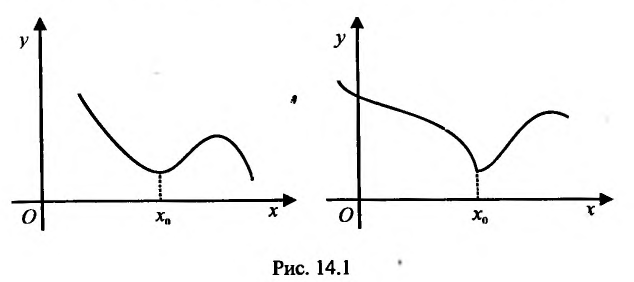
Теорема 14.2.1 .(необходимое условие экстремума) Если точка 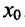 является точкой экстремума функции f определенной в некоторой окрестности точки
является точкой экстремума функции f определенной в некоторой окрестности точки 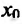 . то либо производная
. то либо производная 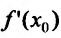 не существует, либо
не существует, либо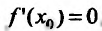
Справедливость этой теоремы следует из теоремы Ферма в силу определения точек экстремума. Действительно, если 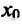 точка экстремума, то согласно определения экстремума это точка, в которой функция достигает наибольшего либо наименьшего значения, и в силу теоремы Ферма
точка экстремума, то согласно определения экстремума это точка, в которой функция достигает наибольшего либо наименьшего значения, и в силу теоремы Ферма 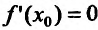 , если производная существует.
, если производная существует.
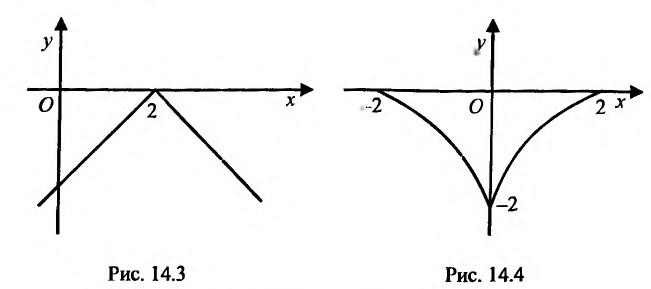
Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция 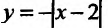 не имеет производной в точке х=2, но достигает в ней максимума: у= 0 при х=2, а для всякой другой точки y
не имеет производной в точке х=2, но достигает в ней максимума: у= 0 при х=2, а для всякой другой точки y 0 (рис. 14.3). Функция
0 (рис. 14.3). Функция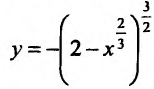 не имеет конечной производной в точке х=0, поскольку
не имеет конечной производной в точке х=0, поскольку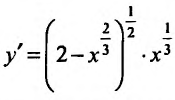 при х=0 обращается в бесконечность, но в этой точке функция имеет Минимум:
при х=0 обращается в бесконечность, но в этой точке функция имеет Минимум:  при
при (рис. 14.4).
(рис. 14.4).
Из приведенных рассуждений следует, что точки экстремума функции нужно искать среди тех точек её области определения, где производная функции равна нулю или не существует.
Если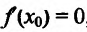 , это еще не значит, что в точке
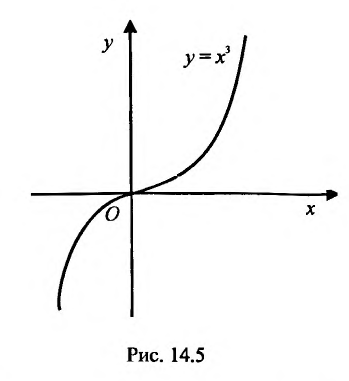
, это еще не значит, что в точке 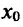 есть экстремум. Примером может служить функция
есть экстремум. Примером может служить функция 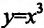 . В точке х=0 её производная
. В точке х=0 её производная 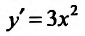 равна нулю, но экстремума в этой точке функция не имеет. График функции изображен на рисунке 14.5.
равна нулю, но экстремума в этой точке функция не имеет. График функции изображен на рисунке 14.5.
Точки области определения функции, в которых производная равна нулю, называются стационарными, а в которых производная не существует, называются критическими.
Каждая стационарная (критическая) точка – это точка возможного экстремума. Однако сделать заключение о том, что в данной стационарной (критической) точке на самом деле экстремум, можно лишь на основании дополнительного исследования, т.е. на основании достаточных условий экстремума.
Теорема 14.2.2. (первое достаточное условие экстремума) Пусть функция f определена, дифференцируема в некоторой окрестности точки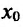 и непрерывна слева и справа от точки
и непрерывна слева и справа от точки 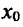 – Тогда если в пределах указанной окрестности производная
– Тогда если в пределах указанной окрестности производная 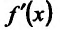 положительна (отрицательна) слева от точки
положительна (отрицательна) слева от точки 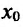 и отрицательна (положительна) справа от точки
и отрицательна (положительна) справа от точки 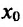 , то функция f имеет в точке
, то функция f имеет в точке 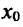 локальный максимум (минимум):
локальный максимум (минимум):
- если
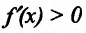 на
на 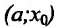 и
и 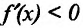 на
на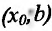 , то точка
, то точка 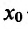 – точка максимума функции f(x);
– точка максимума функции f(x); - если
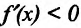 на
на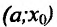 и
и 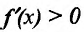 на
на 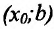 , то точка
, то точка 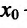 – точка минимума функции f(x);
– точка минимума функции f(x);
Если же в пределах указанной окрестности точки 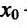 производная
производная 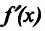 имеет один и тот же знак слева и справа от точки
имеет один и тот же знак слева и справа от точки 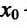 , то экстремума в точке
, то экстремума в точке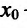 нет.
нет.
Доказательство. Докажем первое утверждение теоремы.
Предположим, что 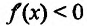 на интервале
на интервале 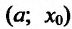 . Поскольку функция
. Поскольку функция  непрерывна в точке
непрерывна в точке 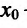 , то, в силу теоремы 14.1.1, она убывает на полуинтервале
, то, в силу теоремы 14.1.1, она убывает на полуинтервале 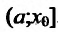 – Следовательно, для любого х
– Следовательно, для любого х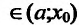 выполняется неравенство
выполняется неравенство 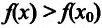 .
.
Пусть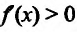 на интервале
на интервале 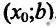 . Так как функция
. Так как функция 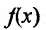 непрерывна в точке
непрерывна в точке 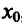 , то она возрастает на полуинтервале
, то она возрастает на полуинтервале 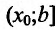 Тогда для любого
Тогда для любого 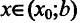 выполняется неравенство
выполняется неравенство 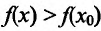 .
.
В результате получается, что при любом 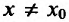 из интервала (а;b) выполняется неравенство
из интервала (а;b) выполняется неравенство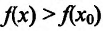 . Это значит, что точка
. Это значит, что точка 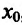 -точка минимума функции
-точка минимума функции 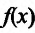 .
.
Второе утверждение теоремы доказывается аналогично. 
Пример:
Найти точки экстремума функции’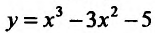 .
.
Решение:
Поскольку 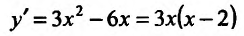 (см. пример 14.1.1) и при переходе через точку х=0 производная меняет знак с плюса на минус, а при переходе через точку х=2- с минуса на’ плюс, то точка х=0 – точка максимума, а х=2 – точка минимума.
(см. пример 14.1.1) и при переходе через точку х=0 производная меняет знак с плюса на минус, а при переходе через точку х=2- с минуса на’ плюс, то точка х=0 – точка максимума, а х=2 – точка минимума.
Производная функции 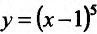 , определенной для
, определенной для 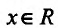 , обращается в нуль в одной точке х=1:
, обращается в нуль в одной точке х=1: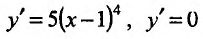 при х=1. Поскольку
при х=1. Поскольку 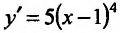 положительна как слева, так и справа от этой точки, то функция
положительна как слева, так и справа от этой точки, то функция 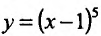 не имеет точек экстремума.
не имеет точек экстремума.
Теорема 14.2.3. (второе достаточное условие экстремума) Если функция f определена в некоторой окрестности точки 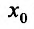 и в точке
и в точке 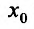 она имеет конечную вторую производную, причем
она имеет конечную вторую производную, причем  то при
то при 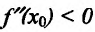 -точка
-точка 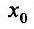 является точкой максимума, а при
является точкой максимума, а при 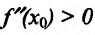 – точка
– точка 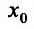 является точкой минимума.
является точкой минимума.
Доказательство: Поскольку функция f дважды дифференцируема в точке 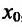 , то для нее справедлива формула Тейлора с остаточным членом в форме Лагранжа и функцию f можно представить
, то для нее справедлива формула Тейлора с остаточным членом в форме Лагранжа и функцию f можно представить
в виде:
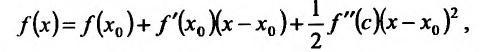
где точка с расположена между 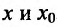 . По условию теоремы
. По условию теоремы 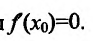 . Тогда формула Тейлора принимает вид:
. Тогда формула Тейлора принимает вид:
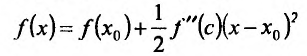
или
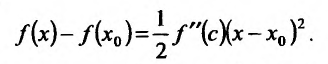
Поскольку 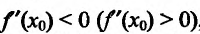 , то существует окрестность точки
, то существует окрестность точки 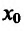 в которой
в которой 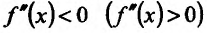 и, следовательно,
и, следовательно,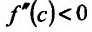
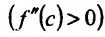 , так как точка с расположена в окрестности точки
, так как точка с расположена в окрестности точки 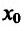 . Если
. Если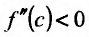 , то слагаемое
, то слагаемое 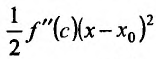 так же меньше нуля. Значит разность
так же меньше нуля. Значит разность 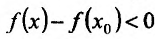 , т.е.
, т.е.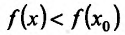 и точка
и точка 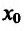 – точка максимума. Если же
– точка максимума. Если же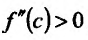 , то
, то 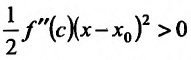 и. следовательно, разность
и. следовательно, разность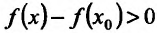 , т.е.
, т.е. 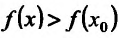 и точка
и точка 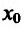 – точка минимума.
– точка минимума.
Пример:
Найти точки экстремума функции 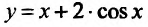 на отрезке
на отрезке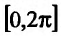 .
.
Решение:
Вычислим первую и вторую производные заданной функции: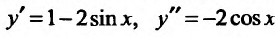 . Из уравнения l-2sinx = 0 определяем стационарные точки на отрезке
. Из уравнения l-2sinx = 0 определяем стационарные точки на отрезке 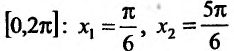 •
•
Теперь находим знак второй производной в каждой стационарной точке и определяем ее характер, используя теорему 14.2.3. Поскольку
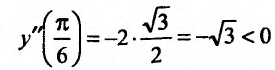 , то
, то 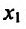 – точка максимума,
– точка максимума,
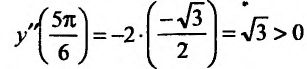 то точка
то точка 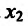 – точка минимума.
– точка минимума.
Теорема 14.2.4. (третье достаточное условие экстремума). Пусть функция f определена в некоторой окрестности точки 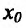 и в точке
и в точке 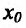 функция f имеет производные до порядка n включительно, причем
функция f имеет производные до порядка n включительно, причем 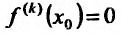 для
для 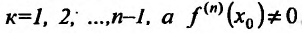 Тогда, если n- четное и
Тогда, если n- четное и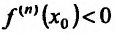 , то
, то 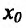 – точка максимума, а если
– точка максимума, а если 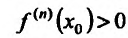 , то
, то 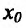 – точка минимума. Если же n – нечетное, то функция f в точке
– точка минимума. Если же n – нечетное, то функция f в точке 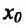 экстремума не имеет.
экстремума не имеет.
Пример:
Исследовать на экстремум функцию 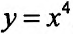 .
.
Решение:
Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем первую производную- 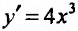 и, приравняв ее к нулю, определяем стационарную точку х=0. Вычисляем последовательно производные
и, приравняв ее к нулю, определяем стационарную точку х=0. Вычисляем последовательно производные 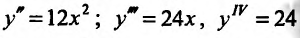 . Применив теорему 14.2.4. определяем, что х=0 – точка минимума.
. Применив теорему 14.2.4. определяем, что х=0 – точка минимума.
Сформулированные теоремы позволяют решать определенный круг задач. Например, требуется определить наибольшее (найме шее) значение функции f на отрезке [а, b]. Для этого следует на ней все точки, в которых производная функции либо равна нулю, ли’ не существует. Затем из этих точек выбираем те, которые принадлежат отрезку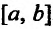 . После этого достаточно лишь сравнить между собой по величине значения функции в отобранных точках и значения функции на концах отрезка
. После этого достаточно лишь сравнить между собой по величине значения функции в отобранных точках и значения функции на концах отрезка 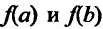 . Наибольшее (найме шее) из этих значений и будет наибольшим (наименьшим) значениях функции на отрезке
. Наибольшее (найме шее) из этих значений и будет наибольшим (наименьшим) значениях функции на отрезке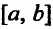 .
.
Пример:
Найти наибольшее и наименьшее значениях функции 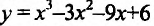 на отрезке [—2;2].
на отрезке [—2;2].
Решение:
Вычислив производную и приравняв ее к ну: 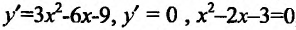 , находим стационарные точки данного функции:
, находим стационарные точки данного функции: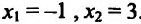
Отрезку [-2;2] принадлежит только одна точка 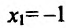 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке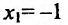 и на концах отрезка:
и на концах отрезка: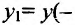
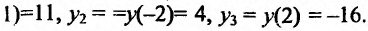 . Сравнивая полученные значения, определяем, что
. Сравнивая полученные значения, определяем, что 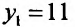 наибольшее значение функции, а
наибольшее значение функции, а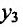
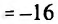 наименьшее значение функции на отрезке [-2;2].
наименьшее значение функции на отрезке [-2;2].
Выпуклость и точки перегиба
Пусть функция f определена на интервале (а; b) и пусть точки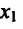 и
и 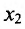 такие, что выполняется неравенство
такие, что выполняется неравенство 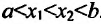 . Проведем прямую через точки графика функции у = f(x). Ее уравнение имеет вид:
. Проведем прямую через точки графика функции у = f(x). Ее уравнение имеет вид: 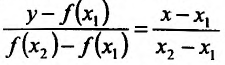
Разрешим это уравнение относительно у:
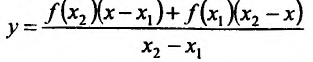
ИЛИ
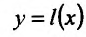 , где
, где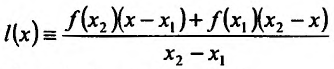
Ясно, что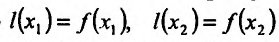 .
.
Определение 14.3.1. Функция f называется выпуклой вверх (выпуклой вниз) на интервале 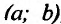 , если для любых точек
, если для любых точек 
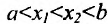 и для любой точки
и для любой точки 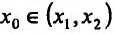 выполняется неравенство
выполняется неравенство

соответственно. А сам интервал называется интервалом выпуклости вверх (выпуклости вниз).
Геометрически это означает, что любая точка хорды АВ (т.е. отрезка прямой у=1(х) с концами в точках А и В) лежит не выше (не ниже) точки графика функции , соответствующей тому же значению аргумента.
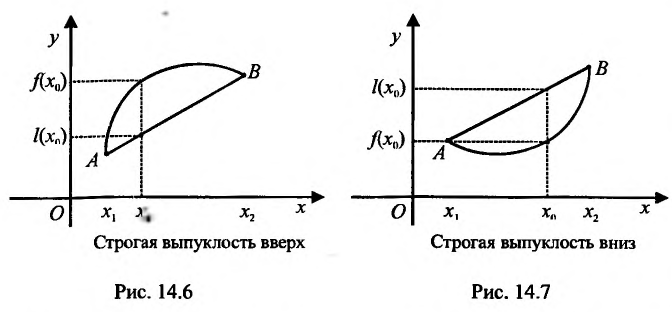
Если неравенства (14.3.1) и (14.3.2) строгие, то функция f называется строго выпуклой вверх (рис. 14.6) (строго выпуклой вниз (рис. 14.7)). В этом случае любая точка хорды АВ, исключая ее концы, лежит ниже (выше) соответствующей точки графика функции
Теорема 14.3.1. (достаточное условие строгой выпуклости) Если функция f определена и дважды дифференцируема на интервале (а,b), то 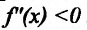 на (а, b) функция f строго выпукла вверх, а при
на (а, b) функция f строго выпукла вверх, а при 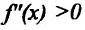 на (а,b) функция f строго выпукла вниз на этом интервале.
на (а,b) функция f строго выпукла вниз на этом интервале.
Доказательство. Пусть функция f определена и дважды непрерывно дифференцируема на интервале (а, b). Возьмем некоторые точки  на интервале (а, b), такие, что
на интервале (а, b), такие, что 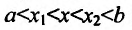 и проведем хорду АВ: у=l(х). Рассмотрим разность:
и проведем хорду АВ: у=l(х). Рассмотрим разность:
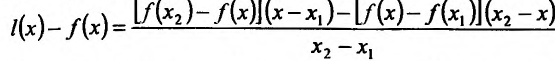
Применяя теорему Лагранжа к каждой разности, т.е. к  . получим
. получим
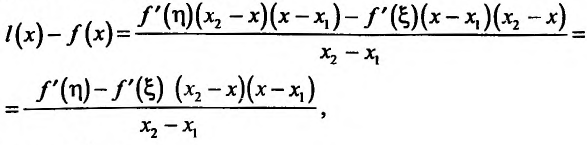
где 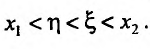
Снова применим теорему Лагранжа к разности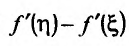 Будем иметь.
Будем иметь.
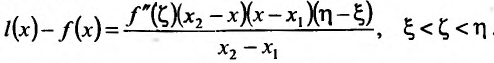
Отсюда видно, что если 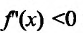 на (а, b) , то и и поэтому-
на (а, b) , то и и поэтому- 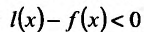 , т.к.
, т.к. 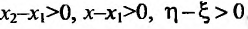 Следовательно. l(х)
Следовательно. l(х) f(x),- функция f строго выпукла вверх; если же
f(x),- функция f строго выпукла вверх; если же на (a, b) , го l(x)> f(x),- функция f строго выпукла вниз. Теорема дока-jaiia.
на (a, b) , го l(x)> f(x),- функция f строго выпукла вниз. Теорема дока-jaiia. 
Заметим, что условие знакопостоянства второй производной не является необходимым условием. Так, функция 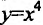 строго выпукла вниз на всей числовой оси, однако ее вторая производная
строго выпукла вниз на всей числовой оси, однако ее вторая производная 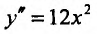 обращается в 0 при x=0. Следовательно, может быть, что для строго выпуклой функции вторая производная и не сохраняет знак. Но если для функции вторая производная сохраняет знак на некотором интервале, то график функции строго выпуклый (при
обращается в 0 при x=0. Следовательно, может быть, что для строго выпуклой функции вторая производная и не сохраняет знак. Но если для функции вторая производная сохраняет знак на некотором интервале, то график функции строго выпуклый (при 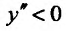 вверх и при
вверх и при 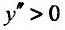 вниз).
вниз).
Определение 14.3.2. Пусть фунщия f определена в некоторой окрестности точки 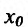 ‘и непрерывна в этой точке. Точка
‘и непрерывна в этой точке. Точка 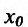 называется точкой перегиба функции f, если она является одновременно концом интервала строгой выпуклости вверх и строгой выпуклости вниз, т.е. она отделяет выпуклые части вверх от выпуклых частей внешнего графика функции.
называется точкой перегиба функции f, если она является одновременно концом интервала строгой выпуклости вверх и строгой выпуклости вниз, т.е. она отделяет выпуклые части вверх от выпуклых частей внешнего графика функции.
Теорема 14.3.2. (необходимое условие точки перегиба) Если функция f определена и дважды непрерывно дифференцируема на (а,b) и 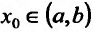 – точка перегиба, то
– точка перегиба, то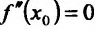
Доказательство. Пусть задана функция f, которая определена и дважды’ непрерывно дифференцируема на (а.b) и пусть точка 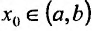 является точкой перегиба. Предположим, что вторая производная
является точкой перегиба. Предположим, что вторая производная 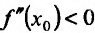 (либо
(либо 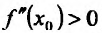 ). Тогда в силу непрерывности второй производной найдется окрестность точки
). Тогда в силу непрерывности второй производной найдется окрестность точки 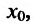 в которой
в которой 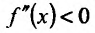 (либо
(либо 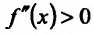 ) и, следовательно, функция f в этой окрестности точки
) и, следовательно, функция f в этой окрестности точки 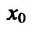 строго выпукла вверх (вниз), что противоречит тому, что
строго выпукла вверх (вниз), что противоречит тому, что 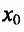 – точка перегиба. Полученное противоречие и доказывает теорему.
– точка перегиба. Полученное противоречие и доказывает теорему. 
Из теоремы вытекает, что точками перегиба дважды дифференцируемой функции могут быть лишь точки, в которых вторая производная обращается в нуль либо не существует.
Сформулируем и докажем теперь достаточные условия точки перегиба.
Теорема 14.3.3. Если функция f определена и дважды дифференцируема на интервале (а,b), кроме, быть может точки 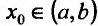 , в которой она, однако, непрерывна, и ее вторая производная меняет знак при переходе аргумента через точку
, в которой она, однако, непрерывна, и ее вторая производная меняет знак при переходе аргумента через точку 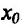 , то точка
, то точка 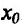 является точкой перегиба функции f
является точкой перегиба функции f
Действительно, в силу теоремы 14.3.1 точка 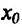 является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз – т.е.
является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз – т.е. 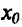 – точка перегиба.
– точка перегиба.
Теорема 14.3.4. Если f трижды непрерывно дифференцируема на (а,b) и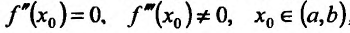 , то
, то 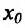 – точка перегиба.
– точка перегиба.
Доказательство (проведем для случая f”(x0) > 0). Так как по предположению 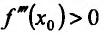 , то существует окрестность точки
, то существует окрестность точки 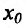 , в которой
, в которой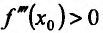 и, следовательно, функция
и, следовательно, функция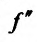 возрастает, обращаясь в нуль при x=
возрастает, обращаясь в нуль при x=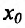 , т.е. функция
, т.е. функция 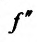 меняет знак при переходе через точку х=
меняет знак при переходе через точку х=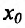 . Следовательно, в силу теоремы 14.3.3, точка
. Следовательно, в силу теоремы 14.3.3, точка 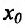 -точка перегиба.
-точка перегиба. 
Теорема 14.3.5. Пусть функция f непрерывно дифференцируема n раз на (а,b), причем
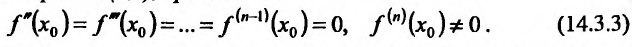 Тогда если п нечетно, то n – точка перегиба, если же n четно, то
Тогда если п нечетно, то n – точка перегиба, если же n четно, то 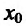 не является точкой перегиба.
не является точкой перегиба.
Итак, из изложенного материала вытекает, что выпуклость вверх или вниз графика функции f зависит от знака ее второй производной. Оказывается, что и расположение графика функции относительно касательной также связано со знаком второй производной, т.е. если функция f имеет вторую производную, все значения которой имеют один и тот же знак, то все точки графика функции f лежат над (под) касательной.
Рассмотрим пример, иллюстрирующий исследование графика функции на выпуклость и точки перегиба.
Пример 14.3.1. Найти интервалы выпуклости и точки перегиба графика функции 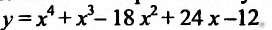
Решение. Функция определена для всех 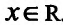 . Вычисляем последовательно первую и вторую производные функции:
. Вычисляем последовательно первую и вторую производные функции:
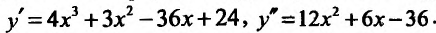
Приравняв вторую производную к нулю 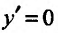 , т.е.
, т.е. 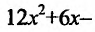
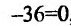 , находим
, находим 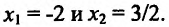
Составляет схему изменения знаков второй производной:

Следовательно, у”>0 на интервалах 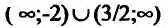 и функция выпукла вниз;
и функция выпукла вниз; 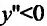 на интервале (-2;3/2) и функция выпукла вверх на этом интервале. Так как при переходе через точки
на интервале (-2;3/2) и функция выпукла вверх на этом интервале. Так как при переходе через точки 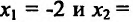 3/2 вторая производная меняет знак, то точки (-2;-124) и (3/2;-129/16) являются точками перегиба графика функции.
3/2 вторая производная меняет знак, то точки (-2;-124) и (3/2;-129/16) являются точками перегиба графика функции.
Рассмотрим пример из микроэкономики:
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
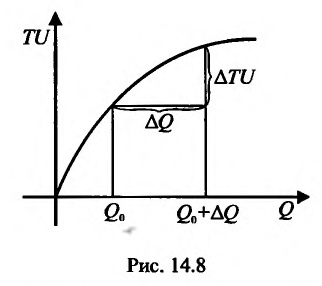
Это означает существование функции полезности TU аргумента Q -количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Построим прямоугольную систему координат и отложим по горизонтальной оси Ох количество потребляемого товара Q, а по вертикальной оси Оу – общую полезность TU (см. рис. 14.3). Рассмотрим график функции TU = TU(Q). Точка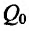 на горизонтальной оси означает количество приобретенного товара, величина
на горизонтальной оси означает количество приобретенного товара, величина 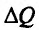 -добавочный приобретенный товар. Разность
-добавочный приобретенный товар. Разность 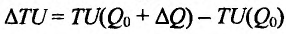 – добавочная полезность, полученная от покупки добавочного товара
– добавочная полезность, полученная от покупки добавочного товара 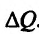 . Добавочная полезность от последней приобретенной порции товара (или единицы товара) вычисляется по формуле
. Добавочная полезность от последней приобретенной порции товара (или единицы товара) вычисляется по формуле 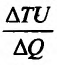 (см. Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Переходя к пределу при
(см. Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Переходя к пределу при 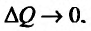 . получим формулу для определения предельной полезности MU:
. получим формулу для определения предельной полезности MU:
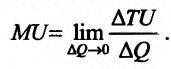
Но предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю, равен производной функции.
Следовательно, предельная полезность равна производной функции полезности TU=TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции 
Асимптоты графика функции
Рассмотрим функцию f определенную на интервале (а;b), . Если 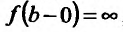 , то прямую х=n называют левосторонней вертикальной асимптотой графика функции f если
, то прямую х=n называют левосторонней вертикальной асимптотой графика функции f если 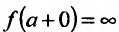 , то прямую х=а называют правосторонней вертикальной асимптотой графика функции f и если , то прямую х=с в плоскости хОу называют двусторонней вертикальной асимптотой графика функции f.
, то прямую х=а называют правосторонней вертикальной асимптотой графика функции f и если , то прямую х=с в плоскости хОу называют двусторонней вертикальной асимптотой графика функции f.
Заметим, что вертикальными асимптотами являются, как правило, нули знаменателей дробно-рациональных функций.
Если функция f определена на и для постоянных 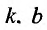 выполняется соотношение
выполняется соотношение

то прямая у = kх + b- называется наклонной асимптотой вправо графика функции f Если соотношение (14.4.1) выполняется и при , то прямая 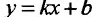 – называется наклонной асимптотой влево. Из (14.4.1) следует, что если
– называется наклонной асимптотой влево. Из (14.4.1) следует, что если 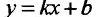 – наклонная вправо (влево) асимптота, то постоянные k и b определяются по формулам (из предельных соотношений):
– наклонная вправо (влево) асимптота, то постоянные k и b определяются по формулам (из предельных соотношений):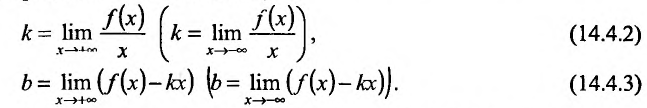
И наоборот, если пределы (14.4.2) и (14.4.3) существуют и конечны, то прямая у = kх + b- наклонная вправо (влево) асимптота графика функции f
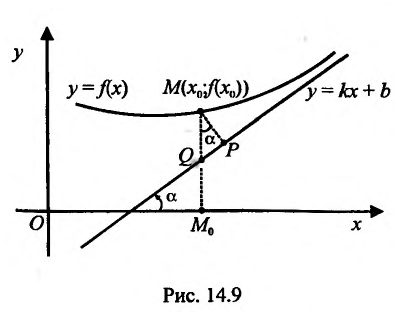
Рассмотрим геометрический смысл асимптоты. Пусть 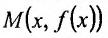 точка графика функцииf, точка
точка графика функцииf, точка 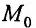 – ее проекция на ось Ох.
– ее проекция на ось Ох.
На рис. 14.9 видно, что отрезок 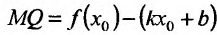 , а MP = MQ cos a.. По определению, прямая y = kx + b называется асимптотой, если
, а MP = MQ cos a.. По определению, прямая y = kx + b называется асимптотой, если 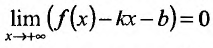 . Это значит, что и
. Это значит, что и 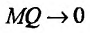 при
при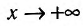 . Расстояние от точки М до прямой, как легко видно, равно MP = MQ cos а. Поэтому, если
. Расстояние от точки М до прямой, как легко видно, равно MP = MQ cos а. Поэтому, если 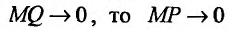 при
при  . Следовательно, асимптота может быть определена как прямая, расстояние до которой от графика функции, т.е. отрезок MP, стремится к нулю, когда точка М стремится к бесконечности по графику функцииf Таким образом, функция f при
. Следовательно, асимптота может быть определена как прямая, расстояние до которой от графика функции, т.е. отрезок MP, стремится к нулю, когда точка М стремится к бесконечности по графику функцииf Таким образом, функция f при  ведет себя почти как линейная функция, если ее график имеет асимптоту у = kх + b.
ведет себя почти как линейная функция, если ее график имеет асимптоту у = kх + b.
Пример:
График функции 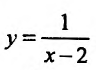 имеет вертикальную асимптоту х = 2, так как
имеет вертикальную асимптоту х = 2, так как 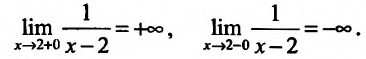
Пример:
Найти асимптоты графика функции 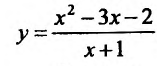
Решение:
Область определения функции D(f): 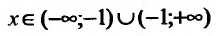 . Вычислим пределы:
. Вычислим пределы:
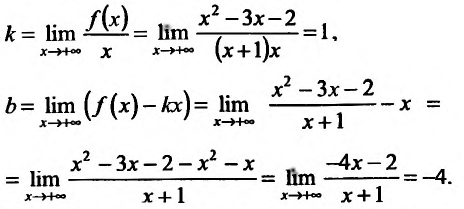
Так как значения пределов останутся такими же и при  , то прямая у = х-4 является наклонной вправо и влево асимптотой графика функции. Кроме того, х = — 1 является двусторонней вертикальной асимптотой, так как
, то прямая у = х-4 является наклонной вправо и влево асимптотой графика функции. Кроме того, х = — 1 является двусторонней вертикальной асимптотой, так как 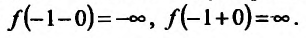
- Заказать решение задач по высшей математике
Общая схема исследования функций и построение их графиков
Под исследованием функций понимается изучение ее изменения в зависимости от изменения аргумента. Исследование функций и построение их графиков можно проводить по следующей схеме:
- Найти область определения и множество значений функции; исследовать на непрерывность, найти точки разрыва и выяснить характер точек разрыва; определить вертикальные асимптоты. Найти точки пересечения с осями координат.
- Исследовать функцию на периодичность; четность, нечетность.
- Исследовать поведение функции на границе области определения; найти асимптоты графика функции.
- Исследовать функцию на монотонность, выяснить характер экстремумов.
- Определить интервалы выпуклости графика функции, точки перегиба.
- Составить таблицу значений функции куда включаются все точки графика функции, найденные на предыдущих этапах исследования и необходимые дополнительные контрольные точки.
- Используя все полученные результаты построить график функции.
Пример:
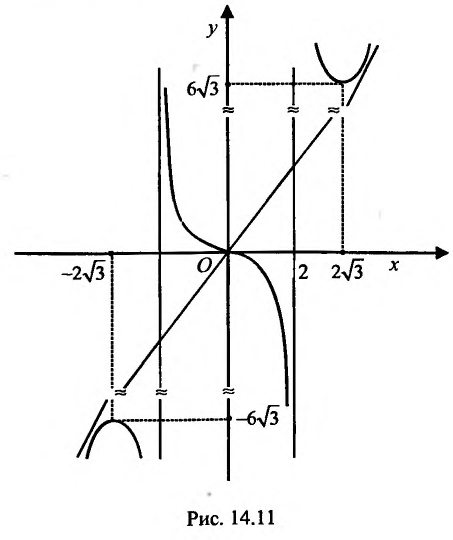
Построить график функции 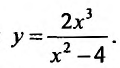
Решение:
Проведем полное исследование функции по указанной схеме.
1. Функция определена и непрерывна при всех 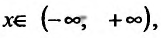 кроме точек х = ±2. Множество значений функции
кроме точек х = ±2. Множество значений функции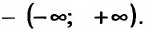
Прямые- х = ±2 являются вертикальными асимптотами, т.к.
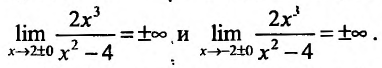
График пересекает оси координат в точке O(0; 0).
2. Функция не периодическая. Функция не четная, т.к. выпол-
няется равенство: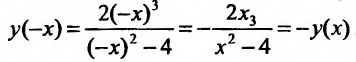 . График
. График
функции симметричный относительно начала координат. Поэтому достаточно провести исследование функции на полуинтервале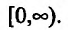
3. Найдем наклонную асимптоту. Для этого вычислим пределы:
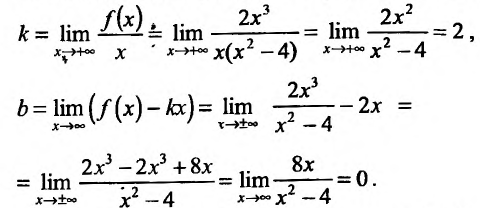
Подставив значения k и b уравнение 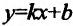 , получим уравнение асимптоты у =2х.
, получим уравнение асимптоты у =2х.
4. Для нахождения промежутков возрастания и убывания найдем первую производную:
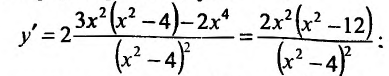
приравняем ее к нулю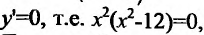 , и найдем стационарные точки
, и найдем стационарные точки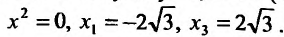 . Составляем схему изменения знаков первой производной:
. Составляем схему изменения знаков первой производной:
 На промежутке
На промежутке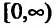 производная
производная 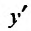 обращается в нуль в точках
обращается в нуль в точках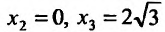 и обращается в бесконечность в точке х = 2. Поскольку при
и обращается в бесконечность в точке х = 2. Поскольку при 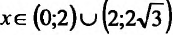 производная
производная 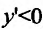 , то функция на этих интервалах убывает, а на интервале
, то функция на этих интервалах убывает, а на интервале 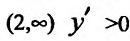 , следовательно, функция возрастает. Очевидно, что точка
, следовательно, функция возрастает. Очевидно, что точка 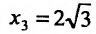 является точкой минимума.
является точкой минимума.
5. Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную 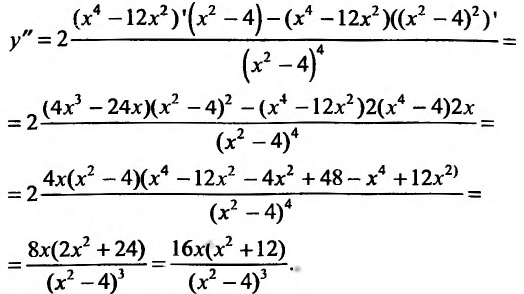
Вторая производная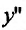 обращается в нуль в точке х = 0 и в бесконечность в точке х = 2. Составляем схему изменения знаков второй производной:
обращается в нуль в точке х = 0 и в бесконечность в точке х = 2. Составляем схему изменения знаков второй производной:
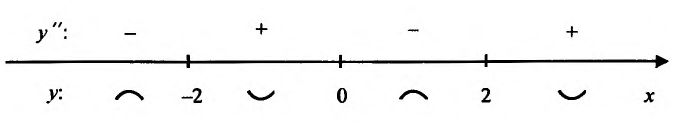
На интервале  и поэтому функция выпукла вверх, а на интервале
и поэтому функция выпукла вверх, а на интервале  и, следовательно, функция выпукла вниз. Кроме того, точка х = 0 является точкой перегиба, т.к. вторая производная меняет знак при переходе через эту точку.
и, следовательно, функция выпукла вниз. Кроме того, точка х = 0 является точкой перегиба, т.к. вторая производная меняет знак при переходе через эту точку.
6. Используя результаты исследования и учитывая нечетность функции, строим график (рис. 14.11).
Пример:
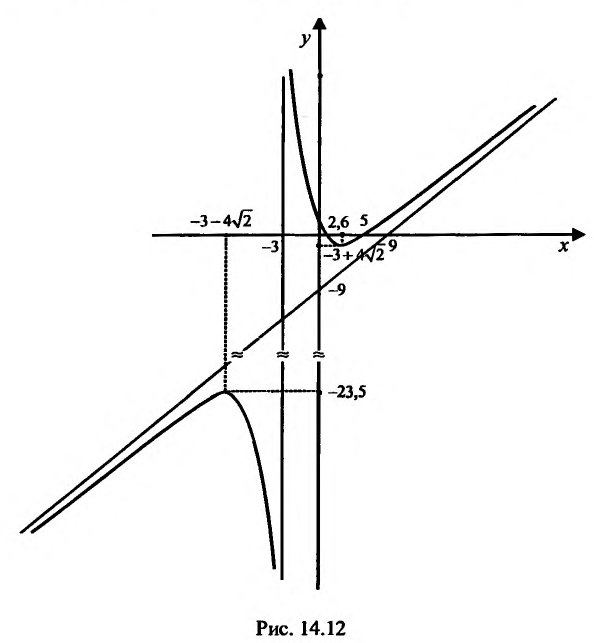
Провести полное исследование целевой функции потребления 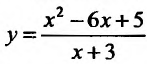 от услуги х и построить её график.
от услуги х и построить её график.
Решение:
Проведём полное и разностороннее изучение свойств функции, применив изложенную выше схему.
1) Функция определена и непрерывна для всех 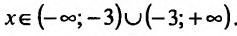 Точка х= -3 является точкой разрыва. Так
Точка х= -3 является точкой разрыва. Так
как 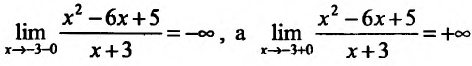 то прямая х =
то прямая х =
-3 является вертикальной асимптотой. Если х=0, то 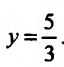 Если
Если
у=О, тс получим уравнение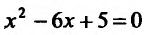 , решив которое найдём
, решив которое найдём
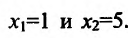 . Итак, график функции
. Итак, график функции 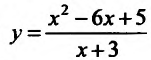 пересекает оси
пересекает оси
координат в точках: 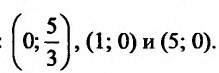
2) Функция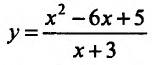 не является периодической
не является периодической
3) Исследуемая функция не является ни чётной, ни нечётной, гак как
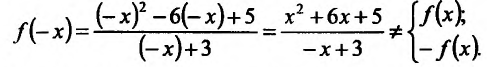
4) Исследуем существование наклонных асимптот. Для этого вычислим пределы;
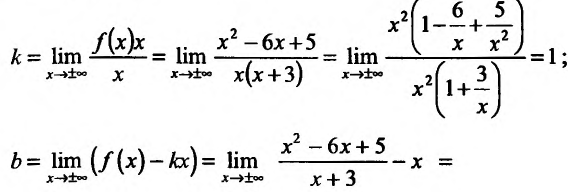
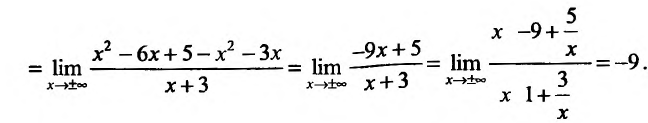
Итак, при  график функции
график функции 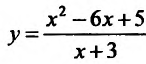 , имеет наклонную асимптоту у=х-9.
, имеет наклонную асимптоту у=х-9.
Исследуем повеление функции на границе области определения. Поведение функции в окрестности точки х = -3 исследовано. Поэтому изучим поведение функции при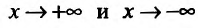 , вычислив пределы:
, вычислив пределы:
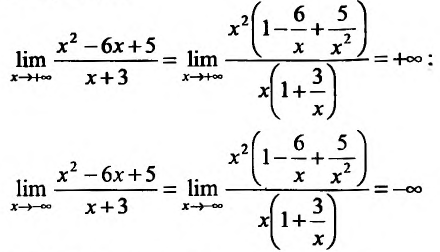
5) Первая производная
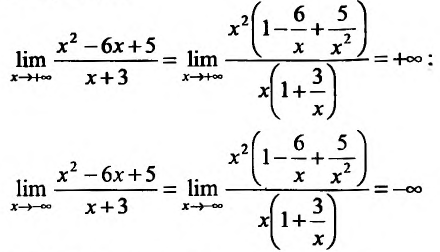
обращается в нуль в точках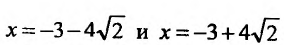 и стремится к бесконечности при
и стремится к бесконечности при 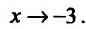 . Для определения интервалов монотонности функции и точек экстремума, построим схему изменения знаков производной:
. Для определения интервалов монотонности функции и точек экстремума, построим схему изменения знаков производной:

Поскольку 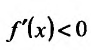 при
при 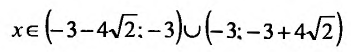 и
и 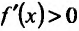 при
при
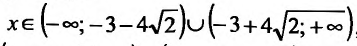 то функция убывает при
то функция убывает при
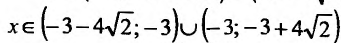 и возрастает при
и возрастает при
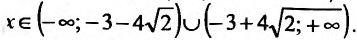 Следовательно, точка
Следовательно, точка
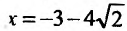 – точка максимума, а точка
– точка максимума, а точка 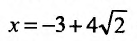 – точка минимума. Значения функции в этих точках равны:
– точка минимума. Значения функции в этих точках равны:
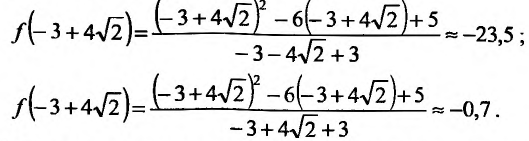
6) Вторая производная не обращается в нуль и стремится к бесконечности при 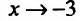 . Построим схему изменения знаков второй производной:
. Построим схему изменения знаков второй производной:
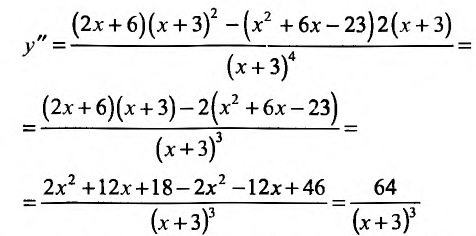
Поскольку  и
и  при
при 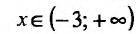 , то график функции является выпуклым вверх на интервале
, то график функции является выпуклым вверх на интервале 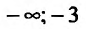 и выпуклым вниз при
и выпуклым вниз при 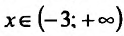 . Точка х = -3 не является точкой перегиба, так как это точка разрыва функции.
. Точка х = -3 не является точкой перегиба, так как это точка разрыва функции.
По результатам исследования строим график функции. Вначале строим систему координат; затем вертикальную и горизонтальную асимптоты; наносим точки пересечения с осями координат и точки экстремума функции. Затем строим график (рис. 14.12).
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
Определение. Множество вещественных чисел ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , называется сегментом или отрезком (обозначается
, называется сегментом или отрезком (обозначается ![]() ), а удовлетворяющих строгому неравенству
), а удовлетворяющих строгому неравенству ![]() – интервалом (обозначается
– интервалом (обозначается ![]() ). Числа
). Числа ![]() и
и ![]() называются концами, а число
называются концами, а число ![]() – длиной как сегмента
– длиной как сегмента ![]() , так и интервала
, так и интервала ![]() .
.
Определение. Множество вещественных чисел ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() или
или ![]() , называется полусегментом или полуинтервалом и обозначается соответственно
, называется полусегментом или полуинтервалом и обозначается соответственно ![]() или
или ![]() .
.
Интервалы и полуинтервалы могут быть и бесконечными. Для обозначения множества вещественных чисел пользуются символом ![]() . Знаки
. Знаки ![]() и
и ![]() не являются числами, (а являются только символами) и для них нельзя указать соответствующих точек прямой. Поэтому в обозначениях интервалов со стороны таких знаков квадратные скобки не ставят. Сегменты, интервалы и полуинтервалы (конечные и бесконечные) объединяют под общим названием – промежутки.
не являются числами, (а являются только символами) и для них нельзя указать соответствующих точек прямой. Поэтому в обозначениях интервалов со стороны таких знаков квадратные скобки не ставят. Сегменты, интервалы и полуинтервалы (конечные и бесконечные) объединяют под общим названием – промежутки.
Определение. Окрестностью точки ![]() называется любой интервал, содержащий эту точку.
называется любой интервал, содержащий эту точку.
Часто рассматривают симметричную окрестность точки ![]() , то есть интервал
, то есть интервал ![]() , при этом
, при этом ![]() называют радиусом окрестности.
называют радиусом окрестности.
Изобразим на прямой окрестность точки 5 радиуса 3:
![]() Для того, чтобы показать, что точка
Для того, чтобы показать, что точка ![]() находится в этой окрестности, воспользуемся неравенством
находится в этой окрестности, воспользуемся неравенством ![]() . В общем случае
. В общем случае ![]() – окрестность
– окрестность ![]() точки
точки ![]() может быть задана неравенством
может быть задана неравенством ![]() .
.
Определение. Окрестностью бесконечно удаленной точки называется внешность некоторого отрезка. Симметричной окрестностью точки ![]() называется внешность любого отрезка, симметричного относительно нуля.
называется внешность любого отрезка, симметричного относительно нуля.
С помощью неравенств ![]() – окрестность бесконечно удаленной точки записывается в виде
– окрестность бесконечно удаленной точки записывается в виде ![]() ,
, ![]() или, объединяя в одно неравенство,
или, объединяя в одно неравенство, ![]() .
.
Определение. Точка ![]() называется предельной точкой множества, если в любой ее окрестности содержится, по крайней мере, одна точка данного множества, отличная от
называется предельной точкой множества, если в любой ее окрестности содержится, по крайней мере, одна точка данного множества, отличная от ![]() .
.
Из определения следует, что в любой окрестности предельной точки содержится бесконечное число точек данного множества. Предельная точка множества может как принадлежать, так и не принадлежать самому множеству.
 Определение. Точка
Определение. Точка ![]() называется внутренней точкой множества, если она принадлежит этому множеству вместе со своей окрестностью.
называется внутренней точкой множества, если она принадлежит этому множеству вместе со своей окрестностью.
Определение. Точка ![]() называется граничной точкой множества, если в любой ее окрестности есть точки как принадлежащие множеству, так и не принадлежащие ему. Сама граничная точка может как принадлежать множеству, так и не принадлежать ему.
называется граничной точкой множества, если в любой ее окрестности есть точки как принадлежащие множеству, так и не принадлежащие ему. Сама граничная точка может как принадлежать множеству, так и не принадлежать ему.
Совокупность граничных точек множества называется его границей.
Определение. Множество, содержащее все свои граничные точки, называется замкнутым, в противном случае – открытым.
Примеры: 1) для множества рациональных чисел ![]() граничными являются все точки отрезка
граничными являются все точки отрезка ![]() как рациональные, так и иррациональные;
как рациональные, так и иррациональные;
2) для множества точек  граничными являются сами точки этого множества и нуль.
граничными являются сами точки этого множества и нуль.
5.03 Числовая последовательность и ее предел
Если каждому натуральному числу ![]() сопоставить вещественное число
сопоставить вещественное число ![]() , тем самым зададим некоторые вещественные числа, определенным образом перенумерованные:
, тем самым зададим некоторые вещественные числа, определенным образом перенумерованные: ![]() имеет номер 1,
имеет номер 1, ![]() – номер 2 и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность:
– номер 2 и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность:
![]() , (1)
, (1)
Которая кратко обозначается ![]() .
.
Числа, составляющие последовательность, называются ее членами, а ![]() – общим или
– общим или ![]() -м членом последовательности. В отличие от числового множества, у которого все элементы различны, последовательность может иметь среди своих членов одинаковые, например:
-м членом последовательности. В отличие от числового множества, у которого все элементы различны, последовательность может иметь среди своих членов одинаковые, например: ![]() или
или ![]() Числовое значение
Числовое значение ![]() зависит от
зависит от ![]() , то есть является функцией от
, то есть является функцией от ![]() , поэтому числовая последовательность может рассматриваться как функция натурального аргумента.
, поэтому числовая последовательность может рассматриваться как функция натурального аргумента.
Пример 1. Последовательность задана общим членом  . Написать
. Написать ![]() члены последовательности.
члены последовательности.
Решение.  ,
,  ,
,  ,
,  .
.
Для сокращения записей в дальнейшем будем использовать логические символы: квантор общности ![]() и квантор существования
и квантор существования ![]() . Запись
. Запись ![]() означает: любой (всякий)
означает: любой (всякий) ![]() , а
, а ![]() – существует (найдется)
– существует (найдется) ![]() .
.
Определение. Последовательность (1) называется ограниченной, если ![]() , такое, что
, такое, что ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Пример 2. Доказать, что последовательности  и
и  – ограниченные, а последовательность
– ограниченные, а последовательность  – не ограничена.
– не ограничена.
Решение. Очевидно, что для любого ![]() справедливо неравенство
справедливо неравенство  . Умножая на 3, получим
. Умножая на 3, получим  .
.
Оценим по модулю общий член последовательности ![]() :
:  .
.
Предположим, что последовательность ![]() ограничена сверху, то есть существует число
ограничена сверху, то есть существует число ![]() такое, что
такое, что  , тогда
, тогда ![]() или
или ![]() , т. е. неравенство
, т. е. неравенство ![]() выполняется не для всех
выполняется не для всех ![]() , а только для
, а только для ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , следовательно,
, следовательно, ![]() не ограничена.
не ограничена.
Определение. Число ![]() называется пределом числовой последовательности
называется пределом числовой последовательности ![]() при
при ![]() , если для всякого
, если для всякого ![]() можно указать номер
можно указать номер ![]() , такой, что для всех членов последовательности с номерами
, такой, что для всех членов последовательности с номерами ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Обозначают ![]() или
или ![]() и говорят, что последовательность сходится к
и говорят, что последовательность сходится к ![]() . Если последовательность не имеет конечного предела, то ее называют расходящейся. Заметим, что величина
. Если последовательность не имеет конечного предела, то ее называют расходящейся. Заметим, что величина ![]() зависит от
зависит от ![]() , которое выбирается произвольно. Чем меньше
, которое выбирается произвольно. Чем меньше ![]() , тем
, тем ![]() , вообще говоря, будет больше (за исключением случая, когда последовательность состоит из одинаковых членов). Очевидно, что если
, вообще говоря, будет больше (за исключением случая, когда последовательность состоит из одинаковых членов). Очевидно, что если ![]() и неравенство
и неравенство ![]() выполняется при
выполняется при ![]() , то оно подавно будет выполняться при
, то оно подавно будет выполняться при ![]() .
.
Пример 3. Показать, что последовательность  имеет своим пределом число 1.
имеет своим пределом число 1.
Решение. По определению предела числовой последовательности ![]()
![]() ,
, ![]()
 .
.
Будем решать последнее неравенство относительно ![]() :
:  . Таким образом, получили, что неравенство
. Таким образом, получили, что неравенство  выполняется не для всех номеров
выполняется не для всех номеров ![]() , а только для тех, которые больше
, а только для тех, которые больше ![]() , следовательно, за
, следовательно, за ![]() можно взять целую часть числа
можно взять целую часть числа ![]() , то есть
, то есть  . Если окажется, что
. Если окажется, что  , то
, то ![]() можно взять равным 1. В определении говорится, что
можно взять равным 1. В определении говорится, что ![]() может быть любым положительным числом, в частности, если
может быть любым положительным числом, в частности, если ![]() , то
, то  , если
, если  , то
, то  и т. д.
и т. д.
Пример 4. Показать, что последовательность, заданная общим числом  , имеет своим пределом число
, имеет своим пределом число ![]() .
.
Решение. Возьмем любое ![]() . Так как
. Так как 
 , то из неравенства
, то из неравенства  получим
получим  , то есть достаточно взять
, то есть достаточно взять  и тогда
и тогда  при
при ![]() .
.
Пример 5. Показать, что числовая последовательность с общим членом ![]() не имеет предела.
не имеет предела.
Решение. В подробной записи эта последовательность имеет вид: ![]()
Будем рассуждать от противного. Пусть последовательность имеет своим пределом некоторое число ![]() . Тогда по определению предела для любого
. Тогда по определению предела для любого ![]() , в том числе и для
, в том числе и для ![]() , найдется
, найдется ![]() , что
, что  для
для ![]() . Так как
. Так как ![]() принимает попеременно значения 1 и –1, то должно быть
принимает попеременно значения 1 и –1, то должно быть  и
и  . Тогда получим
. Тогда получим  , то есть
, то есть ![]() , чего быть не может.
, чего быть не может.
Для доказательства того, что некоторое число ![]() не является пределом последовательности, достаточно убедиться, что не все требования, сформулированные в определении предела, выполнены. Допустим, что
не является пределом последовательности, достаточно убедиться, что не все требования, сформулированные в определении предела, выполнены. Допустим, что ![]() не является пределом данной последовательности. Это значит, что Нельзя для Любого
не является пределом данной последовательности. Это значит, что Нельзя для Любого ![]() найти соответствующий
найти соответствующий ![]() , о котором говорится в определении, то есть существует хотя бы одно
, о котором говорится в определении, то есть существует хотя бы одно ![]() , для которого невозможно найти такого
, для которого невозможно найти такого ![]() , чтобы неравенство
, чтобы неравенство ![]() выполнялось бы для всех
выполнялось бы для всех ![]() . Иначе говоря, найдется хотя бы одно значение
. Иначе говоря, найдется хотя бы одно значение ![]() , для которого
, для которого ![]() .
.
Пример 6. Доказать, пользуясь определением предела, что число ![]() не является пределом последовательности с общим членом
не является пределом последовательности с общим членом  .
.
Решение. Оценим снизу абсолютную величину разности ![]() :
:  , так как
, так как  при любом
при любом ![]() . Следовательно, если взять в качестве
. Следовательно, если взять в качестве  , то
, то  и искать
и искать ![]() в соответствии с определением бессмысленно.
в соответствии с определением бессмысленно.
Дадим геометрическое истолкование предела числовой последовательности.
 |
Числовую последовательность можно рассматривать как последовательность точек прямой и о пределе можно говорить как о точке на прямой. Так как неравенство ![]() равносильно неравенству
равносильно неравенству ![]() , то определение предела можно сформулировать так: точка
, то определение предела можно сформулировать так: точка ![]() будет пределом последовательности точек
будет пределом последовательности точек ![]() если, какую бы окрестность
если, какую бы окрестность ![]() точки
точки ![]() мы ни задали, найдется
мы ни задали, найдется ![]() такое, что все точки последовательности с номерами
такое, что все точки последовательности с номерами ![]() попадут в заданную окрестность.
попадут в заданную окрестность.
![]()
![]() Вне этой окрестности может оказаться лишь Конечное число точек
Вне этой окрестности может оказаться лишь Конечное число точек ![]() .
.
Общий член последовательности можно рассматривать как переменную, принимающую эту последовательность значений, поэтому предел последовательности (1) называют также и пределом переменной ![]() .
.
Вопросы для самопроверки и упражнения.
1. Дана последовательность точек ![]()
![]() Все точки этой последовательности, начиная с пятой, находятся в окрестности нуля
Все точки этой последовательности, начиная с пятой, находятся в окрестности нуля ![]() . Почему из этого, однако, не следует, что точка нуль является пределом данной последовательности?
. Почему из этого, однако, не следует, что точка нуль является пределом данной последовательности?
2. Пользуясь определением предела числовой последовательности, доказать, что  . Начиная с какого
. Начиная с какого ![]() , будет
, будет ![]()
 ?
?
3. Доказать, что число 1 не является пределом переменной  .
.
4. Привести пример ограниченной последовательности, не имеющей предела.
| < Предыдущая | Следующая > |
|---|
