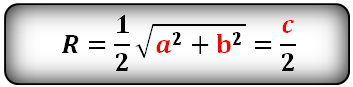Радиус описанной окружности около прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
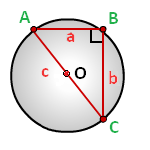
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.
На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
( small R=frac<large c> <large 2 sin C>)
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
( small R=frac<large c><large 2 sin 90°>=frac<large c><large 2>, )
| ( small R=frac<large c><large 2>. ) | (1) |
Пример 1. Известна гипотенуза ( small с=frac<9> <2>) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac<9> <2>) в (1):
Ответ:
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).
Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
| ( small c=sqrt. ) | (2) |
Подставляя (2) в (1), получим:
| ( small R=frac<large sqrt><large 2>. ) | (3) |
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):
Ответ:
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
 |
(4) |
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.
Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
( small angle A+angle B=90°. )
| ( small angle A=90°-angle B. ) | (5) |
Подставляя (5) в (4), получим:
( small R=frac<large a><large 2 sin A>=frac<large a><large 2 sin(90°-B)>) ( small =frac<large a> <large 2 cos B>)
| ( small R=frac<large a><large 2 cos B>. ) | (6) |
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):
Ответ:
Узнать ещё
Знание — сила. Познавательная информация
Окружность, вписанная в прямоугольный треугольник
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.
Дано: ∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) По свойству отрезков касательных, проведенных из одной точки,
AK=AM=6 см,
2) AB=AM+BM=6+4=10 см,
3) По теореме Пифагора:
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
Ответ: 24 см, 24 см², 2 см.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.
Дано:∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a , b – катеты прямоугольного треугольника
c – гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Калькулятор – вычислить, найти радиус описанной окружности прямоугольного треугольника
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-22-04-52-48
[/spoiler]
Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b – катеты прямоугольного треугольника
c – гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Калькулятор – вычислить, найти радиус описанной окружности прямоугольного треугольника
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Утверждение.
Радиус вписанной в прямоугольный треугольник окружности равен
где a и b — катеты, c — гипотенуза.
Доказательство:
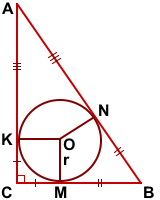
Проведём радиусы OK, OM, ON к сторонам треугольника.
(как радиусы, проведённые в точку касания).
(как отрезки касательных, проведённых из одной точки).
Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.
Следовательно,
то есть
Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности
Что и требовалось доказать.
ВИДЕОУРОК
Вписанная окружность
прямоугольного треугольника.
Радиус окружности,
вписанной в прямоугольный треугольник,
можно найти по формуле:
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности
равен произведению катетов, делённому на сумму
катетов и гипотенузы,
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:
где р – полупериметр
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки 2 см и 8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
ВМ
= ВN = х.
(2 + х)2 + (2 + 8)2 = (8
+ х)2,
х2 + 4х + 4
+ 100 =
= х2 + 16х + 64,
12х = 40,
х =
10/3 (см).
Р = (2 + 8) + (8 + 10/3) + (10/3 + 2) = 262/3 (см).
ЗАДАЧА:
Вписанная окружность прямоугольного треугольника АВС касается гипотенузы АВ в точке
К. Найдите радиус
вписанной окружности, если АК = 4 см, ВК
= 6 см.
РЕШЕНИЕ:
За свойством касательных имеем:
АК = АМ = 4 см,
ВК = ВN = 6 см.
Обозначим радиус вписанной окружности
через х:
СN = СM = NО = МО = х.
Тогда
АС =
(4 + х) см.
ВС = (6 + х) см,
АВ =
4 см +
6 см =
10 см.
По теореме Пифагора для треугольника АВС
можно записать соотношение:
(4 + х)2 + (6 + х)2 = 102.
Решим это квадратное уравнение:
16 + 8x + x2
+ 36 + 12x + x2 = 100,
2x2 + 20x + 52 – 100 = 0,
2x2 + 20x – 48 = 0,
x2 + 10x – 24 = 0,
x1 = 2, x2 = –10.
x2 не
удовлетворяет условию задачи.
ОТВЕТ: 2 см.
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки 8 см и 12
см. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
(8 + 12)2
= (8 + х)2 + (12 + х)2,
400 = 64 + 16x + x2
+ x2 + 24x + 144,
2x2 + 40x – 192 = 0,
x2 + 20x – 96 = 0,
x1 = 4, x2 = –24.
x2 не
подходит.
Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).
ОТВЕТ: 48 см.
Описанная окружность
прямоугольного треугольника.
Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.
Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.
Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.
ОА = ОВ = ОС = R
Радиус описанной окружности равен половине
гипотенузы:
ЗАДАЧА:
Отрезок ВС – диаметр окружности, изображённой на рисунку.
Угол АВС = 55°.
Найдите
величину
угла АСВ
?
РЕШЕНИЕ:
ВС – диаметр,
поэтому ∠ ВАС = 90°,
∠ АСВ = 180° – (90° + 55°) = 35°.
ЗАДАЧА:
Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.
РЕШЕНИЕ:
Пусть АВ – диаметр окружности с
центром в точке О, СD ⊥ АВ,
где С – точка окружности,
СD = 6 см, АD = х см,
ВD – АD = 5 см.
Тогда
DВ = (х + 5) см.
Треугольник АСВ – прямоугольный (угол С прямой, так как
он вписанный и опирается на диаметр).
СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:
АD ∙ DВ = СD2,
х(х + 5) = 62,
х2
+ 5х – 36 = 0,
x1 = –9, x2 = 4.
x1 не подходит.
Поэтому, АD = 4 см,
DВ = 4 + 5 = 9 (см).
АВ
= АD
+ DВ
=
=
4
+ 9 = 13 (см).
Тогда
r = АВ :
2 = 13 : 2 = 6,5 (см).
ОТВЕТ: 6,5 см
ЗАДАЧА:
Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна 4 см. Найдите эти хорды, если радиус окружности равен 10
см.
РЕШЕНИЕ:
Пусть задана окружность радиуса R,
в
которой
проведены
хорды АВ и
АС (АВ ⊥ АС),
R = АО = ВО = СО =
10 см,
АС – АВ =
4
см.
Пусть АВ = х см, тогда
АС = (4
+ х) см.
Так как ∠ А = 90°, то треугольник
ВАС –
прямоугольный,
в
котором
ВС = 2ОВ= 2 ∙ 10 = 20 см.
Из
прямоугольного треугольника ВАС имеем:
АВ2 + АС2
= ВС2,
х2 + (4 + х)2
= 202,
х2 + 16 + 8х
+ х2 = 400,
х2 + 4х –
192 = 0,
х1 = 12,
х2
= –16 – не подходит.
Поэтому,
АВ = 12 см,
АС
= 4 + 12 = 16 (см).
ОТВЕТ: 12
см, 16 см
ЗАДАЧА:
Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.
РЕШЕНИЕ:
Начертим чертёж.
Так как треугольник
прямоугольный и медиана ВМ иcходит
из прямого угла В, то точка М является центром
описанной окружности вокруг треугольника
АВС.
Следовательно,
АМ
= МС = МВ = R,
где R –
радиус описанной окружности.
Найдём сначала угол МВС.
Учитывая, что BD – биссектриса, то
∠ DВС = 90/2 = 45°. Тогда
∠ МВС = ∠ МВD + ∠ DВС,
∠ МВС = 14° + 45° = 59°.
Рассмотрим
равнобедренный треугольник МВС со сторонами
МВ = МС,
в
котором углы при основании ВС равны, то есть
∠ С = ∠ МВС
= 59°.
Так
как сумма острых углов в прямоугольном треугольнике равна 90°, то
∠ А + ∠ С = 90°,
∠ А = 90° – ∠ С =
= 90° – 59° = 31°.
ЗАДАЧА:
Периметр
прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.
РЕШЕНИЕ:
DO = OF = OE = r = 6 м.
Поэтому AD =
AF =
6 м.
FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)
Пусть
BD = BE = x,
FC = EC = y,
Тогда
AB
= x + 6, AC = y + 6,
BC = x + y.
AB + AC + BC =
= x + 6 + y + 6
+ x + y = 72.
2x + 2y + 12 = 72,
2x + 2y = 60,
x + y = 30.
(x + y) – гипотенуза, или диаметр описанной окружности.
ОТВЕТ: 30 м.
ЗАДАЧА:
В окружности на расстоянии 6
см от его центра проведена хорда длинной 16
см. Найдите радиус окружности.
РЕШЕНИЕ:
Начертим чертёж:
Пользуясь теоремой
Пифагора, находим радиус.
ЗАДАЧА:
Две окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.
РЕШЕНИЕ:
ВК ⊥ АD, АК = 9 – 4 = 5 см.
Из ∆ ВКА:
Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1)
β=90°-α
a=c sinα
b=c cosα
Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов.
P=a+b+c=c sinα+c cosα+c=c(sinα+cosα+1)
Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения.
S=ab/2=(sinα cosα)/2
Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2)
h=b sinα=c cosα sinα
Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.3)
m_с=c/2
m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗α+〖c^2 cos^2〗α )/2=(с√(3 sin^2α+1))/2
m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2α+sin^2α )/2=(с√(3 cos^2α+1))/2
Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.4)
l_с=(ab√2)/(a+b)=(c sinα cosα √2)/(sinα+cosα )
l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cosα √(2c(c cosα+c) ))/(c cosα+c)=(c cosα √(2(cosα+1) ))/(cosα+1)
l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sinα √(2c(c sinα+c) ))/(c sinα+c)=(c sinα √(2(sinα+1) ))/(sinα+1)
Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7)
M_a=a/2=(c sinα)/2
M_b=b/2=(c cosα)/2
M_c=c/2
Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее. Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два. Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6)
r=(a+b-c)/2=(c sinα+c cosα-c)/2=c/2 (sinα+cosα-1)
R=c/2