Как найти операцию mod

Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом^[1]. Пусть и  — целые числа, причём Деление с остатком («делимого») на («делитель») означает нахождение таких целых чисел и , что выполняется равенство:

Таким образом, результатами деления с остатком являются два целых числа: называется неполным частным от деления, а  — остатком от деления. На остаток налагается дополнительное условие: то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения при заданных выше условиях. Если остаток равен нулю, говорят, что нацело делится на

Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Примеры

Проверка:

Проверка:

Проверка:

Проверка:

Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.

Определение[править | править код]

Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль^[2], либо теория сразу формулируется для целых чисел, как указано выше^[1].

Для вычисления неполного частного от деления на положительное число следует разделить (в обычном смысле) на и округлить результат до ближайшего целого в меньшую сторону:

когда .

где полускобки обозначают взятие целой части. Значение неполного частного позволяет вычислить значение остатка по формуле:

Для отрицательного делителя нужно округлять частное в большую сторону:

когда .

Операция «mod» и связь со сравнениями[править | править код]

Величина остатка может быть получена бинарной операцией «взятия остатка» от деления на , обозначаемой mod:

Не следует путать это обозначение с обозначением сравнения по модулю . Формула для влечёт выполнение сравнения:

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства , необходимого для того, чтобы было остатком.

В программировании[править | править код]

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:

78 mod 33 = 12
78 div 33 = 2

Знак остатка[править | править код]

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

• Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
• Знак остатка совпадает со знаком делителя: неполное частное округляет к .

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти^[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.

Как запрограммировать, если такой операции нет?[править | править код]

Неполное частное можно вычислить через деление и взятие целой части: , где , в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды mod остаток программируется как .

Если положительно, а знак совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой .

Неполное частное и неотрицательный остаток от деления на степень двойки  — это битовый сдвиг (для чисел со знаком — арифметический) и .

Обобщения[править | править код]

Вещественные числа[править | править код]

Если два числа и (отличное от нуля) относятся к множеству вещественных чисел, может быть поделено на без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

Формально:

если , то , где .

Пример

Деление 7,9 на 2,1 с остатком даёт:

(неполное частное);

(остаток).

Гауссовы целые числа[править | править код]

Гауссово число — это комплексное число вида , где  — целые числа. Для них можно определить деление с остатком: любое гауссово число можно разделить с остатком на любое ненулевое гауссово число , то есть представить в виде:

,

где частное и остаток  — гауссовы числа, причём
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, можно разделить на тремя способами:

Многочлены[править | править код]

При делении с остатком двух многочленов и для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:

, причём .

Пример

(остаток 3), так как: .

См. также[править | править код]

• Алгоритм Евклида
• Делимость
• Наибольший общий делитель
• Непрерывная дробь
• Сравнение по модулю

Примечания[править | править код]

Так как в воскресенье на сайте открывается новая рубрика — решение задач,  мы с вами должны по-быстрому изучить основную часть математических операций, функций и процедур.

Давайте разберемся, что такое функция и процедура. Это подпрограмма — часть программы, выполняющая определенный алгоритм и допускающая обращение к ней из различных частей общей программы. В чем же разница между процедурой и функцией?

Процедуры — мини-программы.

Процедуры используются в случаях, когда в подпрограмме необходимо получить несколько результатов. Из картинки, расположенной ниже вы видите, как работает процедура. Входных данных может не быть вовсе, а может быть сто.

Например, программист хочет в своем суперкоде между блоками выходящих значений прописывать 20 амперсандов. Чтобы облегчить себе задачу, он напишет простую подпрограмму.

program superpuper;
var очень много буковок; 
procedure ampersand; 
begin 
write('&&&&&&&&&&&&&&&&&&&&'); 
end;
begin 
суперсложный код;
ampersand; 
суперсложный код;
ampersand; 
суперсложный код; 
ampersand; 
суперсложный код; 
ampersand; 
end.

Функции в Паскале — мега переменные.

Функции отличается от процедуры тем, что после выполнения функции на ее месте в коде ставится одно число, буква, строка и т.д. Набор встроенных функций в языке Паскаль достаточно широк. Например, для того, чтобы подсчитать квадрат числа можно воспользоваться стандартной функцией sqr(x). Как вы, наверное, уже поняли sqr(x) требует лишь один фактический параметр — число.

Пример: a:=sqr(4).

Обратите внимание! Функции необходимо присваивать! Просто написав их в тексте программы, как процедуры, вы ничего не добьетесь!

Структура функции представлена на картинке ниже.

Если в программу необходимо включить новую уникальную функцию, ее надо описать также, как процедуру. Более подробно о том, как делать собственные процедуры и функции, мы поговорим через 10 уроков. Ниже вы видите таблицу основных стандартных функций и процедур в Паскаль.

Иногда нам требуется найти частное либо же остаток от деления. В такие моменты на помощь нам приходят такие операции, как div и mod. Заметим, что эти операции выполняются только над целыми числами.

Div

Для того, чтобы найти частное от деления, мы используем операцию div.

   Примеры:

• 25 div 20 = 1;
• 20 div 25 = 0;
• 39 div 5 = 7;
• 158 div 3 = 52.

Mod

Для того, чтобы найти остаток от деления, мы используем операцию mod.

    Примеры:

• 25 mod 20 = 5;
• 20 mod 25 = 0;
• 39 mod 5 = 4;
• 158 mod 3 = 2.

Чтобы окончательно понять, с чем мы имеем дело, решим следующую задачу:

Задача 1. Найти сумму цифр двухзначного числа.

Так как эта задача очень простая, мы с вами обойдемся блок-схемой и программой.

program Sumoftwo;
var Number, Num1, Num2, Sum: integer;
begin
write('Введите двухзначное число: ');
read(Number);  { Возьмем число 25 }
Num1 := Number div 10; { 25 div 10 = 2 }
Num2 := Number mod 10; { 25 mod 10 = 5 }
Sum := Num1 + Num2; { 2 + 5 = 7 }
write('Сумма двух чисел -- ', Sum);
end.

Задача 2. Найти сумму цифр трехзначного числа.

Чуть усложненная версия предыдущей задачи. Самая большая сложность — вторая цифра.

program Sumoftree;
var Number, Sum: integer;
begin
write('Введите трехзначное число: ');
read(Number);  { Возьмем число 255 }
Sum := Number div 100 + Number mod 10 + Number div 10 mod 10; { 255 div 100 + 255 mod 10 + 255 div 10 mod 10 = 12 }
write('Сумма трёх чисел -- ', Sum);
end.

Вот и всё. На следующем уроке мы с вами начнём изучать особенности PascalABC.Net.

Теги: sql, java, оператор, mod, запросы, таблицы, деление, operator, остаток

Оператор mod обозначается символом % и является оператором деления по модулю. Он возвращает остаток от деления 1-го операнда на 2-й и широко используется в разных языках программирования для решения ряда задач.

Оператор mod в Java

В Java operator mod может работать как с целыми числами (byte/int/short/long), так и с плавающей точкой (byte/int/short/long). Давайте приведём пример работы оператора mod при делении:

class Modulus { 
public static void main (String args []) { 
int x = 42; 
double у = 42.3; 
System.out.print("x mod 10 = " + x % 10); 
System.out.println("y mod 10 = " + у % 10); 
} 
}


После выполнения этой программы вы получите результат следующего вида:
х mod 10 = 2 у mod 10 = 2.3


Как видим, оператор mod — это прекрасный способ найти остаток от деления. Зачем это может понадобиться на практике? Например, при нахождении кратности числа и определении, является ли некоторое число, введённое с клавиатуры, чётным. Также с помощью оператора mod можно узнать, делится ли одно число на другое без остатка или определить последнюю цифру числа. В общем, оператор mod очень полезен при решении различных задач по программированию. 
Оператор mod в SQL
Не менее интересно использование mod в базах данных. Аналогично, mod находит остаток от деления. При этом вместо mod можно задействовать операцию %, делающую то же самое. Синтаксис в SQL следующий:
SELECT MOD(что_делить, на_что_делить) FROM имя_таблицы WHERE условие


Но можно написать и иначе, используя %:



  


                       
  




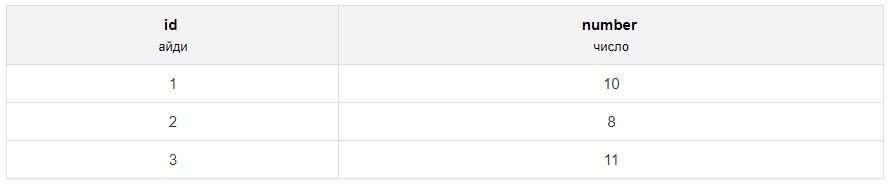
SELECT что_делить % на_что_делить FROM имя_таблицы WHERE условие


Давайте приведём пример использования mod в базах данных. Вот, например, таблица numbers:

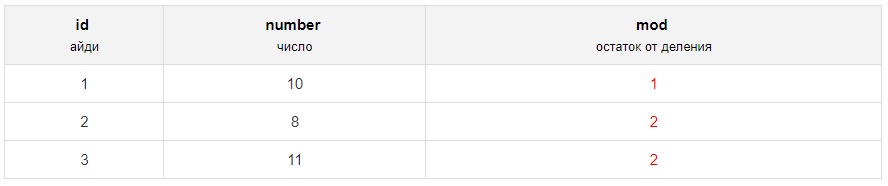
Найдём остаток от деления столбца number на три:
SELECT *, MOD(number, 3) as mod FROM numbers


В результате запрос SQL выберет следующие строки:

Но, как мы уже говорили выше, этот же запрос можно без проблем переписать:
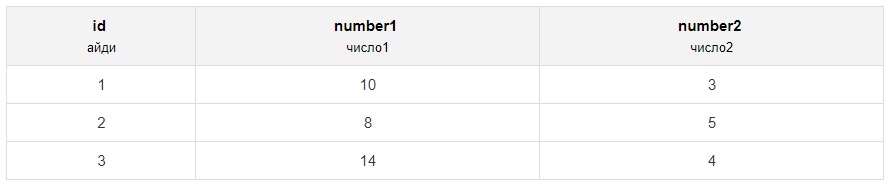
SELECT id, number % 3 as mod FROM numbers


Идём дальше. Теперь возьмём таблицу посложнее:



  


                       
  





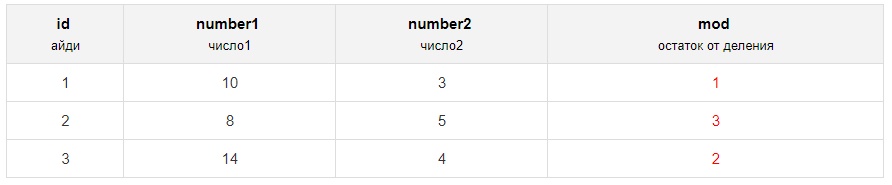
Здесь найдём остаток от деления столбца number1 на number2:
SELECT *, MOD(number1, number2) as mod FROM numbers


Получим следующие строки:

Опять же, этот же самый запрос можно оформить иначе:
SELECT *, number1 % number2 as mod FROM numbers


А где вы используете mod? Пишите в комментариях!

Время на прочтение
4 мин

Количество просмотров 229K

Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!

Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.

Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.

В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»

Позовите ребят из секты «mod не остаток»! Это для вас.

Что такое mod?

Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.

Термин mod означает операцию modulo, с модулем 2 в данном случае. Большинство языков программирования используют % для обозначения такой операции: 5 % 2 = 1.

Вот где мы попадаем в странную серую область.

Математика циферблата

Помню, как учил это в школе, а потом забыл. Существует тип математики, называемый «модульной арифметикой», которая имеет дело с циклическими структурами. Самый простой способ представить это — циферблат с циклом 12. Для математика циферблат — это mod 12. Если хотите понять, можно ли равномерно разделить 253 часа на дни, то можете применить операцию 253 mod 24, результатом будет 13, поэтому ответ «нет»! Мы можем ответить «да» только если результат 0.

Другой вопрос, который вы можете задать: «Если я выеду в 6 вечера, сколько времени будет по приезду через 16 часов?». Это будет 6 + 16 mod 12, то есть 10.

Криптографы любят mod, потому что при использовании с действительно большими числами можно создать нечто, известное как «односторонние функции». Это специальные функции, которые позволяют легко вычислить что-то в одном направлении, но не в обратном.

Если я скажу вам, что 9 является результатом возведения в квадрат, вы можете легко определить, что на входе было 3. Перед вами весь процесс от начала до конца. Если я скажу, что 9 является результатом mod 29, то будет сложнее понять, что на входе.

Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.

Впрочем, не будем отклоняться от темы.

Остатки и математика циферблата

Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.

Рассмотрим такую задачу:

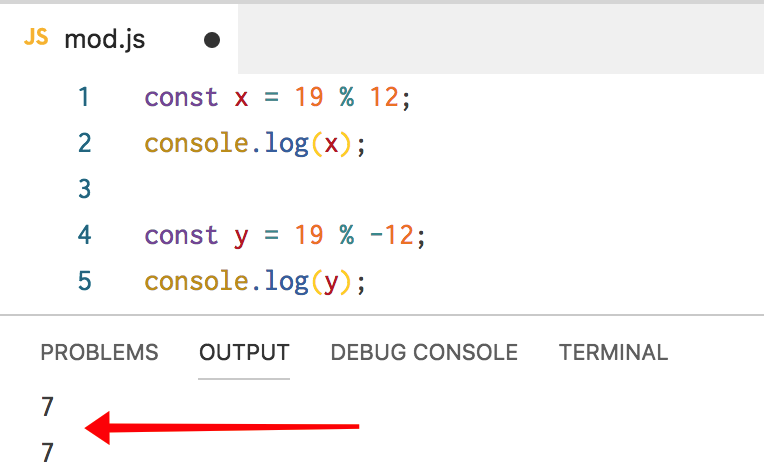
const x = 19 % 12;
console.log(x);

Каково значение x? Делим числа и получаем 7 как остаток от 12. Это верный ответ. Как насчет такого:

const y = 19 % -12;
console.log(y);

Используя обычную математику, мы можем умножить -12 на -1, что даёт 12, и у нас по-прежнему остаётся 7, поэтому наш ответ снова 7.

JavaScript с этим согласен:

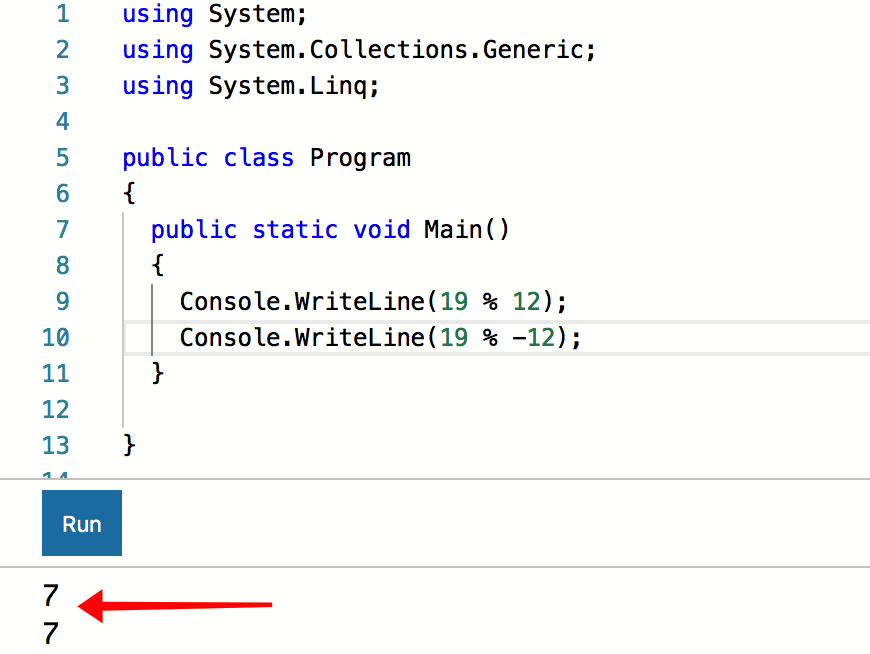
C# тоже согласен:

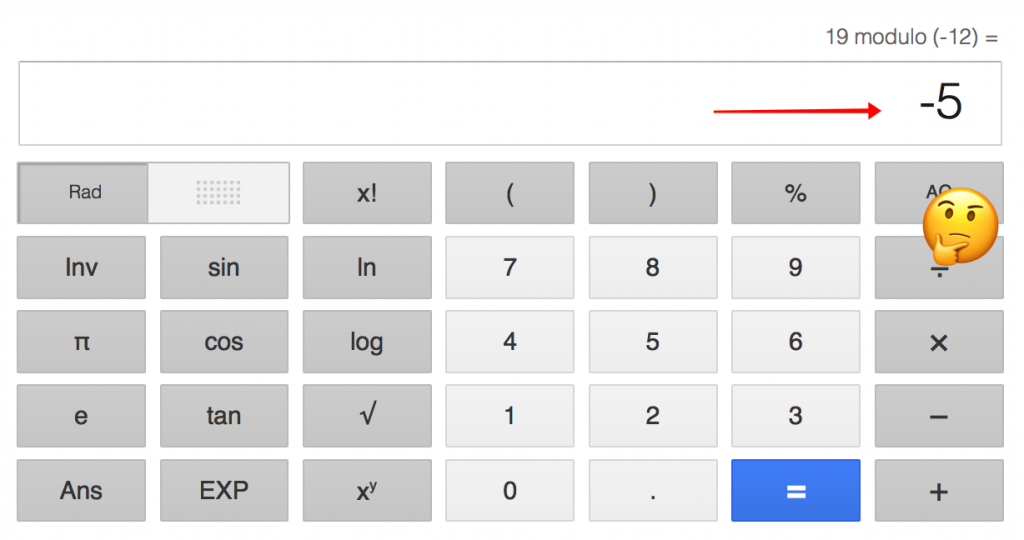
Google согласен с первым утверждением, но не согласен со вторым:

Ruby согласен с Google:

Во имя Дейкстры, что здесь происходит?

Вращение часов назад

Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.

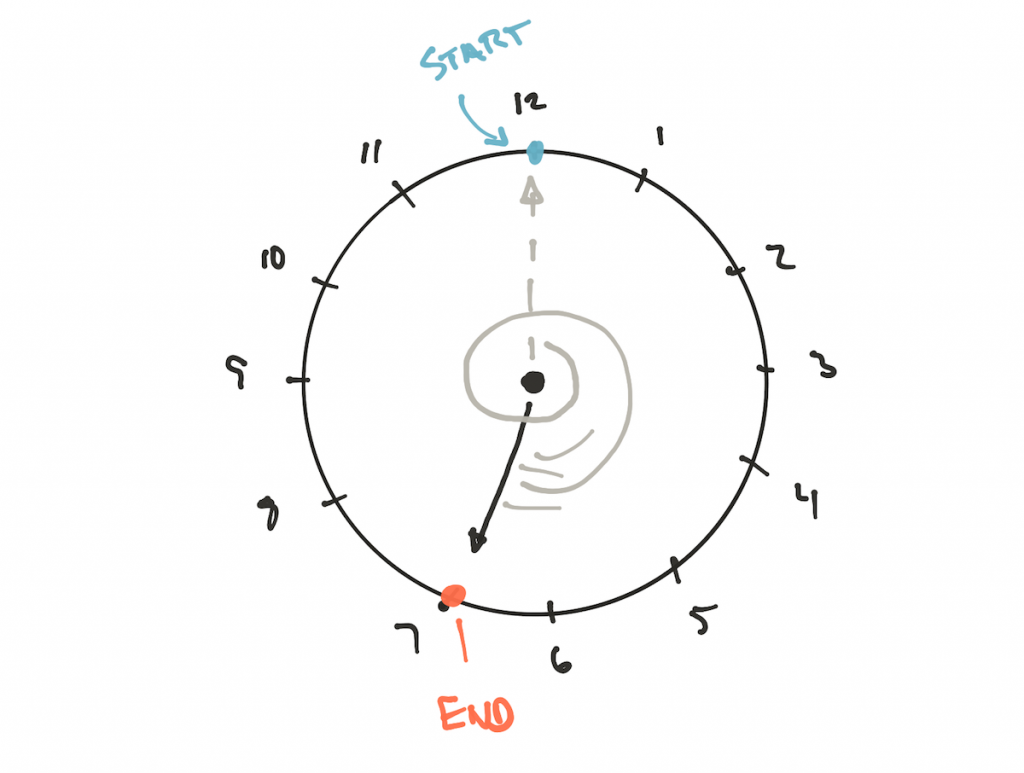
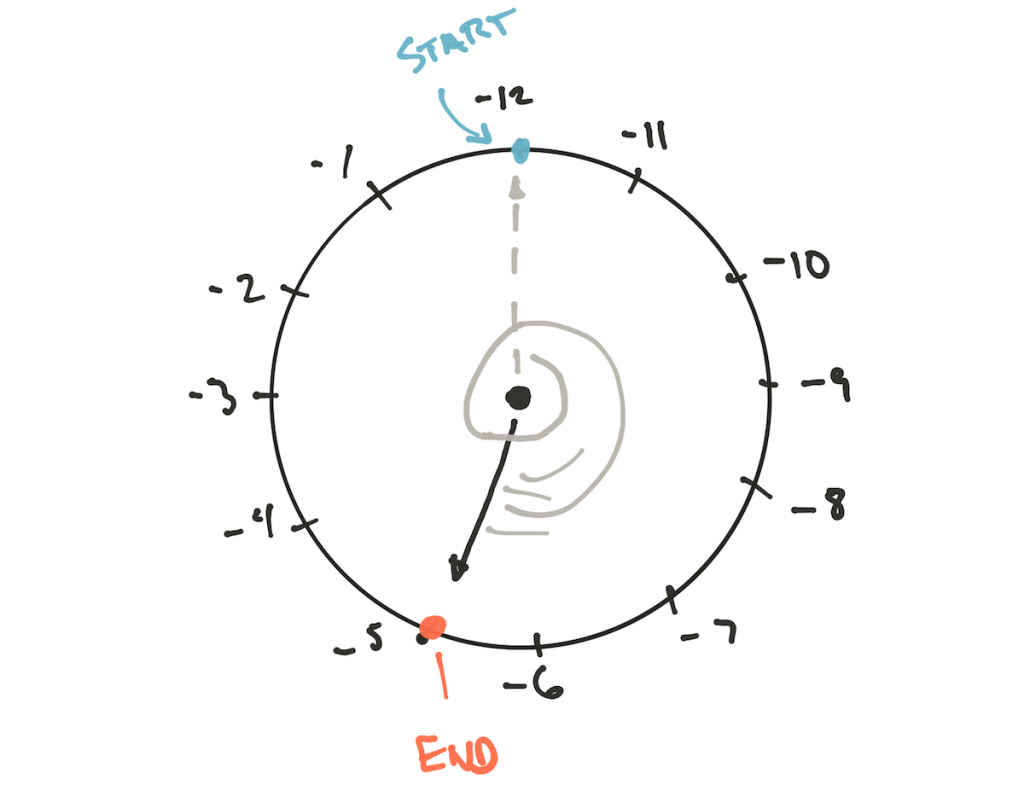
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:

Конечный результат 7. Мы это знаем и мы можем доказать математически. Но что насчёт 19 mod -12? Здесь нужно использовать другие часы:

Модуль равен -12, и мы не можем игнорировать или изменить его, умножив на -1, поскольку модульная арифметика так не работает. Единственный способ правильно рассчитать результат — переставить метки на часах так, чтобы мы двигались от -12 или вращали часы против часовой стрелки, что даёт тот же результат.

Почему не начать метки с -1, двигаясь к -2, и т.д.? Потому что в таком случае мы будем двигаться назад и постоянно уменьшать результат, пока не достигнем -12, и в этот момент сделаем прыжок +12, а modulo так не работает.

Это известная вещь

Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:

Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.

Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:

Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.

А как на вашем языке?

Ну и что?

Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:

1. Я представляю, как этот вопрос займёт меня врасплох на собеседовании.
2. Я представляю, как этот попадёт в продакшн, а разработчики будут несколько часов выяснять, почему математика не работает.

Это также забавный факт на случай, если рядом появится ваш педантичный друг-программист.