Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 марта 2022 года; проверки требуют 2 правки.
Опера́тор Лапла́са (лапласиа́н, оператор дельта) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом 

в n-мерном пространстве.
Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции: 


Оператор Лапласа для вектора 

Лапласиан вектора – тоже вектор.
Другое определение оператора Лапласа[править | править код]
Оператор Лапласа является естественным обобщением на функции нескольких переменных обычной второй производной функции одной переменной. В самом деле, если функция 


при
,
при
вторая производная есть предел
Если, переходя к функции 





функции 







Одновременно с предыдущим представлением для оператора Лапласа функции 
где
— объём окрестности
Эта формула выражает непосредственную связь лапласиана функции с её объёмным средним в окрестности данной точки.
Доказательство этих формул можно найти, например, в[3].
Вышеизложенные пределы, во всех случаях, когда они существуют, могут служить определением оператора Лапласа функции 
Выражения для оператора Лапласа в различных криволинейных системах координат[править | править код]
В произвольных ортогональных криволинейных координатах в трёхмерном пространстве 
- где
— коэффициенты Ламе.
Цилиндрические координаты[править | править код]
В цилиндрических координатах вне прямой 
Сферические координаты[править | править код]
В сферических координатах вне начала отсчёта (в трёхмерном пространстве):
или
В случае если 
Параболические координаты[править | править код]
В параболических координатах (в трёхмерном пространстве) вне начала отсчёта:
Цилиндрические параболические координаты[править | править код]
В координатах параболического цилиндра вне начала отсчёта:
Общие криволинейные координаты и римановы пространства[править | править код]
Пусть на гладком многообразии 


.
Обозначим через 

.
Дивергенция векторного поля 


,
а компоненты градиента функции f — по формуле
Оператор Лапласа — Бельтрами на 
Значение 
Применение[править | править код]
С помощью данного оператора удобно записывать уравнения Лапласа, Пуассона и волновое уравнение. В физике оператор Лапласа применим в электростатике и электродинамике, квантовой механике, во многих уравнениях физики сплошных сред, а также при изучении равновесия мембран, плёнок или поверхностей раздела фаз с поверхностным натяжением (см. Лапласово давление), в стационарных задачах диффузии и теплопроводности, которые сводятся, в непрерывном пределе, к обычным уравнениям Лапласа или Пуассона или к некоторым их обобщениям.
Вариации[править | править код]
- Оператор Д’Аламбера — обобщение оператора Лапласа для гиперболических уравнений. Включает в себя вторую производную по времени.
- Векторный оператор Лапласа — обобщение оператора Лапласа на случай векторного аргумента.
См. также[править | править код]
- Оператор набла
- Оператор Д’Аламбера
- Уравнение Лапласа
- Гармоническая функция
- Матрица Кирхгофа
- В.Г.Воднев, А.Ф.Наумович, Н.Ф.Наумович “Математический словарь высшей школы”. Издательство МПИ 1984.
Примечания[править | править код]
- ↑ Стоит избегать обозначения для оператора Лапласа в виде квадрата оператора набла, поскольку из такой записи непонятно, скалярное или векторное произведение подразумевается под возведением в квадрат.
- ↑ В.Г.Воднев, А.Ф.Наумович, Н.Ф.Наумович “Математический словарь высшей школы”. Издательство МПИ 1984. Статья “Оператор Лапласа” и “Ротор векторного поля”.
- ↑ Тиман А. Ф., Трофимов В. Н. Введение в теорию гармонических функций. М. Наука. 1968 г. 208с.
Ссылки[править | править код]
- MathWorld description of Laplacian Архивная копия от 17 июня 2020 на Wayback Machine
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols 



The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that density distribution. Solutions of Laplace’s equation Δf = 0 are called harmonic functions and represent the possible gravitational potentials in regions of vacuum.
The Laplacian occurs in many differential equations describing physical phenomena. Poisson’s equation describes electric and gravitational potentials; the diffusion equation describes heat and fluid flow, the wave equation describes wave propagation, and the Schrödinger equation describes the wave function in quantum mechanics. In image processing and computer vision, the Laplacian operator has been used for various tasks, such as blob and edge detection. The Laplacian is the simplest elliptic operator and is at the core of Hodge theory as well as the results of de Rham cohomology.
Definition[edit]
The Laplace operator is a second-order differential operator in the n-dimensional Euclidean space, defined as the divergence (



|
|
(1) |
where the latter notations derive from formally writing:
Explicitly, the Laplacian of f is thus the sum of all the unmixed second partial derivatives in the Cartesian coordinates xi:
|
|
(2) |
As a second-order differential operator, the Laplace operator maps Ck functions to Ck−2 functions for k ≥ 2. It is a linear operator Δ : Ck(Rn) → Ck−2(Rn), or more generally, an operator Δ : Ck(Ω) → Ck−2(Ω) for any open set Ω ⊆ Rn.
Motivation[edit]
Diffusion[edit]
In the physical theory of diffusion, the Laplace operator arises naturally in the mathematical description of equilibrium.[1] Specifically, if u is the density at equilibrium of some quantity such as a chemical concentration, then the net flux of u through the boundary ∂V of any smooth region V is zero, provided there is no source or sink within V:
where n is the outward unit normal to the boundary of V. By the divergence theorem,
Since this holds for all smooth regions V, one can show that it implies:
The left-hand side of this equation is the Laplace operator, and the entire equation Δu = 0 is known as Laplace’s equation. Solutions of the Laplace equation, i.e. functions whose Laplacian is identically zero, thus represent possible equilibrium densities under diffusion.
The Laplace operator itself has a physical interpretation for non-equilibrium diffusion as the extent to which a point represents a source or sink of chemical concentration, in a sense made precise by the diffusion equation. This interpretation of the Laplacian is also explained by the following fact about averages.
Averages[edit]
Given a twice continuously differentiable function 










and
Density associated with a potential[edit]
If φ denotes the electrostatic potential associated to a charge distribution q, then the charge distribution itself is given by the negative of the Laplacian of φ:
where ε0 is the electric constant.
This is a consequence of Gauss’s law. Indeed, if V is any smooth region with boundary ∂V, then by Gauss’s law the flux of the electrostatic field E across the boundary is proportional to the charge enclosed:
where the first equality is due to the divergence theorem. Since the electrostatic field is the (negative) gradient of the potential, this gives:
Since this holds for all regions V, we must have
The same approach implies that the negative of the Laplacian of the gravitational potential is the mass distribution. Often the charge (or mass) distribution are given, and the associated potential is unknown. Finding the potential function subject to suitable boundary conditions is equivalent to solving Poisson’s equation.
Energy minimization[edit]
Another motivation for the Laplacian appearing in physics is that solutions to Δf = 0 in a region U are functions that make the Dirichlet energy functional stationary:
To see this, suppose f : U → R is a function, and u : U → R is a function that vanishes on the boundary of U. Then:
where the last equality follows using Green’s first identity. This calculation shows that if Δf = 0, then E is stationary around f. Conversely, if E is stationary around f, then Δf = 0 by the fundamental lemma of calculus of variations.
Coordinate expressions[edit]
Two dimensions[edit]
The Laplace operator in two dimensions is given by:
In Cartesian coordinates,
where x and y are the standard Cartesian coordinates of the xy-plane.
In polar coordinates,
where r represents the radial distance and θ the angle.
Three dimensions[edit]
In three dimensions, it is common to work with the Laplacian in a variety of different coordinate systems.
In Cartesian coordinates,
In cylindrical coordinates,
where 
In spherical coordinates:
or
where φ represents the azimuthal angle and θ the zenith angle or co-latitude.
In general curvilinear coordinates (ξ1, ξ2, ξ3):
where summation over the repeated indices is implied,
gmn is the inverse metric tensor and Γl mn are the Christoffel symbols for the selected coordinates.
N dimensions[edit]
In arbitrary curvilinear coordinates in N dimensions (ξ1, …, ξN), we can write the Laplacian in terms of the inverse metric tensor, 
from the Voss-Weyl formula[3] for the divergence.
In spherical coordinates in N dimensions, with the parametrization x = rθ ∈ RN with r representing a positive real radius and θ an element of the unit sphere SN−1,
where ΔSN−1 is the Laplace–Beltrami operator on the (N − 1)-sphere, known as the spherical Laplacian. The two radial derivative terms can be equivalently rewritten as:
As a consequence, the spherical Laplacian of a function defined on SN−1 ⊂ RN can be computed as the ordinary Laplacian of the function extended to RN∖{0} so that it is constant along rays, i.e., homogeneous of degree zero.
Euclidean invariance[edit]
The Laplacian is invariant under all Euclidean transformations: rotations and translations. In two dimensions, for example, this means that:
for all θ, a, and b. In arbitrary dimensions,
whenever ρ is a rotation, and likewise:
whenever τ is a translation. (More generally, this remains true when ρ is an orthogonal transformation such as a reflection.)
In fact, the algebra of all scalar linear differential operators, with constant coefficients, that commute with all Euclidean transformations, is the polynomial algebra generated by the Laplace operator.
Spectral theory[edit]
The spectrum of the Laplace operator consists of all eigenvalues λ for which there is a corresponding eigenfunction f with:
This is known as the Helmholtz equation.
If Ω is a bounded domain in Rn, then the eigenfunctions of the Laplacian are an orthonormal basis for the Hilbert space L2(Ω). This result essentially follows from the spectral theorem on compact self-adjoint operators, applied to the inverse of the Laplacian (which is compact, by the Poincaré inequality and the Rellich–Kondrachov theorem).[4] It can also be shown that the eigenfunctions are infinitely differentiable functions.[5] More generally, these results hold for the Laplace–Beltrami operator on any compact Riemannian manifold with boundary, or indeed for the Dirichlet eigenvalue problem of any elliptic operator with smooth coefficients on a bounded domain. When Ω is the n-sphere, the eigenfunctions of the Laplacian are the spherical harmonics.
Vector Laplacian[edit]
The vector Laplace operator, also denoted by 
The vector Laplacian of a vector field 
In Cartesian coordinates, this reduces to the much simpler form as
where 




For expressions of the vector Laplacian in other coordinate systems see Del in cylindrical and spherical coordinates.
Generalization[edit]
The Laplacian of any tensor field 
For the special case where 
If 
And, in the same manner, a dot product, which evaluates to a vector, of a vector by the gradient of another vector (a tensor of 2nd degree) can be seen as a product of matrices:
This identity is a coordinate dependent result, and is not general.
Use in physics[edit]
An example of the usage of the vector Laplacian is the Navier-Stokes equations for a Newtonian incompressible flow:
where the term with the vector Laplacian of the velocity field 
Another example is the wave equation for the electric field that can be derived from Maxwell’s equations in the absence of charges and currents:
This equation can also be written as:
where
is the D’Alembertian, used in the Klein–Gordon equation.
Generalizations[edit]
A version of the Laplacian can be defined wherever the Dirichlet energy functional makes sense, which is the theory of Dirichlet forms. For spaces with additional structure, one can give more explicit descriptions of the Laplacian, as follows.
Laplace–Beltrami operator[edit]
The Laplacian also can be generalized to an elliptic operator called the Laplace–Beltrami operator defined on a Riemannian manifold. The Laplace–Beltrami operator, when applied to a function, is the trace (tr) of the function’s Hessian:
where the trace is taken with respect to the inverse of the metric tensor. The Laplace–Beltrami operator also can be generalized to an operator (also called the Laplace–Beltrami operator) which operates on tensor fields, by a similar formula.
Another generalization of the Laplace operator that is available on pseudo-Riemannian manifolds uses the exterior derivative, in terms of which the “geometer’s Laplacian” is expressed as
Here δ is the codifferential, which can also be expressed in terms of the Hodge star and the exterior derivative. This operator differs in sign from the “analyst’s Laplacian” defined above. More generally, the “Hodge” Laplacian is defined on differential forms α by
This is known as the Laplace–de Rham operator, which is related to the Laplace–Beltrami operator by the Weitzenböck identity.
D’Alembertian[edit]
The Laplacian can be generalized in certain ways to non-Euclidean spaces, where it may be elliptic, hyperbolic, or ultrahyperbolic.
In Minkowski space the Laplace–Beltrami operator becomes the D’Alembert operator 
It is the generalization of the Laplace operator in the sense that it is the differential operator which is invariant under the isometry group of the underlying space and it reduces to the Laplace operator if restricted to time-independent functions. The overall sign of the metric here is chosen such that the spatial parts of the operator admit a negative sign, which is the usual convention in high-energy particle physics. The D’Alembert operator is also known as the wave operator because it is the differential operator appearing in the wave equations, and it is also part of the Klein–Gordon equation, which reduces to the wave equation in the massless case.
The additional factor of c in the metric is needed in physics if space and time are measured in different units; a similar factor would be required if, for example, the x direction were measured in meters while the y direction were measured in centimeters. Indeed, theoretical physicists usually work in units such that c = 1 in order to simplify the equation.
The d’Alembert operator generalizes to a hyperbolic operator on pseudo-Riemannian manifolds.
See also[edit]
- Laplace–Beltrami operator, generalization to submanifolds in Euclidean space and Riemannian and pseudo-Riemannian manifold.
- The vector Laplacian operator, a generalization of the Laplacian to vector fields.
- The Laplacian in differential geometry.
- The discrete Laplace operator is a finite-difference analog of the continuous Laplacian, defined on graphs and grids.
- The Laplacian is a common operator in image processing and computer vision (see the Laplacian of Gaussian, blob detector, and scale space).
- The list of formulas in Riemannian geometry contains expressions for the Laplacian in terms of Christoffel symbols.
- Weyl’s lemma (Laplace equation).
- Earnshaw’s theorem which shows that stable static gravitational, electrostatic or magnetic suspension is impossible.
- Del in cylindrical and spherical coordinates.
- Other situations in which a Laplacian is defined are: analysis on fractals, time scale calculus and discrete exterior calculus.
Notes[edit]
- ^ Evans 1998, §2.2
- ^ Ovall, Jeffrey S. (2016-03-01). “The Laplacian and Mean and Extreme Values” (PDF). The American Mathematical Monthly. 123 (3): 287–291. doi:10.4169/amer.math.monthly.123.3.287. S2CID 124943537.
- ^ Archived at Ghostarchive and the Wayback Machine: Grinfeld, Pavel. “The Voss-Weyl Formula”. YouTube. Retrieved 9 January 2018.
- ^ Gilbarg & Trudinger 2001, Theorem 8.6
- ^ Gilbarg & Trudinger 2001, Corollary 8.11
- ^ MathWorld. “Vector Laplacian”.
References[edit]
- Evans, L. (1998), Partial Differential Equations, American Mathematical Society, ISBN 978-0-8218-0772-9
- The Feynman Lectures on Physics Vol. II Ch. 12: Electrostatic Analogs
- Gilbarg, D.; Trudinger, N. (2001), Elliptic Partial Differential Equations of Second Order, Springer, ISBN 978-3-540-41160-4.
- Schey, H. M. (1996), Div, Grad, Curl, and All That, W. W. Norton, ISBN 978-0-393-96997-9.
Further reading[edit]
- The Laplacian – Richard Fitzpatrick 2006
External links[edit]
- “Laplace operator”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. “Laplacian”. MathWorld.
- Laplacian in polar coordinates derivation
- equations on the fractal cubes and Casimir effect
Опера́тор Лапла́са (Лапласиан) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом 


- В произвольных ортогональных криволинейных координатах
:
![{displaystyle Delta f(q_{1}, q_{2}, q_{3})=operatorname {div} ,operatorname {grad} ,f(q_{1}, q_{2}, q_{3})={frac {1}{H_{1}H_{2}H_{3}}}left[{frac {partial }{partial q_{1}}}left({frac {H_{2}H_{3}}{H_{1}}}{frac {partial f}{partial q_{1}}}right)+{frac {partial }{partial q_{2}}}left({frac {H_{1}H_{3}}{H_{2}}}{frac {partial f}{partial q_{2}}}right)+{frac {partial }{partial q_{3}}}left({frac {H_{1}H_{2}}{H_{3}}}{frac {partial f}{partial q_{3}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40c2d06fc95558660125a801701dcad4406e5f6b)
где 
- В цилиндрических координатах:

- В сферических координатах:

или

Оператор Лапласа часто записывается следующим образом 
Применение
Через данный оператор удобно записывать уравнения Лапласа, Пуассона и волновое уравнение, хотя наиболее простой вид последнее принимает с использованием оператора Даламбера (Даламбертиана).
См. также
- Оператор набла
cs:Laplaceův operátor
nl:Laplace-operator
pl:Operator Laplace’a
sk:Laplaceov operátor
sl:Laplaceov operator
sr:Лапласов оператор
sv:Laplaceoperatorn
“Del Squared” перенаправляется сюда. Для использования в других целях, см Del Squared (значения) .
В математике , то оператор Лапласа или лапласиан является дифференциальный оператор задается дивергенции от градиента о наличии скалярной функции на евклидовом пространстве . Обычно обозначается символами , (где – оператор набла ), или . В декартовой системе координат лапласиан задается суммой вторых частных производных функции по каждой независимой переменной . В других системах координат , таких как цилиндрические и сферические координаты , лапласиан также имеет полезную форму. Неформально, лапласиан Δ f ( p ) функции f в точке p измеряет, насколько среднее значение f по маленьким сферам или шарам с центром в p отклоняется от f ( p ) .
Оператор Лапласа назван в честь французского математика Пьера-Симона де Лапласа (1749–1827), который первым применил оператор к изучению небесной механики , где оператор дает постоянную, кратную плотности массы, когда он применяется к гравитационному исследованию. потенциал из-за распределения массы с данной плотностью. Решения уравнения Δ f = 0 , теперь называемого уравнением Лапласа , являются так называемыми гармоническими функциями и представляют возможные гравитационные поля в областях вакуума .
Лапласиан встречается в дифференциальных уравнениях, которые описывают многие физические явления, такие как электрические и гравитационные потенциалы , уравнение диффузии для потока тепла и жидкости , распространение волн и квантовую механику . Лапласиан представляет собой плотность потока от потока градиента функции. Например, чистая скорость, с которой химическое вещество, растворенное в жидкости, движется к некоторой точке или от нее, пропорциональна лапласиану химической концентрации в этой точке; выраженное символически, результирующее уравнение является уравнением диффузии. По этим причинам он широко используется в науке для моделирования различных физических явлений. Лапласиан – простейший эллиптический оператор, он лежит в основе теории Ходжа, а также результатов когомологий де Рама . В обработке изображений и компьютерном зрении оператор Лапласа использовался для различных задач, таких как обнаружение пятен и краев .
Определение
Оператор Лапласа – это дифференциальный оператор второго порядка в n- мерном евклидовом пространстве , определяемый как дивергенция ( ) градиента ( ). Таким образом, если – дважды дифференцируемая вещественнозначная функция , то лапласиан функции определяется следующим образом:

-
( 1 )
где последние обозначения происходят от формального написания:
Эквивалентно, лапласиан f является суммой всех несмешанных вторых частных производных в декартовых координатах x i :
-
( 2 )
Как дифференциальный оператор второго порядка, оператор Лапласа отображает функции C k в функции C k −2 при k ≥ 2 . Выражение ( 1 ) (или, что эквивалентно ( 2 )) определяет оператор Δ: C k ( R n ) → C k −2 ( R n ) или, в более общем смысле, оператор Δ: C k (Ω) → C k – 2 (Ω) для любого открытого множества Ω .
Мотивация
Диффузия
В физической теории диффузии оператор Лапласа (через уравнение Лапласа ) естественным образом возникает при математическом описании равновесия . В частности, если у есть плотность в равновесии некоторой величины , такие как химические концентрации, то результирующий поток из U через границу любой гладкой области V равен нуль, при условии , что нет источника или раковин в пределах V :
где п есть внешнее единичный вектор нормали к границе V . По теореме о дивергенции ,
Поскольку это верно для всех гладких областей V , можно показать, что это влечет:
Левая часть этого уравнения – оператор Лапласа. Сам оператор Лапласа имеет физическую интерпретацию неравновесной диффузии как степень, в которой точка представляет источник или сток химической концентрации, в смысле, уточненном уравнением диффузии .
Средние
Учитывая дважды непрерывно дифференцируемую функцию , точку и действительное число , мы позволяем быть средним значением по шару с радиусом с центром в , и быть средним значением по сфере с радиусом с центром в . Тогда у нас есть:
а также
Плотность, связанная с потенциалом
Если φ обозначает электростатический потенциал, связанный с распределением заряда q , то само распределение заряда задается отрицанием лапласиана φ :
где ε 0 – электрическая постоянная .
Это следствие закона Гаусса . Действительно, если V – любая гладкая область, то по закону Гаусса поток электростатического поля E пропорционален приложенному заряду:
где первое равенство следует из теоремы о расходимости . Поскольку электростатическое поле представляет собой (отрицательный) градиент потенциала, теперь это дает:
Итак, поскольку это верно для всех областей V , мы должны иметь
Тот же подход подразумевает, что отрицательным элементом лапласиана гравитационного потенциала является распределение масс . Часто приводится распределение заряда (или массы), а связанный с ним потенциал неизвестен. Нахождение потенциальной функции с подходящими граничными условиями эквивалентно решению уравнения Пуассона .
Минимизация энергии
Другая причина появления лапласиана в физике состоит в том, что решения для Δ f = 0 в области U являются функциями, которые делают функционал энергии Дирихле стационарным :
Чтобы убедиться в этом, предположим , что F : U → R является функцией, и у : U → R является функцией , которая обращается в нуль на границе U . Потом:
где последнее равенство следует из первого тождества Грина . Этот расчет показывает, что если Δ f = 0 , то E неподвижен вокруг f . Наоборот, если E стационарно вокруг f , то Δ f = 0 по основной лемме вариационного исчисления .
Координатные выражения
Два измерения
Оператор Лапласа в двух измерениях определяется выражением:
В декартовой системе координат ,
где х и у являются стандартными декартовы координаты по ху плоскости.
В полярных координатах ,
где r представляет собой радиальное расстояние, а θ – угол.
Три измерения
В трех измерениях обычно работают с лапласианом в различных системах координат.
В декартовой системе координат ,
В цилиндрических координатах ,
где представляет собой радиальное расстояние, φ – азимутальный угол, а z – высоту.
В сферических координатах :
где φ представляет собой азимутальный угол, а θ – зенитный угол или со-широту .
В общих криволинейных координатах ( ξ 1 , ξ 2 , ξ 3 ):
где подразумевается суммирование по повторяющимся индексам ,
g mn – обратный метрический тензор, а Γ l mn – символы Кристоффеля для выбранных координат.
Размеры N
В произвольных координатах криволинейных в N измерениях ( £ , 1 , …, ξ N ), то можно записать лапласиан в терминах обратного метрического тензора , :
из формулы Фосса – Вейля для расходимости .
В сферических координатах в N измерениях , с параметризацией x = rθ ∈ R N, где r представляет положительный действительный радиус, а θ – элемент единичной сферы S N −1 ,
где Δ S N −1 – оператор Лапласа – Бельтрами на ( N – 1) -сфере, известный как сферический лапласиан. Два члена с радиальной производной могут быть эквивалентно переписаны как:
Как следствие, сферический лапласиан функции , определенный на S N -1 ⊂ R N может быть вычислен как обычный лапласиан функции распространяется на R N ∖ {0} , так что он является постоянным вдоль лучей, то есть, однородные степеней нуль.
Евклидова инвариантность
Лапласиан инвариантен относительно всех евклидовых преобразований : вращений и сдвигов . Например, в двух измерениях это означает, что:
для всех θ , a и b . В произвольных размерах,
всякий раз, когда ρ – вращение, и аналогично:
всякий раз, когда τ – перевод. (В более общем смысле это остается верным, когда ρ – ортогональное преобразование, такое как отражение .)
Фактически, алгебра всех скалярных линейных дифференциальных операторов с постоянными коэффициентами, коммутирующих со всеми евклидовыми преобразованиями, является алгеброй полиномов, порожденной оператором Лапласа.
Спектральная теория
Спектр оператора Лапласа состоит из всех собственных значений А , для которых есть соответствующий собственная функция F с:
Это известно как уравнение Гельмгольца .
Если Ω является ограниченная область в R п , то собственные функции лапласиана являются ортонормированный базис для гильбертова пространства L 2 (Q) . Этот результат по существу следует из спектральной теоремы о компактных самосопряженных операторах , примененной к обратному лапласиану (компактному в силу неравенства Пуанкаре и теоремы Реллиха – Кондрахова ). Также можно показать, что собственные функции являются бесконечно дифференцируемыми функциями. В более общем смысле, эти результаты верны для оператора Лапласа – Бельтрами на любом компактном римановом многообразии с краем или даже для проблемы собственных значений Дирихле любого эллиптического оператора с гладкими коэффициентами в ограниченной области. Когда Ω является n- сферой , собственными функциями лапласиана являются сферические гармоники .
Векторный лапласиан
Оператор Лапласа вектор , также обозначается , является дифференциальным оператором , определенным над векторным полем . Векторный лапласиан аналогичен скалярному лапласиану; в то время как скалярный лапласиан применяется к скалярному полю и возвращает скалярную величину, векторный лапласиан применяется к векторному полю , возвращая векторную величину. При вычислении в ортонормированных декартовых координатах возвращаемое векторное поле равно векторному полю скалярного лапласиана, примененного к каждому компоненту вектора.

Вектор лапласиана из векторного поля определяется как
В декартовых координатах это сводится к гораздо более простой форме, как
где , и – компоненты векторного поля , а слева от каждой компоненты векторного поля находится (скалярный) оператор Лапласа. Это можно рассматривать как частный случай формулы Лагранжа; см. тройное произведение вектора .
Для выражения векторного лапласиана в других системах координат см. Del в цилиндрических и сферических координатах .
Обобщение
Лапласиан любого тензорного поля ( «тензор» включает в себя скалярное и векторное) определяется как дивергенции от градиента тензора:
Для частного случая, когда – скаляр (тензор нулевой степени), лапласиан принимает знакомый вид.
Если – вектор (тензор первой степени), градиент представляет собой ковариантную производную, которая приводит к тензору второй степени, и дивергенция этого снова является вектором. Формула для векторного лапласиана, приведенная выше, может использоваться, чтобы избежать тензорной математики, и может быть показана как эквивалентная дивергенции матрицы Якоби, показанной ниже для градиента вектора:
И таким же образом скалярное произведение, которое оценивается как вектор, вектора градиентом другого вектора (тензор 2-й степени) можно рассматривать как произведение матриц:
Эта идентичность является результатом, зависящим от координат, и не является общим.
Использование в физике
Примером использования векторного лапласиана являются уравнения Навье-Стокса для ньютоновского потока несжимаемой жидкости :
где член с вектором лапласианом скорости поля представляет собой вязкие напряжения в жидкости.

Другой пример – волновое уравнение для электрического поля, которое может быть получено из уравнений Максвелла в отсутствие зарядов и токов:
Предыдущее уравнение также можно записать как:
куда
– даламбертиан , используемый в уравнении Клейна – Гордона .
Обобщения
Версия лапласиана может быть определена везде, где имеет смысл функционал энергии Дирихле , а именно теория форм Дирихле . Для пространств с дополнительной структурой можно дать более явное описание лапласиана следующим образом.
Оператор Лапласа – Бельтрами
Лапласиан также может быть обобщен до эллиптического оператора, называемого оператором Лапласа – Бельтрами, определенным на римановом многообразии . Оператор Даламбера обобщается до гиперболического оператора на псевдоримановых многообразиях . Оператор Лапласа – Бельтрами, примененный к функции, представляет собой след ( tr ) гессиана функции :
где след берется относительно обратного к метрическому тензору . Оператор Лапласа – Бельтрами также может быть обобщен на оператор (также называемый оператором Лапласа – Бельтрами), который работает с тензорными полями , по аналогичной формуле.
Другое обобщение оператора Лапласа, доступное на псевдоримановых многообразиях, использует внешнюю производную , в терминах которой «лапласиан геометра» выражается как
Здесь δ – кодифференциал , который также может быть выражен через звезду Ходжа и внешнюю производную. Этот оператор отличается по знаку от «лапласиана аналитика», определенного выше. В более общем смысле лапласиан «Ходжа» определяется на дифференциальных формах α формулой
Это известно как оператор Лапласа – де Рама , который связан с оператором Лапласа – Бельтрами тождеством Вайтценбека .
Даламбертиан
Лапласиан может быть определенным образом обобщен на неевклидовы пространства, где он может быть эллиптическим , гиперболическим или ультрагиперболическим .
В пространстве Минковского оператор Лапласа-Бельтрами становится оператором Даламбера или даламбертиана:
Это обобщение оператора Лапласа в том смысле, что это дифференциальный оператор, инвариантный относительно группы изометрий основного пространства, и он сводится к оператору Лапласа, если ограничиваться функциями, не зависящими от времени. Общий знак метрики здесь выбран таким, чтобы пространственные части оператора допускали отрицательный знак, что является обычным соглашением в физике частиц высоких энергий . Оператор Даламбера также известен как волновой оператор, потому что это дифференциальный оператор, фигурирующий в волновых уравнениях , а также часть уравнения Клейна – Гордона , которое сводится к волновому уравнению в безмассовом случае.
Дополнительный коэффициент c в метрике необходим в физике, если пространство и время измеряются в разных единицах; аналогичный коэффициент потребовался бы, если, например, направление x измерялось в метрах, а направление y – в сантиметрах. Действительно, физики-теоретики обычно работают с такими единицами, что c = 1 , чтобы упростить уравнение.
Смотрите также
- Оператор Лапласа – Бельтрами , обобщение на подмногообразия в евклидовом пространстве, риманово и псевдориманово многообразие.
- Вектор Лапласа оператор, обобщение лапласиана в векторных полей .
- Лапласиан в дифференциальной геометрии .
- Дискретный оператор Лапласа является конечно-разностным аналогом непрерывного лапласиана, определенный на графиках и сетках.
- Лапласиан – распространенный оператор в обработке изображений и компьютерном зрении (см. Лапласиан гаусса , детектор капель и масштабное пространство ).
- Список формул в римановой геометрии содержит выражение для лапласиана в терминах символов Кристоффеля.
- Лемма Вейля (уравнение Лапласа) .
- Теорема Ирншоу, которая показывает, что стабильная статическая гравитационная, электростатическая или магнитная подвеска невозможна.
- Del в цилиндрических и сферических координатах .
- Другими ситуациями, в которых определяется лапласиан, являются: анализ фракталов , исчисление шкалы времени и дискретное внешнее исчисление .
Примечания
использованная литература
- Эванс, Л. (1998), Уравнения в частных производных , Американское математическое общество, ISBN 978-0-8218-0772-9
- Feynman, R .; Leighton, R; Сэндс, М. (1970), «Глава 12: Электростатические аналоги», Лекции Фейнмана по физике , 2 , Аддисон-Уэсли-Лонгман
- Gilbarg, D .; Трудингер Н. (2001), Эллиптические дифференциальные уравнения с частными производными второго порядка , Springer, ISBN 978-3-540-41160-4.
- Schey, HM (1996), Div, Grad, Curl, и все такое , WW Norton, ISBN 978-0-393-96997-9.
дальнейшее чтение
- http://farside.ph.utexas.edu/teaching/em/lectures/node23.html
внешние ссылки
- «Оператор Лапласа» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В. «Лапласиан» . MathWorld .
- Вывод лапласиана в полярных координатах
Опера́тор Лапла́са (лапласиа́н) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом 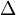
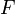

Оператор Лапласа часто обозначается следующим образом 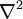
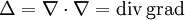
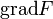
Содержание
- 1 Другое определение оператора Лапласа
- 2 Выражения для оператора Лапласа в различных криволинейных системах координат
- 2.1 Цилиндрические координаты
- 2.2 Сферические координаты
- 2.3 Параболические координаты
- 2.4 Цилиндрические параболические координаты
- 3 Применение
- 4 Вариации и обобщения
- 5 См. также
- 6 Литература
- 7 Внешние ссылки
Другое определение оператора Лапласа
Оператор Лапласа является естественным обобщением на функции нескольких переменных обычной второй производной функции одного переменного. В самом деле, если функция 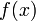
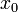
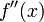
при
,
при
вторая производная есть предел
Eсли, переходя к функции 
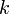
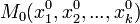
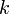

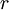
функции 
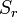
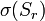
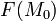
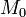

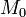
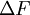
Одновременно с предыдущим представлением для оператора Лапласа функции 
где
– объём окресности
Эта формула выражает непосредственную связь лапласиана функции с её объёмным средним в окрестности данной точки.
Доказательство этих формул можно найти, например, в [1].
Вышеизложенные пределы, во всех случаях, когда они существуют, могут служить определением оператора Лапласа функции 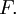
Выражения для оператора Лапласа в различных криволинейных системах координат
В произвольных ортогональных криволинейных координатах в трехмерном пространстве 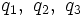
- где
— коэффициенты Ламе.
Цилиндрические координаты
В цилиндрических координатах вне прямой 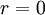
Сферические координаты
В сферических координатах вне начала отсчёта:
или
В случае если
Параболические координаты
В параболических координатах (в трёхмерном пространстве) вне начала отсчёта:
Цилиндрические параболические координаты
В координатах параболического цилиндра вне начала отсчёта:
Применение
С помощью данного оператора удобно записывать уравнения Лапласа, Пуассона и волновое уравнение, хотя наиболее простой вид последнее принимает с использованием оператора Д’Aламбера (Даламбертиана). Впрочем, последний представляет собой не более, чем оператор Лапласа в пространстве Минковского (формально пространство Минковского можно ввести для любого поля, подчиняющегося волновому уравнению, хотя, конечно, параметр c может быть в каждом конкретном случае своим, например, скорость звука).
В физике оператор Лапласа применим в электростатике и электродинамике, во многих уравнениях физики сплошных сред, а также при изучении равновесия мембран, пленок или поверхностей раздела фаз с поверхностным натяжением (см. Лапласово давление), стационарных задач диффузии и теплопроводности, которые сводятся в непрерывном пределе к обычным уравнениям Лапласа или Пуассона или к некоторым их обобщениям.
Вариации и обобщения
- Оператор Д’Аламбера
См. также
- Оператор набла
- Уравнение Лапласа
- Гармоническая функция
Литература
- ↑ Тиман А.Ф., Трофимов В.Н. Введение в теорию гармонических функций. М. Наука. 1968г. 208с.
Внешние ссылки
- MathWorld description of Laplacian
Wikimedia Foundation.
2010.











![=frac{1}{H_1H_2H_3}left[ frac{partial}{partial q_1}left( frac{H_2H_3}{H_1}frac{partial f}{partial q_1} right) + frac{partial}{partial q_2}left( frac{H_1H_3}{H_2}frac{partial f}{partial q_2} right) + frac{partial}{partial q_3}left( frac{H_1H_2}{H_3}frac{partial f}{partial q_3} right)right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/20976c3be6b574fb20939f284033ac2c05f005ac)




![Delta f= frac{1}{sigma^{2} + tau^{2}}
left[
frac{1}{sigma} frac{partial }{partial sigma}
left( sigma frac{partial f}{partial sigma} right) +
frac{1}{tau} frac{partial }{partial tau}
left( tau frac{partial f}{partial tau} right)right] +
frac{1}{sigma^2tau^2}frac{partial^2 f}{partial varphi^2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70817e419f2c0c845d8e553d32111fb9d54f2971)
![Delta F(u,v,z)={frac {1}{c^{2}(u^{2}+v^{2})}}left[{frac {partial ^{2}F}{partial u^{2}}}+{frac {partial ^{2}F}{partial v^{2}}}right]+{frac {partial ^{2}F}{partial z^{2}}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b52cf63665f311548adc0b0285c91488fe08de4)



















































 при
при  ,
,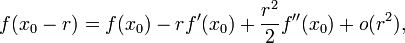 при
при 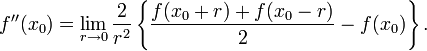

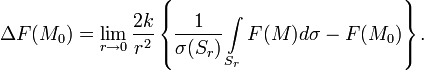
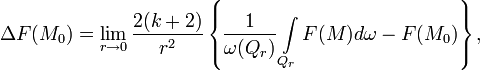 где
где 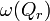 – объём окресности
– объём окресности 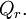
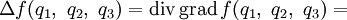
![=frac{1}{H_1H_2H_3}left[ frac{partial}{partial q_1}left( frac{H_2H_3}{H_1}frac{partial f}{partial q_1} right) + frac{partial}{partial q_2}left( frac{H_1H_3}{H_2}frac{partial f}{partial q_2} right) + frac{partial}{partial q_3}left( frac{H_1H_2}{H_3}frac{partial f}{partial q_3} right)right],](https://dic.academic.ru/pictures/wiki/files/48/0fc8a2f7852abfc561572a6d358d9391.png)
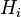 — коэффициенты Ламе.
— коэффициенты Ламе.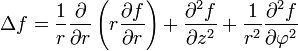


![Delta f= frac{1}{sigma^{2} + tau^{2}}
left[
frac{1}{sigma} frac{partial }{partial sigma}
left( sigma frac{partial f}{partial sigma} right) +
frac{1}{tau} frac{partial }{partial tau}
left( tau frac{partial f}{partial tau} right)right] +
frac{1}{sigma^2tau^2}frac{partial^2 f}{partial varphi^2}](https://dic.academic.ru/pictures/wiki/files/55/7e9a6e157bec490dfb0fe18d8bfb05cd.png)
![Delta F(u,v,z) = frac{1}{c^2(u^2+v^2)} left[ frac{partial^2 F }{partial u^2}+ frac{partial^2 F }{partial v^2}right] + frac{partial^2 F }{partial z^2}](https://dic.academic.ru/pictures/wiki/files/97/af2500787981eca027be57cfe66d0ef0.png)
