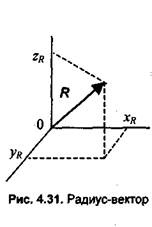
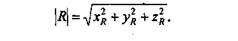|
Линейный |
12.1. Понятие линейного оператора
Определение
1. Пусть
– линейное пространство и каждому вектору
,
принадлежащему,
поставлен в соответствие вектор
,
.
Соответствиеназывается оператором,
определенным в линейном пространстве
.
Принята
также запись:
.
Векторназываетсяпрообразом,
а
–образом
при отображении оператором
.
Определение
2.
Оператор
,
определенный в линейном пространстве
,
называется линейным,
если:
1)
;
2)
– вещественного числа
.
П
1.
–
линейное пространство всех геометрических
векторов плоскости,
– зеркальное отражение относительно
оси(рис. 12.1).
– линейный оператор.
Убедимся,
что выполняется требование 2) в определении
2.
Пусть
– произвольное вещественное число, по
определению умножения надля геометрического вектора
вектор
имеет то же направление, что и
,
если,
и противоположное, если,
и.
Рис.
12.2 соответствует случаю
,
(
рассматривается аналогично).
П
,
,
– зеркальное отражение вектора
относительно оси
,
– зеркальное отражение вектора
.
Тогда~
и, значит,
.
Но,
поэтому.
Кроме того, направление векторасовпадает с направлением вектора
,
следовательно,.
Таким образом, имеем

Так
же, исходя из геометрических соображений,
можно доказать, что
,
следовательно, операторзеркального отражения относительно
осиявляется линейным оператором.
Упражнения.
1.
–
линейное пространство всех многочленов
степени,
– оператор дифференцирования,
.
Доказать, что– линейный оператор.
2.
–
линейное пространство всех непрерывных
на отрезкефункций. Для любой
оператор
определен следующим равенством:

.
Доказать,
что
– линейный оператор.
Определение
3.
Пусть
–
линейное пространство,
–
базис в,
–
линейный оператор в.
Матрицей линейного операторав базисе
называется матрица
,
,такая,
что
,
,
……………………………………..
(12.1)
.
Замечание
1.
Столбцы матрицы
являются координатами в разложении
векторовпо базису
.
П
2.
Найти
матрицу линейного оператора зеркального
отражения относительно оси
в базисе
.
По
определению оператора
(рис. 12.3).
Используя
разложение векторов
и
по базису
,
находим:,
.
Полученные строки координат располагаем
по столбцам:
.
Упражнение.
–
линейное пространство всех геометрических
векторов,
– декартов базис,
– декартова система координат,
– оператор проектирования на ось
.
Доказать, что–
линейный оператор, и найти его матрицу
в базисе.
Замечание
2.
Пусть
–
линейное пространство,–
линейный оператор в,
(I)
– базис в
.
Матрица оператора в базисе (I)
определена однозначно.
Для
того, чтобы в этом убедиться, разложим
векторы
по базису (I).
Столбцы матрицы
представляют собой координаты этих
векторов, которые согласно теореме 3
лекции 10 определяются единственным
образом, следовательно, матрицаоператора
в (I)
определена однозначно.
Теорема
1.
Пусть
–
линейное пространство,
(I)
– базис в
,
–
линейный оператор в,
– матрица линейного оператора
в базисе(I),
,
,
,
.
Тогда

Доказательство.
Имеем

По
условию
.
Используя
теорему о единственности разложения
вектора по базису (теорема 3 из лекции
10), получим
.
(12.2)
Заметим,
что в последнем равенстве числа
– элементыk-й
строки матрицы
.
Привлекая
правило умножения матриц, равенство
(12.2) запишем в виде

Теорема доказана.
Пример
3.
Для линейного оператора зеркального
отражения относительно оси
найти, как преобразуются координаты
произвольного вектора.
Решение.
Матрица
оператора была найдена в примере 2:

В
силу теоремы 1, если
– прообраз, а
– образ,
,
то,
т.е. первая координата образа остается
без изменения, а вторая меняет лишь знак
(рис. 12.4).
Пример
4.
–
линейное пространство всех многочленов
степени,
–
линейный оператор дифференцирования.
Найти его матрицу в базисеи, используя теорему 1, продифференцировать
многочлен.
Решение.
Находим
образы векторов базиса
и разлагаем полученные векторы по базису
:
,
,
.
Матрица
оператора
в базисе
имеет вид

а
вектор
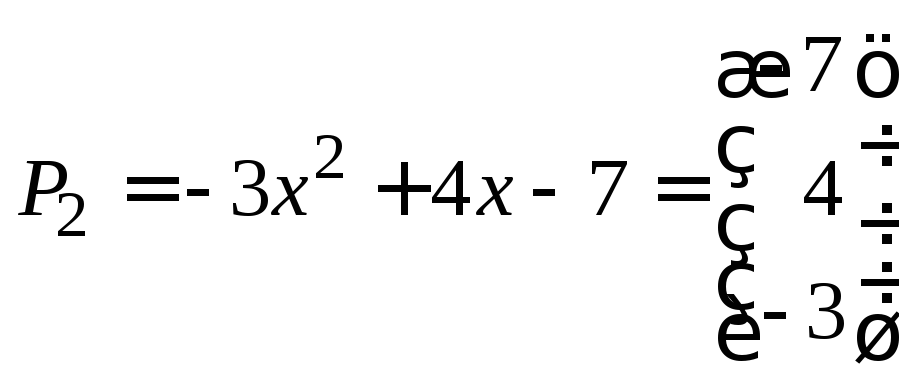
Обозначим
По теореме 1 имеем

или
в виде разложения по базису
:
.
Упражнение.
–
линейное пространство всех геометрических
векторов плоскости,–
декартов базис,–
декартова система координат,–
оператор поворота плоскости вокруг
начала координат на уголпротив часовой стрелки. Доказать, что
– линейный оператор, найти матрицу
оператора
в базисе
и координаты образа вектора
.
Соседние файлы в папке ржавинская лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом
ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
Линейный оператор
Линейное отображение линейного (векторного) пространства $ mathbb V_{} $ в себя
$$ mathcal A : mathbb V longmapsto mathbb V $$
называется линейным преобразованием $ mathbb V_{} $ или линейным оператором1) на $ mathbb V_{} $.
В дальнейшем под выражением оператор понимается исключительно линейный оператор (и линейное пространство $ mathbb V_{} $ предполагается конечномерным!).
Напомню свойство линейности:
$$
mathcal A (X_1 +X_2)= mathcal A(X_1) + mathcal A(X_2),quad mathcal A (alpha_1 X_1)=
alpha_1 mathcal A (X_1),
$$
или, в эквивалентном виде:
$$
mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) + alpha_2 mathcal A(X_2)
$$
для $ forall {X_1,X_2} subset mathbb V,
forall {alpha_1,alpha_2 } subset mathbb R mbox{ или } mathbb C $
(здесь $ alpha_1,alpha_ 2 $ — константы из $ mathbb R_{} $ если $ mathbb V_{} $
вещественное пространство, и из $ mathbb C_{} $, если оно комплексное).
Примеры линейных операторов
Бóльшую часть примеров пункта
☞
ПРИМЕРЫ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ представляют именно линейные операторы. Укажу еще несколько, к которым буду часто обращаться.
П
Пример 1. В пространстве $ mathbb R^{3} $ рассмотрим следующие действия над вектором2) $ (x_{},y,z) $:
-
поворот вокруг прямой $ x=y=2,z $ на угол $ pi/3 $;
-
зеркальное отражение относительно плоскости $ 3,x-y+z = 0 $;
-
растяжение в $ 3.14 $ раза.
Все это — примеры линейных операторов. Но вот отображение сдвига $ (x,y,z) mapsto (x+1,y,z+2) $ оператором не является поскольку
$$ {color{RubineRed} alpha } (x,y,z) = ( {color{RubineRed} alpha } x, {color{RubineRed} alpha } y, {color{RubineRed} alpha } z) mapsto ( {color{RubineRed} alpha } x+1, {color{RubineRed} alpha } y, {color{RubineRed} alpha } z+2) ne {color{RubineRed} alpha } (x+1,y,z+2) . $$
П
Пример 2. В пространстве $ mathbb R^{3} $ отображение ортогонального проецирования на плоскость $ x+y-7, z=0 $ будет линейным оператором (а вот на плоскость $ x+y-7, z=1 $ — не будет!). Вообще, в произвольном пространстве $ mathbb V_{} $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ отображение, сопоставляющее вектору $ X_{} $ его проекцию на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $, будет оператором.
П
Пример 3. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степеней $ le 3 $ отображение $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Это отображение будет оператором в $ mathbb P_3 $. Действительно, если
$$
begin{array}{l}
f_1(x)(x^2-2) equiv q_1(x)(x^4-x^3-x^2+x)+ r_1(x), , \
f_2(x)(x^2-2) equiv q_2(x)(x^4-x^3-x^2+x)+ r_2(x) ,
end{array}
$$
при $ {q_1(x),q_2(x),r_1(x),r_2(x)} subset mathbb R[x], deg r_1(x) le 3, deg r_2(x) le 3 $,
то
$$ (alpha_1 f_1(x)+alpha_2 f_2(x)) (x^2-2) equiv (alpha_1 q_1(x)+alpha_2 q_2(x))(x^4-x^3-x^2+x)+ (alpha_1 r_1(x)+alpha_2 r_2(x)) ;
$$
очевидно, что $ deg (alpha_1 r_1(x)+alpha_2 r_2(x)) le 3 $.
♦
П
Пример 4. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array} qquad npu qquad { x_{1}, dots, x_{n}, y_{1},dots,y_{n} } subset mathbb C
$$
будем считать узлы $ { x_j}_{j=1}^n $ фиксированными, а значения $ { y_j}_{j=1}^n $ — переменными. Эта таблица однозначно определяет интерполяционный полином $ f(x)=A_{0}+A_1x+dots+A_{n-1}x^{n-1} $ со свойством $ f(x_j)=y_j $ при $ j in {1,dots,n} $. При этом $ {A_{j} }_{j=0}^{n-1} subset mathbb C $. Будет ли получившееся отображение
$$ (y_1,dots,y_n) mapsto (A_0,A_1,dots,A_{n-1}) $$
оператором на $ mathbb C^n $? Покажем, что отображение
$$ mathcal A(y_1,dots,y_n) = f(x) in mathbb C[x] $$
является линейным отображением. Действительно, решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & alpha y_1 & alpha y_2 &dots & alpha y_n
end{array}
qquad npu qquad forall alpha in mathbb C
$$
является полином $ alpha f(x) $. Если же, вдобавок, решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & z_1 & z_2 &dots & z_n
end{array}
qquad npu qquad { z_{1},dots,z_{n} } subset mathbb C
$$
является полином $ g(x)in mathbb C[x], deg g(x) le n-1 $, то
решением задачи интерполяции для таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1+z_1 & y_2+z_2 &dots & y_n+z_n
end{array}
qquad
$$
будет полином $ f(x)+g(x) $ и этот полином будет единственным решением среди полиномов степеней $ le n-1 $. Таким образом, линейность отображения $ mathcal A $ установлена. Далее, множество $ mathbb P_{n-1} $ полиномов из $ mathbb C[x] $ степеней $ le n-1 $ изоморфно пространству $ mathbb C^n $. Следовательно, «сложное» отображение
$$
(y_1,dots,y_n) mapsto f(x)=A_{0}+A_1x+dots+A_{n-1}x^{n-1} mapsto (A_0,A_1,dots,A_{n-1})
$$
является линейным отображением из $ mathbb C^n $ в $ mathbb C^n $, т.е. оператором на $ mathbb C^n $.
По аналогии с задачей алгебраической интерполяции, можно поставить и задачу тригонометрической интерполяции. Имеем здесь «точку входа» в теорию дискретного преобразования Фурье.
♦
Этот пример можно «развернуть»: НИЖЕ будет показано, что произвольный оператор,
действующий в пространстве размерности $ n_{} $ полностью определяется своими значениями в $ n_{} $ точках пространства. Важное отличие от традиционной, числовой интерполяции: условие различности этих точек не является достаточным для однозначного определения оператора
!
?
В пространстве $ mathbb P_2 $ оператор действует следующим образом:
$$ mathcal A (x^2+x+1) =2,x+1, mathcal A (x^2-x-1) =2,x^2-1, mathcal A (x+1) =-x^2+x+1 . $$
Вычислить $ mathcal A (x^2) $ и $ mathcal A (x^2+1) $.
П
Пример 5. В пространстве полиномов степени не выше $ n_{} $ с вещественными коэффициентами от $ m_{} $ переменных $ x_1,x_2,dots,x_{m} $ отображение
$$ f(x_1,x_2,dots,x_m) mapsto frac{partial^2 f}{partial x_1^2} +frac{partial^2 f}{partial x_2^2}+ dots+ frac{partial^2 f}{partial x_m^2}
$$
яыляется линейным оператором. Этот оператор известен как оператор Лапласа и для него используется символьное обозначение
$$ Delta = frac{partial^2 }{partial x_1^2} +frac{partial^2 }{partial x_2^2}+ dots+ frac{partial^2 }{partial x_m^2} , .
$$
П
Пример 6. В линейном пространстве квадратных матриц порядка $ n_{} $ с вещественными элементами рассмотрим коммутирующее отображение
$$ mathcal K (X) = AX-XA , $$
а также отображение Ляпунова
$$ mathcal V (X) = A^{top}X+XA $$
при произвольной фиксированной квадратной матрице $ A_{} $ и $ {}^{top} $ означающем транспонирование. Легко проверить, что оба отображения $ mathcal K $ и $ mathcal V $ являются операторами.
♦
Основные определения
Все введенные для линейного отображения понятия переносятся на этот частный случай. Например, ядром оператора называется множество векторов, отображаемых оператором в нулевой вектор:
$$mathcal{K}er (mathcal A)= left{Xin mathbb V big| mathcal A(X)=mathbb O right} ; $$
а образом оператора называется множество всех векторов из
$ mathbb V_{} $, для каждого из которых существует прообраз в том же пространстве:
$$mathcal{I}m (mathcal A)= left{Yin mathbb V mid exists X in mathbb V, mathcal A(X)= Y
right} .$$
Т
Теорема 1. Множества $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m (mathcal A) $ являются подпространствами пространства $ mathbb V_{} $.
?
Доказать, что для оператора в $ mathbb R^4 $
$$
mathcal A
left(begin{array}{c}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)=
left(begin{array}{c}
x_3 \ x_4 \ 0 \ 0
end{array}
right)
$$
имеет место равенство $ mathcal{K}er (mathcal A) = mathcal{I}m (mathcal A) $.
Для оператора $ mathcal A_{} $ его дефектом его называется размерность ядра,
а его рангом — размерность образа:
$$ operatorname{dfc}(mathcal A )=dim (mathcal{K}er (mathcal A )) ,
operatorname{rank}(mathcal A )= dim (mathcal{I}m (mathcal A )) .
$$
Оператор называется невырожденным если $ operatorname{dfc}(mathcal A )=0 $.
П
Пример. В пространстве $ mathbb R^{3} $ оператор проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right)
$$
является вырожденным поскольку его ядро нетривиально: $ mathcal{K}er (mathcal A)={(0,0,z) | z in mathbb R } $.
♦
Следующий результат является следствием теоремы $ 4 $ из
☞
ПУНКТА.
Т
Теорема 2. Имеет место равенство:
$$ dim mathbb V=dim left( mathcal{K}er (mathcal A) right) + dim left( mathcal{I}m (mathcal A) right) = operatorname{dfc}(mathcal A )+ operatorname{rank}(mathcal A ) .$$
В чем смысл свойства вырожденности оператора? — В том, что такой оператор «схлопывает» пространство, в котором действует: $ dim left( mathcal{I}m (mathcal A) right) < dim mathbb V $. Происходит уменьшение размерности подобное тому, что описано в предыдущем примере: трехмерное пространство прообразов оператором проецирования отображается в двухмерное пространство всевозможных образов.
Отображение $ mathcal P: mathbb V longmapsto mathbb V $ называется произведением оператора $ mathcal A $ на оператор $ mathcal B $ если
$ mathcal P(X)=mathcal A (mathcal B(X)) $ для любого $ Xin mathbb V_{} $. Записывать этот факт будем в виде $ mathcal P=mathcal A , mathcal B $.
Фактически, произведение операторов — частный случай понятия сложной функции.
Т
Теорема 3. Произведение операторов является оператором на $ mathbb V_{} $.
Операция произведения ассоциативна.
Доказательство. Имеем на основании свойства линейности
$$mathcal P (alpha_1X_1+alpha_2X_2)=
mathcal A (mathcal B(alpha_1X_1+alpha_2X_2))=mathcal A (alpha_1mathcal B(X_1)+
alpha_2mathcal B(X_2))=$$
$$=alpha_1mathcal A (mathcal B(X_1))+
alpha_2mathcal A (mathcal B(X_2))=alpha_1mathcal P(X_1)+alpha_2{mathcal P}(X_2).$$
Далее, для любого вектора $ X_{} $:
$$mathcal A_1(mathcal A_2mathcal A_3(X))= mathcal A_1(mathcal A_2(mathcal A_3(X)))=mathcal A_1mathcal A_2({mathcal A}_3(X))
,$$
откуда и следует ассоциативность.
♦
Говорят, что операторы $ mathcal A $ и $ mathcal B $ коммутируют если $ mathcal A , mathcal B = mathcal B , mathcal A $.
П
Пример. В пространстве полиномов $ mathbb P_{n} $ рассмотрим
дифференциальный оператор
$$mathcal A = xfrac{d}{d, x}times Box – 1times Box :
mathcal A(p(x)) = x p'(x) – p(x) .$$
Этот оператор не коммутирует с обычным оператором дифференцирования
$ displaystyle mathcal B= frac{d}{d, x} $:
$$mathcal A (x^2)=x^2, quad mathcal B (mathcal A(x^2))=2,x, quad
mathcal B (x^2)=2,x, quad mathcal A (mathcal B (x^2))=0 .$$
♦
Оператор $ mathcal E $, отображающий произвольный вектор $ Xin mathbb V_{} $ в себя : $ mathcal E(X)= X $, называется тождественным на $ mathbb V_{} $. Оператор $ mathcal B $ называется (левым)
обратным оператору $ mathcal A_{} $, если $ mathcal Bmathcal A=mathcal E $.
В этом случае оператор $ mathcal A_{} $ называют обратимым и записывают:
$ mathcal B=mathcal A^{-1} $.
Не всякий оператор обратим.
П
Пример. В пространстве $ mathbb R^{3} $ для оператора проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right)
$$
обратного не существует, т.к. $ mathcal A(0,0,1)=(0,0,0) $ и ни при каком выборе оператора $ mathcal B $ нельзя добиться выполнения равенства $ mathcal B(0,0,0)=(0,0,1) $.
♦
?
Показать, что обратным для оператора
$$frac{1}{x}int_0^x : p(x) longmapsto frac{1}{x}int_{0}^{x}
p(t) d, t ,$$
на $ mathbb P_{n} $ является оператор
$$ frac{d}{d,x}left(xtimes Box right) : p(x) longmapsto
(xp(x))’ .$$
Т
Теорема 4. Оператор $ mathcal A_{} $ обратим тогда и только тогда, когда
когда он невырожден: $ operatorname{dfc} (mathcal A) =0 $. В этом случае $ mathcal A^{-1} $ единствен и коммутирует с $ mathcal A $.
Из теоремы следует, что левый обратный оператор к оператору $ mathcal A_{} $ — если он существует — совпадает с правым обратным оператором. Это утверждение не будет справедливым для бесконечномерных пространств. См. задачу
7
☞
ЗДЕСЬ.
При $ Kin mathbb N $ и $ K>1 $, $ K_{} $-я степень оператора $ mathcal A $ определяется
рекурсивной формулой
$$mathcal A^{, K}=mathcal A (mathcal A^{, K-1}) .$$
Если, вдобавок, $ mathcal A $ невырожден, то отрицательная степень оператора определяется формулой
$$mathcal A^{-K}=left(mathcal A^{-1}right)^K . $$
Полагают также $ mathcal A^{, 0}= {mathcal E} $ для любого $ mathcal A ne {mathcal O} $.
Т
Теорема 5. Степени оператора $ mathcal A $ коммутируют:
$$mathcal A^{, K} mathcal A^{, L}=mathcal A^{, L}mathcal A^{, K}=mathcal A^{, K+L} .$$
П
Пример. $ K_{} $-й степенью оператора дифференцирования в пространстве полиномов $ mathbb P_{n} $ будет оператор нахождения $ K_{} $-й производной:
$$left( frac{d}{d,x} right)^K = frac{d^K}{d,x^K} .$$
Очевидно, что при $ K_{}>n $ этот оператор будет нулевым.
♦
П
Пример. В произвольном пространстве $ mathbb V_{} $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ оператор проецирования $ mathcal P $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $ обладает свойством $ mathcal P^2 = mathcal P $ (проецирование проекции оставляет ее на месте).
♦
Оператор $ mathcal A $, обладающий свойством $ mathcal A^2 = mathcal A $, называется идемпотентным3).
П
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ отображение $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Для этого оператора $ K_{} $-й его степенью является оператор
$$ mathcal B (f(x)) = f(x) (x^2-2)^K pmod{x^4-x^3-x^2+x} . $$
Действительно, если
$$
f(x)(x^2-2) equiv q(x)(x^4-x^3-x^2+x)+ r(x)
$$
при $ {q(x),r(x)} subset mathbb R[x] $ и $ deg r(x) le 3 $, то
$$
f(x)(x^2-2)^2 equiv q(x)(x^4-x^3-x^2+x)(x^2-2)+ r(x)(x^2-2) .
$$
Но тогда
$$ mathcal A^2 (f(x))= mathcal A (r(x)) = r(x) (x^2-2) pmod{x^4-x^3-x^2+x} equiv
$$
$$
equiv f(x)(x^2-2)^2 pmod{x^4-x^3-x^2+x} .
$$
Завершает доказательство святая индукция по степени $ K_{} $…
♦
Пусть задан произвольный полином
$ g(x)=b_{0}x^m+b_1x^{m-1}+dots+b_m $ из $ mathbb R[x] $ или $ mathbb C[x] $. Выражение
$$g(mathcal A )= b_0mathcal A^{m}+b_1mathcal A^{m-1}+dots+b_m{mathcal E}$$
будем называть операторным полиномом.
?
Доказать, что операторные полиномы коммутируют:
$ g_1(mathcal A )g_2(mathcal A )=g_2(mathcal A )g_1(mathcal A ) $.
?
Доказать, что для любого $ mathcal A in {mathcal H}om(mathbb V,mathbb V) $
всегда найдется полином $ g_{}(x) $, $ deg g le n^2+1 $ такой, что
$ g(mathcal A)={mathcal O} $.
Сформулируем еще один результат, являющийся частным случаем приведенного в пункте
☞
СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.
Т
Теорема 6. Пусть $ {X_1,X_2,dots,X_n} $ — произвольный базис $ mathbb V_{} $,
а $ Y_1,Y_2,dots,Y_n $ — произвольные векторы того же пространства. Существует единственный оператор $ mathcal A: mathbb V longmapsto mathbb V $ такой, что
$$ mathcal A(X_1)=Y_1,mathcal A(X_2)=Y_2, dots,mathcal A(X_n)=Y_n .$$
Доказательство. Искомый оператор строится следующим образом. Если $ X=x_1X_1+x_2X_2+dots+x_nX_n $ — разложение произвольного вектора $ X in mathbb V $ по базису, то
$$ mathcal A(X)=x_1 Y_1+x_2Y_2+dots+ x_nY_n . $$
Единственность этого оператора доказывается от противного. Любой другой оператор $ mathcal B $, удовлетворяющий условиям $ {mathcal B(X_j)=Y_j}_{j=1}^n $, будет действовать на тот же вектор $ X_{} $ с тем же результатом:
$$ mathcal B(X)=x_1 mathcal B(X_1)+x_2mathcal B(X_2) +dots+ x_nmathcal B(X_n)=
x_1 Y_1+x_2Y_2+dots+ x_nY_n= mathcal A(X) . $$
♦
Таким образом, оператор — как функция, действующая в $ n_{} $-мерном линейном пространстве, однозначно определяется заданием на $ n_{} $ линейно независимых векторах. В доказательстве теоремы дается и конструктивный способ представления оператора по этим значениям (т.е. строится его “интерполяционная формула” ).
Матрица оператора
Рассмотрим оператор $ mathcal A $ на $ mathbb V_{} $ и пусть $ {X_1,dots,X_n} $ — базис $ mathbb V_{} $. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от
рассмотренного в пункте
☞
МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для $ mathcal{I}m (mathcal A) $. Поскольку $ mathcal{I}m (mathcal A) $ является
подпространством $ mathbb V_{} $, то было бы слишком большой роскошью
иметь два разных базиса для одного и того же пространства.
Найдем координаты образов базисных векторов
$ mathcal A (X_1),dots,mathcal A (X_n) $ в том же базисе $ {X_1,dots,X_n} $:
$$
left{ begin{array}{ccc}
mathcal A(X_1)&=&{{color{RubineRed} alpha }}_{11}X_1+{{color{RubineRed} alpha }}_{21}X_2+dots+{{color{RubineRed} alpha }}_{n1}X_n, \
mathcal A(X_2)&=&{{color{Green} alpha }}_{12}X_1+{{color{Green} alpha }}_{22}X_2+dots+{{color{Green} alpha }}_{n2}X_n, \
dots & & qquad dots , \
mathcal A(X_n)&=&alpha_{1n}X_1+alpha_{2n}X_2+dots+alpha_{nn}X_n.
end{array} right.
$$
Матрица
$$
mathbf A= left(begin{array}{cccc}
{{color{RubineRed} alpha }}_{11} & {{color{Green} alpha }}_{12}& dots & alpha_{1n} \
{{color{RubineRed} alpha }}_{21} & {{color{Green} alpha }}_{22}& dots & alpha_{2n} \
dots & & & dots \
{{color{RubineRed} alpha }}_{n1} & {{color{Green} alpha }}_{n2}& dots & alpha_{nn}
end{array}
right)_{ntimes n},
$$
в столбцах которой стоят координаты образов базисных векторов,
называется матрицей оператора $ mathcal A_{} $ в базисе $ {X_1,dots,X_n} $.
П
Пример. Известны образы базисных векторов $ mathbb R^{3} $
под действием оператора $ mathcal A_{} $:
$$mathcal A left( begin{array}{r}
5 \ 3 \ 1
end{array}right)=
left( begin{array}{r}
-2 \ 1 \ 0
end{array}right)
,
mathcal A left( begin{array}{r}
1 \ -3 \ -2
end{array}right) =
left( begin{array}{r}
-1 \ 3 \ 0
end{array}right)
,
mathcal A
left( begin{array}{r}
1\ 2 \ 1
end{array}right)=
left( begin{array}{r}
-2 \ -3 \ 0
end{array}right) .
$$
Найти матрицу этого оператора в исходном базисе.
Решение. Элементы матрицы $ {mathbf A} $ ищутся по формулам из определения, которые можно переписать в матричном виде:
$$left[ X_1,dots,X_n right] {mathbf A}=left[ mathcal A (X_1),dots,mathcal A (X_n) right]
.$$
Откуда
$${mathbf A}= left[ X_1,dots,X_n right]^{-1} left[ mathcal A (X_1),dots,mathcal A (X_n)
right] ,$$
и для нашего примера эта формула дает
$$
{mathbf A}=
left(begin{array}{rrr}
5&1&1 \
3&-3&2 \
1&-2&1
end{array}right)^{-1}
left(begin{array}{rrr}
-2&-1&-2 \
1&3&-3 \
0&0&0
end{array}right)
=
$$
$$
=left(begin{array}{rrr} 1&-3&5\
-1&4&-7\
-3&11&-18
end{array}right)
left(begin{array}{rrr}
-2&-1&-2 \
1&3&-3 \
0&0&0
end{array}right)
=
left(begin{array}{rrr}
-5&-10&7\
6&13&-10\
17&36&-27
end{array}
right).
$$
♦
?
В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^3+2,x^2+1) pmod{x^4+4} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^3+2,x^2+1) $ на $ x^4+4 $. Найти матрицу оператора $ mathcal A_{} $ в базисе $ {1,x,x^2,x^3} $.
Ответ.
$$
left(begin{array}{rrrr}
1 & -4 & -8 & 0 \
0 & 1 & -4 & -8 \
2& 0 & 1 & -4 \
1 & 2 & 0 & 1
end{array}
right) .
$$
Т
Теорема 1. Координаты произвольного вектора $ X=x_1X_1+dots+x_nX_n $ и его образа $ Y=mathcal A(X)=y_1X_1+dots+y_nX_n $ связаны формулой
$$
left(begin{array}{c}
y_1 \ vdots \ y_n
end{array}
right) =
{mathbf A}left(begin{array}{c}
x_1 \ vdots \ x_n
end{array}
right) .
$$
Как изменяется матрица оператора при переходе к новому базису?
Т
Теорема 2. Если $ C_{} $ — матрица перехода от старого базиса
к новому, то матрицы $ {mathbf A} $ и $ {mathbf B} $ оператора в старом и новом
базисах связаны формулой:
$$
{mathbf B}=C^{-1}cdot {mathbf A} cdot C .
$$
Доказательство
☞
ЗДЕСЬ.
П
Пример. Оператор $ mathcal A $ в базисе пространства $ mathbb R^{3} $
$$
underbrace{left( begin{array}{r}
8 \ -6 \ 7
end{array}right)}_{X_1},
underbrace{left( begin{array}{r}
-16 \ 7 \ -13
end{array}right)}_{X_2} ,
underbrace{left( begin{array}{r}
9\ -3 \ 7
end{array}right)}_{X_3}
qquad
mbox{ имеет матрицу }
qquad
left( begin{array}{rrr}
1&-18&15\
-1&-22&20\
1&-25 &22
end{array}right).
$$
Найти его матрицу в базисе
$$
underbrace{left( begin{array}{r}
1\ -2 \ 1
end{array}right)}_{mathfrak X_1} ,
underbrace{left( begin{array}{r}
3\ -1 \ 2
end{array}right)}_{mathfrak X_2} ,
underbrace{left( begin{array}{r}
2\ 1 \ 2
end{array}right)}_{mathfrak X_3}.
$$
Решение. Матрица $ C_{} $ перехода от старого базиса к новому
находится по
☞
формуле
$$ C= left[X_1|X_2|X_3right]^{-1} cdot left[{mathfrak X}_1|{mathfrak X}_2|{mathfrak X}_3right]= $$
$$
=left( begin{array}{rrr}
8&-16&9\
-6&7&-3\
7&-13 &7
end{array}right)^{-1}
left( begin{array}{rrr}
1&3&2\
-2&-1&1\
1&2 &2
end{array}right)
=
$$
$$
=left (begin{array}{rrr}
2&-1&-3\
{scriptstyle 21}/{scriptstyle 5}& -{scriptstyle 7}/{scriptstyle 5}&-6\
{scriptstyle 29}/{scriptstyle 5}&-{scriptstyle 8}/{scriptstyle 5}&-8
end{array}right)
left( begin{array}{rrr}
1&3&2\
-2&-1&1\
1&2 &2
end{array}right)=
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right) .
$$
По теореме:
$$
{mathbf B}=C^{-1} {mathbf A} C=
left(begin{array}{rrr}
3&-3&1\
1&-3&2\
1&-2&1
end{array}right)
left( begin{array}{rrr}
1&-18&15\
-1&-22&20\
1&-25 &22
end{array}right)
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right)=
$$
$$
=left(begin{array}{rrr}
7&-13&7\
6&-2&-1\
4&1&-3
end{array}right)
left(begin{array}{rrr}
1&1&-3\
1&2&-5\
1&3&-6
end{array}right)=left(begin{array}{rrr}
1&2&2\
3&-1&-2 \
2&-3&1
end{array}right).
$$
♦
Матрицы $ {mathbf A} $ и $ {mathbf B} $, связанные соотношением
$ {mathbf B}=C^{-1}cdot {mathbf A} cdot C $ при какой-то неособенной матрице $ C_{} $, называются подобными, этот факт будем записывать: $ {mathbf A}doteq {mathbf B} $.
?
Доказать, что отношение подобия есть отношение эквивалентности, и если $ {mathbf A}doteq {mathbf B} $ то $ g({mathbf A})doteq g({mathbf B}) $ при любом полиноме $ g_{}(x) $.
Т
Теорема 3. Для оператора $ mathcal A_{} $ ранг его матрицы является инвариантом, т.е. не зависит от выбора базиса пространства. Этот ранг совпадает с рангом оператора $ mathcal A_{} $.
Доказательство. Если $ {mathbf A} $ и $ {mathbf B} $ — матрицы оператора в двух разных базисах, то они являются подобными: $ {mathbf B}=C^{-1}{mathbf A} C $. По свойству ранга матрицы имеем:
$ operatorname{rank}( {mathbf B})= operatorname{rank}({mathbf A}) $.
♦
=>
Дефект оператора $ mathcal A_{} $ совпадает с дефектом его матрицы в произвольном базисе пространства.
Т
Теорема 4. Для оператора $ mathcal A_{} $ определитель и след его матрицы являются инвариантами, т.е. не зависят от выбора базиса пространства.
Доказательство. Действительно, для подобных матриц $ {mathbf A} $ и $ {mathbf B} $, на основании теоремы Бине-Коши имеем:
$$ det ({mathbf B}) = det (C^{-1}{mathbf A} C) = det (C^{-1}) cdot det ({mathbf A}) cdot det (C) =det ({mathbf A}) . $$
Далее, по свойству следа матрицы:
$$ operatorname{Sp}({mathbf B}) = operatorname{Sp}(C^{-1}{mathbf A} C)=operatorname{Sp}({mathbf A} cdot C cdot C^{-1})=operatorname{Sp}({mathbf A}) . $$
♦
Этот результат позволяет ввести понятие определителя и следа оператора $ mathcal A_{} $ — посредством матрицы этого оператора в произвольном базисе пространства. Такое определение оказывается корректным поскольку оба значения не зависят от выбора базиса.
Каков “физический” смысл определителя оператора?
— Для ответа на этот вопрос рассмотрим оператор в $ mathbb R^2 $, заданный формулой:
$$
left(begin{array}{l} y_1 \ y_2 end{array} right)=
left(begin{array}{rr} 1 & – 3 \ 1 & -1 end{array} right)
left(begin{array}{l} x_1 \ x_2 end{array} right) .
$$
Свойство линейности оператора как отображения плоскости проявляется в том, что параллельные отрезки он отображает в параллельные же отрезки (см. упражнение к теореме 2 из
☞
ПУНКТА ), и, следовательно, любой параллелограмм отображается им в параллелограмм. Площади соответствующих параллелограммов оказываются связанными через определитель матрицы — более точно, через модуль этого определителя. В частном случае настоящего примера это проверяется непосредственно; что касается обобщения на произвольное евклидово пространство, в котором понятие объема вводится аксиоматически то сошлюсь на упражнение 3
☞
ЗДЕСЬ.
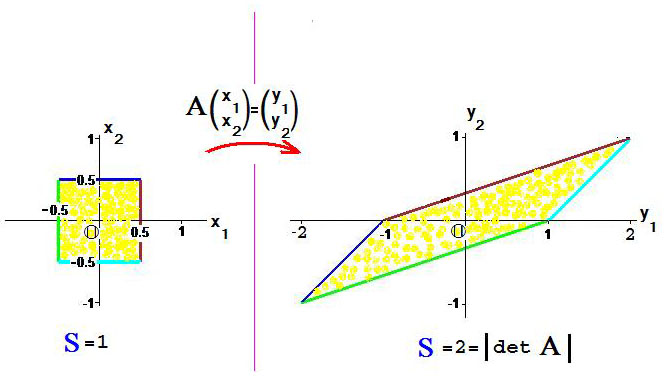
Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения4)объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.
А вот объяснить «физический» смысл следа оператора посложнее будет…
Т
Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.
Т
Теорема 6. Линейное пространство $ {mathcal H}om(mathbb V,mathbb V) $ операторов на $ mathbb V_{}, dim mathbb V = n $ изоморфно линейному пространству квадратных матриц порядка $ n_{} $ (с элементами из $ mathbb R_{} $ или из $ mathbb C_{} $).
Это утверждение является простым следствием теоремы 2, приведенной в пункте
☞
МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ.
Однако в случае операторов установленный изоморфизм сохранит не только результат операции сложения, но и результат операции умножения:
$$ . mbox{ если } mathcal A_1 leftrightarrow mathbf A_1,
mathcal A_2 leftrightarrow mathbf A_2, mbox{ то } mathcal A_1+ mathcal A_2 leftrightarrow mathbf A_1 + mathbf A_2, lambda mathcal A_1
leftrightarrow lambda mathbf A_1 , mathcal A_1 mathcal A_2 leftrightarrow mathbf A_1 mathbf A_2 .
$$
Я сформулирую этот «усиленный вариант» изоморфизма в виде набора свойств, которыми буду пользоваться по мере возникновения потребности.
Т
Теорема 7. В любом базисе пространства
а) матрица нулевого оператора $ mathcal O $ является нулевой матрицей $ mathbb O_{} $, а матрица тождественного оператора $ mathcal E $ является единичной матрицей $ E_{} $; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);
б) матрица произведения операторов совпадает с произведением матриц этих операторов5);
в) коммутирующим операторам соответствуют коммутирующие матрицы;
г) если $ {mathbf A} $ — матрица оператора, то $ {mathbf A}^{-1} $ — матрица обратного оператора;
д) если $ {mathbf A} $ — матрица оператора $ mathcal A $, то матрицей операторного полинома $ g (mathcal A) $ является матрица $ g({mathbf A}) $ .
Матрица оператора и матрица перехода от базиса к базису
Эти матрицы как-то взаимодействовали между собой в предыдущем пункте, хотя вторая была определена совершенно в другом разделе. Обе матрицы квадратные, обе имеют в определении «завязку» на базис пространства $ mathbb V_{} $. У начинающих изучать теорию часто возникает путаница при различении этих определений.
«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).
Тем не менее, с чисто формальной точки зрения, матрица $ C_{} $ перехода от базиса $ {X_1,X_2,dots,X_n } $ пространства $ mathbb V_{} $ к какому-то другому базису $ {mathfrak X_1,mathfrak X_2,dots,mathfrak X_n } $ того же пространства может считаться матрицей некоторого оператора, действующего в этом пространстве. В самом деле, на основании теоремы 6, существует единственный оператор $ mathcal C $, переводящий старые базисные векторы в новые, взятые в той же последовательности:
$$ mathcal C (X_1)=mathfrak X_1, mathcal C (X_2)= mathfrak X_2, dots, mathcal C (X_n)= mathfrak X_n . $$
Но тогда матрица оператора $ mathcal C $ в базисе $ {X_1,X_2,dots,X_n } $ совпадает с матрицей $ C_{} $ перехода от базиса $ {X_1,X_2,dots,X_n } $ к базису $ {mathfrak X_1,mathfrak X_2,dots,mathfrak X_n } $.
Я буду записывать матрицы операторов и матрицы переходов от базиса к базису в разных стилях: $ mathbf A, mathbf B,dots $ и, соответственно, $ C, P, T, dots $ —
с целью быстрого распознавания их «физической» сущности.
Матрица оператора проецирования
Настоящий пункт может быть пропущен при первоначальном чтении.
T
Теорема. Рассмотрим линейную оболочку линейно независимой системы столбцов $ {Y_1,dots, Y_k } subset mathbb R^n $.
$$ mathbb M =left{ lambda_1 Y_1 + dots + lambda_k Y_k big| {lambda_1,dots,lambda_k} subset mathbb R right}= mathcal L (Y_1,dots,Y_k) , . $$
Пусть скалярное произведение векторов $ X_{} $ и $ Y_{} $ задается стандартным способом, т.е. $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Ближайшей к точке $ X_0 subset mathbb R^n $ точкой многообразия (или ортогональной проекцией точки $ X_0 $ на многообразие) $ mathbb M_{} $ является
$$ X_{ast} = mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} X_0 , . $$
Здесь $ mathbf L=[Y_1 |dots |Y_k]_{ntimes k} $.
Матрица $ mathbf L^{top} mathbf L $ невырождена, поскольку является матрицей Грама
$$
mathbf L^{top} mathbf L=
left(begin{array}{cccc}
Y_1^{top} Y_1 & Y_1^{top} Y_2 & dots & Y_1^{top} Y_k \
Y_2^{top} Y_1 & Y_2^{top} Y_2 & dots & Y_2^{top} Y_k \
dots & & & dots \
Y_k^{top} Y_1 & Y_k^{top} Y_2 & dots & Y_k^{top} Y_k
end{array}
right)
$$
системы линейно независимых столбцов $ {Y_1,dots, Y_k } $.
Доказательство. Пусть $ X_0=X_0^{^{parallel}}+X_0^{^{bot}} $, где $ X_0^{^{parallel}} $ — ортогональная проекция точки $ X_0 $ на $ mathbb M $, а $ X_0^{^{bot}} $ — ортогональная составляющая.
Тогда
$$ mathbf L^{top} X_0^{^{bot}}=mathbb O $$
поскольку $ Y_1^{top} X_0^{^{bot}}=0,dots, Y_k^{top} X_0^{^{bot}}=0 $. Далее, $ X_0^{^{parallel}} $ можно разложить по базису $ {Y_1,dots, Y_k } $:
$$ X_0^{^{parallel}}=alpha_1 Y_1+dots+ alpha_k Y_k quad npu quad {alpha_1,dots,alpha_k} subset mathbb R , .
$$
Следовательно,
$$
mathbf L^{top} X_0=mathbf L^{top} (X_0^{^{parallel}}+X_0^{^{bot}})=mathbf L^{top} X_0^{^{parallel}}=
mathbf L^{top} (alpha_1 Y_1+dots+ alpha_k Y_k)=
$$
$$
=left(
begin{array}{c}
alpha_1 Y_1^{top} Y_1 +dots + alpha_k Y_1^{top} Y_k \
alpha_1 Y_2^{top} Y_1 +dots + alpha_k Y_2^{top} Y_k \
dots \
alpha_1 Y_k^{top} Y_1 +dots + alpha_k Y_k^{top} Y_k
end{array}
right)= mathbf L^{top} mathbf L
left(
begin{array}{c}
alpha_1 \
alpha_2 \
vdots \
alpha_k
end{array}
right), .
$$
Тогда
$$
mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} X_0=
mathbf L
left(
begin{array}{c}
alpha_1 \
alpha_2 \
vdots \
alpha_k
end{array}
right)
=alpha_1 Y_1+dots+ alpha_k Y_k= X_0^{^{parallel}} , .
$$
На основании теорем $ 1_{} $ и $ 2_{} $, приведенных
☞
ЗДЕСЬ,
точка $ X_0^{^{parallel}} $ является ближайшей точкой многообразия $ mathbb M $ к точке $ X_{0} $.
♦
Матрица $ P=mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top} $ является матрицей оператора ортогонального проецирования на многообразие $ mathbb M_{} $
в стандартном базисе
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n , . $$
Она симметрична и идемпотентна, т.е. обладает свойством $ P^2=P $.
П
Пример. В $ mathbb R^{3} $ найти матрицу проецирования на плоскость $ x+y+z=0 $.
Решение. Параметрическое задание плоскости:
$$
mathbb M={ lambda_1 underbrace{[1,-1,0]^{top}}_{Y_1} + lambda_2 underbrace{[0,1,-1]^{top}}_{Y_2} big| {lambda_1,lambda_2} subset mathbb R } , .
$$
Имеем:
$$
mathbf L=
left(begin{array}{rr}
1 & 0 \
-1 & 1 \
0 & -1
end{array}
right) Rightarrow
mathbf L^{top} mathbf L=
left(begin{array}{rr}
2 & -1 \
-1 & 2
end{array}
right) Rightarrow (mathbf L^{top} mathbf L )^{-1}=
left(begin{array}{rr}
2/3 & 1/3 \
1/3 & 2/3
end{array}
right) Rightarrow
$$
$$
Rightarrow mathbf L (mathbf L^{top} mathbf L )^{-1} mathbf L^{top}=
frac{1}{3} left(begin{array}{rrr}
2 & -1 & -1 \
-1& 2 & -1 \
-1 & -1 & 2
end{array}
right) , .
$$
♦
В общем случае отображение точки $ X_{0} $ на ближайшую к ней точку произвольного многобразия
$$ mathbb M =left{ Y_0+lambda_1 Y_1 + dots + lambda_k Y_k big| {lambda_1,dots,lambda_k} subset mathbb R right} $$
при $ Y_0 $ линейно независимом от $ {Y_1,dots,Y_k} $ не является линейным оператором, а относится к типу аффинных отображений. Выражение для этого отображения см. в разделе
☞
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ.
Матрица оператора отражения (оператора Хаусхолдера)
Настоящий пункт может быть пропущен при первоначальном чтении.
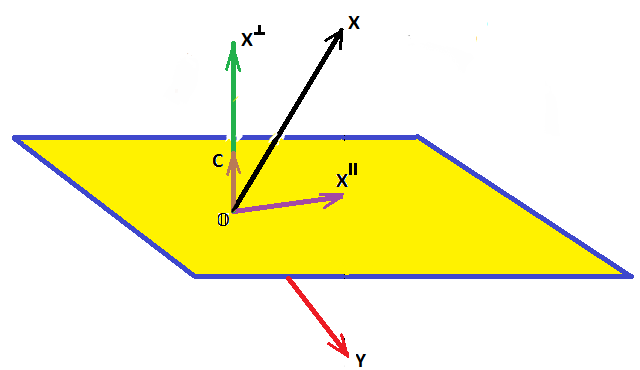
В пространстве $ mathbb R^n $ со стандартным скалярным произведением рассмотрим плоскость, заданную уравнением
$$ C^{top}X= c_1x_1+c_2x_2+dots+c_nx_n = 0 $$
при векторе нормали $ C^{top}=(c_1,c_2,dots,c_n) $ единичной длины: $ |C|^2= C^{top}C=1 $. Действие оператора зеркального отражения или оператора Хаусхолдера6) относительно этой плоскости на вектор (точку) $ X in mathbb R^n $ определим правилом
$$ mathcal H( X^{^{parallel}} + X^{^{bot}})= X^{^{parallel}} – X^{^{bot}} ; $$
здесь $ X^{^{parallel}} $ — ортогональная проекция вектора $ X_{} $ на заданную плоскость, а $ X^{^{bot}} $ — ортогональная составляющая вектора $ X_{} $ относительно этой плоскости.
Т
Теорема. Оператор $ mathcal H $ задается уравнением
$$ mathcal H(X)=X-2, langle X,C rangle C=X-2, C (C^{top}X)= X-2, C^{top}XC , . $$
Последний вариант формулы никогда не встречал, но он имеет формальное право на существование!
Доказательство.
$$ mathcal H( X^{^{parallel}} + X^{^{bot}})=X^{^{parallel}} + X^{^{bot}}-2, langle X^{^{parallel}},C rangle C-2,
langle X^{^{bot}},C rangle C = $$
Поскольку $ X^{^{parallel}} $ ортогонален, а вектор $ X^{^{bot}} $ коллинеарен вектору $ C $ единичной длины, то
$$= X^{^{parallel}} + X^{^{bot}} – 2, X^{^{bot}} = X^{^{parallel}} – X^{^{bot}} , . $$
♦
Т
Теорема. Матрица оператора $ mathcal H $ в стандартном базисе
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n , . $$
имеет вид
$$ mathbf H_{C}= E-2, C cdot C^{top} =
left( begin{array}{cccc}
1-2c_1^2 & -2,c_1c_2 & dots & – 2 c_1 c_n \
-2,c_1c_2 & 1-2c_2^2 & dots & – 2 c_2 c_n \
vdots & & & vdots \
– 2 c_1 c_n & – 2 c_2 c_n & dots & 1-2c_n^2
end{array}
right) , .
$$
П
Пример. Найти зеркальное отражение точки $ [3,2,3] $ относительно плоскости $ 2,x-2,y+z = 0 $.
Решение. Здесь $ C^{top}=[2/3,-2/3,1/3] $ и
$$ mathcal H(X)= left( begin{array}{r} 3 \ 2 \ 3 end{array} right) – 2langle [3,2,3],[2/3,-2/3,1/3] rangle
left( begin{array}{r} 2/3\ -2/3 \ 1/3 end{array} right)=
left( begin{array}{r} 7/9 \ 38/9 \ 17/9 end{array} right) , .
$$
Проверим результат посредством матричного представления:
$$
mathbf H_C=
left( begin{array}{rrr}
1/9 & 8/9 & -4/9 \
8/9 & 1/9 & 4/9 \
-4/9 & 4/9 & 7/9
end{array}
right) quad Rightarrow quad mathbf H left( begin{array}{r} 3 \ 2 \ 3 end{array} right)=
left( begin{array}{r} 7/9 \ 38/9 \ 17/9 end{array} right) , .
$$
♦
=>
Матрица $ mathbf H_{C} $ одновременно симметрична и ортогональна, и $ det mathbf H_{C}=-1 $. Следовательно, ей обратная существует и совпадает с ней самой:
$$ mathbf H_{C}^{-1}= mathbf H_{C} , . $$
Инвариантное подпространство
Задача. Подобрать базис пространства $ mathbb V_{} $ так, чтобы матрица заданного оператора $ mathcal A_{} $ имела наиболее простой вид.
Исследуем действие оператора $ mathcal A $ на произвольное подпространство
$ mathbb V_1 subset mathbb V $:
$$mathcal A (mathbb V_1)= left{Yin mathbb V mid Y=mathcal A (X), X in mathbb V_1
right} .$$
Вообще говоря, множества $ mathbb V_1 $ и $ mathcal A (mathbb V_1) $ будут различными, т.е.
$ exists X_1 in mathbb V_1 $ такой, что $ mathcal A (X_1)notin mathbb V_1 $.
Подпространство $ mathbb V_1 $ называется инвариантным подпространством оператора $ mathcal A $, если оно отображается этим оператором в себя:
$$ mathcal A(mathbb V_1)subset mathbb V_1 .$$
$ mathbb V_1={mathbb O } $ и $ mathbb V_1=mathbb V $ — тривиальные инвариантные подпространства произвольного оператора $ mathcal A $.
Нас будут интересовать нетривиальные инвариантные подпространства.
П
Пример. Оператор
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
left(begin{array}{rrr}
{scriptstyle 1}/{scriptstyle sqrt 2} &
-{scriptstyle 1}/{scriptstyle sqrt 2} & 0 \
{scriptstyle 1}/{scriptstyle sqrt 2} &
{scriptstyle 1}/{scriptstyle sqrt 2} & 0 \
0 & 0 & 1
end{array}
right)
left(begin{array}{c}
x \ y \ z
end{array}
right)
$$
задает в пространстве поворот вокруг оси $ mathbb O z $ на угол
$ +pi /4 $.
Нетривиальными инвариантными подпространствами будут
а) ось вращения $ mathbb V_1={(0,0,z)^{^{top}} mid z in mathbb R} $, $ dim mathbb V_1=1 $ и
б) плоскость, перпендикулярная оси вращения $ mathbb V_2={(x,y,0)^{^{top}} mid {x,y} subset mathbb R} $, $ dim mathbb V_2= 2 $.
♦
П
Пример. Оператор
$$left(begin{array}{c}
x \ y
end{array}
right) longmapsto
left(begin{array}{c}
lambda_1 x \ lambda_2 y
end{array}
right)
$$
задает на плоскости «растяжение»: $ x_{} $-компонента увеличивается
в $ lambda_{1} $ раз, а $ y_{} $-компонента — в $ lambda_{2} $ раз.
При любой комбинации коэффициентов растяжения координатные оси будут инвариантными подпространствами. Однако в частном случае $ lambda_1=lambda_2 $ инвариантной будет также любая
прямая, проходящая через начало координат.
♦
П
Пример. Оператор в $ mathbb R^{n}_{} $ задан блочной матрицей
$$X longmapsto left( begin{array}{cc}
{mathbf A}_1 & {mathbf *}\
mathbb O & {mathbf A}_2
end{array}
right) X
$$
где $ {mathbf A}_1 $ — $ n_1times n_1 $-матрица, $ {mathbf A}_2 $ —
$ (n-n_1)times (n-n_1) $-матрица. Множество столбцов
$$mathbb V_1=left{X=[x_1,dots,x_{n_1},0,dots,0]^{^{top}} bigg| { x_1,
dots, x_{n_1} } subset mathbb R right}$$
образует инвариантное подпространство, $ dim mathbb V_1=n_1 $. Если же, вдобавок,
матрица, обозначенная $ {mathbf *} $ — нулевая, то вторым инвариантным
подпространством будет
$$ mathbb V_2=left{X=[0,dots,0,x_{n_1+1},dots,x_n]^{^{top}} bigg| {x_{n_1+1},dots, x_n } subset mathbb R right} .$$
♦
Т
Теорема. $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ —
инвариантные подпространства оператора $ mathcal A $.
?
Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.
Т
Теорема. Если пространство $ mathbb V_{} $ раскладывается в прямую сумму подпространств, инвариантных относительно оператора $ mathcal A $, то существует базис пространства, в котором матрица оператора будет блочно-диагональной.
Теорема обобщается очевидным образом на произвольное число слагаемых
подпространств: $ mathbb V=mathbb V_1oplus mathbb V_2 oplus dots oplus mathbb V_k $.
Если при этом $ dim mathbb V_1= dots = dim mathbb V_k=1 $, то матрица оператора в базисе, полученном объединением базисных векторов слагаемых подпространств, становится диагональной — это и является решением задачи, поставленной в начале пункта.
Собственное число и собственный вектор
Задача. Найти одномерные инвариантные подпространства оператора.
Вектор $ X_{}in mathbb V $ называется собственным вектором оператора $ mathcal A_{} $, если
$$ {mathbf a)} X ne mathbb O, quad u quad {mathbf b)} exists lambda in mathbb C qquad mbox{ такое, что } qquad
mathcal A(X)=lambda X .$$
В этом случае число $ lambda_{} $ называется
собственным или характеристическим числом оператора, соответствующим (или принадлежащим) данному собственному вектору; обратно, говорят, что вектор $ X_{} $ принадлежит собственному числу $ lambda_{} $.
Вопрос существования хотя бы одного собственного числа для произвольного оператора $ mathcal A_{} $ остается пока открытым. Однако, свойство линейности оператора гарантирует, что если это число существует, то ему соответствует бесконечное множество собственных векторов:
$$ mathcal A(X)=lambda X quad Rightarrow quad mathcal A(t,X)=t mathcal A(X)= tlambda, X , $$
т.е. если вектор $ X in mathbb V_{} $ является собственным, то и вектор $ t, X $ будет собственным при любом скаляре $ tne 0 $. Заметим, что собственное число разыскивается во множестве комплексных чисел: вопрос о существовании вещественного собственного числа — даже в случае вещественного пространства $ mathbb V_{} $ — остается открытым. Геометрический смысл вещественных собственных чисел и векторов проясняет следующий пример.
П
Пример. Оператор
$$left(begin{array}{c}
x \ y
end{array}
right) longmapsto
left(begin{array}{rr}
1 & – 5/2 \
-1/2 & 2
end{array}
right)
left(begin{array}{c}
x \ y
end{array}
right)
$$
задает отображение плоскости $ mathbb R^2 $. На рисунке показан результат действия этого отображения на единичную окружность. Все точки плоскости, за исключением начала координат $ mathbb O_{} $, изменят свое положение — ни одна не останется на месте.
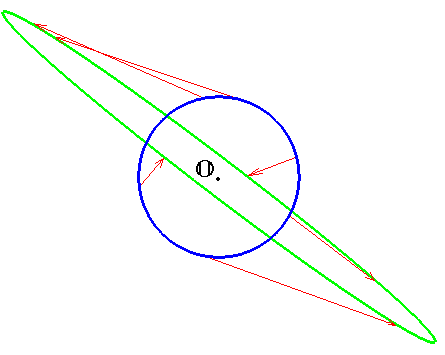
Если рассмотреть эти точки как концы векторов, имеющих начало в $ mathbb O_{} $, то смещения точек под действием оператора можно представить в виде двух составляющих: растяжения (т.е. увеличения расстояния до начала координат) и поворота вокруг начала координат на некоторый угол. И только по двум направлениям плоскости поворота не происходит. Точки окружности с координатами
$$
pm left( 0.823, -0.568 right)^{top} quad u quad
pm left( 0.960, 0.278 right)^{top}
$$
будут смещаться без поворота. Эти точки и задают координаты конца собственного вектора. А соответствующие им собственные числа $ 2.725 $ и $ 0.275 $ определяют коэффициенты сдвига.
Если вообразить оператор как деформацию физической среды, заполняющей плоскость, то можно сказать, что cобственный вектор задает направление, на котором действие оператора сводится к растяжению, при этом коэффициент растяжения и будет собственным числом.
А
Анимация процесса
☞
ЗДЕСЬ (1500 Kb, gif).
Пример другого оператора
$$
left(begin{array}{l} x \ y end{array} right) longmapsto
left(begin{array}{rr} 1 & – 3 \ 1 & -1 end{array} right)
left(begin{array}{l} x \ y end{array} right)
$$
показывает, что существование вещественных собственных чисел вовсе не гарантировано даже в случае оператора в вещественном пространстве: в этом примере все точки плоскости повернутся вокруг начала координат.
♦
Я «замыливаю» ответ на вопрос какой физический смысл имеют отрицательные собственные числа…
?
Доказать, что $ operatorname{dfc} (mathcal A) ne 0 $ тогда и только тогда, когда оператор $ mathcal A_{} $ имеет собственное число, равное нулю.
Т
Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства
оператора является собственным вектором.
П
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_{} $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
т.е. полином $ f_{}(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Найти собственные векторы этого оператора.
Решение. В пространстве $ mathbb P_3 $ векторами являются полиномы, а условие того, что полином $ f_{}(x) $ является собственным, принадлежащим числу $ lambda_{} $, записывается в виде:
$$ f(x)(x^2-2)equiv lambda f(x) pmod{x^4-x^3-x^2+x} quad iff $$
$$ iff quad f(x)(x^2-2-lambda)equiv 0 pmod{x^4-x^3-x^2+x} . $$
Поскольку $ deg f le 3 $, то последнее может выполняться тогда и только тогда, когда полином
$ x^2-2-lambda $ имеет общие корни с $ x^4-x^3-x^2+x equiv x(x+1)(x-1)^2 $. Из этого условия вытекает, что число $ lambda_{} $ может принимать только два значения: $ lambda_1=-2 $ и
$ lambda_2=-1 $. Если $ lambda_1=-2 $ является собственным числом, то ему соответствующий собственный вектор — полином степени $ le 3 $ — должен определяться из условия делимости $ f(x)x^2 $ на $ x(x+1)(x-1)^2 $. Такой полином имеет вид $ t(x+1)(x-1)^2 $ при произвольной константе $ t_{} $. Следовательно множество
$$ { t(x^3-x^2-x+1)= t(x+1)(x-1)^2 mid tne 0 } $$
является множеством собственных векторов, принадлежащих $ lambda_1=-2 $.
С числом $ lambda_2=-1 $ поступаем аналогично. Условие делимости полинома $ f(x)(x^2-1) $ на $ x(x+1)(x-1)^2 $ дает также бесконечное множество:
$$ { (t_1x+t_2)x(x-1) mid {t_1,t_2} subset mathbb R } . $$
Однако в этом случае бесконечность множества качественно иная, чем в предыдущем случае; она — «двумерная».
♦
Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.
Т
Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.
Доказательство. Пусть $ {X_1,dots,X_{n} } $ — произвольный базис пространства $ mathbb V_{} $ и
$ mathbf A_{} $ — матрица оператора $ mathcal A_{} $ в этом базисе. Тогда для
того чтобы вектор $ X=x_1X_1+cdots+x_nX_n ne mathbb O $ был собственным,
принадлежащим собственному числу $ lambda_{} $, необходимо и достаточно чтобы выполнялось
равенство
$$
{mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) =
lambda left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) quad
Longleftrightarrow quad
left(begin{array}{cccc}
alpha_{11} – lambda & alpha_{12}& dots & alpha_{1n} \
alpha_{21} & alpha_{22}- lambda& dots & alpha_{2n} \
dots & & & dots \
alpha_{n1} & alpha_{n2}& dots & alpha_{nn}- lambda
end{array}
right)
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) = mathbb O_{ntimes 1}
$$
Покажем, что существуют комплексные числа $ lambda_{} $ и не все нулевые $ x_1,dots,x_{n} $, удовлетворяющие этой системе. Необходимым и достаточным
условием существования нетривиального решения у однородной системы линейных уравнений с квадратной матрицей является равенство нулю определителя этой матрицы:
$$
det ({mathbf A}-lambda E)=left|begin{array}{cccc}
alpha_{11} – lambda & alpha_{12}& dots & alpha_{1n} \
alpha_{21} & alpha_{22}- lambda& dots & alpha_{2n} \
dots & & & dots \
alpha_{n1} & alpha_{n2}& dots & alpha_{nn}- lambda
end{array}
right|=0 .
$$
Этот определитель является полиномом степени $ n_{} $ по $ lambda_{} $. По
основной теореме высшей алгебры этот полином имеет по крайней мере один комплексный корень $ lambda=lambda_{ast} $. Подставив его в
систему, получаем однородную систему уравнений с нулевым
определителем. Находим нетривиальное решение этой системы:
$$ x_1=x_{1}^{ast},dots,x_n=x_{n}^{ast}, quad exists x_{j}^{ast} ne 0 ; $$
но тогда вектор
$ {mathfrak X}_{ast}= x_{1}^{ast}X_1+cdots+x_{n}^{ast}X_n $ будет собственным вектором оператора $ mathcal A_{} $, принадлежащим $ lambda_{ast}^{} $.
♦
Уравнение $ det ({mathbf A}-lambda E)= 0 $ называется характеристическим или вековым уравнением, а полином в левой его части — характеристическим полиномом матрицы $ {mathbf A} $. Любой корень характеристического полинома матрицы называется собственным числом этой матрицы. Набор всех собственных чисел матрицы (корней характеристического полинома с учетом кратностей) называется спектром матрицы. Ненулевой вектор $ X in mathbb C^n $, удовлетворяющий условию $ {mathbf A} X= lambda X $, где $ lambda $ — собственное число матрицы, называется собственным вектором матрицы, соответствующим (или принадлежащим) данному собственному числу.
П
Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.
Решение. Базисом в пространстве $ mathbb P_3 $ выберем $ {1,,x,,x^2,, x^3} $. Образы базисных векторов под действием оператора $ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} $:
$$
left{begin{array}{lrrrr}
mathcal A (1) =&-2& &+x^2& ,\
mathcal A (x) =&&-2,x &&+x^3 ,\
mathcal A (x^2) =& &-x &-x^2 &+x^3, \
mathcal A (x^2) =& &-x & & ,
end{array} right. qquad Rightarrow qquad {mathbf A}=
left(begin{array}{rrrr}
-2 & 0 & 0 & 0 \
0 & -2 & -1 & -1 \
1& 0 & -1 & 0 \
0 & 1 & 1 & 0
end{array}
right) .
$$
Характеристический полином матрицы $ {mathbf A} $:
$$
left|begin{array}{cccc}
-2-lambda & 0 & 0 & 0 \
0 & -2-lambda & -1 & -1 \
1& 0 & -1-lambda & 0 \
0 & 1 & 1 & -lambda
end{array}
right|equiv (lambda+2)(lambda^3+3,lambda^2+3,lambda+1)equiv (lambda+2)(lambda+1)^3 .
$$
Собственные числа $ lambda_1=-2 $ и $ lambda_2=-1 $, спектр матрицы $ {-1,-1,-1,-2} $. Подставляем каждое из собственных чисел в матрицу $ {mathbf A}-lambda E $ и решаем получившиеся системы однородных уравнений. Поскольку каждая из них должна иметь бесконечное множество решений, то мы строим фундаментальные системы решений (ФСР)
$$
begin{array}{ccc}
& ({mathbf A}-lambda E)X=mathbb O & \
{color{Red} swarrow } & & {color{Red} searrow } \
lambda_1=-2 & & lambda_2=-1 \
Downarrow & & Downarrow \
left(begin{array}{rrrr}
0 & 0 & 0 & 0 \
0 & 0 & -1 & -1 \
1& 0 & 1 & 0 \
0 & 1 & 1 & 2
end{array}
right)
left(begin{array}{l}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)= mathbb O
& &
left(begin{array}{rrrr}
-1 & 0 & 0 & 0 \
0 & -1 & -1 & -1 \
1& 0 & 0 & 0 \
0 & 1 & 1 & 1
end{array}
right) left(begin{array}{l}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right)= mathbb O . \
{color{Red} Downarrow } & & {color{Red} Downarrow } \
x_1=1,x_2=-1,x_3=-1,x_4=1 & & left{begin{array}{c}
x_1=0,x_2=-1,x_3=1,x_4=0 \
x_1=0,x_2=-1,x_3=0,x_4=1
end{array} right}
end{array}
$$
Таким образом, собственному числу $ lambda_1=-2 $ соответствует собственнный вектор — полином $ 1-x-x^2+x^3 $, и он полностью совпадает с полученным при решении предыдущего примера. В то же время собственному числу $ lambda_2=-1 $ соответствует два линейно независимых собственнных вектора — полиномы $ -x+x^2 $ и $ -x+x^3 $. Любой (не тождественно нулевой) полином множества
$$ { tau_1(-x+x^2) +tau_2(-x+x^3) mid {tau_1,tau_2 } subset mathbb R } $$
будет также являться собственным, принадлежащим $ lambda_2=-1 $. Это множество также совпадает с полученным при решении предыдущего примера.
♦
Итак, два формально различных подхода к решению одного и того же примера не привели к противоречию. Хотелось бы, однако, гарантировать глобальную непротиворечивость определения собственных чисел и векторов — т.е. независимость (инвариантность) этих объектов относительно способов их нахождения, и, в частности, от выбора базиса пространства $ mathbb V_{} $.
Т
Теорема. Характеристические полиномы подобных матриц одинаковы.
Доказательство. $ {mathbf A}doteq {mathbf B} {color{Red} iff } exists $ неособенная матрица $ C_{} $,
такая что $ {mathbf B}=C^{-1} {mathbf A} C $. Имеем:
$$det ({mathbf B}-lambda E)=det (C^{-1} {mathbf A} C-lambda E)=$$
$$=
det (C^{-1} {mathbf A} C-lambda C^{-1}EC)=det left[ C^{-1} ({mathbf A} -lambda
E)C right] = det ({mathbf A}-lambda E) .$$
♦
Иначе говоря, для оператора $ mathcal A_{} $ характеристический полином его матрицы не
зависит от выбора базиса пространства. Поэтому можно говорить о характеристическом полиноме оператора $ mathcal A_{} $.
Характеристический полином матрицы подробнее исследуется
☞
ЗДЕСЬ. В частности, в указанном разделе приведен результат, на основании которого (а также на основании пунктов а) и д) теоремы 7, приведенной в пункте
☞
МАТРИЦА ОПЕРАТОРА ) выводится следующее нетривиальное утверждение:
Т
Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.
П
Пример. Для рассмотренного в предыдущих примерах оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
действующего в $ mathbb P_3 $,
характеристический полином равен
$$ lambda^4+5,lambda^3+9,lambda^2+7,lambda+2 , .$$
Проверим утверждение теоремы Гамильтона-Кэли — должно быть выполнено условие
$$ mathcal A^4+5,mathcal A^3+9,mathcal A^2+7,mathcal A +2, mathcal E = mathcal O . $$
Степени данного оператора $ mathcal A_{} $ обсуждались в примере
☞
ПУНКТА. Переписанное в терминах остатков, последнее условие превращается в
$$ (x^2-2)^4f(x)+5,(x^2-2)^3f(x)+9,(x^2-2)^2f(x)+7,(x^2-2)f(x) + $$
$$+2,f(x) equiv 0 pmod{x^4-x^3-x^2+x} , $$
т.е. полином, стоящий в левой части сравнения, должен делиться нацело на $ x^4-x^3-x^2+x $ при любом выборе полинома $ f_{}(x) $. Проверяем:
$$ (x^2-2)^4+5,(x^2-2)^3+9,(x^2-2)^2+7,(x^2-2)+2 equiv $$
$$equiv x^8-3,x^6+3,x^4-x^2 equiv (x^4+x^3-x^2-x)(x^4-x^3-x^2+x) , $$
т.е. утверждение оказывается справедливым.
♦
Диагонализуемость матрицы оператора
Т
Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 2. Если оператор имеет $ n=dim mathbb V $ линейно независимых собственных векторов, то в базисе ими образуемом матрица оператора диагональна. Обратно: если матрица оператора в некотором базисе диагональна, то каждый вектор этого базиса является собственным для оператора.
Базис линейного пространства, состоящий из собственных векторов оператора $ mathcal A_{} $, называется каноническим.
=>
[Матричная версия теоремы]. Пусть $ A_{} $ — квадратная матрица. Неособенная матрица
$ C_{} $, удовлетворяющая равенству
$$C^{-1} A C= A_{diag} quad mbox{ при матрице } A_{diag} quad mbox{ – диагональной} $$
существует тогда и только тогда, когда существует базис пространства $ mathbb C^{n}_{} $,
состоящий из собственных векторов матрицы $ A_{} $. Тогда матрица $ C_{} $ является матрицей перехода от
стандартного базиса
$$ bigg{{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} bigg}_{j=1}^n $$
к каноническому, а на диагонали $ A_{diag} $ стоят собственные числа матрицы $ A_{} $:
$$
A_{diag}=
left(
begin{array}{cccc}
lambda_1 & 0 & dots & 0 \
0 & lambda_2 & dots & 0 \
vdots & & ddots & vdots \
0 & 0 & dots & lambda_n
end{array}
right) .
$$
Доказательство. Проведем формальное доказательство данного конкретного частного случая. Рассмотрим матричное равенство
$$ A C= CA_{diag} $$
при некоторой диагональной матрице $ A_{diag} $.
Легко видеть, что оно эквивалентно системе равенств относительно столбцов матрицы $ C_{} $:
$$
AC_{[1]}=d_1 C_{[1]},dots, AC_{[n]}=d_n C_{[n]} , .
$$
Если все столбцы $ { C_{[j]} }_{j=1}^n $ ненулевые, то тогда они являются собственными векторами для матрицы $ A_{} $, а числа $ { d_{[j]} }_{j=1}^n $ — собственными числами, соответствующими этим собственным векторам. Если матрица $ C_{} $ невырождена, то все ее столбцы линейно независимы. Но тогда они образуют базис пространства $ mathbb C^n $, состоящий из собственных векторов. Обратное тоже верно.
♦
При выполнении условия предыдущего следствия говорят, что матрица $ A_{} $ диагонализуема или приводится к диагональной форме7).
Теорема позволяет сформулировать достаточное условие диагонализуемости.
Т
Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.
Для проверки условия теоремы не требуется явного вычисления корней: оно проверяется по коэффициентам характеристического полинома «чисто алгебраически» (т.е. за конечное число элементарных алгебраических операций). Оно эквивалентно отличию от нуля дискриминанта характеристического полинома.
Это условие не является необходимым, как показывает пример тождественного оператора.
Случай существования кратного корня у характеристического полинома является
«пограничным»: существуют примеры как диагонализуемых, так и недиагонализуемых матриц. Так, для матриц
$$ A= left( begin{array}{rr}
0 &1 \
-1 &2
end{array}
right) quad mbox{ или } quad
A= left( begin{array}{cc}
1 &0 \
1&1
end{array}
right)
$$
при попытке подобрать матрицу $ C_{} $, удовлетворяющую равенству
$$AC=C left( begin{array}{cc}
alpha_1 &0 \
0 & alpha_2
end{array}
right) qquad npu forall {alpha_1 , alpha_2 } subset mathbb C
$$
получим: $ det C=0 $.
В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.
Т
Теорема 4. Множество собственных векторов оператора, принадлежащих его собственному числу $ lambda_{ast}^{} $ , дополненное нулевым вектором, образует линейное подпространство пространства $ mathbb V_{} $.
Это подпространство
$$ mathbb V_{ast} = mathcal{K}er (mathcal A- lambda_{ast} mathcal E) $$
пространства $ mathbb V_{} $ называется собственным подпространством оператора, соответствующим $ lambda_{ast}^{} $.
Величина
$$ dim (mathcal{K}er (mathcal A- lambda_{ast} mathcal E)) $$
называется геометрической кратностью собственного числа $ lambda_{ast}^{} $.
Можно доказать, что геометрическая кратность собственного числа не превосходит кратности собственного числа в характеристическом полиноме. Для акцентирования различий в определениях двух кратностей, кратность собственного числа в характеристическом полиноме называют еще алгебраической кратностью собственного числа.
Если оператор (в некотором базисе пространства) задан своей матрицей $ mathbf A^{} $, то базисные векторы собственного подпространства $ mathbb V_{ast} $ вычисляются посредством нахождения фундаментальной системы решений (ФСР) системы линейных уравнений
$$ (mathbf A- lambda_{ast} E) X=mathbb O . $$
Т
Теорема 5. Матрица оператора диагонализуема тогда и только тогда,
когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:
$$
operatorname{dfc} ({mathbf A}-lambda_{ast}, E)= mbox{ кратность } lambda_{ast} .
$$
?
Диагонализуема ли матрица оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod{x^4-x^3-x^2+x} , $$
рассмотренного в примерах предыдущего пункта?
П
Пример. Найти все вещественные значения параметра $ {color{Red}{ alpha} } $, при которых матрица
$$
left( begin{array}{rcc}
1 &2, {color{Red}{ alpha} } & {color{Red}{ alpha} } -2 \
-1 &2 &1 \
2 & 0 & -3
end{array}
right)
$$
диагонализуема.
Решение. Характеристический полином
$ f(lambda)=-lambda^3+3, lambda-2,(3, {color{Red}{ alpha} } -1) $
имеет кратные корни только тогда когда его дискриминант $ mathcal D(f)=-324, {color{Red}{ alpha} }
(3, {color{Red}{ alpha} } -2) $ обращается в нуль. При $ {color{Red}{ alpha} } =0 $ корень $ lambda=-1 $
имеет алгебраическую кратность $ 2_{} $. Найдем дефект матрицы $ A+E $:
$$left( begin{array}{rrr}
2 &0 & -2 \
-1 &3 &1 \
2 & 0 & -2
end{array}
right) longrightarrow
left( begin{array}{rrr}
1 &0 & -1 \
0 &3 &0 \
0 & 0 & 0
end{array}
right) {color{Red} Longrightarrow } operatorname{rank} (A+E) =2 Longrightarrow operatorname{dfc} (A+E)=1 .
$$
Таким образом, геометрическая кратность собственного числа $ lambda=-1 $ равна $ 1_{} $ и
условие теоремы $ 5 $ не выполнено. Оно не будет выполнено
и при $ {color{Red}{ alpha} } = 2/3 $ (здесь корень $ lambda=1 $ имеет кратность $ 2_{} $).
Ответ. Матрица диагонализуема при всех значениях параметра, за исключением $ {color{Red}{ alpha} } = 0 $ и $ {color{Red}{ alpha} } = 2/3 $.
Диагонализуемость матрицы оператора над полем вещественных чисел
В предыдущем пункте мы рассматривали операторы, не всегда акцентируя внимания на поле, над которым они были определены — над $ mathbb R_{} $ или над $ mathbb C_{} $. Сама теорема существования собственного числа гарантирует нам только лишь наличие этих чисел в поле $ mathbb C_{} $. Как следствие, даже если рассматриваются операторы над полем $ mathbb R_{} $ (что чаще всего и случается на практике), то существование для них вещественного канонического базиса вовсе не гарантировано.
Задача. Найти условия диагонализуемости матрицы оператора $ mathcal A $ над полем вещественных чисел.
Необходимое условие следует из теоремы $ 2 $ предыдущего пункта: все собственные числа
матрицы должны быть вещественными.
Теорема $ 3 $ позволяет сформулировать и достаточный критерий диагонализуемости матрицы оператора $ mathcal A $ над $ mathbb R_{} $.
Т
Теорема. Если характеристический полином оператора имеет только простые вещественные корни, то матрица оператора диагонализуема над $ mathbb R_{} $.
Условие различности и вещественности корней произвольного полинома $ f(lambda)=lambda^n+a_1lambda^{n-1}+dots+ a_n in mathbb R[x] $
можно проверить по коэффициентам этого полинома «чисто алгебраически», т.е. за конечное число элементарных алгебраических операций над этими коэффициентами. Воспользуемся, например,
теоремой Якоби из раздела
☞
ЛОКАЛИЗАЦИЯ КОРНЕЙ ПОЛИНОМА. По коэффициентам $ a_1,dots,a_n $ можно определить сумму Ньютона полинома
$ f(lambda) $, т.е. величину
$$
s_k=sum_{1le j le n} lambda_j^k .
$$
Далее, после нахождения всех этих сумм для значений $ k in {0,dots,2n-2} $, из них составляется ганкелева матрица
$$
S=left[ s_{j+k} right]_{j,k=0}^{n-1}
$$
и вычисляются ее главные миноры $ S_1,dots, S_{n} $.
Для различности всех корней полинома необходимо и достаточно выполнение условия $ S_n ne 0 $ (этот минор совпадает с дискриминантом $ mathcal D(f) $ полинома $ f(lambda) $); для различности и вещественности всех корней необходимо и достаточно, чтобы были выполнены неравенства
$$
S_1ge 0,dots,S_{n-1} ge 0,S_n > 0 .
$$
П
Пример. Найти все вещественные значения параметра $ {color{Red}{ alpha} } $, при которых матрица
$$
left( begin{array}{rcc}
1 &2, {color{Red}{ alpha} } & {color{Red}{ alpha} } -2 \
-1 &2 &1 \
2 & 0 & -3
end{array}
right)
$$
диагонализуема над $ mathbb R_{} $.
Решение. На основании теоремы нам нужно установить условия вещественности корней характеристического полинома $ f(lambda)=-lambda^3+3, lambda-2,(3, {color{Red}{ alpha} } -1) $.
Вычисляем суммы Ньютона:
$ s_0=3, s_1= 0, s_2=6, s_3=18, {color{Red}{ alpha} } -6, s_4=18 $, составляем матрицу:
$$ S=left(begin{array}{ccc}
3 & 0 & 6 \
0 & 6 & 18, {color{Red}{ alpha} } -6 \
6 & 18, {color{Red}{ alpha} } -6 & 18
end{array}
right)
$$
и вычисляем ее главные миноры:
$$S_1=3, S_2=18, S_3=-324, {color{Red}{ alpha} } , (3, {color{Red}{ alpha} } -2)=mathcal D(f) . $$
При $ {color{Red}{ alpha} } ne 0 $ и $ {color{Red}{ alpha} } ne 2/3 $ все собственные числа различны,
условие теоремы выполняется при $ {color{Red}{ alpha} } in ]0,, 2/3[ $. Граничные
точки последнего интервала следовало бы исследовать отдельно: хотя этим
значениям параметра и соответствует случай кратных вещественных корней
характеристического полинома, но матрица $ A_{} $ может оказаться диагонализуемой на
основании теоремы 5 предыдущего пункта. Но при решении примера в предыдущем пункте мы уже установили, что это условие не выполняется.
Ответ. Матрица диагонализуема над $ mathbb R_{} $ при $ {color{Red}{ alpha} } in ]0,, 2/3[ $.
Примером гарантировано диагонализуемых над $ mathbb R_{} $ матриц являются вещественные симметричные матрицы. См.
☞
ЗДЕСЬ.
Жорданова нормальная форма
Если матрица оператора оказывается недиагонализуемой над $ mathbb C_{} $, то к какому простейшему виду ее можно привести
?
— Этим видом является, например,
☞
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА.
Задачи
Источники
[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.
[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960
[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965
Помогите пожалуйста решить, потому что пытаюсь решить сама-получается что-то страшное
Знаток
(291),
закрыт
3 недели назад
Наталья А
Ученик
(158)
5 лет назад
Пусть оператор σ – зеркальное отражение относительно плоскости x-y+z=0.
Каждый вектор переходит в вектор, симметричный (зеркально отраженный) относительно указанной плоскости.
Формула проекции вектора a на плоскость р (в этой формуле проекция рассматривается как вектор): прₚа=a-(a,n)·n/|n|², n-произвольный ненулевой вектор, нормальный к данной плоскости.
Вектор d, симметричный данному вектору a относительно данной плоскости p: d=a-2(a,n)·n/|n|².
В нашем случае в качестве такового можно взять вектор {1; -1; 1}.
Найдем образы базисных векторов:
σ(i)={1/3;2/3;-2/3}; σ(j)={2/3;1/3;2/3}; σ(k)={-2/3;2/3;1/3}.
Составим матрицу этого линейного оператора Aσ=
⎛ ⅓ ⅔ -⅔⎞
⎜ ⅔ ⅓ ⅔ ⎜
⎝-⅔ ⅔ ⅓⎠
Матрица A невырождена (det Aσ=-1), и, следовательно, оператор σ обратим.
Поскольку линейный оператор σ обратим, то у него нулевое ядро, а его образ есть все пространство.
(Так как любой вектор имеет прообраз, то образ совпадает со всем пространством R³. Что же касается ядра, то это по определению множество всех векторов, переходящих в нуль. Так как при отражении длина вектора не меняется, то таковым может быть только нулевой вектор. Итак, ядро в данном случае равно нулевому подпространству. Можно воспользоваться общим утверждением: если линейный оператор обратим, то у него нулевое ядро, а его образ есть все пространство.)
Задачи для подготовки к экзамену и контрольной работе по теме №3
«Линейные операторы». (2 семестр)
3.1. В базисе линейный оператор А имеет матрицу
. Найти его матрицу в базисе
.
Решение:
Матрица данного линейного оператора имеет вид:
,
матрица перехода от базиса к базису
имеет вид:
.
Следовательно, матрица данного линейного оператора в базисе имеет вид:
3.2. В пространстве V3 линейный оператор А – проекция на ось OY. Найти матрицу оператора А в базисе . Найти образ вектора
. Найти ядро и образ оператора А. Существует ли обратный оператор?
Решение:
Проекция на ось OY в пространстве V3 переводит точку с координатами (a;b;c) в точку с координатами (0;b;0), т.е. матрица данного оператора имеет вид:

Находим образ данного вектора:

Находим ядро данного оператора:
Для получения базиса образа данного линейного оператора находим:

Полученный вектор может быть выбран в качестве базиса образа данного оператора, т.е. .
Данный оператор имеет ненулевое ядро, следовательно, он не имеет обратного.
3.3. В пространстве V3 линейный оператор А – зеркальное отражение относительно плоскости YOZ. Найти матрицу оператора А в базисе . Найти образ вектора
. Найти ядро и образ оператора А. Существует ли обратный оператор? Если да, то описать его действие.
Решение:
Зеркальное отражение относительно плоскости YOZ в пространстве V3 переводит точку с координатами (a;b;c) в точку с координатами (-a;b;c), т.е. матрица данного оператора имеет вид:

Находим образ данного вектора:

Находим ядро данного оператора: detA = -1 ≠1, следовательно, KerA=0, ImA= V3.
Поскольку данный оператор имеет нулевое ядро, он обратим, т.е. имеет обратный оператор A-1. В пространстве V3 оператор А-1 = А, т.е совпадает с исходным оператором.
3.4. Пусть А – матрица линейного оператора из задачи 3.3. Найти Аn. Объяснить геометрический смысл полученного результата.
Решение:
Матрица линейного оператора из задачи 3.3 имеет вид:

и тогда

При четном n Аn = E, поскольку четное число отражений соответствует тождественному оператору Е, не меняющему вектора.
При нечетном n Аn = А, поскольку нечетное число отражений дает тот же результат, что и единственное отражение.
3.5. Линейный оператор А – проекция на ось . Найти матрицу оператора А в базисе
. Найти ядро и образ оператора А. Существует ли обратный оператор?
Решение:
Проекция на ось переводит точку с координатами (a;b) в точку с координатами (a–b;b–a):

т.е. матрица данного оператора имеет вид:
Находим ядро данного оператора:
Для получения базиса образа данного линейного оператора находим:
Полученный вектор может быть выбран в качестве базиса образа данного оператора, т.е. .
Данный оператор имеет ненулевое ядро, следовательно, он не имеет обратного.
3.6. Линейный оператор А – поворот на плоскости вокруг начала координат на угол по часовой стрелке. Найти матрицу оператора А в базисе
и образ вектора
. Найти ядро и образ оператора А. Существует ли обратный оператор? Если да, то описать его действие.
Решение:
В пространстве V2 оператор с матрицей – оператор поворота плоскости вокруг начала координат на угол α против часовой стрелки. Тогда данный оператор имеет матрицу

Находим образ данного вектора:

Находим ядро данного оператора: detA = 1 ≠1, следовательно, KerA=0, ImA= V2.
Поскольку данный оператор имеет нулевое ядро, он обратим, т.е. имеет обратный оператор A-1. В пространстве V2 оператор А-1 – поворот на угол вокруг начала координат против часовой стрелки.
3.7. Найти
Решение:
В пространстве V2 оператор с матрицей – оператор поворота плоскости вокруг начала координат на угол α против часовой стрелки. Тогда оператор
– n-кратное повторение оператора А – соответствует повороту плоскости вокруг начала координат на угол nα и такой оператор имеет матрицу
Отсюда получаем:
3.8. В пространстве V3 оператор А – поворот на угол вокруг оси OY по часовой стрелке. Найти матрицу оператора А в базисе
. Найти образ вектора
. Найти ядро и образ оператора А. Существует ли обратный оператор? Если да, то описать его действие.
Решение:
Матрица данного оператора в базисе имеет вид:

Находим образ вектора :

Находим ядро данного оператора: detA = 1 ≠1, следовательно, KerA=0, ImA= V3.
Поскольку данный оператор имеет нулевое ядро, он обратим, т.е. имеет обратный оператор A-1. В пространстве V3 оператор А-1 – поворот на угол вокруг оси OY против часовой стрелки.
3.9. В пространстве V3 оператор действует по правилу где
. Показать линейность оператора, найти его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?
Решение:
Проверяем линейность данного оператора:
Свойства линейности выполнены – оператор линеен.
Если , то
т.е. матрица данного оператора имеет вид:

Находим ядро данного оператора:

Для получения базиса образа данного линейного оператора находим:

Полученный вектор (или любой коллинеарный ему) может быть выбран в качестве базиса образа данного оператора, т.е. .
Данный оператор имеет ненулевое ядро, следовательно, он не имеет обратного.
3.10. В пространстве V3 оператор действует по правилу .
Показать линейность оператора, найти его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?
Решение:
Проверяем линейность данного оператора:
Свойства линейности выполнены – оператор линеен.
Если , то

т.е. матрица оператора в каноническом базисе имеет вид:

Находим ядро данного оператора:
Для получения базиса образа данного линейного оператора находим:


Полученные векторы линейно независимы и могут быть выбраны в качестве базиса образа данного оператора, т.е. .
Данный оператор имеет ненулевое ядро, следовательно, он не имеет обратного.
3.11. В пространстве V3 оператор действует по правилу .
Показать линейность оператора, найти его матрицу в каноническом базисе и в базисе . Сделать проверку с помощью матрицы перехода.
Решение:
Проверяем линейность данного оператора:
Свойства линейности выполнены – оператор линеен.
Если , то

т.е. матрица оператора в каноническом базисе имеет вид:

Матрица перехода от канонического базиса к базису имеет вид:

следовательно, матрица данного оператора в базисе S имеет вид:

3.12. В каноническом базисе пространства R3 операторы А и В действуют по правилу ,
. Показать линейность операторов А и В. Как действует в этом базисе оператор
?
Решение:
Линейность операторов следует из линейности арифметических операций сложения и умножения на число, например, для оператора А:

Матрицы операторов А и В имеют вид:


поэтому оператор будет иметь в том же базисе матрицу


т.е. будет действовать по правилу
3.13. В каноническом базисе пространства R3 операторы А и В действуют по правилу ,
. Показать линейность операторов А и В. Как действует в этом базисе оператор
?
Решение:
Линейность операторов следует из линейности арифметических операций сложения и умножения на число, например, для оператора А:

Матрицы операторов А и В имеют вид:


поэтому оператор будет иметь в том же базисе матрицу

т.е. будет действовать по правилу
3.14. В каноническом базисе пространства R3 оператор А действует по правилу . Является ли оператор А невырожденным? Если да, то найти явный вид обратного оператора.
Решение:
Матрица данного оператора имеет вид:

Поскольку detA=2≠0,k то данный оператор – невырожденный и имеет обратный. Матрица обратного оператора имеет вид:

т.е. обратный оператор действует по правилу:
3.15. В каноническом базисе пространства R4 оператор А действует по правилу . Показать линейность оператора. Обратим ли оператор? Найти ядро и образ оператора.
Решение:
Линейность оператора следует из линейности арифметических операций сложения и умножения на число, например::

Матрица данного оператора имеет вид:

Находим ядро данного оператора:
Для получения базиса образа данного линейного оператора находим:


Полученные векторы линейно независимы:

и могут быть выбраны в качестве базиса образа данного оператора, т.е.
Данный оператор имеет ненулевое ядро, следовательно, он необратим.
3.16. Оператор А действует на матрицы второго порядка по правилу , где
. Показать, что А – линейный оператор. Составить его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?
Говорят, что операторы $ mathcal A $ и $ mathcal B $ коммутируют если $ mathcal A , mathcal B = mathcal B , mathcal A $.
Пример. В пространстве полиномов $ mathbb P_ $ рассмотрим дифференциальный оператор
$$mathcal A = xfractimes Box – 1times Box : mathcal A(p(x)) = x p'(x) – p(x) .$$ Этот оператор не коммутирует с обычным оператором дифференцирования $ displaystyle mathcal B= frac $: $$mathcal A (x^2)=x^2, quad mathcal B (mathcal A(x^2))=2,x, quad mathcal B (x^2)=2,x, quad mathcal A (mathcal B (x^2))=0 .$$ ♦
Оператор $ mathcal E $, отображающий произвольный вектор $ Xin mathbb V_<> $ в себя : $ mathcal E(X)= X $, называется тождественным на $ mathbb V_<> $. Оператор $ mathcal B $ называется (левым) обратным оператору $ mathcal A_<> $, если $ mathcal Bmathcal A=mathcal E $. В этом случае оператор $ mathcal A_<> $ называют обратимым и записывают: $ mathcal B=mathcal A^ <-1>$.
Не всякий оператор обратим.
Пример. В пространстве $ mathbb R^ <3>$ для оператора проецирования на плоскость:
$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right) $$ обратного не существует, т.к. $ mathcal A(0,0,1)=(0,0,0) $ и ни при каком выборе оператора $ mathcal B $ нельзя добиться выполнения равенства $ mathcal B(0,0,0)=(0,0,1) $. ♦
$$frac<1>int_0^x : p(x) longmapsto frac<1>int_<0>^ p(t) d, t ,$$ на $ mathbb P_ $ является оператор $$ fracleft(xtimes Box right) : p(x) longmapsto (xp(x))’ .$$
Теорема 4. Оператор $ mathcal A_<> $ обратим тогда и только тогда, когда когда он невырожден: $ operatorname (mathcal A) =0 $. В этом случае $ mathcal A^ <-1>$ единствен и коммутирует с $ mathcal A $.
При $ Kin mathbb N $ и $ K>1 $, $ K_<> $-я степень оператора $ mathcal A $ определяется рекурсивной формулой $$mathcal A^<, K>=mathcal A (mathcal A^<, K-1>) .$$ Если, вдобавок, $ mathcal A $ невырожден, то отрицательная степень оператора определяется формулой $$mathcal A^<-K>=left(mathcal A^<-1>right)^K . $$ Полагают также $ mathcal A^<, 0>= <mathcal E>$ для любого $ mathcal A ne <mathcal O>$.
Теорема 5. Степени оператора $ mathcal A $ коммутируют:
$$mathcal A^ <, K>mathcal A^<, L>=mathcal A^<, L>mathcal A^<, K>=mathcal A^ <, K+L> .$$
Пример. $ K_<> $-й степенью оператора дифференцирования в пространстве полиномов $ mathbb P_ $ будет оператор нахождения $ K_<> $-й производной:
$$left( frac right)^K = frac .$$ Очевидно, что при $ K_<>>n $ этот оператор будет нулевым. ♦
Пример. В произвольном пространстве $ mathbb V_<> $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ оператор проецирования $ mathcal P $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $ обладает свойством $ mathcal P^2 = mathcal P $ (проецирование проекции оставляет ее на месте). ♦
Оператор $ mathcal A $, обладающий свойством $ mathcal A^2 = mathcal A $, называется идемпотентным 3) .
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ отображение $ mathcal A_<> $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_<>(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Для этого оператора $ K_<> $-й его степенью является оператор $$ mathcal B (f(x)) = f(x) (x^2-2)^K pmod . $$ Действительно, если $$ f(x)(x^2-2) equiv q(x)(x^4-x^3-x^2+x)+ r(x) $$ при $ subset mathbb R[x] $ и $ deg r(x) le 3 $, то $$ f(x)(x^2-2)^2 equiv q(x)(x^4-x^3-x^2+x)(x^2-2)+ r(x)(x^2-2) . $$ Но тогда $$ mathcal A^2 (f(x))= mathcal A (r(x)) = r(x) (x^2-2) pmod equiv $$ $$ equiv f(x)(x^2-2)^2 pmod . $$ Завершает доказательство святая индукция по степени $ K_<> $… ♦
Пусть задан произвольный полином $ g(x)=b_<0>x^m+b_1x^+dots+b_m $ из $ mathbb R[x] $ или $ mathbb C[x] $. Выражение $$g(mathcal A )= b_0mathcal A^+b_1mathcal A^+dots+b_m<mathcal E>$$ будем называть операторным полиномом.
Доказать, что операторные полиномы коммутируют: $ g_1(mathcal A )g_2(mathcal A )=g_2(mathcal A )g_1(mathcal A ) $.
Доказать, что для любого $ mathcal A in <mathcal H>om(mathbb V,mathbb V) $ всегда найдется полином $ g_<>(x) $, $ deg g le n^2+1 $ такой, что $ g(mathcal A)= <mathcal O>$.
Сформулируем еще один результат, являющийся частным случаем приведенного в пункте ☞ СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.
Теорема 6. Пусть $ $ — произвольный базис $ mathbb V_<> $, а $ Y_1,Y_2,dots,Y_n $ — произвольные векторы того же пространства. Существует единственный оператор $ mathcal A: mathbb V longmapsto mathbb V $ такой, что
Доказательство. Искомый оператор строится следующим образом. Если $ X=x_1X_1+x_2X_2+dots+x_nX_n $ — разложение произвольного вектора $ X in mathbb V $ по базису, то $$ mathcal A(X)=x_1 Y_1+x_2Y_2+dots+ x_nY_n . $$ Единственность этого оператора доказывается от противного. Любой другой оператор $ mathcal B $, удовлетворяющий условиям $ <mathcal B(X_j)=Y_j>_^n $, будет действовать на тот же вектор $ X_<> $ с тем же результатом: $$ mathcal B(X)=x_1 mathcal B(X_1)+x_2mathcal B(X_2) +dots+ x_nmathcal B(X_n)= x_1 Y_1+x_2Y_2+dots+ x_nY_n= mathcal A(X) . $$ ♦
Таким образом, оператор — как функция, действующая в $ n_<> $-мерном линейном пространстве, однозначно определяется заданием на $ n_<> $ линейно независимых векторах. В доказательстве теоремы дается и конструктивный способ представления оператора по этим значениям (т.е. строится его “интерполяционная формула” ).
Рассмотрим оператор $ mathcal A $ на $ mathbb V_<> $ и пусть $ $ — базис $ mathbb V_<> $. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от рассмотренного в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для $ mathcalm (mathcal A) $. Поскольку $ mathcalm (mathcal A) $ является подпространством $ mathbb V_<> $, то было бы слишком большой роскошью иметь два разных базиса для одного и того же пространства.
Найдем координаты образов базисных векторов $ mathcal A (X_1),dots,mathcal A (X_n) $ в том же базисе $ $: $$ left< begin mathcal A(X_1)&=& <<coloralpha >>_<11>X_1+ <<coloralpha >>_<21>X_2+dots+ <<coloralpha >>_X_n, \ mathcal A(X_2)&=& <<coloralpha >>_<12>X_1+ <<coloralpha >>_<22>X_2+dots+ <<coloralpha >>_X_n, \ dots & & qquad dots , \ mathcal A(X_n)&=&alpha_<1n>X_1+alpha_<2n>X_2+dots+alpha_X_n. end right. $$ Матрица $$ mathbf A= left(begin <<coloralpha >>_ <11>& <<coloralpha >>_<12>& dots & alpha_ <1n>\ <<coloralpha >>_ <21>& <<coloralpha >>_<22>& dots & alpha_ <2n>\ dots & & & dots \ <<coloralpha >>_ & <<coloralpha >>_& dots & alpha_ end right)_, $$ в столбцах которой стоят координаты образов базисных векторов, называется матрицей оператора $ mathcal A_<> $ в базисе $ $.
Пример. Известны образы базисных векторов $ mathbb R^ <3>$ под действием оператора $ mathcal A_<> $:
$$mathcal A left( begin 5 \ 3 \ 1 endright)= left( begin -2 \ 1 \ 0 endright) , mathcal A left( begin 1 \ -3 \ -2 endright) = left( begin -1 \ 3 \ 0 endright) , mathcal A left( begin 1\ 2 \ 1 endright)= left( begin -2 \ -3 \ 0 endright) . $$ Найти матрицу этого оператора в исходном базисе.
Решение. Элементы матрицы $ <mathbf A>$ ищутся по формулам из определения, которые можно переписать в матричном виде: $$left[ X_1,dots,X_n right] <mathbf A>=left[ mathcal A (X_1),dots,mathcal A (X_n) right] .$$ Откуда $$<mathbf A>= left[ X_1,dots,X_n right]^ <-1>left[ mathcal A (X_1),dots,mathcal A (X_n) right] ,$$ и для нашего примера эта формула дает $$ <mathbf A>= left(begin 5&1&1 \ 3&-3&2 \ 1&-2&1 endright)^ <-1>left(begin -2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = $$ $$ =left(begin 1&-3&5\ -1&4&-7\ -3&11&-18 endright) left(begin -2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = left(begin -5&-10&7\ 6&13&-10\ 17&36&-27 end right). $$ ♦
В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_<> $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^3+2,x^2+1) pmod , $$ т.е. полином $ f_<>(x) $ отображается в остаток от деления произведения $ f(x) (x^3+2,x^2+1) $ на $ x^4+4 $. Найти матрицу оператора $ mathcal A_<> $ в базисе $ <1,x,x^2,x^3>$.
Ответ. $$ left(begin 1 & -4 & -8 & 0 \ 0 & 1 & -4 & -8 \ 2& 0 & 1 & -4 \ 1 & 2 & 0 & 1 end right) . $$
Теорема 1. Координаты произвольного вектора $ X=x_1X_1+dots+x_nX_n $ и его образа $ Y=mathcal A(X)=y_1X_1+dots+y_nX_n $ связаны формулой
$$ left(begin y_1 \ vdots \ y_n end right) = <mathbf A>left(begin x_1 \ vdots \ x_n end right) . $$
Как изменяется матрица оператора при переходе к новому базису?
Доказательство ☞ ЗДЕСЬ.
Пример. Оператор $ mathcal A $ в базисе пространства $ mathbb R^ <3>$
Матрицы $ <mathbf A>$ и $ <mathbf B>$, связанные соотношением $ <mathbf B>=C^<-1>cdot <mathbf A>cdot C $ при какой-то неособенной матрице $ C_<> $, называются подобными, этот факт будем записывать: $ <mathbf A>doteq <mathbf B>$.
Доказать, что отношение подобия есть отношение эквивалентности, и если $ <mathbf A>doteq <mathbf B>$ то $ g(<mathbf A>)doteq g(<mathbf B>) $ при любом полиноме $ g_<>(x) $.
Теорема 3. Для оператора $ mathcal A_<> $ ранг его матрицы является инвариантом, т.е. не зависит от выбора базиса пространства. Этот ранг совпадает с рангом оператора $ mathcal A_<> $.
Доказательство. Если $ <mathbf A>$ и $ <mathbf B>$ — матрицы оператора в двух разных базисах, то они являются подобными: $ <mathbf B>=C^<-1> <mathbf A>C $. По свойству ранга матрицы имеем: $ operatorname( <mathbf B>)= operatorname(<mathbf A>) $. ♦
Дефект оператора $ mathcal A_<> $ совпадает с дефектом его матрицы в произвольном базисе пространства.
Теорема 4. Для оператора $ mathcal A_<> $ определитель и след его матрицы являются инвариантами, т.е. не зависят от выбора базиса пространства.
Доказательство. Действительно, для подобных матриц $ <mathbf A>$ и $ <mathbf B>$, на основании теоремы Бине-Коши имеем: $$ det (<mathbf B>) = det (C^<-1> <mathbf A>C) = det (C^<-1>) cdot det (<mathbf A>) cdot det (C) =det (<mathbf A>) . $$ Далее, по свойству следа матрицы: $$ operatorname(<mathbf B>) = operatorname(C^<-1> <mathbf A>C)=operatorname( <mathbf A>cdot C cdot C^<-1>)=operatorname(<mathbf A>) . $$ ♦
Этот результат позволяет ввести понятие определителя и следа оператора $ mathcal A_<> $ — посредством матрицы этого оператора в произвольном базисе пространства. Такое определение оказывается корректным поскольку оба значения не зависят от выбора базиса.
Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения 4) объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.
Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.
Теорема 6. Линейное пространство $ <mathcal H>om(mathbb V,mathbb V) $ операторов на $ mathbb V_<>, dim mathbb V = n $ изоморфно линейному пространству квадратных матриц порядка $ n_<> $ (с элементами из $ mathbb R_<> $ или из $ mathbb C_<> $).
Это утверждение является простым следствием теоремы 2, приведенной в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ. Однако в случае операторов установленный изоморфизм сохранит не только результат операции сложения, но и результат операции умножения: $$ . mbox < если >mathcal A_1 leftrightarrow mathbf A_1, mathcal A_2 leftrightarrow mathbf A_2, mbox < то >mathcal A_1+ mathcal A_2 leftrightarrow mathbf A_1 + mathbf A_2, lambda mathcal A_1 leftrightarrow lambda mathbf A_1 , mathcal A_1 mathcal A_2 leftrightarrow mathbf A_1 mathbf A_2 . $$ Я сформулирую этот «усиленный вариант» изоморфизма в виде набора свойств, которыми буду пользоваться по мере возникновения потребности.
Теорема 7. В любом базисе пространства
а) матрица нулевого оператора $ mathcal O $ является нулевой матрицей $ mathbb O_<> $, а матрица тождественного оператора $ mathcal E $ является единичной матрицей $ E_<> $; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);
б) матрица произведения операторов совпадает с произведением матриц этих операторов 5) ;
в) коммутирующим операторам соответствуют коммутирующие матрицы;
г) если $ <mathbf A>$ — матрица оператора, то $ <mathbf A>^ <-1>$ — матрица обратного оператора;
д) если $ <mathbf A>$ — матрица оператора $ mathcal A $, то матрицей операторного полинома $ g (mathcal A) $ является матрица $ g(<mathbf A>) $ .
Матрица оператора и матрица перехода от базиса к базису
Эти матрицы как-то взаимодействовали между собой в предыдущем пункте, хотя вторая была определена совершенно в другом разделе. Обе матрицы квадратные, обе имеют в определении «завязку» на базис пространства $ mathbb V_<> $. У начинающих изучать теорию часто возникает путаница при различении этих определений.
«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).
Тем не менее, с чисто формальной точки зрения, матрица $ C_<> $ перехода от базиса $ $ пространства $ mathbb V_<> $ к какому-то другому базису $ <mathfrak X_1,mathfrak X_2,dots,mathfrak X_n >$ того же пространства может считаться матрицей некоторого оператора, действующего в этом пространстве. В самом деле, на основании теоремы, приведенной в конце ☞ ПУНКТА, существует единственный оператор $ mathcal C $, переводящий старые базисные векторы в новые, взятые в той же последовательности: $$ mathcal C (X_1)=mathfrak X_1, mathcal C (X_2)= mathfrak X_2, dots, mathcal C (X_n)= mathfrak X_n . $$ Но тогда, по определению, матрица оператора $ mathcal C $ в базисе $ $ совпадает с матрицей $ C_<> $ перехода от базиса $ $ к базису $ <mathfrak X_1,mathfrak X_2,dots,mathfrak X_n >$.
Я буду записывать матрицы операторов и матрицы переходов от базиса к базису в разных стилях: $ mathbf A, mathbf B,dots $ и, соответственно, $ C, P, T, dots $ — с целью быстрого распознавания их «физической» сущности.
Матрица оператора проецирования
Настоящий пункт может быть пропущен при первоначальном чтении.
Теорема. Рассмотрим линейную оболочку линейно независимой системы столбцов $ subset mathbb R^n $.
$$ mathbb M =left < lambda_1 Y_1 + dots + lambda_k Y_k big| <lambda_1,dots,lambda_k>subset mathbb R right>= mathcal L (Y_1,dots,Y_k) , . $$ Пусть скалярное произведение векторов $ X_<> $ и $ Y_<> $ задается стандартным способом, т.е. $ langle X,Y rangle =x_1y_1+dots+x_ny_n $. Ближайшей к точке $ X_0 subset mathbb R^n $ точкой многообразия (или ортогональной проекцией точки $ X_0 $ на многообразие) $ mathbb M_<> $ является $$ X_ <ast>= mathbf L (mathbf L^ <top>mathbf L )^ <-1>mathbf L^ <top>X_0 , . $$ Здесь $ mathbf L=[Y_1 |dots |Y_k]_ $.
Доказательство. Пусть $ X_0=X_0^<^<parallel>>+X_0^<^<bot>> $, где $ X_0^<^<parallel>> $ — ортогональная проекция точки $ X_0 $ на $ mathbb M $, а $ X_0^<^<bot>> $ — ортогональная составляющая. Тогда $$ mathbf L^ <top>X_0^<^<bot>>=mathbb O $$ поскольку $ Y_1^ <top>X_0^<^<bot>>=0,dots, Y_k^ <top>X_0^<^<bot>>=0 $. Далее, $ X_0^<^<parallel>> $ можно разложить по базису $ $: $$ X_0^<^<parallel>>=alpha_1 Y_1+dots+ alpha_k Y_k quad npu quad <alpha_1,dots,alpha_k>subset mathbb R , . $$ Следовательно, $$ mathbf L^ <top>X_0=mathbf L^ <top>(X_0^<^<parallel>>+X_0^<^<bot>>)=mathbf L^ <top>X_0^<^<parallel>>= mathbf L^ <top>(alpha_1 Y_1+dots+ alpha_k Y_k)= $$ $$ =left( begin alpha_1 Y_1^ <top>Y_1 +dots + alpha_k Y_1^ <top>Y_k \ alpha_1 Y_2^ <top>Y_1 +dots + alpha_k Y_2^ <top>Y_k \ dots \ alpha_1 Y_k^ <top>Y_1 +dots + alpha_k Y_k^ <top>Y_k end right)= mathbf L^ <top>mathbf L left( begin alpha_1 \ alpha_2 \ vdots \ alpha_k end right), . $$ Тогда $$ mathbf L (mathbf L^ <top>mathbf L )^ <-1>mathbf L^ <top>X_0= mathbf L left( begin alpha_1 \ alpha_2 \ vdots \ alpha_k end right) =alpha_1 Y_1+dots+ alpha_k Y_k= X_0^<^<parallel>> , . $$ На основании теорем $ 1_<> $ и $ 2_<> $, приведенных ☞ ЗДЕСЬ, точка $ X_0^<^<parallel>> $ является ближайшей точкой многообразия $ mathbb M $ к точке $ X_ <0>$. ♦
Матрица $ P=mathbf L (mathbf L^ <top>mathbf L )^ <-1>mathbf L^ <top>$ является матрицей оператора ортогонального проецирования на многообразие $ mathbb M_<> $ в стандартном базисе $$ bigg<<mathfrak e>_j = big[underbrace<0,dots,0,1>_,0,dots,0big]^ <top>bigg>_^n , . $$ Она симметрична и идемпотентна, т.е. обладает свойством $ P^2=P $.
Пример. В $ mathbb R^ <3>$ найти матрицу проецирования на плоскость $ x+y+z=0 $.
Решение. Параметрическое задание плоскости: $$ mathbb M=< lambda_1 underbrace<[1,-1,0]^<top>>_ + lambda_2 underbrace<[0,1,-1]^<top>>_ big| <lambda_1,lambda_2>subset mathbb R > , . $$ Имеем: $$ mathbf L= left(begin 1 & 0 \ -1 & 1 \ 0 & -1 end right) Rightarrow mathbf L^ <top>mathbf L= left(begin 2 & -1 \ -1 & 2 end right) Rightarrow (mathbf L^ <top>mathbf L )^<-1>= left(begin 2/3 & 1/3 \ 1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow mathbf L (mathbf L^ <top>mathbf L )^ <-1>mathbf L^<top>= frac<1> <3>left(begin 2 & -1 & -1 \ -1& 2 & -1 \ -1 & -1 & 2 end right) , . $$ ♦
Матрица оператора отражения (оператора Хаусхолдера)
Настоящий пункт может быть пропущен при первоначальном чтении.
В пространстве $ mathbb R^n $ со стандартным скалярным произведением рассмотрим плоскость, заданную уравнением $$ C^<top>X= c_1x_1+c_2x_2+dots+c_nx_n = 0 $$ при векторе нормали $ C^<top>=(c_1,c_2,dots,c_n) $ единичной длины: $ |C|^2= C^<top>C=1 $. Действие оператора зеркального отражения или оператора Хаусхолдера 6) относительно этой плоскости на вектор (точку) $ X in mathbb R^n $ определим правилом $$ mathcal H( X^<^<parallel>> + X^<^<bot>>)= X^<^<parallel>> – X^<^<bot>> ; $$ здесь $ X^<^<parallel>> $ — ортогональная проекция вектора $ X_<> $ на заданную плоскость, а $ X^<^<bot>> $ — ортогональная составляющая вектора $ X_<> $ относительно этой плоскости.
Теорема. Оператор $ mathcal H $ задается уравнением
$$ mathcal H(X)=X-2, langle X,C rangle C=X-2, C (C^<top>X)= X-2, C^<top>XC , . $$
Доказательство. $$ mathcal H( X^<^<parallel>> + X^<^<bot>>)=X^<^<parallel>> + X^<^<bot>>-2, langle X^<^<parallel>>,C rangle C-2, langle X^<^<bot>>,C rangle C = $$ Поскольку $ X^<^<parallel>> $ ортогонален, а вектор $ X^<^<bot>> $ коллинеарен вектору $ C $ единичной длины, то $$= X^<^<parallel>> + X^<^<bot>> – 2, X^<^<bot>> = X^<^<parallel>> – X^<^<bot>> , . $$ ♦
Теорема. Матрица оператора $ mathcal H $ в стандартном базисе
$$ bigg<<mathfrak e>_j = big[underbrace<0,dots,0,1>_,0,dots,0big]^ <top>bigg>_^n , . $$ имеет вид $$ mathbf H_= E-2, C cdot C^ <top>= left( begin 1-2c_1^2 & -2,c_1c_2 & dots & – 2 c_1 c_n \ -2,c_1c_2 & 1-2c_2^2 & dots & – 2 c_2 c_n \ vdots & & & vdots \ – 2 c_1 c_n & – 2 c_2 c_n & dots & 1-2c_n^2 end right) , . $$
Пример. Найти зеркальное отражение точки $ [3,2,3] $ относительно плоскости $ 2,x-2,y+z = 0 $.
Решение. Здесь $ C^<top>=[2/3,-2/3,1/3] $ и $$ mathcal H(X)= left( begin 3 \ 2 \ 3 end right) – 2([3,2,3],[2/3,-2/3,1/3]) left( begin 2/3\ -2/3 \ 1/3 end right)= left( begin 7/9 \ 38/9 \ 17/9 end right) , . $$ Проверим результат посредством матричного представления: $$ mathbf H_C= left( begin 1/9 & 8/9 & -4/9 \ 8/9 & 1/9 & 4/9 \ -4/9 & 4/9 & 7/9 end right) quad Rightarrow quad mathbf H left( begin 3 \ 2 \ 3 end right)= left( begin 7/9 \ 38/9 \ 17/9 end right) , . $$ ♦
Матрица $ mathbf H_ $ одновременно симметрична и ортогональна, и $ det mathbf H_=-1 $. Следовательно, ей обратная существует и совпадает с ней самой: $$ mathbf H_^<-1>= mathbf H_ , . $$
Инвариантное подпространство
Задача. Подобрать базис пространства $ mathbb V_<> $ так, чтобы матрица заданного оператора $ mathcal A_<> $ имела наиболее простой вид.
Исследуем действие оператора $ mathcal A $ на произвольное подпространство $ mathbb V_1 subset mathbb V $: $$mathcal A (mathbb V_1)= left .$$ Вообще говоря, множества $ mathbb V_1 $ и $ mathcal A (mathbb V_1) $ будут различными, т.е. $ exists X_1 in mathbb V_1 $ такой, что $ mathcal A (X_1)notin mathbb V_1 $.
Подпространство $ mathbb V_1 $ называется инвариантным подпространством оператора $ mathcal A $, если оно отображается этим оператором в себя: $$ mathcal A(mathbb V_1)subset mathbb V_1 .$$
$ mathbb V_1= <mathbb O >$ и $ mathbb V_1=mathbb V $ — тривиальные инвариантные подпространства произвольного оператора $ mathcal A $.
Нас будут интересовать нетривиальные инвариантные подпространства.
Пример. Оператор
$$left(begin x \ y \ z end right) longmapsto left(begin <scriptstyle 1>/ <scriptstyle sqrt 2>& -<scriptstyle 1>/ <scriptstyle sqrt 2>& 0 \ <scriptstyle 1>/ <scriptstyle sqrt 2>& <scriptstyle 1>/ <scriptstyle sqrt 2>& 0 \ 0 & 0 & 1 end right) left(begin x \ y \ z end right) $$ задает в пространстве поворот вокруг оси $ mathbb O z $ на угол $ +pi /4 $. Нетривиальными инвариантными подпространствами будут
а) ось вращения $ mathbb V_1=<(0,0,z)^<^<top>> mid z in mathbb R> $, $ dim mathbb V_1=1 $ и
б) плоскость, перпендикулярная оси вращения $ mathbb V_2=<(x,y,0)^<^<top>> mid subset mathbb R> $, $ dim mathbb V_2= 2 $. ♦
Пример. Оператор
$$left(begin x \ y end right) longmapsto left(begin lambda_1 x \ lambda_2 y end right) $$ задает на плоскости «растяжение»: $ x_<> $-компонента увеличивается в $ lambda_ <1>$ раз, а $ y_<> $-компонента — в $ lambda_ <2>$ раз. При любой комбинации коэффициентов растяжения координатные оси будут инвариантными подпространствами. Однако в частном случае $ lambda_1=lambda_2 $ инвариантной будет также любая прямая, проходящая через начало координат. ♦
Пример. Оператор в $ mathbb R^_<> $ задан блочной матрицей
$$X longmapsto left( begin <mathbf A>_1 & <mathbf *>\ mathbb O & <mathbf A>_2 end right) X $$ где $ <mathbf A>_1 $ — $ n_1times n_1 $-матрица, $ <mathbf A>_2 $ — $ (n-n_1)times (n-n_1) $-матрица. Множество столбцов $$mathbb V_1=left,0,dots,0]^<^<top>> bigg| < x_1, dots, x_> subset mathbb R right>$$ образует инвариантное подпространство, $ dim mathbb V_1=n_1 $. Если же, вдобавок, матрица, обозначенная $ <mathbf *>$ — нулевая, то вторым инвариантным подпространством будет $$ mathbb V_2=left,dots,x_n]^<^<top>> bigg| ,dots, x_n > subset mathbb R right> .$$ ♦
Теорема. $ mathcaler (mathcal A) $ и $ mathcalm(mathcal A) $ — инвариантные подпространства оператора $ mathcal A $.
Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.
Теорема. Если пространство $ mathbb V_<> $ раскладывается в прямую сумму подпространств, инвариантных относительно оператора $ mathcal A $, то существует базис пространства, в котором матрица оператора будет блочно-диагональной.
Теорема обобщается очевидным образом на произвольное число слагаемых подпространств: $ mathbb V=mathbb V_1oplus mathbb V_2 oplus dots oplus mathbb V_k $. Если при этом $ dim mathbb V_1= dots = dim mathbb V_k=1 $, то матрица оператора в базисе, полученном объединением базисных векторов слагаемых подпространств, становится диагональной — это и является решением задачи, поставленной в начале пункта.
Собственное число и собственный вектор
Задача. Найти одномерные инвариантные подпространства оператора.
Вектор $ X_<>in mathbb V $ называется собственным вектором оператора $ mathcal A_<> $, если $$ <mathbf a)>X ne mathbb O, quad u quad <mathbf b)> exists lambda in mathbb C qquad mbox < такое, что >qquad mathcal A(X)=lambda X .$$ В этом случае число $ lambda_<> $ называется собственным или характеристическим числом оператора, соответствующим (или принадлежащим) данному собственному вектору; обратно, говорят, что вектор $ X_<> $ принадлежит собственному числу $ lambda_<> $.
Пример. Оператор
$$left(begin x \ y end right) longmapsto left(begin 1 & – 5/2 \ -1/2 & 2 end right) left(begin x \ y end right) $$ задает отображение плоскости $ mathbb R^2 $. На рисунке показан результат действия этого отображения на единичную окружность. Все точки плоскости, за исключением начала координат $ mathbb O_<> $, изменят свое положение — ни одна не останется на месте.
Если рассмотреть эти точки как концы векторов, имеющих начало в $ mathbb O_<> $, то смещения точек под действием оператора можно представить в виде двух составляющих: растяжения (т.е. увеличения расстояния до начала координат) и поворота вокруг начала координат на некоторый угол. И только по двум направлениям плоскости поворота не происходит. Точки окружности с координатами $$ pm left( 0.823, -0.568 right)^ <top>quad u quad pm left( 0.960, 0.278 right)^ <top>$$ будут смещаться без поворота. Эти точки и задают координаты конца собственного вектора. А соответствующие им собственные числа $ 2.725 $ и $ 0.275 $ определяют коэффициенты сдвига. Если вообразить оператор как деформацию физической среды, заполняющей плоскость, то можно сказать, что cобственный вектор задает направление, на котором действие оператора сводится к растяжению, при этом коэффициент растяжения и будет собственным числом.
Анимация процесса ☞ ЗДЕСЬ (1500 Kb, gif).
Пример другого оператора $$ left(begin x \ y end right) longmapsto left(begin 1 & – 3 \ 1 & -1 end right) left(begin x \ y end right) $$ показывает, что существование вещественных собственных чисел вовсе не гарантировано даже в случае оператора в вещественном пространстве: в этом примере все точки плоскости повернутся вокруг начала координат. ♦
Доказать, что $ operatorname (mathcal A) ne 0 $ тогда и только тогда, когда оператор $ mathcal A_<> $ имеет собственное число, равное нулю.
Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства оператора является собственным вектором.
Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_<> $ действует по правилу
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_<>(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Найти собственные векторы этого оператора.
Решение. В пространстве $ mathbb P_3 $ векторами являются полиномы, а условие того, что полином $ f_<>(x) $ является собственным, принадлежащим числу $ lambda_<> $, записывается в виде: $$ f(x)(x^2-2)equiv lambda f(x) pmod quad iff $$ $$ iff quad f(x)(x^2-2-lambda)equiv 0 pmod . $$ Поскольку $ deg f le 3 $, то последнее может выполняться тогда и только тогда, когда полином $ x^2-2-lambda $ имеет общие корни с $ x^4-x^3-x^2+x equiv x(x+1)(x-1)^2 $. Из этого условия вытекает, что число $ lambda_<> $ может принимать только два значения: $ lambda_1=-2 $ и $ lambda_2=-1 $. Если $ lambda_1=-2 $ является собственным числом, то ему соответствующий собственный вектор — полином степени $ le 3 $ — должен определяться из условия делимости $ f(x)x^2 $ на $ x(x+1)(x-1)^2 $. Такой полином имеет вид $ t(x+1)(x-1)^2 $ при произвольной константе $ t_<> $. Следовательно множество $$ < t(x^3-x^2-x+1)= t(x+1)(x-1)^2 mid tne 0 >$$ является множеством собственных векторов, принадлежащих $ lambda_1=-2 $.
С числом $ lambda_2=-1 $ поступаем аналогично. Условие делимости полинома $ f(x)(x^2-1) $ на $ x(x+1)(x-1)^2 $ дает также бесконечное множество: $$ < (t_1x+t_2)x(x-1) mid \subset mathbb R > . $$ Однако в этом случае бесконечность множества качественно иная, чем в предыдущем случае; она — «двумерная». ♦
Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.
Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.
Уравнение $ det (<mathbf A>-lambda E)= 0 $ называется характеристическим или вековым уравнением, а полином в левой его части — характеристическим полиномом матрицы $ <mathbf A>$. Любой корень характеристического полинома матрицы называется собственным числом этой матрицы. Набор всех собственных чисел матрицы (корней характеристического полинома с учетом кратностей) называется спектром матрицы. Ненулевой вектор $ X in mathbb C^n $, удовлетворяющий условию $ <mathbf A>X= lambda X $, где $ lambda $ — собственное число матрицы, называется собственным вектором матрицы, соответствующим (или принадлежащим) данному собственному числу.
Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.
Решение. Базисом в пространстве $ mathbb P_3 $ выберем $ <1,,x,,x^2,, x^3>$. Образы базисных векторов под действием оператора $ mathcal A (f(x)) = f(x) (x^2-2) pmod $: $$ left<begin mathcal A (1) =&-2& &+x^2& ,\ mathcal A (x) =&&-2,x &&+x^3 ,\ mathcal A (x^2) =& &-x &-x^2 &+x^3, \ mathcal A (x^2) =& &-x & & , end right. qquad Rightarrow qquad <mathbf A>= left(begin -2 & 0 & 0 & 0 \ 0 & -2 & -1 & -1 \ 1& 0 & -1 & 0 \ 0 & 1 & 1 & 0 end right) . $$ Характеристический полином матрицы $ <mathbf A>$: $$ left|begin -2-lambda & 0 & 0 & 0 \ 0 & -2-lambda & -1 & -1 \ 1& 0 & -1-lambda & 0 \ 0 & 1 & 1 & -lambda end right|equiv (lambda+2)(lambda^3+3,lambda^2+3,lambda+1)equiv (lambda+2)(lambda+1)^3 . $$ Собственные числа $ lambda_1=-2 $ и $ lambda_2=-1 $, спектр матрицы $ <-1,-1,-1,-2>$. Подставляем каждое из собственных чисел в матрицу $ <mathbf A>-lambda E $ и решаем получившиеся системы однородных уравнений. Поскольку каждая из них должна иметь бесконечное множество решений, то мы строим фундаментальные системы решений (ФСР) $$ begin & (<mathbf A>-lambda E)X=mathbb O & \ <colorswarrow > & & <colorsearrow > \ lambda_1=-2 & & lambda_2=-1 \ Downarrow & & Downarrow \ left(begin 0 & 0 & 0 & 0 \ 0 & 0 & -1 & -1 \ 1& 0 & 1 & 0 \ 0 & 1 & 1 & 2 end right) left(begin x_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O & & left(begin -1 & 0 & 0 & 0 \ 0 & -1 & -1 & -1 \ 1& 0 & 0 & 0 \ 0 & 1 & 1 & 1 end right) left(begin x_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O . \ <colorDownarrow > & & <colorDownarrow > \ x_1=1,x_2=-1,x_3=-1,x_4=1 & & left<begin x_1=0,x_2=-1,x_3=1,x_4=0 \ x_1=0,x_2=-1,x_3=0,x_4=1 end right> end $$ Таким образом, собственному числу $ lambda_1=-2 $ соответствует собственнный вектор — полином $ 1-x-x^2+x^3 $, и он полностью совпадает с полученным при решении предыдущего примера. В то же время собственному числу $ lambda_2=-1 $ соответствует два линейно независимых собственнных вектора — полиномы $ -x+x^2 $ и $ -x+x^3 $. Любой (не тождественно нулевой) полином множества $$ < tau_1(-x+x^2) +tau_2(-x+x^3) mid <tau_1,tau_2 >subset mathbb R > $$ будет также являться собственным, принадлежащим $ lambda_2=-1 $. Это множество также совпадает с полученным при решении предыдущего примера. ♦
Итак, два формально различных подхода к решению одного и того же примера не привели к противоречию. Хотелось бы, однако, гарантировать глобальную непротиворечивость определения собственных чисел и векторов — т.е. независимость (инвариантность) этих объектов относительно способов их нахождения, и, в частности, от выбора базиса пространства $ mathbb V_<> $.
Теорема. Характеристические полиномы подобных матриц одинаковы.
Доказательство. $ <mathbf A>doteq <mathbf B>iff exists $ неособенная матрица $ C_<> $, такая что $ <mathbf B>=C^ <-1> <mathbf A>C $. Имеем: $$det (<mathbf B>-lambda E)=det (C^ <-1> <mathbf A>C-lambda E)=$$ $$= det (C^ <-1> <mathbf A>C-lambda C^<-1>EC)=det left[ C^ <-1>( <mathbf A>-lambda E)C right] = det (<mathbf A>-lambda E) .$$ ♦
Иначе говоря, для оператора $ mathcal A_<> $ характеристический полином его матрицы не зависит от выбора базиса пространства. Поэтому можно говорить о характеристическом полиноме оператора $ mathcal A_<> $.
Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.
Пример. Для рассмотренного в предыдущих примерах оператора
$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ действующего в $ mathbb P_3 $, характеристический полином равен
$$ lambda^4+5,lambda^3+9,lambda^2+7,lambda+2 , .$$ Проверим утверждение теоремы Гамильтона-Кэли — должно быть выполнено условие $$ mathcal A^4+5,mathcal A^3+9,mathcal A^2+7,mathcal A +2, mathcal E = mathcal O . $$ Степени данного оператора $ mathcal A_<> $ обсуждались в примере ☞ ПУНКТА. Переписанное в терминах остатков, последнее условие превращается в $$ (x^2-2)^4f(x)+5,(x^2-2)^3f(x)+9,(x^2-2)^2f(x)+7,(x^2-2)f(x) + $$ $$+2,f(x) equiv 0 pmod , $$ т.е. полином, стоящий в левой части сравнения, должен делиться нацело на $ x^4-x^3-x^2+x $ при любом выборе полинома $ f_<>(x) $. Проверяем: $$ (x^2-2)^4+5,(x^2-2)^3+9,(x^2-2)^2+7,(x^2-2)+2 equiv $$ $$equiv x^8-3,x^6+3,x^4-x^2 equiv (x^4+x^3-x^2-x)(x^4-x^3-x^2+x) , $$ т.е. утверждение оказывается справедливым. ♦
Диагонализуемость матрицы оператора
Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.
Теорема 2. Если оператор имеет $ n=dim mathbb V $ линейно независимых собственных векторов, то в базисе ими образуемом матрица оператора диагональна. Обратно: если матрица оператора в некотором базисе диагональна, то каждый вектор этого базиса является собственным для оператора.
Базис линейного пространства, состоящий из собственных векторов оператора $ mathcal A_<> $, называется каноническим.
[Матричная версия теоремы]. Пусть $ A_<> $ — квадратная матрица. Неособенная матрица $ C_<> $, удовлетворяющая равенству
$$C^ <-1>A C= A_ quad mbox < при матрице >A_ quad mbox < – диагональной>$$ существует тогда и только тогда, когда существует базис пространства $ mathbb C^_<> $, состоящий из собственных векторов матрицы $ A_<> $. Тогда матрица $ C_<> $ является матрицей перехода от стандартного базиса $$ bigg<<mathfrak e>_j = big[underbrace<0,dots,0,1>_,0,dots,0big]^ <top>bigg>_^n $$ к каноническому, а на диагонали $ A_ $ стоят собственные числа матрицы $ A_<> $: $$ A_= left( begin lambda_1 & 0 & dots & 0 \ 0 & lambda_2 & dots & 0 \ & & ddots & \ 0 & 0 & dots & lambda_n end right) . $$
Доказательство. Проведем формальное доказательство данного конкретного частного случая. Рассмотрим матричное равенство $$ A C= CA_ $$ при некоторой диагональной матрице $ A_ $. Легко видеть, что оно эквивалентно системе равенств относительно столбцов матрицы $ C_<> $: $$ AC_<[1]>=d_1 C_<[1]>,dots, AC_<[n]>=d_n C_ <[n]>, . $$ Если все столбцы $ < C_<[j]>>_^n $ ненулевые, то тогда они являются собственными векторами для матрицы $ A_<> $, а числа $ < d_<[j]>>_^n $ — собственными числами, соответствующими этим собственным векторам. Если матрица $ C_<> $ невырождена, то все ее столбцы линейно независимы. Но тогда они образуют базис пространства $ mathbb C^n $, состоящий из собственных векторов. Обратное тоже верно. ♦
При выполнении условия предыдущего следствия говорят, что матрица $ A_<> $ диагонализуема или приводится к диагональной форме 7) .
Теорема позволяет сформулировать достаточное условие диагонализуемости.
Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.
Это условие не является необходимым, как показывает пример тождественного оператора .
Случай существования кратного корня у характеристического полинома является «пограничным»: существуют примеры как диагонализуемых, так и недиагонализуемых матриц. Так, для матриц $$ A= left( begin 0 &1 \ -1 &2 end right) quad mbox < или >quad A= left( begin 1 &0 \ 1&1 end right) $$ при попытке подобрать матрицу $ C_<> $, удовлетворяющую равенству $$AC=C left( begin alpha_1 &0 \ 0 & alpha_2 end right) qquad npu forall <alpha_1 , alpha_2 >subset mathbb C $$ получим: $ det C=0 $.
В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.
Теорема 4. Множество собственных векторов оператора, принадлежащих его собственному числу $ lambda_<ast>^<> $ , дополненное нулевым вектором, образует линейное подпространство пространства $ mathbb V_<> $.
Это подпространство $$ mathbb V_ <ast>= mathcaler (mathcal A- lambda_ <ast>mathcal E) $$ пространства $ mathbb V_<> $ называется собственным подпространством оператора, соответствующим $ lambda_<ast>^<> $. Величина $$ dim (mathcaler (mathcal A- lambda_ <ast>mathcal E)) $$ называется геометрической кратностью собственного числа $ lambda_<ast>^<> $. Можно доказать, что геометрическая кратность собственного числа не превосходит кратности собственного числа в характеристическом полиноме. Для акцентирования различий в определениях двух кратностей, кратность собственного числа в характеристическом полиноме называют еще алгебраической кратностью собственного числа.
Если оператор (в некотором базисе пространства) задан своей матрицей $ mathbf A^<> $, то базисные векторы собственного подпространства $ mathbb V_ <ast>$ вычисляются посредством нахождения фундаментальной системы решений (ФСР) системы линейных уравнений $$ (mathbf A- lambda_ <ast>E) X=mathbb O . $$
Теорема 5. Матрица оператора диагонализуема тогда и только тогда, когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:
Диагонализуема ли матрица оператора $$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ рассмотренного в примерах предыдущего пункта?
Пример. Найти все вещественные значения параметра $ <color < alpha>> $, при которых матрица
Решение. Характеристический полином $ f(lambda)=-lambda^3+3, lambda-2,(3, <color < alpha>> -1) $ имеет кратные корни только тогда когда его дискриминант $ mathcal D(f)=-324, <color < alpha>> (3, <color < alpha>> -2) $ обращается в нуль. При $ <color < alpha>> =0 $ корень $ lambda=-1 $ имеет алгебраическую кратность $ 2_<> $. Найдем дефект матрицы $ A+E $: $$left( begin 2 &0 & -2 \ -1 &3 &1 \ 2 & 0 & -2 end right) longrightarrow left( begin 1 &0 & -1 \ 0 &3 &0 \ 0 & 0 & 0 end right) Longrightarrow operatorname (A+E) =2 Longrightarrow operatorname (A+E)=1 . $$ Таким образом, геометрическая кратность собственного числа $ lambda=-1 $ равна $ 1_<> $ и условие теоремы $ 5 $ не выполнено. Оно не будет выполнено и при $ <color < alpha>> = 2/3 $ (здесь корень $ lambda=1 $ имеет кратность $ 2_<> $).
Ответ. Матрица диагонализуема при всех значениях параметра, за исключением $ <color < alpha>> = 0 $ и $ <color < alpha>> = 2/3 $.
Диагонализуемость матрицы оператора над полем вещественных чисел
В предыдущем пункте мы рассматривали операторы, не всегда акцентируя внимания на поле, над которым они были определены — над $ mathbb R_<> $ или над $ mathbb C_<> $. Сама теорема существования собственного числа гарантирует нам только лишь наличие этих чисел в поле $ mathbb C_<> $. Как следствие, даже если рассматриваются операторы над полем $ mathbb R_<> $ (что чаще всего и случается на практике), то существование для них вещественного канонического базиса вовсе не гарантировано.
Задача. Найти условия диагонализуемости матрицы оператора $ mathcal A $ над полем вещественных чисел.
Необходимое условие следует из теоремы $ 2 $ предыдущего пункта: все собственные числа матрицы должны быть вещественными.
Теорема $ 3 $ позволяет сформулировать и достаточный критерий диагонализуемости матрицы оператора $ mathcal A $ над $ mathbb R_<> $.
Теорема. Если характеристический полином оператора имеет только простые вещественные корни, то матрица оператора диагонализуема над $ mathbb R_<> $.
Условие различности и вещественности корней произвольного полинома $ f(lambda)=lambda^n+a_1lambda^+dots+ a_n in mathbb R[x] $ можно проверить по коэффициентам этого полинома «чисто алгебраически», т.е. за конечное число элементарных алгебраических операций над этими коэффициентами. Воспользуемся, например, теоремой Якоби из раздела ☞ ЛОКАЛИЗАЦИЯ КОРНЕЙ ПОЛИНОМА. По коэффициентам $ a_1,dots,a_n $ можно определить сумму Ньютона полинома $ f(lambda) $, т.е. величину $$ s_k=sum_ <1le j le n>lambda_j^k . $$ Далее, после нахождения всех этих сумм для значений $ k in <0,dots,2n-2>$, из них составляется ганкелева матрица $$ S=left[ s_ right]_^ $$ и вычисляются ее главные миноры $ S_1,dots, S_ $. Для различности всех корней полинома необходимо и достаточно выполнение условия $ S_n ne 0 $ (этот минор совпадает с дискриминантом $ mathcal D(f) $ полинома $ f(lambda) $); для различности и вещественности всех корней необходимо и достаточно, чтобы были выполнены неравенства $$ S_1ge 0,dots,S_ ge 0,S_n > 0 . $$
Пример. Найти все вещественные значения параметра $ <color < alpha>> $, при которых матрица
$$ left( begin 1 &2, <color < alpha>> & <color < alpha>> -2 \ -1 &2 &1 \ 2 & 0 & -3 end right) $$ диагонализуема над $ mathbb R_<> $.
Решение. На основании теоремы нам нужно установить условия вещественности корней характеристического полинома $ f(lambda)=-lambda^3+3, lambda-2,(3, <color < alpha>> -1) $. Вычисляем суммы Ньютона: $ s_0=3, s_1= 0, s_2=6, s_3=18, <color < alpha>> -6, s_4=18 $, составляем матрицу: $$ S=left(begin 3 & 0 & 6 \ 0 & 6 & 18, <color < alpha>> -6 \ 6 & 18, <color < alpha>> -6 & 18 end right) $$ и вычисляем ее главные миноры: $$S_1=3, S_2=18, S_3=-324, <color < alpha>> , (3, <color < alpha>> -2)=mathcal D(f) . $$ При $ <color < alpha>> ne 0 $ и $ <color < alpha>> ne 2/3 $ все собственные числа различны, условие теоремы выполняется при $ <color < alpha>> in ]0,, 2/3[ $. Граничные точки последнего интервала следовало бы исследовать отдельно: хотя этим значениям параметра и соответствует случай кратных вещественных корней характеристического полинома, но матрица $ A_<> $ может оказаться диагонализуемой на основании теоремы 5 предыдущего пункта. Но при решении примера в предыдущем пункте мы уже установили, что это условие не выполняется.
Ответ. Матрица диагонализуема над $ mathbb R_<> $ при $ <color < alpha>> in ]0,, 2/3[ $.
Жорданова нормальная форма
Если матрица оператора оказывается недиагонализуемой над $ mathbb C_<> $, то к какому простейшему виду ее можно привести ? — Этим видом является, например, ☞ ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА.
Задачи
Источники
[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.
[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960
[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965
Скалярное произведение в разработке игр: проекции и прыгающие мячики в Unity ⛹
furry.cat
Скалярное произведение – простой, но чрезвычайно полезный математический инструмент. Он кодирует отношение между величинами и направлениями двух векторов в единственное скалярное значение. Его можно использовать для вычисления проекции, отражения, расчета тени и постановки освещения. Из этого руководства вы узнаете:
- Геометрический смысл скалярного произведения.
- Как спроецировать один вектор на другой.
- Как измерить размер объекта вдоль произвольной оси.
- Как отразить вектор относительно плоскости.
- Как создать эффект отскока мяча от наклонной поверхности.
Скалярное произведение
Представьте два вектора a и b . Вектор характеризуется только направлением и величиной (длиной), поэтому не имеет значения, в каком месте плоскости он расположен. Допустим, оба вектора начинаются в одной точке:
a и b , выходящие из одной точки плоскости” data-src=”https://media.proglib.io/posts/2020/04/04/182e211c01704ab48d14f469d9838df4.png” > Два вектора a и b , выходящие из одной точки плоскости
Проекцию одного вектора на другой можно представить как отбрасывание тени от первого вектора в направлении, перпендикулярном второму:
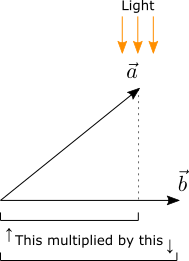
Как вы знаете, операция вычисления произведения векторов записывается так:
Далее в статье мы будем использоваться запись a * b .
Если между векторами острый угол, то длина проекции будет положительной величиной, если больше – то отрицательной.
Если b – единичный вектор, то величина проекции a на b – это просто произведение a * b .
Вычисление скалярного произведения через косинус угла
На схеме изображен прямоугольный треугольник. Угол между векторами a и b равен θ .

Для начала требуется рассчитать величину проекции вектора a на вектор b – это нижний катет в нарисованном нами треугольнике. Длину катета стороны можно найти, умножив длину гипотенузы треугольника на косинус прилежащего угла.
a на вектор b – это катет прямоугольного треугольника” data-src=”https://media.proglib.io/posts/2020/04/04/c4a332573e7bdc88dcc72dddf457044d.png” > Проекция вектора a на вектор b – это катет прямоугольного треугольника
Итак, длина проекции равна произведению модуля вектора a на косинус угла θ . Скалярное произведение можно выразить следующим образом:
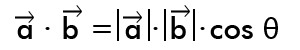
Эта формула лишний раз подтверждает, что порядок умножения не важен – в результат входят беззнаковые длины обоих векторов. Если оба вектора – единичные, правая часть формулы упрощается до cos(θ) . А если угол равен 90° (векторы перпендикулярны), то их произведение равно 0 .
Если угол острый (меньше 90°), результат будет положительным, так как косинус такого угла больше 0. Аналогично для тупого угла получится отрицательный результат. Таким образом, знак скалярного произведения дает нам некоторое представление о направлениях векторов.
Функция косинуса монотонно убывает на промежутке от 0 до 180° (от 1 до -1 ). Следовательно, чем ближе направления двух векторов, тем больше их скалярное произведение и наоборот.
- Направления совпадают, угол θ равен 0°, произведение равно |a| * |b| .
- Направления противоположны, угол θ равен 180°, произведение – -1* |a| * |b| .
Вычисление скалярного произведения через компоненты векторов
Если наши векторы расположены в 3D-пространстве и имеют по три координаты каждый, не совсем понятно, где тот угол, косинус которого нужно вычислить. К счастью, существует другой способ расчета скалярного произведения – без всякой тригонометрии! Для начала нужно разложить каждый вектор на компоненты:
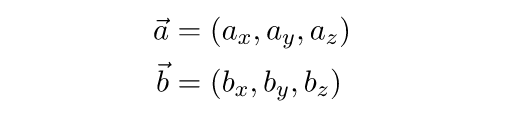
Намного проще и без всяких косинусов! В Unity есть встроенный метод Vector3.Dot для вычисления скалярного произведения двух векторов:
Его реализация выглядит следующим образом:
Нам известно, как найти длину вектора по его координатам:
Но ее можно выразить и через скалярное произведение вектора на себя:
Вернемся к формуле a * b = |a| * |b| * cos θ . При известных длинах векторов мы можем вычислить угол между ними с помощью функции арккосинуса:
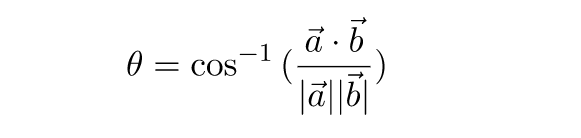
Если оба вектора являются единичными, мы можем упростить формулы:
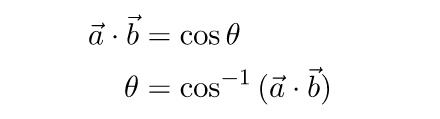
Проекция вектора
Теперь, когда нам известно геометрическое значение скалярного произведения векторов (произведение длины со знаком первого проецируемого вектора и длины второго вектора), мы можем перейти к практическому применению этого знания. Например, спроецируем один вектор на другой.
Пусть вектор с = project ba – это проекция вектора a на вектор b .
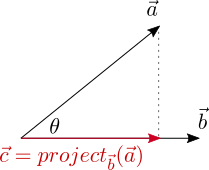
Возьмем единичный вектор в направлении вектора b . Он будет равен b / |b| . Если мы возьмем величину проекции a на b со знаком и умножим на этот единичный вектор, то получим вектор c . Cкалярное произведение a * b – это результат умножения длины b на длину проекции a на b . Отсюда получаем, что длину c со знаком можно найти, разделив скалярное произведение a * b на длину b :
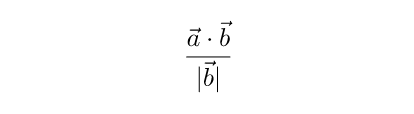
Умножив полученное значение на единичный вектор b / |b| , получаем формулу для нахождения проекции вектора:
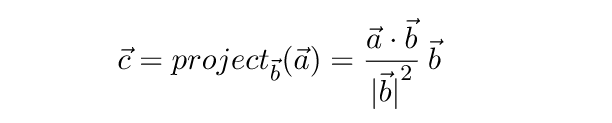
Вспомним теперь, что квадрат длины вектора равен его скалярному произведению на самого себя, и перепишем формулу:
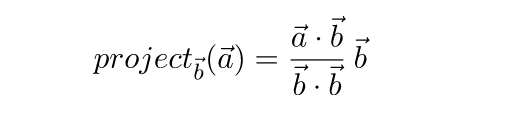
Если b – единичный вектор, то можно упростить еще больше:
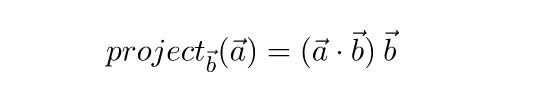
В Unity для вычисления проекции одного вектора на другой есть специальная функция Vector3.Project :
Вот так выглядит ее реализация:
Следует остерегаться возможного вырожденного случая, когда вектор, на который происходит проекция, – нулевой или имеет малую величину. При этом произойдет численный «взрыв» из-за деления на 0 или близкое к нему значение. Один из способов решить проблему – заранее вычислять величину вектора и при необходимости использовать резервный вариант (единичный вектор).
Упраженение #1. Линейка
В качестве упражнения для закрепления знаний о векторной проекции сделаем линейку, которая измеряет размер объекта вдоль произвольной оси.
Линейка характеризуется базовой позицией (точка) и осью (единичный вектор):
Как спроецировать какую-либо точку ( Point ) на линейку? Прежде всего, найдем относительный вектор от базовой позиции линейки ( Base ) до этой точки. Затем спроецируем его на ось линейки ( Axis ). Проекция точки ( Projection ) – это базовое положение линейки, смещенное на проекцию относительного вектора.
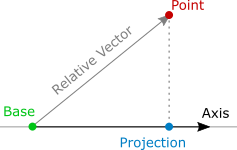
Промежуточное значение relativeDot в коде отражает, насколько далеко проекция точки находится от базового положения линейки – в направлении оси линейки, если она положительная, или в противоположном направлении, если отрицательная.
Чтобы найти размер объекта вдоль оси линейки, нужно провести такие измерения для каждой вершины меша (Mesh) и найти минимальное и максимальное значение. Ответ будет равен разнице между ними.
Отражение вектора
Еще одно практическое применение скалярного произведения – отражение вектора относительно плоскости. Рассмотрим вектор v и плоскость с нормальным вектором (перпендикуляром) n .
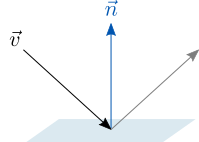
Мы можем разложить отражаемый вектор на параллельную и перпендикулярную к плоскости составляющие:
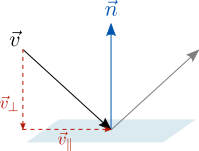
Сам вектор является суммой параллельной и перпендикулярной составляющих:
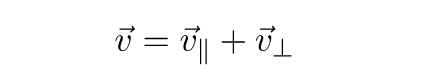
Перпендикулярный компонент, как вы уже догадались – это проекция вектор на нормаль плоскости. Параллельный компонент можно получить вычитанием этой проекции из самого вектора:
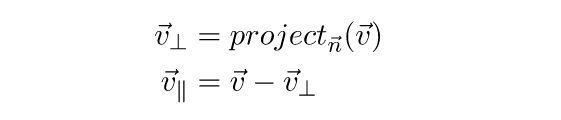
Теперь, чтобы получить искомый отраженный вектор, нужно перевернуть перпендикулярную составляющую и прибавить ее к параллельной:
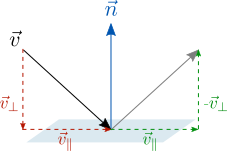
Параллельный компонент можно заменить разностью самого вектора и перпендикулярной составляющей, тогда получим следующий вид формулы:
То есть разность самого вектора и его удвоенной проекции на нормаль плоскости.
В Unity, конечно же, есть встроенная функция для расчета отраженного вектора – Vector3.Reflect :
Так выглядит реализация согласно первой выведенной нами формуле:
Упражнение #2. Отскок мяча от наклонной плоскости
Теперь, когда мы знаем все об отражении вектора от плоскости, можно переходить на следующий уровень сложности. Попробуем сымитировать движение мяча, отскакивающего от склона.
Для моделирования траектории движения шара под действием силы тяжести мы будем использовать метод Эйлера.
Чтобы определить, когда мяч ударяется о склон, нужно как-то определить момент, когда мяч проникает в плоскость.
Сфера может быть определена центром ( C ) и радиусом ( R ). Плоскость определяется нормальным вектором ( n ) и точкой на плоскости ( P ). Вектор от P до С обозначим u .
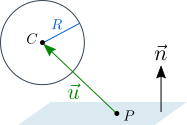
Если сфера НЕ проникает в плоскость, перпендикулярный плоскости компонент вектора u , должен иметь то же направление, что и вектор n , а также длину не менее R .
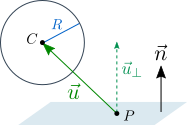
Другими словами, сфера не проникает в плоскость, если скалярное произведение векторов u и n больше R . В противном случае величина проникновения составляет R – u * n , и положение сферы нужно исправить.
Чтобы это сделать, можно просто переместить сферу в направлении нормали плоскости n на величину проникновения. Это лишь приближенное решение, которое не является физически правильным, но для упражнения оно хорошо подходит.
Добавим логику для коррекции позиции:
Нам также нужно отразить скорость, с которой движется сфера, относительно наклона, чтобы она правильно отскакивала.
Эта анимация демонстрирует идеальное отражение и выглядит неестественной. Мы ожидаем, что с каждым отскоком скорость мяча будет уменьшаться.
Это поведение обычно моделируется значением реституции (восстановления) между двумя сталкивающимися объектами. При 100% реституции мяч идеально отскакивает от плоскости. При 50% – величина перпендикулярной к плоскости составляющей скорости мяча будет уменьшена вдвое.
Величина реституции – это отношение величин перпендикулярного к плоскости компонента скорости мяча до и после отскока.
Вот пересмотренный с учетом коэффициента восстановления скорости вариант функции отражения:
Вот так выглядит обновленная функция SphereVsPlane :
Логика корректировки позиции заменяется логикой полноценного отскока:
Теперь мы можем устанавливать разные коэффициенты реституции для разных шариков:
Заключение
Мы ответили на все вопросы, заданные в начале этого руководства.
- Скалярное произведение двух векторов – это произведение проекции первого вектора на второй (с учетом знака) и модуля второго вектора.
- Существует две формулы вычисления скалярного произведения: через косинус угла и через компоненты векторов.
- Скалярное произведение имеет множество полезных практических применений. Например, оно позволяет рассчитать проекцию вектора на другой вектор.
- С помощью скалярного произведения можно найти отраженный от плоскости вектор. На этой основе строятся различные физические модели, например, имитация отскока шарика от плоскости.
Расскажите в комментариях – разрабатываете ли вы сейчас какую-нибудь игру и если да, то о чем она. Каких уроков по Unity вам не хватает?
Вычисление нормалей и углов отражения
Тема9. Построение реалистических изображений
В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками.
Модели отражения света
Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.
Зеркальное отражение света.Угол между нормалью и падающим лучом (Θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).
Поверхность считается идеально зеркальной, если на ней отсутствуют какие либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм
Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.
При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов, близких к 90 градусам.
Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемые по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cosа) p , где а— угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:
где I— интенсивность излучения источника, Ks— коэффициент пропорциональности, который изменяется от 0 до 1.
Диффузное отражение.Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).
где I— интенсивность источника света, Kd— коэффициент, который учитывает свойства материала поверхности. Значение Kd находится в диапазоне от 0 до 1 . Интенсивность отраженного света не зависит от расположения наблюдателя.
Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.
При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:
где константы Kd, KS определяют отражательные свойства материала.
Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов Θ и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:
где Iа — интенсивность рассеянного света, Ка — константа, изменяется от 0 до 1.
Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:
где R — расстояние от центра проекции до поверхности, k — константа.
Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвет (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициент! Ка и Kd различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент Ks будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.
Алгебра векторов
Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как R|и вычисляется следующим образом:
Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.
1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а
[spoiler title=”источники:”]
http://proglib.io/p/skalyarnoe-proizvedenie-v-razrabotke-igr-proekcii-i-prygayushchie-myachiki-v-unity-2020-04-05
http://poisk-ru.ru/s19716t20.html
[/spoiler]