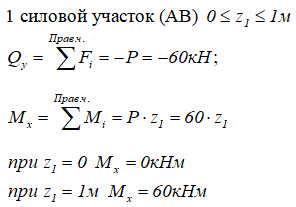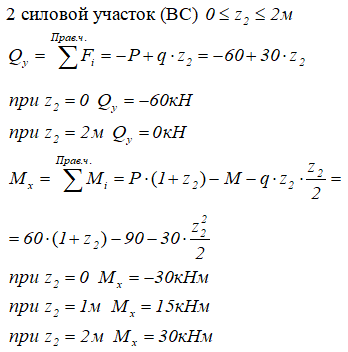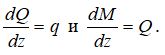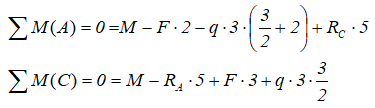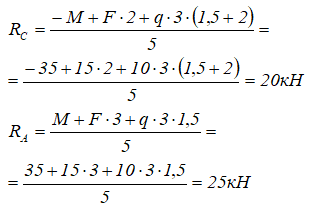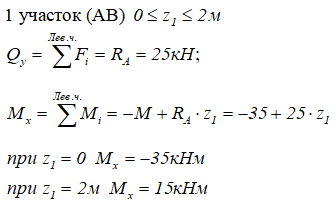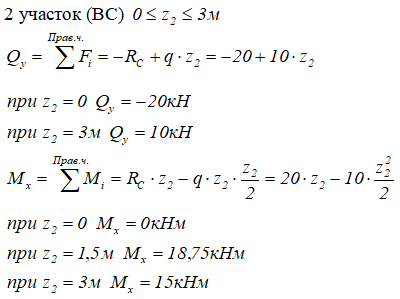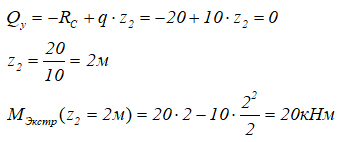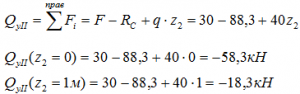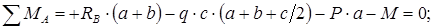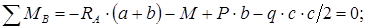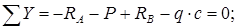Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

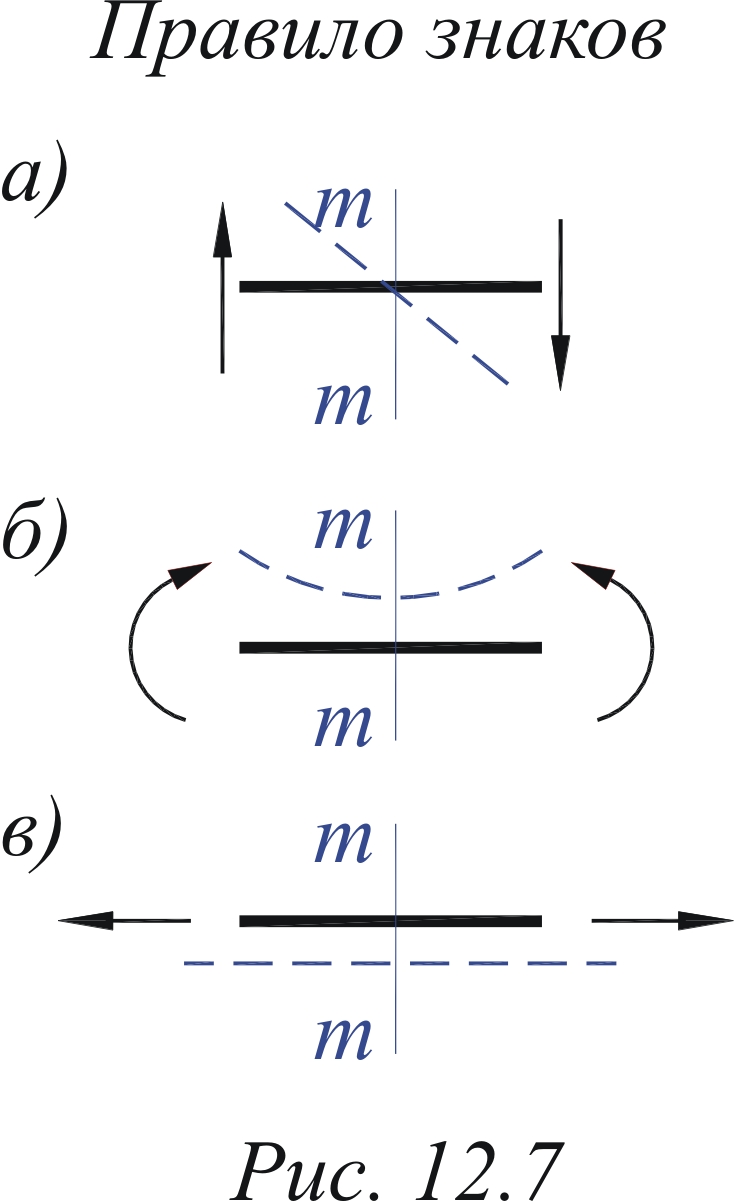
Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
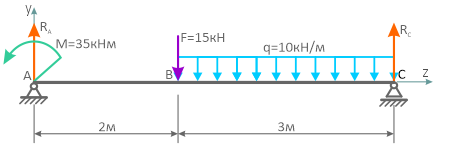
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
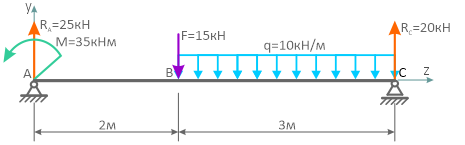
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Задача. Расчет рамы. Для рамы построить эпюры продольных сил N, поперечных сил Q и изгибающих моментов М.
- Определим опорные реакции
Нанесем значения опорных реакций на расчетную схему.
2. Строим эпюру продольных сил N методом сечений. Имеем три характерных участка и три сечения на них.
Правило знаков продольных сил – продольная сила считается положительной, если сила растягивает стержень, и отрицательной, если сила сжимает стержень. Положительные значения откладываем влево от стойки и вверх от ригеля.
Строим эпюру продольных сил.
3. Строим эпюру поперечных сил Q методом сечений. Правило знаков – если сила относительно сечения направлена по часовой стрелке, то поперечная сила считается положительной и наоборот. Положительные значения откладываются влево от стоек и вверх от ригеля.
Строим эпюру поперечных сил
4. Строим эпюру изгибающих моментов М методом характерных точек. Расставляем точки: А – опора, В,С, — узлы рамы, D – свободный конец, К – середина равномерно распределенной нагрузки (точки экстремума при построении эп.Q не обнаружено). Эпюру М строим на сжатых волокнах (для машиностроительных специальностей), знак не ставим.
Строим эпюру моментов.
5. Вырезаем узлы С и В и проверяем их равновесие.
Узлы находятся в равновесии, значит эпюры построены верно.
Для балки с жесткой заделкой построить эпюры Q и М.
Расставляем сечения от свободного конца балки — в этом случае можно построить эпюры, не определяя опорных реакций. Рассматривать в каждом случае будем правую часть — справа от сечения. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 2 участка, 2 сечения.
Сечение 2-2 проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Определяем поперечные силы в сечениях. Правило знаков см. — здесь.
Строим эпюру Q.
Построим эпюру М методом характерных точек. Расставляем точки на балке — это точки начала и конца балки (D,A), сосредоточенного момента (B), а также отметим в качестве характерной точки середину равномерно распределенной нагрузки (K) — это дополнительная точка для построения параболической кривой.
Определяем изгибающие моменты в точках. Правило знаков см. — здесь.
Момент в т. В будем определять следующим образом. Сначала определим:
Теперь:
Точку К возьмем в середине участка с равномерно распределенной нагрузкой.
Строим эпюру M. Участок АВ – параболическая кривая (правило «зонтика»), участок ВD – прямая наклонная линия.
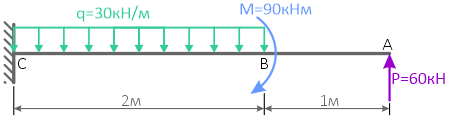
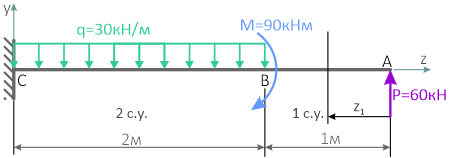
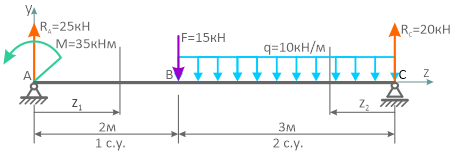
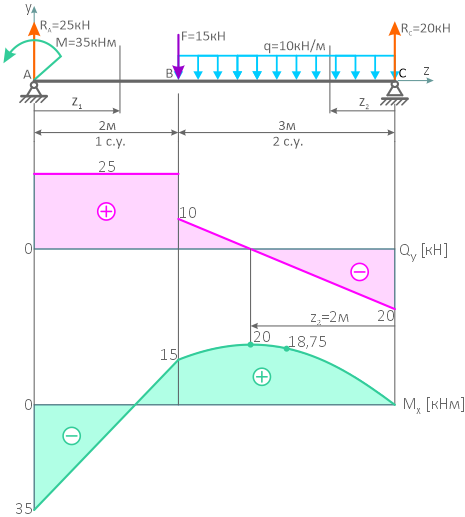
Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).
- Обозначаем опоры буквами А и В и направляем опорные реакции RА и RВ.
Составляем уравнения равновесия.
Проверка
Записываем значения RА и RВ на расчетную схему.
2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.
сеч. 1-1 ход слева.
Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.
Строим по найденным значением эпюру Q.
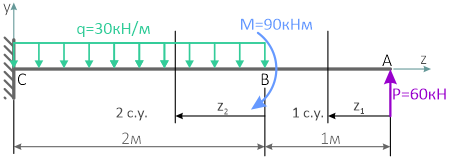
сеч. 2-2 ход справа.
Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Длина участка 6 м.
Строим эпюру Q.
сеч. 3-3 ход справа.
сеч. 4-4 ход справа.
Строим эпюру Q.
3. Построение эпюры М методом характерных точек.
Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.
Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.
Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.
Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.
Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.
Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)
Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.
Получаем уравнение:
Теперь, зная х, определим момент в точке К с правой стороны.
Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».
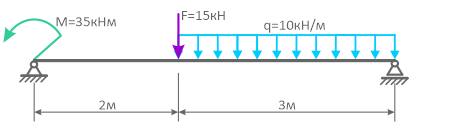
Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.
Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м
Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.
1. Определим опорные реакции.
Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН
В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.
Найдем вертикальную реакцию опоры RA и опорный момент МA из уравнений равновесия.
2. Строим эпюру поперечных сил.
На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции RA.
4.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения
Таким образом, подбираем сечение с диаметром 25 см.
Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.
1.Определение реакций:
Сумма моментов относительно опор:
Опора А:
Опора В:
Сумма проекций всех сил на ось У (проверка):
2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
1) Первый участок:
2) Второй участок:
3) Третий участок:
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:
С эпюры берем максимальный момент:
По сортаменту подбираем двутавр № 20 с
Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:
Для заданной балки требуется построить эпюры Q и M, найти Mmax и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала Ru=10 МПа.
1.Определение реакций:
Сумма проекций всех сил на ось z:
Сумма проекций всех сил на ось y:
Сумма моментов относительно точки А:
После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).
2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.
M— изгибающий момент, считается положительным, если растягивает нижние волокна.
1)Первый участок:
2) Второй участок:
3) Третий участок:
Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подберем деревянную балку круглого поперечного сечения при Ru=10 МПа
С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.
Задача 1. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).
Теперь из него найдем МА
Следующее уравнение из него найдем RА
2. Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть
3. Строим эпюру М
Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. МК , для этого определим положение точки К.
Это уравнение первого участка, на котором находится точка К
в точке К
Строим эпюры. Задача решена.
Задача 2. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть правую часть, то в уравнении будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.
Знак «-» говорит о том, что реакция RВ направлена в обратную сторону.
Проверка:
2. Построение эпюры Q.
Участок первый – ЕА, смотрим левую часть
Участок второй – АС, смотрим левую часть
Участок третий – СВ, смотрим левую часть
Участок четвертый – ВД, смотрим правую часть
3. Построение эпюры М
Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД
Строим эпюры, задача решена.
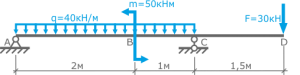
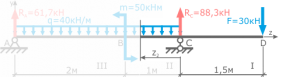
Задача 1. Построить эпюры внутренних усилий для рамы ( рис.а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=1,8м, h=2м.
Решение.
Для рассматриваемой рамы опорные реакции можно не определять, поскольку будем рассматривать участки, идя от свободных концов рамы к заделке.
Вычислим значения внутренних усилий N, Q и М в характерных сечениях рамы. Правило знаков для поперечных сил Q и изгибающих моментов М такие же,как в балках. Эпюры моментов построим на сжатых волокнах. Для продольной N, силы правило знаков: растягивающая сила – положительна, сжимающая – отрицательна.
Участок ВС: (сжаты нижние волокна).
(сжаты нижние волокна).
Участок DC: 
Участок СК: (сжаты левые волокна)
(сжаты левые волокна)
На рисунке – эпюры нормальных (продольных) сил — (б), , поперечных сил — (в) и изгибающих моментов — (г).
Проверка равновесия узла С:
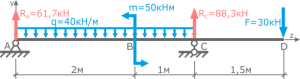
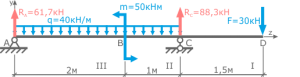
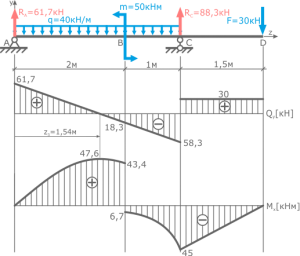
Задача 2 Построить эпюры внутренних усилий для рамы (рис. а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=3м, h=2м.
Определим опорные реакции рамы:
Из этих уравнений найдем:
Поскольку значения реакции RK имеет знак минус, на рис. а изменяется направление данного вектора на противоположное, при этом записывается RK=83,33кН.
Определим значения внутренних усилий N, Q и М в характерных сечениях рамы:
Участок ВС:
(сжаты правые волокна).
Участок CD:
(сжаты правые волокна);
(сжаты правые волокна).
Участок DE:
(сжаты нижние волокна);
(сжаты нижние волокна).
Участок КС
(сжаты левые волокна).
Построим эпюры нормальных (продольных) сил (б), поперечных сил (в) и изгибающих моментов (г).
Рассмотрим равновесие узлов D и Е
Из рассмотрения узлов Dи Е видно, что они находятся в равновесии.
Задача 3. Для рамы с шарниром построить эпюры внутренних усилий.
Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.
Решение. Определим опорные реакции. Следует отметить ,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых ,так и от правых сил равен нулю. Рассмотрим левую часть.
Уравнения равновесия для рассматриваемой рамы можно записать в виде:
Из решения данных уравнений следует:
На схеме рамы направление действия силы НВ изменяется на противоположное (НB=15кН).
Определим усилия в характерных сечениях рамы.
Участок BZ:
(сжаты левые волокна).
Участок ZC:
(сжаты левые волокна);
Участок КD:
(сжаты левые волокна);
(сжаты левые волокна).
Участок DС:
(сжаты нижние волокна);
Определение экстремального значения изгибающего момента на участке CD :
(сжаты верхние волокна).
Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы.
Узлы C и D находятся в равновесии.
Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.
1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции VA; С – точка приложения сосредоточенной силы; D, B– начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:
Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис,б).
2. Построение эпюры моментов
Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка приложения сосредоточенного момента и силы F; D и В — начало и конец действия равномерно распределенной нагрузки. Поскольку эпюра Qx на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.
Ход слева:
Ходом справа находим MB = 0.
По найденным значениям строим эпюру изгибающих моментов (см. рис. в).
Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.
1. Построение эпюры Qу. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Qу ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Qу в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно .
Строим эпюру Qу методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:
Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Qу. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Qу (рис. б).
Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, равный значению силы. Если наклонная линия под распределенной нагрузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Qу и Мx, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпюре Qу себя никак не проявляет, так как сумма проекций сил, образующих пару, равна нулю.
2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, методом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значения изгибающих моментов в начале участка, конце его и в одном промежуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в котором эпюра Qу пересекает нулевую линию, т.е. где Qу= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Qу не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если нагрузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпюры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и будет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.
Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствующих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соответствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.
Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Qу = 0.
Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,
Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):
Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Qу (рис.б).
Определяем момент в точке К:
Пройдем оставшуюся часть балки ходом справа.
Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).
Примеры построения эпюр для решения задач сопротивления материалов, строительной и технической механики со всеми расчетами, подробными пояснениями и видеоуроками.
Примечание: студентам строительных специальностей эпюры изгибающих моментов надо строить на растянутых слоях балки, поэтому положительные значения Mx необходимо откладывать вниз, а отрицательные — вверх от базовой линии.
Сохранить или поделиться с друзьями
Рассмотрим пару упрощенных и несколько максимально подробных примеров построения эпюр внутренних силовых факторов, напряжений и перемещений для всех способов закрепления и нагружения балок, стержней и валов.
Построение эпюр Qy и Mx для консольной балки
Для заданной консольной балки требуется построить эпюры внутренних силовых факторов Qy и Mx.
Решение
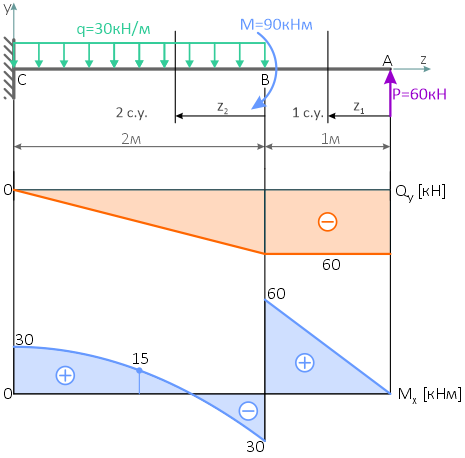
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.
Показываем оси системы координат y-z и обозначаем характерные сечения балки.
Для построения эпюр внутренних силовых факторов консольных балок, опорные реакции можно не определять.
Тогда для расчета значений Qy и Mx необходимо рассматривать противоположную от заделки часть балки, где все внешние усилия известны.
Балка имеет 2 силовых участка.
Рассчитаем, с учетом правил знаков при изгибе, значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.
На первом участке оба силовых фактора рассчитаны.
Переходим ко второму
Так как эпюра Qy на втором силовом участке не пересекает базовую линию, экстремума на эпюре Mx не будет.
По полученным данным строим эпюры внутренних поперечных сил Qy и изгибающих моментов Mx.
При ручном оформлении решения, эпюры заштриховываются тонкими линиями перпендикулярно базовой (нулевой) линии.
Оформление в электронном виде допускает сплошную однородную заливку площади эпюры.
Проверка построенных эпюр:
- по дифференциальным зависимостям
- в сечениях балки, где приложены сосредоточенные силы, на эпюре Qy имеются скачки значений на величину соответствующей силы;
- в сечениях балки, где приложены изгибающие моменты, на эпюре Mx скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.
Как строить эпюры для балки на двух опорах
Для заданной расчетной схемы балки на двух шарнирных опорах требуется определить значения и построить эпюры внутренних поперечных сил и изгибающих моментов.
Решение
При построении эпюр для участков балки расположенных между опорами необходимо знать величину хотя бы одной из реакций.
Определение реакций в шарнирных опорах балки
Направим реакции опор, например, вверх
и запишем, с учетом правила знаков, суммы моментов нагрузок приложенных к балке относительно точек на опорах
Из составленных уравнений выражаем и находим реакции
Положительные значения указывают на то, что произвольно заданное направление реакций оказалось верным.
Расчет и построение эпюр
Используя метод сечений и соответствующие правила знаков, рассчитаем по каждому участку значения для построения эпюр.
Балка имеет 2 силовых участка.
На первом участке расчет произведем, рассматривая левую отсеченную часть балки
На втором — правую
Значения поперечной силы Qy на границах участка имеют разные знаки, следовательно, на этом участке, на эпюре Mx будет экстремум.
Определим его:
По полученным данным строим эпюры внутренних поперечных сил и изгибающих моментов.
Алгоритм проверки эпюр показан в решении предыдущей задачи.
Более подробно ход расчетов и построения эпюр для балки с тремя силовыми участками рассмотрен в следующих задачах.
Подробные примеры построения эпюр
При растяжении-сжатии
Примеры построения эпюр внутренних продольных сил, нормальных напряжений и линейных перемещений для стержней при их растяжении и сжатии.
- эпюра внутренних продольных сил
- эпюра нормальных напряжений в стержне
- построение эпюр внутренних сил, напряжений и перемещений для стального бруса
- построение эпюры внутренних продольных сил для стержня с продольно распределенной нагрузкой
- расчет напряжений с построением эпюры в стержне заданной формы
- построение эпюры перемещений сечений стержня
При кручении
Примеры построения эпюр внутренних крутящих моментов и угловых перемещений сечений вала при кручении.
- Построение эпюры крутящих моментов для вала
- Построение эпюр крутящих моментов и углов закручивания сечений вала
Построение эпюр при изгибе
Примеры построения эпюр внутренних поперечных сил и изгибающих моментов, нормальных и касательных напряжений для балок и рам при изгибе.
Эпюры внутренних силовых факторов
- Построение эпюр поперечных сил Qy и изгибающих моментов Mx для балки (3 участка)
- Эпюра внутренних поперечных сил
- Эпюра внутренних изгибающих моментов балки
- Построение эпюр для рамы
- Проверка эпюр внутренних силовых факторов в рамах
Эпюры напряжений
- эпюра нормальных напряжений двутавра
- эпюра касательных напряжений для двутавра
- эпюра нормальных напряжений прямоугольного сечения
Видеоурок расчетов для построения эпюр внутренних силовых факторов для балки:
Другие видео
Другие примеры решения задач >
Порядок построения эпюр
В рассмотренных выше примерах для построения эпюр выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
Расчетная схема балки - Обозначаются характерные сечения бруса;
- Определяются опорные реакции;
Опорные реакции балки - Рассматриваемый элемент разбивается на силовые участки;
Обозначение силовых участков - Для каждого силового участка выбирается рассматриваемая часть бруса (балки)
Выбранная часть балки и записываются выражения для рассчитываемых внутренних силовых факторов, напряжений или перемещений;Выражения для расчета поперечной силы в сечении балки - Рассчитываются значения на границах участков. В случаях, когда переменная в выражении имеет вторую или более степень можно дополнительно определить значение в середине участка;
- В некоторых случаях необходимо определять экстремумы эпюр;
- После расчета всех значений выполняется построение эпюр.
Эпюры поперечных сил и изгибающих моментов для балки
После построения эпюр желательно выполнять их проверку.
|
СОВЕТУЕМ! |
Перед изучением |
Для
определения опорных реакций в статически
определимых рамах
(12.1)
достаточно использовать условия
равновесия тела (2.14).
При этом, также как и для определения
опорных реакций в балках(6.3),
уравнения пытаются составить так, чтобы
в каждом из них было не более одной
неизвестной. Это позволит облегчить
процесс решения задачи, избегая решения
систем уравнений.
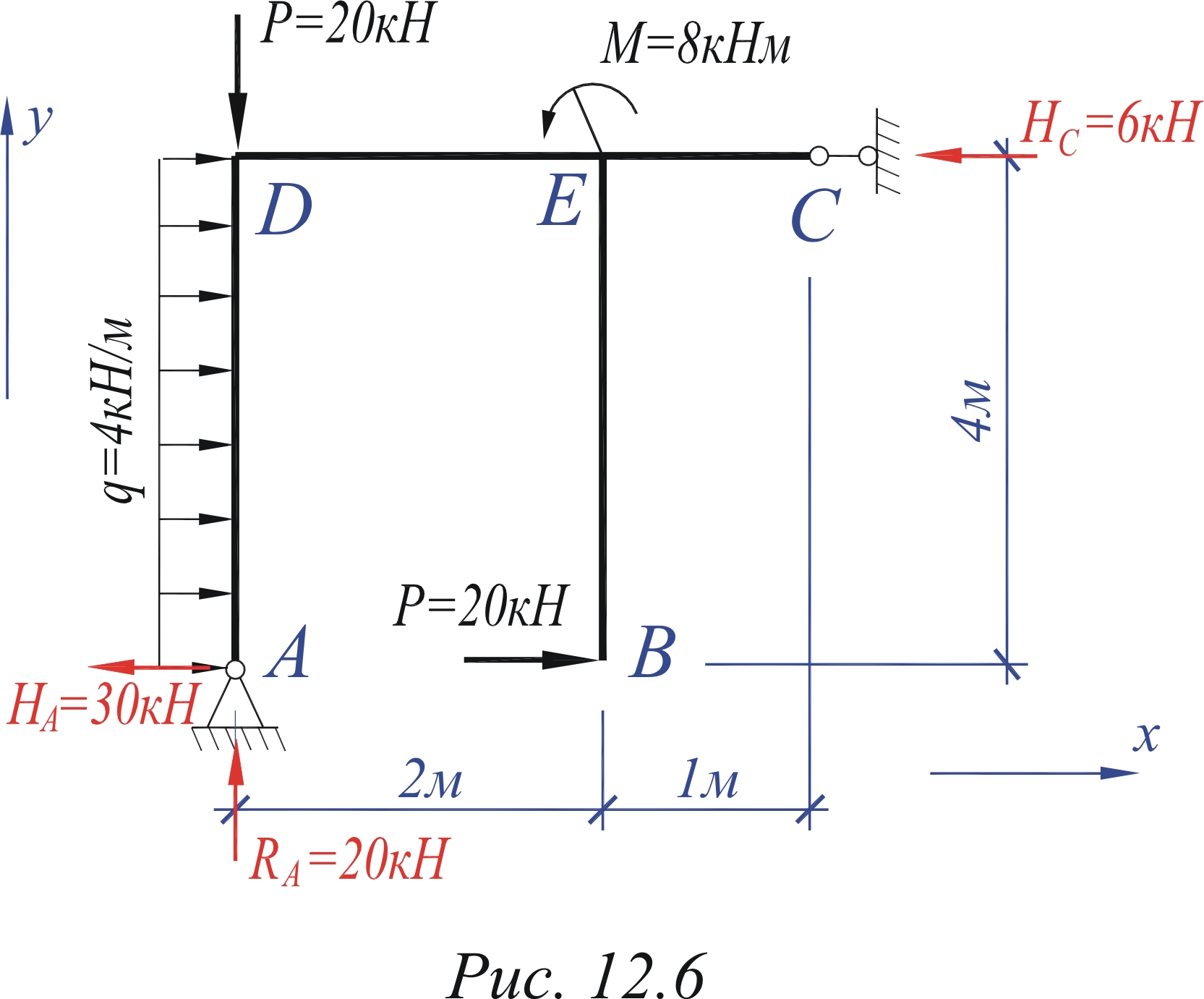
Рассмотрим раму
на рис. 12.6 и определим опорные реакции
в этой раме. Опоры рамы находятся в
точках А и С. Отбрасываем
связи, заменяя их силами опорных реакций.
В точке А расположена шарнирно
неподвижная опора, которую заменяем на
две силы реакции RA
и HA.
В точке С расположена шарнирно
подвижная опора, которую заменяем на
реакцию Hс. Направление опорных
реакций изначально выбирается произвольно.
Анализируем уравнения
|
проекций – содержит
В
|
|
,
откуда
.
,
откуда
.
Наносим
полученные значения реакций на расчетную
схему и корректируем при необходимости
начальное направление реакций. Напоминаем,
что для реакций, полученных со знаком
минус, следует изменить исходное
направление на противоположное, а само
значение записать положительным.
Проверяем
правильность найденных реакций. Для
этого используем уравнение:
.
Для
построения эпюр
(5.3) в рамах
(12.1)
необходимо знать, что вследствие
произвольного расположения стержней
рамы и нагрузок, в
общем случае
в
поперечном сечении элементов рамы
возникают: изгибающие моменты, поперечные
силы и продольные силы.
Построение эпюр можно разделить на
отдельные этапы:
1)
Раму разбивают на участки. Участками
рамы называются части рамы, между точками
приложения сосредоточенных нагрузок,
точками начала или окончания распределенной
нагрузки и точками узлов
(12.4) рамы.
2)
На каждом участке производят рассечение
рамы на две части, одну из которых
рассматривают в равновесии
(1.1). При
этом удобно расположить отсеченную
часть рамы так, чтобы она заняла
горизонтальное положение, и применить
при этом все правила построения эпюр
(5.3) поперечных
сил (6.5),
изгибающих
моментов (6.6)
и продольных сил для этого участка
балки. Построение эпюр продольных сил
в некотором роде было рассмотрено ранее.
Дадим определение продольной силы в
сечении.
Продольной силой называется равнодействующая
потока нормальных усилий в поперечном
сечении. Продольная сила равна сумме
проекций всех внешних сил, расположенных
по одну сторону от сечения, на продольную
ось стержня, и взятых с определенным
знаком.
|
12.6.
Продольной силой
Вернитесь |
|
|
Продольная
Записывают |
|
3)
По аналитическим зависимостям строят
эпюры в раме. При этом положительные
значения ординат эпюры откладывают в
раме, как правило, сверху на ригелях
(12.2) и слева
на стойках
(12.3). На
эпюрах поперечных и продольных сил
указывают знак, на эпюрах изгибающих
моментов знак не указывают, а эпюру
строят на растянутых волокнах.
Проще всего определить расположение
растянутых волокон по уже построенной
эпюре изгибающих моментов для данного
участка как для балки. Для этого
рекомендуется замаркировать соответствующие
точки эпюры в раме и эпюры в балке, а
затем совместить их, убирая знак.
Штриховка
всех эпюр в рамах осуществляется линиями
перпендикулярными осям стержней рамы.
4)
После построения эпюр в рамах выполняют
проверку равновесия
(1.1) узлов (12.4).
Суть проверки заключается в том, что из
рамы вырезают узел
(12.4), в
соответствии с эпюрами указывают
направление и величину внутренних
усилий и проверяют выполнение условий
равновесия тела (2.14).
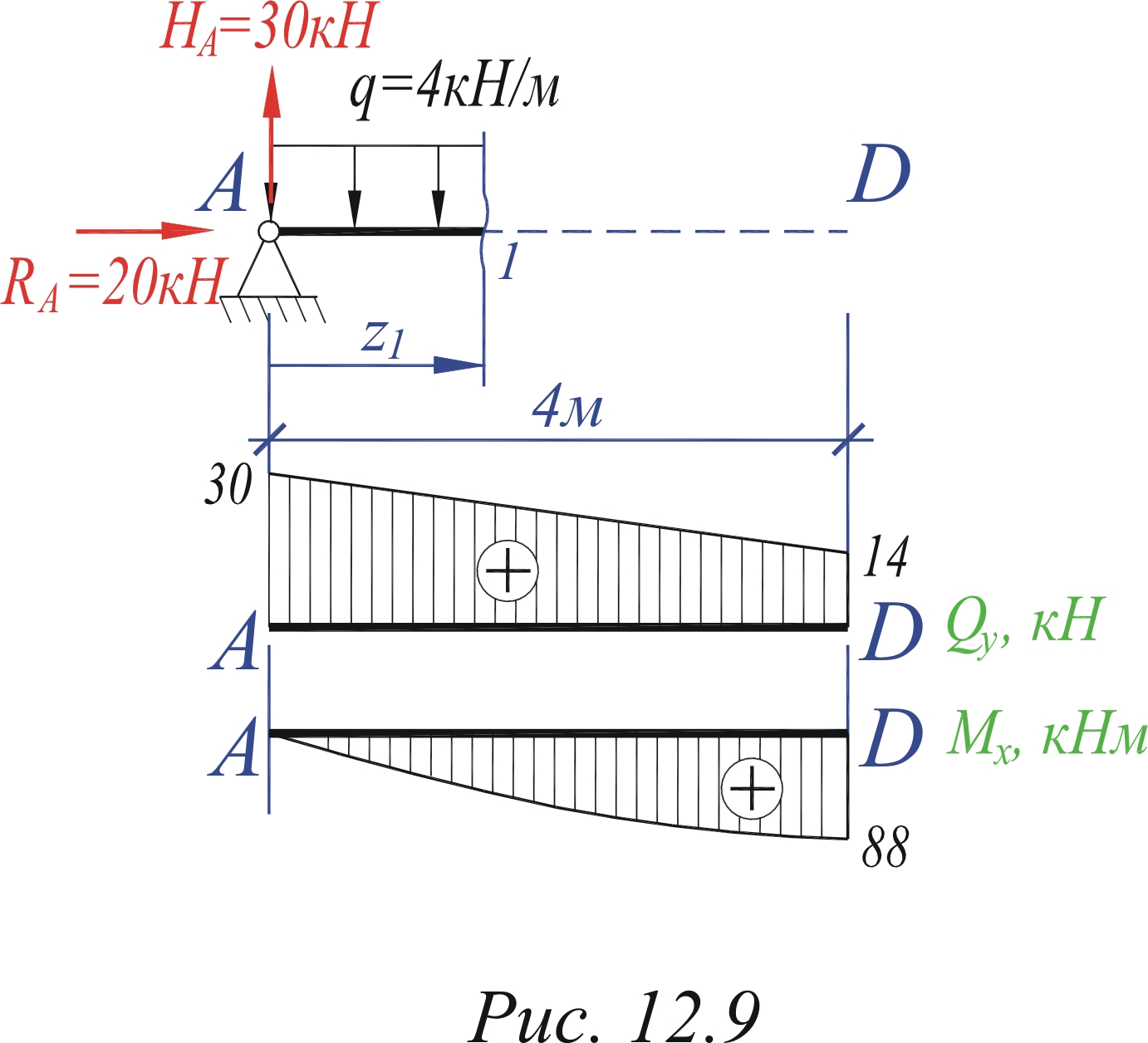
Построим эпюры на
примере рамы на рис. (12.7).
|
Разбиваем C-E.
Рассмотрим Участок Qy=НA Qy(0)=30 Qy(4)=14
Mx(0)=0; Mx(4)=88 Nz= Строим
Рассмотрим Участок Qy=RA
=120 Nz= Эпюру
Рассмотрим Участок Qy=–P
Mx(0) Mx(4)= Nz= Эпюру
Рассмотрим Участок Qy=0. Mx Nz Все |
|
После построения
эпюр выполняют проверку равновесия
узлов (2.4) рамы (2.1). Для
этого из рамы вырезают узел сечениями,
проходящими бесконечно близко к узлу,
и изображают его отдельно с указанием
внутренних усилий в местах рассечения.
Рассмотрим проверку равновесия узла
на примере узла D рамы (рис. 2.14).
Вырезаем данный узел из рамы и прикладываем
внешние нагрузки, оставшиеся на отсеченном
узле. Поскольку сечение проходят
бесконечно близко к узлу, то такие
нагрузки могут быть только узловые
(напомним, что распределенная
сила (1.6) характеризуется длиной
приложения, которая в данном случае
будет бесконечно малой). В узле D на
исходной схеме (12.8) приложена сосредоточенная
сила P, которая очевидно и останется на
отсеченном узле. В местах рассечения
вместо отброшенной части рамы указываем
внутренние усилия. Значения внутренних
усилий в сечениях берем с соответствующих
эпюр (рис. 12.13). Направление усилий
назначаем с учетом знака. Проще всего
рассуждать так: закрепим мысленно
рассматриваемый узел в точке D. Тогда
положительная продольная сила, должна
растягивать
|
стержни, |
|
Узел
D
находится в равновесии. Отметим, что
полученная система сил на рис. 12.14 –
сходящаяся, поэтому в последнем уравнении
данной системы важно проверить равновесие
только моментов
пар сил (2.11)
(сосредоточенных моментов). В этом случае
моментная
точка (2.8)
может быть любой и может вообще не
указываться.
Аналогично проверяем
равновесие узла Е (рис. 2.15).
|
Узел |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение опорных реакций
Способы определения опорных реакций изучаются в курсе теоретической механики. Остановимся только практических вопросах методики вычисления опорных реакций, в частности для шарнирно опертой балки с консолью (рис. 7.4).

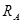
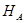
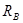
Нахождение и проверка опорных реакций в шарнирной опоре
Для вычисления значений реакций опор составим уравнения статики:
Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: 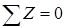
Поскольку на балку действуют только вертикальные нагрузки (перпендикулярные к оси балки), то из этого уравнения находим: горизонтальная реакция неподвижной шарнирной опоры 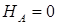
Сумма моментов всех сил относительно опоры А равна нулю: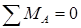
Правило знаков для момента силы: считаем момент силы положительным, если он вращает балку относительно точки против хода часовой стрелки.
Необходимо найти равнодействующую распределенной погонной нагрузки. Распределенная погонная нагрузка равна площади эпюры распределенной нагрузки 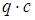
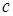
Тогда
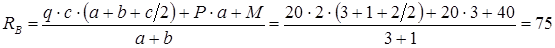
Сумма моментов всех сил относительно опоры B равна нулю: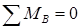
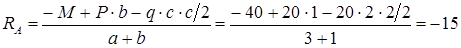
Знак «минус» в результате говорит: предварительное направление опорной реакции 
Проверка опорных реакций
Сумма проекций всех сил на ось y должна быть равна нулю: 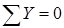
Силы, направление которых совпадает с положительным направлением оси y, проектируются на нее со знаком «плюс»:
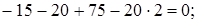
Нахождение опорных реакций в жесткой заделке
Найдем реакции опор в жесткой заделке. Для определения опорных реакций составляются уравнения статики:
Из первого уравнения определяется реакция 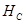
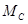
Проверка, как правило, не производится.