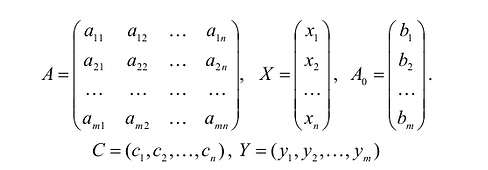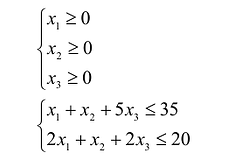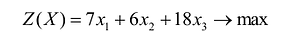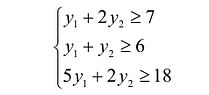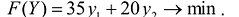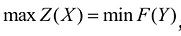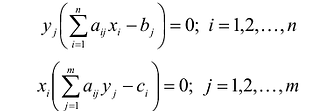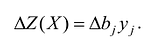его
взаимосвязь с угловыми точками.
Рассмотрим
каноническую задачу ЛП в векторной
записи (см.(2.1.2)):
,
,
(4.4.1)
.
Определение
4.4.1.Опорным решением задачи ЛПназывается такое допустимое решение,
для которого соответствующие положительным
координатамвекторы
,
,…,
в (4.4.1) линейно независимы.
Число
отличных от нуля координат опорного
решения не может быть больше ранга
системы векторов условия (т.е. числа
линейно независимых уравнений системы
ограничений). В дальнейшем будем считать,
что система ограничений состоит из
линейно независимых уравнений, т.е..
Если число отличных от нуля координат
опорного решения равно,
то оно (решение) называется невырожденным,
в противном случае (меньшевырожденным.
Определение
4.4.2.Базисом опорного решения
называется базис системы векторов
условия задачи (4.4.1), в состав которого
входят векторы, соответствующие отличным
от нуля координатам опорного решения.
Приведём
без доказательства две теоремы о
взаимосвязи опорных решений и угловых
точек множества допустимых решений.
Теорема
4.4.1.Любое опорное решение является
угловой точкой области допустимых
решений.
Теорема
4.4.2.Любая угловая точка области
допустимых решений является опорным
решением.
Доказательства
теорем 4.4.1 и 4.4.2 проводятся методом от
противного (см. [3], с.537-539).
5. Симплексный метод решения задач
линейного
программирования
Симплексный метод
– это метод целенаправленного перебора
опорных решений задачи ЛП. Он позволяет
за конечное число шагов либо найти
оптимальное решение, либо установить,
что его не существует. Основное содержание
метода состоит в следующем:
1.
Указать способ нахождения начального
опорного плана.
2.
Указать способ перехода от одного
опорного плана к другому, на котором
значение целевой функции ближе к
оптимальному.
3.
Задать критерии, которые позволяют
своевременно прекратить проверку
решений на оптимальность или сделать
заключение об отсутствии оптимального
решения.
5.1. Нахождение начального опорного плана и переход к новому опорному решению
Предположим,
что необходимо найти минимум целевой
функции
при следующей системе ограничений:

Запишем
систему (5.1.1) в векторной форме:
(5.1.2)





Векторы
,
,..,
образуют базис в
.
Поэтому в соотношении (5.1.2) за базисные
переменные принимаем,
,…,
,
а остальные переменные
(будем
называть их свободными) приравниваем
нулю. Учитывая, что
,
получаем, что опорное решение задачи
(5.1.1) имеет вид
Рассмотрим,
как, исходя из начального опорного
решения, можно построить другое опорное
решение, которое будет более близким к
оптимальному, т.е. на котором значение
целевой функции будет меньше. Систему
ограничений (5.1.1) перепишем в виде:

Выражая
значения
,
,…,
через свободные неизвестные, целевую
функциюполучим в виде:
.
(5.1.4)
Итак,
первоначальный опорный план
,
а соответствующее значение.
Возможны следующие ситуации:
1)
все
,
,
…,.
Тогда минимумдостигается при
,
т.е. планявляется оптимальным и
;
2)
среди чисел
,
,
…,имеются положительные. Пусть
,
гдеодно из чисел
,
,..;,
.
Тогда полагаем все,
,
…,равными нулю, кроме
.
Из (5.1.3) следует, что

и
.
Здесь,
в свою очередь, могут представиться два
случая:
а)
все числа
,
,
…,,
тогда для любоговсе значения
,
,…,
.
В этом случаене достигается, так как при
функция
;
б)
среди чисел
,
,
…,имеются положительные. Пусть, например,
.
Так как все компоненты плана должны
быть положительны, тонельзя увеличивать более, чем
( иначе
станет отрицательным ).
Поэтому
найдём
называется разрешающим элементом.
Положим,…,
,
,
,…,
.
Найдём значения остальных неизвестных:
Получено
новое опорное решение:
.
Значение
целевой функции при этом уменьшается:
.
Идея
симплекс-метода заключается в том, что
на каждом этапе один из векторов
выводится из базиса, а вместо него
вводится другой –.
При этом удобно, чтобы он стал бы
единичным. Поэтому в системе ограничений-е
уравнение, содержащее разрешающий
элемент,
делим на.
Исключаемиз всех остальных уравнений, т.е.
осуществляем преобразование Жордана-Гаусса.
Итак,
алгоритм симплекс-метода состоит в
следующем:
1.
Приводим систему к виду, содержащему
единичных векторов, и определяем
первоначальный опорный план.
2.
Выражаем
через свободные переменные в виде:
.
Если
при этом все коэффициенты
,
,..,
не являются положительными, то найденный
первоначальный план являетсяоптимальным.
3.
Пусть среди чисел
,
,..,
имеются положительные. Берём любой из
них, например,,
и просматриваем весь соответствующий
столбец.
Он называется разрешающим столбцом.
Если все числа этого столбца отрицательны,
тоЗадача решения не имеет.
4.
Если в этом столбце есть положительные
числа, то находим разрешающий
элемент – это элемент, для которого
отношениеминимально. Пусть это элемент
.
5.
Выводим переменную
из числа свободных и меняем её с базисной
переменной.
6.
Эту процедуру выполняем до тех пор, пока
все коэффициенты
при свободных неизвестных станут
неположительными, (это признак
оптимальности
плана) либо неположительными станут
все элементы в разрешающем столбце (
т.е.
).
Замечание.
На практике этот алгоритм реализуется
с помощью симплекс-таблиц (см. пример
5.1.).
Пример
5.1. Строительное управление ведёт
капитальный ремонт жилых домов.
Перегородки внутри этих домов могут
быть изготовлены гипсобетонными или
каркасными ( с обшивкой листами сухой
штукатурки ). Ресурсы на месяц заданы в
таблице:
Потребности
на
площади перегородок
|
Гипсобетон Пиломатериалы Сухая Трудоресурсы |
Каркасные |
Гипсобетонные |
|
―
|
―
|
Рассчитать
общее количество
как каркасных, так и гипсобетонных
перегородок, которые следует возвести
в текущем месяце, чтобы их площадь была
наибольшей, если строительное управление
имеет в наличии гипсобетона –,
пиломатериалов –,
сухой штукатурки –,
трудоресурсов –.
Решение.
Составим математическую модель задачи.
Пусть требуется возвести
каркасных и
гипсобетонных перегородок. Из условия
на это уйдёт: гипсобетона,
пиломатериалов,
сухой штукатурки,
трудоресурсов.
Учитывая лимиты материалов и трудоресурсов,
составляем систему ограничений –
неравенств:
Для
решения задачи симплекс-методом вводим
дополнительные переменные:
Полагаем
.
Принимаем,
в качестве свободных переменных,
,
,
,
в
качестве базисных. Начальный опорный
план имеет вид:,
.
Составляем симплекс-таблицу (в сокращённой
форме), соответствующую начальному
опорному плану. Обратим внимание, что
коэффициенты при свободных переменных
пишутся с противоположным знаком.
|
Выбираем |
столбца:
,
,
.
Элемент
ведущего столбца, для которого отношение
минимально ( в нашем случае 0,25) объявляем
ведущим. Строка, в которой находится
элемент, также называется ведущей и
помечается стрелкой слева.
Теперь
запишем правила перехода к новой
симплекс-таблице, соответствующие
приведённому выше алгоритму симплекс-метода:
1.
Базисная переменная, находящаяся в
ведущей строке, и свободная переменная,
находящаяся в ведущем столбце, меняются
местами.
2.
Ведущий элемент заменяется величиной,
ему обратной.
3.
Все элементы ведущей строки (включая
свободный член), кроме ведущего элемента,
заменяются их отношениями к ведущему
элементу.
4.
Все элементы ведущего столбца (кроме
ведущего элемента) заменяются взятыми
с обратными знаками
их отношениями к ведущему элементу.
5.
Остальные элементы заменяются по
«правилу 4 элементов»: любой такой
элемент умножается на ведущий и из
произведения вычитается произведение
двух других элементов, составляющих с
первыми вершины прямоугольника, после
чего результат делится на ведущий
элемент.
Проводя
вычисление по этим правилам, получаем
следующую симплекс-таблицу:
|
|
Значение |
Аналогично
составляем следующую симплекс-таблицу:
|
И |
||||||||||||||||||||||||
|
Пересчитывая |
,
.
Замечание. При
построении симплекс-таблиц можно
рассуждать иначе. Пусть решаем ЗЛП в
виде
,
В
этом случае общая схема симплекс-методапретерпевает некоторые изменения. А
именно:
1) Пусть дан базис
некоторого опорного решения и
соответствующая ему симплекс-таблица.В верхней строке этой таблицы (заголовки
столбцов) располагаются свободные
переменные, в крайнем левом столбце –
базисные переменные; крайний правый
столбец – это столбец свободных членов,
а самая нижняя строка является строкой
целевой функции и называется вектором
относительных оценок. Остальное
содержимое таблицы – столбцы матрицы
ограничений, отвечающие соответствующим
столбцам свободных переменных. Координаты
вектора относительных оценок (1,2,…n)
находят по правилу: для нахождения
коэффициентаkвектор из коэффициентов при базисных
переменных в целевой функции скалярно
умножить на k-й
столбец симплекс-таблицы и вычесть из
найденного числа коэффициент целевой
функции при соответствующем свободном
переменномxk.
2) Если все
относительные оценки (нижняя строка
этой таблицы) неотрицательны, то построено
оптимальное опорное решение.
3) Если существует
отрицательная оценка и соответствующий
ей столбец (разрешающий) состоит из
неположительных элементов, то имеет
место неразрешимость целевой функции
Z(X),
то естьmaxZ(X)+.
4) Иначе, выбрать
ведущий элемент (задаёт ведущую строку)
и сделать с ним шаг жордановых исключений,
перейдя к новой симплекс-таблице, которую
проанализировать как в пункте 2).
Соседние файлы в папке математика_2
- #
- #

Введение
Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных xj, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения (они также линейные) в форме равенств или неравенств. Требуется найти план Х <n> = <x1, x2, …, xn>, который обеспечивает получение целевой функцией с экстремальным значением. Идеи моделей линейного планирования (программирования) впервые были высказаны и опубликованы советским математиком Л. В. Канторовичем в 1939 году в работе “математические методы организации и планирования производства”. В 1975 году Л. В. Канторович и Т. Купманс получили Нобелевскую премию по экономическим наукам с формулировкой «за их вклад в теорию оптимального распределения ресурсов». В 1947 г. очень близкие идеи высказаны американским математиком Дж. Данцигом. А еще позднее стали массово появляться работы, посвященные проблемам выбора оптимальных решений в силу их исключительной важности. Признание приоритета за Л. В. Канторовичем не оспаривалось практически никогда, а после присуждения Нобелевской премии тем более.
Общая постановка задачи
Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных xj, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения в форме равенств или неравенств. Требуется найти план Х <n> = <x1, x2, …, xn>, который обеспечивает получение целевой функцией экстремального значения
а) Если система ограничений ЗЛП обладает хотя бы одним решением, она называется совместной в противном случае несовместной; б) Допустимое множество решений ЗЛП не пусто, если система ограничений совместна; в) Множество допустимых решений ЗЛП (если оно не пусто) в общем случае является многогранным множеством. Линейная функция Q(X<n>) называется функцией цели, целевой функцией (ЦФ), множество планов {X<n>} удовлетворяющих системе ограничений (2) – (5), - множеством допустимых решений (альтернатив) и обозначается символом R, X<n>є Ω Допустимый план X<n>є Ω, доставляющий целевой функции (1) экстремальное значение, называется оптимальным. Задача в форме (1) – (5) представляет общую задачу линейного программирования.
Cтандартная форма задачи
Если все ограничения задачи заданы в виде строгих равенств и на переменные величины наложено условие неотрицатаельности xj ≥0, j = 1(1)n, то такую формулировку называют стандартной:
Экстремумы функций в общем случае связаны простыми соотношениями
Переход от общей задачи к стандартной
-
Для удобства применения методов решения выполняют преобразование исходной общей задачи. Ограничения неравенства преобразуют в равенства. Вводятся дополнительные переменные по числу неравенств, т. е. формулируют расширенную задачу xn+1 ≥0, xn+2 ≥0, … , xn+k ≥0. Неравенства ai1x1+ai2x2+…+ainxn ≥bi введением переменной xn+1≥0 преобразуются в равенства ai1x1+ai2x2+…+ainxn + ai(n+1)xn+1=bi. В ЦФ вновь введённые переменные имеют коэффициенты равные нулю cn+1=cn+2=…=cn+k =0.
-
а) Если в исходной общей задаче на некоторые переменные xj , j = 1(1)n, не наложено условие их неотрицательности, то каждую такую переменную представляют в виде разности положительных новых переменных x’j – x”j , где x’j≥0 и x”j≥0 , j>r . Способ устранения отрицательных переменных прост, но при этом размерность (число неотрицательных переменных) задачи возрастает. б) Имеется другой более сложный путь. Каждую xj ≯ 0 выражают явно через другие, для которых условие xj ≥0 выполняется. Затем найденные выражения подставляют в ограничения, чтобы исключить их из рассмотрения. При этом размерность задачи даже уменьшается.
Каноническая форма задачи
Удобство этой формы ЗЛП состоит в том, что она позволяет предельно просто получить первое допустимое решение. Для этой формы должны быть выполнены условия:
-
правые части в ограничениях – неотрицательны bi ≥ 0, i = 1(1)m;
-
каждое уравнение содержит переменную xj ≥0 с коэффициентом при ней равным “1” в этом уравнении и с коэффициентом “0” во всех других уравнениях; эти переменные называют дополнительными или искусственными;
-
в ЦФ эти переменные входят с коэффициентом “0”;
-
определение опорного плана (начальной вершины) выполняют методом искусственного базиса, что ещё до решения задачи позволяет выяснить факт существования решения.
Если исходная задача имеет хотя бы один план, то расширенная задача (после введения искусственных переменных в систему ограничений) также содержит этот план в качестве своего допустимого решения
Переменные x1, x2, …, xm называют базисными – остальные свободными (внебазисными). Вершина допустимой области решений записывается в виде точки <β1, β2, …, βm, 0, 0,…,0>, так как векторы условий для x1, x2, …, xm являются линейно независимыми (образуют подматрицу, где единицы помещаются только на главной диагонали).
Геометрическая интерпретация ЗЛП
Будем рассматривать пример ЗЛП в производстве двух видов продукции на предприятии, использующем при этом четыре виды сырья (см. ранее эту задачу). Этот пример удобен для геометрической интерпретации тем, что пространство решений является двумерным (т. е. плоскость) и все элементы ЗЛП допускают наглядное представление (изображение) в трёхмерном пространстве. Начнём с рассмотрения системы неравенств (ограничений ЗЛП). Заметим, что каждое i-е неравенство в ограничениях ЗЛП определяет полуплоскость в системе координат х1Ох2 с граничной прямой ai1x1 + ai2x2 = bi , i = 1(1)m.
Выпишем их и присвоим им имена
Область, формируемая полуплоскостями, может быть получена в виде замкнутого или разомкнутого (неограниченного) многогранника. Путём непосредственного построения границ (прямых) и выявления области пересечения полупространств выясним, является ли многогранное множество ограниченным и не пусто ли оно (рис.). Имеем на плоскости х1 О х2 многоугольник А Ո В Ո C Ո D Ո E Ո F . Он является выпуклым (всегда ли?), его граница образована отрезками прямых.
Целевая функция. Что можно сказать о линейной форме (ЦФ)? Это функция двух переменных x1 и x2, её образ в трёхмерном пространстве – плоскость, проходящая через начало координат. Найдём частные производные ЦФ по хj
Так как частная производная по переменной хj представляет наибольшую скорость изменения функции Q в направлении этой оси, то вектор C<n>= <c1, c2> – это вектор наибольшего изменения ЦФ, вектор градиентного направления. Если значения Q зафиксировать Q =Q1 = const , то уравнение ЦФ превращается в уравнение прямой c1x1 + c2x2= Q1= const плоскости х1О х2
В трёхмерном пространстве это плоскость параллельная х1О х2 на высоте Q1, в каждой точке <x1, x2, Q1> которой значение ЦФ постоянно и равно Q1. . На плоскости Q этой прямой соответствует линия параллельная плоскости х1О х2, которую называют линией уровня (плотницкий уровень) функции c1x1 + c2x2 . Изменяя Q, получим семейство линий уровня параллельных друг другу. Требованию задачи – поиску экстремума Q соответствует смещение точки по поверхности функции Q в направлении вектора C<n>= <c1, c2> от начала координат.
Ограничения ЗЛП не позволяют аргументам ЦФ Q(x1, x2) выходить за пределы многоугольной допустимой области. Другими словами, надо найти точку на плоскости Q наиболее удалённую от плоскости х1О х2 и проекция которой на х1О х2 лежит в области допустимых решений. Координаты x*1, x*2 найденной точки и определяют оптимальный план ЗЛП. Покажем, что семейство линий уровня (изолиний) перпендикулярно C<n>, т. е. перпендикулярно прямой х2 =с2х1/c1. Из векторного анализа известно, что все линии уровня ЦФ Q перпендикулярны вектору градиенту ЦФ, вычисленному в некоторой точке
Таким образом, перемещаясь вдоль вектора C<n> или по прямой х2 =с2х1/c1, легко построить линию уровня (она перпендикулярна х2 = с2х1/c1 ) и вычислить значение ЦФ Q для этой линии. Экстремум Q, очевидно, будет достигаться в положении касания линией уровня (её проекцией) границы множества допустимых решений. Такое касание может быть трёх типов: в вершине, по ребру, по грани многогранника. Этим типам касания соответствуют: единственное решение в вершине и бесконечное множество решений в других случаях. Область допустимых решений. Рассмотрим случаи ограниченной и неограниченной области допустимых решений. В последнем случае поиск экстремума Q может приводить к отсутствию решения, так как extr Q → ±∞ или существует опорная прямая линия, касающаяся неограниченного многогранника, и тогда решение существует.
Пример. Описание области допустимых решений.
Мы можем записать уравнение границы области D заданной неравенствами:
Основные понятия и теоремы линейной алгебры Важным понятием линейной алгебры является понятие линейного векторного пространства. Определение 2.1. Упорядоченная совокупность n действительных чисел называется n-мерным вектором. Определение 2.2. Совокупность всевозможных n-мерных векторов после введения в нее операций сложения и умножения на действительное число называется n-мерным линейным векторным пространством. Частными случаями линейных пространств являются прямая, плоскость, трехмерное пространство. Определение 2.3. Система векторов X1, X2, …, Xn называется линейно зависимой, если существуют такие числа λ1, λ2, …, λn, не равные нулю одновременно, при которых имеет место равенство: λ1X1+ λ2X2 …+ λn Xn=0 , где все λi ≥0 и λ1+ λ2+ …+ λn =1. Если же это равенство возможно лишь в случае, когда все λi = 0 (i = 1(1)n) , то система векторов называется линейно независимой. Определение 2.4. Базисом n-мерного векторного пространства называется любая совокупность n линейно независимых векторов этого пространства. В двумерном пространстве за базис могут быть взяты любые два неколлинеарных вектора, в частности, е1 = (1,0), е2 = (0, 1). В трехмерном пространстве – любые три некомпланарных вектора, например, е1 = (1,0,0), е2 = (0,1,0), е3 = (0,0,1).
Выпуклой линейной комбинацией точек X1, X2, …, Xn называется линейная комбинация вида: X= λ1X1+ λ2X2 …+ λn Xn где все λi ≥0 и λ1+ λ2+ …+ λn =1. В частности, когда имеются две точки X1 и X2, то их выпуклая комбинация λX1+(1- λ)X2, λ ∈[0,1] представляет собой точку на отрезке, соединяющем эти точки.
Теорема 1. Любой вектор n-мерного векторного пространства можно представить, как линейную комбинацию векторов базиса, притом единственным образом. Определение 2.5. Максимальное число линейно независимых векторов линейного пространства называется размерностью линейного пространства. Линейное пространство обычно обозначают, Rn где n – его размерность. Выпуклой оболочкой точек называется множество всевозможных выпуклых комбинаций этих точек. Множество называется выпуклым, если вместе с двумя любыми его точками оно содержит и их произвольную выпуклую линейную комбинацию. С геометрической точки зрения это означает, что выпуклое множество содержит вместе с любыми двумя своими точками и соединяющий их отрезок. Выпуклое множество совпадает со своей выпуклой оболочкой. Примерами выпуклых множеств являются прямолинейный отрезок, квадрат, круг, прямая, полуплоскость, куб, шар, полупространство и другие. Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, угловыми точками круга – точки окружности. Таким образом, выпуклое множество может иметь конечное или бесконечное число угловых точек, но может не иметь их совсем. Например, прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют. Одним из основных понятий теории линейного программирования является понятие выпуклого многогранника в n-мерном пространстве, частными случаями которого являются при n = 1 отрезок на прямой, при n = 2 выпуклый многоугольник на плоскости. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество точек на плоскости, имеющее конечное число угловых точек, называемых вершинами. Прямолинейные отрезки, соединяющие две вершины и образующие границу, называются сторонами многоугольника.
Опорной прямой выпуклого многоугольника называется прямая, имеющая с многоугольником, расположенным по одну сторону от нее, хотя бы одну общую точку.
Выпуклым многогранником называется выпуклое замкнутое ограниченное множество точек пространства, имеющее конечное число угловых точек, называемых его вершинами. Многоугольники, ограничивающие многогранник, называются его гранями, а отрезки, по которым пересекаются грани, называются ребрами. Опорной плоскостью многогранника называется плоскость, имеющая с многогранником, расположенным по одну сторону от нее, хотя бы одну общую точку.
Теорема 2.2. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек.
Следствие 2.3. Из теоремы вытекает, что выпуклый многогранник порождается своими угловыми точками (вершинами): отрезок – двумя точками, треугольник – тремя точками, n – угольник на плоскости – n точками и т. д. В тоже время выпуклая многогранная область, содержащая бесконечно удаленную точку, являясь неограниченным множеством, не определяется однозначно своими угловыми точками: любую ее точку нельзя представить в виде выпуклой линейной комбинации угловых точек.
Элементы выпуклых множеств
Определение 1. Множеством называется совокупность элементов любой природы, для которых задано правило принадлежности к данному множеству.
Определение 2. е – о к р е с т н о с т ь ю точки х называется множество всех точек, расстояние которых до точки х меньше е.
Определение 3. Точка х1 называется внутренней точкой множества M, если существует такая – окрестность данной точки, все точки которой принадлежат множеству M.
Определение 4. Точка х2 называется в н е ш н е й т о ч к о й м н о ж е с т в а M, если существует такая – окрестность данной точки, все точки которой не принадлежат множеству М.
Определение 5. Точка х3 называется г р а н и ч н о й т о ч к о й м н о ж е с т в а M, если в любой её – окрестности существуют точки как принадлежащие множеству M, так и не принадлежащие этому множеству.
Определение 6. Множество М называется з а м к н у т ы м, если оно содержит все свои граничные точки. х 2– незамкнутое множество, Пример. х 2 – замкнутое множество.
Определение 7. Множество М называется в ы п у к л ы м, если вместе с любыми двумя точками, принадлежащими данному множеству, оно содержит и отрезок их соединяющий. В общей форме ЗЛП каждый символ R1, R2, …, Rm означает один из знаков: = или ≠. В такой форме задачи линейного программирования часть переменных может быть подчинена условию неотрицательности (xi ≥ 0), часть – условию неположительности (xj ≤ 0), а какие-то переменные, возможно, могут принимать любые значения.
Общий алгоритм симплексного метода ЗЛП
Решается задача
Пусть система невырожденна и совместна, т.е. rA = rB = r = m<n – ранг.
Выделим m = r базисных переменных x1, x2, …, xm , ф = 1(1)m и k = n – m свободных переменных xm+1, xm+2, …, xn , j = m + 1(1)n ; ЦФ и базисные переменные выразим через свободные
Все введённые переменные в новых обозначениях удобно свести в таблицу, которая называется симплексной.
Алгоритм решения
1) Формируем исходный план при свободных переменных; xj =0, j = m+1(1)n, xj = βф, ф = 1(1)m при βф > 0 план xo<n> допустим Q(x) =xo.
2) Проверяем этот план на оптимальность, используя значения γj коэффициентов ЦФ в последней строке таблицы. Могут быть два случая:
а) все γj ≤0, j = m+1(1)n , при этом увеличение никакой переменной (из свободных) не приведёт к уменьшению ЦФ Q, т. е. план xo<n> улучшить нельзя, и он уже оптимален, таким образом, условием оптимальности плана является – отсутствие в таблице γj >0.
б) некоторые γj > 0. В этом случае увеличение значений соответствующих свободных переменных xj (γj > 0) будет минимизировать Q, так как
Чтобы Q уменьшалось, такие переменные следует вводить (последовательно) в базис, но, чтобы размерность пространства не изменялась из базиса должны выводиться переменные в число свободных (по одной) формируем множество индексов Г = { j | γj >0}. Какая переменная должна первой вводиться в базис? Вообще последовательно перебирая (вершины симплекса) решение отыскивается при произвольном выборе, но для определённости выбираем новую базисную переменную с индексом v = argmax {xj}, где j ∈ Г. Теперь определим переменную (базисную), которая будет выводиться из базиса.
В системе уравнений
Начинаем увеличивать хv до тех пор, пока некоторый хф станет отрицательным. Первый же хф ≤ 0 будет выводиться из базиса. Определение. Столбец с индексом v и строка с индексом ф = i называются направляющими.
3) Проверка существования решения (ограниченность ЗЛП). В выражениях, связывающих х, ∝, β, хф = βф -∝фvхv, ф=1(1)m, могут быть все ∝фv < 0 и тогда рост хv будет неограниченно увеличивать все хф, т.е. ни одно отрицательное значение не будет принимать. Это случай, когда ЦФ Q не ограничена снизу и, следовательно, ЗЛП не имеет оптимального решения.
Признаком неограниченности ЦФ является отсутствие в направляющем v– м столбце значений ∝фv > 0. Пусть ЦФ ограничена и некоторые ∝фv > 0. Сформируем множество индексов S = { ф | ∝фv >0}. Из базиса необходимо выводить переменную с индексом i, так как она первая обращается в нуль, i = argmin(βф/∝фv), где ф∈S, таким образом, базисная переменная xi выводится из базиса.
Определение. Коэффициент ∝фv=∝iv , стоящий на пересечении направляющих строки и столбца называется направляющим (разрешающим, генеральным) элементом таблицы.
4) Формируем новые множества:
Дальнейшие действия алгоритма:
-
преобразуем задачу, т.е. все базисные переменные и целевую функцию выражаем через свободные переменные;
-
заполняем новую симплексную таблицу;
-
делаем все свободные переменные хj = 0 и находим опорный план;
Опорный план (вектор) такой Х’<n>=< β1,β2,…,βv,,…,βm, 0, 0…,0>; Q(Х’<n>) ≤ Q0 ;
-
если план не оптимален, то определяем направляющий столбец;
-
проверяем существует ли оптимальный план;
-
если оптимальный план существует, то находим направляющую строку и вновь изменяем базис и т. д.
-
Переход от одной таблицы к другой связан с трудоемкими расчетами (о чем надо еще написать) Вводимую в базис переменную хν (икс ню) выражаем через свободные переменные и выводимую хi. Действуем так.
При ручном счете все эти действия проще выполнять с использованием вспомогательных таблиц по правилам специального алгоритма. Эти таблицы имеют прежнюю структуру, но клетки делятся на две полуклетки. В верхней полуклетке оставляем содержимое из прежней таблицы.
При решении задач линейного программирования вычисляются ранги у матрицы ограничений и расширенной матрицы ранги должны быть равны r=m.
Матрица и её ранг. Система mn чисел, расположенных в форме прямоугольной таблицы из m строк и n столбцов, называется матрицей.
Определение. Рангом матрицы [A] называется наибольший порядок, который могут иметь её миноры, не обращающиеся в нуль. Для определения ранга матрицы следует рассмотреть все её миноры порядка р (где р – меньшее из чисел m, n, если m ≠ n или р = m = n); если хотя бы один из них ≠ 0, то ранг [A] равен р; если же все они равны (= 0), то следует рассмотреть все миноры порядка р – 1 и т. д. Практически поступают наоборот: переходят от миноров меньшего порядка к минорам большего порядка, в соответствии со следующим правилом. Если найден минор k-го порядка Dk, отличный от нуля, то остается вычислить только те миноры (k + 1) -го порядка, которые представляют собой «окаймление» Dk, например,
Определение. Минором k-го порядка матрицы [A] (k ≤ m, k ≤ n) называется определитель D, составленный (с сохранением порядка) из k2 элементов матрицы, лежащих на пересечении некоторых её k столбцов и k строк См. схему выше минор D из 3-х строк и 3-х столбцов. Обозначается матрица символами:
Приведем пример вычисления ранга матрицы.
С выполнением каждого шага связаны процедуры:
1. Получение опорного плана; 2. устанавливается, является ли данный опорный план оптимальным; 3. если нет, то существует ли оптимальный план вообще, или задача является неограниченной; 4. если оптимальный план существует, то, как перейти на следующем шаге, к новому опорному плану с меньшим значением ЦФ.
Алгоритм СМ применяется к ЗЛП после её приведения к канонической форме, т.е. отыскивается минимум целевой функции min Q(X) на множестве векторов Х<n>.
Система ограничений совместна rA = rB и detA ≠ 0 невырожденная, т.е. ранг r =m матрицы A[m, n] и расширенной матрицы системы равен m. Имеется множество решений. Для решения системы произвольным (n – m) переменным могут быть приданы любые, в частности, нулевые значения. Эти переменные называются свободными. Обычно их индексируют xe, e =(m+1)(1)n. Остальные переменные (их называют базисными), однозначно определяются из решения системы
(здесь xe, e =(m+1)(1)n). Матрица этой системы неособенная и, следовательно, система имеет единственное решение xj , j =1(1)m.
Исходный опорный план ЗЛП – вектор, содержащий значения всех переменных задачи как базисных, так и свободных, т.е. этот вектор Х<n>, удовлетворяет ограничениям, но не обеспечивает, как правило, экстремума ЦФ. Общее число опорных планов очевидно равно числу сочетаний из n по m. Оптимальный план можно выявить, перебрав их все. Такой путь громоздок и неприемлем уже при n, m ≈ 10 ÷15.
Алгоритм СМ тоже перебирает опорные планы, но не все, а направленно, т.е. на каждом шаге ЦФ уменьшается. Число шагов имеет тот же порядок, что и число уравнений в ограничениях.
Приведем пояснения некоторым понятиям и терминам, широко используемым в алгоритме решения задач линейного программирования симплексным методом и тесно связанными с ним методами.
Определение. Системой линейных уравнений называют систему следующего вида. Ранг матрицы определяется через миноры r = – 5.
Решение системы уравнений. Решаем относительно переменных x и y, полагаем z = 1. Получаем единственное решение х = –2/5, y = 3/5, z =1. Все другие решения получаются из этого линейно-независимого фундаментального решения: х = –2k/5; y = 3k/5; z = k или х = 2k , y = 3k, z = 5k. Подобные системы возникают при описании ограничений ЗЛП. Существенную роль при решении ЗЛП играют определители подобных систем (Δ = 0, Δ ≠ 0). При однородной системе определитель должен быть равен нулю.
Определение. Симплекс – выпуклый многоугольник в n-мерном пространстве с n + 1 вершинами, не лежащими в одной гиперплоскости. Симплексы выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости. Другими словами, симплекс – это простейший многоугольник, содержащий некоторый объем n-мерного пространства. В обычном (трехмерном) пространстве симплекс – это тетраэдр; трехмерный объем совпадает с объемом тела. На плоскости симплекс – это треугольник, двумерный объем – площадь; на прямой – симплекс – отрезок, объем – длина отрезка.
Определение. Гиперпространство, гиперплоскость. Гиперпространство многомерного (n-мерного) пространства – это его подпространство размерности (n – 1). Главное свойство гиперпространства – то, что оно «самое большое» подпространство. Иначе говоря, если к базису выбранного гиперпространства добавить еще один линейно независимый вектор, то можно получить базис всего пространства.
Например, для трехмерного пространства гиперпространством является плоскость (любая), проходящая через начало координат. Для двумерного пространства – гиперпространство – это прямая линия, проходящая через нуль.
Гиперплоскость в n-мерном пространстве обобщает наши представления о роли прямой на плоскости и плоскости в пространстве. Например, в n-мерном пространстве через любые n точек можно провести единственную гиперплоскость (как в трехмерном через три точки общего положения, т.е. не лежащие на одной прямой).
Гиперплоскость определяется линейной формой: а1х1 + а2х2 + … + аnxn = k, где коэффициенты (а1, а2, …, аn) представляют собой координаты вектора А.
Гиперплоскость делит пространство (соответствующей размерности) на два полупространства. Все точки каждого из них определяются неравенствами. Например, в случае прямой линии на плоскости: а1х1 + а2х2 ≥Z, или а1х1 + а2х2 >Z , а1х1 + а2х2 <Z а1х1 + а2х2 ≤Z. Эти два варианта различаются тем, к какой полуплоскости мы относим разделяющую прямую.
Литература
-
Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
-
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
-
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
-
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
-
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
-
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
-
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.
Содержание:
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.
Построение математической модели экономической задачи включает следующие этапы:
- выбор переменных задачи;
- составление системы ограничений;
- выбор целевой функции.
Переменными задачи называются величины
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 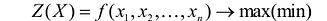
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (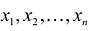
Допустимым решением (планом) задачи линейного программирования называется любойX = (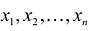
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
Используя знак суммирования эту задачу можно записать следующим образом:
Каноническая задача линейного программирования в векторной форме имеет вид:
В данном случае введены векторы:
Здесь С – X – скалярное произведение векторов С и X.
Каноническая задача линейного программирования в матричной форме записи имеет вид:
где:
Здесь А – матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 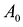
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:
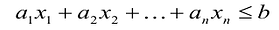
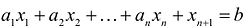
Неотрицательная переменная 
Основания для возможности такого преобразования дает следующая теорема.
Теорема. Каждому решению 
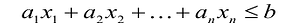
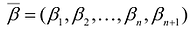
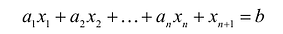
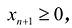

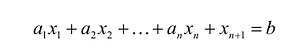

Доказательство. Пусть 
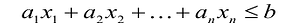
Если в уравнение 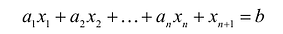
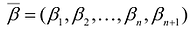
Таким образом, решение 
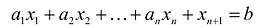

Доказана первая часть теоремы.
Пусть 
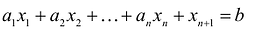

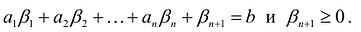
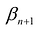
т.е. 
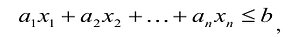
Если в левую часть неравенств системы ограничений вида
добавить переменную 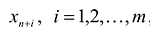
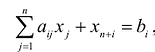
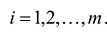
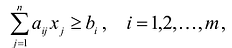
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 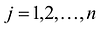
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 
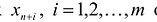
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
Множества допустимых решений
Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.
Выпуклой линейной комбинацией произвольных точек 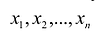
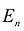
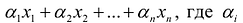
Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.
Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.
Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.
Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.
Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.
Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.
Так, угловые точки треугольника – его вершины, круга – точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.
Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.
Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.
Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.
Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.
Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.
Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.
Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 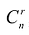
Опорным решением задачи линейного программирования называется такое допустимое решение 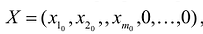
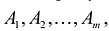
Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример:
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.
Построим математическую модель задачи, для чего обозначим 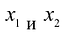
Тогда прибыль предприятия от реализации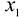
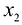
Ограничения по ресурсам будут иметь вид:
Естественно, объемы производства должны быть неотрицательными
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 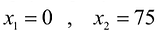
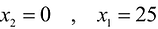
Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
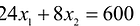
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 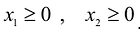
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции
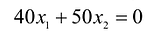
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
Решив эту систему, получаем, что
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
Алгоритм решения задачи линейного программирования графическим методом таков:
- Строится область допустимых решений;
- Строится вектор нормали к линии уровня с точкой приложении в начале координат;
- Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
- Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
- Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
- Множество всех планов задачи линейного программирования выпукло.
- Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
- Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
- Заказать решение задач по высшей математике
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
- если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
- если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 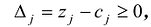
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 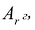
Строка 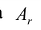
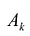
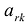
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
а элементы любой другой i-й строки пересчитываются по формулам:
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы 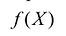
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
Переменные двойственной задачи 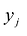
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум – вид
- Матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, в двойственной задаче получаются друг из друга транспонированием;
- Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;
- Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;
- Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.
где:
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья 
При исследовании первой возможности (наладить выпуск товаров 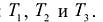
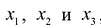
Прибыль, которую получит предприятие от реализации товара, составит:
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи 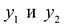
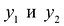
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 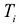
Это требование можно представить в виде системы неравенств:
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара 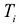
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины
Теоремы двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.
Возможны следующие случаи:
- обе задачи из пары двойственных имеют оптимальные решения;
- одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:
- В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
- В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
- В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
- Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственностн (теорема о дополняющей нежесткости):
Пусть 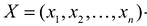
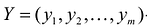
Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Теорема об оценках:
Значения переменных 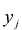
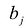
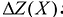
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 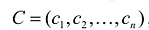
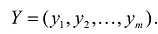
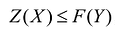
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R”
- Неопределённый интеграл
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
Каноническая задача линейного программирования в векторной форме имеет вид:
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное , где
– число неизвестных,
– ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
Опорным решением задачи линейного программирования называется такое допустимое решение , для которого векторы условий, соответствующие положительным координатам
, линейно независимы.
Число отличных от нуля координат опорного решения не может превосходить ранга Системы векторов условий (т. е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно , то такое решение называется Невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше
, такое решение называется Вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример.
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при
= 2.
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Решение:
|
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн. руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль. |
Построим математическую модель задачи, для чего обозначим и
– объемы производства изделий А и В соответственно.
Тогда прибыль предприятия от реализации изделий А и
изделий В составит:
.
Ограничения по ресурсам будут иметь вид:
Естественно, объемы производства должны быть неотрицательными .
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: при , а при
. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку
и, подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка
лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
. На рис. 14.1 расположение полуплоскости относительно первой прямой отмечено стрелками.
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям , находятся в первом квадранте.
Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник .
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т. е. многовариантна. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор–градиент прямой функции имеет координаты
.
 |
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
Решив эту систему, получаем, что .
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
(млн. руб.).
Алгоритм решения задачи линейного программирования графическим методом таков:
1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой приложении в начале координат;
3. Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т. к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж. Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
· Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
· Множество всех планов задачи линейного программирования выпукло.
· Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
· Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью . В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые Т Векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: .
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т. д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
, где

То можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
1. Если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
2. Если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие , то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор , давший минимальную отрицательную величину симплекс-разности:
.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Г, Который дает минимальное положительное отношение:

,
.
Строка Называется Направляющей, Столбец
и элемент
— Направляющими (последний называют также Разрешающим Элементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

А элементы любой другой -й Строки пересчитываются по формулам:

,
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

;

для
.
Если наименьшее значение достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс-метода к минимизации линейной формы следует искать максимум функции
, затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М–Задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М–Задачи содержит искусственные векторы или М–Задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
| < Предыдущая | Следующая > |
|---|
Решение задачи линейного программирования. Симплекс метод
Задача линейного программирования (ЗЛП) − это задача нахождения наибольшего (или наименьшего) значения линейной функции на выпуклом многогранном множестве.
Симплекс метод − это метод решения задачи линейного программирования. Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи.
Рассмотрим следующую задачу линейного программирования в канонической форме:
 |
(1) |
 |
(2) |
 |
(3) |
где A-mxn-матрица, rank(A)=m, b− неотрицательный вектор столбец длины m (b∈ Rm, b≥0), c − вектор строка длины n (c∈Rn), x − вектор столбец длины n (x∈Rn).
Определение 1. Допустимым планом или планом задачи линейного программирования (1)−(3) называется вектор 
Определение 2. Опорным планом задачи линейного программирования (1)−(3) называется план 
Из определения 2 следует, что понятие опорный план совпадает с понятием вершины выпуклого многогранного множества, определяемого условиями (2)−(3).
Определение 3. Опорный план задачи линейного программирования (1)−(3) называется невырожденным , если число его положительных компонент в точности равен m.
Определение 4. Задача линейного программирования называется невырожденным , если все ее опорные планы невырождены.
Определение 5. Целевой функцией задачи линейного программирования (1)−(3) называется линейная функция cx, которую нужно максимизировать (в данном случае) на заданном выпуклом многогранном множестве (2)−(3).
Определение 6. Оптимальное решение или оптимальный план − это допустимый план, при котором целевая функция достигает своего максимума (в данном случае) на заданном выпуклом многогранном множестве (2)−(3).
Суть симплекс метода заключается в переходе от одного опорного плана к другому, до достижения оптимального плана или выяснения неразрешимости задачи. Неразрешимость задачи фиксируется, если допустимая область пуста или целевая функция неограничена сверху при максимизации целевой функции, или неограничена снизу, при минимизации целевой функции.
Симплекс метод включает в себя два этапа. Первый этап − нахождение начального допустимого плана. Второй этап − нахождение оптимального плана путем постепенного улучшения допустимого плана задачи.
Начнем рассмотрение метода со второго этапа. Мы будем предполагать, что ЗЛП невырождена (Определение 4).
Симплекс метод
Рассмотрим следующую задачу линейного программирования
где
Очевидно, что 
Запишем ЗЛП (4)-(6) в векторном виде:
 |
(4′) |
 |
(5′) |
 |
(6′) |
где E−единичная матрица порядка m×m,
 |
Разделим x на базисные и свободные компоненты (базисные компоненты − это положительные компоненты вектора, а свободные компоненты − это нулевые компоненты):
 |
(7) |
где
Тогда (5′) можно записать так:
или
 . . |
(9) |
Отсюда
 |
(10) |
Представим c в виде объединения базисных и свободных компонент:
 , , |
(11) |
где
Тогда, учитывая (7), (10) и (11), получим
Обозначим
 . . |
(12′) |
Тогда (12) можно записать так:
 . . |
(12”) |
В выражении (12) ничего не изменится, если к правой части добавить нулевой элемент:
где 
Обозначим
 . . |
(14) |
Выражение (14) эквивалентно следующему выражению:
 |
(14′) |
или
Тогда (13) можно записать так:
или
Заметим, что первые m элементы вектора Δ и последние n−m элементы вектора x нулевые (

Посмотрев на выражение (16), замечаем, что если среди элементов 


Учитывая (7′) перезапишем (5) следующим образом:
 |
(17) |
где 
Постепенно увеличивая из нуля 






Другими словами нужно решить систему линейных неравенств
 |
(18) |
Из (18) следует
Тогда
Подставляя 
 . . |
(20) |
Тогда при 
 |
а при 
 . . |
Из вышеизложенного можно сформулировать следующие теоремы:
Теорема 1 (признак оптимальности опорного плана). Опорный план 

Теорема 2. Если 

Теорема 3. Если опорный план x задачи (4)-(6) не вырожден и 

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность и вычислительный процесс удобнее вести, если первоначальные данные, полученные после определения исходного опорного плана записать в так называемой симплекс таблице.
В таблице 1, в первом столбце записвыаются базисные элементы текущего опорного плана. Во втором столбце записываются элементы правой части ограничений. С правой стороны второго столбца записываются элементы матрицы A. В нижней части таблицы записываются соответствующие элементы вектора Δ, а 
Далее рассматривают элементы 

Пусть 

Пусть среди 

Тогда из базиса выходит k-я переменная, а в базис входит p– я переменная, значение которой равно 
Далее делают исключение Гаусса для столбца p выбирая в качестве ведущего элемента 



Здесь
 , , |
 , , |
 , , |
 . . |
Теперь рассматривают элементы 

Для решения задач линейного программирования онлайн, пользуйтесь калькулятором симплекс метод онлайн.
Метод искусственного базиса
Как было паказано выше, для задачи, записанной в канонической форме, если среди векторов столбцов матрицы A есть m единичных и линейно независимых, можно непосредственно указать опорный план. Однако для многих задач линейного программирования, записанных в канонической форме и имеющих опорные планы, среди векторов столбцов матрицы A не всегда есть m единичных и линейно независимых. Рассмотрим такую задачу:
Пусть требуется найти максимум функции
 |
(21) |
при условиях
 |
(22) |
 |
(23) |
где 
 |
нет mединичных и линейно независимых.
Определение 7. Задача, состоящая в определении максимального значения функции
при условиях
где M − некоторое достаточно больное положительное число (конкретное значение обычно не задается), называется расширенной задачей по отношению к (21)−(23).
Расширенная задача (24)−(26) имеет опорный план
 , , |
(27) |
где первы n элементы нули. Переменные 
образуют так называемый искусственный базис m-мерного векторного пространства.
Так как расширенная задача имеет опорный план, то ее решение можно найти симплекс методом.
Теорема 4. Если в оптимальном плане 


Таким образом, если в найденном оптимальном плане расширенной задачи, значения искусственных переменных равны нулю, то получен оптимальный план исходной задачи. Остановимся более подробно на нахождении решения расширенной задачи.
Значение целевой функции при опорном плане (27):
Значения 
Замечаем, что F(X) и
После вычисления F(X) и
При переходе от одного опорного плана к другому, в базис вводят вектор, соответствующий наибольшему по абсолютной величине отрицательному числу (m+2) строки. Искусственный вектор, исключенный из базиса не имеет смысла вновь ввести в базис. При переходе к другому опорному плану, может случится так, что ни один из искусственных векторов из базиса не будет исключен. Пересчет симплекс таблицы при переходе от одного опорного плана к другому производят по обычным правилам симплекс метода (смотри выше).
Итерационный процесс ведут по m+2 строке до тех пор, пока элементы m+2 строки, соответствующие переменным 
Если же не все искусственные переменные исключены из базиса и элемент m+2 строки, столбца x0 отрицателен, то исходная задача не имеет решения.
Если же не все искусственные переменные исключены из базиса и элемент m+2 строки, столбца x0 равен нулю, то опорный план исходной задачи является вырожденным и базис содержит минимум один из векторов искусственного базиса.
Если исходная задача содержит несколько единичных векторов, то их следует включить в искусственный базис.
Если в ходе итераций m+2 строка больше не содержит отрицательных элементов, то итерационный процесс продолжают с m+1 строкой, до тех пор, пока не найден оптимальный план расширенной задачи или не выявлен неразрешимость задачи.
Таким образом, процесс нахождения решения задачи линейного программирования (21)−(23) методом искусственного базиса включает следующие основные этапы:
- Составляют расширенную задачу (24)−(26).
- Находят опорный план расширенной задачи.
- Используя симплекс метод исключают искусственные векторы из базиса. В результате находят опорный план исходной задачи или фиксируют ее неразрешимость.
- Используя найденный опорный план ЗЛП (21)−(23), или находят оптимальный план исходной задачи, или устанавливают ее неразрешимость.
Для решения задач линейного программирования онлайн, пользуйтесь калькулятором симплекс метод онлайн.





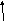




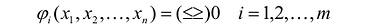
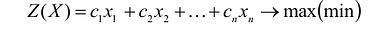
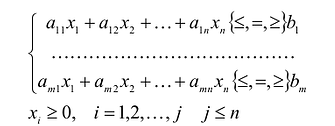
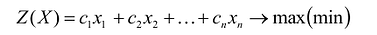
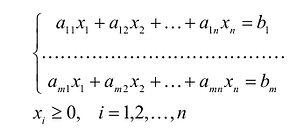
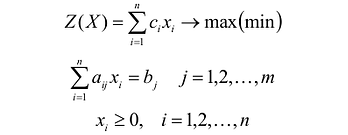
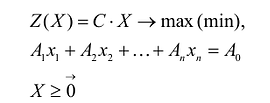
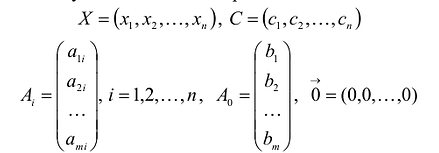
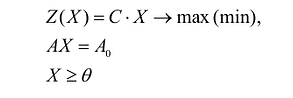
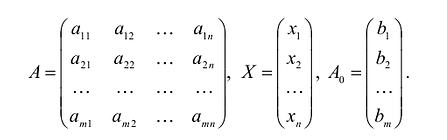
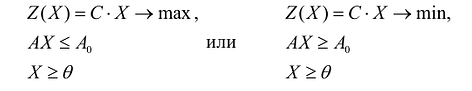
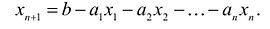
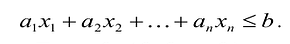
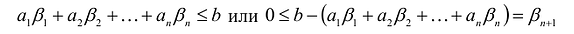
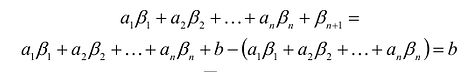
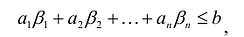
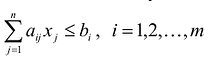
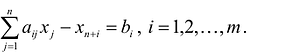
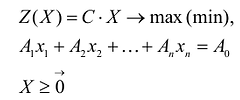
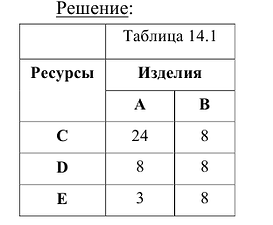
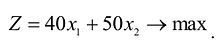
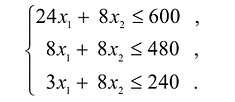
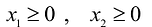
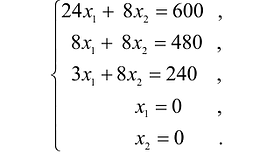
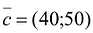
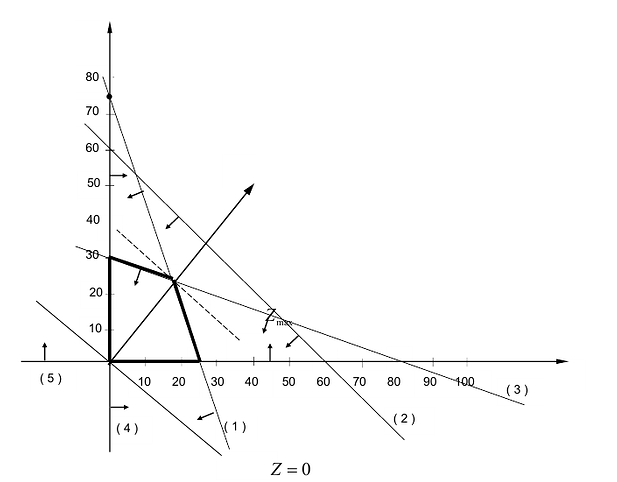
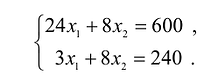
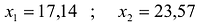
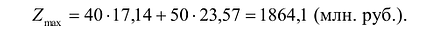
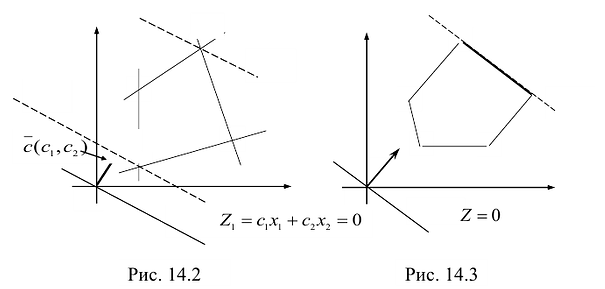
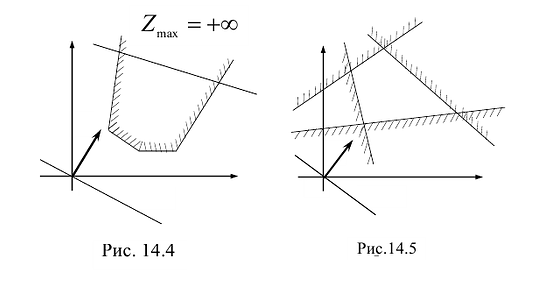
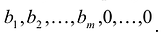
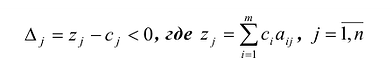
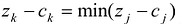
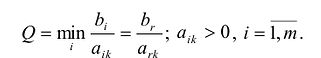
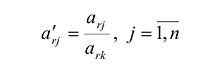
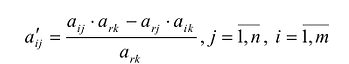
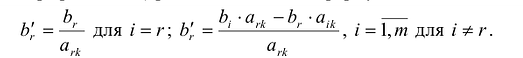
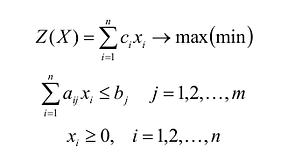
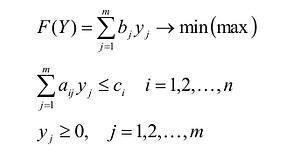
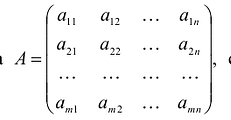 , составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 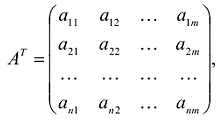 , в двойственной задаче получаются друг из друга транспонированием;
, в двойственной задаче получаются друг из друга транспонированием;