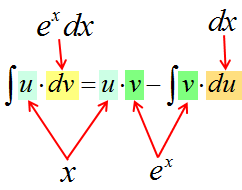
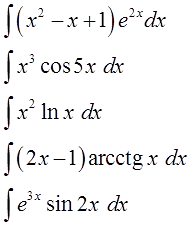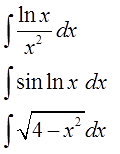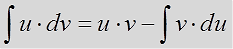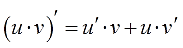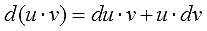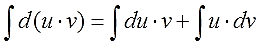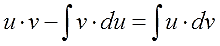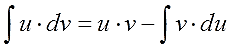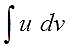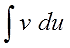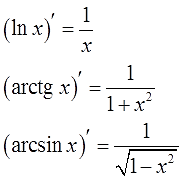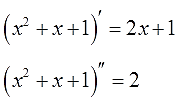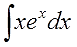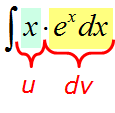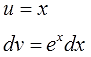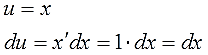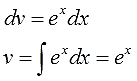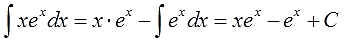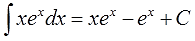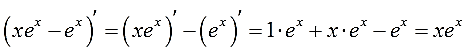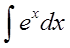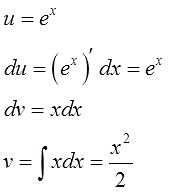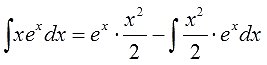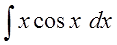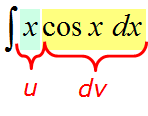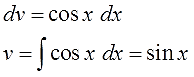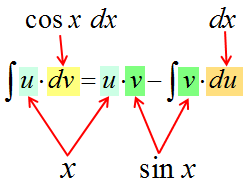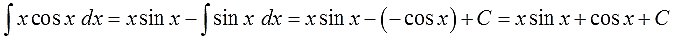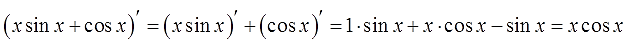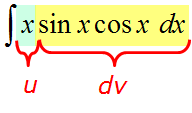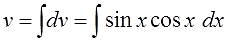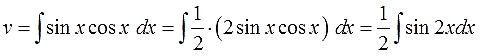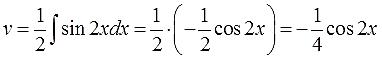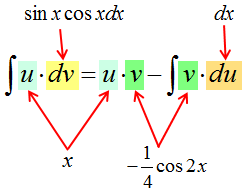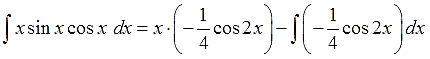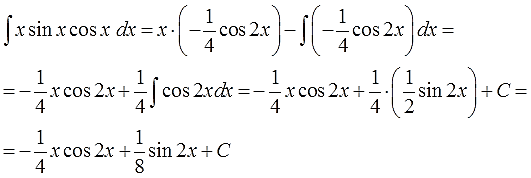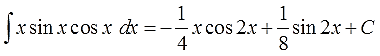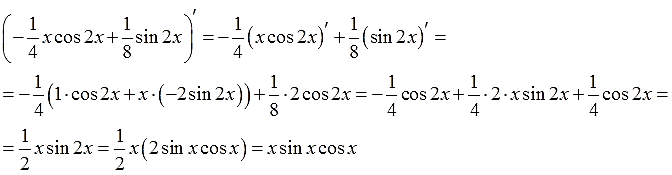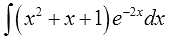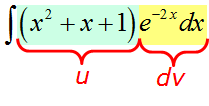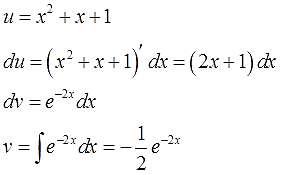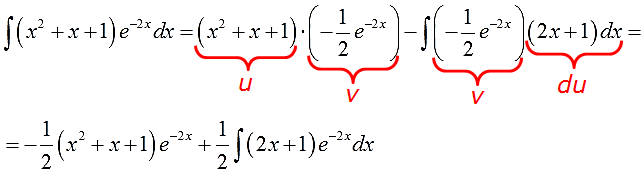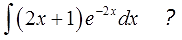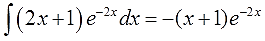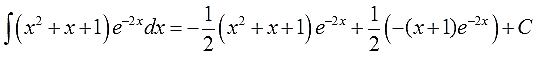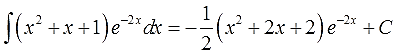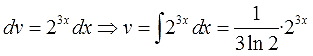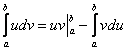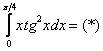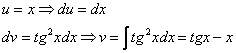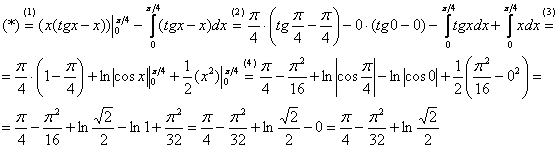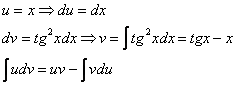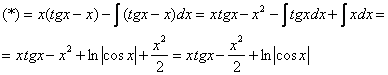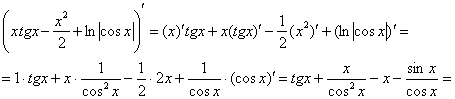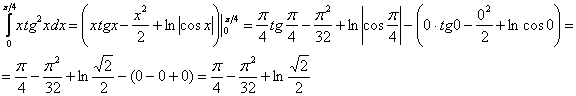Как найти определенный интеграл от произведения - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.

Интегрирование по частям

Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.

Формула для неопределенного интеграла:

$$ int udv = uv – int vdu $$

Формула для определенного интеграла:

$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$

Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.

Пример 1

Найти интеграл $ int xe^xdx $

Решение

Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $

Подставляем найденные значения в первую формулу интегрирования и получаем

$$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int xe^x dx = xe^x – e^x + C $$

Пример 2

Найти интеграл $ int xcos x dx $

Решение

В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $.

Подставим функции $ u $ и $ v $ в первую формулу

$$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$

Ответ

$$ int x cos x dx = x sin x + cos x + C $$

Пример 3

Вычислить интеграл $ int limits_1 ^e xln x dx $

Решение

В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения

$$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$

Осталось подставить это в формулу

$$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$

$$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$

Ответ

$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$

Пример 4

Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $

Решение

По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так

$$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$

Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу

$$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$

$$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$

Ответ

$$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$

Источник

Метод интегрирования по частям.

Продолжаем осваивать базовые приёмы интегрирования. В предыдущих уроках мы рассмотрели три таких приёма – непосредственное интегрирование (то бишь, по таблице), метод подведения функции под знак дифференциала и метод замены переменной. Три ножки для стула. Сидеть уже можно, но… как-то неудобно.)

Сегодняшний наш урок будет началом изучения ещё одной обширной темы интегрального исчисления. Последней, четвёртой ножки для нашего стула.) А именно – метода интегрирования по частям. Великого и могучего. Фраза “интегрируем по частям” вселяет уверенность и так же обнадёживает студентов, как и фраза “решаем через дискриминант” у школьников. 🙂

В чём же заключается столь сильная мощь данного метода и почему именно он так популярен при вычислении львиной доли неопределённых интегралов? А дело вот в чём.

Ключевой момент №1

Как мы уже знаем, в отличие от производных, в матанализе не существует стандартных правил для интегралов от произведения, частного и сложной функции. Но в процессе интегрирования такие операции с функциями встречаются сплошь и рядом. И очень часто именно метод интегрирования по частям позволяет свести вычисление интеграла от навороченной функции к совсем простенькому выражению, проинтегрировать которое не составит труда. Если таблицу знать, конечно.

Ключевой момент №2

Нередко под интегралом могут стоять всякие нехорошие трансцендентные конструкции — логарифмы, арксинусы, арктангенсы и прочие ужасы. Таблица интегралов не катит: нету в ней ни логарифмов, ни арков. И замена не годится тоже.

И в таких случаях тоже надо уметь как-то выкручиваться, да…

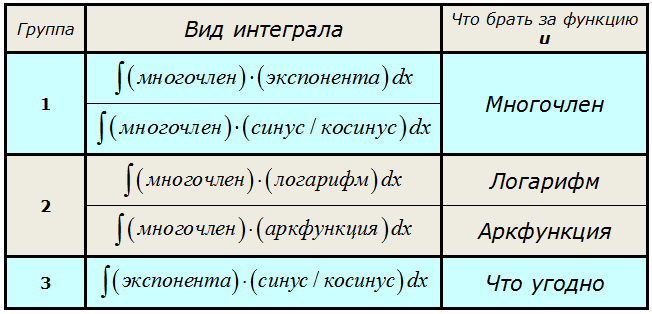
Какие же именно интегралы берутся по частям?

Вот типовые схемы подынтегральных функций:

Например, что-то в таком духе:

Что общего во всех таких интегралах? А общее то, что подынтегральная функция представляет собой произведение (а в ряде случаев и частное) “разнородных” функций. Многочлена и логарифма, синуса и экспоненты и так далее… Или же под интегралом тусуются всякие там арксинусы, арктангенсы и прочая жесть.

Под последним шестым пунктом стоит слово “прочие”. Это такие функции, которые не относятся к предыдущим пяти типам, но которые также вполне можно проинтегрировать по частям (а иногда и только по частям). Как правило, сочетая в себе и другие способы интегрирования — замену переменной, подведение под дифференциал и т.п. Это всякие сложные экзотические функции, а также некоторые дроби и функции с корнями.

Например:

И тому подобные примеры. Их разберём в соответствующем уроке.

Ну вот. Про таинственный метод упомянули, какие именно интегралы с его помощью вычисляются — тоже. Пора бы уже начать более близкое знакомство. Знакомимся? Поехали!

Формула интегрирования по частям — вывод и смысл.

Итак, прошу любить и жаловать:

Это и есть формула интегрирования по частям собственной персоной.)

Откуда же она берётся и почему так называется? Она берётся из обычного правила дифференцирования произведения.

Все вы (надеюсь) его хорошо помните ещё со школы:

Или почти то же самое, только по-взрослому, через дифференциалы:

Все формулы в матанализе, если слева и справа стоят функции или их производные (или дифференциалы), можно почленно интегрировать. Вот и проинтегрируем левую и правую части нашего правила. Имеем полное право!

Подвешиваем на крючки левую и правую части и получаем:

Осталось сообразить, что значок интеграла всегда “съедает” значок дифференциала (согласно соответствующему свойству). Стало быть, слева останется просто произведение u∙v. А справа приведём первый интеграл к приличному виду и отправим его влево к u·v (со сменой знака, разумеется). Получим:

И, наконец, финальный бросок. Меняем местами левую и правую части и получаем:

Всё! Больше никаких научных хитростей.)

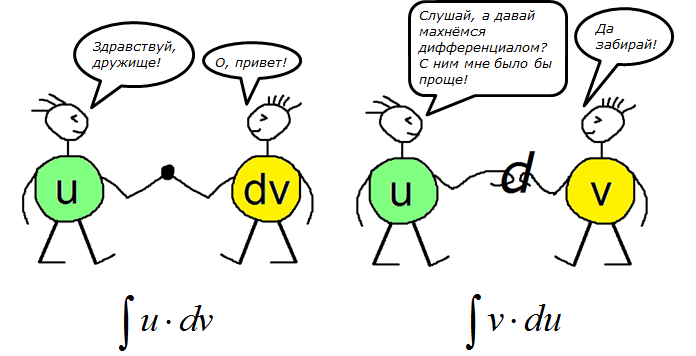
Собственно, формула производной произведения и формула интегрирования по частям — это две взаимно обратных формулы. 🙂 Так же, как и операции дифференцирования сложной функции и подведения функции под знак дифференциала. Вот и вся суть.

Запоминается формула на удивление легко и просто. Чаще всего, в виде секретного заклинания:

Интеграл у-дэ-вэ равен у на вэ минус интеграл вэ-дэ-у. 🙂

Итак, будем считать, что с происхождением формулы разобрались. Теперь разбираемся с названием – что ещё там за части какие-то. 🙂

Смотрим на формулу ещё разок:

В чём основная суть? Исходное подынтегральное выражение (то, что слева) разбивается на два кусочка. Или две части.) Причём только с помощью умножения! Именно поэтому в общей формуле я отдельно и выделяю знаки умножения.

Первая часть (первый множитель) — это некоторая функция u. Функция как функция. Выражаемая какой-то формулой.

Вторая часть (второй множитель) — это не функция, а дифференциал некоторой другой функции v. То есть, dv.

Что это за таинственные u и v? Об этом дальше подробненько будет. Никаких тайн.)

Что же происходит при применении формулы? С точки зрения математики ничего особенного не происходит:

1. Первый множитель — u — дифференцируется. Было u, а становится du.

2. Второй множитель – dv – наоборот, интегрируется. Было dv, а после интегрирования стало просто v.

Зато с точки зрения наших хотелок происходит оч-чень много полезного! Исходный интеграл:

который, по каким-то причинам, нам не очень нравится, заменяется на другой интеграл

вычисление которого должно оказаться проще исходного.

Вот и всё. Вот и вся ключевая идея применения формулы!

Что брать за u, а что за dv?

Вопрос хороший! Этот момент – стратегически самый важный при применении формулы. Давайте разбираться. В самых общих чертах.) Выпишем ещё раз формулу:

Как видно из формулы, нам надо интегрировать новое выражение v∙du. И оно должно оказаться проще старого подынтегрального выражения u∙dv. Вот такая ключевая идея — упростить исходное подынтегральное выражение!

Поскольку в новом подынтегральном выражении стоит дифференциал du, то за функцию u всегда принимается функция, упрощающаяся при дифференцировании.

И какие же функции упрощаются при дифференцировании? Как правило, это всякие ужасы типа логарифмов или “арков”. Почему же они упрощаются при дифференцировании? А потому, что их производные — гораздо более простые функции! Рациональные дроби или, в худшем случае, выражения с корнями (для арксинуса/арккосинуса). Вспоминаем нашу старую добрую таблицу производных:

И так далее. С дробью 1/х всяко проще работать в процессе интегрирования, чем с логарифмом, правда? И с арками та же история.

Точно так же упрощаются при дифференцировании и многочлены, степень которых после каждого дифференцирования понижается на единичку:

В общем, принцип выбора функции u предельно ясен — упрощение после дифференцирования. А что же со вторым множителем dv?

Поскольку множитель dv нам придётся интегрировать, то за dv всегда берётся конструкция, не усложняющаяся при интегрировании!

Например, это вполне может быть экспонента. Или же тригонометрическая функция — синус там или косинус… Или степенная функция или многочлен. Эти функции никак не усложняются при интегрировании! Почему? Вспоминаем теперь уже таблицу интегралов (первообразных): экспонента при интегрировании превращается сама в себя, синус/косинус — друг в друга (с точностью до знака), а любой многочлен степени n — также в многочлен, но степени n+1.

Запоминаем:

За функцию u всегда принимаем выражение, упрощающееся при дифференцировании.

За dv принимаем выражение, не усложняющееся при интегрировании.

Разумеется, сразу увидеть и сообразить в уме, что упростится/усложнится после дифференцирования/интегрирования, не всегда возможно. Всё от конкретного примера и от опыта зависит. Не всегда с первого раза получается. Бывает.)

Но для некоторых типовых схем я всё же приведу небольшую сводную табличку. Пользуйтесь на здоровье! 🙂

Что ж, думаю, хватит грузной теории, давайте перейдём к конкретным примерам — всё станет куда понятнее.) В этом уроке рассмотрим интегралы из группы №1.

Произведение многочлена и показательной/тригонометрической функции.

Это интегралы из первой группы нашей сводной таблички.

Общий рецепт здесь следующий:

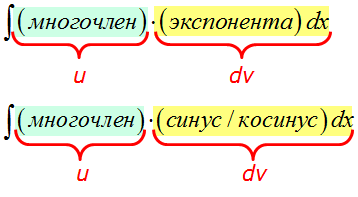
Если под интегралом стоит произведение многочлена и показательной/тригонометрической функции, то за функцию u всегда берётся МНОГОЧЛЕН.

А что берётся за dv? А за dv всегда берётся оставшаяся часть подынтегрального выражения вместе с dx! Что уж там осталось, то и берётся, так уж формула интегрирования по частям устроена: всё подынтегральное выражение надо по кусочкам распределить между u и dv.

Вот так:

Ну что, посмотрим на формулу интегрирования по частям в действии?)

Например, пусть надо найти вот такой интересный интеграл:

Пример 1

Казалось бы, всё просто. Под знаком интеграла стоит произведение знакомых табличных функций — икса и e^x. Вроде, всё хорошо. Но есть одна проблемка: общей стандартной формулы для интеграла от произведения не существует! По отдельности каждая функция интегрируется без проблем, а вот произведение — уже проблема, да…) Как быть?

Как-как… Надо разделить разные типы функций!

Вот и разбиваем наше подынтегральное выражение на кусочки! Наша задача представить конструкцию

xe^xdx

в виде произведения функции u и дифференциала другой функции dv.

Определяемся, что выбираем за u и за dv!

Работаем прямо по правилу для группы №1. В роли показательной функции у нас, очевидно, e^x. А множитель х служит как раз тем самым многочленом, который целесообразно брать в качестве функции u. Не так очевидно, что это многочлен, но это именно он.) Состоящий всего из одного члена — икса. Бывает.)

А вот к dv мы должны отнести то, что осталось — выражение e^xdx.

Так и пишем:

Да-да, именно так и выделяем, прямо в тетрадке!

Итак, выбор u и dv сделан. Вот он:

Теперь следующим шагом мы начинаем операцию, которую я условно называю “миграция дифференциала”: функцию u мы будем дифференцировать и превращать в du, а dv — наоборот интегрировать и превращать в v. Таким образом, под дифференциалом вместо функции v окажется функция u. Вспоминаем нашу картинку с пляшущими человечками.)

Поехали!

Дифференцируем функцию u, считаем du:

Интегрируем множитель dv и ищем функцию v:

Внимание! Не прибавляем константу С после отыскания функции v! Ведь в качестве функции v нам нужна только какая-то одна конкретная первообразная! А не всё бесконечное множество, да…) Самая простая такая первообразная — очевидно, с константой С, равной нулю (С=0). Именно поэтому я и пишу

v = e^x,

а не

v = e^x + C.

А теперь берём формулу интегрирования по частям

и аккуратно подставляем все исходные данные на свои места:

И считаем:

Вот и все дела.)

Ответ:

Как всегда, для пущей уверенности, дифференцируем результат:

Ура! Совпало! 🙂

Что у нас произошло после применения формулы интегрирования по частям? А произошло то, что мешающий нам множитель х исчез из примера, и исходный интеграл от нехорошего произведения

свёлся к табличному (!) интегралу от безобидной экспоненты

Берущемуся в уме. Если таблицу знать.) Здорово, правда?

Именно так и работает формула интегрирования по частям. Разделяет разнотипные функции и превращает ужасный на вид интеграл в белый и пушистый. Вот и вся суть метода интегрирования по частям.)

А что будет, если поступить наоборот – за u принять e^x, а за dv — xdx?

Не вопрос, давайте посмотрим:

Тогда, подставляя всё в формулу, получим:

Хм… И что нам с таким интегралом делать?! Даже ещё хуже стало, чем было…

Да! При таком выборе u и dv новый интеграл не упрощается, а, наоборот, усложняется! Экспоненте-то всё равно, что с ней делают — дифференцируют/интегрируют. У неё ко всем воздействиям врождённый иммунитет.) В отличие от многочлена, который при таком раскладе не понижает свою степень, а повышает. Что никак не делает пример проще, да…)

Собственно в этом-то и кроется причина выбора именно многочлена в качестве функции u для интегралов первой группы — понизить его степень.

А для общего развития запоминаем:

Если после применения формулы новый интеграл получился сложнее исходного, то, скорее всего, неудачно сделан выбор u и dv. Не падаем духом и пробуем другую комбинацию.

Эта рекомендация относится не только к этому уроку, на примеры из первой группы, а ко всему интегрированию по частям вообще.

Но самое надёжное — не бездумно расчленять подынтегральное выражение и комбинировать кусочки, задумчиво глядя на пример, а понимать общий смысл формулы и принцип выбора u и dv для конкретного типа интеграла. Уметь заранее просчитывать ситуацию и оценивать последствия того или иного выбора. Такой опыт только с практикой приходит. Прорешаете хотя бы 20-30 примеров — и проблема выбора u и dv отпадёт сама собой.)

Ну вот. Первый пример разобран по косточкам. Разумеется, так подробно расписывать следующие примеры я уже не буду. Это чисто для знакомства сделано. Чтобы общую идею уловить.)

А теперь можно записать и общий алгоритм вычисления неопределённых интегралов по частям.

Алгоритм вычисления неопределённых интегралов по частям.

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.

Ну что, потренируемся в применении алгоритма?)

Пример 2

И опять под интегралом стоит произведение функций разной природы — икса и косинуса. Значит, разделяем разнородные функции и интегрируем по частям: у нас просто нет других вариантов!

Работаем строго по пунктам.

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

Очевидно, это интеграл из первой группы — типа “многочлен на синус/косинус”. Переходим к пункту 2.

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

Наше правило для первой группы гласит, что за функцию u следует принимать многочлен — то есть, просто множитель x.

Ну, а за dv, ясен перец, принимаем то что осталось, т.е. cos x dx.

Вот так:

Итак, выбор сделан. Переходим к пунктам 3 и 4. Тут всё просто, без фокусов:

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

Итак, все исходные данные для применения формулы подготовлены. Подставляем:

Вперёд!

Ответ:

Готово дело.)

Проверяем ответ дифференцированием:

Всё путём.)

Мы видим, что новый интеграл опять оказался табличным и берущимся в уме! От синуса. Халява! 🙂 Но далеко не всегда выпадает такое счастье. Иногда при поиске функции v надо дополнительно потрудиться. Поэтому теперь решим что-нибудь посложнее. Чтобы в ступор не впасть, в случае чего…

Пример 3

Чем-то похоже на предыдущий пример, правда? Только синус ещё затесался, в качестве третьего множителя. Поскольку перед нами снова произведение разнородных функций — икса и тригонометрии, то такой интеграл можно попробовать взять только по частям. Но под интегралом произведение трёх функций, а не двух, как обычно! Что делать?

Что-что… Не бояться, вот что! Ибо из трёх множителей всегда можно сделать два. Нас спасут… скобочки! Вот так:

А дальше опять по алгоритму. Поехали!

1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

Всё ясно. Это первая группа, т.к. под интегралом произведение многочлена (икса) и тригонометрии (sinx∙cosx).

2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

И здесь вопросов нет. Икс — это u. То, что осталось (т.е. sinx∙cosxdx) — это dv.

Итого имеем следующее:

3. Дифференцируем функцию u и считаем дифференциал du.

4. Интегрируем дифференциал dv и ищем саму функцию v.

А вот здесь начинается самое интересное.) Для поиска v нам надо проинтегрировать выражение sinx∙cosxdx.

Вот так:

Вот тут уже с ходу, в уме, этот интеграл не возьмёшь. В одно действие. Подумать надо.)

Варианта два. Можно внести косинус (или синус) под знак дифференциала и старым добрым способом, но в данном случае гораздо выгоднее искусственно выделить под интегралом синус двойного угла:

А проинтегрировать синус двойного угла уже никакого труда не составляет. В уме интегрируется. Как это делается, смотрим этот урок. Самое главное — не забываем про дополнительные коэффициенты и про знаки.

Всё. Функцию v мы нашли. Идём дальше по алгоритму.

5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

И снова мы видим, что новый интеграл, от косинуса двойного угла, много проще старого интеграла от сборной солянки x∙sinx∙cosx. Интегрируем косинус двойного угла, “причёсываем” ответ и добиваем наш злой пример.

Пишу подробно, со всеми знаками и коэффициентами, поскольку именно в них народ и косячит на 99%:

Ответ:

Вот и все дела.) Кому не нравятся двойные углы, те могут перейти обратно к одинарным по соответствующим формулам, но в таком виде ответ выглядит гораздо компактнее.

Что, сомнения нахлынули? Не ленимся, дифференцируем:

Нет, всё честно.)

Всё бы ничего, но… могут случаться и такие сюрпризы, когда по частям приходится интегрировать несколько раз. Разберём ещё один пример.

Пример 4

Надеюсь, общий алгоритм интегрирования по частям уже запомнился? Можно не расписывать подробно в четвёртый раз?)

В этот раз на экспоненту умножается не одинокий икс, а вполне себе полноценный многочлен. Но схема выбора u и dv та же самая.

Действуем в соответствии с алгоритмом:

Отлично. Функции u и v, а также их дифференциалы du и dv найдены. Пора приступать к интегрированию по частям. Снова прямо по формуле вставляем все исходные данные, упрощаем что упрощается и получаем:

А вот и обещанный сюрприз! Что делать с новым интегралом

В таблице такого и близко нет, обычными преобразованиями с подынтегральной функцией тоже ничего не сделаешь… Но! Можно заметить, что под новым интегралом у нас опять произведение многочлена и экспоненты! Поэтому… снова интегрируем по частям (да-да!). Утешает то, что новый многочлен (2х+1) стал уже линейным (а не квадратичным, как был изначально)! Казалось бы, мелочь, но очень существенная: новый интеграл в целом проще старого! Как и должно быть.)

Если мы сейчас отдельно возьмём этот интеграл по частям и упростим до упора, то получим такой результат:

Что, у вас не так получилось? А за знаками следили? А за коэффициентами? Не забываем, что е^-2х — сложная функция! Со всеми вытекающими.)

Вот практически и всё. Возвращаемся к исходному примеру, вставляем результат промежуточного интегрирования по частям на своё место и константу не забываем.)

Получим:

В принципе, интеграл мы уже нашли. Если требуются дальнейшие упрощения и наведение марафета, то, раскрыв скобки и приведя подобные, окончательно получим:

Ответ:

Вот такой ответ. Проверочное обратное дифференцирование предлагаю провести самостоятельно.)

Чем поучителен этот пример? Как видите, здесь нам пришлось интегрировать по частям два раза! Почему? Всему виной является вторая степень нашего многочлена x²+x+1. Проблема в том, что после каждого применения формулы (т.е. взятии дифференциала du) степень многочлена понижается лишь на единичку. Как и при любом дифференцировании, да.

Например, если бы под интегралом стоял многочлен 10-й степени (да даже хотя бы простое произведение x¹⁰e^x), то последовательно интегрировать по частям пришлось бы (о, ужас!) десять раз! Это огорчает. Но зато при каждом новом интегрировании степень многочлена будет становиться всё ниже. Пускай на единичку, но — ниже. Это радует.)

Запоминаем:

Интегрировать по частям требуется столько раз, какова степень многочлена.

Между прочим, в качестве показательной функции совершенно не обязательно должна стоять именно экспонента (e^x, е^2х и тому подобные конструкции). Запросто может оказаться вообще не “е”, а что-то типа 2^3х и т. п. Не надо пугаться. Принцип интегрирования тот же самый. Отличие состоит лишь в том, что при вычислении функции v будут всплывать дополнительные коэффициенты с логарифмами, которые ни в коем случае нельзя терять.

Например:

И так далее…

Итак, с первой группой интегралов, берущихся по частям, поработали. Переходим ко второй группе — логарифмам, аркам и прочим питомцам нашего зоопарка элементарных функций. В следующей теме.)

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 апреля 2020 года; проверки требуют 6 правок.

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие равенства

для неопределённого интеграла

или в другой записи

{displaystyle int u,v'dx=u,v-int v,u'dx}

для определённого интеграла: $int limits _{a}^{b}u,dv=u,v,{bigg |}_{a}^{b}-int limits _{a}^{b}v,du$

Предполагается, что нахождение интеграла проще, чем . В противном случае применение метода не оправдано.

Получение формул[править | править код]

Для неопределённого интеграла[править | править код]

Функции и гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

$int {frac {dx}{x}}={frac {1}{x}}cdot x-int {frac {-1}{x^{2}}}cdot xdx=1+int {frac {dx}{x}}$

Отсюда «следствие»: 0=1 , что очевидно неверно.

Для определённого интеграла[править | править код]

В целом аналогично случаю неопределённого интеграла:

$int limits _{a}^{b}d(u,v)=int limits _{a}^{b}v,du+int limits _{a}^{b}u,dv$

$int limits _{a}^{b}u,dv=u,v,{bigg |}_{a}^{b}-int limits _{a}^{b}v,du$

Данные формулы справедливы, если каждая из функций и непрерывно дифференцируема на области интегрирования.

Табличное интегрирование по частям[править | править код]

Основной процесс приведённой выше формулы может быть обобщено в таблице.

Например, рассмотрим интеграл

${displaystyle int x^{3}cos x,dxquad }$

${displaystyle quad u^{(0)}=x^{3},quad v^{(n)}=cos x.}$

Начнем перечислять в столбце D функцию ${displaystyle u^{(0)}=x^{3}}$ и ее последующие производные ${displaystyle u^{(i)}}$ до тех пор, пока не будет получен 0. Затем, перечисляем в столбце I функцию ${displaystyle v^{(n)}=cos x}$ и ее последующие первообразные ${displaystyle v^{(n-i)}}$ до тех пор, пока размер столбца I не будет таким же, как и в столбце D. Результат выглядит следующим образом:

# i	Знак	D: производные u⁽ⁱ⁾
0	+	$x^{3}$
1	−	${displaystyle 3x^{2}}$
2	+
3	−
4	+

Произведение значений в ряду i столбцов D и I вместе с соответствующим им знаком выдают соответствующие интегралы на шаге i в течение повторяющихся шагов интегрирования по частям. Шаг i = 0 несет в себе исходный интеграл. для полного результата в шаге i > 0 i-й интеграл должен быть добавлен к предыдущим произведениям(0 ≤ j < i) j-го значения столбца D и (j + 1)-го значения столбца I (т.е., умножить 1-ое значение столбца D на 2-ое значение столбца I, 2-ое значение столбца D на 3-е значение столбца I, и т.д. …) не забывая о j-м знаке. Процесс завершается, когда произведение, которое несет в себе интеграл, принимает значение 0 (i = 4 в нашем примере). Конечный результат следующий: (включая разные знаки в каждом сегменте):

${displaystyle underbrace {(+1)(x^{3})(sin x)} _{j=0}+underbrace {(-1)(3x^{2})(-cos x)} _{j=1}+underbrace {(+1)(6x)(-sin x)} _{j=2}+underbrace {(-1)(6)(cos x)} _{j=3}+underbrace {int (+1)(0)(cos x),dx} _{i=4:;to ;C}.}$

В итоге:

${displaystyle underbrace {int x^{3}cos x,dx} _{text{шаг 0}}=x^{3}sin x+3x^{2}cos x-6xsin x-6cos x+C.}$

Примеры[править | править код]

$int x^{2}sin x,dx=int x^{2},d(-cos x)=-x^{2}cos x-int -2xcos x,dx=$

$=-x^{2}cos x+int 2x,d(sin x)=-x^{2}cos x+2xsin x-int 2sin x,dx=-x^{2}cos x+2xsin x+2cos x+C$

Данный метод также используется для нахождения интегралов от элементарных функций:

$int ln x,dx=xln x-int {frac {1}{x}}x,dx=xln x-x+C$

$int operatorname {arctg},x,dx=x,operatorname {arctg},x-int {frac {x}{1+x^{2}}},dx=x,operatorname {arctg},x-{frac {1}{2}}ln(1+x^{2})+C$

В некоторых случаях интегрирование по частям не даёт прямого ответа:

$I_{1}=int e^{{alpha x}},sin {beta x},dx=$

$=int e^{{alpha x}},d{Big (}-{frac {1}{beta }}cos {beta x}{Big )}=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }}int e^{{alpha x}},cos {beta x},dx=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }},I_{2}$

$I_{2}=int e^{{alpha x}},cos {beta x},dx=$

$=int e^{{alpha x}},d{Big (}{frac {1}{beta }}sin {beta x}{Big )}={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }}int e^{{alpha x}},sin {beta x},dx={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }},I_{1}$

Таким образом один интеграл выражается через другой:

${begin{cases}I_{1}=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }},I_{2}\I_{2}={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }},I_{1}end{cases}}$

Решив полученную систему, получаем:

$I_{1}={frac {e^{{alpha x}}}{alpha ^{2}+beta ^{2}}}{Big (}alpha sin {beta x}-beta cos {beta x}{Big )}+C$

$I_{2}={frac {e^{{alpha x}}}{alpha ^{2}+beta ^{2}}}{Big (}alpha cos {beta x}+beta sin {beta x}{Big )}+C$

Многомерный случай[править | править код]

Существует обобщение формулы интегрирования по частям для функций от нескольких переменных. В таком случае вместо интервала рассматривается подмножество $mathbb {R} ^{n}$ , а вместо производной − частная производная.

Пусть Omega открытое ограниченное подмножество $mathbb {R} ^{n}$ с кусочно-гладкой границей . Если и гладкие функции на замыкании Omega , то

$int _{Omega }{frac {partial u}{partial x_{i}}}v,dx=int _{{partial Omega }}uvn_{i},dsigma -int _{Omega }u{frac {partial v}{partial x_{i}}},dx$

где − внешняя нормаль к , а $n_{i}$ − её i-ая координата, i от 1 до n, sigma – мера на .

См. также[править | править код]

Интеграл
Интеграл Римана
Преобразование Лежандра
Методы интегрирования
Дискретное преобразование Абеля — аналог интегрирования по частям для сумм.

Литература[править | править код]

Маслов А. П., Белоус Е. А. Тема 5.2 // Математика для инженеров (2 курс).
Тимофеев А. Ф. Интегрирование функций. — М.—Лен.: ОГИЗ, Гостехиздат, 1948. — С. 37—42.

Также см. Математический анализ#Библиография.

Ссылки[править | править код]

Математика для заочников и не только. Дата обращения: 11 мая 2011.
Канал СЗТУ на сайте youtube.com. Дата обращения: 11 мая 2011.

Источник

Здесь новизны еще меньше. Всё, что справедливо для неопределенного интеграла, в полной мере справедливы и для определенного интеграла. Плюсом идёт то, что в формуле интегрирования по частям добавляются пределы интегрирования:

Формулу Ньютона-Лейбница здесь нужно применить дважды: для произведения и после того, как мы возьмём интеграл . Ну и, конечно, подынтегральные функции должна быть непрерывны на , ибо на «нет» и интеграла нет.

Пример я подобрал не самый простой, но очень и очень познавательный:

Пример 8
Вычислить определенный интеграл

Сразу начинаем решение и сразу прерываем его «звёздочкой». Этот тип интеграла не встречался ранее, он тоже берётся по частям. Используем стандартную схему интегрирования по частям:

Интеграл от квадрата тангенса я разбирал в 1-й части курса, но на чистовике, естественно, всё расписываем подробно, вспоминая заодно насущные тригонометрические формулы:

Далее открываем решение и на первом шаге

(1) расписываем правую часть формулы :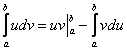

(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойство линейности, разделяя его на два интеграла. Не путаемся в знаках!

(3) Берем два оставшихся интеграла. Интеграл также разобран ранее, однако, не поленюсь:

(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.

Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.

Если честно, я недолюбливаю формулу 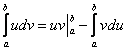и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален:

На первом этапе находим неопределенный интеграл:

Интегрируем по частям:

Первообразная функция найдена. …Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу ?

В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования.

На втором этапе проводим проверку (обычно на черновике).

Тоже логично. Ведь если неправильно найден неопределённый интеграл, то… правильно! И это лучше выяснить немедленно, дифференцируем ответ:

– получена исходная подынтегральная функция, значит, первообразная найдена верно.

И третий этап – применение формулы Ньютона-Лейбница:

Здесь тоже есть существенная выгода! – это гораздо меньший риск запутаться в подстановках и вычислениях, т.к. формула Ньютона-Лейбница применяется всего лишь один раз.

Рассмотренный алгоритм решения
можно применить для любого определенного интеграла!

И нужно, если интеграл трудный. Так, если «чайник» решит разобранный интеграл по формуле 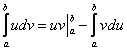(1-м способом), то 99% где-нибудь допустит ошибку.

Уважаемый студент, распечатай и наклей рядом с формулой Ньютона-Лейбница:

1) Сначала находим неопределенный интеграл (первообразную функцию). Если не получилось, повышаем свои навыки интегрирования.

2) Проверяем найденную первообразную дифференцированием. Здесь, кстати, может статься, позабылись производные – и тогда самое время подтянуть свои навыки!

3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания. Царь тут!

И на холодную закуску интеграл для самостоятельного решения.

Пример 9
Вычислить определенный интеграл

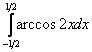
1.7. Геометрический смысл определённого интеграла

1.5. А если подвести функцию под знак дифференциала?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Пусть
и– непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем

Отсюда

Интегрируя,
получим:

или окончательно

(4)

Формула (4) называется формулой
интегрирования по частям.

Выведенная формула показывает, что
интеграл
приводится к интегралу,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражениепредставляется в виде произведения
множителейuиdv.
При этом dx обязательно входит в
dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим,
а затем.

Пример 1.

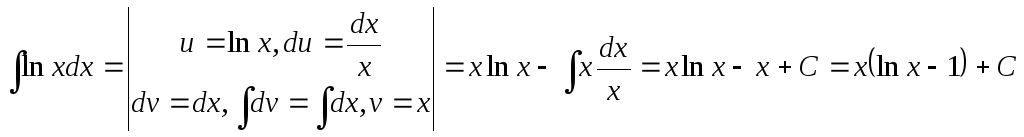
В представленном примере, как и в
дальнейших, вертикальными черточками
отделены вспомогательные записи. Отметим
также, что в качестве vможно взять любую функцию видаx+C,гдеС– постоянная. Мы взялиv=x,
т.е.С=0.

Пример
2.
.

Пример
3.

Пример 4.

Иногда для вычисления
интеграла формулу интегрирования по
частям приходится применять несколько
раз.

Пример
5.

Таким образом, интеграл
вычислен двукратным интегрированием
по частям.

Пример 6.

Если бы выражение
u
и dv
мы выбрали иначе, т.е.
,
то получили бы,
откуда,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.

Приведенный пример показывает, что при
вычислении интегралов методом
интегрирования по частям главным
является разумное разбиение подынтегрального
выражения на множители uиdv. Общих установок
по этому вопросу не имеется. Однако, для
некоторых типов интегралов сделать это
возможно.

а) В интегралах вида

где
P(х)
– многочлен относительно x,
а –
некоторое число, полагают u=P(x),
а остальные сомножители за
.

Пример 7.
Найти
.


Положим
,,
тогда,.
Следовательно,



б) В интегралах вида

полагают

а
остальные сомножители – заu.

Пример 8.
Найти
.

Следовательно,

Вычислим отдельно последний интеграл:

Итак,
.

Отметим, что на
практике важно научиться применять
формулу (4), не выписывая по возможности
в стороне выражения для функций u
и v.

Так, решение приведенного примера может
быть представлено в виде:



=.

Возвращение к исходному интегралу

Формула интегрирования
по частям применима и для нахождения
интегралов вида
и,
гдеа
и b
– числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u
выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.