Как найти определенный интеграл по частям

Как найти определенный интеграл по частям

Интегрирование по частям

Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.

Формула для неопределенного интеграла:

$$ int udv = uv – int vdu $$

Формула для определенного интеграла:

$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$

Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.

Пример 1
Найти интеграл $ int xe^xdx $
Решение

Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $

Подставляем найденные значения в первую формулу интегрирования и получаем

$$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ

$$ int xe^x dx = xe^x – e^x + C $$
Пример 2
Найти интеграл $ int xcos x dx $
Решение

В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $.

Подставим функции $ u $ и $ v $ в первую формулу

$$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$
Ответ

$$ int x cos x dx = x sin x + cos x + C $$
Пример 3
Вычислить интеграл $ int limits_1 ^e xln x dx $
Решение

В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения

$$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$

Осталось подставить это в формулу

$$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$

$$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$
Ответ

$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$
Пример 4
Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $
Решение

По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так

$$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$

Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу

$$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$

$$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$
Ответ
$$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$
Источник

Интегрирование по частям

Пусть U(x) и V(x) – дифференцируемые функции. Тогда d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение

Интегрирование по частям

называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

  • Решение онлайн
  • Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

Также рекомендуется изучить сервис вычисление интегралов онлайн

Примеры

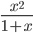≡ x^2/(x+2)

cos2(2x+π) ≡ (cos(2*x+pi))^2

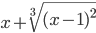≡ x+(x-1)^(2/3)

Применение метода интегрирования по частям

В связи с особенностями нахождения определенных величин, формулу интегрирования по частям очень часто используют в следующих задачах:

  1. Математическое ожидание непрерывной случайной величины. Формула для нахождения математического ожидания и дисперсии непрерывной случайной величины включает в себя два сомножителя: функцию полинома от x и плотность распределения f(x).
  2. Разложение в ряд Фурье. При разложении необходимо определять коэффициенты, которые находятся интегрированием от произведения функции f(x) и тригонометрической функции cos(x) или sin(x).

Типовые разложения по частям

Вид интеграла Разложения на части
∫Pn(x)cos(ax)dx, ∫Pn(x)sin(ax)dx, ∫Pn(x)eaxdx, где Pn(x) – некоторый полином (многочлен) степени n U(x)=Pn(x), dV(x)=cos(ax)dx
∫ln(P(x))dx U=ln(P(x)); dV=dx
∫arcsin(ax)dx U=arcsin(ax); dV=dx
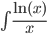U=ln(x); dV=dx/x

При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=ex, dV=xdx. Тогда dU=exdx, 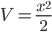и Вряд ли интеграл ∫x2exdx можно считать проще исходного.

Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла ∫x2sin(x)dx.

Интегралы ∫eaxcos(bx)dx и ∫eaxsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.

Пример №1. Вычислить ∫xexdx.

Положим U=x, dV=exdx. Тогда dU=dx, V=ex. Поэтому ∫xexdx=xex-∫exdx=xex-ex+C.

Пример №2. Вычислить ∫xcos(x)dx.

Полагаем U=x, dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) - ∫sin(x)dx = xsin(x)+cos(x)+C

Пример №3. ∫(3x+4)cos(x)dx

Решение:

Ответ: (3x+4)sin(x)+3cos(x)+C

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Интегрирование определенного интеграла по частям

Требуется вычислить
интеграл
,
гдеифункции
от.
Используя последний вариант формулы
Ньютона-Лейбница, получаем,
в правой части стоит неопределенный
интеграл, для интегрирования которого
можно использовать формулу.
В результате

.

Итак, формула
интегрирования по частям определенного
интеграла

.

Пример.
.

Примеры для
самостоятельного решения

12.1. , 12.2., 12.3..

Ответы. 12.1.
, 12.2.,
12.3..

Замена переменной в определенном интеграле

Замену переменной
в определенном интеграле можно осуществить
двумя способами. Первый – непосредственное
применение формулы Ньютона-Лейбница,
то есть переход от определенного
интеграла к неопределенному
,
затем замена переменной в неопределенном
интеграле, его вычисление, возвращение
к старой переменной

и подстановка
верхнего и нижнего пределов интегрирования
в соответствии с формулой Ньютона
Лейбница

.

Здесь
первообразная
функции,
аобратная
функция функции.

Возможен и другой
путь, основанный на том, что в отличие
от неопределенного интеграла, когда
результатом вычисления является функция,
определенный интеграл представляет
собой число. Введем обозначения
,
тогда

.

Отсюда имеем

.

Нопервообразная
функции,
следовательно,

,

откуда следует
формула, реализующая замену переменной
без возвращения к старой переменной

.

Другими словами,
вместо возвращения к старой переменной
осуществляется корректировка пределов
интегрирования в интеграле после замены
переменной. В процессе этой корректировки
устанавливается, каковы пределы
интегрирования по новой переменной
,
если пределы интегрирования по старой
переменной отдо.

Замечание.
Поскольку при любом способе интегрирования
осуществляется переход от определенного
интеграла к неопределенному, все
теоретические наработки, связанные с
заменой переменной в неопределенном
интеграле, справедливы и при замене
переменной в определенном интеграле.
При одном условии – существование
интеграла относительно новой переменной
также должно гарантироваться.

Примеры.

1.

.

Отметим, что при
осуществлении замены переменной в
соответствии с рекомендациями теории
необходимо эту замену уточнять, чтобы
не напутать при корректировке пределов.
В вычисленном интеграле теория рекомендует
замену
,
если корректировку пределов интегрирования
осуществлять с помощью этой формулы,
тои,и.
Чтобы избежать путаницы в знаках, формулуследует записать либо в виде,
либо.
И тот, и другой варианты приводят к
желаемому результату – избавлению от
иррациональностей. Однако до установления
пределов интегрирования следует
остановиться на одной из формул. В
примере была выбрана первая формула.

2.

.

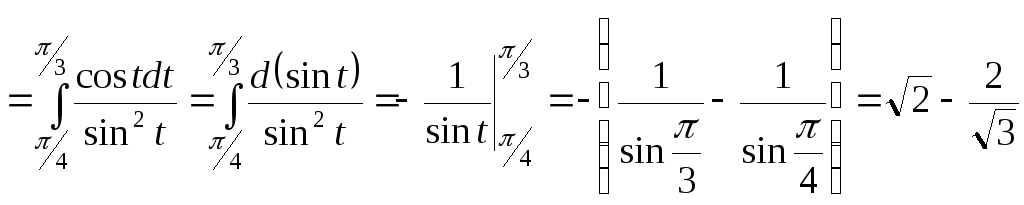Для корректировки
пределов использовалась формула ,
из которой следует, что
имеет место при,
ареализуется при.

Вычисление определенного интеграла с помощью максимы

В этом случае
используется команда, мало отличающаяся
от команды для вычисления неопределенного
интеграла, лишь после переменной
интегрирования добавляются пределы
интегрирования, причем в порядке их
возрастания.

Например, команда
integrate(x^5,x,0,1)
и Shift+Enter
вычисляет интеграл

Интеграл
,
вычисленный ранее вручную,

Интеграл

Примеры для
самостоятельного решения

12.4.
,
12.5., 12.6.,

12.7.
,
12.8.,
12.9..

Ответы.

12.4.
,
12.5.,
12.6.,
12.7.,
12.8.,
12.9. 2.

Разные задачи

12.10.
,
12.11.
,

12.12.
,
12.13.,

12.14.
,
12.15.
,
12.16.

,

12.17.
,
12.18.
,
12.19.
.

Ответы.

12.10.  ,
12.11. ,
12.12. ,
12.13. ,

12.14. ,
12.15. ,
12.16. ,

12.17. ,
12.18.
,
12.19..

Приложения
определенного интеграла

Площадь фигуры

Декартова система
координат

Выше было показано,
что геометрический смысл определенного
интеграла – площадь криволинейной
трапеции. Покажем, как с его помощью
определяются площади более сложных
плоских фигур.

Явное задание
функции

Поскольку значение
интеграла
может быть как отрицательным, так и
положительным, а площадь фигуры –
величина положительная, следует
руководствоваться следующим правилом.

Если подынтегральная
функция на интервале
меняет знак, скажем, в точкахи,
причем,
площадь фигуры определяется формулой

.

Покажем на примере
1, что может получиться, если не следовать
этому правилу. Пусть необходимо вычислить
площадь фигуры, ограниченной осью
абсцисс и кривой
на интервале.
Если не заметить, что на этом интервале
синусоида меняет знак, проходя через
точку,
то решение принимает вид.
Ясно, что получен неверный результат,
площадь этой фигуры не равна нулю. Теперь
применим вышеприведенную формулу

=2+2=4.

В рассмотренном
примере ошибочное решение видно сразу,
так как оно противоречит ожидаемому
результату, но бывают случаи, когда
ошибку в расчетах заметить трудно, а
иногда и невозможно. Это происходит,
когда площадь части фигуры, расположенной
ниже оси абсцисс, скажем, значительно
меньше площади части фигуры, расположенной
в верхней полуплоскости. Тогда результат,
полученный без разбиения интеграла на
части будет не очень заметно отличаться
от правильного результата. Эту ошибку
без надлежащей проверки можно не
заметить, хотя она может оказаться
важной.

Пример 2. Вычислить
площадь фигуры, ограниченной линиями

.

Кривая пересекает
ось абсцисс при
и.
Очевидно, интересующая нас фигура
находится в области,
причем подынтегральная функция в этой
области отрицательна (рисунок 41)

Рисунок 41.

.

Пример 3. Вычислить
площадь фигуры, ограниченной линиями
,,.
Сделаем рисунок

Рисунок 42.

Из рисунка 42 видно,
что часть фигуры расположена ниже оси
,
другая выше ее, причем кривая пересекает
ось абсцисс при.
Итак,

.

Пример 4. Вычислить
площадь фигуры, находящейся в правой
полуплоскости
и ограниченной линиями,.
Сделаем рисунок

Рисунок 43.

Из рисунка 43
следует, что заданная фигура представляет
разность двух трапеций и занимает
область
,
формула ее площади имеет вид,
где,.
Тогда

.

Параметрическое
задание функции

Чтобы получить
формулу площади плоской фигуры, когда
уравнение кривой, ограничивающей фигуру,
задано параметрически
,
следует в

формуле
произвести замену переменной

,

здесь
значение
переменной,
соответствующее,значение
переменной,
соответствующее.
Итак, для параметрически заданной
функции

.

Здесь, как и в
предыдущем параграфе, необходимо следить
за точками, в которых функция меняет
знак.

Пример 1. Вычислить
площадь фигуры, ограниченной одной
аркой циклоиды
и осью абсцисс. Определим два ближайших
друг к другу значения параметра,
при которых.
Этои.
Именно в этой области располагается
одна арка циклоиды, и в этих пределах
нужно производить интегрирование.
Сделаем рисунок

Рисунок 44.

Из рисунка видно,
что внутри области
кривая знака не меняет. Тогда

.

Получим тот же
результат с помощью МАКСИМЫ

Пример 2. Вычислить
площадь эллипса
.

Запишем уравнение
эллипса в параметрической форме
.
Если вычислить площадь фигуры,
расположенной в верхней полуплоскости,
полученный результат умножить на 2,
получим искомую площадь. Но эта часть
кривой реализуется при.
Таким образом,

.

Полярная система
координат

Определим площадь
криволинейного сектора, ограниченного
лучами
,и кривой.
Разобьем областьнаподобластей – элементарных секторов.
Заменим каждый элементарный сектор
сектором круга, радиус которогои угол.
Тогда площадь элементарного сектора
равна.
Площадь всего криволинейного сектора
приближенно описывается интегральной
суммой.
При этом с возрастанием числа разбиений
областизначение интегральной суммы приближается
к истинному значению площади криволинейного
сектора, так как уменьшается погрешность
замены каждого элементарного сектора
частью круга. Очевидно,.
Однако, предел интегральной суммы, если
он не зависит от способа разбиения
области и выбора точекравен определенному интегралу.
Следовательно, площадь криволинейного
сектора определяется формулой

.

Пример 1. Вычислить
площадь фигуры, ограниченной одним
витком спирали Архимеда
.

Рисунок 45.

Один виток спирали
проходится при изменении угла
от 0 до.
Тогда.

Пример 2. Вычислить
площадь фигуры, ограниченной кардиоидой
.
Рисунок

Рисунок 46.

Очевидно,

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник


Здесь новизны еще меньше. Всё, что справедливо для неопределенного интеграла, в полной мере справедливы и для определенного интеграла. Плюсом идёт то, что в формуле интегрирования по частям добавляются пределы интегрирования:

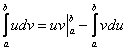
Формулу Ньютона-Лейбница здесь нужно применить дважды: для произведения   и после того, как мы возьмём интеграл . Ну и, конечно, подынтегральные функции должна быть непрерывны на , ибо на «нет» и интеграла нет.

Пример я подобрал не самый простой, но очень и очень познавательный:

Пример 8
Вычислить определенный интеграл

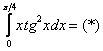
Сразу начинаем решение и сразу прерываем его «звёздочкой». Этот тип интеграла не встречался ранее, он тоже берётся по частям. Используем стандартную схему интегрирования по частям:

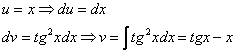
Интеграл от квадрата тангенса я разбирал в 1-й части курса, но на чистовике, естественно, всё расписываем подробно, вспоминая заодно насущные тригонометрические формулы:

Далее открываем решение и на первом шаге

(1) расписываем правую часть формулы :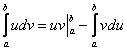

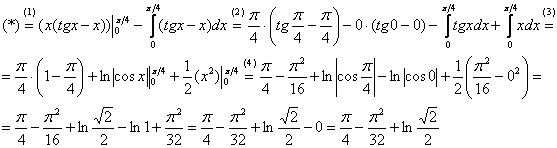
(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойство линейности, разделяя его на два интеграла. Не путаемся в знаках!

(3) Берем два оставшихся интеграла. Интеграл  также разобран ранее, однако, не поленюсь:

(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.

Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.

Если честно, я недолюбливаю формулу 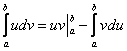 и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален:

На первом этапе находим неопределенный интеграл:

Интегрируем по частям:

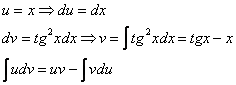
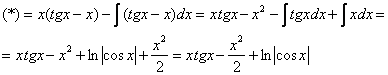
Первообразная функция найдена. …Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу ?

В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования.

На втором этапе проводим проверку (обычно на черновике).

Тоже логично. Ведь если неправильно найден неопределённый интеграл, то… правильно! И это лучше выяснить немедленно, дифференцируем ответ:

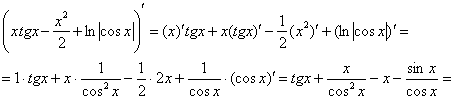
 – получена исходная подынтегральная функция, значит, первообразная найдена верно.

И третий этап – применение формулы Ньютона-Лейбница:

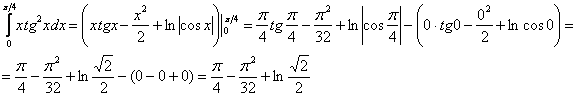
Здесь тоже есть существенная выгода! – это гораздо меньший риск запутаться в подстановках и вычислениях, т.к. формула Ньютона-Лейбница применяется всего лишь один раз.

Рассмотренный алгоритм решения
можно применить для любого определенного интеграла!

И нужно, если интеграл трудный. Так, если «чайник» решит разобранный интеграл по формуле 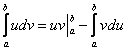 (1-м способом), то 99% где-нибудь допустит ошибку.

Уважаемый студент, распечатай и наклей рядом с формулой Ньютона-Лейбница:

1) Сначала находим неопределенный интеграл (первообразную функцию). Если не получилось, повышаем свои навыки интегрирования.

2) Проверяем найденную первообразную дифференцированием. Здесь, кстати, может статься, позабылись производные – и тогда самое время подтянуть свои навыки!

3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания. Царь тут!

И на холодную закуску интеграл для самостоятельного решения.

Пример 9
Вычислить определенный интеграл

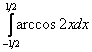
1.7. Геометрический смысл определённого интеграла

1.5. А если подвести функцию под знак дифференциала?

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 апреля 2020 года; проверки требуют 6 правок.

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие равенства

для неопределённого интеграла
int u,dv=u,v-int v,du

или в другой записи

{displaystyle int u,v'dx=u,v-int v,u'dx}
для определённого интеграла
int limits _{a}^{b}u,dv=u,v,{bigg |}_{a}^{b}-int limits _{a}^{b}v,du

Предполагается, что нахождение интеграла int v,du проще, чем {displaystyle int u,dv}. В противном случае применение метода не оправдано.

Получение формул[править | править код]

Для неопределённого интеграла[править | править код]

Функции textstyle {mathit {u}} и textstyle {mathit {v}} гладкие, следовательно, возможно дифференцирование:

d(u,v)=v,du+u,dv

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

int d(u,v)=int v,du+int u,dv

Операция интегрирования обратна дифференцированию:

u,v=int v,du+int u,dv

После перестановок:

int u,dv=u,v-int v,du

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

int {frac {dx}{x}}={frac {1}{x}}cdot x-int {frac {-1}{x^{2}}}cdot xdx=1+int {frac {dx}{x}}

Отсюда «следствие»: 0=1, что очевидно неверно.

Для определённого интеграла[править | править код]

В целом аналогично случаю неопределённого интеграла:

d(u,v)=v,du+u,dv
int limits _{a}^{b}d(u,v)=int limits _{a}^{b}v,du+int limits _{a}^{b}u,dv
int limits _{a}^{b}u,dv=u,v,{bigg |}_{a}^{b}-int limits _{a}^{b}v,du

Данные формулы справедливы, если каждая из функций u и v непрерывно дифференцируема на области интегрирования.

Табличное интегрирование по частям[править | править код]

Основной процесс приведённой выше формулы может быть обобщено в таблице.

Например, рассмотрим интеграл

{displaystyle int x^{3}cos x,dxquad } {displaystyle quad u^{(0)}=x^{3},quad v^{(n)}=cos x.}

Начнем перечислять в столбце D функцию {displaystyle u^{(0)}=x^{3}} и ее последующие производные {displaystyle u^{(i)}} до тех пор, пока не будет получен 0. Затем, перечисляем в столбце I функцию {displaystyle v^{(n)}=cos x} и ее последующие первообразные {displaystyle v^{(n-i)}} до тех пор, пока размер столбца I не будет таким же, как и в столбце D. Результат выглядит следующим образом:

# i Знак D: производные u(i) I: интегралы v(n−i)
0 + x^{3} cos x
1 − {displaystyle 3x^{2}} sin x
2 + {displaystyle 6x} {displaystyle -cos x}
3 − 6 {displaystyle -sin x}
4 + {displaystyle 0} cos x

Произведение значений в ряду i столбцов D и I вместе с соответствующим им знаком выдают соответствующие интегралы на шаге i в течение повторяющихся шагов интегрирования по частям. Шаг i = 0 несет в себе исходный интеграл. для полного результата в шаге i > 0 i-й интеграл должен быть добавлен к предыдущим произведениям(0 ≤ j < i) j-го значения столбца D и (j + 1)-го значения столбца I (т.е., умножить 1-ое значение столбца D на 2-ое значение столбца I, 2-ое значение столбца D на 3-е значение столбца I, и т.д. …) не забывая о j-м знаке. Процесс завершается, когда произведение, которое несет в себе интеграл, принимает значение 0 (i = 4 в нашем примере). Конечный результат следующий: (включая разные знаки в каждом сегменте):

{displaystyle underbrace {(+1)(x^{3})(sin x)} _{j=0}+underbrace {(-1)(3x^{2})(-cos x)} _{j=1}+underbrace {(+1)(6x)(-sin x)} _{j=2}+underbrace {(-1)(6)(cos x)} _{j=3}+underbrace {int (+1)(0)(cos x),dx} _{i=4:;to ;C}.}

В итоге:

{displaystyle underbrace {int x^{3}cos x,dx} _{text{шаг 0}}=x^{3}sin x+3x^{2}cos x-6xsin x-6cos x+C.}

Примеры[править | править код]

int x^{2}sin x,dx=int x^{2},d(-cos x)=-x^{2}cos x-int -2xcos x,dx=
=-x^{2}cos x+int 2x,d(sin x)=-x^{2}cos x+2xsin x-int 2sin x,dx=-x^{2}cos x+2xsin x+2cos x+C
  • Данный метод также используется для нахождения интегралов от элементарных функций:
int ln x,dx=xln x-int {frac {1}{x}}x,dx=xln x-x+C
int operatorname {arctg},x,dx=x,operatorname {arctg},x-int {frac {x}{1+x^{2}}},dx=x,operatorname {arctg},x-{frac {1}{2}}ln(1+x^{2})+C
  • В некоторых случаях интегрирование по частям не даёт прямого ответа:
I_{1}=int e^{{alpha x}},sin {beta x},dx=
=int e^{{alpha x}},d{Big (}-{frac {1}{beta }}cos {beta x}{Big )}=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }}int e^{{alpha x}},cos {beta x},dx=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }},I_{2}
I_{2}=int e^{{alpha x}},cos {beta x},dx=
=int e^{{alpha x}},d{Big (}{frac {1}{beta }}sin {beta x}{Big )}={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }}int e^{{alpha x}},sin {beta x},dx={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }},I_{1}
Таким образом один интеграл выражается через другой:
{begin{cases}I_{1}=-{frac {1}{beta }},e^{{alpha x}},cos {beta x}+{frac {alpha }{beta }},I_{2}\I_{2}={frac {1}{beta }},e^{{alpha x}},sin {beta x}-{frac {alpha }{beta }},I_{1}end{cases}}
Решив полученную систему, получаем:
I_{1}={frac {e^{{alpha x}}}{alpha ^{2}+beta ^{2}}}{Big (}alpha sin {beta x}-beta cos {beta x}{Big )}+C
I_{2}={frac {e^{{alpha x}}}{alpha ^{2}+beta ^{2}}}{Big (}alpha cos {beta x}+beta sin {beta x}{Big )}+C

Многомерный случай[править | править код]

Существует обобщение формулы интегрирования по частям для функций от нескольких переменных. В таком случае вместо интервала рассматривается подмножество mathbb {R} ^{n}, а вместо производной − частная производная.

Пусть Omega открытое ограниченное подмножество mathbb {R} ^{n} с кусочно-гладкой границей partial Omega . Если u и v гладкие функции на замыкании Omega , то

int _{Omega }{frac {partial u}{partial x_{i}}}v,dx=int _{{partial Omega }}uvn_{i},dsigma -int _{Omega }u{frac {partial v}{partial x_{i}}},dx

где {vec {n}} − внешняя нормаль к partial Omega , а n_{i} − её i-ая координата, i от 1 до n, sigma – мера на partial Omega .

См. также[править | править код]

  • Интеграл
  • Интеграл Римана
  • Преобразование Лежандра
  • Методы интегрирования
  • Дискретное преобразование Абеля — аналог интегрирования по частям для сумм.

Литература[править | править код]

  • Маслов А. П., Белоус Е. А. Тема 5.2 // Математика для инженеров (2 курс).
  • Тимофеев А. Ф. Интегрирование функций. — М.—Лен.: ОГИЗ, Гостехиздат, 1948. — С. 37—42.

Также см. Математический анализ#Библиография.

Ссылки[править | править код]

  • Математика для заочников и не только. Дата обращения: 11 мая 2011.
  • Канал СЗТУ на сайте youtube.com. Дата обращения: 11 мая 2011.
Источник

Добавить комментарий