Как найти определенный интеграл в питоне – Сайт, где вы сможете решить свои вопросы

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Definite integrals are the extension after indefinite integrals, definite integrals have limits [a, b]. It gives the area of a curve bounded between given limits.

$int_{a}^b F(x)dx$

It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.

In this article, we will discuss how we can solve definite integrals in python, and would also visualize the area between them using matplotlib. We would also use the NumPy module for defining the range of the variable we are integrating. Let’s Begin with installing the modules.

Module needed:

matplotlib: We would use this to visualize our area under the graph formed by a definite integral.
numpy: Helper library to define ranges of definite integrals.
sympy: Library to calculate the numerical solution of the integral easily.

Approach

For calculating area under curve

Import module
Declare function
Integrate.

Syntax :

sympy.integrate(expression, reference variable)

For plotting

Import module
Define a function
Define a variable
Draw the curve
Fill the color under it using some condition.
Display plot

Given below is the implementation for the same.

The area between a curve and standard axis

Example 1 :

Python

import matplotlib.pyplot as plt

import numpy as np

import sympy as sy

def f(x):

return x**2

x = sy.Symbol("x")

print(sy.integrate(f(x), (x, 0, 2)))

Output:

8/3

Example 2:

Python3

import matplotlib.pyplot as plt

import numpy as np

def f(x):

return x**2

x = np.linspace(0, 2, 1000)

plt.plot(x, f(x))

plt.axhline(color="black")

plt.fill_between(x, f(x), where=[(x > 0) and (x < 2) for x in x])

plt.show()

Output:

The area between two curves

Example 1:

Python3

import matplotlib.pyplot as plt

import numpy as np

import sympy as sy

def f(x):

return x**2

def g(x):

return x**(1/2)

x = sy.Symbol("x")

print(sy.integrate(f(x)-g(x), (x, 0, 2)))

Output:

0.781048583502540

Example 2:

Python3

import matplotlib.pyplot as plt

import numpy as np

def f(x):

return x**2

def g(x):

return x**(1/2)

x = np.linspace(0, 2, 1000)

plt.plot(x, f(x))

plt.plot(x, g(x))

plt.fill_between(x, f(x), g(x), where=[(x > 0) and (x < 2) for x in x])

plt.show()

Output:

Last Updated :
15 Mar, 2021

Like Article

Save Article

Источник

Дадим определение, что такое интеграл – одно из важнейших понятий математического анализа, которое возникает при решении задач: о нахождении площади под кривой; пройденного пути при неравномерном движении; массы неоднородного тела, и тому подобных; а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых.

Но мы будем рассматривать определенный интеграл

Общее определение определенного интеграла

Здесь числа aa и bb называются пределами интегрирования (по аналогии с пределами суммирования): aa — нижним, bb — верхним.

А теперь самое важное! Неопределённый интеграл от функции — это семейство первообразных функций (ключевое слово тут — функций). То есть это выражения, содержащие неизвестную.

А вот определённый интеграл — это число. Как и площадь под графиком кривой — это число. Для нахождения этого числа существует специальная формула.

То есть определённый интеграл функции f(x)f(x) равен разности значений любой её первообразной F(x)F(x) в правой и левой точках отрезка.

Первообразной для данной функции F(x), называют, такую функцию F(x) производная, которой равна f. Нахождение первообразной является операцией, обратной дифференцированию – последнее по заданной функции находит её производную, а найдя первообразную, мы, наоборот, по заданной производной определили исходную функцию.

Посмотрим, как вычислять определённые интегралы с помощью Python.

В этом поможет библиотека SciPy. Её часто используют для научных исследований, так как в ней содержатся реализации многих математических операций. Нам пригодится метод scipy.integrate.quad — он вычисляет значение определённого интеграла функции при заданных пределах интегрирования.

На вход метода quad(f, a, b) подаются подынтегральная функция f, нижний предел интегрирования a и верхний предел b.

Внутри метод заменяет исходную функцию на комбинацию более простых — таких, у которых интеграл легко вычисляется. То есть quad находит значение интеграла приближённо. В таких случаях нужна оценка погрешности — чтобы понимать, на сколько приближённое значение может отличаться от точного.

Поэтому quad возвращает два числа (res, err): приближённое значение интеграла res и оценку погрешности err.

Функция quad возвращает два значения, но сохранить нужно только первое — результат интегрирования. Можно получить его так: quad(f, a, b)[0].

Пример кода:

from scipy.integrate import quad

def d(t):

return (1/4)*(-5*t**2+14*t+50)

res = quad(d, 0, 4)[0]

print(res)

Оператор def задает функцию в данном случае (d(t).

return – оператор возврата.

Оператор ** -возводит число в степень, в данном случае , во вторую.

res- переменная в которую мы записываем результат вычислений

quad(d, 0, 4)[0] -нижний предел 0, а верхний 4.

print- печатает на экран, то что мы положили в переменную res.

Результат

51.33333333333333

А, если пятую строчку кода написать без [0], то результат будет 51.33333333333333, 5.69914485974247e-13, справа выводится погрешность вычисления.

Библиотеку scipy нужно устанавливать с помощью cmd.exe, если это windows при помощи команды pip install scipy, но перед этим должна быть установлена актуальная версия Python.

Чтобы запустить этот код в среде разработки Python нужно в меню выбрать пункт File->New File, в появившемся окне набрать код или скопировать его туда, проверить ошибки, в меню появившегося окна выбрать Run->Run Module, программа выполнится.

Вот, такой не сложный, но полезный способ подсчета определенного интеграла, хотелось показать вам.

Источник

Вычисление определённых интегралов: базовые алгоритмы

Время на прочтение
13 мин

Количество просмотров 82K

В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают “под капотом”, и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.

Определение интеграла

Интегралом (по Риману) от функции $f(x)$ на отрезке $[a;b]$ называется следующий предел:

$int_a^b f(x)dx = lim_{Delta x to 0} sum_{i=0}^{n-1} f(xi_i)(x_{i+1} - x_i),~~(1)$

где $Delta x = maxlbrace x_{i+1} - x_irbrace$ — мелкость разбиения, $x_0 = a$ , $x_n = b$ , $xi_i$ — произвольное число на отрезке $[x_i; x_{i+1}]$ .

Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.

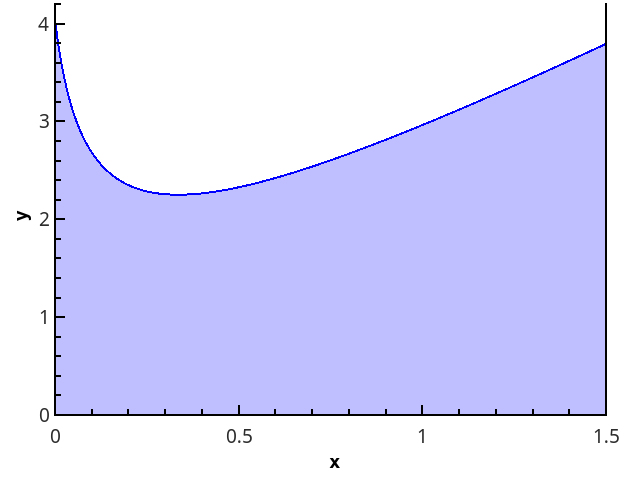
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).

Квадратурные формулы

Определение интеграла (1) можно переписать в виде

$I = int_a^b f(x)dx approx I_n = (b - a)sum_{i=0}^{n-1} w_i f(xi_i),~~(2)$

где $w_i$ — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа $n$ точек, в которых вычисляется функция.

Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки $lbrace xi_i rbrace$ и веса $w_i$ таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.

Вычислительная задача

Задана функция $f(x)$ , для которой есть алгоритм вычисления значений в любой точке отрезка $[a;b]$ (имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).

Требуется найти приближённое значение интеграла $int_a^b f(x)dx$ .
Решения будут реализованы на языке Python 3.6.

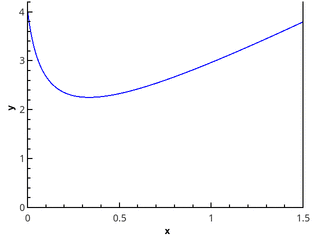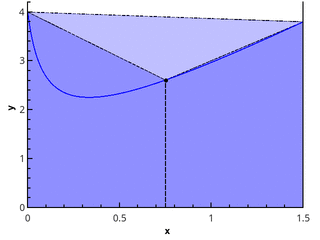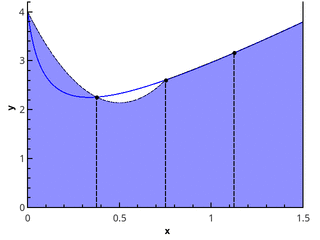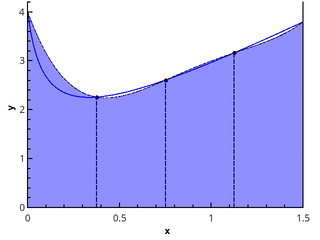
Для проверки методов используется интеграл $int_0^{3/2} left[ 2x + frac{1}{sqrt{x + 1/16}}right]dx = 17/4$ .

Кусочно-постоянная аппроксимация

Идейно простейшие квадратурные формулы возникают из применения выражения (1) “в лоб”:

$I_n = sum_{i=0}^{n-1} f(xi_i) (x_{i+1} - x_i)$

Т.к. от метода разбиения отрезка точками $lbrace x_irbrace$ и выбора точек $lbracexi_irbrace$ значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1) $xi_i = x_i$ ; 2) $xi_i = x_{i+1}$ ; 3) $xi_i = (x_i + x_{i+1}) / 2$ .

Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.

Реализация

def _rectangle_rule(func, a, b, nseg, frac):
    """Обобщённое правило прямоугольников."""
    dx = 1.0 * (b - a) / nseg
    sum = 0.0
    xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки, 
                           # в которой вычисляется функция,
                           # от левого края отрезка dx
    for i in range(npoints):
        sum += func(xstart + i * dx)

    return sum * dx

def left_rectangle_rule(func, a, b, nseg):
    """Правило левых прямоугольников"""
    return _rectangle_rule(func, a, b, nseg, 0.0)

def right_rectangle_rule(func, a, b, nseg):
    """Правило правых прямоугольников"""
    return _rectangle_rule(func, a, b, npoints, 1.0)

def midpoint_rectangle_rule(func, a, b, nseg):
    """Правило прямоугольников со средней точкой"""
    return _rectangle_rule(func, a, b, nseg, 0.5)

Для анализа производительности квадратурных формул построим график погрешности в координатах “число точек — отличие численного результата от точного”.

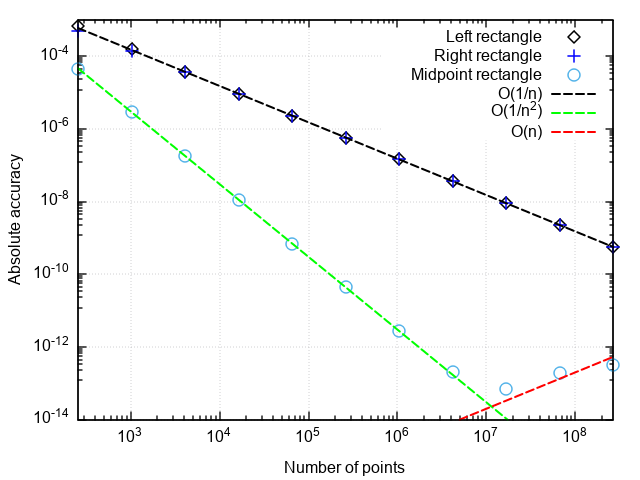
Что можно заметить:

Формула со средней точкой гораздо точнее, чем с правой или левой точками
Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е. , а формулы правых и левых прямоугольников — первый порядок, т.е. .
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как , что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).

Кусочно-линейная аппроксимация

Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

$I_n = sum_{i=0}^{n-1} frac{f(x_i) + f(x_{i+1})}{2}(x_{i+1} - x_i)~~(3)$

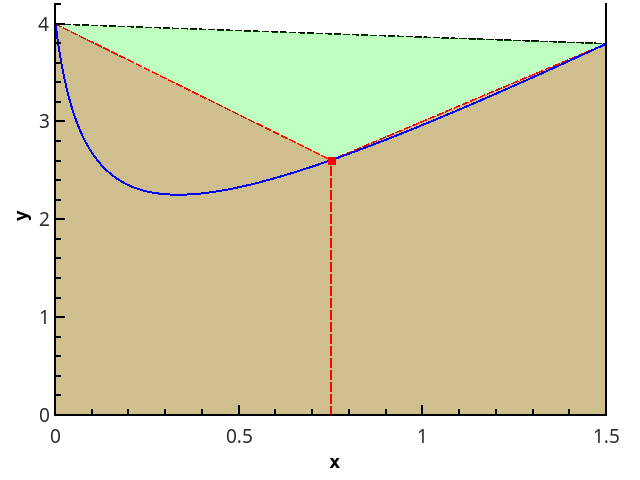
Иллюстрация метода трапеций для n=1 и n=2.

В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид

$I_n = hleft(frac{f(a) + f(b)}{2} + sum_{i=1}^{n-1} f(a + ih)right),~h=frac{b-a}{n}~~(3a)$

Реализация

def trapezoid_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    dx = 1.0 * (b - a) / nseg
    sum = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        sum += func(a + i * dx)

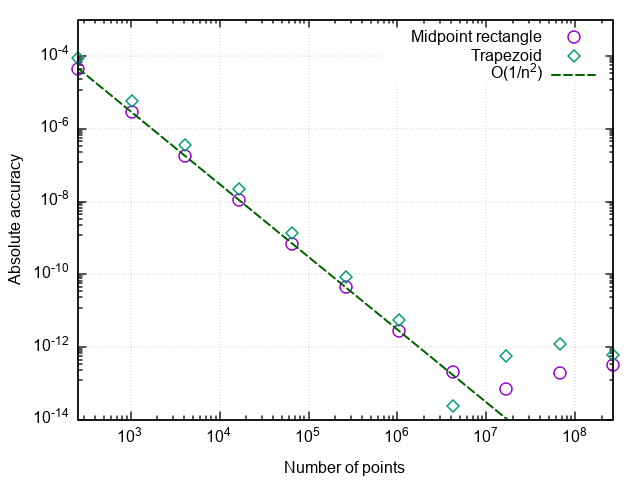
    return sum * dx

Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).

Контроль точности вычисления

Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.

Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: $Delta_{2n} approx |I_{2n} - I_n|$ . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.

Чем ещё хорош метод прямоугольников

Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x^-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.

Отсюда получаем следующий код для метода трапеций с контролем точности:

def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
    """Правило трапеций
       rtol - желаемая относительная точность вычислений
       nseg0 - начальное число отрезков разбиения"""
    nseg = nseg0
    old_ans = 0.0
    dx = 1.0 * (b - a) / nseg
    ans = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        ans += func(a + i * dx)

    ans *= dx
    err_est = max(1, abs(ans))
    while (err_est > abs(rtol * ans)):
        old_ans = ans
        ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
                                                                      # добавляются ровно в середины предыдущих отрезков
        nseg *= 2
        err_est = abs(ans - old_ans)

    return ans

С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.

Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.

Кусочно-параболическая аппроксимация

Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x₀=a, x₁, x₂), (x₂, x₃, x₄), …, (x_n-2, x_n-1, x_n=b)}.

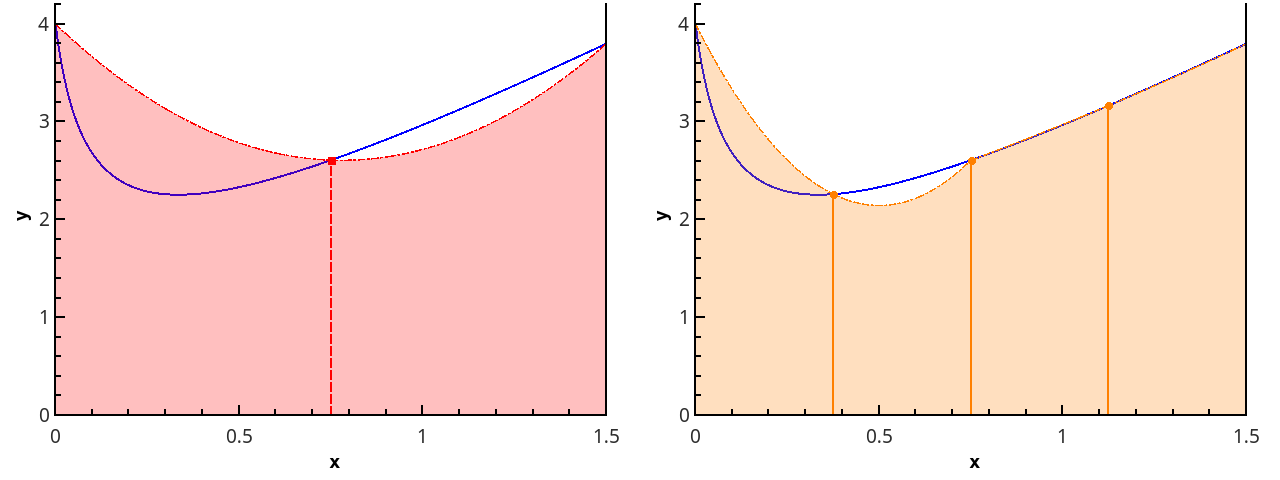
Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).

Приближая интеграл от функции на каждом из отрезков [x_k;x_k+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (x_k+1=x_k+h), получаем формулу Симпсона:

$I_{Simps, n} = sum_{i=0}^{n/2-1}frac{h}{3}[f(x_{2i})+4f(x_{2i+1})+f(x_{2i + 2})] = \ =frac{h}{3}[f(a)+4f(a+h)+2f(a+2h) + ... +4f(b-h) + f(b)]~~(4)$

Из формулы (4) напрямую получается “наивная” реализация метода Симпсона:

Заголовок спойлера

def simpson_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    if nseg%2 = 1:
        nseg += 1
    dx = 1.0 * (b - a) / nseg
    sum = (func(a) + 4 * func(a + dx) + func(b))
    for i in range(1, nseg / 2):
        sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)

    return sum * dx / 3

Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.

Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам $(a, f_0),~(a+h, f_1),~(a+2h, f_2)$ :

$I_{Simps,2} = frac{h}{3}(f_0 + 4f_1 + f_2) = frac{4}{3}hleft(frac{f_0 + f_1}{2} + frac{f_1 + f_2}{2}right) - frac{1}{3}cdot2hfrac{f_0 + f_2}{2} = \ =frac{4I_{trap,2} - I_{trap,1}}{3}$

Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.

Как-то так…

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
        """Интегрирование методом трапеций с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        ans = Quadrature.__restart(func, x0, x1, nseg0)
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            ans = Quadrature.__double_nseg(func, x0, x1)
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

    def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
        """Интегрирование методом парабол с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
        new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
        ans = (4 * new_trapez_sum - old_trapez_sum) / 3
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            old_trapez_sum = new_trapez_sum
            new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
            ans = (4 * new_trapez_sum - old_trapez_sum) / 3
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Сравним эффективность метода трапеций и парабол:

>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985

Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!

Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования $|I_{Simps, n} - I| = O(1/n^4)$ (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).

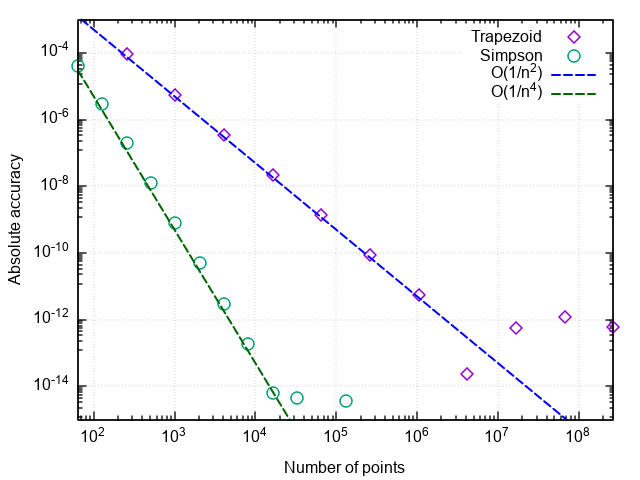
Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.

Что дальше?

Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов w_i в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.

Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:

$I_{trap,n}[f, a, b] = int_a^b f(x)dx + C_2h^2 + C_4h^4 + C_6h^6 + ...,~h = frac{b-a}{n}~~~(5)$

На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла $I(h)$ строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.

Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.

Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.

$I_{trap,n} - I approx C_2h^2;~I_{trap,2n} - I approx C_2left(frac{h}{2}right)^2$

Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:

$I = I_{trap,2n} - C_2left(frac{h}{2}right)^2 + O(h^4) approx I_{trap,2n} - frac{I_{trap,2n}-I_{trap,n}}{1-2^2} = I_{Simps,2n}$

Повторяя аналогичную процедуру для формулы Симпсона, получаем:

$I_{Simps,2n} - I approx C_4left(frac{h}{2}right)^4;~I_{Simps,n} - I approx C_4h^4$

$I = I_{Simps,2n} - C_4left(frac{h}{2}right)^4 + O(h^6) approx I_{Simps,2n} - frac{I_{Simps,2n}-I_{Simps,n}}{1-2^4}$

Если продолжить, вырисовывается такая таблица:

2 порядок	4 порядок	6 порядок
I_0,0
I_1,0	I_1,1
I_2,0	I_2,1	I_2,2
…	…	…

В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).

Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:

$I_{i,j} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-left(frac{h_{i-j}}{h_i}right)^2} = I_{i,j-1} - frac{I_{i,j-1}-I_{i-1,j-1}}{1-2^{2j}}~~~(6)$

Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.

$Delta_{i,j} approx I_{i,j} - I_{i,j-1}$

Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.

Реализация

Дополнительный метод добавляется в класс Quadrature

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
        """Интегрирование методом Ромберга
           nseg0 - начальное число отрезков разбиения
           maxcol - максимальный столбец таблицы"""
        # инициализация таблицы
        Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
        i = 0
        maxcol = max(0, maxcol)
        ans = Itable[i][i]
        error_est = max(1, abs(ans))
        while (error_est > abs(rtol * ans)):
            old_ans = ans
            i += 1
            d = 4.0
            ans_col = min(i, maxcol)
            Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
            for j in range(0, ans_col):
                diff = Itable[i][j] - Itable[i - 1][j]
                Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
                d *= 4.0

            ans = Itable[i][ans_col]
            if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
                error_est = abs(ans - Itable[i - 1][-1])
            elif (i > maxcol):
                error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
            else:
                error_est = abs(ans - Itable[i - 1][i - 1])

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Проверим, как работает аппроксимация высокого порядка:

>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
4.250000001644076

Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:

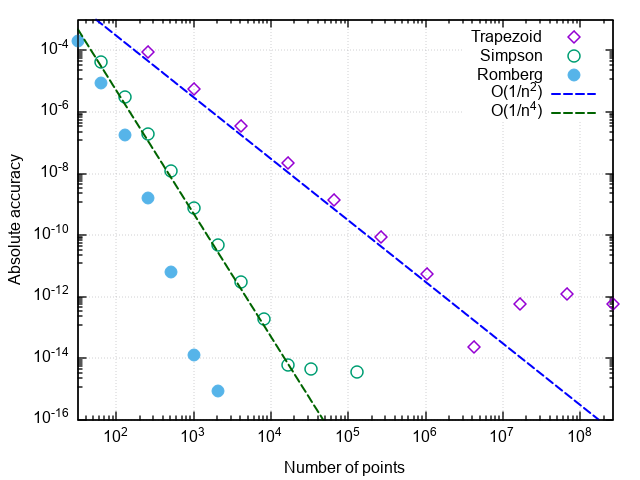
Некоторые замечания

Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10^-15, метод парабол — при желаемой точности 2×10^-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.

Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.

Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:

>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357

Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4^j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/n_i)^2j ~ 4^–ij. C учётом деления получается ~4^-(i+1)j ~ 4^–j². Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.

Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла $int_0^1sqrt{x}sin{x}dx$ и эквивалентного ему $int_0^1 2t^2sin{t^2}dt$ . Как говорится, почувствуйте разницу.

Заключение

Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования “обычных” функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.

Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).

Литература

А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

Источник

The integrals module in SymPy implements methods to calculate definite and indefinite integrals of expressions.

Principal method in this module is integrate()

integrate(f, x) returns the indefinite integral (int f,dx)

integrate(f, (x, a, b)) returns the definite integral (int_{a}^{b} f,dx)

Examples#

SymPy can integrate a vast array of functions. It can integrate polynomial functions:

>>> from sympy import *
>>> init_printing(use_unicode=False, wrap_line=False)
>>> x = Symbol('x')
>>> integrate(x**2 + x + 1, x)
 3    2
x    x
-- + -- + x
3    2

Rational functions:

>>> integrate(x/(x**2+2*x+1), x)
               1
log(x + 1) + -----
             x + 1

Exponential-polynomial functions. These multiplicative combinations of polynomials and the functions exp, cos and sin can be integrated by hand using repeated integration by parts, which is an extremely tedious process. Happily, SymPy will deal with these integrals.

>>> integrate(x**2 * exp(x) * cos(x), x)
 2  x           2  x                         x           x
x *e *sin(x)   x *e *cos(x)      x          e *sin(x)   e *cos(x)
------------ + ------------ - x*e *sin(x) + --------- - ---------
     2              2                           2           2

even a few nonelementary integrals (in particular, some integrals involving the error function) can be evaluated:

>>> integrate(exp(-x**2)*erf(x), x)
  ____    2
/ pi *erf (x)
--------------
      4

Integral Transforms#

SymPy has special support for definite integrals, and integral transforms.

sympy.integrals.transforms.mellin_transform(f, x, s, **hints)[source]#

Compute the Mellin transform (F(s)) of (f(x)),

[F(s) = int_0^infty x^{s-1} f(x) mathrm{d}x.]

For all “sensible” functions, this converges absolutely in a strip: (a < operatorname{Re}(s) < b).

Explanation

The Mellin transform is related via change of variables to the Fourier
transform, and also to the (bilateral) Laplace transform.

This function returns (F, (a, b), cond)
where F is the Mellin transform of f, (a, b) is the fundamental strip
(as above), and cond are auxiliary convergence conditions.

If the integral cannot be computed in closed form, this function returns
an unevaluated MellinTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit(). If noconds=False,
then only (F) will be returned (i.e. not cond, and also not the strip
(a, b)).

Examples

>>> from sympy import mellin_transform, exp
>>> from sympy.abc import x, s
>>> mellin_transform(exp(-x), x, s)
(gamma(s), (0, oo), True)

class sympy.integrals.transforms.MellinTransform(*args)[source]#

Class representing unevaluated Mellin transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute Mellin transforms, see the mellin_transform()
docstring.

sympy.integrals.transforms.inverse_mellin_transform(F, s, x, strip, **hints)[source]#

Compute the inverse Mellin transform of (F(s)) over the fundamental
strip given by strip=(a, b).

Explanation

This can be defined as

[f(x) = frac{1}{2pi i} int_{c – iinfty}^{c + iinfty} x^{-s} F(s) mathrm{d}s,]

for any (c) in the fundamental strip. Under certain regularity
conditions on (F) and/or (f),
this recovers (f) from its Mellin transform (F)
(and vice versa), for positive real (x).

One of (a) or (b) may be passed as None; a suitable (c) will be
inferred.

If the integral cannot be computed in closed form, this function returns
an unevaluated InverseMellinTransform object.

Note that this function will assume x to be positive and real, regardless
of the SymPy assumptions!

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().

Examples

>>> from sympy import inverse_mellin_transform, oo, gamma
>>> from sympy.abc import x, s
>>> inverse_mellin_transform(gamma(s), s, x, (0, oo))
exp(-x)

The fundamental strip matters:

>>> f = 1/(s**2 - 1)
>>> inverse_mellin_transform(f, s, x, (-oo, -1))
x*(1 - 1/x**2)*Heaviside(x - 1)/2
>>> inverse_mellin_transform(f, s, x, (-1, 1))
-x*Heaviside(1 - x)/2 - Heaviside(x - 1)/(2*x)
>>> inverse_mellin_transform(f, s, x, (1, oo))
(1/2 - x**2/2)*Heaviside(1 - x)/x

class sympy.integrals.transforms.InverseMellinTransform(*args)[source]#

Class representing unevaluated inverse Mellin transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse Mellin transforms, see the
inverse_mellin_transform() docstring.

sympy.integrals.transforms.laplace_transform(f, t, s, legacy_matrix=True, **hints)[source]#

Compute the Laplace Transform (F(s)) of (f(t)),

[F(s) = int_{0^{-}}^infty e^{-st} f(t) mathrm{d}t.]

Explanation

For all sensible functions, this converges absolutely in a
half-plane

[a < operatorname{Re}(s)]

This function returns (F, a, cond) where F is the Laplace
transform of f, (a) is the half-plane of convergence, and (cond) are
auxiliary convergence conditions.

The implementation is rule-based, and if you are interested in which
rules are applied, and whether integration is attempted, you can switch
debug information on by setting sympy.SYMPY_DEBUG=True. The numbers
of the rules in the debug information (and the code) refer to Bateman’s
Tables of Integral Transforms [1].

The lower bound is (0-), meaning that this bound should be approached
from the lower side. This is only necessary if distributions are involved.
At present, it is only done if (f(t)) contains DiracDelta, in which
case the Laplace transform is computed implicitly as

[F(s) = lim_{tauto 0^{-}} int_{tau}^infty e^{-st}
f(t) mathrm{d}t]

by applying rules.

If the Laplace transform cannot be fully computed in closed form, this
function returns expressions containing unevaluated
LaplaceTransform objects.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit(). If
noconds=True, only (F) will be returned (i.e. not cond, and also
not the plane a).

Deprecated since version 1.9: Legacy behavior for matrices where laplace_transform with
noconds=False (the default) returns a Matrix whose elements are
tuples. The behavior of laplace_transform for matrices will change
in a future release of SymPy to return a tuple of the transformed
Matrix and the convergence conditions for the matrix as a whole. Use
legacy_matrix=False to enable the new behavior.

Examples

>>> from sympy import DiracDelta, exp, laplace_transform
>>> from sympy.abc import t, s, a
>>> laplace_transform(t**4, t, s)
(24/s**5, 0, True)
>>> laplace_transform(t**a, t, s)
(gamma(a + 1)/(s*s**a), 0, re(a) > -1)
>>> laplace_transform(DiracDelta(t)-a*exp(-a*t), t, s, simplify=True)
(s/(a + s), -re(a), True)

References

class sympy.integrals.transforms.LaplaceTransform(*args)[source]#

Class representing unevaluated Laplace transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute Laplace transforms, see the laplace_transform()
docstring.

If this is called with .doit(), it returns the Laplace transform as an
expression. If it is called with .doit(noconds=False), it returns a
tuple containing the same expression, a convergence plane, and conditions.

doit(**hints)[source]#

Try to evaluate the transform in closed form.

Explanation

Standard hints are the following:
– noconds: if True, do not return convergence conditions. The
default setting is (True).
– simplify: if True, it simplifies the final result. The
default setting is (False).

sympy.integrals.transforms.inverse_laplace_transform(F, s, t, plane=None, **hints)[source]#

Compute the inverse Laplace transform of (F(s)), defined as

[f(t) = frac{1}{2pi i} int_{c-iinfty}^{c+iinfty} e^{st}
F(s) mathrm{d}s,]

for (c) so large that (F(s)) has no singularites in the
half-plane (operatorname{Re}(s) > c-epsilon).

Explanation

The plane can be specified by
argument plane, but will be inferred if passed as None.

Under certain regularity conditions, this recovers (f(t)) from its
Laplace Transform (F(s)), for non-negative (t), and vice
versa.

If the integral cannot be computed in closed form, this function returns
an unevaluated InverseLaplaceTransform object.

Note that this function will always assume (t) to be real,
regardless of the SymPy assumption on (t).

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().

Examples

>>> from sympy import inverse_laplace_transform, exp, Symbol
>>> from sympy.abc import s, t
>>> a = Symbol('a', positive=True)
>>> inverse_laplace_transform(exp(-a*s)/s, s, t)
Heaviside(-a + t)

class sympy.integrals.transforms.InverseLaplaceTransform(*args)[source]#

Class representing unevaluated inverse Laplace transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse Laplace transforms, see the
inverse_laplace_transform() docstring.

doit(**hints)[source]#

Try to evaluate the transform in closed form.

Explanation

sympy.integrals.transforms.fourier_transform(f, x, k, **hints)[source]#

Compute the unitary, ordinary-frequency Fourier transform of f, defined
as

[F(k) = int_{-infty}^infty f(x) e^{-2pi i x k} mathrm{d} x.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated FourierTransform object.

For other Fourier transform conventions, see the function
sympy.integrals.transforms._fourier_transform().

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import fourier_transform, exp
>>> from sympy.abc import x, k
>>> fourier_transform(exp(-x**2), x, k)
sqrt(pi)*exp(-pi**2*k**2)
>>> fourier_transform(exp(-x**2), x, k, noconds=False)
(sqrt(pi)*exp(-pi**2*k**2), True)

sympy.integrals.transforms._fourier_transform(f, x, k, a, b, name, simplify=True)[source]#

Compute a general Fourier-type transform

[F(k) = a int_{-infty}^{infty} e^{bixk} f(x), dx.]

For suitable choice of a and b, this reduces to the standard Fourier
and inverse Fourier transforms.

class sympy.integrals.transforms.FourierTransform(*args)[source]#

Class representing unevaluated Fourier transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute Fourier transforms, see the fourier_transform()
docstring.

sympy.integrals.transforms.inverse_fourier_transform(F, k, x, **hints)[source]#

Compute the unitary, ordinary-frequency inverse Fourier transform of (F),
defined as

[f(x) = int_{-infty}^infty F(k) e^{2pi i x k} mathrm{d} k.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated InverseFourierTransform object.

For other Fourier transform conventions, see the function
sympy.integrals.transforms._fourier_transform().

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import inverse_fourier_transform, exp, sqrt, pi
>>> from sympy.abc import x, k
>>> inverse_fourier_transform(sqrt(pi)*exp(-(pi*k)**2), k, x)
exp(-x**2)
>>> inverse_fourier_transform(sqrt(pi)*exp(-(pi*k)**2), k, x, noconds=False)
(exp(-x**2), True)

class sympy.integrals.transforms.InverseFourierTransform(*args)[source]#

Class representing unevaluated inverse Fourier transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse Fourier transforms, see the
inverse_fourier_transform() docstring.

sympy.integrals.transforms.sine_transform(f, x, k, **hints)[source]#

Compute the unitary, ordinary-frequency sine transform of (f), defined
as

[F(k) = sqrt{frac{2}{pi}} int_{0}^infty f(x) sin(2pi x k) mathrm{d} x.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated SineTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import sine_transform, exp
>>> from sympy.abc import x, k, a
>>> sine_transform(x*exp(-a*x**2), x, k)
sqrt(2)*k*exp(-k**2/(4*a))/(4*a**(3/2))
>>> sine_transform(x**(-a), x, k)
2**(1/2 - a)*k**(a - 1)*gamma(1 - a/2)/gamma(a/2 + 1/2)

class sympy.integrals.transforms.SineTransform(*args)[source]#

Class representing unevaluated sine transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute sine transforms, see the sine_transform()
docstring.

sympy.integrals.transforms.inverse_sine_transform(F, k, x, **hints)[source]#

Compute the unitary, ordinary-frequency inverse sine transform of (F),
defined as

[f(x) = sqrt{frac{2}{pi}} int_{0}^infty F(k) sin(2pi x k) mathrm{d} k.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated InverseSineTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import inverse_sine_transform, exp, sqrt, gamma
>>> from sympy.abc import x, k, a
>>> inverse_sine_transform(2**((1-2*a)/2)*k**(a - 1)*
...     gamma(-a/2 + 1)/gamma((a+1)/2), k, x)
x**(-a)
>>> inverse_sine_transform(sqrt(2)*k*exp(-k**2/(4*a))/(4*sqrt(a)**3), k, x)
x*exp(-a*x**2)

class sympy.integrals.transforms.InverseSineTransform(*args)[source]#

Class representing unevaluated inverse sine transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse sine transforms, see the
inverse_sine_transform() docstring.

sympy.integrals.transforms.cosine_transform(f, x, k, **hints)[source]#

Compute the unitary, ordinary-frequency cosine transform of (f), defined
as

[F(k) = sqrt{frac{2}{pi}} int_{0}^infty f(x) cos(2pi x k) mathrm{d} x.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated CosineTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import cosine_transform, exp, sqrt, cos
>>> from sympy.abc import x, k, a
>>> cosine_transform(exp(-a*x), x, k)
sqrt(2)*a/(sqrt(pi)*(a**2 + k**2))
>>> cosine_transform(exp(-a*sqrt(x))*cos(a*sqrt(x)), x, k)
a*exp(-a**2/(2*k))/(2*k**(3/2))

class sympy.integrals.transforms.CosineTransform(*args)[source]#

Class representing unevaluated cosine transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute cosine transforms, see the cosine_transform()
docstring.

sympy.integrals.transforms.inverse_cosine_transform(F, k, x, **hints)[source]#

Compute the unitary, ordinary-frequency inverse cosine transform of (F),
defined as

[f(x) = sqrt{frac{2}{pi}} int_{0}^infty F(k) cos(2pi x k) mathrm{d} k.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated InverseCosineTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import inverse_cosine_transform, sqrt, pi
>>> from sympy.abc import x, k, a
>>> inverse_cosine_transform(sqrt(2)*a/(sqrt(pi)*(a**2 + k**2)), k, x)
exp(-a*x)
>>> inverse_cosine_transform(1/sqrt(k), k, x)
1/sqrt(x)

class sympy.integrals.transforms.InverseCosineTransform(*args)[source]#

Class representing unevaluated inverse cosine transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse cosine transforms, see the
inverse_cosine_transform() docstring.

sympy.integrals.transforms.hankel_transform(f, r, k, nu, **hints)[source]#

Compute the Hankel transform of (f), defined as

[F_nu(k) = int_{0}^infty f(r) J_nu(k r) r mathrm{d} r.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated HankelTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import hankel_transform, inverse_hankel_transform
>>> from sympy import exp
>>> from sympy.abc import r, k, m, nu, a

>>> ht = hankel_transform(1/r**m, r, k, nu)
>>> ht
2*k**(m - 2)*gamma(-m/2 + nu/2 + 1)/(2**m*gamma(m/2 + nu/2))

>>> inverse_hankel_transform(ht, k, r, nu)
r**(-m)

>>> ht = hankel_transform(exp(-a*r), r, k, 0)
>>> ht
a/(k**3*(a**2/k**2 + 1)**(3/2))

>>> inverse_hankel_transform(ht, k, r, 0)
exp(-a*r)

class sympy.integrals.transforms.HankelTransform(*args)[source]#

Class representing unevaluated Hankel transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute Hankel transforms, see the hankel_transform()
docstring.

sympy.integrals.transforms.inverse_hankel_transform(F, k, r, nu, **hints)[source]#

Compute the inverse Hankel transform of (F) defined as

[f(r) = int_{0}^infty F_nu(k) J_nu(k r) k mathrm{d} k.]

Explanation

If the transform cannot be computed in closed form, this
function returns an unevaluated InverseHankelTransform object.

For a description of possible hints, refer to the docstring of
sympy.integrals.transforms.IntegralTransform.doit().
Note that for this transform, by default noconds=True.

Examples

>>> from sympy import hankel_transform, inverse_hankel_transform
>>> from sympy import exp
>>> from sympy.abc import r, k, m, nu, a

>>> ht = hankel_transform(1/r**m, r, k, nu)
>>> ht
2*k**(m - 2)*gamma(-m/2 + nu/2 + 1)/(2**m*gamma(m/2 + nu/2))

>>> inverse_hankel_transform(ht, k, r, nu)
r**(-m)

>>> ht = hankel_transform(exp(-a*r), r, k, 0)
>>> ht
a/(k**3*(a**2/k**2 + 1)**(3/2))

>>> inverse_hankel_transform(ht, k, r, 0)
exp(-a*r)

class sympy.integrals.transforms.InverseHankelTransform(*args)[source]#

Class representing unevaluated inverse Hankel transforms.

For usage of this class, see the IntegralTransform docstring.

For how to compute inverse Hankel transforms, see the
inverse_hankel_transform() docstring.

class sympy.integrals.transforms.IntegralTransform(*args)[source]#

Base class for integral transforms.

Explanation

This class represents unevaluated transforms.

To implement a concrete transform, derive from this class and implement
the _compute_transform(f, x, s, **hints) and _as_integral(f, x, s)
functions. If the transform cannot be computed, raise IntegralTransformError.

Also set cls._name. For instance,

>>> from sympy import LaplaceTransform
>>> LaplaceTransform._name
'Laplace'

Implement self._collapse_extra if your function returns more than just a
number and possibly a convergence condition.

doit(**hints)[source]#

Try to evaluate the transform in closed form.

Explanation

This general function handles linearity, but apart from that leaves
pretty much everything to _compute_transform.

Standard hints are the following:

simplify: whether or not to simplify the result
noconds: if True, do not return convergence conditions
needeval: if True, raise IntegralTransformError instead of

returning IntegralTransform objects

The default values of these hints depend on the concrete transform,
usually the default is
(simplify, noconds, needeval) = (True, False, False).

property function#: The function to be transformed.

property function_variable#: The dependent variable of the function to be transformed.

property transform_variable#: The independent transform variable.

exception sympy.integrals.transforms.IntegralTransformError(transform, function, msg)[source]#

Exception raised in relation to problems computing transforms.

Explanation

This class is mostly used internally; if integrals cannot be computed
objects representing unevaluated transforms are usually returned.

The hint needeval=True can be used to disable returning transform
objects, and instead raise this exception if an integral cannot be
computed.

Internals#

SymPy uses a number of algorithms to compute integrals. Algorithms are tried
in order until one produces an answer. Most of these algorithms can be enabled
or disabled manually using various flags to integrate() or doit().

SymPy first applies several heuristic algorithms, as these are the fastest:

If the function is a rational function, there is a complete algorithm for
integrating rational functions called the Lazard-Rioboo-Trager and the
Horowitz-Ostrogradsky algorithms. They are implemented in ratint().

sympy.integrals.rationaltools.ratint(f, x, **flags)[source]#

Performs indefinite integration of rational functions.

Explanation

Given a field (K) and a rational function (f = p/q),
where (p) and (q) are polynomials in (K[x]),
returns a function (g) such that (f = g’).

Examples

>>> from sympy.integrals.rationaltools import ratint
>>> from sympy.abc import x

>>> ratint(36/(x**5 - 2*x**4 - 2*x**3 + 4*x**2 + x - 2), x)
(12*x + 6)/(x**2 - 1) + 4*log(x - 2) - 4*log(x + 1)

References

[R540]

M. Bronstein, Symbolic Integration I: Transcendental
Functions, Second Edition, Springer-Verlag, 2005, pp. 35-70

sympy.integrals.rationaltools.ratint_ratpart(f, g, x)[source]#

Horowitz-Ostrogradsky algorithm.

Explanation

Given a field K and polynomials f and g in K[x], such that f and g
are coprime and deg(f) < deg(g), returns fractions A and B in K(x),
such that f/g = A’ + B and B has square-free denominator.

Examples

>>> from sympy.integrals.rationaltools import ratint_ratpart
>>> from sympy.abc import x, y
>>> from sympy import Poly
>>> ratint_ratpart(Poly(1, x, domain='ZZ'),
... Poly(x + 1, x, domain='ZZ'), x)
(0, 1/(x + 1))
>>> ratint_ratpart(Poly(1, x, domain='EX'),
... Poly(x**2 + y**2, x, domain='EX'), x)
(0, 1/(x**2 + y**2))
>>> ratint_ratpart(Poly(36, x, domain='ZZ'),
... Poly(x**5 - 2*x**4 - 2*x**3 + 4*x**2 + x - 2, x, domain='ZZ'), x)
((12*x + 6)/(x**2 - 1), 12/(x**2 - x - 2))

See also

ratint, ratint_logpart

sympy.integrals.rationaltools.ratint_logpart(f, g, x, t=None)[source]#

Lazard-Rioboo-Trager algorithm.

Explanation

Given a field K and polynomials f and g in K[x], such that f and g
are coprime, deg(f) < deg(g) and g is square-free, returns a list
of tuples (s_i, q_i) of polynomials, for i = 1..n, such that s_i
in K[t, x] and q_i in K[t], and:

          ___    ___
d  f   d    `     `
-- - = --  )      )   a log(s_i(a, x))
dx g   dx /__,   /__,
         i=1..n a | q_i(a) = 0

Examples

>>> from sympy.integrals.rationaltools import ratint_logpart
>>> from sympy.abc import x
>>> from sympy import Poly
>>> ratint_logpart(Poly(1, x, domain='ZZ'),
... Poly(x**2 + x + 1, x, domain='ZZ'), x)
[(Poly(x + 3*_t/2 + 1/2, x, domain='QQ[_t]'),
...Poly(3*_t**2 + 1, _t, domain='ZZ'))]
>>> ratint_logpart(Poly(12, x, domain='ZZ'),
... Poly(x**2 - x - 2, x, domain='ZZ'), x)
[(Poly(x - 3*_t/8 - 1/2, x, domain='QQ[_t]'),
...Poly(-_t**2 + 16, _t, domain='ZZ'))]

See also

ratint, ratint_ratpart

trigintegrate() solves integrals of trigonometric functions using
pattern matching

sympy.integrals.trigonometry.trigintegrate(f, x, conds=‘piecewise’)[source]#

Integrate f = Mul(trig) over x.

Examples

>>> from sympy import sin, cos, tan, sec
>>> from sympy.integrals.trigonometry import trigintegrate
>>> from sympy.abc import x

>>> trigintegrate(sin(x)*cos(x), x)
sin(x)**2/2

>>> trigintegrate(sin(x)**2, x)
x/2 - sin(x)*cos(x)/2

>>> trigintegrate(tan(x)*sec(x), x)
1/cos(x)

>>> trigintegrate(sin(x)*tan(x), x)
-log(sin(x) - 1)/2 + log(sin(x) + 1)/2 - sin(x)

References

deltaintegrate() solves integrals with DiracDelta objects.
sympy.integrals.deltafunctions.deltaintegrate(f, x)[source]#
Explanation

The idea for integration is the following:
- If we are dealing with a DiracDelta expression, i.e. DiracDelta(g(x)),
  we try to simplify it.
  
  If we could simplify it, then we integrate the resulting expression.
  We already know we can integrate a simplified expression, because only
  simple DiracDelta expressions are involved.
  
  If we couldn’t simplify it, there are two cases:
  1. The expression is a simple expression: we return the integral,
    taking care if we are dealing with a Derivative or with a proper
    DiracDelta.
  2. The expression is not simple (i.e. DiracDelta(cos(x))): we can do
    nothing at all.
- If the node is a multiplication node having a DiracDelta term:
  
  First we expand it.
  
  If the expansion did work, then we try to integrate the expansion.
  
  If not, we try to extract a simple DiracDelta term, then we have two
  cases:
  1. We have a simple DiracDelta term, so we return the integral.
  2. We didn’t have a simple term, but we do have an expression with
    simplified DiracDelta terms, so we integrate this expression.
Examples
```
>>> from sympy.abc import x, y, z
>>> from sympy.integrals.deltafunctions import deltaintegrate
>>> from sympy import sin, cos, DiracDelta
>>> deltaintegrate(x*sin(x)*cos(x)*DiracDelta(x - 1), x)
sin(1)*cos(1)*Heaviside(x - 1)
>>> deltaintegrate(y**2*DiracDelta(x - z)*DiracDelta(y - z), y)
z**2*DiracDelta(x - z)*Heaviside(y - z)
```
singularityintegrate() is applied if the function contains a SingularityFunction
sympy.integrals.singularityfunctions.singularityintegrate(f, x)[source]#
This function handles the indefinite integrations of Singularity functions.
The integrate function calls this function internally whenever an
instance of SingularityFunction is passed as argument.

Explanation

The idea for integration is the following:
- If we are dealing with a SingularityFunction expression,
  i.e. SingularityFunction(x, a, n), we just return
  SingularityFunction(x, a, n + 1)/(n + 1) if n >= 0 and
  SingularityFunction(x, a, n + 1) if n < 0.
- If the node is a multiplication or power node having a
  SingularityFunction term we rewrite the whole expression in terms of
  Heaviside and DiracDelta and then integrate the output. Lastly, we
  rewrite the output of integration back in terms of SingularityFunction.
- If none of the above case arises, we return None.
Examples
```
>>> from sympy.integrals.singularityfunctions import singularityintegrate
>>> from sympy import SingularityFunction, symbols, Function
>>> x, a, n, y = symbols('x a n y')
>>> f = Function('f')
>>> singularityintegrate(SingularityFunction(x, a, 3), x)
SingularityFunction(x, a, 4)/4
>>> singularityintegrate(5*SingularityFunction(x, 5, -2), x)
5*SingularityFunction(x, 5, -1)
>>> singularityintegrate(6*SingularityFunction(x, 5, -1), x)
6*SingularityFunction(x, 5, 0)
>>> singularityintegrate(x*SingularityFunction(x, 0, -1), x)
0
>>> singularityintegrate(SingularityFunction(x, 1, -1) * f(x), x)
f(1)*SingularityFunction(x, 1, 0)
```
If the heuristic algorithms cannot be applied, risch_integrate() is
tried next. The Risch algorithm is a general method for calculating
antiderivatives of elementary functions. The Risch algorithm is a decision
procedure that can determine whether an elementary solution exists, and in
that case calculate it. It can be extended to handle many nonelementary
functions in addition to the elementary ones. However, the version implemented
in SymPy only supports a small subset of the full algorithm, particularly, on
part of the transcendental algorithm for exponentials and logarithms is
implemented. An advantage of risch_integrate() over other methods is
that if it returns an instance of NonElementaryIntegral, the
integral is proven to be nonelementary by the algorithm, meaning the integral
cannot be represented using a combination of exponentials, logarithms, trig
functions, powers, rational functions, algebraic functions, and function
composition.
sympy.integrals.risch.risch_integrate(f, x, extension=None, handle_first=‘log’, separate_integral=False, rewrite_complex=None, conds=‘piecewise’)[source]#
The Risch Integration Algorithm.

Explanation

Only transcendental functions are supported. Currently, only exponentials
and logarithms are supported, but support for trigonometric functions is
forthcoming.

If this function returns an unevaluated Integral in the result, it means
that it has proven that integral to be nonelementary. Any errors will
result in raising NotImplementedError. The unevaluated Integral will be
an instance of NonElementaryIntegral, a subclass of Integral.

handle_first may be either ‘exp’ or ‘log’. This changes the order in
which the extension is built, and may result in a different (but
equivalent) solution (for an example of this, see issue 5109). It is also
possible that the integral may be computed with one but not the other,
because not all cases have been implemented yet. It defaults to ‘log’ so
that the outer extension is exponential when possible, because more of the
exponential case has been implemented.

If separate_integral is True, the result is returned as a tuple (ans, i),
where the integral is ans + i, ans is elementary, and i is either a
NonElementaryIntegral or 0. This useful if you want to try further
integrating the NonElementaryIntegral part using other algorithms to
possibly get a solution in terms of special functions. It is False by
default.

Examples
```
>>> from sympy.integrals.risch import risch_integrate
>>> from sympy import exp, log, pprint
>>> from sympy.abc import x
```
First, we try integrating exp(-x**2). Except for a constant factor of
2/sqrt(pi), this is the famous error function.
```
>>> pprint(risch_integrate(exp(-x**2), x))
  /
 |
 |    2
 |  -x
 | e    dx
 |
/
```
The unevaluated Integral in the result means that risch_integrate() has
proven that exp(-x**2) does not have an elementary anti-derivative.

In many cases, risch_integrate() can split out the elementary
anti-derivative part from the nonelementary anti-derivative part.
For example,
```
>>> pprint(risch_integrate((2*log(x)**2 - log(x) - x**2)/(log(x)**3 -
... x**2*log(x)), x))
                                         /
                                        |
  log(-x + log(x))   log(x + log(x))    |   1
- ---------------- + --------------- +  | ------ dx
         2                  2           | log(x)
                                        |
                                       /
```
This means that it has proven that the integral of 1/log(x) is
nonelementary. This function is also known as the logarithmic integral,
and is often denoted as Li(x).

risch_integrate() currently only accepts purely transcendental functions
with exponentials and logarithms, though note that this can include
nested exponentials and logarithms, as well as exponentials with bases
other than E.
```
>>> pprint(risch_integrate(exp(x)*exp(exp(x)), x))
 / x
 e /
e
>>> pprint(risch_integrate(exp(exp(x)), x))
  /
 |
 |  / x
 |  e /
 | e     dx
 |
/
```
```
>>> pprint(risch_integrate(x*x**x*log(x) + x**x + x*x**x, x))
   x
x*x
>>> pprint(risch_integrate(x**x, x))
  /
 |
 |  x
 | x  dx
 |
/
```
```
>>> pprint(risch_integrate(-1/(x*log(x)*log(log(x))**2), x))
     1
-----------
log(log(x))
```
class sympy.integrals.risch.NonElementaryIntegral(function, *symbols, **assumptions)[source]#
Represents a nonelementary Integral.

Explanation

If the result of integrate() is an instance of this class, it is
guaranteed to be nonelementary. Note that integrate() by default will try
to find any closed-form solution, even in terms of special functions which
may themselves not be elementary. To make integrate() only give
elementary solutions, or, in the cases where it can prove the integral to
be nonelementary, instances of this class, use integrate(risch=True).
In this case, integrate() may raise NotImplementedError if it cannot make
such a determination.

integrate() uses the deterministic Risch algorithm to integrate elementary
functions or prove that they have no elementary integral. In some cases,
this algorithm can split an integral into an elementary and nonelementary
part, so that the result of integrate will be the sum of an elementary
expression and a NonElementaryIntegral.

Examples
```
>>> from sympy import integrate, exp, log, Integral
>>> from sympy.abc import x
```
```
>>> a = integrate(exp(-x**2), x, risch=True)
>>> print(a)
Integral(exp(-x**2), x)
>>> type(a)
<class 'sympy.integrals.risch.NonElementaryIntegral'>
```
```
>>> expr = (2*log(x)**2 - log(x) - x**2)/(log(x)**3 - x**2*log(x))
>>> b = integrate(expr, x, risch=True)
>>> print(b)
-log(-x + log(x))/2 + log(x + log(x))/2 + Integral(1/log(x), x)
>>> type(b.atoms(Integral).pop())
<class 'sympy.integrals.risch.NonElementaryIntegral'>
```
For non-elementary definite integrals, SymPy uses so-called Meijer G-functions.
Details are described in Computing Integrals using Meijer G-Functions.

All the algorithms mentioned thus far are either pattern-matching based
heuristic, or solve integrals using algorithms that are much different from
the way most people are taught in their calculus courses. SymPy also
implements a method that can solve integrals in much the same way you would in
calculus. The advantage of this method is that it is possible to extract the
integration steps from, so that one can see how to compute the integral “by
hand”. This is used by SymPy Gamma. This is
implemented in the manualintegrate() function. The steps for an integral
can be seen with the integral_steps() function.

sympy.integrals.manualintegrate.manualintegrate(f, var)[source]#

Explanation

Compute indefinite integral of a single variable using an algorithm that
resembles what a student would do by hand.

Unlike integrate(), var can only be a single symbol.

Examples

>>> from sympy import sin, cos, tan, exp, log, integrate
>>> from sympy.integrals.manualintegrate import manualintegrate
>>> from sympy.abc import x
>>> manualintegrate(1 / x, x)
log(x)
>>> integrate(1/x)
log(x)
>>> manualintegrate(log(x), x)
x*log(x) - x
>>> integrate(log(x))
x*log(x) - x
>>> manualintegrate(exp(x) / (1 + exp(2 * x)), x)
atan(exp(x))
>>> integrate(exp(x) / (1 + exp(2 * x)))
RootSum(4*_z**2 + 1, Lambda(_i, _i*log(2*_i + exp(x))))
>>> manualintegrate(cos(x)**4 * sin(x), x)
-cos(x)**5/5
>>> integrate(cos(x)**4 * sin(x), x)
-cos(x)**5/5
>>> manualintegrate(cos(x)**4 * sin(x)**3, x)
cos(x)**7/7 - cos(x)**5/5
>>> integrate(cos(x)**4 * sin(x)**3, x)
cos(x)**7/7 - cos(x)**5/5
>>> manualintegrate(tan(x), x)
-log(cos(x))
>>> integrate(tan(x), x)
-log(cos(x))

sympy.integrals.manualintegrate.integral_steps(integrand, symbol, **options)[source]#

Returns the steps needed to compute an integral.

Returns:: rule : Rule

The first step; most rules have substeps that must also be
considered. These substeps can be evaluated using manualintegrate
to obtain a result.

Explanation

This function attempts to mirror what a student would do by hand as
closely as possible.

SymPy Gamma uses this to provide a step-by-step explanation of an
integral. The code it uses to format the results of this function can be
found at
https://github.com/sympy/sympy_gamma/blob/master/app/logic/intsteps.py.

Examples

>>> from sympy import exp, sin
>>> from sympy.integrals.manualintegrate import integral_steps
>>> from sympy.abc import x
>>> print(repr(integral_steps(exp(x) / (1 + exp(2 * x)), x)))     
URule(integrand=exp(x)/(exp(2*x) + 1), variable=x, u_var=_u, u_func=exp(x),
substep=ArctanRule(integrand=1/(_u**2 + 1), variable=_u, a=1, b=1, c=1))
>>> print(repr(integral_steps(sin(x), x)))     
SinRule(integrand=sin(x), variable=x)
>>> print(repr(integral_steps((x**2 + 3)**2, x)))     
RewriteRule(integrand=(x**2 + 3)**2, variable=x, rewritten=x**4 + 6*x**2 + 9,
substep=AddRule(integrand=x**4 + 6*x**2 + 9, variable=x,
substeps=[PowerRule(integrand=x**4, variable=x, base=x, exp=4),
ConstantTimesRule(integrand=6*x**2, variable=x, constant=6, other=x**2,
substep=PowerRule(integrand=x**2, variable=x, base=x, exp=2)),
ConstantRule(integrand=9, variable=x)]))

Finally, if all the above fail, SymPy also uses a simplified version of the
Risch algorithm, called the Risch-Norman algorithm. This algorithm is tried
last because it is often the slowest to compute. This is implemented in
heurisch():
sympy.integrals.heurisch.heurisch(f, x, rewrite=False, hints=None, mappings=None, retries=3, degree_offset=0, unnecessary_permutations=None, _try_heurisch=None)[source]#
Compute indefinite integral using heuristic Risch algorithm.

Explanation

This is a heuristic approach to indefinite integration in finite
terms using the extended heuristic (parallel) Risch algorithm, based
on Manuel Bronstein’s “Poor Man’s Integrator”.

The algorithm supports various classes of functions including
transcendental elementary or special functions like Airy,
Bessel, Whittaker and Lambert.

Note that this algorithm is not a decision procedure. If it isn’t
able to compute the antiderivative for a given function, then this is
not a proof that such a functions does not exist. One should use
recursive Risch algorithm in such case. It’s an open question if
this algorithm can be made a full decision procedure.

This is an internal integrator procedure. You should use top level
‘integrate’ function in most cases, as this procedure needs some
preprocessing steps and otherwise may fail.

Specification

heurisch(f, x, rewrite=False, hints=None)
where

f : expression
x : symbol

rewrite -> force rewrite ‘f’ in terms of ‘tan’ and ‘tanh’
hints -> a list of functions that may appear in anti-derivate

hints = None –> no suggestions at all

hints = [ ] –> try to figure out

hints = [f1, …, fn] –> we know better
Examples
```
>>> from sympy import tan
>>> from sympy.integrals.heurisch import heurisch
>>> from sympy.abc import x, y
```
```
>>> heurisch(y*tan(x), x)
y*log(tan(x)**2 + 1)/2
```
See Manuel Bronstein’s “Poor Man’s Integrator”:

References

For more information on the implemented algorithm refer to:

[R543]

K. Geddes, L. Stefanus, On the Risch-Norman Integration
Method and its Implementation in Maple, Proceedings of
ISSAC’89, ACM Press, 212-217.

[R544]

J. H. Davenport, On the Parallel Risch Algorithm (I),
Proceedings of EUROCAM’82, LNCS 144, Springer, 144-157.

[R545]

J. H. Davenport, On the Parallel Risch Algorithm (III):
Use of Tangents, SIGSAM Bulletin 16 (1982), 3-6.

[R546]

J. H. Davenport, B. M. Trager, On the Parallel Risch
Algorithm (II), ACM Transactions on Mathematical
Software 11 (1985), 356-362.
sympy.integrals.heurisch.components(f, x)[source]#
Returns a set of all functional components of the given expression
which includes symbols, function applications and compositions and
non-integer powers. Fractional powers are collected with
minimal, positive exponents.

Examples
```
>>> from sympy import cos, sin
>>> from sympy.abc import x
>>> from sympy.integrals.heurisch import components
```
```
>>> components(sin(x)*cos(x)**2, x)
{x, sin(x), cos(x)}
```

API reference#

sympy.integrals.integrals.integrate(f, var, …)[source]#

Explanation

Compute definite or indefinite integral of one or more variables
using Risch-Norman algorithm and table lookup. This procedure is
able to handle elementary algebraic and transcendental functions
and also a huge class of special functions, including Airy,
Bessel, Whittaker and Lambert.

var can be:

a symbol – indefinite integration
a tuple (symbol, a) – indefinite integration with result

given with a replacing symbol
a tuple (symbol, a, b) – definite integration

Several variables can be specified, in which case the result is
multiple integration. (If var is omitted and the integrand is
univariate, the indefinite integral in that variable will be performed.)

Indefinite integrals are returned without terms that are independent
of the integration variables. (see examples)

Definite improper integrals often entail delicate convergence
conditions. Pass conds=’piecewise’, ‘separate’ or ‘none’ to have
these returned, respectively, as a Piecewise function, as a separate
result (i.e. result will be a tuple), or not at all (default is
‘piecewise’).

Strategy

SymPy uses various approaches to definite integration. One method is to
find an antiderivative for the integrand, and then use the fundamental
theorem of calculus. Various functions are implemented to integrate
polynomial, rational and trigonometric functions, and integrands
containing DiracDelta terms.

SymPy also implements the part of the Risch algorithm, which is a decision
procedure for integrating elementary functions, i.e., the algorithm can
either find an elementary antiderivative, or prove that one does not
exist. There is also a (very successful, albeit somewhat slow) general
implementation of the heuristic Risch algorithm. This algorithm will
eventually be phased out as more of the full Risch algorithm is
implemented. See the docstring of Integral._eval_integral() for more
details on computing the antiderivative using algebraic methods.

The option risch=True can be used to use only the (full) Risch algorithm.
This is useful if you want to know if an elementary function has an
elementary antiderivative. If the indefinite Integral returned by this
function is an instance of NonElementaryIntegral, that means that the
Risch algorithm has proven that integral to be non-elementary. Note that
by default, additional methods (such as the Meijer G method outlined
below) are tried on these integrals, as they may be expressible in terms
of special functions, so if you only care about elementary answers, use
risch=True. Also note that an unevaluated Integral returned by this
function is not necessarily a NonElementaryIntegral, even with risch=True,
as it may just be an indication that the particular part of the Risch
algorithm needed to integrate that function is not yet implemented.

Another family of strategies comes from re-writing the integrand in
terms of so-called Meijer G-functions. Indefinite integrals of a
single G-function can always be computed, and the definite integral
of a product of two G-functions can be computed from zero to
infinity. Various strategies are implemented to rewrite integrands
as G-functions, and use this information to compute integrals (see
the meijerint module).

The option manual=True can be used to use only an algorithm that tries
to mimic integration by hand. This algorithm does not handle as many
integrands as the other algorithms implemented but may return results in
a more familiar form. The manualintegrate module has functions that
return the steps used (see the module docstring for more information).

In general, the algebraic methods work best for computing
antiderivatives of (possibly complicated) combinations of elementary
functions. The G-function methods work best for computing definite
integrals from zero to infinity of moderately complicated
combinations of special functions, or indefinite integrals of very
simple combinations of special functions.

The strategy employed by the integration code is as follows:

If computing a definite integral, and both limits are real,
and at least one limit is +- oo, try the G-function method of
definite integration first.
Try to find an antiderivative, using all available methods, ordered
by performance (that is try fastest method first, slowest last; in
particular polynomial integration is tried first, Meijer
G-functions second to last, and heuristic Risch last).
If still not successful, try G-functions irrespective of the
limits.

The option meijerg=True, False, None can be used to, respectively:
always use G-function methods and no others, never use G-function
methods, or use all available methods (in order as described above).
It defaults to None.

Examples

>>> from sympy import integrate, log, exp, oo
>>> from sympy.abc import a, x, y

>>> integrate(x*y, x)
x**2*y/2

>>> integrate(log(x), x)
x*log(x) - x

>>> integrate(log(x), (x, 1, a))
a*log(a) - a + 1

Terms that are independent of x are dropped by indefinite integration:

>>> from sympy import sqrt
>>> integrate(sqrt(1 + x), (x, 0, x))
2*(x + 1)**(3/2)/3 - 2/3
>>> integrate(sqrt(1 + x), x)
2*(x + 1)**(3/2)/3

>>> integrate(x*y)
Traceback (most recent call last):
...
ValueError: specify integration variables to integrate x*y

Note that integrate(x) syntax is meant only for convenience
in interactive sessions and should be avoided in library code.

>>> integrate(x**a*exp(-x), (x, 0, oo)) # same as conds='piecewise'
Piecewise((gamma(a + 1), re(a) > -1),
    (Integral(x**a*exp(-x), (x, 0, oo)), True))

>>> integrate(x**a*exp(-x), (x, 0, oo), conds='none')
gamma(a + 1)

>>> integrate(x**a*exp(-x), (x, 0, oo), conds='separate')
(gamma(a + 1), re(a) > -1)

See also

Integral, Integral.doit

sympy.integrals.integrals.line_integrate(field, Curve, variables)[source]#

Compute the line integral.

Examples

>>> from sympy import Curve, line_integrate, E, ln
>>> from sympy.abc import x, y, t
>>> C = Curve([E**t + 1, E**t - 1], (t, 0, ln(2)))
>>> line_integrate(x + y, C, [x, y])
3*sqrt(2)

The class Integral represents an unevaluated integral and has some methods that help in the integration of an expression.

class sympy.integrals.integrals.Integral(function, *symbols, **assumptions)[source]#

Represents unevaluated integral.

is_commutative#: Returns whether all the free symbols in the integral are commutative.

as_sum(n=None, method=‘midpoint’, evaluate=True)[source]#

Approximates a definite integral by a sum.

Parameters:

n :

The number of subintervals to use, optional.

method :

One of: ‘left’, ‘right’, ‘midpoint’, ‘trapezoid’.

evaluate : bool

If False, returns an unevaluated Sum expression. The default
is True, evaluate the sum.

Notes

These methods of approximate integration are described in [1].

Examples

>>> from sympy import Integral, sin, sqrt
>>> from sympy.abc import x, n
>>> e = Integral(sin(x), (x, 3, 7))
>>> e
Integral(sin(x), (x, 3, 7))

For demonstration purposes, this interval will only be split into 2
regions, bounded by [3, 5] and [5, 7].

The left-hand rule uses function evaluations at the left of each
interval:

>>> e.as_sum(2, 'left')
2*sin(5) + 2*sin(3)

The midpoint rule uses evaluations at the center of each interval:

>>> e.as_sum(2, 'midpoint')
2*sin(4) + 2*sin(6)

The right-hand rule uses function evaluations at the right of each
interval:

>>> e.as_sum(2, 'right')
2*sin(5) + 2*sin(7)

The trapezoid rule uses function evaluations on both sides of the
intervals. This is equivalent to taking the average of the left and
right hand rule results:

>>> e.as_sum(2, 'trapezoid')
2*sin(5) + sin(3) + sin(7)
>>> (e.as_sum(2, 'left') + e.as_sum(2, 'right'))/2 == _
True

Here, the discontinuity at x = 0 can be avoided by using the
midpoint or right-hand method:

>>> e = Integral(1/sqrt(x), (x, 0, 1))
>>> e.as_sum(5).n(4)
1.730
>>> e.as_sum(10).n(4)
1.809
>>> e.doit().n(4)  # the actual value is 2
2.000

The left- or trapezoid method will encounter the discontinuity and
return infinity:

>>> e.as_sum(5, 'left')
zoo

The number of intervals can be symbolic. If omitted, a dummy symbol
will be used for it.

>>> e = Integral(x**2, (x, 0, 2))
>>> e.as_sum(n, 'right').expand()
8/3 + 4/n + 4/(3*n**2)

This shows that the midpoint rule is more accurate, as its error
term decays as the square of n:

>>> e.as_sum(method='midpoint').expand()
8/3 - 2/(3*_n**2)

A symbolic sum is returned with evaluate=False:

>>> e.as_sum(n, 'midpoint', evaluate=False)
2*Sum((2*_k/n - 1/n)**2, (_k, 1, n))/n

See also

Integral.doit: Perform the integration using any hints

References

doit(**hints)[source]#

Perform the integration using any hints given.

Examples

>>> from sympy import Piecewise, S
>>> from sympy.abc import x, t
>>> p = x**2 + Piecewise((0, x/t < 0), (1, True))
>>> p.integrate((t, S(4)/5, 1), (x, -1, 1))
1/3

property free_symbols#

This method returns the symbols that will exist when the
integral is evaluated. This is useful if one is trying to
determine whether an integral depends on a certain
symbol or not.

Examples

>>> from sympy import Integral
>>> from sympy.abc import x, y
>>> Integral(x, (x, y, 1)).free_symbols
{y}

principal_value(**kwargs)[source]#

Compute the Cauchy Principal Value of the definite integral of a real function in the given interval
on the real axis.

Explanation

In mathematics, the Cauchy principal value, is a method for assigning values to certain improper
integrals which would otherwise be undefined.

Examples

>>> from sympy import Integral, oo
>>> from sympy.abc import x
>>> Integral(x+1, (x, -oo, oo)).principal_value()
oo
>>> f = 1 / (x**3)
>>> Integral(f, (x, -oo, oo)).principal_value()
0
>>> Integral(f, (x, -10, 10)).principal_value()
0
>>> Integral(f, (x, -10, oo)).principal_value() + Integral(f, (x, -oo, 10)).principal_value()
0

References

transform(x, u)[source]#

Performs a change of variables from (x) to (u) using the relationship
given by (x) and (u) which will define the transformations (f) and (F)
(which are inverses of each other) as follows:

If (x) is a Symbol (which is a variable of integration) then (u)
will be interpreted as some function, f(u), with inverse F(u).
This, in effect, just makes the substitution of x with f(x).
If (u) is a Symbol then (x) will be interpreted as some function,
F(x), with inverse f(u). This is commonly referred to as
u-substitution.

Once f and F have been identified, the transformation is made as
follows:

[int_a^b x mathrm{d}x rightarrow int_{F(a)}^{F(b)} f(x)
frac{mathrm{d}}{mathrm{d}x}]

where (F(x)) is the inverse of (f(x)) and the limits and integrand have
been corrected so as to retain the same value after integration.

Notes

The mappings, F(x) or f(u), must lead to a unique integral. Linear
or rational linear expression, 2*x, 1/x and sqrt(x), will
always work; quadratic expressions like x**2 - 1 are acceptable
as long as the resulting integrand does not depend on the sign of
the solutions (see examples).

The integral will be returned unchanged if x is not a variable of
integration.

x must be (or contain) only one of of the integration variables. If
u has more than one free symbol then it should be sent as a tuple
(u, uvar) where uvar identifies which variable is replacing
the integration variable.
XXX can it contain another integration variable?

Examples

>>> from sympy.abc import a, x, u
>>> from sympy import Integral, cos, sqrt

>>> i = Integral(x*cos(x**2 - 1), (x, 0, 1))

transform can change the variable of integration

>>> i.transform(x, u)
Integral(u*cos(u**2 - 1), (u, 0, 1))

transform can perform u-substitution as long as a unique
integrand is obtained:

>>> i.transform(x**2 - 1, u)
Integral(cos(u)/2, (u, -1, 0))

This attempt fails because x = +/-sqrt(u + 1) and the
sign does not cancel out of the integrand:

>>> Integral(cos(x**2 - 1), (x, 0, 1)).transform(x**2 - 1, u)
Traceback (most recent call last):
...
ValueError:
The mapping between F(x) and f(u) did not give a unique integrand.

transform can do a substitution. Here, the previous
result is transformed back into the original expression
using “u-substitution”:

>>> ui = _
>>> _.transform(sqrt(u + 1), x) == i
True

We can accomplish the same with a regular substitution:

>>> ui.transform(u, x**2 - 1) == i
True

If the (x) does not contain a symbol of integration then
the integral will be returned unchanged. Integral (i) does
not have an integration variable (a) so no change is made:

>>> i.transform(a, x) == i
True

When (u) has more than one free symbol the symbol that is
replacing (x) must be identified by passing (u) as a tuple:

>>> Integral(x, (x, 0, 1)).transform(x, (u + a, u))
Integral(a + u, (u, -a, 1 - a))
>>> Integral(x, (x, 0, 1)).transform(x, (u + a, a))
Integral(a + u, (a, -u, 1 - u))

See also

sympy.concrete.expr_with_limits.ExprWithLimits.variables: Lists the integration variables
as_dummy: Replace integration variables with dummy ones

Integral subclasses from ExprWithLimits, which is a
common superclass of Integral and Sum.

class sympy.concrete.expr_with_limits.ExprWithLimits(function, *symbols, **assumptions)[source]#

property bound_symbols#

Return only variables that are dummy variables.

Examples

>>> from sympy import Integral
>>> from sympy.abc import x, i, j, k
>>> Integral(x**i, (i, 1, 3), (j, 2), k).bound_symbols
[i, j]

See also

function, limits, free_symbols

as_dummy: Rename dummy variables
sympy.integrals.integrals.Integral.transform: Perform mapping on the dummy variable

property free_symbols#

This method returns the symbols in the object, excluding those
that take on a specific value (i.e. the dummy symbols).

Examples

>>> from sympy import Sum
>>> from sympy.abc import x, y
>>> Sum(x, (x, y, 1)).free_symbols
{y}

property function#

Return the function applied across limits.

Examples

>>> from sympy import Integral
>>> from sympy.abc import x
>>> Integral(x**2, (x,)).function
x**2

property has_finite_limits#

Returns True if the limits are known to be finite, either by the
explicit bounds, assumptions on the bounds, or assumptions on the
variables. False if known to be infinite, based on the bounds.
None if not enough information is available to determine.

Examples

>>> from sympy import Sum, Integral, Product, oo, Symbol
>>> x = Symbol('x')
>>> Sum(x, (x, 1, 8)).has_finite_limits
True

>>> Integral(x, (x, 1, oo)).has_finite_limits
False

>>> M = Symbol('M')
>>> Sum(x, (x, 1, M)).has_finite_limits

>>> N = Symbol('N', integer=True)
>>> Product(x, (x, 1, N)).has_finite_limits
True

property has_reversed_limits#

Returns True if the limits are known to be in reversed order, either
by the explicit bounds, assumptions on the bounds, or assumptions on the
variables. False if known to be in normal order, based on the bounds.
None if not enough information is available to determine.

Examples

>>> from sympy import Sum, Integral, Product, oo, Symbol
>>> x = Symbol('x')
>>> Sum(x, (x, 8, 1)).has_reversed_limits
True

>>> Sum(x, (x, 1, oo)).has_reversed_limits
False

>>> M = Symbol('M')
>>> Integral(x, (x, 1, M)).has_reversed_limits

>>> N = Symbol('N', integer=True, positive=True)
>>> Sum(x, (x, 1, N)).has_reversed_limits
False

>>> Product(x, (x, 2, N)).has_reversed_limits

>>> Product(x, (x, 2, N)).subs(N, N + 2).has_reversed_limits
False

property is_number#: Return True if the Sum has no free symbols, else False.

property limits#

Return the limits of expression.

Examples

>>> from sympy import Integral
>>> from sympy.abc import x, i
>>> Integral(x**i, (i, 1, 3)).limits
((i, 1, 3),)

property variables#

Return a list of the limit variables.

>>> from sympy import Sum
>>> from sympy.abc import x, i
>>> Sum(x**i, (i, 1, 3)).variables
[i]

See also

function, limits, free_symbols

as_dummy: Rename dummy variables
sympy.integrals.integrals.Integral.transform: Perform mapping on the dummy variable

TODO and Bugs#

There are still lots of functions that SymPy does not know how to integrate. For bugs related to this module, see https://github.com/sympy/sympy/issues?q=is%3Aissue+is%3Aopen+label%3Aintegrals

Numeric Integrals#

SymPy has functions to calculate points and weights for Gaussian quadrature of
any order and any precision:

sympy.integrals.quadrature.gauss_legendre(n, n_digits)[source]#

Computes the Gauss-Legendre quadrature [R550] points and weights.

Parameters:

n :

The order of quadrature.

n_digits :

Number of significant digits of the points and weights to return.

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Legendre quadrature approximates the integral:

[int_{-1}^1 f(x),dx approx sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (P_n)
and the weights (w_i) are given by:

[w_i = frac{2}{left(1-x_i^2right) left(P’_n(x_i)right)^2}]

Examples

>>> from sympy.integrals.quadrature import gauss_legendre
>>> x, w = gauss_legendre(3, 5)
>>> x
[-0.7746, 0, 0.7746]
>>> w
[0.55556, 0.88889, 0.55556]
>>> x, w = gauss_legendre(4, 5)
>>> x
[-0.86114, -0.33998, 0.33998, 0.86114]
>>> w
[0.34785, 0.65215, 0.65215, 0.34785]

References

sympy.integrals.quadrature.gauss_laguerre(n, n_digits)[source]#

Computes the Gauss-Laguerre quadrature [R552] points and weights.

Parameters:

n :

The order of quadrature.

n_digits :

Number of significant digits of the points and weights to return.

Returns:

(x, w) : The x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Laguerre quadrature approximates the integral:

[int_0^{infty} e^{-x} f(x),dx approx sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (L_n)
and the weights (w_i) are given by:

[w_i = frac{x_i}{(n+1)^2 left(L_{n+1}(x_i)right)^2}]

Examples

>>> from sympy.integrals.quadrature import gauss_laguerre
>>> x, w = gauss_laguerre(3, 5)
>>> x
[0.41577, 2.2943, 6.2899]
>>> w
[0.71109, 0.27852, 0.010389]
>>> x, w = gauss_laguerre(6, 5)
>>> x
[0.22285, 1.1889, 2.9927, 5.7751, 9.8375, 15.983]
>>> w
[0.45896, 0.417, 0.11337, 0.010399, 0.00026102, 8.9855e-7]

References

sympy.integrals.quadrature.gauss_hermite(n, n_digits)[source]#

Computes the Gauss-Hermite quadrature [R554] points and weights.

Parameters:

n :

The order of quadrature.

n_digits :

Number of significant digits of the points and weights to return.

Returns:

(x, w) : The x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Hermite quadrature approximates the integral:

[int_{-infty}^{infty} e^{-x^2} f(x),dx approx
sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (H_n)
and the weights (w_i) are given by:

[w_i = frac{2^{n-1} n! sqrt{pi}}{n^2 left(H_{n-1}(x_i)right)^2}]

Examples

>>> from sympy.integrals.quadrature import gauss_hermite
>>> x, w = gauss_hermite(3, 5)
>>> x
[-1.2247, 0, 1.2247]
>>> w
[0.29541, 1.1816, 0.29541]

>>> x, w = gauss_hermite(6, 5)
>>> x
[-2.3506, -1.3358, -0.43608, 0.43608, 1.3358, 2.3506]
>>> w
[0.00453, 0.15707, 0.72463, 0.72463, 0.15707, 0.00453]

References

sympy.integrals.quadrature.gauss_gen_laguerre(n, alpha, n_digits)[source]#

Computes the generalized Gauss-Laguerre quadrature [R557] points and weights.

Parameters:

n :

The order of quadrature.

alpha :

The exponent of the singularity, (alpha > -1).

n_digits :

Number of significant digits of the points and weights to return.

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The generalized Gauss-Laguerre quadrature approximates the integral:

[int_{0}^infty x^{alpha} e^{-x} f(x),dx approx
sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of
(L^{alpha}_n) and the weights (w_i) are given by:

[w_i = frac{Gamma(alpha+n)}
{n Gamma(n) L^{alpha}_{n-1}(x_i) L^{alpha+1}_{n-1}(x_i)}]

Examples

>>> from sympy import S
>>> from sympy.integrals.quadrature import gauss_gen_laguerre
>>> x, w = gauss_gen_laguerre(3, -S.Half, 5)
>>> x
[0.19016, 1.7845, 5.5253]
>>> w
[1.4493, 0.31413, 0.00906]

>>> x, w = gauss_gen_laguerre(4, 3*S.Half, 5)
>>> x
[0.97851, 2.9904, 6.3193, 11.712]
>>> w
[0.53087, 0.67721, 0.11895, 0.0023152]

References

sympy.integrals.quadrature.gauss_chebyshev_t(n, n_digits)[source]#

Computes the Gauss-Chebyshev quadrature [R559] points and weights of
the first kind.

Parameters:

n :

The order of quadrature.

n_digits :

Number of significant digits of the points and weights to return.

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Chebyshev quadrature of the first kind approximates the integral:

[int_{-1}^{1} frac{1}{sqrt{1-x^2}} f(x),dx approx
sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (T_n)
and the weights (w_i) are given by:

Examples

>>> from sympy.integrals.quadrature import gauss_chebyshev_t
>>> x, w = gauss_chebyshev_t(3, 5)
>>> x
[0.86602, 0, -0.86602]
>>> w
[1.0472, 1.0472, 1.0472]

>>> x, w = gauss_chebyshev_t(6, 5)
>>> x
[0.96593, 0.70711, 0.25882, -0.25882, -0.70711, -0.96593]
>>> w
[0.5236, 0.5236, 0.5236, 0.5236, 0.5236, 0.5236]

References

sympy.integrals.quadrature.gauss_chebyshev_u(n, n_digits)[source]#

Computes the Gauss-Chebyshev quadrature [R561] points and weights of
the second kind.

Parameters:

n : the order of quadrature

n_digits : number of significant digits of the points and weights to return

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Chebyshev quadrature of the second kind approximates the
integral:

[int_{-1}^{1} sqrt{1-x^2} f(x),dx approx sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (U_n)
and the weights (w_i) are given by:

[w_i = frac{pi}{n+1} sin^2 left(frac{i}{n+1}piright)]

Examples

>>> from sympy.integrals.quadrature import gauss_chebyshev_u
>>> x, w = gauss_chebyshev_u(3, 5)
>>> x
[0.70711, 0, -0.70711]
>>> w
[0.3927, 0.7854, 0.3927]

>>> x, w = gauss_chebyshev_u(6, 5)
>>> x
[0.90097, 0.62349, 0.22252, -0.22252, -0.62349, -0.90097]
>>> w
[0.084489, 0.27433, 0.42658, 0.42658, 0.27433, 0.084489]

References

sympy.integrals.quadrature.gauss_jacobi(n, alpha, beta, n_digits)[source]#

Computes the Gauss-Jacobi quadrature [R563] points and weights.

Parameters:

n : the order of quadrature

alpha : the first parameter of the Jacobi Polynomial, (alpha > -1)

beta : the second parameter of the Jacobi Polynomial, (beta > -1)

n_digits : number of significant digits of the points and weights to return

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Jacobi quadrature of the first kind approximates the integral:

[int_{-1}^1 (1-x)^alpha (1+x)^beta f(x),dx approx
sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of
(P^{(alpha,beta)}_n) and the weights (w_i) are given by:

[w_i = -frac{2n+alpha+beta+2}{n+alpha+beta+1}
frac{Gamma(n+alpha+1)Gamma(n+beta+1)}
{Gamma(n+alpha+beta+1)(n+1)!}
frac{2^{alpha+beta}}{P’_n(x_i)
P^{(alpha,beta)}_{n+1}(x_i)}]

Examples

>>> from sympy import S
>>> from sympy.integrals.quadrature import gauss_jacobi
>>> x, w = gauss_jacobi(3, S.Half, -S.Half, 5)
>>> x
[-0.90097, -0.22252, 0.62349]
>>> w
[1.7063, 1.0973, 0.33795]

>>> x, w = gauss_jacobi(6, 1, 1, 5)
>>> x
[-0.87174, -0.5917, -0.2093, 0.2093, 0.5917, 0.87174]
>>> w
[0.050584, 0.22169, 0.39439, 0.39439, 0.22169, 0.050584]

References

sympy.integrals.quadrature.gauss_lobatto(n, n_digits)[source]#

Computes the Gauss-Lobatto quadrature [R566] points and weights.

Parameters:

n : the order of quadrature

n_digits : number of significant digits of the points and weights to return

Returns:

(x, w) : the x and w are lists of points and weights as Floats.

The points (x_i) and weights (w_i) are returned as (x, w)
tuple of lists.

Explanation

The Gauss-Lobatto quadrature approximates the integral:

[int_{-1}^1 f(x),dx approx sum_{i=1}^n w_i f(x_i)]

The nodes (x_i) of an order (n) quadrature rule are the roots of (P’_(n-1))
and the weights (w_i) are given by:

[begin{split}&w_i = frac{2}{n(n-1) left[P_{n-1}(x_i)right]^2},quad xneqpm 1\
&w_i = frac{2}{n(n-1)},quad x=pm 1end{split}]

Examples

>>> from sympy.integrals.quadrature import gauss_lobatto
>>> x, w = gauss_lobatto(3, 5)
>>> x
[-1, 0, 1]
>>> w
[0.33333, 1.3333, 0.33333]
>>> x, w = gauss_lobatto(4, 5)
>>> x
[-1, -0.44721, 0.44721, 1]
>>> w
[0.16667, 0.83333, 0.83333, 0.16667]

References

Integration over Polytopes#

The intpoly module in SymPy implements methods to calculate the integral of a polynomial over 2/3-Polytopes.
Uses evaluation techniques as described in Chin et al. (2015) [1].

The input for 2-Polytope or Polygon uses the already existing Polygon data structure in SymPy. See
sympy.geometry.polygon for how to create a polygon.

For the 3-Polytope or Polyhedron, the most economical representation
is to specify a list of vertices and then to provide each constituting face(Polygon) as a list of vertex indices.

For example, consider the unit cube. Here is how it would be represented.

unit_cube = [[(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0),(1, 0, 1), (1, 1, 0), (1, 1, 1)],: [3, 7, 6, 2], [1, 5, 7, 3], [5, 4, 6, 7], [0, 4, 5, 1], [2, 0, 1, 3], [2, 6, 4, 0]]

Here, the first sublist is the list of vertices. The other smaller lists such as [3, 7, 6, 2] represent a 2D face
of the polyhedra with vertices having index 3, 7, 6 and 2 in the first sublist(in that order).

Principal method in this module is polytope_integrate()

polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x) returns the integral of (x) over the triangle with vertices (0, 0), (0, 1) and (1, 0)

polytope_integrate(unit_cube, x + y + z) returns the integral of (x + y + z) over the unit cube.

References#

[1] : Chin, Eric B., Jean B. Lasserre, and N. Sukumar. “Numerical integration of homogeneous functions on convex and nonconvex polygons and polyhedra.” Computational Mechanics 56.6 (2015): 967-981

PDF link : http://dilbert.engr.ucdavis.edu/~suku/quadrature/cls-integration.pdf

Examples#

For 2D Polygons#

Single Polynomial:

>>> from sympy.integrals.intpoly import *
>>> init_printing(use_unicode=False, wrap_line=False)
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x)
1/6
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x + x*y + y**2)
7/24

List of specified polynomials:

>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [3, x*y + y**2, x**4], max_degree=4)
          4               2
{3: 3/2, x : 1/30, x*y + y : 1/8}
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [1.125, x, x**2, 6.89*x**3, x*y + y**2, x**4], max_degree=4)
                       2              3  689    4               2
{1.125: 9/16, x: 1/6, x : 1/12, 6.89*x : ----, x : 1/30, x*y + y : 1/8}
                                         2000

Computing all monomials up to a maximum degree:

>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)),max_degree=3)
                        2         3                 2         3                      2         2
{0: 0, 1: 1/2, x: 1/6, x : 1/12, x : 1/20, y: 1/6, y : 1/12, y : 1/20, x*y: 1/24, x*y : 1/60, x *y: 1/60}

For 3-Polytopes/Polyhedra#

Single Polynomial:

>>> from sympy.integrals.intpoly import *
>>> cube = [[(0, 0, 0), (0, 0, 5), (0, 5, 0), (0, 5, 5), (5, 0, 0), (5, 0, 5), (5, 5, 0), (5, 5, 5)], [2, 6, 7, 3], [3, 7, 5, 1], [7, 6, 4, 5], [1, 5, 4, 0], [3, 1, 0, 2], [0, 4, 6, 2]]
>>> polytope_integrate(cube, x**2 + y**2 + z**2 + x*y + y*z + x*z)
-21875/4
>>> octahedron = [[(S(-1) / sqrt(2), 0, 0), (0, S(1) / sqrt(2), 0), (0, 0, S(-1) / sqrt(2)), (0, 0, S(1) / sqrt(2)), (0, S(-1) / sqrt(2), 0), (S(1) / sqrt(2), 0, 0)], [3, 4, 5], [3, 5, 1], [3, 1, 0], [3, 0, 4], [4, 0, 2], [4, 2, 5], [2, 0, 1], [5, 2, 1]]
>>> polytope_integrate(octahedron, x**2 + y**2 + z**2 + x*y + y*z + x*z)
  ___
/ 2
-----
  20

List of specified polynomials:

>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [3, x*y + y**2, x**4], max_degree=4)
          4               2
{3: 3/2, x : 1/30, x*y + y : 1/8}
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [1.125, x, x**2, 6.89*x**3, x*y + y**2, x**4], max_degree=4)
                       2              3  689    4               2
{1.125: 9/16, x: 1/6, x : 1/12, 6.89*x : ----, x : 1/30, x*y + y : 1/8}
                                         2000

Computing all monomials up to a maximum degree:

>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)),max_degree=3)
                        2         3                 2         3                      2         2
{0: 0, 1: 1/2, x: 1/6, x : 1/12, x : 1/20, y: 1/6, y : 1/12, y : 1/20, x*y: 1/24, x*y : 1/60, x *y: 1/60}

API reference#

sympy.integrals.intpoly.polytope_integrate(poly, expr=None, *, clockwise=False, max_degree=None)[source]#

Integrates polynomials over 2/3-Polytopes.

Parameters:

poly : The input Polygon.

expr : The input polynomial.

clockwise : Binary value to sort input points of 2-Polytope clockwise.(Optional)

max_degree : The maximum degree of any monomial of the input polynomial.(Optional)

Explanation

This function accepts the polytope in poly and the function in expr
(uni/bi/trivariate polynomials are implemented) and returns
the exact integral of expr over poly.

Examples

>>> from sympy.abc import x, y
>>> from sympy import Point, Polygon
>>> from sympy.integrals.intpoly import polytope_integrate
>>> polygon = Polygon(Point(0, 0), Point(0, 1), Point(1, 1), Point(1, 0))
>>> polys = [1, x, y, x*y, x**2*y, x*y**2]
>>> expr = x*y
>>> polytope_integrate(polygon, expr)
1/4
>>> polytope_integrate(polygon, polys, max_degree=3)
{1: 1, x: 1/2, y: 1/2, x*y: 1/4, x*y**2: 1/6, x**2*y: 1/6}

Источник

This post shows how to perform integral calculus of continuous and limited real functions of real variables in Python
through the use of common Python libraries frequently used in scientific applications.
The integral calculation techniques here are both primarily numerical since this site deals with computation,
however some analytical techniques are also shown.
The post is organized by examples: each paragraph contains an example of an integral to compute
and the related Python code snippet that calculates it using an appropriate library.

All of the various code snippets described in this post require Python version 3 and the NumPy library,
while individually they require an additional library (and its dependencies, if any) between
SciPy and SymPy.

We thank Prof. Fausta D’Acunzo of Preparazione 2.0 for theoretical support provided on multi-variable integral calculus.

To get the code see the Full code download paragraph at the bottom of this post.

Integration via SciPy

Integral of function of one variable (with finite extremes)

In integral calculus, the definite integral is an operator that, given a real-valued function of a real-valued variable and an interval $[a,b]$ (subset of the domain),
associates to the function the area subtended by its graph in the interval $[a,b]$.
The SciPy library provides several numerical methods for computing the integral of such functions;
the purpose of this chapter is to present a series of demos to show “by examples” the use of such methods;
for complete documentation of these methods, the reader is invited to consult the official documentation of SciPy.

Let the following integral of a function of one variable be given:

$$ int_{1}^{5} 2 x e^{-x} ,dx $$

whose analytical solution is
$ approx 1.3907 $
verifiable online via Wolfram Alpha.

Calculating the integral with quad

Below is the example of Python code that calculates the integral using
the quad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy quad')
print('Example 1-01 quad')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.

result, error = spi.quad(integrand, a, b)
print('Result is ', result, 'with error ', error)

whose output is:

Single integral computed by SciPy quad
Example 1-01 quad
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906624006967436 with error  1.54394541673402e-14

Here is the link to the code on GitHub.

Calculating the integral with fixed_quad

Below is the example of Python code that calculates the integral using
the fixed_quad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy fixed_quad')
print('Example 1-01 fixed_quad')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.

result, none = spi.fixed_quad(integrand, a, b, n=5)
print('Result is ', result)

whose output is:

Single integral computed by SciPy fixed_quad
Example 1-01 fixed_quad
Integral of 2xe^-x from x=1 to x=5
Result is  1.39066368239563

Here is the link to the code on GitHub.

Calculating the integral with quadrature

Below is the example of Python code that calculates the integral using
the quadrature function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy quadrature')
print('Example 1-01 quadrature')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.

result, error = spi.quadrature(integrand, a, b)
print('Result is ', result, 'with error ', error)

whose output is:

Single integral computed by SciPy quadrature
Example 1-01 quadrature
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906624007789083 with error  1.225092050027854e-08

Here is the link to the code on GitHub.

Calculating the integral with romberg

Below is the example of Python code that calculates the integral using
the romberg function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy romberg')
print('Example 1-01 romberg')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.

result = spi.romberg(integrand, a, b)
print('Result is ', result)

whose output is:

Single integral computed by SciPy romberg
Example 1-01 romberg
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906624006967394

Here is the link to the code on GitHub.

Calculating the integral with trapezoid

The trapezoid function is a fixed-sample function integration method,
so the code first discretizes the integration interval evenly spaced and
for all discrete values of $x$ it computes the corresponding values of $y$
and then passes the two sets of discrete values $x$ and $y$ to the integration method.

Below is the example of Python code that calculates the integral using
the trapezoid function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy trapezoid')
print('Example 1-01 trapezoid')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.
step = 1e-4

xs = np.arange(a, b, step)
ys = integrand(xs)

result = spi.trapezoid(ys, xs)
print('Result is ', result)

whose output is:

Single integral computed by SciPy trapezoid
Example 1-01 trapezoid
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906556624352673

Here is the link to the code on GitHub.

Calculating the integral with cumulative_trapezoid

The function cumulative_trapezoid is also a fixed-sample function integration method,
and so what was said about trapezoid applies.

Below is the example of Python code that calculates the integral using
of the cumulative_trapezoid function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy cumulative_trapezoid')
print('Example 1-01 cumulative_trapezoid')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.
step = 1e-4

xs = np.arange(a, b, step)
ys = integrand(xs)

result = spi.cumulative_trapezoid(ys, xs)
result = result[-1]
print('Result is ', result)

whose output is:

Single integral computed by SciPy cumulative_trapezoid
Example 1-01 cumulative_trapezoid
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906556624352677

Here is the link to the code on GitHub.

Calculating the integral with simpson

The function simpson is also a fixed-sample function integration method,
and so what was said about trapezoid applies.

Below is the example of Python code that calculates the integral using
the simpson function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy simpson')
print('Example 1-01 simpson')
print('Integral of 2xe^-x from x=1 to x=5')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = 5.
step = 1e-4

xs = np.arange(a, b, step)
ys = integrand(xs)

result = spi.simpson(ys, xs)
print('Result is ', result)

whose output is:

Single integral computed by SciPy simpson
Example 1-01 simpson
Integral of 2xe^-x from x=1 to x=5
Result is  1.3906556624801614

Here is the link to the code on GitHub.

Integral of function of one variable with quad (with extreme infinity)

Set the following integral of a function of one variable be given:

$$ int_{1}^{+infty} 2 x e^{-x} ,dx $$

whose analytical solution is
$ approx 1.4715 $
verifiable online via Wolfram Alpha.

Below is the example of Python code that calculates the integral using
the quad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Single integral computed by SciPy quad')
print('Example 1-02 quad')
print('Integral of 2xe^-x from x=1 to x-->+inf')

integrand = lambda x : 2 * x * np.exp(-x)
a = 1.
b = np.inf

result, error = spi.quad(integrand, a, b)
print('Result is ', result, 'with error ', error)

whose output is:

Single integral computed by SciPy quad
Example 1-02 quad
Integral of 2xe^-x from x=1 to x-->+inf
Result is  1.4715177646857691 with error  3.7568301883294814e-10

Here is the link to the code on GitHub.

Calculation of the length of a planar curve arc

As is well known, the integrals of a function of one variable can also be used to calculate the length of an arc of a planar curve.
If the curve is expressed in the form $y=f(x)$ and is continuous and derivable
the formula for calculating the length of the;arc of the curve between $ x=a $ and $ x=b $ is as follows:
$$ int_{a}^{b} sqrt{1 + left(frac{,dy}{,dx}right)^2} ,dx $$

If instead curve is expressed in the parametric form $x=f_x(t)$ and $y=f_y(t)$
with both $f_x$ and $f_y$ continuous and derivable,
the formula for calculating the length of the arc of the curve between $ t=a $ and $ t=b $ is as follows:
$$ int_{a}^{b} sqrt{left(frac{,dx}{,dt}right)^2 + left(frac{,dy}{,dt}right)^2} ,dt $$

Note: in the two examples that follow, the prime derivatives are calculated using the AutoGrad library.

Calculation of the length of a planar curve arc expressed in explicit form with quad

Let the following planar curve be given in explicit form:

$$ y=e^{-x^2} $$

by applying the corresponding formula above to calculate the length of the arc between $ x=-1 $ and $ x = 1 $, the integral is obtained:

$$ int_{-1}^{1} sqrt{1 + left(frac{,d(e^{-x^2})}{,dx}right)^2} ,dx $$

whose analytical solution is
$ approx 2.4089 $
verifiable online via Wolfram Alpha.

Here is the example of Python code that calculates length of a planar curve arc expressed in explicit form using
the quad function of SciPy library:

import scipy.integrate as spi
import autograd.numpy as anp   # Thinly-wrapped version of Numpy
import autograd as ag

print('Compute length of an arc of planar curve by SciPy quad')
print('Example 1-03 quad arclength')
print('Length of arc of curve y=e^(-x^2) from x=-1 to x=1')

y = lambda x : anp.exp(-x**2)
dy_dx = ag.grad(y)
integrand = lambda x : anp.sqrt(1 + dy_dx(x) ** 2)
a = -1.
b = 1.

result, error = spi.quad(integrand, a, b)
print('Result is ', result, 'with error ', error)

whose output is:

Compute length of an arc of planar curve by SciPy quad
Example 1-03 quad arclength
Length of arc of curve y=e^(-x^2) from x=-1 to x=1
Result is  2.408882141747104 with error  1.3501578327579367e-12

Here is the link to the code on GitHub.

Calculation of the length of a planar curve arc expressed in parametric form with quad

Let the following planar curve be given in parametric form:

$$ x(t)=cos^3 t $$
$$ y(t)=sin^3 t $$

by applying the corresponding formula above to calculate the length of the arc between $ t=0 $ e $ t = 2pi $, the integral is obtained:

$$ int_{0}^{2 pi} sqrt{left(frac{,d (cos^3 t)}{,dt}right)^2 + left(frac{,d (sin^3 t)}{,dt}right)^2} ,dt $$

whose analytical solution is
$ 6 $
verifiable online via Wolfram Alpha.

Here is the example of Python code that calculates length of a planar curve arc expressed in parametric form using
the quad function of SciPy library:

import scipy.integrate as spi
import autograd.numpy as anp   # Thinly-wrapped version of Numpy
import autograd as ag

print('Compute length of an arc of planar parametric curve by SciPy quad')
print('Example 1-04 quad arclength')
print('Length of arc of parametric curve x(t)=cos^3(t) and y(t)=sin^3(t) from t=0 to t=2pi')

x = lambda t : anp.cos(t) ** 3
y = lambda t : anp.sin(t) ** 3
dx_dt = ag.grad(x)
dy_dt = ag.grad(y)

integrand = lambda t : anp.sqrt(dx_dt(t) ** 2 + dy_dt(t) ** 2)
a = 0.
b = 2 * anp.pi

result, error = spi.quad(integrand, a, b)
print('Result is ', result, 'with error ', error)

whose output is:

Compute length of an arc of planar parametric curve by SciPy quad
Example 1-04 quad arclength
Length of arc of parametric curve x(t)=cos^3(t) and y(t)=sin^3(t) from t=0 to t=2pi
Result is  6.0 with error  6.616929226765933e-14

Here is the link to the code on GitHub.

Double integral of a function of two variables

In integral calculus, the definite double integral is an operator that, given a real-valued function of two real-valued variables and a set included in the domain,
associates to the function the volume of the solid (called cylindroid) between the surface described by the function and the plane containing the given set.

Let the following double integral of a function of two variables be given:

$$ int_{1}^{5} int_{y-1}^{y+1} 2 x y e^{-x y} ,dx dy $$

whose analytical solution is
$ approx 1.0273 $
verifiable online via Wolfram Alpha.

Calculating the integral with dblquad

Below is the example of Python code that calculates the integral using
the dblquad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Double integral computed by SciPy dblquad')
print('Example 2-01 dblquad')
print('Integral of 2xye^-xy from y=1 to y=5 and from x=y-1 to x=y+1')

integrand = lambda x, y : 2 * x * y * np.exp(-x * y)
ya = 1.
yb = 5.

result, error = spi.dblquad(integrand, ya, yb, lambda y: y-1, lambda y: y+1)
print('Result is ', result, 'with error ', error)

whose output is:

Double integral computed by SciPy dblquad
Example 2-01 dblquad
Integral of xye^-xy from y=1 to y=5 and from x=y-1 to x=y+1
Result is  1.0273038469260316 with error  1.3420097685964054e-14

Here is the link to the code on GitHub.

Calculating the integral with nquad

Below is the example of Python code that calculates the integral using
the nquad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Double integral computed by SciPy nquad')
print('Example 2-01 nquad')
print('Integral of 2xye^-xy from y=1 to y=5 and from x=y-1 to x=y+1')

integrand = lambda x, y : 2 * x * y * np.exp(-x * y)

bounds_y = lambda : [1., 5.]
bounds_x = lambda y : [y-1, y+1]

result, error = spi.nquad(integrand, [bounds_x, bounds_y])
print('Result is ', result, 'with error ', error)

whose output is:

Double integral computed by SciPy nquad
Example 2-01 nquad
Integral of 2xye^-xy from y=1 to y=5 and from x=y-1 to x=y+1
Result is  1.0273038469260316 with error  1.3420097685964054e-14

Here is the link to the code on GitHub.

Double integral of a function of two variables with nquad (other example)

Let the following double integral of a function of two variables be given:

$$ int_{1}^{+infty} int_{1}^{+infty} 2 x y e^{-x y} ,dx dy $$

whose analytical solution is
$ approx 1.17453 $
verifiable online via Wolfram Alpha.

Below is the example of Python code that calculates the integral using
the nquad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Double integral computed by SciPy nquad')
print('Example 2-02 nquad')
print('Integral of 2xye^-xy from y=1 to x-->+inf and from x=1 to x-->+inf')

integrand = lambda x, y : 2 * x * y * np.exp(-x * y)
ya = 1.
yb = 5.

result, error = spi.nquad(integrand, [[1, np.inf],[1, np.inf]])
print('Result is ', result, 'with error ', error)

whose output is:

Double integral computed by SciPy nquad
Example 2-02 nquad
Integral of 2xye^-xy from y=1 to y-->+inf and from x=1 to x-->+inf
Result is  1.1745267511339024 with error  1.6321550842479074e-08

Here is the link to the code on GitHub.

Triple Integral of a function of three variables

Let the following triple integral of a function of three variables be given:

$$ int_{1}^{2} int_{z+1}^{z+2} int_{y+z}^{2(y+z)} x + yz^2 ,dx dy dz $$

whose analytical solution is
$ approx 65.7194 $
verifiable online via Wolfram Alpha.

Calculating the integral with tplquad

Below is the example of Python code that calculates the integral using
the tplquad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Triple integral computed by SciPy tplquad')
print('Example 3-01 tplquad')
print('Integral of x + yz^2 from z=1 to z=2, y=z+1 to y=z+2 and from x=y+x to x=2(y+z)')

integrand = lambda x, y, z : x + y * z ** 2
za = 1.
zb = 2.
ya=lambda z: z + 1
yb=lambda z: z + 2
xa=lambda z, y : y + z
xb=lambda z, y : 2 * (y + z)

result, error = spi.tplquad(integrand, za, zb, ya, yb, xa, xb)
print('Result is ', result, 'with error ', error)

whose output is:

Triple integral computed by SciPy tplquad
Example 3-01 tplquad
Integral of x + yz^2 from z=1 to z=2, y=z+1 to y=z+2 and from x=y+x to x=2(y+z)
Result is  65.71944444444445 with error  1.659412309590769e-12

Here is the link to the code on GitHub.

Calculating the integral with nquad

Below is the example of Python code that calculates the integral using
the nquad function of the SciPy library:

import scipy.integrate as spi
import numpy as np

print('Triple integral computed by SciPy nquad')
print('Example 3-01 nquad')
print('Integral of x + yz^2 from z=1 to z=2, y=z+1 to y=z+2 and from x=y+x to x=2(y+z)')

integrand = lambda x, y, z : x + y * z ** 2

bounds_z = lambda : [1., 2.]
bounds_y = lambda z : [z+1, z+2]
bounds_x = lambda z, y : [y+z, 2 * (y+z)]
ya=lambda z: z + 1
yb=lambda z: z + 2
xa=lambda z, y : y + z
xb=lambda z, y : 2 * (y + z)

result, error = spi.nquad(integrand, [bounds_x, bounds_y, bounds_z])
print('Result is ', result, 'with error ', error)

whose output is:

Triple integral computed by SciPy nquad
Example 3-01 nquad
Integral of x + yz^2 from z=1 to z=2, y=z+1 to y=z+2 and from x=y+x to x=2(y+z)
Result is  65.71944444444445 with error  1.659412309590769e-12

Here is the link to the code on GitHub.

Integration via SymPy

Integral of function of one variable (with finite extremes)

Let the following integral of a function of one variable be given:

$$ int_{1}^{5} 2 x e^{-x} ,dx $$

whose analytical solution is
$ approx 1.3907 $
verifiable online via Wolfram Alpha.

Integral of a function of one variable with integrate(f, (x, a, b))

Below is the example of Python code that calculates the integral using
the integrate(f, (x, a, b)) function of the SymPy library:

import sympy as sp

print('Single integral computed by SymPy definite integrate')
print('Example 1-01 definite')
print('Integral of 2xe^-x from x=1 to x=5')

x = sp.Symbol('x')
f = 2 * x * sp.exp(-x)
a = 1.
b = 5.
integral = sp.integrate(f, (x, a, b))
integral = integral.evalf()
print('Result is ', integral)

whose output is:

Single integral computed by SymPy definite integrate
Example 1-01 definite
Integral of 2xe^-x from x=1 to x=5
Result is  1.39066240069674

Here is the link to the code on GitHub.

Integral of a function of one variable with integrate(f, (x, a, b)) via indefinite integral

Below is the example of Python code that calculates the integral using
the integrate(f, x) function of the SymPy library:

import sympy as sp

print('Single integral computed by SymPy indefinite integrate')
print('Example 1-01 indefinite integrate')
print('Integral of 2xe^-x from x=1 to x=5')

x = sp.Symbol('x')
f = 2 * x * sp.exp(-x)
primitive = sp.integrate(f, x)
print('Primitive is ', primitive)

primitive_lambda = sp.lambdify(x, primitive)
a = 1.
b = 5.
integral = primitive_lambda(b) - primitive_lambda(a)
print('Result is ', integral)

whose output is:

Single integral computed by SymPy indefinite integrate
Example 1-01 indefinite integrate
Integral of 2xe^-x from x=1 to x=5
Primitive is  (-2*x - 2)*exp(-x)
Result is  1.3906624006967436

The program first calculates the indefinite integral and then
applying the fundamental theorem of integral calculus,
calculates the value of the integral.

Here is the link to the code on GitHub.

Double integral of a function of two variables

Let the following double integral of a function of two variables be given:

$$ int_{1}^{4} int_{y-1}^{y+2} x y e^{-x} e^{-y} ,dx dy $$

whose analytical solution is
$ approx 0.396134 $
verifiable online via Wolfram Alpha.

Double Integral of a function of two variables with integrate(f, (x, xa, xb), (y, ya, yb))

Below is the example of Python code that calculates the integral using
the integrate(f, (x, xa, xb), (y, ya, yb)) of the SymPy library:

import sympy as sp

print('Double integral computed by SymPy definite integrate')
print('Example 2-03 definite')
print('Integral of xye^-xy from y=1 to y=4 and from x=y-1 to x=y+1')

x, y = sp.symbols('x y')
f = x * y * sp.exp(-x) * sp.exp(-y)
ya = 0.
yb = 4.
xa = y-1.
xb = y+1.

integral = sp.integrate(f, (x, xa, xb), (y, ya, yb))
integral = integral.evalf()
print('Result is ', integral)

whose output is:

Double integral computed by SymPy definite integrate
Example 2-03 definite
Integral of xye^-xy from y=1 to y=4 and from x=y-1 to x=y+1
Result is  0.396134380699524

Here is the link to the code on GitHub.

Download of the complete code

The complete code is available at GitHub.

These materials are distributed under MIT license; feel free to use, share, fork and adapt these materials as you see fit.

Also please feel free to submit pull-requests and bug-reports to this GitHub repository or contact me on my social media channels available on the top right corner of this page.

Источник

Module needed:

Approach

Python

Python3

Python3

Python3

Вычисление определённых интегралов: базовые алгоритмы

Определение интеграла

Квадратурные формулы

Вычислительная задача

Кусочно-постоянная аппроксимация

Кусочно-линейная аппроксимация

Контроль точности вычисления

Кусочно-параболическая аппроксимация

Что дальше?

Некоторые замечания

Заключение

Литература

Examples#

Integral Transforms#

Internals#

API reference#

TODO and Bugs#

Numeric Integrals#

Integration over Polytopes#

References#

Examples#

For 2D Polygons#

For 3-Polytopes/Polyhedra#

API reference#

Integration via SciPy

Integral of function of one variable (with finite extremes)

Calculating the integral with quad

Calculating the integral with fixed_quad

Calculating the integral with quadrature

Calculating the integral with romberg

Calculating the integral with trapezoid

Calculating the integral with cumulative_trapezoid

Calculating the integral with simpson

Integral of function of one variable with quad (with extreme infinity)

Calculation of the length of a planar curve arc

Calculation of the length of a planar curve arc expressed in explicit form with quad

Calculation of the length of a planar curve arc expressed in parametric form with quad

Double integral of a function of two variables

Calculating the integral with dblquad

Calculating the integral with nquad

Double integral of a function of two variables with nquad (other example)

Triple Integral of a function of three variables

Calculating the integral with tplquad

Calculating the integral with nquad

Integration via SymPy

Integral of function of one variable (with finite extremes)

Integral of a function of one variable with integrate(f, (x, a, b))

Integral of a function of one variable with integrate(f, (x, a, b)) via indefinite integral

Double integral of a function of two variables

Double Integral of a function of two variables with integrate(f, (x, xa, xb), (y, ya, yb))

Download of the complete code

Вам также может понравиться

Пилоты даргина как найти

Как найти эцп на носителе

Скайрим как найти своего коня

Добавить комментарий Отменить ответ