Как найти определитель матрицы методом элементарных преобразований

Как найти определитель матрицы методом элементарных преобразований

     
Под элементарными преобразованиями определителей понимаются следующие операции.

N Операция Результат
1 Перестановка местами двух строк или столбцов определителя. Определитель изменяет свой знак на противоположный.
2 Умножение элементов строки или столбца на ненулевое число c. Определитель умножается на число c.
3 Прибавление к строке другой строки, предварительно умноженной на любое число. Определитель не изменяется.

     
Целью таких преобразований является приведение определителя к треугольному виду, что решает проблему
его вычисления.

     
Можно поступать и несколько иначе: с помощью элементарных преобразований получить строку (или столбец),
содержащую только один ненулевой элемент, и затем разложить полученный определитель по элементам этой
строки (столбца).

     
Подобная процедура понижает порядок определителя на одну единицу.

Источник

Теорема
2.2.
Определитель
треугольной матрицы равен произведению
элементов главной диагонали:

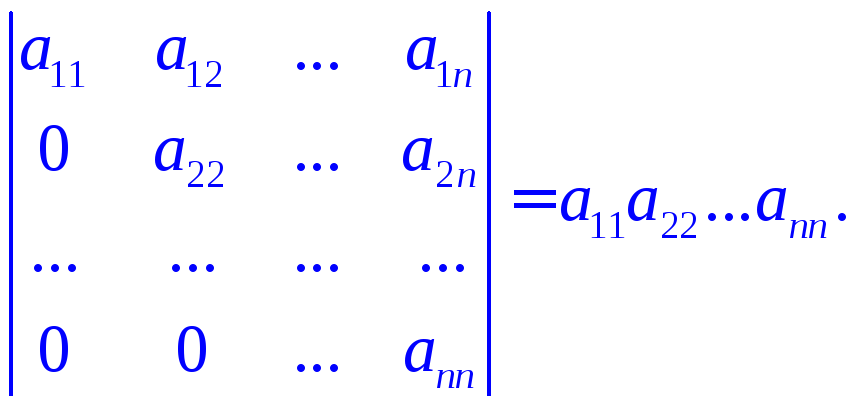
Элементарными
преобразованиями
матрицы
называются следующие преобразования:
1) умножение строки (столбца) на число,
не равное нулю; 2) прибавление одной
строки (столбца) к другой; 3) перестановка
двух строк (столбцов).

Метод
элементарных преобразований
заключается
в том, чтобы при помощи элементарных
преобразований, учитывая свойства
определителей, привести матрицу к
треугольному виду.

Пример
2.5.
Вычислить определитель при помощи
элементарных преобразований, приведя
их к треугольному виду:

Пример
2.6.
Вычислить определитель:

.

Решение.
Упростим данный определитель, а затем
вычислим его:

.

Пример
2.7. Вычислить
определитель
.

Решение.
Способ
1.При
помощи элементарных преобразований
матрицы, учитывая свойства определителей,
будем получать в какой-либо строке или
столбце нули, а затем будем разлагать
полученный определитель по этой строке
или столбцу:


–6

7

-2

-2

.

Способ
2.При
помощи элементарных преобразований
матрицы, учитывая свойства определителей,
приведем матрицу к треугольному виду:

.

Вычисление
определителей при помощи элементарных
преобразований, путем приведения его
к треугольному виду, является одним из
самых распространенных методов. Это
связано с тем, что он является основным
методом при реализации вычислений
определителей на ЭВМ. Точнее он является
одной из модификаций метода
Гаусса,
который обычно используется при решении
систем линейных уравнений.

Пример
2.8.
Вычислить определитель методом Гаусса:

Решение.
Рассмотрим первый столбец и выберем в
нем ту строку, которая содержит 1. Если
единиц нет, то нужно эту единицу создать
при помощи элементарных преобразований:
переставляя строки или столбцы, складывая
или вычитая их друг с другом, умножая
или деля их на какое-либо число (учитывая
при этом, конечно свойства определителей).
Возьмем за основу вторую строку и получим
при помощи ее нули в первом столбце:

После
этого на первую строку больше внимания
не обращаем. Рассмотрим 2-й столбец.
Здесь единиц нет, однако ее можно легко
создать, например, если поменять местами
2-й и 3-й столбцы, или если от второй строки
отнять четвертую. Далее повторяем
предыдущую операцию, т.е. создаем нули
во втором столбце:

Сейчас
рассматриваем 3-й столбец, в котором уже
имеется единица, при этом на первые две
строки не обращаем внимание. Переставляем
третью и четвертую строки и при помощи
отмеченной единицы получаем нули в
четвертой и пятой строках третьего
столбца:

Осталось
рассмотреть четвертый столбец. Вынесем
общий множитель четвертой строки, равный
2, за знак определителя и поменяем местами
две последние стоки. Далее воспользуемся
тем, что 99 кратно 33:

В
результате, получилась треугольная
матрица. Для того чтобы вычислить
определитель, осталось только перемножить
элементы матрицы, находящиеся на главной
диагонали. Таким образом, получаем
ответ: –2(–1)(–1)1334
= –264. 

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Содержание:

  • Вычисления определителей второго порядка
  • Методы вычисления определителей третьего порядка
  • Приведение определителя к треугольному виду
  • Правило треугольника
  • Правило Саррюса
  • Разложение определителя по строке или столбцу
  • Разложение определителя по элементам строки или столбца
  • Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Определитель матрицы по правилу треугольника

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.

Решение.

$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$

$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$

$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:

$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$

Полученный определитель разложим по элементам первого столбца:

$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:

$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$

$$=4 cdot(2 cdot 8-4 cdot 4)=0$$

Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$

$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$

Ответ. $Delta=-80$

Теорема Лапласа

Теорема

Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$

Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$

$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$

$$=-23+128+90=195$$

Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$

Читать дальше: обратная матрица.

Источник

Методы вычисления определителей

При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей. Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя, что соответствует элементарным преобразованиям матрицы.

I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.

II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.

III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.

При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.

Метод приведения определителя к треугольному виду

При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.

Итак, метод состоит из двух шагов.

1. При помощи элементарных преобразований привести определитель к треугольному виду.

2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.

Пример 2.12. Вычислить определитель четвёртого порядка

det{A}= begin{vmatrix}1&2&3&4\ 2&3&4&1\ 3&4&1&2\ 4&1&2&3end{vmatrix}, приводя его к треугольному виду.

Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент a_{11}=1 первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):

begin{vmatrix}1&2&3&4\ 2&3&4&1\ 3&4&1&2\ 4&1&2&3end{vmatrix}= begin{vmatrix}1&2&3&4\ 0&-1&-2&-7\ 0&-2&-8&-10\ 0&-7&-10&-13end{vmatrix}.

Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.

Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на (-1)cdot0,!5=-0,!5, т.е. умножить на (-2):

begin{vmatrix}1&2&3&4\ 0&-1&-2&-7\ 0&-2&-8&-10\ 0&-7&-10&-13end{vmatrix}= -2cdot!begin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&-1&-4&-5\ 0&-7&-10&-13end{vmatrix}.

В полученной матрице нужно сделать равными нулю элементы a_{32}=-1 и a_{42}=-7 второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента a_{22}=1 и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:

-2cdot!begin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&-1&-4&-5\ 0&-7&-10&-13end{vmatrix}= -2cdot!begin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&0&-2&2\ 0&0&4&36end{vmatrix}

Осталось сделать равным нулю элемент a_{43}. К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):

-2cdot!begin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&0&-2&2\ 0&0&4&36end{vmatrix}= -2cdot!begin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&0&-2&2\ 0&0&0&40end{vmatrix}.

Получили определитель треугольного вида.

2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:

det{A}= -2cdotbegin{vmatrix}1&2&3&4\ 0&1&2&7\ 0&0&-2&2\ 0&0&0&40end{vmatrix}= -2cdot1cdot1cdot(-2)cdot40=160.

Метод понижения порядка определителя

Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.

Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.

det{A}= begin{vmatrix}1&0&3&4\ 0&3&0&1\ 3&0&1&2\ 4&1&2&3 end{vmatrix}

Решение. 1. В качестве ведущего элемента возьмем a_{24}=1, а все остальные элементы второй строки при помощи элементарных преобразований сделаем равными нулю. Для этого ко второму столбцу прибавим четвертый, умноженный на (-3):

begin{vmatrix}1&0&3&4\ 0&3&0&1\ 3&0&1&2\ 4&1&2&3 end{vmatrix}= begin{vmatrix}1&-12&3&4\ 0&0&0&1\ 3&-6&1&2\ 4&-8&2&3end{vmatrix}.

2. Разложим определитель по второй строке

begin{vmatrix}1&-12&3&4\ 0&0&0&1\ 3&-6&1&2\ 4&-8&2&3end{vmatrix}= 1cdot(-1)^{2+4}cdot begin{vmatrix}1&-12&3\3&-6&1\4&-8&2end{vmatrix}.

Получили определитель третьего порядка.

Вынесем за знак определителя множитель (2) из второго столбца (точнее все элементы второго столбца умножим на 0,5 , а получившийся определитель умножим на 2):

begin{vmatrix}1&-12&3\3&-6&1\4&-8&2end{vmatrix}= 2cdot begin{vmatrix}1&-6&3\ 3&-3&1\ 4&-4&2end{vmatrix}.

Прибавим ко второму столбцу первый

2cdot begin{vmatrix}1&-6&3\ 3&-3&1\ 4&-4&2end{vmatrix}= 2cdot begin{vmatrix}1&-5&3\ 3&0&1\ 4&0&2end{vmatrix}.

Полученный определитель разложим по второму столбцу

2cdot begin{vmatrix}1&-5&3\ 3&0&1\ 4&0&2end{vmatrix}= 2cdot(-5)cdot(-1)^{1+2}cdot begin{vmatrix}3&1\4&2end{vmatrix}= 10cdot begin{vmatrix}3&1\4&2end{vmatrix}.

Получили определитель 2-го порядка.

Прибавим ко второй строке первую, умноженную на (-2)

10cdot begin{vmatrix}3&1\4&2end{vmatrix}= 10cdot begin{vmatrix}3&1\-2&0 end{vmatrix}.

Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом

10cdot begin{vmatrix}3&1\-2&0 end{vmatrix}= 10cdot(-2)cdot(-1)^{2+1}cdot1=20.

Результат совпадает с полученным в примере 2.7.

Метод изменения всех элементов определителя

При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.

Пусть дана квадратная матрица A n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число lambdane0 определитель умножается на число lambda^ncolon,det(lambda A)=lambda^ndet{A}.

Рассмотрим теперь определитель матрицы B, элементы которой b_{ij}=a_{ij}+x получены из соответствующих элементов матрицы A прибавлением числа xcolon

det{B}= begin{vmatrix} a_{11}+x& a_{12}+x& cdots& a_{1n}+x\ vdots&vdots& ddots&vdots\ a_{n1}+x& a_{n2}+x& cdots& a_{nn}+x end{vmatrix}.

Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей

det{B}= begin{vmatrix} a_{11}+x&a_{12}+ x&cdots& a_{1n}+x\ vdots&vdots&ddots&vdots\ a_{n1}+x&a_{n2}+ x&cdots& a_{nn}+xend{vmatrix}= begin{vmatrix}x&a_{12}+x&cdots&a_{1n}+x\ vdots&vdots&ddots&vdots\ x&a_{n2}+x&cdots&a_{nn}+xend{vmatrix}.

То же свойство применяем к каждому определителю (“раскладывая” второй столбец) и т.д. В итоге получим сумму 2^n определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных x, равны нулю (по свойству 4). Поэтому в сумме остаются только (n+1) слагаемых: определитель матрицы A и n определителей вида

D_{j}= begin{vmatrix}a_{11}&cdots&a_{1,j-1}&x& a_{1,j+1}&cdots&a_{1n}\ vdots&ddots& vdots&vdots& vdots&ddots&vdots\ a_{n1}&cdots&a_{n,j-1}&x&a_{n,j+1}& cdots&a_{nn}end{vmatrix},

отличающихся от определителя матрицы A только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на xcolon

D_{j}= xcdotsum_{i=1}^{n}A_{ij}.

Следовательно, сумма всех таких определителей D_{j},(j=1,2,ldots,n) равна сумме алгебраических дополнений всех элементов матрицы A, умноженной на x:

sum_{j=1}^{n}D_{j}= xcdotsum_{j=1}^{n}sum_{i=1}^{n}A_{ij},.

Окончательно получаем, что при увеличении всех элементов определителя на число x, определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число xcolon

begin{vmatrix}a_{11}+x&cdots&a_{1n}+x\ vdots&ddots&vdots\ a_{n1}+x&cdots&a_{nn}+xend{vmatrix}= begin{vmatrix}a_{11}&cdots&a_{1n}\ vdots&ddots&vdots\ a_{n1}&cdots&a_{nn}end{vmatrix}+ xcdotsum_{i=1}^{n} sum_{j=1}^{n}A_{ij},.

Пример 2.14. Вычислить определитель n-го порядка

D_n= begin{vmatrix}a_1&x&x&cdots&x\ x&a_2&x&cdots&x\ x&x&a_3&cdots&x\ vdots&vdots&vdots&ddots&vdots\ x&x&x&cdots&a_nend{vmatrix}.

Решение. Рассмотрим определитель диагональной матрицы A

det{A}= begin{vmatrix}a_1-x&0&0&cdots&0\ 0&a_2-x&0&cdots&0\ 0&0&a_3-x&cdots&0\ vdots&vdots&vdots&ddots&vdots\ 0&0&0&cdots&a_n-xend{vmatrix}.

Искомый определитель D_n получается прибавлением к каждому элементу определителя матрицы A числа x. Поэтому

D_n=det{A}+xcdot sum_{i=1}^{n}sum_{j=1}^{n}A_{ij},.

Определитель диагональной матрицы A равен произведению диагональных элементов:

det{A}= (a_1-x)cdot(a_2-x)cdotldotscdot(a_n-x)=prod_{i=1}^{n}(a_i-x).

Осталось вычислить сумму алгебраических дополнений всех элементов матрицы A. Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (A_{ij} при ine j, так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.

A_{ij}= (a_1-x)cdotldotscdot(a_{i-1}-x)cdot(a_{i+1}-x)cdotldotscdot(a_n-x).

Поэтому

D_{n}= prod_{i=1}^{n}(a_i-x)+xcdotsum_{k=1}^{n}prod_{i=1}^{k}(a_i-x).

Вычисление определителей с помощью рекуррентных уравнений

Этот метод заключается в том, что исходный определитель Delta_n n-го порядка выражается через определители Delta_{n-1},Delta_{n-2},ldots,Delta_{n-m} того же вида, но меньшего порядка. Получается рекуррентное уравнение

Delta_n= f(Delta_{n-1},Delta_{n-2},ldots,Delta_{n-m}).

Решая это уравнение, находим формулу, выражающую определитель Delta_n через определители Delta_1,Delta_2,ldots,Delta_m и порядок ncolon

Delta_n= F(Delta_1,Delta_2,ldots,Delta_m).

В последнюю формулу подставляем определители Delta_1,Delta_2,ldots,Delta_m невысокого (m<n) порядка, которые нетрудно вычислить каким-либо другим способом.

Замечание 2.6. Рекуррентным уравнением называется равенство вида x_n=f(n,x_{n-1},ldots,x_{n-m})=0, выражающее n-й член x_n искомой числовой последовательности {x_n} через m её предыдущих членов x_{n-1},x_{n-2},ldots,x_{n-m}. Методы решения таких уравнений рассматриваются в разд.

Пример 2.15. Вычислить определитель n-го порядка

Delta_n= begin{vmatrix}3&2&0&cdots&0&0\ -2&3&2&cdots&0&0\ 0&-2&3&cdots&0&0\ vdots&vdots&vdots&ddots&vdots&vdots\ 0&0&0&cdots&3&2\ 0&0&0&cdots&-2&3end{vmatrix}.

Решение. Разложим определитель по первой строке

Delta_n= 3cdot(-1)^{1+1}cdot begin{vmatrix}3&2&cdots&0&0\ -2&3&cdots&0&0\ vdots&vdots&ddots&vdots&vdots\ 0&0&cdots&3&2\ 0&0&cdots&-2&3end{vmatrix}+ 2cdot(-1)^{1+2}cdot begin{vmatrix}-2&2&cdots&0&0\ 0&3&cdots&0&0\ vdots&vdots&ddots&vdots&vdots\ 0&0&cdots&3&2\ 0&0&cdots&-2&3end{vmatrix}.

Первый из полученных определителей (n-l)-ro порядка обозначим Delta_{n-1}, так как он имеет такой же вид, что и Delta_n. Разложив последний определитель по первому столбцу, получим определитель того же вида, что и Delta_n, но (n-2)-го порядка

Delta_n= 3Delta_{n-1}- 2begin{vmatrix}-2&2&0&cdots&0\ 0&3&2&cdots&0\ 0&-2&3&cdots&0\ vdots&vdots&vdots&ddots&vdots\ 0&0&0&cdots&3end{vmatrix}= 3Delta_{n-1}-2(-2)(-1)^{1+1} begin{vmatrix}3&2&cdots&0\ -2&3&cdots&0\ vdots&vdots&ddots&vdots\ 0&0&cdots&3end{vmatrix}.

Следовательно, искомый определитель удовлетворяет рекуррентному уравнению

Delta_n= 3cdotDelta_{n-1}+4cdotDelta_{n-2}.

Решение этого уравнения будем искать в виде Delta_n= a(-1)^n+b4^n, где a и b — неизвестные коэффициенты. Заметим, что эта формула дает решение рекуррентного уравнения при любых коэффициентах a и b. В самом деле, подставляя Delta_n= a(-1)^n+b4^n в уравнение, получаем тождество

begin{gathered} acdot(-1)^n+bcdot4^n= 3cdotBigl[acdot(-1)^{n-1}+bcdot4^{n-1} Bigr] + 4cdotBigl[acdot(-1)^{n-2}+bcdot4^{n-2}Bigr]~~Leftrightarrow\[2pt] Leftrightarrow~~ acdot(-1)^n+bcdot4^n= -3acdot(-1)^n+frac{3}{4}bcdot4^n+4acdot(-1)^n+frac{b}{4}cdot4^n~~Leftrightarrow\[2pt] Leftrightarrow~~ acdot(-1)^n+bcdot4^n= acdot(-1)^n+bcdot4^n.end{gathered}

Подберем теперь коэффициенты a и b в формуле Delta_n= acdot(-1)^n+bcdot4^n так, чтобы при n=1 и n=2 она давала правильные результаты, т.е.

Delta_1= acdot(-1)^1+bcdot4^1=3;quad Delta_2= acdot(-1)^2+bcdot4^2= begin{vmatrix}3&2\-2&3end{vmatrix}=13.

Решая систему уравнений begin{cases}-a+4b=3,\ a+16b=13,end{cases} получаем a=frac{1}{5},,b=frac{4}{5}. Следовательно, искомый определитель равен

Delta_n= frac{1}{5}cdot(-1)^n+frac{4}{5}cdot4^n= frac{1}{5}Bigl[(-1)^n+4^{n+1}Bigr].

Пример 2.16. Вычислить определитель Вандермонда

Delta_n= begin{vmatrix}1&1&cdots&1&1\ x_1&x_2&cdots&x_{n-1}&x_n\ x_1^2&x_2^2&cdots&x_{n-1}^2&x_n^2\ vdots&vdots&ddots&vdots&vdots\ x_1^{n-1}&x_2^{n-1}&cdots&x_{n-1}^{n-1}&x_n^{n-1}end{vmatrix}. где x_1,x_2,ldots,x_n — действительные числа.

Решение. Рассмотрим определитель

Delta_n(x)= begin{vmatrix}1&1&cdots&1&1\ x_1&x_2&cdots&x_{n-1}&x\ x_1^2&x_2^2&cdots&x_{n-1}^2&x^2\ vdots&vdots&ddots&vdots&vdots\ x_1^{n-1}&x_2^{n-1}&cdots&x_{n-1}^{n-1}&x^{n-1}end{vmatrix},

который отличается от определителя Вандермонда последним столбцом, но совпадает с ним при x=x_ncolon,Delta_n(x_n)=Delta_n. Раскладывая определитель Delta_n(x) по последнему столбцу, получаем многочлен (n-1)-й степени действительной переменной xcolon

Delta_n(x)=a_{n-1}x^{n-1}+ldots+a_1x+a_0,

где старший коэффициент a_{n-1} равен алгебраическому дополнению элемента x^{n-1}colon

a_{n-1}= (-1)^{n+n}cdotDelta_{n-1}= Delta_{n-1},

т.е. определителю Delta_{n-1} — определителю Вандермонда (n-l)-ro порядка. Заметим, что при x=x_1 определитель Delta_n(x) равен нулю, так как он имеет два одинаковых столбца (свойство 4). Следовательно, x_1 — корень многочлена Delta_n(x). То же самое можно сказать про числа x_2,x_3,ldots,x_{n-1}. Все они являются корнями многочлена Delta_n(x). Следовательно, этот многочлен имеет вид:

Delta_n(x)= Delta_{n-1}cdot(x-x_1)(x-x_2)cdotldotscdot(x-x_{n-1}).

Подставляя в это равенство x=x_n и учитывая, что Delta_n(x_n)=Delta_n, получаем рекуррентное уравнение

Delta_n= Delta_{n-1}cdot(x_n-x_1)(x_n-x_2)cdotldotscdot(x_n-x_{n-1}).

Записывая аналогичным образом Delta_{n-1},Delta_{n-2},ldots,Delta_2 и учитывая, что Delta_1=1, получаем

Delta_n= (x_2-x_1)(x_3-x_1)(x_3-x_2)cdotldotscdot(x_n-x_1)(x_n-x_2)cdotldotscdot(x_n-x_{n-1})= prod_{1leqslant j<ileqslant n}(x_i-x_j).

Таким образом, определитель Вандермонда равен произведению всех разностей x_i-x_j при 1leqslant j<ileqslant n.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определитель матрицы онлайн

В нашем калькуляторе вы сможете бесплатно найти определитель матрицы онлайн с подробным решением и даже с комплексными числами. Вычисление определителя происходит путем приведения ее к ступенчатому виду, а затем перемножением элементов главной диагонали.

Подробнее о том, как пользоваться нашим онлайн калькулятором, вы можете прочитать в инструкции.

О методе

Чтобы вычислить определитель матрицы, нужно выполнить следующие шаги.

  1. Записываем матрицу (обязательно квадратную).
  2. С помощью элементарных преобразований приводим ее к ступенчатому виду, при котором матрица имеет треугольный вид, так что все элементы, расположенные ниже главной диагонали, нулевые.
  3. После этих манипуляций определитель матрицы равен произведению элементов на главной диагонали.

Чтобы лучше всего понять принцип вычисления, введите любой пример, выберите “очень подробное решение” и изучите полученный ответ.

Источник

Добавить комментарий