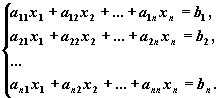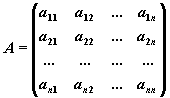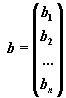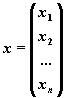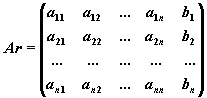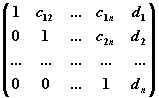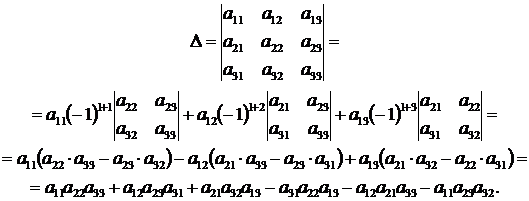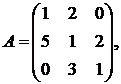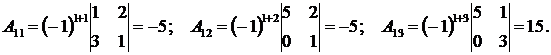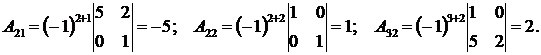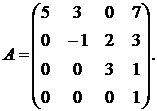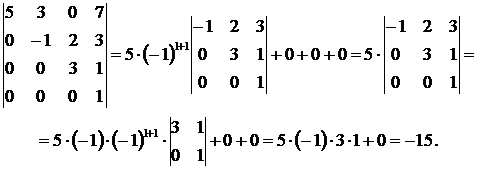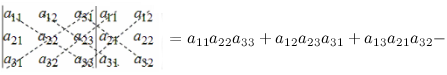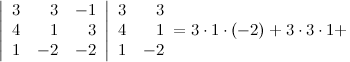Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2022 года; проверки требует 1 правка.
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
Формулировка[править | править код]
Для начала введём несколько определений.
Пусть 
— матрица размера 
, и пусть выбраны любые 
строк матрицы 
с номерами 
и любые столбцов с номерами 
.
Определитель матрицы, получаемой из вычеркиванием всех строк и столбцов, кроме выбранных, называется минором -го порядка, расположенным в строках с номерами 
и столбцах с номерами 
. Он обозначается следующим образом:
А определитель матрицы, получаемой вычеркиванием только выбранных строк и столбцов из квадратной матрицы, называется дополнительным минором к минору 
:
где 
и 
— номера невыбранных строк и столбцов.
Алгебраическое дополнение минора определяется следующим образом:
где 
, 
.
Справедливо следующее утверждение.
Теорема Лапласа
- Пусть выбраны любые
строк матрицы
- где суммирование ведётся по всевозможным номерам столбцов
Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать столбцов из 
, то есть биномиальному коэффициенту 
.
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Примеры
Рассмотрим квадратную матрицу
Выберем вторую и четвертую строки и разложим определитель этой матрицы по теореме Лапласа. Заметим, что в этих строках все миноры второго порядка, кроме 
, содержат нулевые столбцы, т.е. заведомо равны нулю и на сумму в теореме не влияют.
Поэтому определитель будет равен:
Из приведенного примера видно, что теорема Лапласа упрощает вычисление определителей не всех матриц, а только матриц особого вида. Поэтому на практике чаще используются другие методы, например, метод Гаусса. Теорема больше применяется для теоретических исследований.
Разложение определителя по строке (столбцу) (Следствие 1)[править | править код]
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть — квадратная матрица размера . Пусть также задан некоторый номер строки 
либо номер столбца 
матрицы . Тогда определитель может быть вычислен по следующим формулам:
Разложение по
Разложение по
где 
— алгебраическое дополнение к минору, расположенному в строке с номером и столбце с номером . также называют алгебраическим дополнением к элементу 
.
Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить равным 1 и выбрать -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.
Примеры
Рассмотрим квадратную матрицу
Разложим определитель по элементам первой строки матрицы:
(Обратите внимание, что у алгебраического дополнения ко второму элементу первой строки отрицательный знак).
Также определитель можно разложить, например, по элементам второго столбца:
Следствие 2 (фальшивое разложение определителя)[править | править код]
Сумма произведений всех элементов некоторой строки (столбца) матрицы на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
Доказательство
Рассмотрим сумму произведений всех элементов произвольной -ой строки матрицы на алгебраические дополнения соответствующих элементов любой другой, скажем, -ой строки матрицы . Пусть 
– матрица, у которой все строки, кроме -ой, такие же, как у матрицы , а элементами -ой строки матрицы являются соответствующие элементы -ой строки матрицы . Тогда у матрицы две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что 
. С другой стороны, по следствию 1 определитель 
равен сумме произведений всех элементов -ой строки матрицы на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов -ой строки матрицы совпадают с алгебраическими дополнениями соответствующих элементов -ой строки матрицы . Но элементами -ой строки матрицы являются соответствующие элементы -ой строки матрицы . Таким образом, сумма произведений всех элементов -ой строки матрицы на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов -ой строки матрицы на алгебраические дополнения соответствующих элементов -ой строки матрицы .
Примечания[править | править код]
- ↑ Smith, D. E. Project Gutenberg’s History of Modern Mathematics. — P. 18. Архивная копия от 16 сентября 2009 на Wayback Machine
Литература[править | править код]
- Ильин, В. А., Позняк, Э. Г. Линейная алгебра. — 6-е изд. — М.: Физматлит, 2005. — С. 25-27. — ISBN 5-9221-0481-0.
- Прасолов, В. В. Задачи и теоремы линейной алгебры. — 2-е изд. — М., 2008. — С. 42-45.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009. — С. 374-376.
Теорема Лапласа
Определение.
Определитель квадратной матрицы равен
сумме произведений элементов любой
строки (столбца) на их алгебраические
дополнения:
(разложение
по элементам i-й
строки);
(разложение
по элементам j-го
столбца).
Убедимся в
справедливости теоремы Лапласа на
примере определителя матрицы третьего
порядка. Разложим его вначале по элементам
первой строки
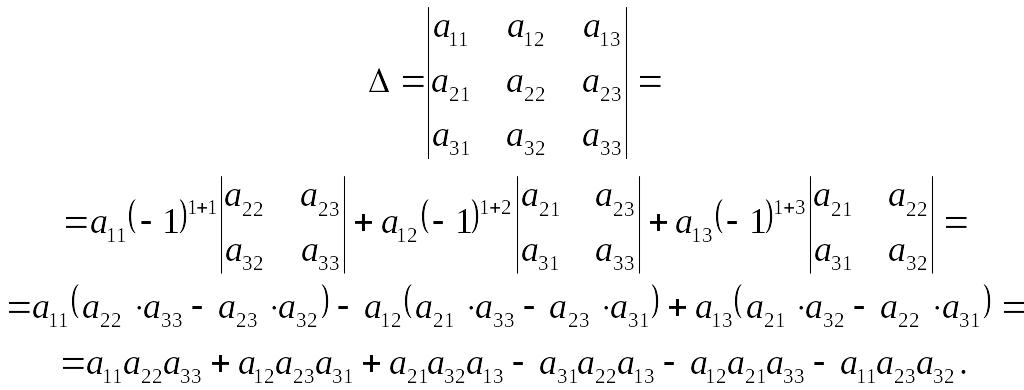
Что совпадает
с определением определителя матрицы
третьего порядка.
Пример:
Вычислить определитель четвертого
порядка треугольной матрицы:
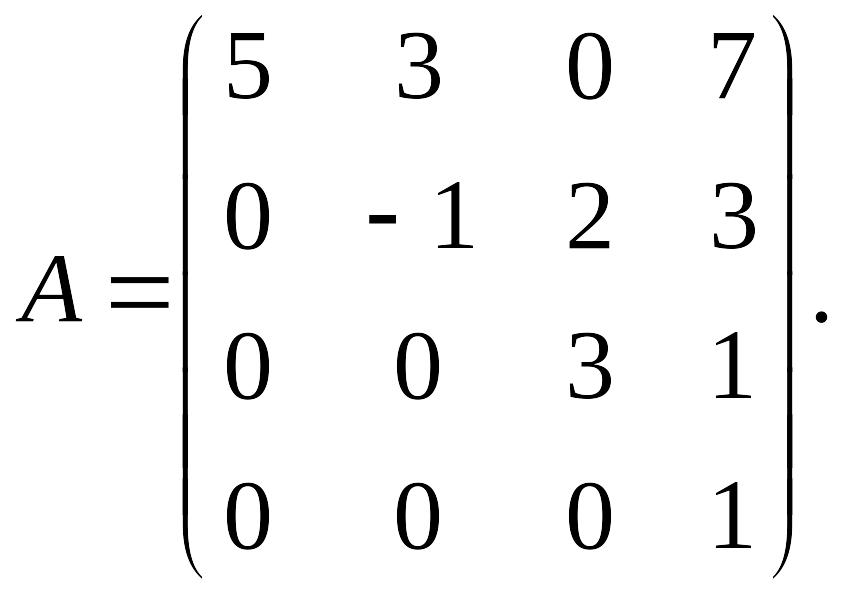
Решение:
Выполним разложение по первому столбцу:
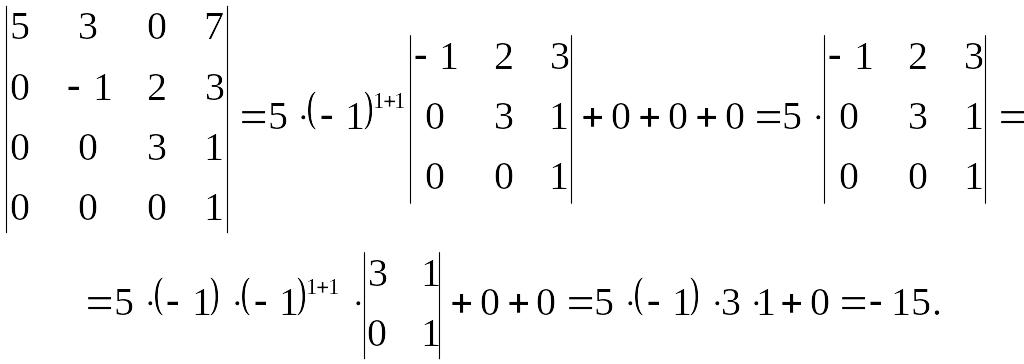
Значение теоремы
Лапласа состоит в том, что она позволяет
свести вычисление определителей n-го
порядка к вычислению определителя
меньшего порядка, то есть (n-1)-го
порядка.
СЛАУ
Р
ассмотрим
систему
линейных алгебраических уравнений
(СЛАУ) относительно n
неизвестных x1
, x2
, …, xn:
(1)
–
числа-коэффициенты.
1
i
m
1
j
n
Эта
система в «свернутом» виде может быть
записана так:
ni=1aij
xj
= bi
В
соответствии с правилом
умножения матриц рассмотренная
система линейных уравнений может быть
записана в матричной
форме
Ax=b,
где
,
,
.
Матрица
A,
столбцами которой являются коэффициенты
при соответствующих неизвестных, а
строками – коэффициенты при неизвестных
в соответствующем уравнении называется
матрицей
системы.
Матрица-столбец b,
элементами которой являются правые
части уравнений системы, называется
матрицей правой части или просто правой
частью
системы.
Матрица-столбец x,
элементы которой – искомые неизвестные,
называется решением
системы.
Система
линейных алгебраических уравнений,
записанная в виде Ax=b,
является матричным
уравнением.
Если
матрица системы невырождена,
то у нее существует обратная матрица и
тогда решение системы Ax=b
дается формулой:
x=A
-1
b.
Решение слау
Определение
Упорядоченный
набор из n
чисел
Решение
системы(1) Если при подстановке этих
чисел в уравнение вместо соответствующих
неизвестных каждое уравнение становится
верным числовым равенством.
Система называется
несовместной, если множество решений
пусто, в противном случае-совместная
система. Если существует единственное
решение, то определённая система,
неопределённая система, если решений
бесчисленное множество.
Квадратные системы. Правило Крамера.
Если
определитель
D=det
A
матрицы системы Ax=b
отличен от нуля, то система имеет
единственное решение x1
, x2
, …, xn,
определяемое формулами
Крамера
Видно,
что
k
это определитель, получающийся из
заменой столбца с номером k
столбцом свободных членов.
Xk
=
k
/
, k=1,2,
…, n.
– Формула Крамера
Если
определитель
0
и система совместна, то она имеет
единственное решение, находящиеся по
формуле Крамера.
Пример. Вычисление
решения системы линейных уравнений по
формулам Крамера.
Решить
систему:
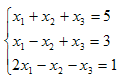
х1
= 12/6=2, х2
=
6/6=1, х3
= 12/6=2.
Универсальный способ решения слау
Метод
Гаусса
применим для решения системы линейных
алгебраических уравнений c
невырожденной матрицей системы. Идея
метода Гаусса состоит в том, что систему
n
линейных алгебраических уравнений
относительно n
неизвестных x1
, x2
, …, xn
приводят
последовательным исключением неизвестных
к эквивалентной системе с треугольной
матрицей
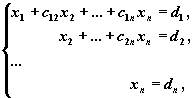
решение которой
находят по рекуррентным формулам:
Матричная
запись
метода Гаусса.
-
Шаг.
Прямой
ход
метода Гаусса: приведение расширенной
матрицы системы
к
ступенчатому виду
с
помощью элементарных
операций над строками
матрицы (под элементарными операциями
понимаются следующие операции:
-перестановка
строк;
-умножение
строки на число, отличное от нуля;
-сложение
строки матрицы с другой строкой,
умноженной на отличное от нуля чиcло).
-
Шаг.
Обратный
ход
метода Гаусса: преобразование полученной
ступенчатой матрицы к матрице, в первых
n
столбцах которой содержится единичная
матрица
,последний, (n+1)-й,
столбец этой матрицы содержит решение
системы.
Пример.
Решить
систему уравнений методом Гаусса.
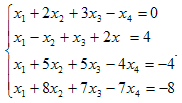
Решение:
Выписав расширенную
матрицу этой системы, после ряда
элементарных преобразований (проследить
порядок которых рекомендуем самостоятельно),
получим:
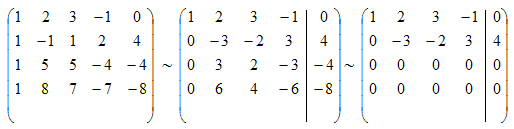
откуда
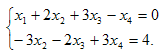
Решая последнюю
систему, находим
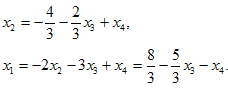
Здесь
ранг расширенной матрицы равен рангу
основной матрицы и равен, очевидно,
двум. Система имеет бесконечно много
решений, каждое из которых можно получить,
придавая х3
и
х4
конкретные значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТЕОРЕМА
ЛАПЛАСА
К оглавлению
I. Теорема ЛАПЛАСА
Определитель квадратной матрицы равен сумме
произведений элементов любой строки (столбца) на их алгебраические дополнения:
(*)
(разложение по
элементам i-й строки);
(**)
(разложение по
элементам j-го столбца).
Убедимся в
справедливости теоремы Лапласа на примере определителя матрицы третьего
порядка. Разложим его вначале по элементам первой строки
Что совпадает с
определением определителя матрицы третьего порядка.
Пример 1. Вычислить определитель
третьего порядка
используя его
разложение по элементам первой строки.
Решение. Находим алгебраические
дополнения элементов первой строки:
Теперь по теореме
Лапласа найдем определитель, используя формулу (*)
Пример 2. Вычислить определитель
предыдущего примера, используя его разложение по элементам второго столбца.
Решение. Находим алгебраические
дополнения элементов второго столбца:
Теперь по формуле (**) найдем определитель матрицы
Значения первого и
второго примеров совпали, что говорит о том, что можно выбирать разложение по
любой строке или любому столбцу.
Пример 3. Вычислить
определитель четвертого порядка треугольной матрицы:
Решение: Выполним
разложение по первому столбцу:
Значение теоремы Лапласа
состоит в том, что она позволяет свести вычисление определителей n-го порядка
к вычислению определителя меньшего порядка, то есть (n-1)-го
порядка.
II. Примеры для
самостоятельного решения
Пример 4. Вычислить шесть определителей
четвертого порядка:
К оглавлению
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы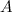 
второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
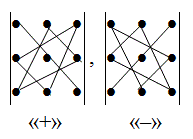
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение. 
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Все курсы > Линейная алгебра > Занятие 5
Введем понятие определителя, который посредством всего лишь одного числа способен многое сказать о свойствах матрицы.
Продолжим работать в том же ноутбуке⧉
Площадь, задаваемая векторами
Возьмем матрицу расширения, которая увеличивает площадь, заданную векторами.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
i = np.array([1, 0]) j = np.array([0, 1]) Scale = np.array([[3, 0], [0, 2]]) ax = plt.axes() plt.xlim([–0.5, 4]) plt.ylim([–0.5, 4]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Scale, i)[0], np.dot(Scale, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Scale, j)[0], np.dot(Scale, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Rectangle((0, 0), 3, 2, fill = False, edgecolor = ‘b’, lw = 2)) plt.show() |
Определитель (determinant) матрицы показывает, какой будет площадь после трансформации.
Так как мы сказали, что мы изменяем не только базисные, но и все остальные векторы пространства, определитель, по сути, показывает насколько сжимается или расширяется векторное пространство при трансформации.
Посмотрим на сдвиг.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Shear = np.array([[1, 1], [0, 1]]) ax = plt.axes() plt.xlim([–0.5, 2.5]) plt.ylim([–0.5, 1.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Shear, i)[0], np.dot(Shear, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Shear, j)[0], np.dot(Shear, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2)) ax.add_patch(Polygon([[0, 0], [1, 0], [2, 1], [1, 1]], fill = False, edgecolor = ‘b’, lw = 2)) plt.show() |
Напомню, что площадь параллелограмма можно найти, умножив основание на высоту.
|
1 * 1, np.linalg.det(Shear) |
Линейно зависимые векторы
Возьмем матрицу с линейно зависимыми столбцами.
|
# второй столбец в два раза больше первого Dependent = np.array([[1, 2], [1, 2]]) |
Такая матрица располагает базисные векторы на прямой линии.
|
ax = plt.axes() plt.xlim([–0.5, 2.5]) plt.ylim([–0.5, 2.5]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, np.dot(Dependent, i)[0], np.dot(Dependent, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) ax.arrow(0, 0, np.dot(Dependent, j)[0], np.dot(Dependent, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.show() |
Как следствие, площадь после трансформации, а значит и определитель, равны нулю.
|
# одномерная оболочка, определитель равен нулю np.linalg.det(Dependent) |
В случае трехмерной матрицы, в которой один из векторов был бы линейной комбинацией двух других, трехмерное пространство «схлопывалось» бы до двумерного (плоскости) и определитель также был бы равен нулю, потому что объем, задаваемый векторами был бы нулевым.
Если определитель равен нулю, то матрица $2 times 2$ преобразует вектор в линию. Если не равен нулю, сохраняет двумерность пространства. Приведем еще один пример.
Возьмем следующую систему уравнений с линейно зависимыми строками и столбцами.
|
# row3 = row1 + row2 # col3 = 2 * col1 + col2 A = np.array([[1.0, 1.0, 3.0, 12.0], [1.0, 2.0, 4.0, 17.0], [2.0, 3.0, 7.0, 29.0]]) |
Такая матрица преобразований (первые три столбца) не описывает три линейно независимых базисных вектора. Один из них зависит от двух других. Если применить метод Гаусса, то получим
$$ begin{bmatrix} 1 & 1 & 3 & 12 \ 0 & 1 & 1 & 5 \ 0 & 0 & 0 & 0 end{bmatrix} $$
Другими словами, $0x_3 = 0$, что предполагает, что у $x_3$ может быть бесконечное количество решений. Это значит, что в имеющейся у нас матрице недостаточно информации для нахождения всех трех неизвестных.
|
Singular Matrix. May have infinitely many solutions. |
Напомню, что сингулярной (singular), вырожденной или необратимой матрицей называют квадратную матрицу, определитель которой равен нулю и которая не имеет обратной матрицы.
Одновременно, у такой матрицы с линейно зависимыми векторами нет обратной матрицы, так как если считать, что обратная матрица «отматывает» преобразование к исходному состоянию, при «схлопывании» пространства мы уже не сможем восстановить куб из плоскости, поскольку при изначальном преобразовании из куба в плоскость была потеряна часть информации.
Какой можно сделать вывод, если обратная матрица все-таки существует? При применении сначала одного преобразования, потом обратного, мы остаемся на месте. Именно это свойство описано в формуле $ AA^{-1} = A^{-1}A = I $, потому что единичная матрица $I$, будучи умноженной на любую матрицу, оставляет ее без изменений $ AI = IA = A $.
Рассмотрим это преобразование с точки зрения системы уравнений. Если определитель равен нулю, то трансформация понижает размерность, и соответственно нет возможности перенести вектор $ mathbf x$ на вектор $ mathbf b$ и обратно вектор $ mathbf b$ на вектор $ mathbf x$.
Единственная возможность найти решение при нулевом определителе, заключается в том, что вектор $mathbf b$ должен находиться в пространстве пониженной размерности, формируемой матрицей $A$. К этой идее мы еще вернемся.
Отрицательный определитель
Отрицательный определитель меняет ориентацию пространства. Наиболее наглядной кажется следующая картинка.
Ссылка на видео про определитель⧉.
Свойства определителя
Рассмотрим свойства определителя более формально.
Свойство 1. Единичная матрица оставляет пространство без изменений. Ее определитель равен единице.
$$ det(I) = I $$
Свойство 2. Перестановка любых двух строк меняет знак определителя. В случае матрицы перестановок $P$
$$ det(P) = begin{cases} 1, text{четное число перестановок} \ -1, text{нечетное число перестановок} end{cases} $$
Это правило легко продемонстрировать на матрице $2 times 2$ с помощью формулы $ad-bc$
$$ det begin{vmatrix} 1 & 0 \ 0 & 1 end{vmatrix} = 1 $$
$$ det begin{vmatrix} 0 & 1 \ 1 & 0 end{vmatrix} = -1 $$
Свойство 3 (а). Если умножить строку матрицы на $t$, то и определитель умножается на $t$. Это логично, умножение константы $t$ на строку (то есть на один и тот же компонент каждого вектор-столбца) увеличивает объем n-мерного параллелепипеда, задаваемый этими векторами, в $t$ раз.
$$ begin{pmatrix} ta & tb \ c & d end{pmatrix} rightarrow t cdot det begin{vmatrix} a & b \ c & d end{vmatrix} $$
Свойство 3 (b).
$$ det begin{vmatrix} a+a’ & b+b’ \ c & d end{vmatrix} = det begin{vmatrix} a & b \ c & d end{vmatrix} + det begin{vmatrix} a’ & b’ \ c & d end{vmatrix} $$
Свойство 4. Если две строки матрицы идентичны, то отпределитель равен нулю.
С одной стороны, перестановка двух одинаковых строк не должна менять знак определителя. С другой, по свойству 2 при перестановке строк знак определителя меняется. Условие $det(A) = -det(A)$ выполняется только, если определитель равен нулю.
Свойство 5. Если строки $i$ и $j$ не равны, то вычитание строки $t cdot i, t in mathbb R$ из строки $j$ не изменит определителя.
Свойство 6. Если есть строка, заполненная нулями, то определитель равен нулю. Следует из свойства 3(а).
Свойство 7. Определитель треугольной матрицы является произведением элементов главной диагонали (решающих элементов). Примеры⧉. Из этого свойства выводится формула определителя.
Примечание. Знак определителя при этом должен соответствовать четному или нечетному количеству перестановок строк, если последние имели место.
Свойство 8. Определитель равен нулю, когда матрица сингулярна. Следует из свойства 6.
Свойство 9. $det(AB) = (detA)(detB) $. Это логично, если считать, что определители $A$ и $B$ увеличивают пространство в $s$ и $t$ раз соотвественно, то вместе они увеличивают пространство в $st$ раз. Отсюда следует, что
$$ det (A^{-1}A) = 1 rightarrow det(A^{-1}) = frac{1}{det(A)} $$
$$ det (A^2) = (det (A))^2 $$
$$ det (2A) = 2^n (det (A)) $$
Последнее следует из свойства 3(а), примененного к каждой строке. Это также соответствует тому факту, что если вдвое увеличить длину, ширину и высоту, то объем вырастет в $2^3 = 8$ раз.
Свойство 10. $det (A^T) = det (A) $. На последующих занятиях мы узнаем, что матрицу $A$ можно разложить на компоненты $LU$, где $L$ — нижнетреугольная матрица с единицами на главной диагонали, а $U$ — верхне диагональная матрица. Тогда,
$$ det(A^T) = det(A) $$
$$ det(U^TL^T) = det(LU)$$
По свойствам 9 и 7,
$$ det(U^T) cdot det(L^T) = det(L) cdot det(U) $$
$$ det(L^T) = det(L) = 1 rightarrow det(U^T)=det(U)$$
Так как $U$ — верхне треугольная матрица, то по свойству 7
$$ U^T = U $$
$$ det(U^T)=det(U) $$
$$ det(A^T) = det(A) $$
Как следствие, свойства, применимые к строкам матрицы, применяются и к столбцам.
Формула определителя и теорема Лапласа
Возьмем матрицу $ underset{n times n} A $. Тогда формулу для нахождения определителя можно записать как
$$ det(A) = sum_{n!} pm a_{1 alpha}, a_{2 beta}, a_{3, gamma},…, a_{n, omega} $$
где ${ alpha, beta, gamma, …, omega }$ — перестановки столбцов $(1, 2, …, n)$.
Кроме этого, определитель можно вычислить по теореме Лапласа (Laplace expansion, cofactor expansion). Подробнее здесь⧉.
Определитель и обратная матрица
Возьмем матрицу и предположим, что она преобразовывает площадь, задаваемую базисными векторами в параллелограмм.
$$ A = begin{pmatrix} a & b \ c & d end{pmatrix} $$
Формула для расчета определителя $ad-bc$ одновременно является площадью этого параллелограмма. Теперь выполним умножение на эту же матрицу, но элементы главной диагонали (leading diagonal) поменяем местами, а у элементов на побочной диагонали (off-diagonal) — знак.
$$ begin{pmatrix} a & b \ c & d end{pmatrix} begin{pmatrix} d & -b \ -c & a end{pmatrix} = begin{pmatrix} ad-bc & 0 \ 0 & ad-bc end{pmatrix} $$
Если элементы этой матрицы разделить на $frac{1}{ad-bc}$, то получится единичная матрица. Как следствие, можно сказать, что
$$ A^{-1} = frac{1}{ad-bc} begin{pmatrix} d & -b \ -c & a end{pmatrix} $$
Идея здесь в следующем: обратная матрица состоит из обратного преобразования, т.е. матрицы $begin{pmatrix} d & -b \ -c & a end{pmatrix}$ и обратного масштабирующего фактора $frac{1}{det(A)}$.
Дополнительные материалы:
- Взаимосвязь обратной матрицы и теоремы Лапласа, метод Крамера⧉
- Геометрическое объяснение метода Крамера⧉
Подведем итог
Мы познакомились с понятием определителя, его связью с линейной независимостью векторов, а также изучили свойства определителя.
Рассмотрим ранг и фундаментальные подпространства матрицы.
