Как найти определитель матрицы третьего порядка

Как найти определитель матрицы третьего порядка

Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.

Вычисление определителей по правилу треугольника

Схематически раскрытие определителя по этому правилу выглядит так:

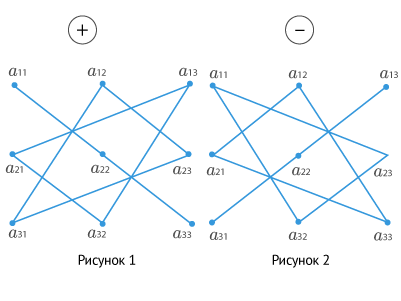
Как вычислить определитель матрицы третьего порядка 1.png

Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».

Произведения, которые берутся со знаком «+» Произведения, которые берутся со знаком «-»
a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31}
a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} a12⋅a33⋅a21a_{12}cdot a_{33}cdot a_{21}
a13⋅a32⋅a21a_{13} cdot a_{32} cdot a_{21} a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32}

На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.

Определитель может быть вычислен по формуле:

∣a11a12a13a21a22a23a31a32a33∣=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=

=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a32⋅a21−a13⋅a22⋅a31−a12⋅a33⋅a21−a11⋅a23⋅a32=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{32}cdot a_{21}-a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{33}cdot a_{21}-a_{11}cdot a_{23}cdot a_{32}.

Примеры

Рассмотрим примеры нахождения определителя по правилу треугольника.

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу треугольника.

По правилу треугольника определитель третьего порядка равен:

∣925148637∣=9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=9cdot4cdot7+2cdot8cdot6+5cdot3cdot1-5cdot4cdot6-2cdot7cdot1-9cdot8cdot3=

=252+96+15−120−14−216=13=252+96+15-120-14-216=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу треугольника.

Искомый определитель третьего порядка равен:

∣21−46−3510−1∣=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=

=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot0cdot6-(-4)cdot(-3)cdot1-1cdot(-1)cdot6-2cdot5cdot0=6+5-12+6=5.

При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».

Вычисление определителей по правилу Саррюса

Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.

Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.

Вычисления будем производить по следующей схеме:

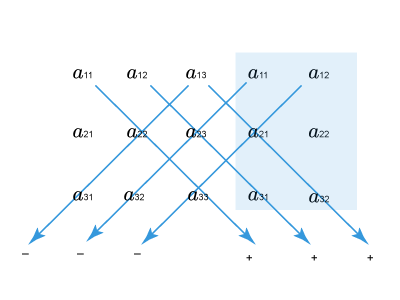
Как вычислить определитель матрицы третьего порядка 2.png

Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.

Произведения, которые берутся со знаком «+» Произведения, которые берутся со знаком «-»
a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31}
a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32}
a13⋅a21⋅a32a_{13} cdot a_{21} cdot a_{32} a12⋅a21⋅a33a_{12}cdot a_{21}cdot a_{33}

В общем виде вычисление по правилу Саррюса можно записать следующим образом:

∣a11a12a13a21a22a23a31a32a33∣=∣a11a12a13a21a22a23a31a32a33∣a11a12a21a22a31a32=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}end{matrix}=

=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a11⋅a23⋅a32−a12⋅a21⋅a33=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{21}cdot a_{32}-a_{13}cdot a_{22}cdot a_{31}-a_{11}cdot a_{23}cdot a_{32}-a_{12}cdot a_{21}cdot a_{33}.

Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.

Примеры

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу Саррюса.

Приписываем два первых столбца справа от определителя и вычисляем его:

∣925148637∣921463=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}begin{matrix}9&2\1&4\6&3end{matrix}=

=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13=9cdot4cdot7+2cdot8cdot6+5cdot1cdot3-5cdot4cdot6-9cdot8cdot3-2cdot1cdot7=252+96+15-120-216-14=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу Саррюса.

Приписываем два первых столбца справа от определителя и вычисляем его:

∣21−46−3510−1∣216−310=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}begin{matrix}2&1\6&-3\1&0end{matrix}=

=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot6cdot0-(-4)cdot(-3)cdot1-2cdot5cdot0-1cdot6cdot(-1)=6+5-12+6=5.

Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.

Минор и алгебраическое дополнение

Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.

Минор

Минор

Минором MijM_{ij} к элементу aija_{ij} определителя n-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.

Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11M_{11} получается вычеркиванием 1-й строки и 1-го столбца, M23M_{23} — вычеркиванием 2-й строки и 3-го столбца.

Алгоритм нахождения миноров:

  1. вычеркиваем ii-ю строку;
  2. вычеркиваем jj-й столбец;
  3. записываем определитель, который получили в результате действий 1 и 2.

Примеры

Пример 1

Найти миноры матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.

Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.

M11=∣925148637∣=∣4837∣=4⋅7−3⋅8=28−24=4M_{11}=begin{vmatrix}color{green}9&color{green}2&color{green}5\color{green}1&4&8\color{green}6&3&7end{vmatrix}=begin{vmatrix}4&8\3&7end{vmatrix}=4cdot7-3cdot8=28-24=4,

M12=∣925148637∣=∣1867∣=1⋅7−6⋅8=7−48=−41M_{12}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&color{green}4&8\6&color{green}3&7end{vmatrix}=begin{vmatrix}1&8\6&7end{vmatrix}=1cdot7-6cdot8=7-48=-41,

M13=∣925148637∣=∣1463∣=1⋅3−6⋅4=3−24=−21M_{13}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}1&4\6&3end{vmatrix}=1cdot3-6cdot4=3-24=-21,

M21=∣925148637∣=∣2537∣=2⋅7−3⋅5=14−15=−1M_{21}=begin{vmatrix}color{green}9&2&5\color{green}1&color{green}4&color{green}8\color{green}6&3&7end{vmatrix}=begin{vmatrix}2&5\3&7end{vmatrix}=2cdot7-3cdot5=14-15=-1,

M22=∣925148637∣=∣9567∣=9⋅7−6⋅5=63−30=33M_{22}=begin{vmatrix}9&color{green}2&5\color{green}1&color{green}4&color{green}8\6&color{green}3&7end{vmatrix}=begin{vmatrix}9&5\6&7end{vmatrix}=9cdot7-6cdot5=63-30=33,

M23=∣925148637∣=∣9263∣=9⋅3−6⋅2=27−12=15M_{23}=begin{vmatrix}9&2&color{green}5\color{green}1&color{green}4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}9&2\6&3end{vmatrix}=9cdot3-6cdot2=27-12=15,

M31=∣925148637∣=∣2548∣=2⋅8−4⋅5=16−20=−4M_{31}=begin{vmatrix}color{green}9&2&5\color{green}1&4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}2&5\4&8end{vmatrix}=2cdot8-4cdot5=16-20=-4,

M32=∣925148637∣=∣9518∣=9⋅8−1⋅5=72−5=67M_{32}=begin{vmatrix}9&color{green}2&5\1&color{green}4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&5\1&8end{vmatrix}=9cdot8-1cdot5=72-5=67,

M33=∣925148637∣=∣9214∣=9⋅4−1⋅2=36−2=34M_{33}=begin{vmatrix}9&2&color{green}5\1&4&color{green}8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&2\1&4end{vmatrix}=9cdot4-1cdot2=36-2=34.

Пример 2

Найти миноры матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.

Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.

M11=∣21−46−3510−1∣=∣−350−1∣=(−3)⋅(−1)−0⋅5=3−0=3M_{11}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\color{green}6&-3&5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}-3&5\0&-1end{vmatrix}=(-3)cdot(-1)-0cdot5=3-0=3,

M12=∣21−46−3510−1∣=∣651−1∣=6⋅(−1)−1⋅5=−6−5=−11M_{12}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&color{green}-3&5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}6&5\1&-1end{vmatrix}=6cdot(-1)-1cdot5=-6-5=-11,

M13=∣21−46−3510−1∣=∣6−310∣=6⋅0−1⋅(−3)=0+3=3M_{13}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}6&-3\1&0end{vmatrix}=6cdot0-1cdot(-3)=0+3=3,

M21=∣21−46−3510−1∣=∣1−40−1∣=1⋅(−1)−0⋅(−4)=−1−0=−1M_{21}=begin{vmatrix}color{green}2&1&-4\color{green}6&color{green}-3&color{green}5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}1&-4\0&-1end{vmatrix}=1cdot(-1)-0cdot(-4)=-1-0=-1,

M22=∣21−46−3510−1∣=∣2−41−1∣=2⋅(−1)−1⋅(−4)=−2+4=2M_{22}=begin{vmatrix}2&color{green}1&-4\color{green}6&color{green}-3&color{green}5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}2&-4\1&-1end{vmatrix}=2cdot(-1)-1cdot(-4)=-2+4=2,

M23=∣21−46−3510−1∣=∣2110∣=2⋅0−1⋅1=0−1=−1M_{23}=begin{vmatrix}2&1&color{green}-4\color{green}6&color{green}-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\1&0end{vmatrix}=2cdot0-1cdot1=0-1=-1,

M31=∣21−46−3510−1∣=∣1−4−35∣=1⋅5−(−3)⋅(−4)=5−12=−7M_{31}=begin{vmatrix}color{green}2&1&-4\color{green}6&-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}
1&-4\-3&5end{vmatrix}=1cdot5-(-3)cdot(-4)=5-12=-7,

M32=∣21−46−3510−1∣=∣2−465∣=2⋅5−6⋅(−4)=10+24=34M_{32}=begin{vmatrix}2&color{green}1&-4\6&color{green}-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&-4\6&5end{vmatrix}=2cdot5-6cdot(-4)=10+24=34,

M33=∣21−46−3510−1∣=∣216−3∣=2⋅(−3)−6⋅1=−6−6=−12M_{33}=begin{vmatrix}2&1&color{green}-4\6&-3&color{green}5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\6&-3end{vmatrix}=2cdot(-3)-6cdot1=-6-6=-12.

Алгебраическое дополнение

Алгебраическое дополнение

Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя nn-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij},

где ii, jj — соответствующие строка и столбец,

MijM_{ij} — минор к элементу aija_{ij}.

Алгоритм нахождения алгебраических дополнений:

  1. найти сумму номеров строки (i)(i) и столбца (j)(j);
  2. найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
  3. подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.

Примеры

Пример 1

Найти алгебраические дополнения матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.

A11=(−1)1+1⋅M11=(−1)2⋅∣4837∣=4A_{11}=(-1)^{1+1}cdot M_{11}= (-1)^{2}cdotbegin{vmatrix}4&8\3&7end{vmatrix}=4,

A12=(−1)1+2⋅M12=(−1)3⋅∣1867∣=41A_{12}=(-1)^{1+2}cdot M_{12}= (-1)^{3}cdotbegin{vmatrix}1&8\6&7end{vmatrix}=41,

A13=(−1)1+3⋅M13=(−1)4⋅∣1463∣=−21A_{13}=(-1)^{1+3}cdot M_{13}= (-1)^{4}cdotbegin{vmatrix}1&4\6&3end{vmatrix}=-21,

A21=(−1)2+1⋅M21=(−1)3⋅∣2537∣=1A_{21}=(-1)^{2+1}cdot M_{21}= (-1)^{3}cdotbegin{vmatrix}2&5\3&7end{vmatrix}=1,

A22=(−1)2+2⋅M22=(−1)4⋅∣9567∣=33A_{22}=(-1)^{2+2}cdot M_{22}= (-1)^{4}cdotbegin{vmatrix}9&5\6&7end{vmatrix}=33,

A23=(−1)2+3⋅M23=(−1)5⋅∣9263∣=−15A_{23}=(-1)^{2+3}cdot M_{23}= (-1)^{5}cdotbegin{vmatrix}9&2\6&3end{vmatrix}=-15,

A31=(−1)3+1⋅M31=(−1)4⋅∣2548∣=−4A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}2&5\4&8end{vmatrix}=-4,

A32=(−1)3+2⋅M32=(−1)5⋅∣9518∣=−67A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}9&5\1&8end{vmatrix}=-67,

A33=(−1)3+3⋅M33=(−1)6⋅∣9214∣=34A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}9&2\1&4end{vmatrix}=34.

Пример 2

Найти алгебраические дополнения матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.

A11=(−1)1+1⋅M11=(−1)2⋅∣−350−1∣=3A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{2}cdotbegin{vmatrix}-3&5\0&-1end{vmatrix}=3,

A12=(−1)1+2⋅M12=(−1)3⋅∣651−1∣=11A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{3}cdotbegin{vmatrix}6&5\1&-1end{vmatrix}=11,

A13=(−1)1+3⋅M13=(−1)4⋅∣6−310∣=3A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{4}cdotbegin{vmatrix}6&-3\1&0end{vmatrix}=3,

A21=(−1)2+1⋅M21=(−1)3⋅∣1−40−1∣=1A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{3}cdotbegin{vmatrix}1&-4\0&-1end{vmatrix}=1,

A22=(−1)2+2⋅M22=(−1)4⋅∣2−41−1∣=2A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{4}cdotbegin{vmatrix}2&-4\1&-1end{vmatrix}=2,

A23=(−1)2+3⋅M23=(−1)5⋅∣2110∣=1A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{5}cdotbegin{vmatrix}2&1\1&0end{vmatrix}=1,

A31=(−1)3+1⋅M31=(−1)4⋅∣1−4−35∣=−7A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}1&-4\-3&5end{vmatrix}=-7,

A32=(−1)3+2⋅M32=(−1)5⋅∣2−465∣=−34A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}2&-4\6&5end{vmatrix}=-34,

A33=(−1)3+3⋅M33=(−1)6⋅∣216−3∣=−12A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}2&1\6&-3end{vmatrix}=-12.

Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.

Вычисление определителя по строке или столбцу

Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.

Алгоритм вычисления определителя по строке или столбцу:

  1. находим алгебраические дополнения элементов строки или столбца;
  2. находим произведения элементов на их алгебраические дополнения;
  3. находим сумму, полученных на шаге 2, произведений.

Примеры

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по 2 столбцу.

∣925148637∣=2⋅A12+4⋅A22+3⋅begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=2cdot A_{12}+4cdot A_{22}+3cdot

A32=2(−1)3M12+4(−1)4M22+3(−1)5M32=2(−1)3∣1867∣+4(−1)4∣9567∣+3(−1)5∣9518∣=A_{32}=2(-1)^{3}M_{12}+4(-1)^{4}M_{22}+3(-1)^{5}M_{32}=2(-1)^{3}begin{vmatrix}1&8\6&7end{vmatrix}+4(-1)^{4}begin{vmatrix}9&5\6&7end{vmatrix}+3(-1)^{5}begin{vmatrix}9&5\1&8end{vmatrix}=

=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13=-2cdot(-41)+4cdot33-3cdot67=82+132-201=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по 3 строке.

∣21−46−3510−1∣=1⋅A31+0⋅A32−1⋅A33=1(−1)4M31+0(−1)5M32−1(−1)6M33=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=1cdot A_{31}+0cdot A_{32}-1cdot A_{33}=1(-1)^{4}M_{31}+0(-1)^{5}M_{32}-1(-1)^{6}M_{33}=

=1(−1)4∣1−4−35∣+0(−1)5∣2−465∣−1(−1)6∣216−3∣=−7+0+12=5=1(-1)^{4}begin{vmatrix}1&-4\-3&5end{vmatrix}+0(-1)^{5}begin{vmatrix}2&-4\6&5end{vmatrix}-1(-1)^{6}begin{vmatrix}2&1\6&-3end{vmatrix}=-7+0+12=5.

Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.

Оформите решение задачи на заказ онлайн, если возникают трудности с выполнением!

Тест по теме «Как вычислить определитель матрицы третьего порядка»

Источник

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Перед тем как находить и считать определитель, дадим определение определителю матрицы. 

Определение 1

Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n. 

|А|, ∆, det A – символы, которыми обозначают определитель матрицы.

Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.

Пример 1​​​​​

Определитель матрицы второго порядка можно вычислять по формуле:

А=1-231.

Решение матрицы:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника 

Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:

  • он может считаться по правилу треугольника;
  • расчет также проводится по правилу Саррюса.

Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

  • дописать слева от определителя два первых столбца;
  • перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
  • перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:

  • разложением по элементам строки;
  • разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

  • раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

  • раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

  • если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
  • если поменять местами строки и столбцы, то знак поменяется на противоположный;
  • определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Замечание 

В рамках темы советуем обратиться к модулю определителя.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Содержание:

  • Вычисления определителей второго порядка
  • Методы вычисления определителей третьего порядка
  • Приведение определителя к треугольному виду
  • Правило треугольника
  • Правило Саррюса
  • Разложение определителя по строке или столбцу
  • Разложение определителя по элементам строки или столбца
  • Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Определитель матрицы по правилу треугольника

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.

Решение.

$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$

$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$

$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:

$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$

Полученный определитель разложим по элементам первого столбца:

$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:

$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$

$$=4 cdot(2 cdot 8-4 cdot 4)=0$$

Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$

$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$

Ответ. $Delta=-80$

Теорема Лапласа

Теорема

Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$

Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$

$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$

$$=-23+128+90=195$$

Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$

Читать дальше: обратная матрица.

Источник
Автор статьи

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Существует несколько способов нахождения определителей матриц третьего порядка. Рассмотрим их подробнее.

Перечислим основные способы, используемые для этого:

  • Правило Саррюса;
  • Правило треугольников;
  • Использование специальной формулы для вычисления;
  • Использование метода Гаусса или иначе метода перестановок.

Правило Саррюса

Правило Саррюса для вычисления матриц 3-ьего порядка применяется просто: достаточно соответственно рисунку переписать 2 первых столбика справа рядом с матричной таблицей, а затем записать произведения, стоящие по диагоналям со знаками.

Замечание 1

Если диагональ идёт сверху слева вниз направо — то произведение записывается со знаком «+», а если диагональ идёт из правого верхнего угла в нижний левый — то со знаком «-».

Формула третьего порядка. Автор24 — интернет-биржа студенческих работ

Рисунок 1. Формула третьего порядка. Автор24 — интернет-биржа студенческих работ

Пример 1

Дана матричная таблица $A$. Вычислите детерминант с помощью правила Саррюса.

$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$

Решение:

Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ

Рисунок 2. Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ

$Δ = 0 cdot 4 cdot 3 + 3 cdot 2 cdot 2 – 1 cdot 1 cdot 5 – 3 cdot 1 cdot 3 – 0 cdot 2 cdot 5 + 1 cdot 4 cdot 2 = 0 + 12 – 5 – 9 – 0 + 8 = 6$

Правило треугольников

Это правило немного похоже на предыдущее. Суть его в том, что произведения элементов с главной диагонали и двух треугольников, задействующих все остальные элементы как показано на рисунке, записываются со знаком плюс, а произведения элементов с побочной диагонали и двух синих треугольников — с противоположным.

«Найти определитель матрицы третьего порядка» 👇

Треугольники. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Треугольники. Автор24 — интернет-биржа студенческих работ

Пример 2

Найдите определитель из прошлого задания, используя метод треугольников.

Решение:

Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ

Рисунок 4. Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ

$Δ= 0 cdot 4 3 + 3 cdot 2 cdot 2 – 1 cdot 5 cdot 1 + 1 cdot 4 cdot 2 – 1 cdot 3 cdot 3 – 2 cdot 5 cdot 0 = 0 + 12 – 5 + 8 – 9 – 0 = 6$

Использование формулы разложения по строчке

$A = begin{pmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{pmatrix}$

Для матрицы 3 на 3, приведённой выше, определитель можно сосчитать по формуле:

$Δ =begin{array}{|ccc|} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{array}=a_{11} cdot begin{array}{|cc|} a_{22} & a_{23} \ a_{32} & a_{33} \ end{array} – a_{12} cdot begin{array}{|cc|} a_{11} & a_{13} \ a_{21} & a_{23} \ a_{31} & a_{33} \ end{array} + a_{13} cdot begin{array}{|cc|} a_{11} & a_{12} \ a_{21} & a_{22} \ a_{31} & a_{32} \ end{array}= a_{11} cdot a_{22} cdot a_{33} – a_{12} cdot a_{23} cdot a_{31} + a_{13} cdot a_{21} cdot a_{32} – a_{13} cdot a_{22} cdot a_{31}$.

Пример 3

Разложите определитель матрицы из предыдущих примеров по 1-ой строчке и найдите его.

Решение:

$Δ = 0 cdot begin{array}{|cc|} 4 & 2 \ 5 & 3 \ end{array} – 3 cdot begin{array} {|cc|} 1 & 2 \ 2 & 3 \ end{array} + (-1) cdot begin{array}{|cc|} 1 & 4 \ 2 & 5 \ end{array} = 0 – 3 cdot (1 cdot 3 – 2 cdot 2) + (-1) cdot (5 – 8) = 0 – 3 cdot(-1) + (-1) cdot (-3) = 3 + 3 = 6$

Метод Гаусса

Чтобы вычислить детерминант этим методом, нужно используя разрешённые преобразования получить треугольную матрицу.

Разрешёнными преобразованиями являются сложение и вычитание строчек и столбцов, в то время как при перестановке строчек и столбцов между собой необходимо помнить о смене знака определителя в конце.

После этого нужно перемножить элементы, стоящие на главной диагонали, их произведение и будет определителем.

Пример 4

Примените метод Гаусса для получения детерминанта матрицы из предыдущих примеров.

Решение:

$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$

Переставим первую строчку со второй, при этом запомним, что знак детерминанта в конце поменяется:

$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 2 & 5 & 3 \ end{pmatrix}$;

Вычтем из третьей строчки 1-ую, умноженную на 2:

$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & -3 & -1 \ end{pmatrix}$;

Сложим между собой третью строчку со второй:

$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}$;

Получили искомый вид матрицы. Теперь можно сосчитать определитель, минус появляется из-за перемены строчек местами:

$Δ=-begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}= -(1 cdot 3 cdot ( – 2) ) = 6 $

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Часто в ВУЗе попадаются задачи по высшей математики, в которых необходимо вычислить определитель матрицы. К слову, определитель может быть только в квадратных матрицах. Ниже рассмотрим основные определения, какими свойствами обладает определитель и как его правильно вычислить.. Также на примерах покажем подробное решение.

Что такое определитель матрицы: вычисление определителя при помощи определения

Определитель матрицы

A = begin{pmatrix} a_1_1&a_1_2\ a_2_1&a_2_2 end{pmatrix}right второго порядка – это число |A| = a_{11}a_{22} - a_{12}a_{21}.

Определитель матрицы обозначается det A – (сокращенно от латинского названия детерминант), или |A|.

Если:A = begin{pmatrix} a_1_1&a_1_2\ a_2_1&a_2_2 end{pmatrix}right, тогда получается |A| = det A = begin{pmatrix} a_1_1&a_1_2\ a_2_1&a_2_2 end{pmatrix}right

Напомним ещё несколько вспомогательных определений:

Упорядоченный набор чисел, который состоит из n элементов называется перестановкой порядка n.

Для множества, которое содержит n элементов есть факториал (n), который всегда обозначается восклицательным знаком: n!. Перестановки отличаются друг от друга всего лишь порядком следования. Чтобы вам было понятнее, приведём пример:

Рассмотрим множество из трёх элементов {3, 6, 7}. Всего перестановок 6, так как 3! = 1 * 2 * 3 = 6.:

1. 3, 6, 7;

2. 3, 7, 6;

3. 6, 3, 7;

4. 6, 7, 3;

5. 7, 3, 6;

6. 7, 6, 3

Инверсия в перестановке порядка n – это упорядоченный набор чисел (его ещё называют биекцией), где из них два числа образуют некий беспорядок. Это когда большее из чисел в данной перестановке расположено левее меньшего числа. 

Выше мы рассматривали пример с инверсией перестановки, где были числа {6, 3, 7}. Так вот, возьмём вторую строку, где судя по данным числам получается, что q = 2, а k = 3, так как второй элемент 7 больше третьего элемента 6. Возьмём для сравнения шестую строку, где расположены числа: 7, 6, 3. Здесь есть три пары: p = 1, а k = 2, так как 7 > 6; p = 1, k = 3, так как 7 > 3; p = 2, k = 3 – 6 > 3.

Саму инверсию мы изучать не будем, а вот перестановки нам очень пригодятся в дальнейшем рассмотрении темы.

Определитель матрицы nxn – число:

det (A) = sum_{a_1, a_2,..., a_n}limits (-1)^{N(a_1, a_2,..., a_n)}* a_alpha_1_1*a_alpha_2_2...*a_alpha_n_n, где

alpha_1, alpha_2, alpha_n – перестановка чисел от 1 до бесконечного числа (n), а {N(a_1, a_2,..., a_n)} – число инверсий в перестановке. Таким образом, в определитель входит n! слагаемых, которые называются “членами определителя”.

Можно вычислять определитель матрицы второго порядка, третьего и даже четвёртого. Также стоит упомянуть: 

определитель матрицы |A| – это число, которое равняется sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j1(k)} * a_{2j2(k)} * ...*a_{njn(k)}.

Чтобы понять данную формулу, опишем её более подробно. Определитель квадратной матрицы n x n – это сумма, которая содержит n! слагаемых, а каждое слагаемое является собой произведением определённого количества (n) элементов матрицы. При этом, в каждом произведении есть элемент из каждой строки и каждого столбца матрицы.

Перед определённым слагаемым может появится (-1) в том случае, если элементы матрицы в произведении идут по порядку (по номеру строку), а количество инверсий N_k в перестановке k множество номеров столбцов нечётно.

Выше упоминалось о том, что определитель матрицы A обозначается |A| или det(A), то есть, определитель часто называют детерминантом.

Итак, вернёмся к формуле:

sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j1(k)} * a_{2j2(k)} * ...*a_{njn(k)}.

Из формулы видно, что определитель матрицы первого порядка – это элемент этой же матрицы |a_{11}| = a_{11}.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Вычисление определителя матрицы второго порядка

Чаще всего на практике определитель матрицы решается методами второго, третьего и реже, четвёртого порядка. Рассмотрим, как вычисляется определитель матрицы второго порядка:

A = begin{vmatrix} a_{11}&a_{12}\ a_{21}&a_{22} end{vmatrix} right

В матрице второго порядка n = 2, отсюда следует, что факториал n! = 2! = 2. Прежде чем применить формулу

A = sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j1(k)} * a_{2j2(k)} * ...*a_{njn(k)}. необходимо определить, какие данные у нас получаются:

1. k = 2;

2. перестановки множеств: 1, 2 и 2, 1;

3. количество инверсий в перестановке N_k: 0 и 1, так как 2 > 1;

4. соответствующие произведения (-1)^{N_k} * a_{1j1(k)} * a_{2j2(k)}: a_{11} * a_{22} и -a_{12} * a_{21}.

Получается:

|A| = begin{vmatrix} a_{11}&a_{12}\ a_{21}&a_{22} end{vmatrix} = sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j1(k)} * a_{2j2(k)} = a_{11} * a_{22} - a_{12} * a_{21}. right

Исходя из вышесказанного мы получаем формулу для вычисления определителя квадратной матрицы второго порядка, то есть 2 x 2:

begin{vmatrix} a_{11}&a_{12}\ a_{21}&a_{22} end{vmatrix} = a_{11} * a_{22} - a_{12} * a_{21} right

Рассмотрим на конкретном примере, как вычислять определитель квадратной матрицы второго порядка:

Задача

Вычислить определитель матрицы 2 x 2:

A = begin{vmatrix} 2&3\ - 6&1 end{vmatrix}right

Решение

Итак, у нас получается a_{11} = 2, a_{12} = 3, a_{21} = - 6, a_{22} = 1.

Для решения необходимо воспользоваться ранее рассмотренной формулой:

A = begin{vmatrix} a_{11}&a_{12}\ a_{21}&a_{22} end{vmatrix} = a_{11} * a_{22} - a_{12} * a_{21} right

Подставляем числа с примера и находим:

A = begin{vmatrix} 2&3\ - 6&1 end{vmatrix} = 2 * 1 - 3 * (-6) = 3 - (-18) = 21 right

Ответ

Определитель матрицы второго порядка = 21.

Вычисление определителя матрицы третьего порядка: пример и решение по формуле

Определитель матрицы третьего порядка – это число, полученное из девяти заданных чисел, расположенных в виде квадратной таблицы,

Определитель третьего порядка находится почти так же, как и определитель второго порядка. Разница лишь в формуле. Поэтому, если хорошо ориентироваться в формуле, тогда и проблем с решением не будет.

Рассмотрим квадратную матрицу третьего порядка 3 * 3:

A = begin{vmatrix} a_{11}&a_{12}&a_{13}\ a_{21}&a_{22}&a_{23}\ a_{31}&a_{32}&a_{33} end{vmatrix} right

Исходя из данной матрицы, понимаем, что n = 3, соответственно, факториал (n) = 3, а это значит, что всего перестановок получается 6

Чтобы применить правильно формулу |A| = sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j_1(k)} * a_{2j_2(k)} ... * a_{nj_n(k), необходимо найти данные:

Итак, всего перестановок множества {1, 2, 3} = 6:

1. 1, 2, 3, количество инверсий в перестановке 0, а соответствующие произведения = a_{11} * a_{22} * a_{33};

2. 1, 3, 2, количество инверсий в перестановке 1 (3 >2), соответствующие произведения = -a_{11} * a_{23} * a_{32};

3. 2, 1, 3, инверсий в перестановке 1 (2 > 1), соответствующие произведение = -a_{12} * a_{21} * a_{33};

4. 2, 3, 1; инверсий в перестановке 2 (2 > 1; 3 > 1), соответствующие произведение = a_{12} * a_{23} * a_{31}

5. 3, 1, 2; инверсий в перестановке 2 (3 > 1; 3 > 2), соответствующие произведение = a_{13} * a_{21} * a_{32}

6. 3, 2, 1; инверсий в перестановке 3 (3 > 1; 3 > 2; 2 >1), соответствующие произведение = -a_{13} * a_{22} * a_{31}.

Теперь у нас получается:

A = begin{vmatrix} a_{11}&a_{12}&a_{13}\ a_{21}&a_{22}&a_{23}\ a_{31}&a_{32}&a_{33} end{vmatrix} = sum_{k = 1}^{n!}limits(-1)^{N_k} * a_{1j_1(k)} * a_{2j_2(k)} * a_{3j_3(k)} = a_{11} * a_{22} * a_{33} - a_{11} * a_{23} * a_{32} + a_{12} * a_{23} * a_{31} + a_{13} * a_{21} * a_{32} - a_{13} * a_{22} * a_{31} right

Таким образом у нас получена формула для вычисления определителя матрицы порядка 3 x 3:

begin{vmatrix} a_{11}&a_{12}&a_{13}\ a_{21}&a_{22}&a_{23}\ a_{31}&a_{32}&a_{33} end{vmatrix} right = a_{11} * a_{22} * a_{33} + a_{12} * a_{23} * a_{31} + a_{13} * a_{21} * a_{32} -\- a_{13} * a_{22} * a_{31} - a_{12} * a_{21} * a_{33} - a_{11} * a_{23} * a_{32}.

Нахождение матрицы третьего порядка по правилу треугольника (правило Саррюса)

Как говорилось выше, элементы определителя 3-го порядка расположены в трёх строках и трёх столбцах. Если ввести обозначение общего элемента a_{ij}(i = 1, 2, 3; j = 1, 2, 3), тогда первый элемент обозначает номер строки, а второй элемент из индексов – номер столбца. Есть главная (элементы a_{11}, a_{22}, a_{33)) и побочная (элементы a_{31}, a_{22}, a_{13}) диагонали определителя. Слагаемые в правой части называются членами определителя).

Видно, что каждый член определителя находится в схеме только по одному элементу в каждой строке и каждого столбца.

Вычислять определитель можно при помощи правила прямоугольника, который изображён в виде схемы. Красным цветом выделены члены определителя из элементов главной диагонали, а также члены из элементов, которые находятся в  вершине треугольников, что имеют по одной стороне, параллельны главной диагонали (лева схема), беруться со знаком "+".

Члены с синими стрелками из элементов побочной диагонали, а также из элементов, которые находятся в вершинах треугольников, что имеют стороны, параллельные побочной диагонали (правая схема) берутся со знаком "-".

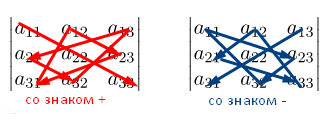
Правило треугольника

На следующем примере научимся, как вычислять определитель квадратной матрицы третьего порядка.

Задача

Вычислить определитель матрицы третьего порядка:

begin{vmatrix} 1&4&-3\ 2&3&5\ -4&1&-1 end{vmatrix} right

Решение

В этом примере:

a_{11} = 1, a_{12} = 4, a_{13} = -3,

a_{21} = 2, a_{22} = 3, a_{23} = 5,

a_{31} = -4, a_{32} = 1, a_{33} = -1.

Вычисляем определитель, применяя формулу или схему, которые рассматривались выше:

begin{vmatrix} 1&4&-3\ 2&3&5\ -4&1&-1 end{vmatrix} = a_{11} * a_{22} * a_{33} + a_{12} * a_{23} * a_{31} + a_{13} * a_{21} * a_{32} - a_{13} * a_{22} * a_{31} - a_{12} * a_{21} * a_{33} - a_{11} * a_{23} * a_{32} = 1 * 3 * (-1) + 4 * 5 * (-4) + (-3) * 2 * 1 - (-3) * 3 * (-4) - 4 * 2 * (-1) - 1 * 5 * 1 = -3 - 80 - 6 - 36 + 8 - 5 = -122 right

Ответ

Определитель матрицы третьего порядка = -122

Рекомендуем запомнить формулы для нахождения определителя матрицы второго и третьего порядка, так как они часто применяются на зачётах и экзаменах.

Основные свойства определителей матрицы третьего порядка

На основании предыдущих определений и формул рассмотрим основные свойства определителя матрицы.

1. Размер определителя не изменится при замене соответствующих строк, столбцов (такая замена называется транспонированием).

left begin{vmatrix} a_1_1&a_1_2&a_1_3\ a_2_1&a_2_2&a_2_3\ a_3_1&a_3_2&a_3_3 end{vmatrix} = begin{vmatrix}a_1_1&a_2_1&a_3_1\a_1_2&a_2_2&a_3_2\a_1_3&a_2_3&a_3_3end{vmatrix}right

На примере убедимся, что определитель матрицы A равен определителю транспонированной матрицы:

|A| = begin{vmatrix} 0&3&1\ 1&2&3\. 3&2&3 end{vmatrix} right

Вспомним формулу для вычисления определителя: a_{11} * a_{22} * a_{33} + a_{12} * a_{23} * a_{31} + a_{13} * a_{21} * a_{32} - a_{13} * a_{22} * a_{31} - a_{12} * a_{21} * a_{33} - a_{11} * a_{23} * a_{32} = 0 * 2 * 3 + 3 * 3 * 3 + 1 * 1 * 2 - 1 * 2 * 3 - 3 * 1 * 3 - 0 * 3 * 2 = 0 + 27 + 2 - (-6) - (-9) - 0 = 44

Транспонируем матрицу:

A^T = begin{vmatrix} 0&3&1\ 1&2&3\. 3&2&3 end{vmatrix}^T = begin{vmatrix} 0&1&3\ 3&2&2\. 1&3&3 end{vmatrix} right

Вычисляем определитель транспонированной матрицы:

A^T = begin{vmatrix} 0&1&3\ 3&2&2\. 1&3&3 end{vmatrix}^T = 0 * 2 * 3 + 1 * 2 * 1 + 3 * 3 * 3 - 3 * 2 * 1 - 1 * 3 * 3 - 0 * 2 * 3 = 0 + 2 + 27 - (-6) - (-9) - 0 = 44 right

Мы убедились, что определитель транспортированной матрицы равен исходной матрице, что говорит о правильном решении.

2. Знак определителя изменится на противоположный, если в нём поменять местами любые два его столбца или две строки.

Рассмотрим на примере:

Даны две матрицы третьего порядка (3 x 3):

A = begin{vmatrix} 1&4&-3\ 2&3&5\ -4&1&-1 end{vmatrix} right

B = begin{vmatrix} -4&1&-1\ 2&3&5\ 1&4&-3 end{vmatrix} right

Нужно показать, что определители данных матриц противоположные.

Решение

В матрице A и в матрице B поменялись строки (третья с первой, и с первой на третью). Согласно второму свойству определители двух матриц должны отличаться знаком. То есть, одна матрица с положительным знаком, а вторая – с отрицательным. давайте проверим данное свойство, применив формулу для вычисления определителя.

|A| = begin{vmatrix} 1&4&-3\ 2&3&5\ -4&1&-1 end{vmatrix} = 1 * 3 * (-1) + 4 * 5 * (-4) + (-3) * 2 * 1 - (-3) * 3 * (-4) - 4 * 2 * (-1) - 1 * 5 * 1 = -3 - 80 - 6 - 36 + 8 - 5 = -122 right

|B| = begin{vmatrix} -4&1&-1 2&3&5\ 1&4&-3 end{vmatrix} = (-4) * 3 * (-3) + 1 * 5 * 1 + (-1) * 2 * 4 - 1 * 3 * (-1) - 2 * 1 * (-3) - (-4) * 5 * 4 = 36 + 5 - 8 + 3 + 6 + 80 = 122 right

Свойство верно, так как - |A| = |B|.

3. Определитель равняется нулю, если в нём есть одинаковые соответствующие элементы в двух строках (столбцах). Пусть у определителя одинаковые элементы первого и второго столбцов:

Delta =begin{vmatrix} a&b&c\ b&b&a_2_3\ c&c&a_3_3 end{vmatrix}right

Поменяв местами одинаковые столбцы, мы, согласно свойству 2 получим новый определитель: Delta_1 = -Delta. С другой стороны, новый определитель совпадает с изначальным, поскольку одинаковые ответы элементы, то есть Delta_1 = Delta. Из этих равенств у нас получается: Delta_1 = -Deltalongrightarrow 2Delta=0longrightarrowDelta = 0.

4. Определитель равняется нулю, если все элементы одной строки (столбца) нули. Это утверждение выплывает из того, что у каждого члена определителя по формуле (1) есть по одному, и только по одному элементу с каждой строки (столбца), у которого одни нули.

Рассмотрим на примере:

Покажем, что определитель матрицы равен нулю:

A = begin{vmatrix} 3&2&2\ -2&3&3\ 8&-2&-2 end{vmatrix} right

В нашей матрицы есть два одинаковых столбца (второй и третий), поэтому, исходя из данного свойства, определитель должен равняться нулю. Проверим:

|A| = begin{vmatrix} 3&2&2\ -2&3&3\ 8&-2&-2 end{vmatrix} = 3 * 3 * (-2) + 2 * 3 * 8 + 2 * (-2) * (-2) - 2 * 3 * 8 - 2 * (-2) * (-2) - 3 * 3 * (-2) = (-18) + 48 + 8 - 48 - 8 + 18 = 0 right

И действительно, определитель матрицы с двумя одинаковыми столбцами равняется нулю.

5. Общий множитель элементов первой строки (столбца) можно вынести за знак определителя:

leftbegin{vmatrix}a_1_1&a_1_2&ka_1_3\a_2_1&a_2_2&ka_2_3\a_3_1&a_3_2&ka_3_3end{vmatrix} = kbegin{vmatrix}a_1_1&a_1_2&a_1_3\a_2_1&a_2_2&a_2_3\a_3_1&a_3_2&a_3_3end{vmatrix}right.

6. Если элементы одной строки или одного столбца определителя пропорциональны соответствующим элементам второй строки (столбца), тогда такой определитель равняется нулю.

Действительно, за свойством 5 коэффициент пропорциональности можно вынести за знак определителя, и тогда воспользоваться свойством 3.

7. Если каждый из элементов строк (столбцов) определителя является суммой двух слагаемых, то этот определитель можно подать в виде суммы соответствующих определителей:

begin{vmatrix} a_1_1&a_1_2&a_1_3 + a'_1_3\ a_2_1&a_2_2&a_2_3 + a'_2_3\ a_3_1&a_3_2&a_3_3 + a'_3_3 end{vmatrix} =begin{vmatrix} a_1_1&a_1_2&a_1_3\ a_2_1&a_2_2&a_2_3\ a_3_1&a_3_2&a_3_3end{vmatrix} +begin{vmatrix} a_1_1&a_1_2&a'_1_3\ a_2_1&a_2_2&a'_2_3\ a_3_1&a_3_2&a'_3_3 end{vmatrix} right.

Для проверки достаточно записать в развёрнутом виде по (1) определитель, что в левой части равенства, тогда отдельно сгруппировать члены, в которых содержатся элементы a_i_3 и a'_i_3 (i = 1, 2, 3).Каждая из полученных групп слагаемых будет соответственно первым и вторым определителем с правой части равенства.

8. Значения определения не изменятся, если к элементу одной строки или одного столбца прибавить соответствующие элементы второй строки (столбца), умноженные на одно и то же число:

begin{vmatrix} a_1_1&a_1_2&a_1_3\ a_2_1&a_2_2&a_2_3\ a_3_1&a_3_2&a_3_3 end{vmatrix} =begin{vmatrix} a_1_1&a_1_2&a_1_3 + ka_1_1\ a_2_1&a_2_2&a_2_3 + ka_2_1\ a_3_1&a_3_2&a_3_3 + ka_3_1end{vmatrix} right.

Это равенство получается исходя из свойств 6 и 7.

9. Определитель матрицы A = |a_{ij}|, i = 1, 2, 3, 4, ..., n, j = 1, 2, 3, 4, ..., n равняется сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.

begin{vmatrix} a_{11}&a_{12}&dots&a_{1n}\ a_{21}&a_{22}&dots&a_{2n}\ vdots&vdots&vdots&vdots\ a_{n1}&a_{n2}&dots&a_{nn} end{vmatrix} = a_{p1} * A_{p1} + a_{p2} * A_{p2} + dots + a_{pn} * A_{pn} =\ = a_{1q} * A_{1q} + a_{2q} * A_{2q} + dots + a_{nq} * A_{nq}. right

Здесь по A_{ij} подразумевается алгебраическое дополнение элемента матрицы a_{ij}. При помощи данного свойства можно вычислять не только матрицы третьего порядка, но и матрицы более высших порядков (4 x 4 или 5 x 5).Другими словами – это рекуррентная формула, которая нужна для того, чтобы вычислить определитель матрицы любого порядка. Запомните её, так как она часто применяется на практике.

Стоит сказать, что при помощи девятого свойства можно вычислять определители матриц не только четвёртого порядка, но и более высших порядков. Однако, при этом нужно совершать очень много вычислительных операций и быть внимательным, так как малейшая ошибка в знаках приведёт к неверному решению. Матрицы высших порядков удобнее всего решать методом Гаусса, и об этом поговорим позже.

10. Определитель произведения матриц одного порядка равен произведению их определителей.

Рассмотрим на примере:

Задача

Убедитесь, что определитель двух матриц A и B равен произведению их определителей. Даны две матрицы:

A = begin{vmatrix} 5&2\ -2&-4 end{vmatrix} right B = begin{vmatrix} 3&-1\ 1&6 end{vmatrix} right

Решение

Сначала находим произведение определителей двух матриц A и B.

|A| = begin{vmatrix} 5&2\ -2&-4 end{vmatrix} = 5 * (-4) - 2 * (-2) = (-20) - (-4) = -16 right

|B| = begin{vmatrix} 3&-1\ 1&6 end{vmatrix} = 3 * 6 - (-1) * 1 = 18 - (1) = 19 right

|A| x |B| = -16 * 19 = -304,

Теперь выполним умножение обеих матриц и таким образом, вычислим определитель:

A * B = begin{pmatrix} 5&2\ -2&-4 end{pmatrix} * begin{pmatrix} 3&-1\ 1&6 end{pmatrix}rightlongleftrightarrow

begin{pmatrix} 5 * 3 + 2 * 1&quadquad{5 * (- 1)+ 2 * 6}\(-2) * 3 + (-4) * 1&quadquad{(-2) * (-1) + (-4) * 6} end{pmatrix} rightlongleftrightarrow begin{pmatrix} 15 + 2quadquad{(-5) + 12}\(-6) + (-4)quadquad{2 + (-24)end{pmatrix}rightlongleftrightarrow  begin{pmatrix}17&7\(-10)&(-22)end{pmatrix} = 17 * (-22) - 7 * (-10) = -374 + 70 = - 304 right

Ответ

Мы убедились, что |A * B| = |A| * |B|

Вычисление определителя матрицы при помощи метода Гаусса

Вспомним, как метод Гаусса помогает находить определитель матрицы: благодаря элементарным преобразованием в матрице все элементы (кроме a_{11}) нужно привести к нулю. Однако, такой метод подходит только к тем матрицам, в которых определитель отличен от нуля. Об этом поговорим позже, а сейчас объясним, для чего проделывается такая процедура.

Нулевые элементы необходимы для того, чтобы самым простым способом разложить определитель, исходя из элементов первого столбца. После такого преобразования, исходя из девятого свойства  и a_{21} = 0, a_{31} = 0,dots, a_{n_1} = 0, получается:

|A| = a_{11} * A_{11} + a_{21} * A_{21} + dots + a_{n1} * A_{n1} = a_{11} * A_{11} = a_{11} * (-1)^{1 + 1} * M_{11} = a_{11} * M_{11}.

Здесь M_{11} – это минор первого порядка, который получился из матрицы A путём вычёркивания элементов первой строки и первого столбца. Такая процедура проделывается до тех пор, пока все элементы первого столбца не превратятся в нулевые элементы.

Конечно же, сразу же назревает вопрос: “А как же получается нулевые элементы?” Рассмотрим алгоритм решения:

Если первый элемент в первой строке и в первом столбце (a_{11}) прибавить к соответствующим элементом k – ой строки, где a_{k1}neq{0}. (Метод Гаусса не нужен только в том случае, если все элементы в первом столбцы нулевые). После данного преобразования “новый” элемент матрицы a_{11}neq{0}. Определитель “новой” матрицы равен определителю исходной матрицы.

Если a_{11}neq{0}, тогда к каждому элементу второй строки прибавляем элемент первой строки, которые заранее умноженные на -{a_{21}over{a_{11}}}, а к элементам третьей строки прибавляем определённые элементы первой строки, которые умножаются на -{a_{31}over{a_{11}}}. И дальше вычисляем по такой же схеме. Метод Гаусса рассмотрен более подробно в отдельно теме. В итоге получится преобразованная матрица, где все элементы первого столбца окажутся нулевыми. Определитель полученной матрицы будет равен определителю изначальной матрицы.

Напомним, что величина определителя n – ого порядка равна сумме произведений элементов какой-либо строки или столбца на соответствующее алгебраическое дополнение.

Рассмотрим записанный сначала формально определитель четвёртого порядка:

Delta = begin{vmatrix} a_{11}&a_{12}&a_{13}&a_{14}\ a_{21}&a_{22}&a_{23}&a_{24}\ a_{31}&a_{32}&a_{33}&a_{34}\ a_{41}&a_{42}&a_43}&1a_{44} end{vmatrix} right

Вычёркивая в Delta i – тую строку и j – тый столбец, на пересечении которого помещается элемент a_{ij}(i, j = 1, 2, 3, 4), получим определитель третьего порядка, который называется минором элемента a_{ij} и обозначается M_{ij}. Тогда A_{ij} = (-1)^{i + j} * M – алгебраическое дополнение элемента a_{ij}. Определитель 4-го порядка можно обозначить, как размещение по элементам, например, первого столбца:

Delta = a_{11} * A_{11} + a_{21} * A_{21} + a_{31} * A_{31} + a_{41} * A_{41}.

Пусть введено понятие определителя (n - 1) – ого порядка, тогда определитель n – ого порядка:

Delta = begin{vmatrix} a_{11}&a_{12}&dots&a_{1j}&dots&a_{1n}\ a_{21}&a_{22}&dots&a_{2j}&dots&a_{2n}\ dots&dots&dots&dots\ a_{i1}&a_{i2}&dots&a_{ij}&dots&a_{in}\ dots&dots&dots&dots\ a_{n1}&a_{n2}&dots&a_{nj}&dots&a_{nn} end{vmatrix} right

Можно изобразить, как размещение по элементам первого столбца:

Delta = a_{11} * A_{11} + a_{21} * A_{21} + dots + a_{i1} * A_{i1} + dots + a_{n1} * A_{n1} = sum_{i = 1}^nlimits,

где A_{i1} = (-1)^{i + 1}quad{M{i1}(i = 1, 2, dots, n)} – алгебраические дополнения, а M{i1} – миноры элементов первого столбца. Последние и есть определители (n - 1) – го порядка.

Чтобы было более понятно, разберём матрицу четвёртого порядка, где нужно найти определитель:

Разберём на примере:

Задача

Нужно вычислить определитель матрицы высшего порядка 4 x 4:

Delta = begin{vmatrix} 1&-2&-1&3\ -1&3&-1&-1\ 3&-8&7&7\ 2&1&-10&17 end{vmatrix} right

Решение

Сначала вспомним тему про определители третьего порядка и превратим в нули элементы 1-го столбца, которые принадлежат 2, 3, 4 строкам. Для этого прибавим соответствующие элементы 1 и 2 строк. На месте элементов a_{21} получим (1 + (-1)) = 0, a_{22} = (-2) + 3 = 1, a_{23} = (-1) + (-1) = -2, a_{24} = 3 + (-1) = 2.

Чтобы получить 0 в 3 строке 1-го столбца, умножим на (-3) элементы 1-ой строки и прибавим к соответствующим элементам третьей строки:

a_{31} = 1 * (-3) + 3 = 0,

a_{32} = (-2) * (-3) + (-8) = - 2,

a_{33} = (-1) * (-3) + 7 = 10,

a_{34} = 3 * (-3) + 7 = -2.

Умножим элементы 1-ой строки на (-2) и добавим к соответствующим элементам 4-ой строки. Получается:

a_{41} = 1 * (-2) + 2 = 0,

a_{42} = (-2) * (-2) + 1 = 5,

a_{43} = (-1)*(-2) +(-10) = -8

a_{44} = 3 * (-2) + 17 = 11.

Изначальный определитель впоследствии преобразований получается:

Delta = begin{vmatrix} 1&-2&-1&3\ -1&3&-1&-1\ 3&-8&7&7\ 2&1&-10&17 end{vmatrix} = begin{vmatrix} 1&-2&-1&3\ 0&1&-2&2\ 0&-2&10&-2\ 0&5&-8&11 end{vmatrix} right

Дальше раскладываем последний определитель за элементами 1-го столбца. Поскольку a_{11} = 1, а остальные элементы 1-го столбца нули, тогда получим один определитель  3-го порядка.

Delta = begin{vmatrix} 1&-2&2\ -2&10&-2\ 5&-8&11 end{vmatrix} = begin{vmatrix} 1&-2&2\ 0&6&2\ 0&2&1 end{vmatrix} = begin{vmatrix} 6&2\ 2&1 end{vmatrix} = 2 right

Ответ

Определитель матрицы четвёртого порядка = 2.

Вычисление определителя матрицы при помощи теоремы Лапласа

Теорема Лапласа – это глубокое разложение определителя по элементам. При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.

Напомним – минор – это определитель матрицы, который составлен методом вычёркивания i – той строки и j – того столбца. А алгебраическое дополнение – соответствующий минор, который берётся со знаком минус (-1)^{i + j}. Знаки же зависят от места элемента a_{ij} в определителе и определяются по схеме:

begin{vmatrix} +&-&+\ -&+&-\ +&-&+ end{vmatrix} right

Приведём пример решения алгебраических дополнений по схеме:

Задача

Найти алгебраические дополнения элементов определителя:

begin{vmatrix} 3&-2&4\ 0&-5&1\ 6&7&8 end{vmatrix} right

Решение

A_{11} = + begin{vmatrix} -5&1\ 7&8 end{vmatrix} = - 47; {A_{12}} = - begin{vmatrix} 0&1\ 6&8 end{vmatrix} = 6; {A_{13}} = + begin{vmatrix} 0&-5\ 6&7 end{vmatrix} = 30 right

A_{21} = - begin{vmatrix} -2&4\ 7&8 end{vmatrix} = 44; {A_{22}} = + begin{vmatrix} 3&4\ 6&8 end{vmatrix} = 0; {A_{23}} = - begin{vmatrix} 3&-2\ 6&7 end{vmatrix} = - 33 right

A_{31} = + begin{vmatrix} -2&4\ -5&1 end{vmatrix} = 18; {A_{32}} = - begin{vmatrix} 3&4\ 0&1 end{vmatrix} = - 3;{A_{33}} = + begin{vmatrix} 3&-2\ 0&-5 end{vmatrix} = - 15 right

Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя):

Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например,

Delta = a_{11} * A_{11} + a_{21} * A_{21} + a_{31} * a_{31}. – это равенство проверяется непосредственно

Delta = begin {vmatrix} a_{11}&a_{12}&a_{13}\ a_{21}&a_{22}&a_{23}\ a_{31}&a_{32}&a_{33} end{vmatrix} = a_{11} * A_{11} + a_{21} * A_{21} + a_{31} * A_{31} =\=a_{11}begin {vmatrix}a_{22}&a_{23\a_{32}&a_{33}end{vmatrix} - a_{21}begin {vmatrix}a_{12}&a_{13}\a_{32}&a_{33}end{vmatrix} + a_{31} begin {vmatrix}a_{12}&a_{13}\a_{22}&a_{23}end{vmatrix} = a_{11}a_{22}a_{33} - a_{11}a_{32}a_{23} -\- a_{21}a_{12}a_{33} + a_{21}a_{32}a_{13} + a_{31}a_{12}a_{23} - a_{31}a_{22}a_{13}. right

Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Давайте по теореме Лапласа разберём несколько примеров:

Задача

Вычислить определитель матрицы, разложив его за элементами третьего порядка:

Delta = begin{vmatrix} 1&1&1\ 4&5&9\ 16&25&81 end{vmatrix} right

Решение

Delta = 16 * begin{vmatrix} 1&1\ 5&9 end{vmatrix} - 25 * begin{vmatrix} 1&1\ 4&9 end{vmatrix} + 81 * begin{vmatrix}1&1\ 4&5 end{vmatrix} = 16 * 4 - 25 * 5 + 81 * 1 = \ = 145 - 125 = 20 right

Ответ

Delta = 20.

Заключение

Итак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя:

  1. через сумму двух произведений сочетаний элементов квадратной матрицы;
  2. по правилу разложения определителя по элементам строк (столбцов) квадратной матрицы;
  3. по методу Гаусса, когда матрицу нужно привести к треугольному виду.

Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков.

Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы.

Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали.

Полезная литература

pdf Белоусов И. В. Матрицы и определители, учеб. Пособие по линейной по алгебре/ – Кишинёв – 2006 – 91 с.

pdf Магазинников Л. И.- Практикум по линейной алгебре и аналитической геометрии: учеб. пособие для вузов/Магазинников Л. И., Магазинникова А. Л. – Томск – 2007 – 150 с.

Источник

Добавить комментарий