Как найти определитель матрицы в квадрате - Сайт, где вы сможете решить свои вопросы

tr(A) = tr(AT ) .

4. При суммировании матриц их следы также суммируются:

tr(A + B) = tr(A) + tr(B) .

5. Хотя коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, однако:

tr(A B) = tr(B A) .

В частности, если А – матрица строка: A = (a1 a2 L an ) , то:

tr(A AT ) = tr(AT A) = ∑ai2

i=1

Основные вопросы темы

1.Определитель квадратной матрицы.

2.Вычисление определителя матриц 1, 2 и 3 порядка.

3.Вычисление определителя матриц произвольного порядка.

2.1Определитель квадратной матрицы.

Вначале дадим качественное определение: определителем квадратной матрицы размера n×n называется число, вычисляемое по строго определенному правилу и характеризующее определенные свойства матрицы. Эта характеристика широко используется для решения различных задач матричного анализа.

Определитель матрицы А обозначается как А , , или detA.

Правила вычисления определителей удобно рассмотреть, начиная с матриц первого, второго и третьего порядка.

2.2. Вычисление определителя матриц 1, 2 и 3 порядка.

Определитель матрицы первого порядка.

Определитель матрицы первого порядка A = (a11 ) равен элементу

1×1

матрицы a11 :

= A = a11 .

Определитель матрицы второго порядка.

Определитель матрицы второго порядка A	a11	a12	вычисля-
=
2×2		a22
	a21

ется по формуле:

=	A	=	a11	a12	= a11a22 − a12 a21 .

			a21	a22

Таким образом, для того чтобы найти определитель второго порядка нужно из произведения элементов, составляющих главную диагональ матрицы, вычесть произведение элементов, составляющих ее вторую диагональ.

4	2		равен:
Например, определитель матрицы A =
	5	6

= 4 6 − 2 5 = 10 .

2.2.3 Определитель матрицы третьего порядка

a11

a12

a13

Определитель матрицы третьего порядка

a22

вы-

A = a21

a23

3×3

a32

a31

a33

числяется по формуле:

			a11	a12	a13	= a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a12 a21a33 − a11a23 a32 .
=	A	=	a21	a22	a23

			a31	a32	a33

Правая часть данного равенства представляет собой алгебраическую сумму шести слагаемых, половина из которых берется со знаком ‘+’ , а другая половина – со знаком ‘–’. Каждое слагаемое содержит произведение трех элементов матрицы (по одному из каждого столбца и каждой строки). Правило определения элементов, входящих в каждое слагаемое, удобно представить в геометрической форме. Такое пред-

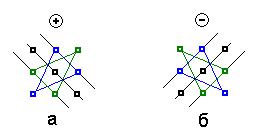
ставление носит название правило треугольников или правило Сарру-

са (см. рис. 2.1).

Рисунок 2.1. Графическая иллюстрация правила Сарруса.

Левая часть рисунка (рис. 2.1.а) отражает правило записи слагаемых со знаком ‘+’ :

–первое слагаемое представляет собой произведение членов матрицы, находящихся на главной диагонали;

–второе и третье слагаемые представляет собой произведение членов матрицы, входящих в треугольники с основаниями параллельными главной диагонали матрицы;

Аналогично находятся слагаемые со знаком ‘ – ’, с той лишь разницей, что все построения реализуются относительно дополнительной диагонали (рис. 2.1.б).

2.2.4Определитель квадратной матрицы произвольного порядка.

Правило вычисления определителя квадратной матрицы произвольного порядка определяется теоремой Лапласа. Однако, чтобы сформулировать эту теорему, необходимо познакомится еще с двумя понятиями: минор – Mij и алгебраическое дополнение – Aij элемента aij

матрицы А.

ОПРЕДЕЛЕНИЕ: Минором – Mij элемента aij матрицы А n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из исходной матрицы путем вычеркивания строки и столбца, в которых находится элемент aij (т.е. i-ой строки и j-го столбца).

Например,

	a11	a12	a13		a12	a13	= a12 a23 − a22 a13 .

M 31 =	a21	a22	a23	=
	a31	a32	a33		a22	a23

ОПРЕДЕЛЕНИЕ: Алгебраическим дополнением – Аij элемента aij матрицы А n-го порядка называется минор этого элемента, взятый со знаком (− 1)i+ j :

Aij = (− 1)i+ j M ij .

Приведенные определения позволяют сформулировать теорему Лапласа, позволяющую вычислить определитель матрицы произвольного порядка.

Теорема Лапласа. Определитель квадратной матрицы равен сумме попарных произведений элементов произвольной строки (столбца) матрицы на их алгебраические дополнения:

A = ai1 Ai1 + ai2 Ai2 + ai3 Ai3 + K+ ain Ain = ∑ aik Aik , k =1

или

A = a1 j A1 j + a2 j A2 j + a3 j A3 j + K+ anj Anj = ∑akj Akj . k =1

Первое выражение определяет разложение определителя матрицы по элементам строки, второе – по элементам столбца.

ЗАМЕЧАНИЕ. Теорема Лапласа показывает, что определитель матрицы n-го порядка может быть вычислен через определители матриц более низкого – (n-1)-го порядка.

2.2.5 Свойства определителя матрицы.

Опираясь на теорему Лапласа, можно показать, что определитель матрицы обладает следующими свойствами.

1.При транспонировании матрицы, значение ее определителя не меняется:

A = AT .

2.При перестановке двух строк (столбцов) матрицы абсолютное значение определителя не меняется, а его знак меняется на противоположный.

3.Определитель матрицы, имеющей две пропорциональные строки (столбцы), равен нулю. В частности, определитель матрицы, имеющей две одинаковые строки (столбцы), равен нулю.

4.Общий множитель элементов отдельной строки (столбца) матрицы можно выносить за знак определителя. Из этого свойства,

вчастности, вытекает следующее равенство:

λА = λn A ,

где: n – порядок квадратной матрицы А; и λ – произвольное число.

5.Определитель матрицы не изменится, если к элементам одной строки (столбца) добавить элементы другой строки (столбца), предварительно умноженные на произвольное (не равное нулю) число.

6.Хотя произведение матриц не обладает законом коммутативности, однако:

A B = B A = А В ,

где А и В квадратные матрицы одного порядка.

7. Определитель единичной матрицы равен единице:

E = 1.

Учет указанных свойств часто значительно облегчает расчет определителя при использовании теоремы Лапласа. Действительно, согласно этой теореме значение определителя равно сумме попарных произведений элементов произвольной строки (столбца) матрицы на их алгебраические дополнения:

A = ai1 Ai1 + ai2 Ai2 + ai3 Ai3 + K+ ain Ain = ∑aik Aik , k =1

или:

A = a1 j A1 j + a2 j A2 j + a3 j A3 j + K+ anj Anj = ∑akj Akj . k =1

Отметим, что чем больше нулевых элементов содержит выбранная для расчета определителя строка (столбец), тем проще выполнить расчет, т.к. соответствующее слагаемое будет заведомо равно нулю. Поэтому, для вычислений целесообразно использовать строку (столбец), содержащую максимальное число нулевых элементов. Если таких строк (столбцов) нет, возможно выполнить ряд операций, которые согласно перечисленным ранее свойствам, не изменяют значение определителя, но увеличивают число нулевых элементов выбранной строки (столбца).

Пример. Вычислить определитель матрицы четвертого порядка

		2	− 3	6	− 2

Â	=	− 3	2	0	1	.

		3	− 1	4	2

		− 8	2	− 3	3

Решение. Воспользуемся теоремой Лапласа, выбрав для разложения вторую строку, т.к. она содержит нулевой элемент. Попытаемся увеличить число нулевых элементов этой строки, воспользовавшись пятым свойством определителей. Прибавим ко второму столбцу – четвертый, предварительно умножив его на “-2” (согласно пятому свойству, значение определителя при этом не изменится). В результате получим:

		2	1	6	− 2

Â	=	− 3	0	0	1	.

		3	− 5	4	2

		− 8	− 4	− 3	3

Число нулевых элементов второй строки – возросло. Теперь прибавим к первому столбцу – четвертый, предварительно умножив его на 3. В результате получим:

		− 4	1	6	− 2

Â	=	0	0	0	1	.

		9	− 5	4	2

		1	− 4	− 3	3

Теперь, вторая строка содержит только один ненулевой элемент. Воспользуемся теоремой Лапласа, используя разложение определителя по второй строке:

B	= b21 A21 + b22 A22 + b23 A23 + b24 A24

	= 0 A21 + 0 A22 + 0 A23 + 1 A24 =
	= A	= (− 1)2+4 M		= M			− 4	1	6

	24	24	=	9	− 5	4	= −279
24
							1	− 4	− 3

ЗАМЕЧАНИЕ. Решение многих задач матричного анализа связано с проверкой равенства нулю определителя матрицы.

ОПРЕДЕЛЕНИЕ. Матрица А называется невырожденной (неособен-

ной), если ее определитель отличен от нуля. В противном случае она называется вырожденной (особенной).

Перечисленные выше свойства определителей позволяют сформулировать необходимое и достаточное условие равенства нулю опре-

делителя: Определитель матрицы равен нулю тогда и только тогда, когда матрица содержит линейно зависимые строки (столбцы).

Пример. Вычислить определитель матрицы четвертого порядка

		5	3	8	1
A	=	7	2	3	8	.

		10	6	16	2

		12	21	7	4

Соседние файлы в папке М

Источник

Содержание

Определитель квадратной матрицы первого порядка
Определитель квадратной матрицы второго порядка
Схема вычисления определителя второго порядка
Примеры вычисления определителей второго порядка
Определитель квадратной матрицы третьего порядка
Правило треугольников нахождения определителя третьего порядка
Примеры вычисления определителей третьего порядка

Используя специальное правило каждой квадратной матрице можно поставить в соответствие число, которое будем называть определителем (детерминантом) и обозначать или или

Определитель квадратной матрицы первого порядка

Определителем квадратной матрицы первого порядка $A=(a_{11})$ называется число

$|A|=|a_{11}|=a_{11}.$

Заметим, что здесь выражение $|a_{11}|$ означает определитель, хоть внешне очень похоже на запись модуля числа $a_{11}.$ Таким образом, определитель матрицы первого порядка равен единственному элементу этой матрицы, например для матриц

определители

Определитель квадратной матрицы второго порядка

Определителем квадратной матрицы второго порядка

$A=left(!!begin{array}{cc}a_{11}^{}& a_{12}^{}\[0.5ex]a_{21}^{}&a_{22}^{}end{array}!!right)$

называется число

$left|Aright|= left|!!begin{array}{cc}a_{11}^{}& a_{12}^{}\[0.5ex]a_{21}^{}&a_{22}^{}end{array}!!right|=a_{11}^{}a_{22}^{}-a_{12}^{}a_{21}.$

Таким образом, для того, что вычислить определитель матрицы 2-го порядка нужно умножить элементы главной диагонали матрицы и от полученного произведения вычесть произведение элементов побочной диагонали матрицы. Схема вычисления определителя второго порядка представлена на рис. 1.

Рис. 1

Рассмотрим примеры, где требуется вычислить определитель второго порядка. У матриц

$A=left(!!begin{array}{cc} 3& -4\[0.5ex] 2&1end{array}!!right),$ $B=left(!!begin{array}{cc} cosalpha & sinalpha\[0.5ex] -sinalpha&cosalpha end{array}!!right)$

определители

$left|Aright|=left|!!begin{array}{cc} 3& -4\[0.5ex] 2&1end{array}!!right|=3cdot 1-({}-4)cdot2=3+8=11,$

$left|Bright|=left(!!begin{array}{cc} cosalpha & sinalpha\[0.5ex] -sinalpha&cosalpha end{array}!!right) =cosalphacosalpha-sinalpha({}-sinalpha)=$

Определитель квадратной матрицы третьего порядка

Определителем квадратной матрицы третьего порядка

$A=left(!!begin{array}{ccc}a_{11}^{}& a_{12}^{}&a_{13}^{}\[0.5ex]a_{21}^{}& a_{22}^{}&a_{23}^{}\[0.5ex]a_{31}^{}& a_{32}^{}&a_{33}^{}end{array}!!right)$

называется число

$left|Aright|=left|!!begin{array}{ccc}a_{11}^{}& a_{12}^{}&a_{13}^{}\[0.5ex]a_{21}^{}& a_{22}^{}&a_{23}^{}\[0.5ex]a_{31}^{}& a_{32}^{}&a_{33}^{}end{array}!!right|=$

$=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-$ $(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+ a_{11}a_{23}a_{32}).$

Как видим, для того чтобы вычислить определитель матрицы третьего порядка необходимо использовать достаточно сложную для запоминания формулу, однако, заучивать ее вовсе не обязательно. Гораздо легче понять и запомнить схему вычисления определителя третьего порядка (рис. 2) (ее еще называют правилом треугольников). Используя эту схему решаются задачи на вычисление определителей матриц 3×3, и с ее помощью всегда можно восстановить формулу нахождения определителя 3-го порядка.

Рис. 2

Как видно из схемы (рис. 2), для того чтобы найти определитель третьего порядка необходимо вычислить 6 чисел, каждое из которых представляет собой произведение трех чисел. Для нахождения первого числа требуется найти произведение элементов главной диагонали, второе и третье числа представляют собой произведения элементов, находящихся в вершинах равнобедренных треугольников (см. рис. 2), чьи основания параллельны главной диагонали матрицы. Аналогично, четвертое число в схеме есть произведение элементов второй (побочной) диагонали матрицы, а пятое и шестое числа находятся как произведения элементов-вершин равнобедренных треугольников с основаниями параллельными второй диагонали матрицы. Затем следует сложить первые три числа и из этой суммы вычесть сумму чисел с номерами 4 — 6.

Рассмотрим пример вычисления определителя матрицы третьего порядка. Определитель

$left|!!begin{array}{ccc}2& 3&-1\[0.5ex] 1& 3&{}-1\[0.5ex] 1& {}-3&0}end{array}!!right|= 2cdot3cdot0+3cdot(-1)cdot1+(-1)cdot 1cdot(-3)-$

Источник

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Перед тем как находить и считать определитель, дадим определение определителю матрицы.

Определение 1

Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.

|А|, ∆, det A – символы, которыми обозначают определитель матрицы.

Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.

Пример 1

Определитель матрицы второго порядка можно вычислять по формуле:

А=1-231.

Решение матрицы:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника

Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:

он может считаться по правилу треугольника;
расчет также проводится по правилу Саррюса.

Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

дописать слева от определителя два первых столбца;
перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:

разложением по элементам строки;
разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
если поменять местами строки и столбцы, то знак поменяется на противоположный;
определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Замечание

В рамках темы советуем обратиться к модулю определителя.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Содержание:

Вычисления определителей второго порядка
Методы вычисления определителей третьего порядка
Приведение определителя к треугольному виду
Правило треугольника
Правило Саррюса
Разложение определителя по строке или столбцу
Разложение определителя по элементам строки или столбца
Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.

Решение.

$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$

$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$

$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:

$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$

Полученный определитель разложим по элементам первого столбца:

$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:

$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$

$$=4 cdot(2 cdot 8-4 cdot 4)=0$$

Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$

$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$

Ответ. $Delta=-80$

Теорема Лапласа

Теорема

Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$

Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$

$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$

$$=-23+128+90=195$$

Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$

Читать дальше: обратная матрица.

Источник

Определитель матрицы

Пусть задана матрица второго порядка $ A = begin{pmatrix} a_{11}&a_{12}\a_{21}&a_{22} end{pmatrix} $. Тогда её определитель находится по формуле:

$$ Delta = begin{vmatrix} a_{11}&a_{12}\a_{21}&a_{22} end{vmatrix} = a_{11}cdot a_{22} – a_{12}cdot a_{21} $$

Из произведения элементов, стоящих на главной диагонали $ a_{11}cdot a_{22} $, вычитается произведение элементов, расположенных на побочной диагонали $ a_{12}cdot a_{21} $. Это правило верно только (!) для определителя 2-го порядка.

Если дана матрица третьего порядка $ A = begin{pmatrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{pmatrix} $, то вычислить её определитель следует по формуле:

$$ Delta = begin{vmatrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{vmatrix} = $$

$$ = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13} – a_{13}a_{22}a_{31}-a_{23}a_{32}a_{11}-a_{12}a_{21}a_{33} $$

Пример 1

Найти определитель матрицы $ A = begin{pmatrix} 1&2\3&4 end{pmatrix} $

Решение

Обратим внимание на то что матрица квадратная второго порядка, то есть количество столбцов равно количеству строк и они содержат по 2 элемента. Поэтому применим первую формулу. Перемножим элементы, стоящие на главной диагонали и вычтем из них произведение элементов, стоящих на побочной диагонали:

$$ Delta = begin{vmatrix} 1&2\3&4 end{vmatrix} = 1 cdot 4 – 2 cdot 3 = 4-6 = -2 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ Delta = -2 $$

Пример 2

Вычислить определитель $ A = begin{pmatrix} 2&2&1\1&-3&-1\3&4&-2 end{pmatrix} $

Решение

Так как в задаче квадратная матрица 3-го порядка, то найти определитель матрицы следует по второй формуле. Для простоты решения задачи достаточно подставить вместо $ a_{ij} $ переменных, стоящих в формуле значения из матрицы нашей задачи:

$$ Delta = begin{vmatrix} 2&2&1\1&-3&-1\3&4&-2 end{vmatrix} = $$

$$ = 2cdot (-3) cdot (-2) + 2cdot (-1) cdot 3 + 1cdot 4cdot 1 – $$ $$ – 1cdot (-3)cdot 3 – (-1)cdot 4cdot 2 – 2cdot 1cdot (-2) = $$

$$ = 12 – 6 + 4 + 9 + 8 + 4 = 31 $$

Стоит отметить когда мы находим произведения элементов на побочной диагонали и подобных её, то перед произведениями ставится знак минус.

Ответ

$$ Delta = 31 $$

Пример 3

Найти определитель матрицы $ A = begin{pmatrix} 1&3&-2\-2&4&1 end{pmatrix} $

Решение

Замечаем сразу, что количество строк не равно количеству столбцов, поэтому матрица не является квадратной. Так как определить существует только у квадратных матриц, то задача не имеет решения.

Ответ

Невозможно посчитать определитель

Источник

Основные вопросы темы

1.Определитель квадратной матрицы.

Правила вычисления определителей удобно рассмотреть, начиная с матриц первого, второго и третьего порядка.

2.2. Вычисление определителя матриц 1, 2 и 3 порядка.

Определитель квадратной матрицы первого порядка

Определитель квадратной матрицы второго порядка

Определитель квадратной матрицы третьего порядка

Определитель матрицы 3-го порядка: правило треугольника

Правило Саррюса

Методы разложения по элементам строки и столбца

Свойства определителя

Вычисления определителей второго порядка

Методы вычисления определителей третьего порядка

Правило треугольника

Правило Саррюса

Разложение определителя по строке или столбцу

Разложение определителя по элементам строки или столбца

Приведение определителя к треугольному виду

Теорема Лапласа

Определитель матрицы

Вам также может понравиться

Как найти свою половинку от бога

Web of science id автора как найти

Как найти куда посадили человека после суда

Добавить комментарий Отменить ответ