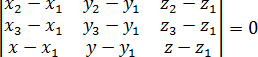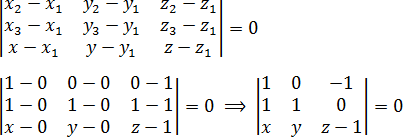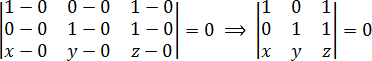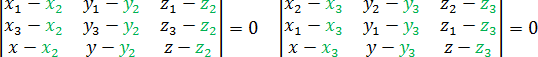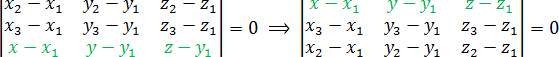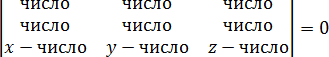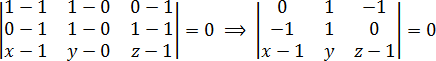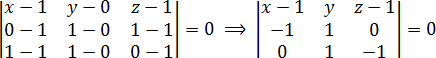Как найти определитель плоскости

23 ноября 2012

В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:

M = (x₁, y₁, z₁);
N = (x₂, y₂, z₂);
K = (x₃, y₃, z₃);

Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:

Ax + By + Cz + D = 0

где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x₁, y₁, z₁); N = (x₂, y₂, z₂); K = (x₃, y₃, z₃). Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

Задача. Составьте уравнение плоскости, проходящей через точки:

A₁ = (0, 0, 1);
B = (1, 0, 0);
C₁ = (1, 1, 1);

Составляем определитель и приравниваем его к нулю:

Раскрываем определитель:

a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x, y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Задача. Составьте уравнение плоскости, проходящей через точки:

A = (0, 0, 0);
B₁ = (1, 0, 1);
D₁ = (0, 1, 1);

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x₂ или x₃, а в какой — просто x. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Откуда берется формула с определителем?

Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.

Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:

M = (x₁, y₁, z₁);
N = (x₂, y₂, z₂);
K = (x₃, y₃, z₃).

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

T = (x, y, z)

Берем любую точку из первой тройки (например, точку M) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:

MN = (x₂ − x₁, y₂ − y₁, z₂ − z₁);
MK = (x₃ − x₁, y₃ − y₁, z₃ − z₁);
MT = (x − x₁, y − y₁, z − z₁).

Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x, y, z) — как раз то, что мы искали.

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x; y; z) в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные x, y и z, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax + By + Cz + D = 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Задача. Составьте уравнение плоскости, проходящей через точки:

B₁ = (1, 0, 1);
C = (1, 1, 0);
D₁ = (0, 1, 1).

Итак, рассматриваем 4 точки:

B₁ = (1, 0, 1);
C = (1, 1, 0);
D₁ = (0, 1, 1);
T = (x, y, z).

Для начала составим стандартный определитель и приравниваем его к нулю:

Раскрываем определитель:

a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

Все, мы получили ответ: x + y + z − 2 = 0.

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x, y, z не внизу, а вверху:

Вновь раскрываем полученный определитель:

a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку B₁ = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D₁ = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.

Смотрите также:

1. Видеоурок по задачам C2: уравнение плоскости через определитель
2. Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
3. Тест к уроку «Что такое числовая дробь» (легкий)
4. Сводный тест по задачам B15 (1 вариант)
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: тарифы на сотовую связь

Задача C2: уравнение плоскости через определитель

В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:

Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:

Ax + By + Cz + D = 0

где числа A , B , C и D — коэффициенты, которые, собственно, и требуется найти.

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием обоснований и доказательств.

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

Задача. Составьте уравнение плоскости, проходящей через точки:

Составляем определитель и приравниваем его к нулю:

a = 1 · 1 · ( z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · ( z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (− x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Задача. Составьте уравнение плоскости, проходящей через точки:

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − ( x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, рекомендуется — чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит а в какой — Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Откуда берется формула с определителем?

Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.

Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

Берем любую точку из первой тройки (например, и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:

Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка как раз то, что мы искали.

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax + By + Cz + D = 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Задача. Составьте уравнение плоскости, проходящей через точки:

Итак, рассматриваем 4 точки:

Для начала составим стандартный определитель и приравниваем его к нулю:

a = 0 · 1 · ( z − 1) + 1 · 0 · ( x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · ( x − 1) + 1 · (−1) · ( z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

Все, мы получили ответ: .

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными не внизу, а вверху:

Вновь раскрываем полученный определитель:

a = ( x − 1) · 1 · (−1) + ( z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = ( z − 1) · 1 · 0 + y · (−1) · (−1) + ( x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Мы получили точно такое же уравнение плоскости: Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку но вполне можно было взять В общем, любую точку с известными координатами, лежащую на искомой плоскости.

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

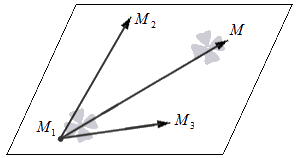
Допустим, у нас имеется прямоугольная система координат. Обозначим ее O x y z . В ней лежат три точки M с координатами M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , которые нельзя соединить прямой линией. Исходя из этих условий, мы можем записать уравнение необходимой нам плоскости. Есть два подхода к решению этой задачи.

1. Первый подход использует общее уравнение плоскости. В буквенном виде оно записывается как A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . С его помощью можно задать в прямоугольной системе координат некую плоскость альфа, которая проходит через первую заданную точку M 1 ( x 1 , y 1 , z 1 ) . У нас получается, что нормальный вектор плоскости α будет иметь координаты A , B , C .

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

Таким образом, согласно условиям задачи, мы имеем координаты искомой точки (даже трех), через которую проходит плоскость. Чтобы найти уравнение, нужно вычислить координаты ее нормального вектора. Обозначим его n → .

Вспомним правило: любой не равный нулю вектор данной плоскости является перпендикулярным нормальному вектору этой же плоскости. Тогда мы имеем, что n → будет перпендикулярным по отношению к векторам, составленным из исходных точек M 1 M 2 → и M 1 M 3 → . Тогда мы можем обозначить n → как векторное произведение вида M 1 M 2 → · M 1 M 3 → .

Поскольку M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) а M 1 M 3 → = x 3 – x 1 , y 3 – y 1 , z 3 – z 1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора по координатам точек), тогда получается, что:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

Если мы вычислим определитель, то получим необходимые нам координаты нормального вектора n → . Теперь мы можем записать нужное нам уравнение плоскости, проходящей через три заданные точки.

2. Второй подход нахождения уравнения, проходящей через M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , основан на таком понятии, как компланарность векторов.

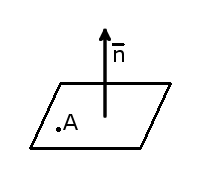
Если у нас есть множество точек M ( x , y , z ) , то в прямоугольной системе координат они определяют плоскость для заданных точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) только в том случае, когда векторы M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) будут компланарными.

На схеме это будет выглядеть так:

Это будет означать, что смешанное произведение векторов M 1 M → , M 1 M 2 → , M 1 M 3 → будет равно нулю: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , поскольку это является основным условием компланарности: M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) .

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

После того, как мы вычислим определитель, мы сможем получить нужное нам уравнение плоскости для трех не лежащих на одной прямой точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) .

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Есть три точки, не лежащие на одной прямой, с координатами M 1 ( – 3 , 2 , – 1 ) , M 2 ( – 1 , 2 , 4 ) , M 3 ( 3 , 3 , – 1 ) . Составьте уравнение плоскости, проходящей через них.

Решение

Используем поочередно оба способа.

1. Найдем координаты двух нужных нам векторов M 1 M 2 → , M 1 M 3 → :

M 1 M 2 → = – 1 – – 3 , 2 – 2 , 4 – – 1 ⇔ M 1 M 2 → = ( 2 , 0 , 5 ) M 1 M 3 → = 3 – – 3 , 3 – 2 , – 1 – – 1 ⇔ M 1 M 3 → = 6 , 1 , 0

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

У нас получился нормальный вектор плоскости, которая проходит через три искомые точки: n → = ( – 5 , 30 , 2 ) . Далее нам нужно взять одну из точек, например, M 1 ( – 3 , 2 , – 1 ) , и записать уравнение для плоскости с вектором n → = ( – 5 , 30 , 2 ) . Мы получим, что: – 5 · ( x – ( – 3 ) ) + 30 · ( y – 2 ) + 2 · ( z – ( – 1 ) ) = 0 ⇔ – 5 x + 30 y + 2 z – 73 = 0

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

2. Используем другой подход. Запишем уравнение для плоскости с тремя точками M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

Сюда можно подставить данные из условия задачи. Поскольку x 1 = – 3 , y 1 = 2 , z 1 = – 1 , x 2 = – 1 , y 2 = 2 , z 2 = 4 , x 3 = 3 , y 3 = 3 , z 3 = – 1 , в итоге мы получим:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

Ответ: – 5 x + 30 y + 2 z – 73 .

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

У нас есть прямоугольная система координат в трехмерном пространстве, в которой размещены три точки с координатами M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) . Необходимо составить уравнение плоскости, проходящей через нее.

Решение

Используем первый способ и начнем с вычисления координат двух векторов M 1 M 2 → и M 1 M 3 → . Подсчитаем их координаты: M 1 M 2 → = ( – 4 , 6 , 2 ) , M 1 M 3 → = – 6 , 9 , 3 .

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Поскольку M 1 M 2 → × M 1 M 3 → = 0 → , то наши векторы будут коллинеарными (перечитайте статью о них, если забыли определение этого понятия). Таким образом, исходные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой, и наша задача имеет бесконечно много вариантов ответа.

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Из получившегося равенства также следует, что заданные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой.

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

1. Записать уравнение прямой М 1 М 2 , М 1 М 3 или М 2 М 3 (при необходимости посмотрите материал об этом действии).

2. Взять точку M 4 ( x 4 , y 4 , z 4 ) , которая не лежит на прямой М 1 М 2 .

3. Записать уравнение плоскости, которая проходит через три различных точки М 1 , М 2 и M 4 , не лежащих на одной прямой.

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

x – x 1	y – y 1	z – z 1	= 0
x 2 – x 1	y 2 – y 1	z 2 – z 1
x 3 – x 1	y 3 – y 1	z 3 – z 1

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-kotoraja-prohodit-cherez-tri-z/

http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/plane/

[/spoiler]

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Во-первых, мы должны запомнить аксиому, которая звучит так:

Если три точки не совпадают между собой и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Другими словами, если у нас есть три разные точки, координаты которых не совпадают и которые не могут быть соединены линией, мы можем определить плоскость, которая ее пересекает.

Допустим, у нас есть прямоугольная система координат. Назовем его Oxyz. Он содержит три точки M с координатами M1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3, y3, z3), которые нельзя соединить прямой линией. Исходя из этих условий, мы можем написать необходимое нам уравнение плоскости. Есть два подхода к решению этой проблемы.

• Первый подход использует общую уравнение плана. В буквальном виде он записывается как A (x-x1) + B (y-y1) + C (z-z1) = 0. С его помощью можно указать некую альфа-плоскость в прямоугольной системе координат, которая проходит через первую заданную точку M1 (x1, y1, z1). Оказывается, нормальный вектор плоскости α будет иметь координаты A, B, C.
• Зная координаты вектора нормали и координаты точки, через которую проходит плоскость, мы можем написать общее уравнение этой плоскости.

Из этого и будем исходить в дальнейшем.

Тогда по условиям задачи у нас есть координаты искомой точки (даже трех), через которую проходит самолет. Чтобы найти уравнение, необходимо вычислить координаты его вектора нормали. Обозначим его через n→.

Напомним правило: любой ненулевой вектор данной плоскости перпендикулярен вектору нормали той же плоскости. Тогда мы имеем, что n → будет перпендикулярно векторам, составленным из исходных точек M1M2 → и M1M3 →. Тогда мы можем обозначить n → как векторное произведение вида M1M2 → M1M3→.

Поскольку M1M2 → = (x2-x1, y2-y1, z2-z1) и M1M3 → = x3-x1, y3-y1, z3-z1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора из координат точек), то получается, что:

n → = M1M2 → × M1M3 → = i → j → k → x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1

Если вычислить определитель, то получим нужные нам координаты вектора нормали n →. Теперь мы можем написать желаемое уравнение плоскости, проходящей через три точки данных.

• Второй подход к нахождению уравнения, проходящего через M1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3, y3, z3), основан на концепции компланарности векторов.

Если у нас есть набор точек M (x, y, z), то в прямоугольной системе координат они определяют плоскость для заданных точек M1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3 , y3, z3), только если векторы M1M → = (x-x1, y-y1, z-z1), M1M2 → = (x2-x1, y2-y1, z2-z1) и M1M3 → = (x3-x1 , y3-y1, z3-z1) будет компланарным.

На схеме это будет выглядеть так:

Это будет означать, что смешанное произведение векторов M1M →, M1M2 →, M1M3 → будет равно нулю: M1M → M1M2 → M1M3 → = 0, поскольку это главное условие компланарности: M1M → = (x-x1, y -y1, z-z1), M1M2 → = (x2-x1, y2-y1, z2-z1) и M1M3 → = (x3-x1, y3-y1, z3-z1).

Запишем полученное уравнение в виде координат:

x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1 = 0

После вычисления определителя мы можем получить необходимое уравнение плоскости для трех точек M1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3, y3, z3), которые не лежат на одной прямой).

От полученного уравнения можно перейти к уравнению сегментированной плоскости или уравнению нормали к плоскости, если этого требуют условия задачи.

В следующем разделе мы приведем примеры того, как эти подходы реализуются на практике.

Уравнение плоскости через определитель

Хватит лирики, приступим к работе. Начнем с теоремы о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Даны координаты трех точек, через которые необходимо провести плоскость: M = (x1, y1, z1); N = (x2, y2, z2); К = (х3, у3, z3). Итак, уравнение этой плоскости можно записать через определитель:

Например, давайте попробуем найти пару плоскостей, которые действительно встречаются в задачах C2. Посмотрите, насколько быстро все это имеет значение:

Задача. Сопоставьте план по пунктам:

A1 = (0, 0, 1);
В = (1,0,0);
C1 = (1, 1, 1);

Составляем определитель и отождествляем его с нулем:

Расширяя определитель:

a = 1 1 (z — 1) + 0 0 x + (−1) 1 y = z — 1 — y;
b = (−1) 1 x + 0 1 (z — 1) + 1 0 y = −x;
d = a — b = z — 1 — y — (−x) = z — 1 — y + x = x — y + z — 1;
d = 0 ⇒ x — y + z — 1 = 0;

Как видите, при вычислении числа d я немного прочесал уравнение, чтобы переменные x, y и z находились в правильной последовательности. Это все! Уравнение плана готово!

Задача. Сопоставьте план по пунктам:

А = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);

Сразу подставляем координаты точек в определитель:

Снова разверните определитель:

а = 1 1 z + 0 1 x + 1 0 y = z;
б = 1 1 х + 0 0 г + 1 1 у = х + у;
d = a — b = z — (x + y) = z — x — y;
d = 0 ⇒ z — x — y = 0 ⇒ x + y — z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем этапе нам пришлось изменить знаки, чтобы получить более «красивую» формулу. В настоящем решении это вовсе не обязательно, но все же рекомендуется, чтобы упростить дальнейшее решение проблемы.

Как видите, уравнение плана теперь намного проще. Подставляем точки в матрицу, вычисляем определитель и все, уравнение готово.

Это могло закончить урок. Однако многие студенты постоянно забывают, что находится внутри определителя. Например, какая строка содержит x2 или x3, а какая строка содержит только x. Чтобы наконец добраться до конца, давайте проследим, откуда взялось каждое число.

Откуда берется формула с определителем?

Итак, попробуем разобраться, откуда взялось такое сложное уравнение с определителем. Это поможет вам запомнить и успешно применить его.

Все плоскости, встречающиеся в задаче C2, обозначены тремя точками. Эти точки всегда отмечены на чертеже или даже указаны прямо в тексте задачи. В любом случае, чтобы составить уравнение, нам нужно записать их координаты:

M = (x1, y1, z1);
N = (x2, y2, z2);
К = (х3, у3, z3).

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

Т = (х, у, г)

Берем любую точку первой тройки (например, точку M) и из нее строим векторы для каждой из трех оставшихся точек. Получаем три вектора:

MN = (x2 — x1, y2 — y1, z2 — z1);
MK = (x3 — x1, y3 — y1, z3 — z1);
MT = (x — x1, y — y1, z — z1).

Теперь мы составим квадратную матрицу из этих векторов и сделаем их равными нулю. Координаты векторов станут строками матрицы — и мы получим тот же определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, произвольная точка T = (x, y, z) — это именно то, что мы искали.

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax cdot + By + Cz + D = 0left(1right)$,

при этом: ${A; B; C}$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

$A(x-x_0)+B(y-y_0) + C(z-z_0)=0left(2right)$,

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec{M_1M_2}$, $vec{M_1M_3}$ и $vec{M_1M}$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

«Уравнение плоскости через 3 точки» 👇

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

$vec{M_1M_2}={x_2-x_1; y_2-y_1; z_2-z_1}$;

$vec{M_1M_3}= {x_3-x_1; y_3-y_1; z_3-z_1}$;

$vec{M_1M} = {x-x_1; y-y_1; z-z_1}$.

Составим определитель, описывающий смешанное произведение векторов:

$begin{array}{|ccc|} x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end{array}=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$begin{array}{|cc|} y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end{array} cdot ( x-x_1) + begin{array}{|cc|} x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end{array} cdot (y-y_1) + begin{array}{|cc|} x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end{array} cdot (z-z_1) = 0left(3right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec{M_1M_2}×vec{M_1M_3}$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec{M_1M_2}$ и $vec{M_1M_3}$:

$[vec{M_1M_2} × vec{M_1M_3}]= begin{array}{|ccc|} vec{i} &&vec{j} &&vec{k} \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end{array}=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

$n_x(x-x_3)+n_y(y-y_3)+n_z(z-z_3)=0$.

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec{M_1M_2}$ и $vec{M_1M_3}$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.