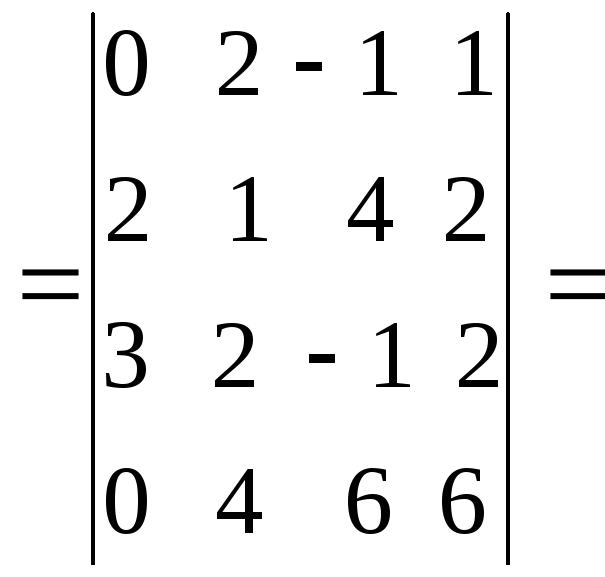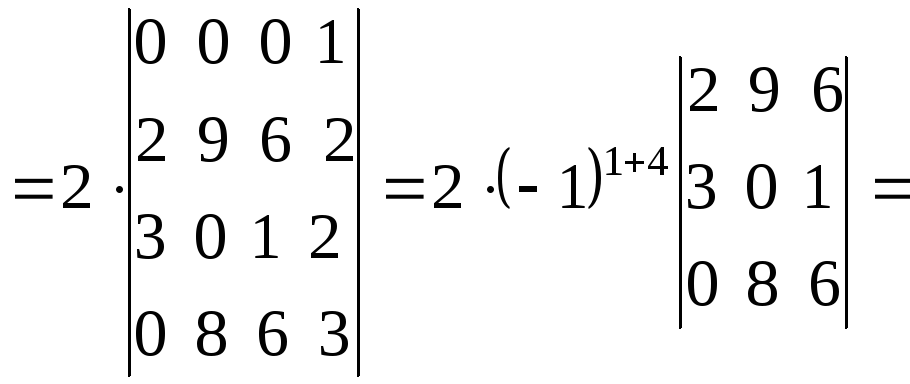Как найти определитель системы линейных уравнений

1. Определители и системы линейных уравнений

1.1.
Системы двух линейных уравнений и
определители второго порядка

Рассмотрим
систему двух линейных уравнений с двумя
неизвестными:

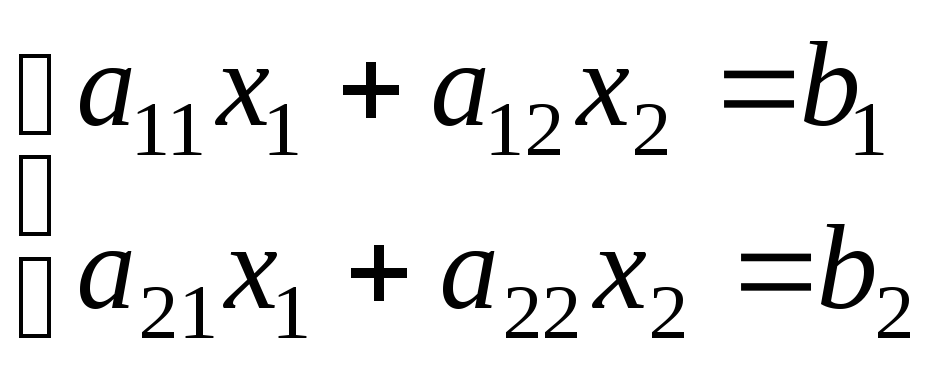
Коэффициенты

при неизвестных
и
имеют два индекса: первый указывает
номер уравнения, второй – номер
переменной.

Главным определителем системы называется таблица, составленная из коэффициентов при неизвестных и заключенная в прямые скобки:

Вспомогательным определителем называют определитель, полученный из главного определителя заменой одного из столбцов на столбец свободных членов:

Главнаядиагональ определителя – это диагональ, направленная из левого верхнего угла в правый нижний угол. Вторая диагональ называетсяпобочной.

Определитель второго порядка равен разности между произведением элементов главной диагонали и произведением элементов побочной диагонали:

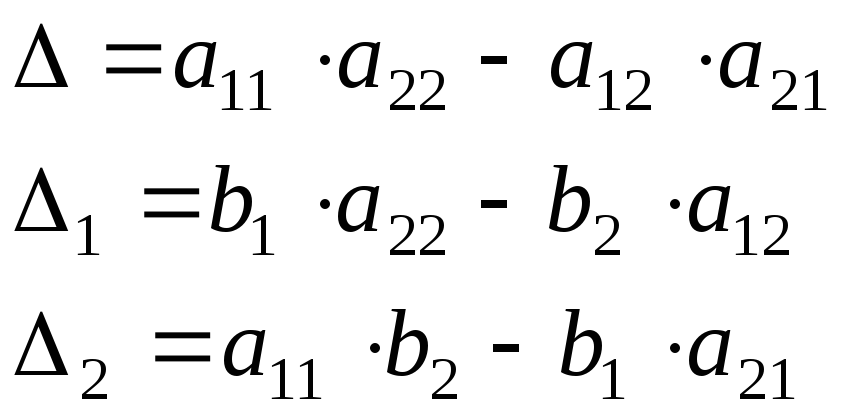
Правило
Крамера: Решение системы находят
путем деления вспомогательных
определителей на главный определитель
системы

,

Замечание
1.Использование правила Крамера
возможно, если определитель системы
не равен нулю.

Замечание
2.Формулы Крамера обобщаются и на
системы большего порядка.

Пример
1. Решить систему:
.

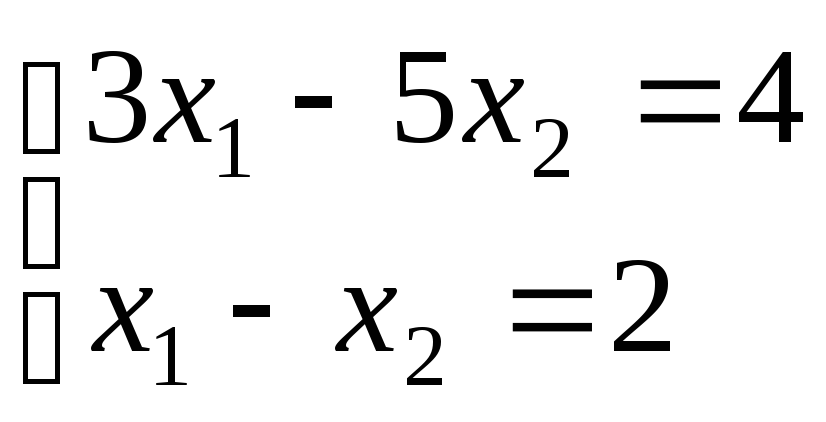Решение.

;

;

;

Проверка:

Вывод:
Система решена верно:
.

1.2. Системы трех линейных уравнений и определители третьего порядка

Рассмотрим
систему трех линейных уравнений с тремя
неизвестными:

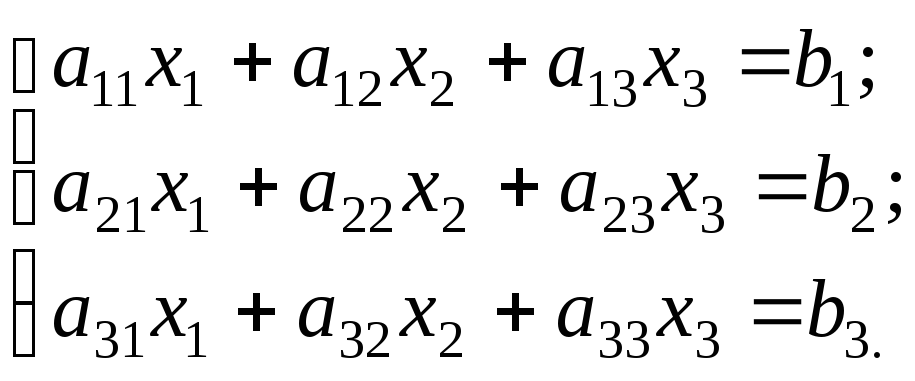
Определитель,
составленный из коэффициентов при
неизвестных, называется определителем
системы или главным определителем:

.

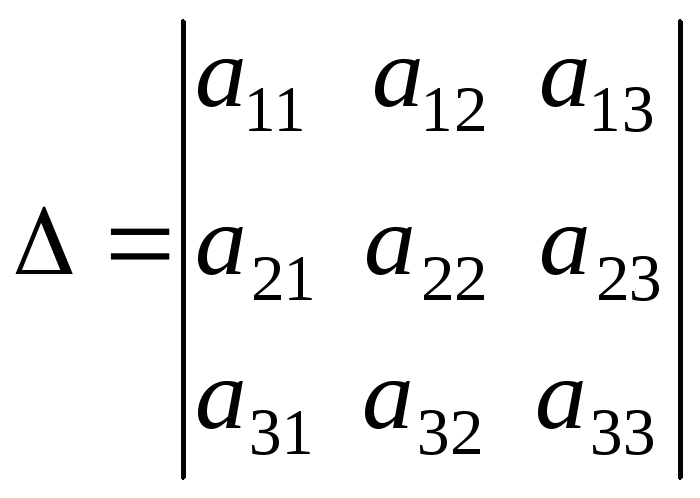Если

то система имеет единственное решение,
которое определяется по формулам
Крамера:

где

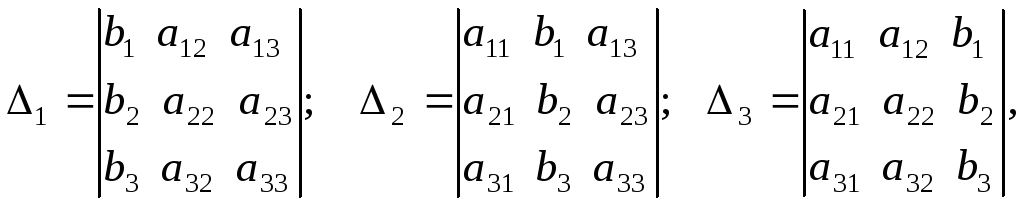
где
определители
– называются вспомогательными и
получаются из определителя
путем замены его первого, второго или
третьего столбца столбцом свободных
членов системы.

Пример
2.Решить систему
.

Сформируем
главный и вспомогательные определители:

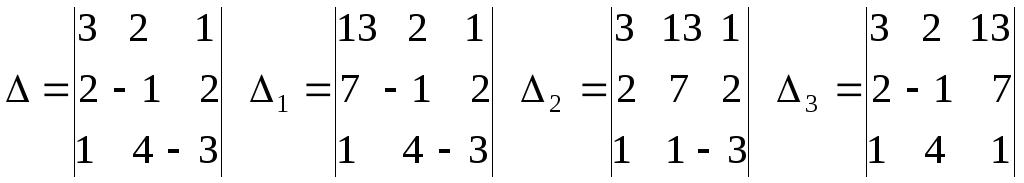
Осталось
рассмотреть правила вычисления
определителей третьего порядка. Их три:
правило дописывания столбцов, правило
Саррюса, правило разложения.

а)
Правило дописывания первых двух столбцов
к основному определителю:

.

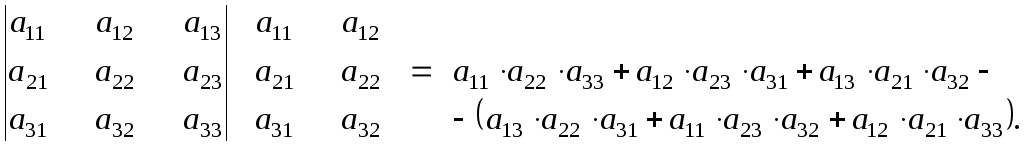
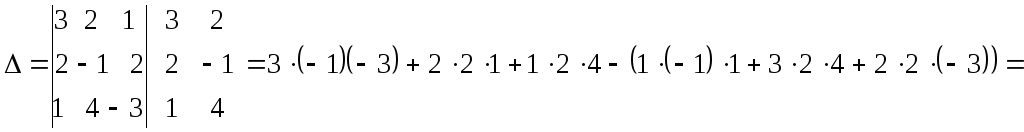
Вычисление
проводятся следующим образом: со своим
знаком идут произведения элементов
главной диагонали и по параллелям к
ней, с обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней.

б)
Правило Саррюса:

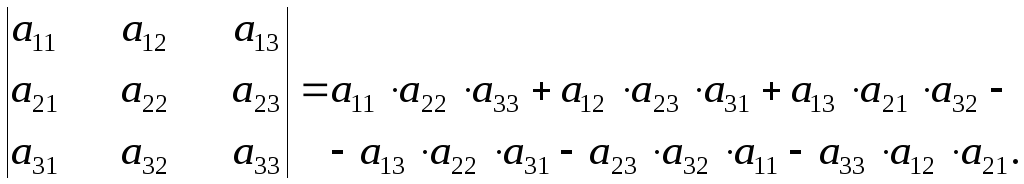
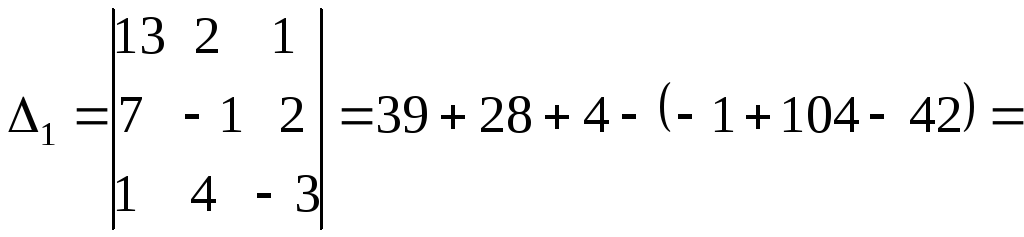
Со
своим знаком берут произведения элементов
главной диагонали и по параллелям к
ней, причем недостающий третий элемент
берут из противоположного угла. С
обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней, третий элемент берут
из противоположного угла.

в)
Правило разложения по элементам строки
или столбца:

Определитель равен сумме произведений элементов какой-нибудь строки (столбца) на их соответствующие алгебраические дополнения.

Если

,
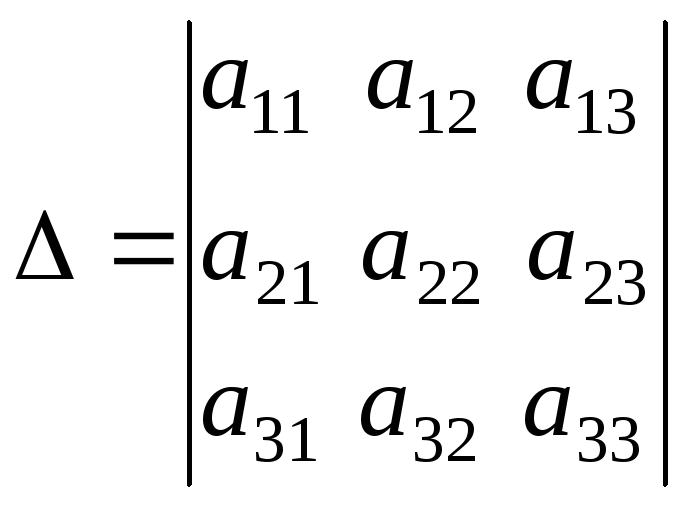тогда
.

Алгебраическое
дополнение– это определитель более
низкого порядка, получаемый путем
вычеркивания соответствующей строки
и столбца и учитывающий знак
,
где– номер строки,– номер столбца.

Например,

,

,
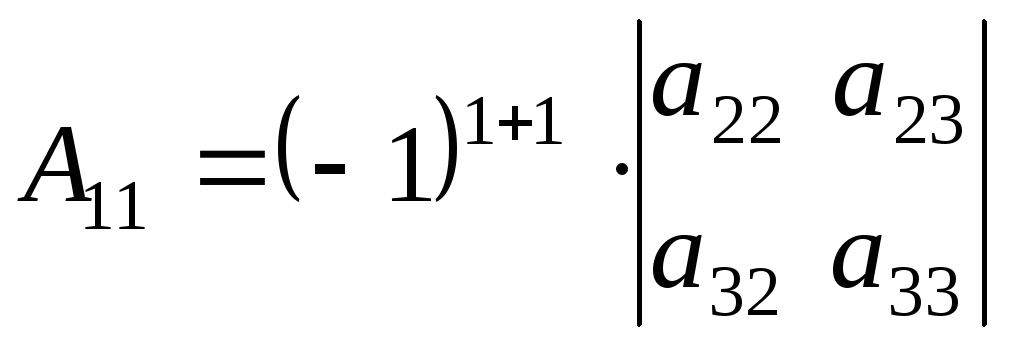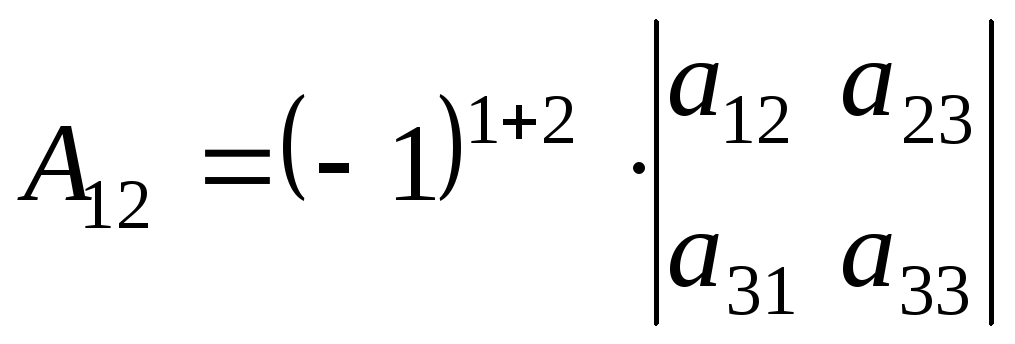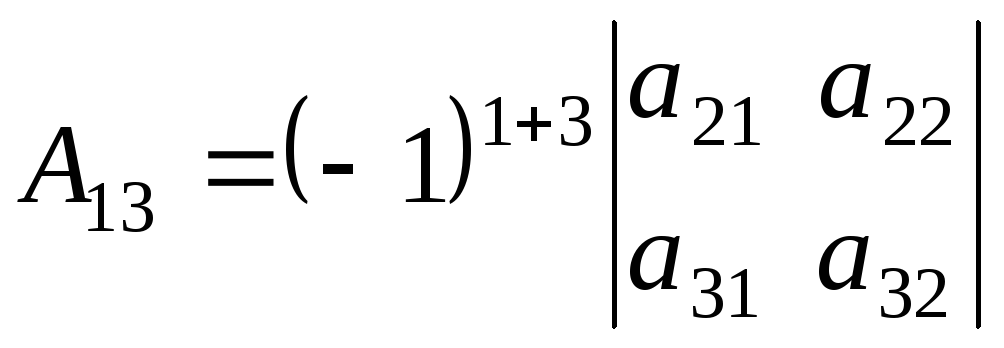и т.д.

Вычислим
по этому правилу вспомогательные
определители
и
,
раскрывая их по элементам первой строки.

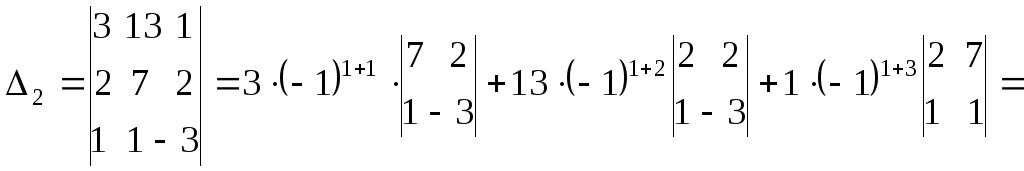
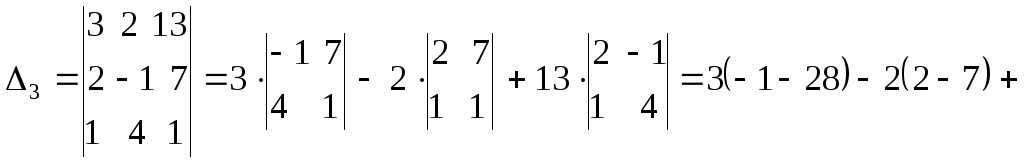
Вычислив
все определители, по правилу Крамера
найдем переменные:

Проверка:

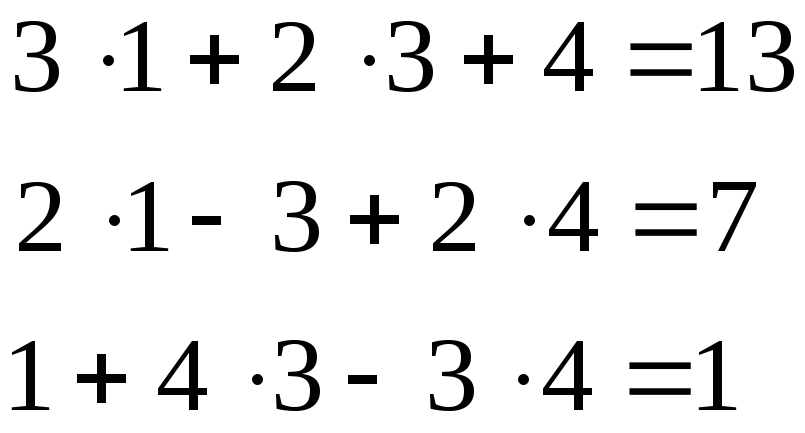
Вывод:
система решена верно:
.

1. Основные
   свойства определителей

Необходимо
помнить, что определитель – это число,
найденное по некоторым правилам. Его
вычисление может быть упрощено, если
пользоваться основными свойствами,
справедливыми для определителей любого
порядка.

Свойство
1.Значение определителя не изменится
от замены всех его строк соответствующими
по номеру столбцами и наоборот.

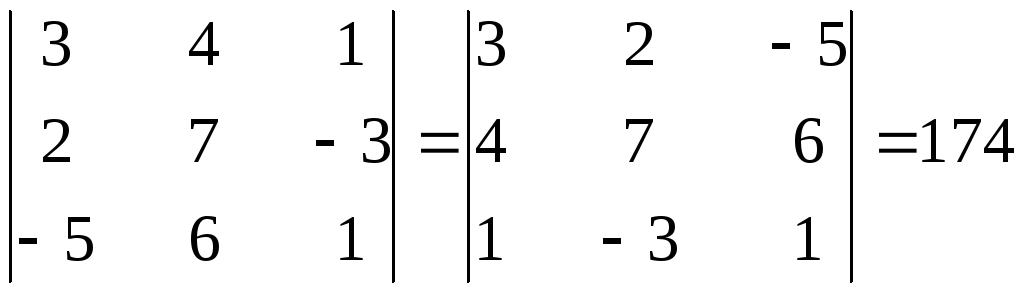
Операция
замены строк столбцами называется
транспонированием. Из этого свойства
вытекает, что всякое утверждение,
справедливое для строк определителя,
будет справедливым и для его столбцов.

Свойство
2.Если в определителе поменять
местами две строки (столбца), то знак
определителя поменяется на противоположный.

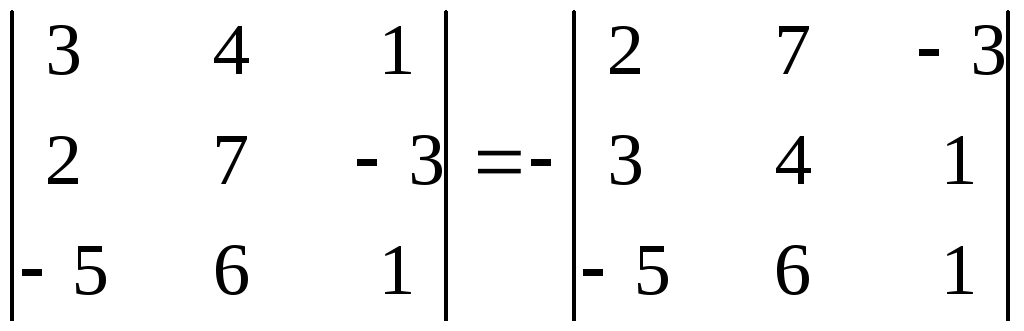
Свойство
3.Если все элементы какой-нибудь
строки определителя равны 0, то определитель
равен 0.

Свойство
4.Если элементы строки определителя
умножить (разделить) на какое-нибудь
число
,
то и значение определителя увеличится
(уменьшится) в
раз.

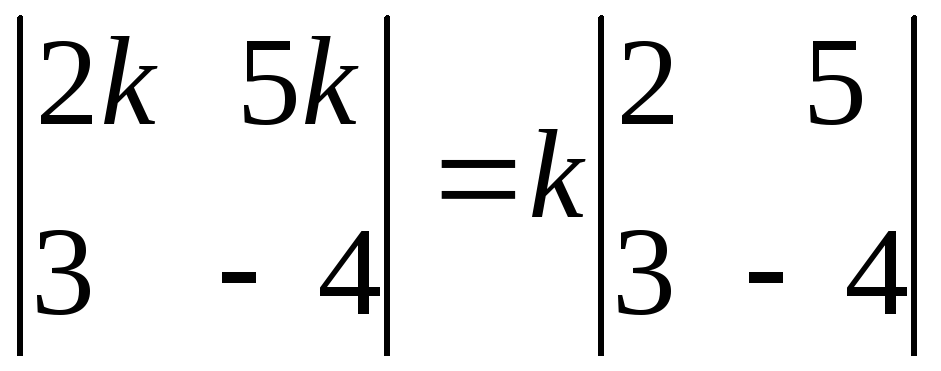
Если
элементы какой-нибудь строки, имеют
общий множитель, то его можно вынести
за знак определителя.

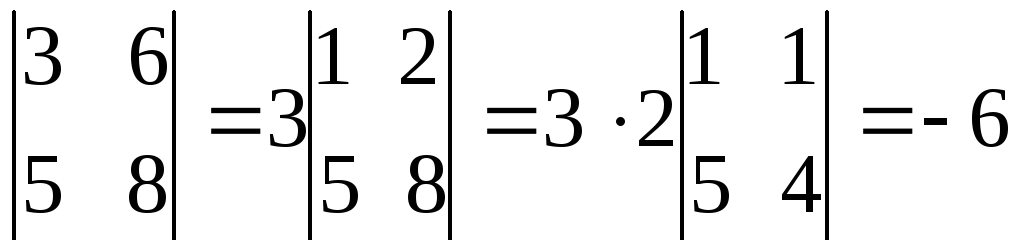
Свойство
5. Если определитель имеет две
одинаковые или пропорциональные строки,
то такой определитель равен 0.

Свойство
6. Если элементы какой-нибудь строки
определителя представляют собой сумму
двух слагаемых, то определитель равен
сумме двух определителей.

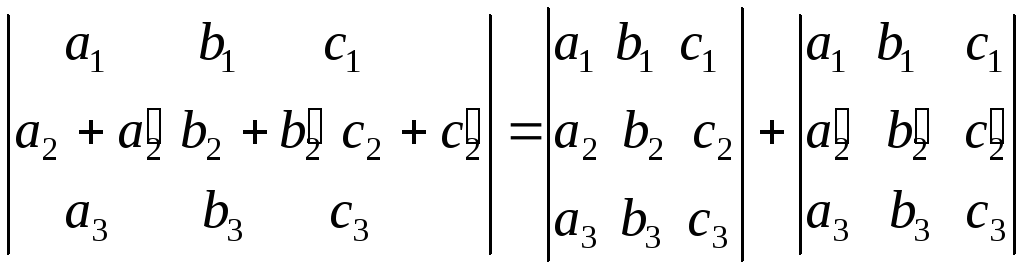
Свойство
7. Значение определителя не изменится,
если к элементам какой-нибудь строки
добавить элементы другой строки,
умноженной на одно и то же число.

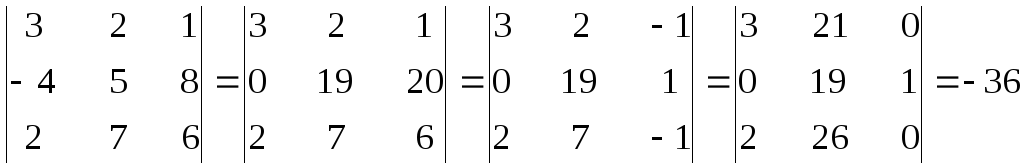
В
этом определителе вначале ко второй
строке прибавили третью, умноженную на
2, затем из третьего столбца вычли второй,
после чего вторую строку прибавили к
первой и третьей, в результате получили
много нулей и упростили подсчет.

Элементарными
преобразованиями определителя
называются упрощения его благодаря
использованию указанных свойств.

Пример
1.Вычислить определитель

Непосредственный
подсчет по одному из рассмотренных выше
правил приводит к громоздким вычислениям.
Поэтому целесообразно воспользоваться
свойствами:

а)
из І строки вычтем вторую, умноженную
на 2;

б)
из ІІ строки вычтем третью, умноженную
на 3.

В
результате получаем:

Разложим
этот определитель по элементам первого
столбца, содержащего лишь один ненулевой
элемент.

.

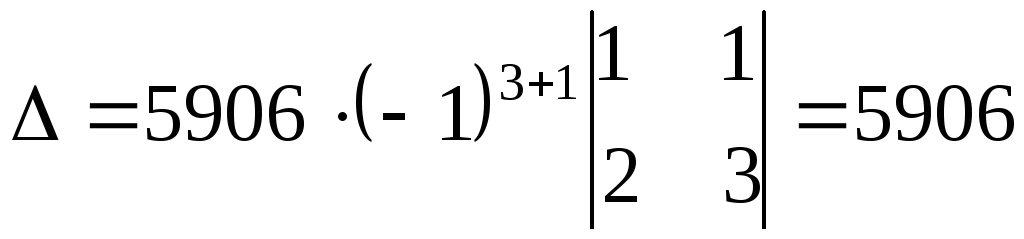1. Системы
   и определители высших порядков

Систему

линейных уравнений с
неизвестными можно записать в таком
виде:

Для
этого случая также можно составить
главный и вспомогательные определители,
а неизвестные определять по правилу
Крамера. Проблема состоит в том, что
определители более высокого порядка
могут быть вычислены только путем
понижения порядка и сведения их к
определителям третьего порядка. Это
может быть осуществлено способом прямого
разложения по элементам строк или
столбцов, а также с помощью предварительных
элементарных преобразований и дальнейшего
разложения.

Пример
4. Вычислить определитель четвертого
порядка

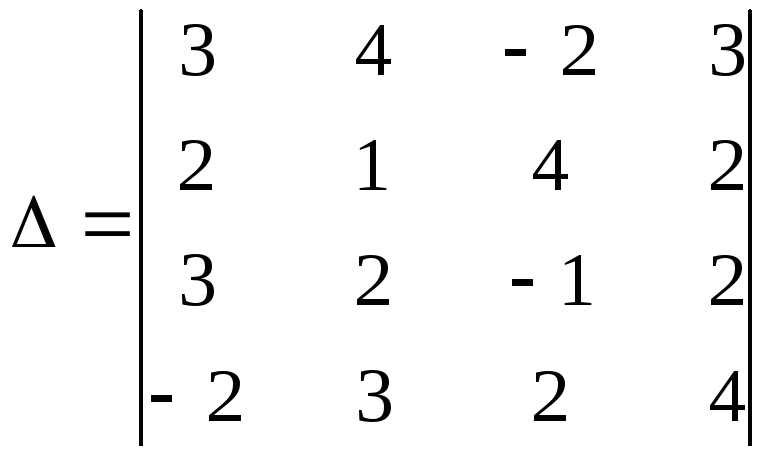
Решение
найдем двумя способами:

а)
путем прямого разложения по элементам
первой строки:

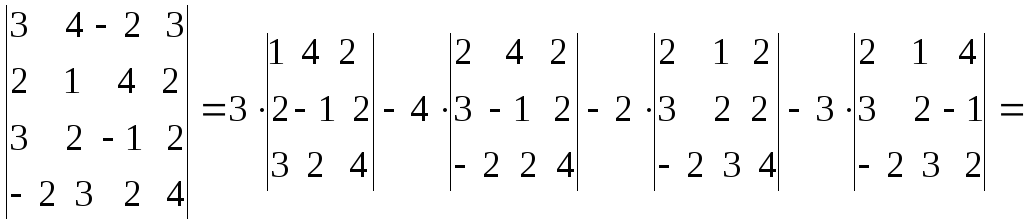
б)
путем предварительных преобразований
и дальнейшего разложения

	а) из І строки вычтем ІІІ
б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

Пример
5.Вычислить определитель пятого
порядка, получая нули в третьей строке
с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

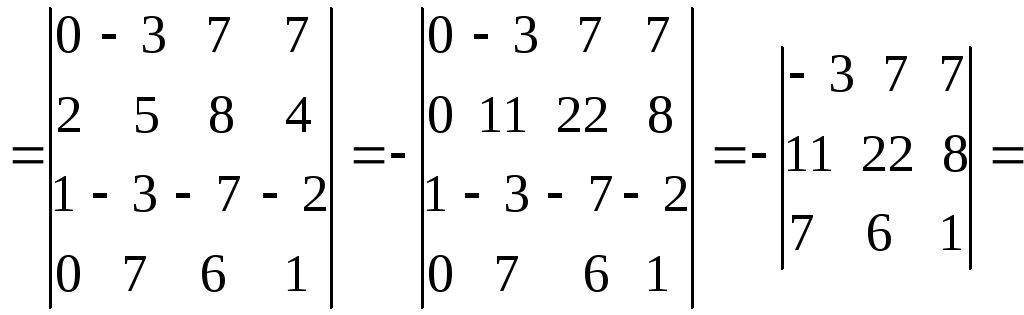
из
второго столбца вычтем третий:

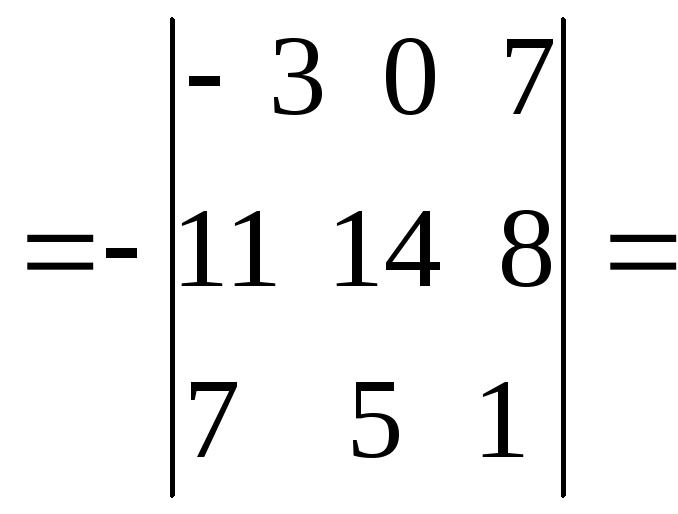
из
второй строки вычтем третью:

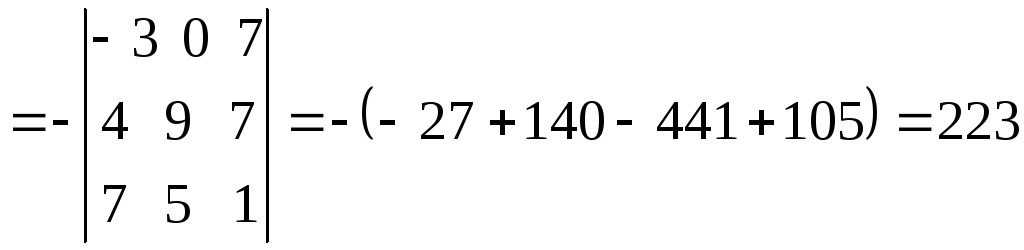
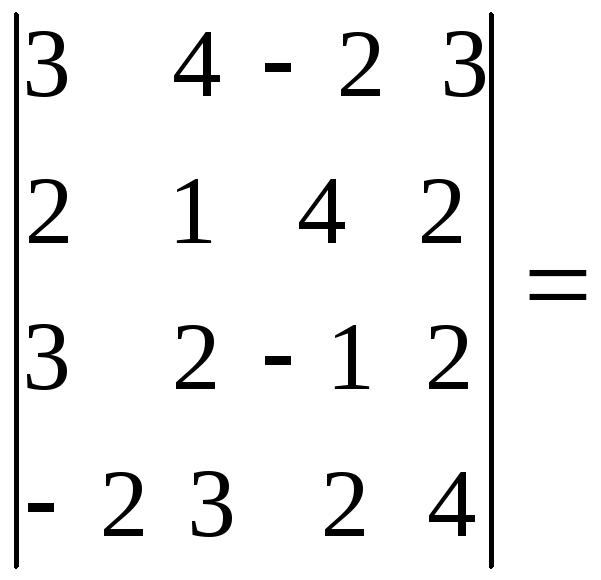
Пример
6.Решить систему:

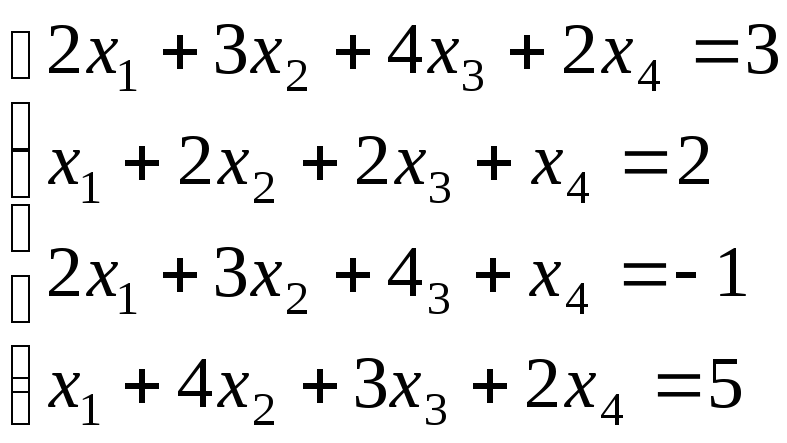
Решение.Составим определитель системы и, применив
свойства определителей, вычислим его:

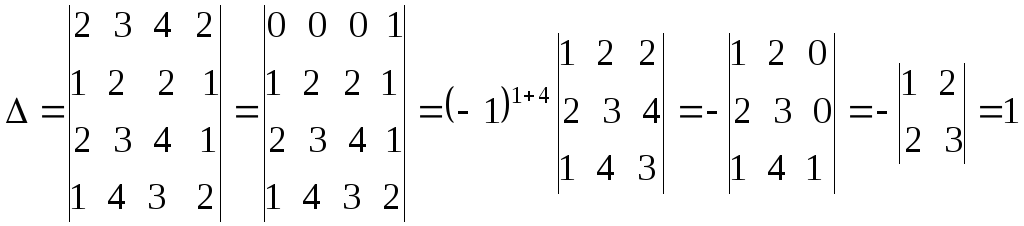
(из
первой строки вычтем третью, а затем в
полученном определителе третьего
порядка из третьего столбца вычитаем
первый, умноженный на 2). Определитель

,
следовательно, формулы Крамера применимы.

Вычислим
остальные определители:

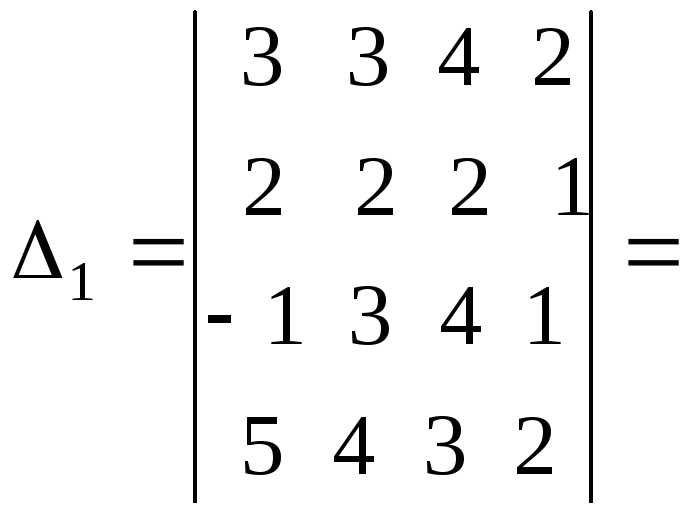
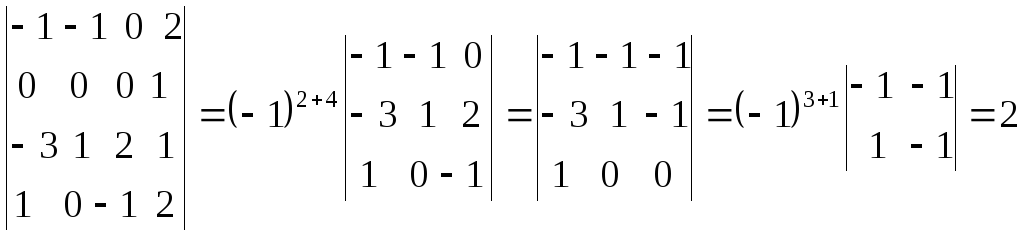
Четвертый
столбец умножили на 2 и вычли из остальных

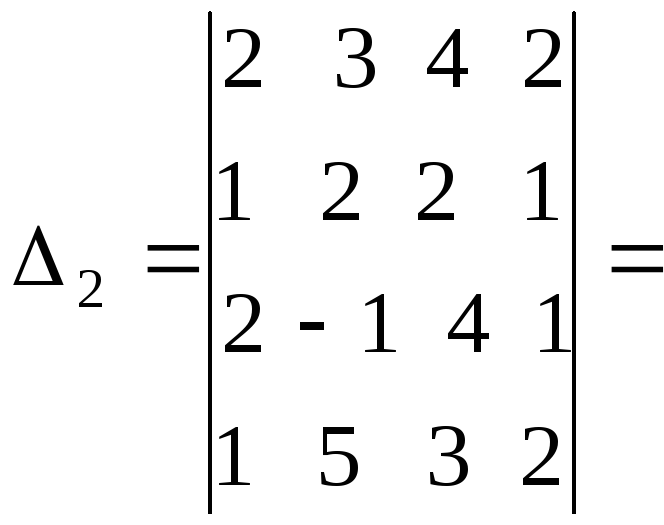
Четвертый
столбец вычли из первого, а затем, умножив
на 2, вычли из второго и третьего столбцов.

.

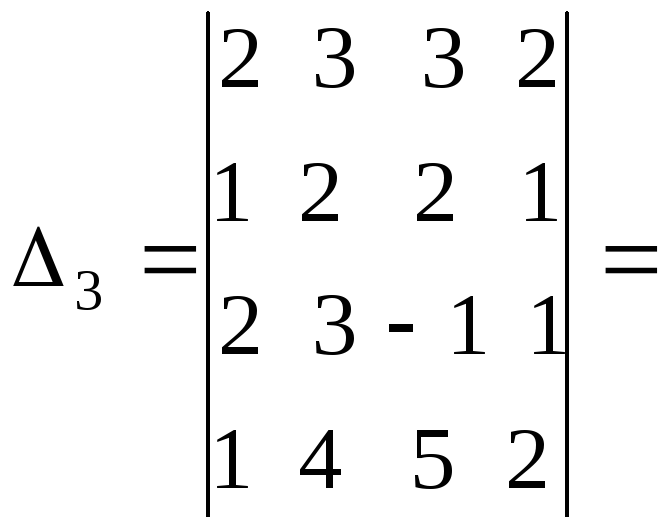
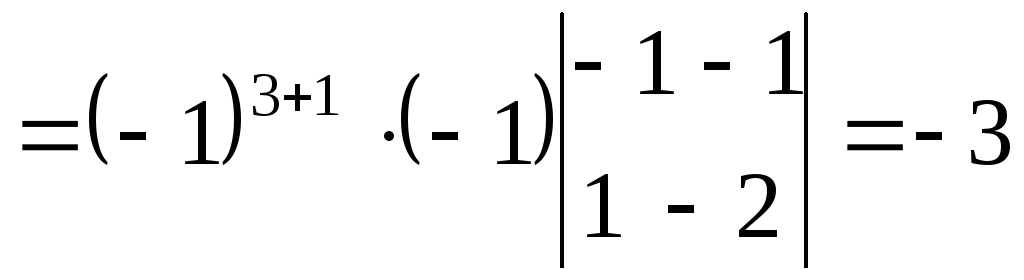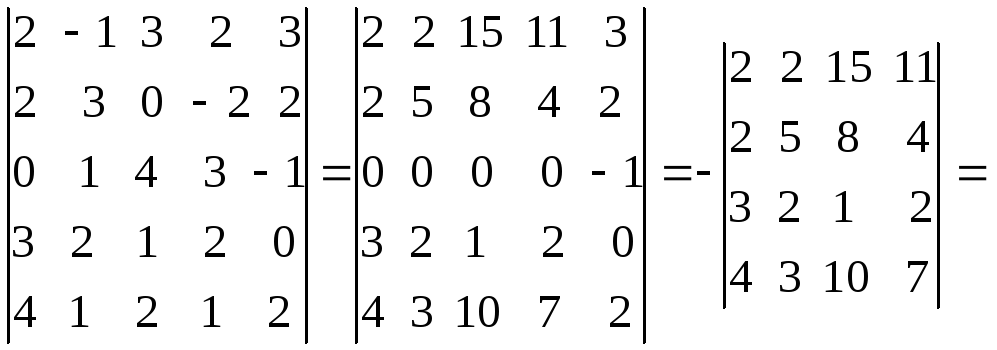
Здесь
выполнили те же преобразования, что и
для
.

.

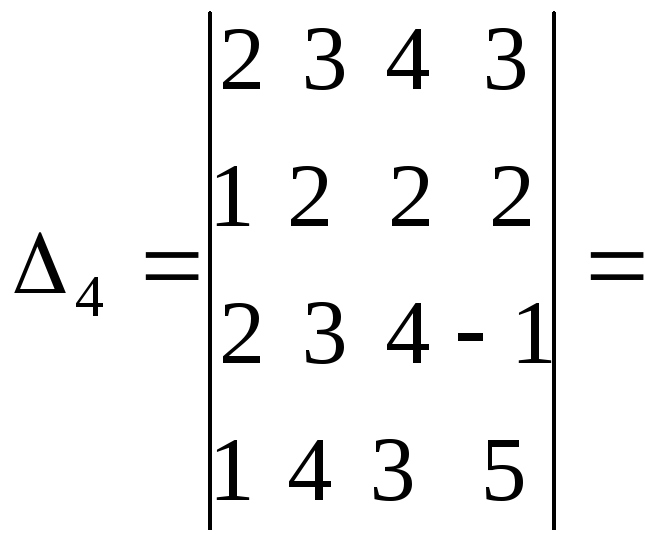
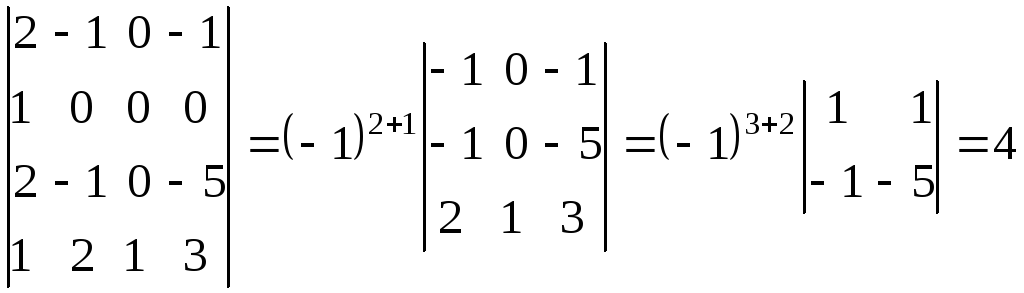При
нахождении
первый столбец умножили на 2 и вычли из
остальных.

По
правилу Крамера имеем:

.

После
подстановки в уравнения найденных
значений убеждаемся в правильности
решения системы.

2.
МАТРИЦЫ и
ИХ
ИСПОЛЬЗОВАНИЕ

В
РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1.1. Определители и матрицы

1.1.1. Понятие числовой матрицы

1.1.2. Определители второго порядка

1.1.3. Подматрица, минор, алгебраическое дополнение

1.1.4. Определители третьего порядка

1.1.5. Свойства определителей

1.1.6. Определители порядка n

1.2. Решение систем линейных уравнений методом Крамера

1.2.1. Понятие системы линейных уравнений

1.2.2. Формулы Крамера

1.3. Матрицы. Операции над матрицами

1.3.1. Умножение матрицы на число

1.3.2. Сложение матриц

1.3.3. Произведение матриц

1.3.4. Транспонирование матриц

1.3.5. Понятие обратной матрицы

1.3.6. Нахождение обратной матрицы методом Крамера

1.3.7. Алгоритм нахождения обратной матрицы методом Крамера

1.3.8. Элементарные преобразования матриц

1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований

1.4. Решение системы линейных уравнений

1.4.1. Системы линейных уравнений. Основные понятия

1.4.2. Метод Гаусса

1.5. Исследование систем линейных уравнений

1.5.1. Теоремы о ранге матриц

1.5.2. Исследование систем линейных уравнений

1.5.3. Теорема Кронекера-Капелли

1.5.4. Однородные системы линейных уравнений

1.5.5. Свойства решений линейной однородной системы уравнений

1.1. Определители и матрицы

1.1.1. Понятие числовой матрицы

Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.

Пример:

A= 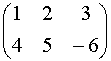или A=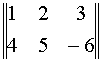

Общее обозначение:

A= или A=, где – элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца:

Если M=N, то матрица называется квадратной. В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:

. . .
.

. . главная
. . .
побочная

. .

. .

Пример:

A = 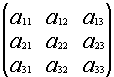главную диагональ образуют эл-ты:

, а побочную

1.1.2. Определители второго порядка

Пусть дана матрица второго порядка
A= .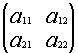

Определителем второго порядка называется число, вычисляемое по правилу:

Определитель второго порядка равен произведению элементов Главной диагонали минус произведение элементов Побочной диагонали.

=
1*(-4)-6 = -10

1.1.3. Подматрица, минор, алгебраическое дополнение

Пусть дана какая-либо матрица (например, порядка 3):

А=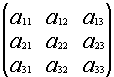

Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.

Например, если вычеркнуть первую строку и второй столбец, то получим подматрицу данной матрицы:

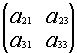
Минором элемента определителя называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.

Алгебраическим дополнением элемента называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.

Обозначение: =

Если i+j – четное число , то знак алгебраического дополнения и минора одинаковы, если нечетное , то их знаки противоположны.

Символически покажем положительные и отрицательные места в определителе:

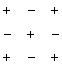или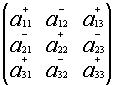

1.1.4. Определители третьего порядка

Определителем третьего порядка называется число, вычисляемое по правилу:

= =

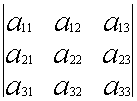Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.

Заменим алгебраические дополнения на миноры:

=

= – +

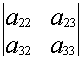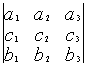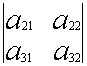
Вычисляя миноры, получим:

=

1.1.5. Свойства определителей

Свойство 1. При замене строк на столбцы определитель не меняется.

=

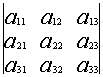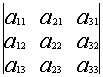
(такая операция называется транспонированием).

Следствие: строки и столбцы равноправны, т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.

Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.

= –

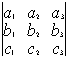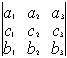
Следствие: любую строку (столбец) можно поставить первой (первым)

Свойство 3. Определитель с двумя равными строками равен нулю.

= 0

Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.

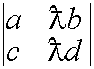
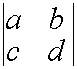
Следствие: Постоянный множитель можно внести в какую-нибудь строку

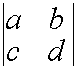
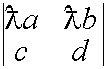
Свойство 5. Если элементы какой–либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей.

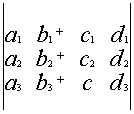
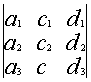
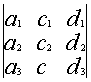
Свойство 6. Определитель не меняется, если любую строку умножить на любое число и прибавить к любой другой строке.

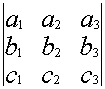
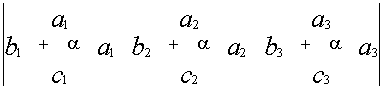
Случаи, когда определитель равен нулю:

1. Все элементы какой-либо строки равны нулю
2. Две строки одинаковы
3. Элементы двух строк пропорциональны

1.1.6. Определители порядка n

Вычисление определителей порядка n.

Для вычисления порядка n используется метод разложения по cтроке.

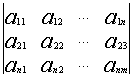
Алгебраическое дополнение получается вычеркиванием i-строки и j-столбца. Этот процесс мы будем продолжать до тех пор пока не получим определители порядка 2 или 3

Формулу (1) используют как правило при i=1

Пример:

1.2. Решение систем линейных уравнений методом Крамера

1.2.1. Понятие системы линейных уравнений

Система линейных уравнений порядка n имеет вид:

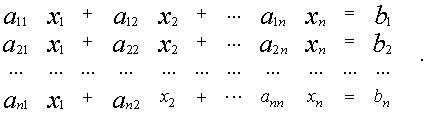
При этом числа – называются коэффициентами
при неизвестных

– свободные члены

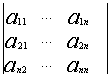Матрица называется матрицей системы

Числа 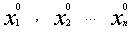– решение системы, если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.

Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.

Если система линейных уравнений не имеет решений, то система называется несовместной.

1.2.2. Формулы Крамера

Рассмотрим систему уравнений (*). И пусть А – матрица системы

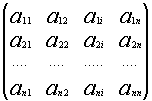
Если i – столбец заменим свободными членами, то соответствующую матрицу обозначим

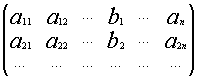
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, которое находится по формуле:

1.3. Матрицы. Операции над матрицами

Две матрицы A и B называются равными, если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.

К линейным операциям относятся:

1.3.1. Умножение матрицы на число

Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:

1.3.2. Сложение матриц

Складывать можно только матрицы одинаковых размеров:

Свойства линейных операций

Если матрица в качестве элементов имеет нули, то такая матрица называется нулевой.

1.3.3. Произведение матриц

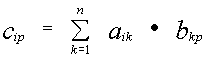
Пример:

.==

.=

.

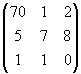
Если для матриц А и В выполняется равенство А*В=В*А, то матрицы называются перестановочными.

Если для матриц А, В, С имеет смысл операция произведения, то выполняются равенства

A(B*C)=(A*B)*C

A(B+C)=AB+AC

(B+C)A=BA+CA

1.3.4. Транспонирование матриц

Рассмотрим матрицы

A^T называется транспонированной по отношению к A

Если A_T получена из матрицы А заменой строк на столбцы то

называют главной диагональю

Очевидно:

Если для квадратной матрицы выполняется условие

то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.

1.3.5. Понятие обратной матрицы

Обратные матрицы существуют только для квадратных матриц. Квадратная матрица, у которой на главной диагонали стоят единицы, а
вне главной диагонали – нули, называется единичной матрицей.

Например, единичная матрица второго порядка:

Теорема.

Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:

Определение обратной матрицы:

Матрица В называется обратной для матрицы А, если А и В перестановочны и А*В=В*А=Е

Обозначение обратной матрицы:

Теорема.

Если матрица А имеет обратную, то ее определитель отличен от нуля.

Доказательство.

Так как А имеет обратную матрицу, то

Воспользуемся теоремой о том, что определитель произведения равен произведению определителей.

что и требовалось доказать.

1.3.6. Нахождение обратной матрицы методом Крамера

Теорема.

Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.

Доказательство.

Пусть матрица А такова, что её определитель отличен от нуля.

Докажем, что существует матрица В, такая что:

*=

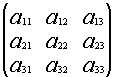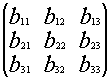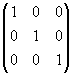
Отсюда, в частности, следует:

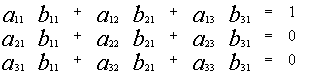
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля, то эту систему можно решить методом Крамера причем решение (3) – единственно.

Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.

1.3.7. Алгоритм нахождения обратной матрицы методом Крамера

Первоначально находим определитель матрицы А и если он равен нулю, то обратной матрицы не существует.

Если определитель отличен от нуля, то находим союзную

матрицу

состоящую из алгебраических дополнений элементов матрицы А.

1.3.8. Элементарные преобразования матриц

Эквивалентные матрицы.

К элементарным преобразованиям относятся:

1. 1. умножение любой строки матрицы на число, отличное от нуля;

пример

=

1. к любой строке можно добавить любую другую строку, умноженную на любое число;
2. перестановка двух строк.

Матрицы, полученные с помощью элементарных преобразований называются эквивалентными

А~
В, В~
С, А~
С

1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований

Рассмотрим квадратную матрицу А и предположим, что

тогда используя элементарные преобразования эту матрицу можно привести к единичной матрице. Таким образом единичная матрица эквивалентна любой невырожденной матрице того же порядка.

Теорема

Если элементарные преобразования:

переводят невырожденную матрицу А в единичную, то те же самые преобразования, взятые в том же порядке, переводят единичную матрицу в обратную для A.

Доказательство:

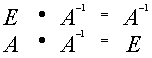
отсюда

1.4. Решение системы линейных уравнений

1.4.1. Системы линейных уравнений. Основные понятия

Система уравнений вида:

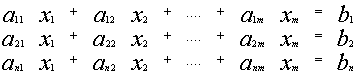
называется линейной системой из n уравнений с m неизвестными.

(a_ij) коэффициенты при неизвестных x₁, x₂,…,x_m

b₁,b₂,…,b_n – свободные члены

Матрица А системы (*) состоит из коэффициентов a_ij, размера n*m .

Если неизвестные и свободные члены представим в виде:

,

то систему уравнений (*) мы можем переписать в виде: (3)

Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*). Следует особо обратить внимание на то, что m может быть неравно n. Если m=n и матрица А является невырожденной , то из соотношения (3) вытекает: (4)

Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной.
Решить систему – означает найти все её решения.

1.4.2. Метод Гаусса

Рассмотрим систему (*):

Припишем к матрице А
матрицу-столбец В

Припишем к матрице А матрицу-столбец
В:

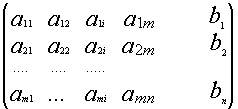
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной. Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: 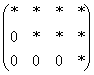то, система решений не имеет.

Если треугольная матрица получается вида: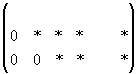 , то система имеет бесконечно много решений. При этом какие-то неизвестные
объявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: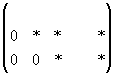 , то в этом случае система имеет единственное решение.

Пример:

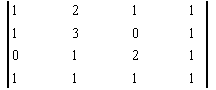
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:

~~

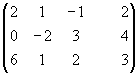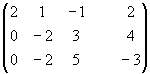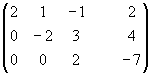
В итоге получим систему: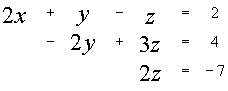

Откуда получим значения неизвестных: y = -7,25 x = 2,875

Пример: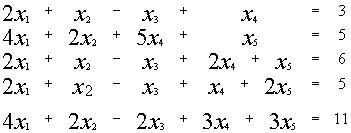

~~~

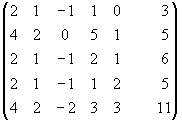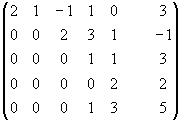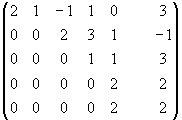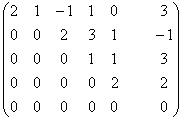
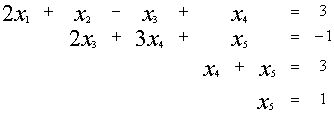
1.5. Исследование систем линейных уравнений

Рассмотрим систему линейных уравнений.

Задача: определить:

• Совместна или нет данная система
• Если совместна, то сколько имеет решений а) единственное б) бесконечное множество

Понятие ранга матрицы

А=() i= j=

Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.

Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.

Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.

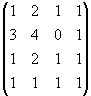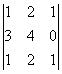М==0 М==-20 М==0 М=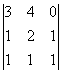=3 Ранг равен 3.

Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг1.
С другой стороны если матрица имеет порядок MxN, то r(A)min(M,N).

1.5.1. Теоремы о ранге матриц

Теорема 1

Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).

Доказательство

Для доказательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.

1) А~B B получена умножением строки(столбца) на отличное от нуля число.

А=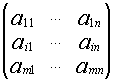 B=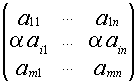

Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В=А (по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.

2) A~B B получена прибавлением строк

А=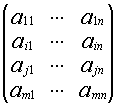 В=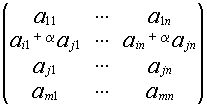

Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В0.

Если выбранные миноры содержат i-ю и j-ю строки, тогда
М(А)=А=

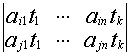
В=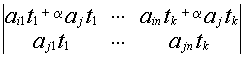

минор В получен из А путем прибавления строки.

Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.

Теорема 2

Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Вычисление ранга матрицы

Используя утверждение доказанной теоремы, легко вычислить ранг матрицы

1. с помощью элементарных преобразований матрица приводится к ступенчатому виду.
2. считается число ненулевых строк ступенчатой матрицы

Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.

ПРИМЕР

~ ~

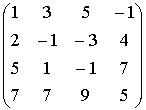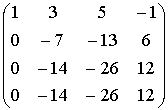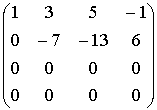
Ответ: r(A)=2

1.5.2. Исследование систем линейных уравнений

Рассмотрим систему линейных уравнений

(*)

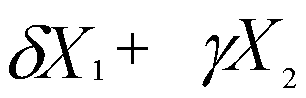
А=()
H=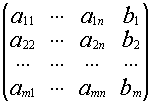

1.5.3. Теорема Кронекера-Капелли

Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)

Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.

Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных объявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.

1.5.4. Однородные системы линейных уравнений

Если в системе (*) все свободные члены равны нулю, то такая система является однородной.

Однородные системы всегда совместны т.к. ====0 всегда является решением. Такое решение называется тривиальным.

1) то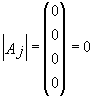

2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений

1.5.5. Свойства решений линейной однородной системы уравнений

1) Если 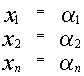является решением системы, то 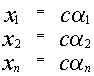также является решением.

Доказательство.

2) Если 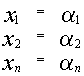является решением системы

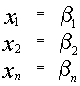также является решением той же самой системы, то и

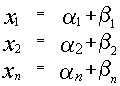также является решением системы

Доказательство.

+

откуда получим

3) Есл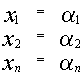и и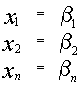
два различных решения системы, то их линейная комбинация, равная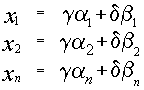

также является решением системы.

Доказательство.

+

откуда получим

Каждое из решений системы можно записать в виде строки матрицы, тогда на основании свойств можно утверждать, что матрицы есть решения, то также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.

Пример.

~~

{ {

{{

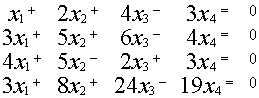
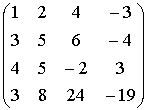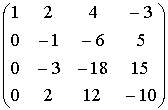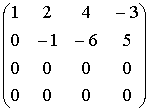
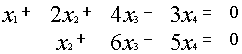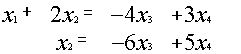
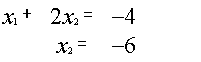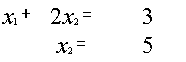
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец – на -ый столбец – на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй – при неизвестной у, третий – при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

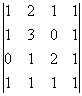
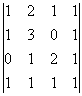
Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера – Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов
• Преобразования декартовой системы координат
• Бесконечно малые и бесконечно большие функции
• Критерий совместности Кронекера-Капелли
• Формулы Крамера
• Матричный метод
• Экстремум функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Основной определитель системы линейных уравнений

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:

Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным определителем и обозначается ∆.

Вспомогательный определитель ∆ _i получается из главного определителя путем замены i -го столбца на столбец свободных членов .

Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:

Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).

В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆ _i = 0), либо несовместной (при отличии хотя бы одного из ∆ _i от нуля).

После этого следует провести проверку полученного решения.

Пример 1.4. Решить систему методом Крамера

Решение. Так как главный определитель системы

отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители

Воспользуемся формулами Крамера (1.6):

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

Определить стоимость 1 единицы продукции молокоцеха каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):

Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.

В MathCAD для нахождения определителя пользуются палитрой оператора Matrix

Основной определитель системы линейных уравнений

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

[spoiler title=”источники:”]

http://www.sites.google.com/site/vyssaamatem/kupit-sklad/i-3-metod-kramera-resenia-sistem-linejnyh-algebraiceskih-uravnenij

http://toehelp.ru/theory/math/lecture14/lecture14.html

[/spoiler]

(схема 16)

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной,
если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее
свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи
подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она
имеет хотя бы одно решение, и несовместной, если она решений не
имеет.

Совместная система уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет более
одного решения.

Рассмотрим неоднородную систему линейных
алгебраических уравнений, имеющую при n=m следующий
общий вид:

.                                                                                                                                                  (1.5) 

Главной матрицей A системы
линейных алгебраических уравнений называется матрица, составленная из
коэффициентов, стоящих при неизвестных:

.

Определитель главной матрицы системы называется главным
определителем и обозначается ∆.

Вспомогательный определитель ∆_i  получается
из главного определителя путем замены i-го
столбца на столбец свободных членов.

Теорема 1.1
(теорема Крамера). Если главный
определитель системы линейных алгебраических уравнений отличен от нуля, то
система имеет единственное решение, вычисляемое по формулам:

.                                                                                                                                                                        (1.6)

 Если
главный определитель ∆=0, то система либо 
имеет бесконечное множество решений (при всех нулевых вспомогательных
определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного
из вспомогательных определителей).

В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если
главный определитель системы линейных алгебраических уравнений отличен от нуля,
то система является совместной определенной и при этом ; если главный определитель нулевой, то система является
либо совместной неопределенной (при всех ∆_i=0),
либо несовместной (при отличии хотя бы одного из ∆_i от нуля).

После этого следует провести проверку полученного
решения.

Пример 1.4.  Решить
систему методом Крамера 

Решение.  Так
как главный определитель системы

 отличен от нуля, то система имеет единственное
решение. Вычислим вспомогательные определители

Воспользуемся
формулами Крамера (1.6):
 

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла
и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

                                                                   
                                     Таблица 1.4                                 

Определить стоимость 1 единицы продукции молокоцеха
каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z –
1 кг
творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из
трех дней реализации можно отобразить следующей системой:

.

Решим систему методом Крамера. Найдем главный
определитель системы по формуле (1.2):

         

     Так
как он отличен от нуля, то система имеет единственное решение. Вычислим
вспомогательные определители с помощью формулы (1.2):

        

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1
литра молока равна 44 рубля, 1
кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с
помощью калькулятора трудоемок, поэтому на практике используют персональный
компьютер. Так, для решения систем линейных алгебраических уравнений методом
Крамера в MS Excel высчитывают ее главный и вспомогательные определители
с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек
и элементы матрицы, определитель которой находится.

В MathCAD для
нахождения определителя пользуются палитрой оператора Matrix

Вопросы для
самопроверки