Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.
Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.
Тонкая линза: задачи
Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению.
Задача №1. Формула тонкой линзы
Условие
Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?
Решение
Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:
1F=1d+1f
Учтем, что F=1D, подставим значения из условия, и запишем:
2,5=10,5+1+ff=2 м
Ответ: 2м
Задача №2. Формула тонкой линзы
Условие
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению светящейся точки.
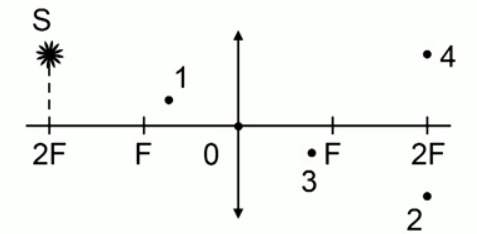
Решение
Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.
Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.
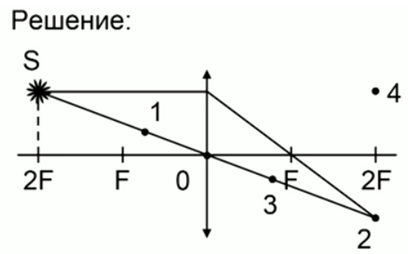
Ответ: изображению точки S соответствует точка 2.
Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.
Задача №3. Формула тонкой линзы
Условие
Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.
Решение
Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:
1F=1d+1f ; Г=Hh=fd
Перепишем эти соотношения, с учетом того, что F=1D
H=h·fd1f=D-1d
Отсюда найдем f:
f=dD·d-1
Осталось подставить значения в формулу для H и вычислить:
H=hdD·d-1=0,03·0,44·0,4-1=0,05 м
Ответ: 0,05 м.
Задача №4. Формула тонкой линзы
Условие
Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?
Решение
Фокусное расстояние найдем из формулы линзы:
1F=1d+1fF=fdd+f
Запишем формулу увеличения линзы и выразим d:
Г=Hh=fd ; d=fhH
Запишем окончательный ответ:
F=hfH+h≈0,08 м
Ответ: 0,08 м.
Задача №5. Формула тонкой линзы
Условие
Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?
Решение
Посторим изображение в соответствии с правилами геометрической оптики:
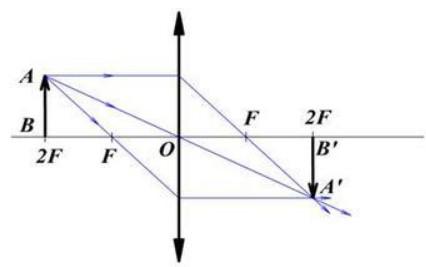
Данное изображение:
- действительное;
- перевернутое;
- равное предмету.
Ответ: см. выше.
Вопросы на тему «Тонкая линза»
Вопрос 1. Какое равенство называют формулой тонкой линзы?
Ответ. Формула тонкой линзы имеет следующий вид:
1F=1d+1±f
Здесь:
- F – фокусное расстояние;
- d – расстояние от линзы до предмета;
- f – расстояние от линзы до изображения.
Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?
Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.
Вопрос 3. Что такое фокусное расстоняние линзы?
Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.
Вопрос 4. Что такое оптическая сила линзы?
Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.
Вопрос 5. Может ли оптическая сила линзы быть отрицательной?
Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.
Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!
Решение задач на линзы имеет большое значение в контексте ЕГЭ по физике и других вступительных экзаменов, особенно для студентов, выбравших естественнонаучные направления. Задачи на линзы могут быть представлены в различных форматах, включая теоретические вопросы и практические задания, и могут быть частью как физического, так и математического разделов экзаменов. Понимание принципов работы линз и способности решать задачи на линзы являются необходимыми навыками для успешной сдачи экзаменов и продолжения образования в области физики, оптики и других естественных наук.
В этой статье мы говорили об изображениях, даваемые линзой. Она так же будет полезна при решении задач на линзы.
Линзы характеризуются величиной, которая называется оптической силой линзы. Оптическая сила обозначается буквой D.
Оптическая сила линзы – это величина, обратная её фокусному расстоянию.
D
=
1
F
За единицу оптической силы принята диоптрия (дптр). 1 дптр =
1
м
.
В задачах школьного курса, как правило речь идёт о тонких линзах. Тонкой линзой называют такую линзу, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей линзы и расстоянием предмета от линзы.
Формула тонкой линзы
Опыты и расчёты показывают, что между расстоянием d от предмета до линзы, расстоянием f от линзы до изображения и фокусным расстоянием линзы F существует соотношение, которое называется формулой тонкой линзы:
1
d
+
1
f
=
1
F
В этой формуле расстояние до изображения берут со знаком “плюс”, если изображение действительное, и со знаком “минус”, если изображение мнимое. Фокусное расстояние собирающей линзы берут со знаком “плюс”, а рассеивающей – со знаком минус.
Далее будет подразумеваться всегда тонкая линза.
Приступим к решению задач.
Задачи на линзы
Задача (Классическая)
Какое расстояние нужно выбрать между собирающей линзой и предметом, чтобы получить его прямое изображение, увеличенное в 2 раза? Известно, что оптическая сила линзы D=+10 дптр. Найдите это расстояние в сантиметрах и округлите до целого числа.
Решение:
Как мы знаем, с помощью собирающей линзы можно получить прямое (не перевёрнутое) увеличенное изображение только, если предмет находится между фокусом и линзой.
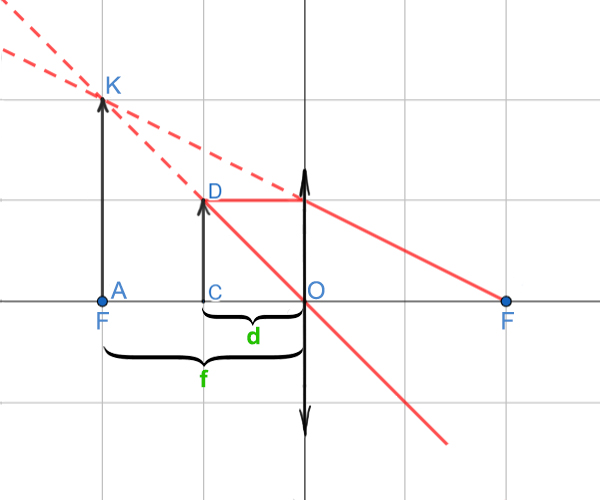
Из рисунка видно, что треугольники △АКО и △CDO подобны, т.к. оба треугольника прямоугольные и ∠O – общий. В задаче сказано, что изображение предмета должно быть увеличено в 2 раза. Значит, коэффициент подобия треугольников будет равен:
k
=
A
K
D
C
=
2
Следовательно,
f
=
2
d
Воспользуемся формулой для тонкой линзы. Изображение у нас мнимое, значит, перед f ставим знак минус.
1
d
−
1
f
=
1
F
=
D
1
d
−
1
2
d
=
D
1
2
d
=
D
d
=
1
2
D
=
1
2
⋅
10 дптр
=
0
,
05 м
Ответ: 5 см
Задача (Действительное изображение)
Найдите коэффициент увеличения изображения предмета.
a)
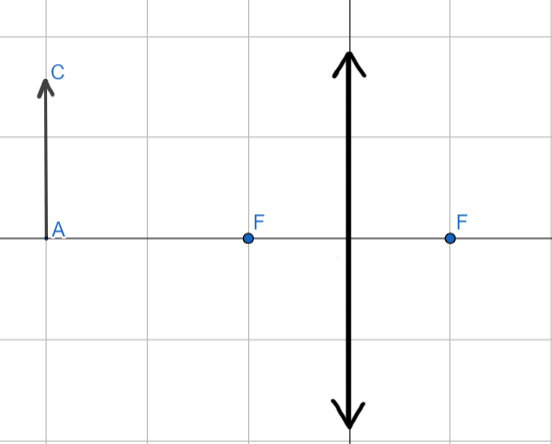
б)
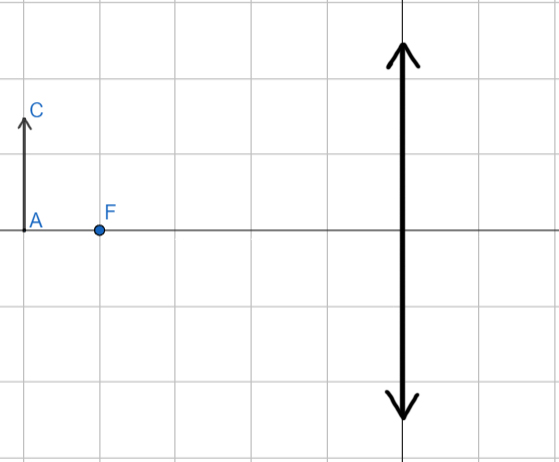
Решение:
Решим пункт a.
Здесь изображение находится за двойным фокусом. Значит, как мы знаем, в этом случае изображение получается действительным, перевёрнутым, уменьшенным.
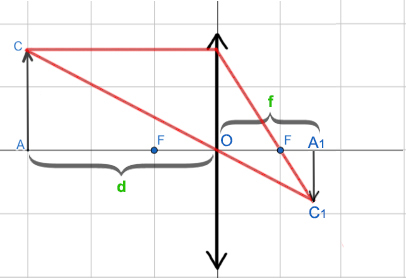
Чтобы узнать коэффициент увеличения, нужно найти отношение C1A1:CA. Другими словами, нужно найти коэффициент подобия треугольников △A1C1O и △ACO. Воспользуемся формулой тонкой линзы.
1
d
+
1
f
=
1
F
F – одна единица (1 клетка), d – 3 единицы (3 клетки).
1
3
+
1
f
=
1
1
f
=
3
2
Коэффициент подобия треугольников △A1C1O и △ACO:
k
=
f
d
=
1
,
5
3
=
0
,
5
Значит, коэффициент увеличения изображение тоже равен:
k
=
A
1
C
1
A
C
=
0
,
5
Решим пункт б.
Когда предмет находится между фокусом и двойным фокусом собирающей линзы, то изображение получается действительным, увеличенным, перевёрнутым.
Нарисуем примерный рисунок, не соблюдая изначальный масштаб, для экономия места.
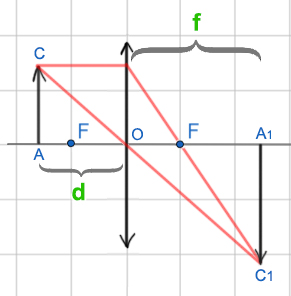
Здесь вновь получаются подобные треугольники △A1C1O и △ACO, и их коэффициент подобия покажет степень увеличения изображения.
На изначальном рисунке d = 5, F = 4. Применим формулу для тонкой линзы.
1
5
+
1
f
=
1
4
1
f
=
1
20
f
=
20
Коэффициент подобия треугольников △A1C1O и △ACO равен
k
=
f
d
=
20
5
=
4
k
=
A
1
C
1
A
C
=
4
Ответ: a) 0,5 б) 4
Исходя из этих примеров, можно сказать, что увеличение предмета в тонкой линзе будет равно
Г
=
Н
h
=
f
d
H – размер изображения, h – размер предмета, в м.
Задача (Пользуемся формулой)
На рисунке показан ход двух лучей от точечного источника света A через тонкую линзу.
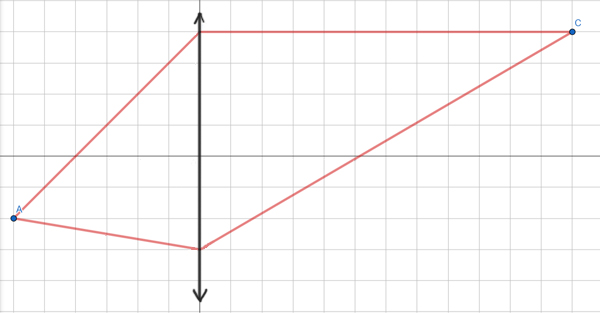
Какова оптическая сила линзы, если одна клетка на рисунке соответствует 2 см ?
Решение:
Мы видим, что изображение точки A, будет действительным, т.к. лучи пересекаются за самой линзой.
Расстояние от точки до линзы равно d = 6 клеток ∙ 0,02 м = 0,12 м. Расстояние от линзы до изображения точки равно f = 12 клеток ∙ 0,02 м = 0,24 м. Применим формулу тонкой линзы.
1
0
,
12 м
+
1
0
,
24 м
=
1
F
=
D
D
=
12
,
5 дптр
Ответ: 12,5 дптр
Задача (Рассеивающая линза)
В тонкой рассеивающей линзе получено уменьшенное в 5 раз изображение предмета. Определите модуль фокусного расстояния линзы, если предмет находится на расстоянии d = 20 см от линзы.
Решение:
Воспользуемся формулой увеличения линзы. Изображение уменьшено, поэтому формула принимает перевёрнутый вид
d
f
=
0
,
2 м
f
=
5
f
=
0
,
2 м
5
=
0
,
04 м
Теперь не проблема найти фокусное расстояние.
В рассеивающей линзе фокусное расстояние в формулу тонкой линзы подставляем со знаком “минус”. Изображение получается в рассеивающей линзе мнимым, поэтому перед f тоже ставим знак “минус”.
1
0
,
2 м
−
1
0,04 м
=
−
1
F
F
=
0,05 м
Ответ: 0,05 м
Задача (Скорость изображения муравья)
Муравей движется перпендикулярно главной оптической оси тонкой собирающей линзы, которая имеет фокусное расстояние F. Он находится на расстоянии
8
3
∙F от линзы и движется со скоростью V = 5 см/с. Какая скорость u будет у движущегося изображения муравья?
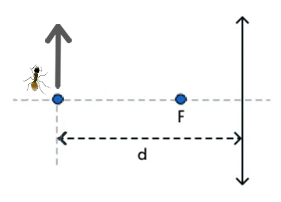
Решение:
d
=
8
3
⋅
F
За 1 с муравей реально проползёт 5 см. Узнаем, сколько его изображение проползёт за 1 с.
{
x
5
=
f
d
1
8
F
3
+
1
f
=
1
F
Составим систему уравнений. Первое уравнение – это формула увеличения линзы, вторая – формула тонкой линзы.
Из второго уравнения выражаем f.
f
=
8
⋅
F
5
Подставляем в первое.
x
5
=
8
F
3
8
F
5
=
3 см
Получается за 1 с изображение муравья пройдёт 3 см.
Ответ: u = 3 см/c
Таким образом, решение задач на линзы требует понимания основных определений и формул, связанных с тонкими линзами. Важно уметь правильно выбирать знаки величин и следить за единицами измерения. Решение задач на линзы не только позволяет лучше понять оптику, но и развивает навыки анализа, логического мышления и применения математических методов.
Задачи на оптическую силу линзы
Вопрос 1. Если изображение предмета, помещенного на расстоянии 10 см
от собирающей линзы, получается на расстоянии 20 см от нее, то чему равно
увеличение линзы?
Вопрос 2. Определите оптическую силу линзы, если действительное
изображение предмета, помещенного на расстоянии 15 см от собирающей линзы,
получается на расстоянии 30 см от нее.
Вопрос 3. Фокусное расстояние собирающей линзы 0,2 м. На каком
расстоянии (см) от линзы следует установить предмет, чтобы его изображение
получилось в натуральную величину?
Вопрос 4. Определите наибольшее расстояние (см) между предметом и
собирающей линзой с оптической силой 2,5 дптр, при котором получается прямое
изображение предмета.
Вопрос 5. На тонкую собирающую линзу падает сходящийся пучок лучей.
Продолжения лучей пересекаются за линзой на расстоянии 50 см, а преломленные –
на расстоянии 25 см. Определите фокусное расстояние (см), если обе точки лежат
на главной оптической оси линзы.
Вопрос 6. Предмет расположен на главной оптической оси собирающей
линзы на расстоянии 20 см от нее. Определите F (фокусное расстояние, см), если
действительное изображение предмета получено на расстоянии 4F от линзы.
Вопрос 7. Определите оптическую силу линзы, если мнимое изображение
предмета, расположенного на расстоянии 15 см от собирающей линзы, получается на
расстоянии 30 см от нее.
Вопрос 8. Линейные размеры действительного изображения предмета в 2
раза больше предмета. Определите расстояние (см) от линзы до изображения, если
расстояние от предмета до линзы 40 см.
Вопрос 9. Предмет расположен на расстоянии 50 см от линзы с оптической
силой 2,5 дптр. Если предмет приблизить к линзе на 5 см, то на сколько
увеличится его изображение?
Вопрос 10. На пути сходящегося пучка поставили собирающую линзу с
фокусным расстоянием 10 см, в результате чего лучи сошлись на расстоянии 5 см
от линзы. Если линзу убрать, то расстояние от места, где она стояла, до точки
схождения лучей в этом случае составит… см.
Вопрос 11. Линза формирует действительное изображение, увеличенное в 3
раза. Если при неизменном расстоянии между предметом и линзой ее оптическую
силу уменьшить вдвое, то чему будет равно увеличение?
Вопрос 12. Главные оптические оси собирающей (фокусное расстояние 48
см) и рассеивающей линзы совпадают. Цилиндрический пучок лучей, параллельных
главной оптической оси, после прохождения через обе линзы остается
параллельным. Определите фокусное расстояние (см) рассеивающей линзы, если его
диаметр при этом увеличивается в 1,2 раза.
Условие задачи:
Найти оптическую силу собирающей линзы, если изображение предмета, помещенного в 15 см от линзы, получается на расстоянии 30 см от нее.
Задача №10.5.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(d=15) см, (f=30) см, (D-?)
Решение задачи:
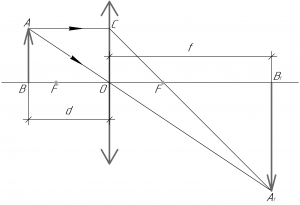Легко догадаться, что в данном случае мы имеем дело с собирающей линзой. Почему? Дело в том, что в рассеивающей линзе расстояние от линзы до предмета (d) всегда больше расстояния от линзы до изображения (f), то есть ({d} > {f}) (то есть изображение находится между предметом и линзой), а это противоречит условию задачи.
Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A1. Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и увеличенным ((Gamma > 1)).
Запишем формулу тонкой линзы:
[D = frac{1}{d} + frac{1}{f}]
В этой формуле (D) – оптическая сила линзы, она положительная, поскольку линза – собирающая, (d) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), (f) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).
Приведем под общий знаменатель (хотя делать это совсем не обязательно):
[D = frac{{f + d}}{{fd}}]
Если подставить в эту формулу значения величин из условия задачи, то мы получим ответ (не забываем переводить эти значения в систему СИ):
[D = frac{{0,3 + 0,15}}{{0,3 cdot 0,15}} = 10;дптр]
Ответ: 10 дптр.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.4.20 Световой луч падает на стеклянную пластинку квадратного сечения. Каким должен быть
10.5.2 На расстоянии 25 см от двояковыпуклой линзы, оптическая сила которой 5 дптр
10.5.3 Предмет находится на расстоянии 8 см от переднего фокуса линзы, а его изображение
Данная
тема посвящена решению задач на тему: «Оптическая сила линзы. Формула тонкой
линзы. Линейное увеличение линзы»
Задача
1.
На каком расстоянии находится фокус тонкой линзы от её оптического центра, если
оптическая сила линзы равна 5 дптр? На каком расстоянии находился бы фокус при
оптической силе −5 дптр? −10 дптр?
|
ДАНО: |
РЕШЕНИЕ Оптическая сила линзы определяется по формуле: Тогда фокус линзы равен В ходе решения получены Изобразим собирающую линзу и Расстояние между оптическим Для рассеивающей линзы: Поэтому, физический смысл результатов |
|
|
Задача
2.
На рисунке изображен предмет. Постройте его изображения на для собирающей и
рассеивающей линзы. Исходя из чертежа оцените линейное увеличение линзы.
РЕШЕНИЕ
Точка
А находится на главной оптической оси, а, значит, её изображение тоже
будет на главной оптической оси, поскольку лучи, проходящие через оптический
центр линзы не преломляются. Чтобы получить изображение точки В, понадобится
два луча.
Рассмотрим
построение изображения для рассеивающей линзы. Для этого также используем два
луча.
Линейное
увеличение линзы, в данном случае, определяется отношением размера изображения
к предмету. Произведя соответствующие измерения, получим, что для собирающей
линзы
для рассеивающей линзы
Нужно
понимать, что в таком задании каждый ученик может получить свой собственный
ответ, поскольку в данном случае фокус линзы выбирается произвольно при
построении чертежа. Главное построить корректный чертёж и произвести правильные
измерения.
Задача
3.
Изображение предмета сформировалось на расстоянии 30 см от линзы. Известно, что
оптическая сила этой линзы равна 4 дптр. Найдите линейное увеличение.
|
ДАНО: |
СИ |
РЕШЕНИЕ Оптическая сила линзы Формула тонкой линзы Тогда Линейное увеличение |
|
|
Задача
4.
Изображение предмета, находящегося на расстоянии 40 см от линзы, образуется на
расстоянии 30 см от линзы. Найдите фокусное расстояние данной линзы. Также
найдите, на каком расстоянии нужно поместить предмет, чтобы изображение
оказалось на расстоянии 80 см.
|
ДАНО: |
СИ |
РЕШЕНИЕ Формула тонкой линзы Тогда Формула тонкой линзы: |
|
|
Ответ:
F = 17 см;
d1 = 21,6 м.
Задача
5.
Предмет находится от тонкой собирающей линзы на расстоянии 10 см. Если его
отодвинуть от линзы на 5 см, то изображение предмета приблизится к линзе вдвое.
Найдите оптическую силу этой линзы.
|
ДАНО: |
СИ |
РЕШЕНИЕ Формула тонкой линзы Оптическая сила линзы Тогда Приравняем первое и второе уравнение из системы уравнений |
|
|
