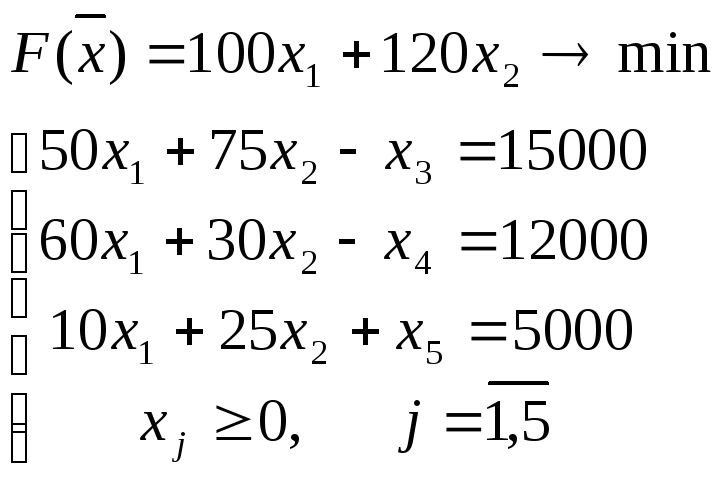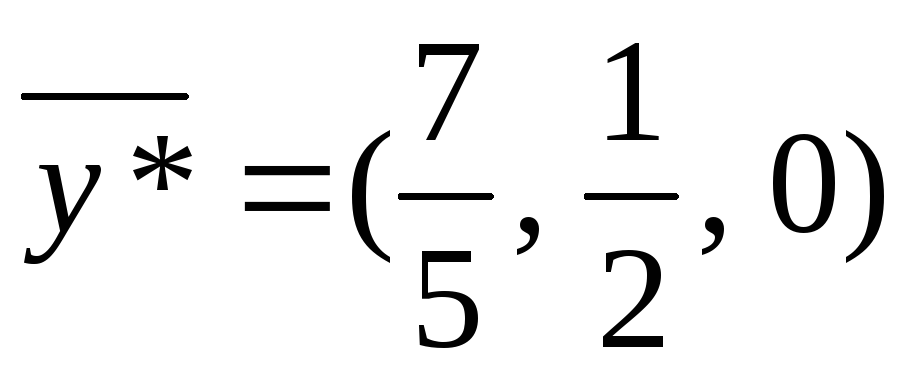Как найти оптимальное решение двойственной задачи - Сайт, где вы сможете решить свои вопросы

Двойственная задача линейного программирования

Время на прочтение
9 мин

Количество просмотров 26K

Прочие статьи цикла

Обычно с задачей линейного программирования (ЗЛП) связана другая линейная задача, называемая двойственной. Обе эти задачи можно считать двойственными одну по отношению к другой, считать равносильными. Первая задача называется обычно исходной, или прямой, другая – обратной. Переменные, используемые в двойственной задаче называются двойственными или множителями Лагранжа. На них не накладывается ограничений по знаку. Рассматриваются двойственные критерии оптимальности. Специальные случаи называют симметричными двойственными задачами линейного программирования. Связь между оптимальными решениями двойственных задач устанавливается теоремой двойственности.

Теорема двойственности

Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.

Теорема двойственности

Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.

Теорема существования решения

Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.

Теорема (принцип) дополняющей нежесткости

Если (x_Q, x_L) – оптимальное решение прямой задачи, а (y_Q, y_L) – решение двойственной задачи, то (x_Q, x_L, y_Q, y_L) – решение задачи Лагранжа. В частности, в этом случае удовлетворяются соотношения между переменными прямой и двойственной задач и условия дополняющей нежесткости.
Оптимальное решение прямой задачи программирования получается только при одном значении x_Q. Это справедливо и для переменной y_Q в двойственной задаче.

Теоремы двойственности

Основное неравенство двойственности. Для любых допустимых решений Х_<n>и Y_<n>пары двойственных ЗЛП имеет место неравенство

Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.

Теорема существования (малая тероема двойственности)

Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.

Теорема 1 двойственности.

Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. C_j – стоимость единицы продукции (внешняя оценка) y_i – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место x_j <-> y_m +_j; x_n+i<-> y_i_.

Теорема 2 двойственности (о дополняющей нежесткости)

Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:

То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.

Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.

Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.

Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:

Минимальное число линий, покрывающих все единицы матрицы [C_ij], найдем, решив линейную задачу:

Оптимальному решению (u*_i, v*_j) последней задачи отвечает минимальное покрытие, состоящее из множества строк I, для которых u*_i= 1 и столбцов J, для которых u*_j=1.

Матрицы А и А^Т коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:

Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.

Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.

Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину

Принцип двойственности в задачах линейного программирования.

Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.

С этой целью руководство должно назначить стоимости y_i за единицу сырья вида S_i, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ⁴_i=1 b_iy_i

Выручка предприятия от продажи сырья, расходуемого на единицу продукции П_i, составит: Σ⁴_i=1 a_ijy_i

И по условию она не должна быть меньше С_j (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).

Сформулируем исходную и двойственную задачи:

Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:

Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.
Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.
Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.
Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.
Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.

Оптимальный план X^opt_<n>одной из задач тесно связан с оптимальным планом Y^opt_<n> другой. Если одна из задач имеет решение, то другая также разрешена, причем для оптимальных клонов X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> справедливо равенство Q( X^opt ) =Q’( Y^opt ). Если линейная форма одной из задач неограниченна, то условия другой задачи несовместны. Если A^-1 обратная матрица к матрице В, состоящей из векторов базиса оптимального плана исходной задачи, то оптимальный план двойственной задачи равен Y^opt_<m> =СВ ^-1, здесь С – вектор базисных переменных. Решение двойственной задачи получается в последней симплексной таблице исходной задачи, в (m+1) строке, в столбцах, соответствующих дополнительным параметрам.

Для того чтобы векторы X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:

Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие y_i≥ 0.

Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*_j y*_m _+j; x*_n+i y*_i ; i = 1(1)m.

Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.

Пример. Двойственный симплекс метод.

Исходная задача. Имеется три вида продуктов П_j, причем единица веса каждого из видов продуктов содержит a_ij единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее b_i единиц вещества B_i в сутки. Стоимость единицы продукта П_j равняется C_j. Требуется составить оптимальный суточный рацион питания, т.е. найти количество x_j продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что

такие значения его компонентов x_j, j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x₁+ 2x₂+ x₃ и удовлетворяют ограничениям неравенствам

0,3x₁+ 0,2x₂+ 0, 4x₃≥ 0,2;

0,4x₁+ 0,3x₂+ 0,45x₃≥ 0,5;

0,2x₁+ 0,3x₂+ 0, 1 x₃≥ 0,6;

0,1x₁+ 0,2x₂+ 0,05x₃≥ 0,1;

x_j ≥ 0;j = 1(1)3 = n

Для приведения задачи к каноническому виду введем дополнительные переменные x₄, x₅, x₆, x₇, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств

0,3x₁+ 0,2x₂+ 0,4x₃– x₄= 0,2;

0,4x₁+ 0,3x₂+ 0,45x₃– x₅= 0,5;

0,2x₁+ 0,3x₂+ 0,1x₃– x₆= 0, 6;

0,1x₁+ 0,2x₂+ 0,05x₃– x₇= 0, 1;

x_j ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.

Назначаем опорный план. Выбор в качестве базисных переменных x₄, x₅, x₆, x₇ приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x₁ = x₂ = x₃= 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.

Двойственная задача. Коэффициентами линейной формы в двойственной задаче выступают правые части b_i , i = 1(1)4 = m, исходной основной задачи. Переменные получают другие имена y₁, y₂, y₃, y₄, и формулируется двойственная задача иначе. Найти максимум линейной формы Q’:

Q’=0,2y₁+ 0,5y₂+ 0,6y₃+ 0,1y₄;

при ограничениях

0,3y₁+ 0, 4y₂+ 0,2y₃+ 0,1y₄≤ 3;

0,2y₁+ 0, 3y₂+ 0,3y₃+ 0,2y₄≤ 2;

0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₄≤ 1;

y_i ≥ 0; i = 1(1)4.

Приведем задачу к каноническому виду, вводим дополнительные неотрицательные переменные y₅, y₆ , y₇:

Найти минимум ЦФ (знаки у коэффициентов ЦФ поменяли на противоположные): Q’= – 0,2y₁– 0,5y₂– 0, 6y₃– 0,1y₄;

при ограничениях (в ограничения добавили новые переменные):

0,3y₁+ 0, 4y₂+ 0,2y₃+ 0, 1y₄+ y₅= 3;

0,2y₁+ 0, 3y₂+ 0,3y₃+ 0, 2y₄+ y₆= 2;

0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₄+ y₇= 1,

y_i ≥ 0; i = 1(1)7.

Задача решается симплекс методом. Исходный опорный план в качестве переменных может иметь y₅, y₆, y₇ и свободные переменные y₁= y₂= y₃= y₄= 0, т.е. Y_<7> = [0, 0, 0, 0, 3, 2, 1] .

Базисные переменные y₅, y₆, y₇и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γ_i) вычитаем левые части ограничений

y₅= 3 – (0,3y₁+ 0,4y₂+ 0,2y₃+ 0,1y₄);

y₆= 2 – (0,2y₁+ 0,3y₂+ 0,3y₃+ 0,2y₄);

y₇= 1 – (0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₆);

Q’₁=γ₀ – Σ⁴_i=1 γ_iy_i= 0 -(0,2y₁+ 0,5y₂+ 0, 6y₃+ 0,1y₄);

γ₀=0, так как ЦФ не содержит свободного члена.

и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y₃, направляющая строка y₆.

Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y_<7> не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.

Находим γ = max{γ_i} =max {0,2; 0,5; 0,6; 0,1} = 0,6. Переменную y₃ надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y₃,тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y₆ и ее исключаем из базиса.

После замены переменных в базисе переходим к новой симплексной таблице.

Анализ этой таблицы показывает, что все коэффициенты в выражении ЦФ свободных переменных отрицательны. Следовательно, опорный план Y_<7>= [0, 0, 20/3, 0, 5/3, 0, 1/3] является оптимальным. ЦФ при этом Q’₁= – 4 достигла наименьшего значения. Возвращаемся к двойственной задаче. Используя соответствие между оптимальными планами двойственных задач ЛП, определяем: базисными переменными в оптимальном плане будут x₂ x₄ x₅ x₇; их значения с противоположным знаком записаны в последней строке таблицы. Таким образом, X^opt_<n> =<0; 2; 0; 0; 2; 0; 1; 0; 1/30>, т.е. оптимальный рацион из двух единиц продукта П₂. Стоимость такого рациона минимальна и составляет 4 единицы. Это значение с противоположным знаком записано в той же таблице.

Литература

Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
Квейд Э. Методы системного анализа // Новое в теории и практике управления производством в США.–М.: Прогресс, 1971.– с.78-99. .
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

Источник

(1)

(2)

(3)

усть исходная задача дана в
канонической форме

(4)

Оптимальное решение
получено симплекс-методом,–
базисная матрица оптимального решения.

Оптимальное решение
двойственной задачи (по первой теореме
двойственности)

элементы
строки оценок в оптимальной симплекс-таблице
прямой задачи вычисляются по формулам

(5)

Подставляя (4) в
(5) получим

Памятуя о том, что
ограничение двойственной задачи,
соответствующее переменной
прямой задачи, имеет вид

(6)

, или
,
выводим
из (6) важное свойство оценок:

Оценка
переменнойв симплекс-таблице равна разнице левой
и правой части соответствующего
ограничения двойственной задачи.

Из соотношения
(6) легко найти компоненты оптимального
решения двойственной задачи.

Действительно,
пусть
– единичный вектор с единицей вi-ой
строке. В исходной симплекс-таблице
всегда есть такие вектора.

Оценка
переменнойсогласно (6) запишется

(7)

откуда

Таким образом, для
определения компоненты
оптимального решения двойственной
задачи следует в исходной симплекс-таблице
выбрать единичный столбецс единицей вi-ой
строке. Тогда компонента
равна оценкепеременнойиз оптимальной симплекс-таблицы плюс
коэффициент критерия этой переменной

Пример:

Найдем оптимальное
решение двойственной задачи к задаче
раздела 5.2 о работе предприятия по двум
технологиям.

Воспроизведем для
наглядности решение симплекс-методом

	F	8	3	0	0	-M
Св	Бп	x₁	x₂	x₃	x₄	x₅	b
0	x₃	2	1	1	0	0	12
0	x₄	1	0	0	1	0	4
-M	x₅	1	1	0	0	1	6
	F	-8-M	-3-M	0	0	0	-6M
0	x₃	0	1	1	-2	0	4
8	x₁	1	0	0	1	0	4
-M	x₅	0	1	0	-1	1	2
	F	0	-3-M	0	8+M	0	-2M+32
0	x₃	0	0	1	-1	-1	2
8	x₁	1	0	0	1	0	4
3	x₂	0	1	0	-1	1	2
	F	0	0	0	5	3+M	38

Единичная матрица
в исходной симплекс таблице расположена
в столбцах
3, 4, 5.

Оптимальное решение
двойственной задачи будет находиться
в строке оценок оптимальной симплекс-таблицы
под единичной матрицей исходной
симплекс-таблицы:

5.5. Двойственный симплексный метод

Рассмотрим базисное
недопустимое решение
.

Пусть
все оценки на этом решении неотрицательные.
Такое базисное решение называетсяпсевдо-планом
или псевдо-оптимальным решением. У него
значение критерия лучше, чем у оптимального,
но оно является недопустимым.

Для этого решения

,
.
А это означает, что псевдо-план исходной
задачи соответствует опорному плану
двойственной задачи:.
При этом каждому псевдо-плану исходной
задачи соответствует угловая точка
двойственной.

Двойственная
задача может быть решена симплекс-методом.

Двойственный
симплекс-метод решения прямой задачи
использует соответствующее решение
двойственной задачи, но операции
выполняются в симплекс-таблице исходной
задачи. Перемещение происходит от одного
псевдо-плана к другому с приближением
к области. Когда очередное базисное
решение станет допустимым, будет получено
оптимальное решение.

Если симплексный
метод – метод последовательного
улучшения плана (улучшаются планы
),
то двойственный симплекс-метод – метод
последовательного улучшения оценок
(улучшаются решения двойственной задачи
– двойственные оценки).

Условия применимости
двойственного симплекс-метода:

в
матрице условий задачи, записанной в
канонической форме, должна быть единичная
подматрица, при этом правые части
ограничений не обязаны быть положительными.

все
оценки должны быть неотрицательны,
если задача на максимум, и неположительны,
если задача на минимум.

Итерации в
двойственном симплекс-методе выполняются
по следующим правилам:

определяется
переменная ,
выводимая из списка базисных. Она
определяется по отрицательной компоненте
.
Если их несколько, то лучше брать
максимальную по модулю.
определяется
свободная переменная ,
вводимая в список базисных.
При этом разрешающий
столбец определяется по минимальному
по модулю отношению оценок свободных
переменных к отрицательным коэффициентам
разрешающей строки.

Это правило
гарантирует, что новое базисное решение
будет псевдо-планом.

далее
выполняются операции однократного
замещения (как и в симплекс-методе) с
разрешающим элементом .
процесс
повторяется до тех пор, пока очередное
базисное решение не станет допустимым.

Замечание:
если в разрешающей строке нет отрицательных
элементов, то область допустимых решений
пуста.

Пример:

Содержательное
описание.

Целлюлозно-бумажный
комбинат (ЦБК) на берегу озера Байкал
может работать по двум технологическим
режимам. По первому режиму в течение
смены расходуется 100 м³
древесины, производится 50 тонн целлюлозы,
60 центнеров лигнитов (вещества,
используемые в химической промышленности)
и сбрасывается в озеро 10 кг отравляющих
веществ. По второму режиму в течение
смены расходуется 120 м³
древесины, производится 75 тонн целлюлозы,
30 центнеров лигнитов, сбрасывается в
озеро 25 кг отравляющих веществ. Годовой
план производства составляет 15000 тонн
целлюлозы, 1200 тонн лигнитов. Предельные
годовые нормы выброса отравляющих
веществ составляют 5 тонн. Определить
годовой план работы ЦБК, требующий
минимального расхода древесины.

Математическая
модель.

Управляемые
параметры.

[см]
– время работы (в сменах) по первой
технологии;

[см]
– время работы (в сменах) по второй
технологии;

–годовой план
работы.

2.2 Ограничения.

–годовое
производство целлюлозы в тоннах должно
быть не меньше плана;

–годовое
производство лигнитов в центнерах
должно быть не меньше плана;

–годовой выброс
отравляющих веществ в килограммах не
должен превосходить предельно-допустимых
норм выброса.

–время работы по
каждой из технологий неотрицательно

Формулировка
цели.

–годовой расход
древесины должен быть минимален.

Получили следующую
задачу линейного программирования

(1)

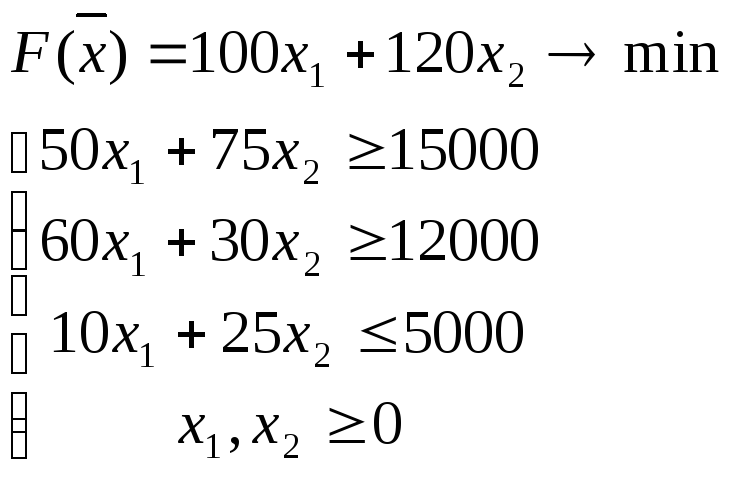
Приведем её к
каноническому виду

–очевидное
базисное решение, но оно не является
допустимым.

Обеспечим условия
применения двойственного симплекс-метода.
Сменим знаки левых и правых частей
первых двух уравнений

(2)

Занесем данные в
симплекс-таблицу. Видим, что оценки
переменных в последней строке первой
симплекс-таблицы не положительны, то
есть базисное решение
является псевдо-планом, условия
применимости двойственного симплекс-метода
выполняются.

		100	120	0	0	0
Св	Бп	x₁	x₂	x₃	x₄	x₅	b
0	x₃	-50	-75	1	0	0	-15000
0	x₄	-60	-30	0	1	0	-12000
0	x₅	10	25	0	0	1	5000
	F	-100	-120	0	0	0	0
120	x₂	2/3	1	-1/75	0	0	200
0	x₄	-40	0	-2/5	1	0	-6000
0	x₅	-20/3	0	1/3	0	1	0
	F	-20	0	-8/5	0	0	24000
120	x₂	0	1	-1/50	1/60	0	100
100	x₁	1	0	1/100	-1/40	0	150
0	x₅	0	0	2/5	-1/6	1	1000
	F	0	0	-7/5	-1/2	0	27000

–псевдо-план.

На первой итерации
выбирается первая разрешающая строка
(-15000<0) и второй разрешающий столбец
(120/75<100/50). Выполняются операции
однократного замещения. Получаем
следующее приближение к области.

На второй итерации
разрешающая строка вторая (-6000,0),
разрешающий столбец первый (20/40=0.5<
8/5:2/5=4).

Следующее решение

–допустимое
базисное, значит оптимальное.

Экономическая
интерпретация полученного решения: для
обеспечения минимального расхода
древесины нужно работать 150 смен по
первой технологии, 100 смен по второй
технологии, при этом расход древесины
будет составлять 27000 м³.
Производство целлюлозы и лигнитов
совпадает с плановым (так как x₃=x₄=0),
выброс отравляющих веществ на 1000 кг
меньше предельно-допустимых норм
выброса.

Построим двойственную
задачу. Для применения правил построения
двойственных задач необходимо согласовать
знаки неравенств с типом критерия:

(3)

Введем переменные
двойственной задачи:

–оценка полезности
1 тонны целлюлозы;

–оценка полезности
1 центнера лигнитов;

–оценка «полезности»
1 кг отравляющих веществ. Значение у₃
на оптимальном плане будет показывать,
на сколько изменится критерий при
увеличении b₃на единицу
(с -5000 до -4999). В терминах исходной задачи
– это приращение расхода древесины от
ужесточения (уменьшения) предельно
допустимых норм выброса отравляющих
веществ на один килограмм.

Тогда двойственная
задача запишется в виде

(4)

Найдем оптимальное
решение двойственной задачи из оптимальной
симплекс-таблицы прямой задачи:

(5)

Казалось бы,
полученное решение опровергает теорию
получения оптимального решения
двойственной задачи из оптимальной
симплекс-таблицы прямой. Полученное
решение
даже
недопустимое – нарушаются условия
неотрицательности в (4).

Действительно,
(5) – это не оптимальное решение задачи
(4), двойственной к задаче (3). Вектор
– это оптимальное решение задачи,
двойственной к задаче (2). Именно эта
задача представлена в исходной
симплекс-таблице.

Хотя задачи (2) и
(3) эквивалентны, имеют совпадающие
области допустимых решений, но формы
представления задач разные и двойственные
к ним задачи будут отличаться не только
формой, но и значением оптимальных
решений. Однако оптимальные решения
этих задач легко могут быть получены
друг из друга.

Построим двойственную
задачу к задаче (2):

(6)

После замены
переменных

задача
(6) обращается в задачу (4).

Таким образом,
если из симплекс-таблицы получено
оптимальное решение

задачи, двойственной
к задаче (2), то решение двойственной к
задаче (3) может быть получено сменой
знаков компонент решения:

Экономический
смысл двойственных переменных:

показывает, что
при увеличении плана выпуска целлюлозы
на 1 тонну расход древесины возрастет
на 1.4 м³.

показывает, что
при увеличении плана выпуска лигнитов
на 1 центнер расход древесины возрастет
на 0.5 м³.

показывает, что
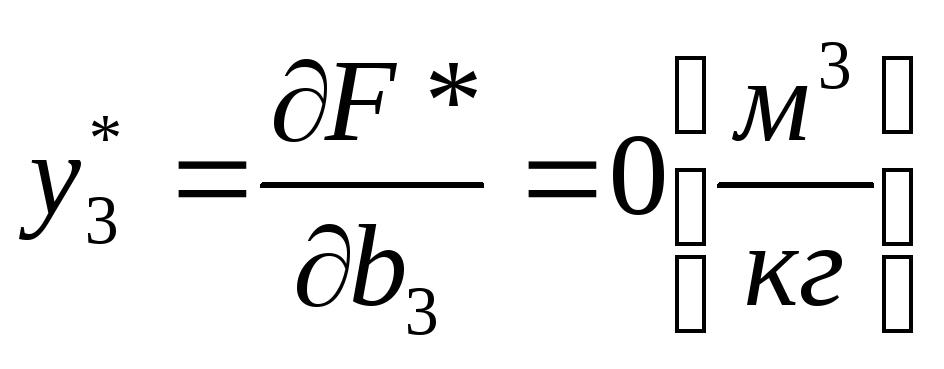
при уменьшении годовых предельно
допустимых норм выброса отравляющих
веществ на 1 килограмм расход древесины
не изменится. Действительно, на оптимальном
решении ограничение по выбросу отравляющих
веществ не активное, выброс (4000) не
достигает предельной нормы (5000), поэтому
уменьшение нормы не только на 1, но и на
величину в пределах 1000 килограммов не
повлияет на оптимальный план работы
комбината.

Полученные оценки
влияния рассмотренных параметров на
оптимальное значение критерия справедливы
в области устойчивости двойственных
оценок.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Двойственная задача линейного программирования

Краткая теория

С каждой задачей линейного
программирования тесно связана другая линейная задача, называемая двойственной.
Первоначальная задача называется прямой или исходной. Многие задачи линейного
программирования первоначально ставятся в виде исходных или двойственных задач,
поэтому говорят о паре взаимно двойственных задач линейного программирования.
Пара симметричных двойственных ЗЛП имеет следующий вид:

Прямая
задача:

Двойственная
задача

Рассмотренная пара взаимно
двойственных задач может быть экономически интерпретирована, например, так.

Прямая задача: сколько и
какой продукции

надо
произвести, чтобы при заданных объемах имеющихся ресурсов

и
нормах расходов

максимизировать
выпуск продукции в стоимостном выражении?

Двойственная задача: какова
должна быть оценка единицы каждого из ресурсов

, чтобы при заданных

минимизировать
общую оценку затрат на ресурсы?

Для построения двойственной
задачи необходимо пользоваться следующими правилами:

Основное неравенство теории двойственности

Для любых допустимых планов

пары
двойственных задач справедливо неравенство

. Его экономическое содержание состоит в
том, что для любого допустимого плана производства

и
любого допустимого вектора оценок ресурсов

общая
созданная стоимость не превосходит суммарной оценки ресурсов.

Критерий оптимальности Канторовича (достаточный признак оптимальности)

Если для некоторых
допустимых планов

пары
двойственных задач выполняется равенство

, то

являются оптимальными планами
соответствующих задач. Экономический смысл критерия следующий: план
производства

и
вектор оценок ресурсов

являются оптимальными, если цена всей
произведенной продукции и суммарная оценка ресурсов совпадают.

Теорема существования оптимальных планов пары двойственных задач

Для существования
оптимального плана любой из пары двойственных задач необходимо и достаточно
существования допустимого плана для каждой из них.

Первая теорема двойственности

Если одна из двойственных
задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем
экстремальные значения целевых функций совпадают

. Если одна из двойственных задач
неразрешима вследствие неограниченности целевой функции на множестве допустимых
решений, то система ограничений другой задачи противоречива.

Экономическое содержание
первой теоремы двойственности состоит в следующем: если задача определения
оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима
и задача определения оценок ресурсов. Причем цена продукта, полученного в
результате реализации оптимального плана, совпадает с суммарной оценкой
ресурсов. Совпадения значений целевых функций для соответствующих решений пары
двойственных задач достаточно для того, чтобы эти решения были оптимальными.
Это значит, что план производства и вектор оценок ресурсов являются
оптимальными тогда и только тогда, когда цена произведенной продукции и
суммарная оценка ресурсов совпадают. Оценки выступают как инструмент
балансирования затрат и результатов. Двойственные оценки обладают тем
свойством, что они гарантируют рентабельность оптимального плана, то есть
равенство общей оценки продукции и ресурсов обусловливает убыточность всякого
другого плана, отличного от оптимального. Двойственные оценки позволяют
сопоставлять и балансировать затраты и результаты системы.

Связь между задачами
двойственной пары глубже, чем указано в формулировке теоремы. Решая симплексным
методом одну из них, автоматически получаем решение другой. Для этого
достаточно воспользоваться соответствием переменных прямой и двойственной задач
и оценок в последней симплексной таблице.

Отсюда имеем оптимальный
план двойственной задачи. Если прямая задача решается на максимум, то пользуясь
соответствием переменных:

и так далее.

Если прямая задача решается
на минимум, то:

и так далее.

Вторая теорема двойственности (о дополняющей нежесткости)

Для того, чтобы планы

пары
двойственных задач были оптимальными, необходимо и достаточно выполнение
условий:

Эти условия называются
условиями дополняющей нежесткости. Из них следует: если какое-либо неравенство
системы ограничений одной из задач не обращается в строгое равенство
оптимальным планом этой задачи, то соответствующая компонента оптимального
плана двойственной задачи должна равняться нулю. Если же какая-либо компонента
оптимального плана одной из задач положительна, то соответствующее ограничение
в двойственной задаче ее оптимальным планом должно обращаться в строгое
равенство.

Экономически это означает,
что если по некоторому оптимальному плану

производства расход i-го ресурса строго меньше его запаса

, то в оптимальном плане соответствующая двойственная
оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане
оценок его i-я компонента строго
больше нуля, то в оптимальном плане производства расход соответствующего
ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить
мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по
оптимальному плану производства) имеет положительную оценку, а избыточный
ресурс (используемый не полностью) имеет нулевую оценку.

Третья теорема двойственности

Двойственные оценки
показывают приращение функции цели, вызванное малым изменением свободного члена
соответствующего ограничения ЗЛП, то есть:

Выясним экономическое
содержание третьей теоремы двойственности. Для этого в последнем выражении
дифференциалы заменим приращениями. Получим:

При

имеем

То есть двойственная оценка
численно равна изменению целевой функции
при изменении соответствующего ресурса на единицу. Двойственные оценки

часто
называют скрытыми, теневыми или маргинальными оценками ресурсов.

Примеры решения задач

Задача 1

Постройте
модель двойственной задачи для данной задачи линейного программирования,
заданной в произвольной форме.

Решение

Воспользуемся правилами для
построения двойственной задачи.Заполним вспомогательную таблицу.

ДЗ/ПЗ				min	СП/ЦФ
	-18	7	-12		-2
	-12	16	-12		3
	-11	3	-7	=	-2
	0	13	-12		-1
max		=
ЦФ/СП	-18	1	-3

Двойственная задача будет
иметь следующий вид:

–любого
знака,

Задача 2

Для приведенной ниже задачи
записать двойственную. Решить одну из них симплексным методом и получить решение
другой.

Решение

Приведем задачу к каноническому виду.

Воспользуемся правилами для
построения двойственной задачи.

Двойственная задача будет иметь следующий вид:

Приведем двойственную задачу к каноническому виду.

Заполняем симплексную таблицу 0-й итерации.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Переходим к таблице 1-й итерации:

В индексной строке все члены неотрицательные, поэтому получено
следующее решение задачи линейного программирования (выписываем из столбца
свободных членов):

Соответствие между переменными исходной и двойственной задачи:

На основании симплексной таблицы получено следующее решение
двойственной задачи линейного программирования:

Задача 3

Дана
задача линейного программирования:

Решение прямой задачи:

Найти
оптимальное решение двойственной задачи линейного программирования.

Решение

Исходя из вышеописанных
правил построения модели двойственной задачи, двойственная задача будет иметь
следующий вид:

Найдем оптимальное решение
двойственной задачи:

Условия
дополняющей нежесткости (вторая теорема двойственности): для оптимальных планов
двойственных задач имеют место соотношения:

Так
как для оптимального решения прямой задачи 3-е и 4-е ограничения выполняются
как неравенство, то

Для
нахождения значений

, получаем:

Ответ

Решение двойственной задачи:

Источник

Двойственная задача^[1] для заданной задачи линейного программирования (ЛП, англ. Linear programming, LP) — это другая задача линейного программирования, которая получается из исходной (прямой) задачи следующим образом:

Каждая переменная в прямой задаче становится ограничением двойственной задачи;
Каждое ограничение в прямой задаче становится переменной в двойственной задаче;
Направление цели обращается – максимум в прямой задаче становится минимумом в двойственной, и наоборот.

Теорема о слабой двойственности утверждает, что значение двойственной задачи для любого допустимого решения всегда ограничено значением прямой задачи для любого допустимого решения (верхняя или нижняя граница, в зависимости от того, это задача максимизации или минимизации).

Теорема о сильной двойственности утверждает, что более того, если прямая задача имеет оптимальное решение, то двойственная задача имеет также оптимальное решение, и эти два оптимума равны^[2].

Эти теоремы принадлежат более широкому классу теорем двойственности в оптимизации. Теорема о сильной двойственности является одним из случаев, в котором разрыв двойственности (разрыв между оптимумом прямой задачи и оптимумом двойственной) равен 0.

О геометрическом смысле двойственной задачи можно почитать в книге Юдина и Гольштейна^[3]. Там же можно прочитать об экономическом смысле задачи^[4].

Построение двойственной задачи[править | править код]

Если дана прямая задача линейного программирования, для построения двойственной задачи может быть использован следующий алгоритм^[5].

Пусть прямая задача определена как:

Двойственная задача строится следующим образом.

Каждое ограничение прямой задачи становится двойственной переменной. Таким образом, получаем m переменных: ${displaystyle y_{1},ldots ,y_{m}}$ .
Знак ограничения каждой двойственной переменной «противоположен» знаку ограничения в прямой задаче. Таким образом, « ${displaystyle geqslant b_{j}}$ » становится ${displaystyle y_{j}leqslant 0}$ , « ${displaystyle leqslant b_{j}}$ » превращается в ${displaystyle y_{j}geqslant 0}$ , а « ${displaystyle =b_{j}}$ » превращается в ${displaystyle y_{j}in mathbb {R} }$ .
Целевая функция двойственной задачи равна (минимизировать) ${displaystyle b_{1}y_{1}+cdots +b_{m}y_{m}}$
Каждая переменная прямой задачи становится двойственным ограничением. Таким образом, получаем n ограничений. Коэффициент двойственной переменной в двойственных ограничениях равен коэффициенту переменной из ограничения прямой задачи. Таким образом, каждое ограничение i есть: ${displaystyle a_{1i}y_{1}+cdots +a_{mi}y_{m}lesseqqgtr c_{i}}$ , где символ перед $c_{i}$ аналогичен ограничению на переменную i в прямой задаче. Так, ${displaystyle x_{i}leqslant 0}$ превращается в « ${displaystyle leqslant c_{i}}$ », ${displaystyle x_{i}geqslant 0}$ превращается в « ${displaystyle geqslant c_{i}}$ », а ${displaystyle x_{i}in mathbb {R} }$ превращается в « ${displaystyle =c_{i}}$ ».

Из этого алгоритма легко видеть, что двойственная задача двойственной задачи совпадает с прямой задачей.

Векторные формулировки[править | править код]

Если все ограничения имеют один и тот же знак, можно представить вышеизложенный метод в более короткой форме с помощью векторов и матриц. Следующая таблица представляет связи между различными видами прямых и двойственных задач.

Прямая	Двойственная	Примечания
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {y} geqslant 0}$	Такая задача называется «симметричной» двойственной задачей
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} =mathbf {c} ,mathbf {y} geqslant 0}$	Такая задача называется «асимметричной» двойственной задачей
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} }$

Теоремы двойственности[править | править код]

Ниже мы предполагаем, что прямая задача поставлена как «Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях [ограничения]», а двойственная задача поставлена как «Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях [ограничения]».

Слабая двойственность[править | править код]

Теорема о слабой двойственности утверждает, что для каждого допустимого решения x прямой задачи и каждого допустимого решения y двойственной задачи: ${displaystyle mathbf {c} ^{T}mathbf {x} leqslant mathbf {b} ^{T}mathbf {y} }$ . Другими словами, значение целевой функции для каждого допустимого решения двойственной задачи является верхней границей целевой функции прямой задачи, а значение целевой функции любого допустимого решения прямой задачи является нижней границей для целевой функции двойственной задачи. Из этого следует, что

${displaystyle max _{mathbf {x} }mathbf {c} ^{T}mathbf {x} leqslant min _{mathbf {y} }mathbf {b} ^{T}mathbf {y} }$

В частности, если прямая задача не ограничена (сверху), то двойственная задача не имеет допустимого решения, а если не ограничена двойственная задача (снизу), то не имеет допустимого решения прямая задача.

Теорему о слабой двойственности относительно легко доказать^[6]. Предположим, что прямая задача линейного программирования звучит как «Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях ». Предположим, что мы создаём линейную комбинацию ограничений с положительными коэффициентами, такую, что коэффициенты при x не меньше ${displaystyle mathbf {c} ^{T}}$ . Эта линейная комбинация даёт нам верхнюю грань для целевой функции. Переменные y двойственной задачи являются коэффициентами этой линейной комбинации. Двойственная задача пытается найти такие коэффициенты, которые минимизируют результирующую правую часть. Это даёт задачу линейного программирования «Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {y} geqslant 0}$ »^[7]. См. «Простой пример» ниже.

Сильная двойственность[править | править код]

Теорема о сильной двойственности утверждает, что границы, определяемые теоремой о слабой двойственности жёсткие, то есть

${displaystyle max _{mathbf {x} }mathbf {c} ^{T}mathbf {x} =min _{mathbf {y} }mathbf {b} ^{T}mathbf {y} }$

Теорему о сильной двойственности существенно труднее доказать. Обычно доказательство использует теорему о слабой двойственности в качестве леммы^[8].

Одно доказательство использует симплекс-метод и опирается на доказательство того, что, при подходящем правиле выбора выводимого столбца, он даёт правильное решение. Доказательство устанавливает, что, когда симплекс-метод завершается решением прямой задачи линейного программирования, можно из конечной таблицы прочесть решение двойственной задачи. Таким образом, после прогона симплекс-алгоритма мы получим решения как прямой, так и двойственной задачи одновременно^[9].

Другое доказательство использует лемму Фаркаша^[10]

Теоретическое приложение[править | править код]

Слабая двойственность имеет интересное теоретическое приложение — она показывает, что нахождение отдельного допустимого решения настолько же трудно, насколько нахождение оптимального допустимого решения. Предположим, что мы имеем систему предсказывания, что данная задача линейного программирования находит произвольное допустимое решение (если оно существует). Если задача звучит как «Максимизировать ${displaystyle mathbf {c} ^{mathbf {x} }}$ при ограничениях », мы можем построить другую задачу путём комбинирования её с двойственной ей задачей. Комбинированная задача имеет как x, так и y в качестве переменных:

Максимизировать 1

при ограничениях ${displaystyle mathbf {Ax} leqslant mathbf {b} ,mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {c} ^{T}mathbf {x} geqslant mathbf {b} ^{T}mathbf {y} ,mathbf {x} geqslant 0,mathbf {y} geqslant 0}$

Если комбинированная задача имеет допустимое решение (x,y), то по слабой двойственности ${displaystyle mathbf {c} ^{T}mathbf {x} =mathbf {b} ^{T}mathbf {y} }$ . Таким образом, x должно быть максимальным решением прямой задачи, а y должно быть минимальным решением двойственной задачи. Если комбинированная задача не имеет допустимого решения, то и прямая задача допустимого решения не имеет.

Примеры[править | править код]

Простой пример[править | править код]

Рассмотрим прямую задачу с двумя переменными и одним ограничением:

Максимизировать ${displaystyle 3x_{1}+4x_{2}}$

При условиях

${displaystyle {begin{aligned}&5x_{1}+6x_{2}=7\&x_{1}geqslant 0,x_{2}geqslant 0end{aligned}}}$

Применив вышеизложенный рецепт построения двойственной задачи, получим задачу с одной переменной и двумя ограничениями:

Минимизировать ${displaystyle 7y_{1}}$

При условиях

${displaystyle {begin{aligned}&&5y_{1}geqslant 3\&&6y_{1}geqslant 4\&&y_{1}in mathbb {R} end{aligned}}}$

Легко видеть, что максимум прямой задачи достигается, когда переменная x₁ минимизируется до её нижней границы (0), а переменная x₂ максимизируется до её верхней границы, заданной ограничением (7/6). Максимум равен .

Аналогично, минимум двойственной задачи достигается, когда y₁ минимизируется до его нижнего значения при ограничениях: первое ограничение даёт значение 3/5, в то время как второе даёт более строгую границу 4/6, так что фактический минимум равен 4/6 и минимум целевой функции равен .

Согласно теореме о сильной двойственности максимум прямой задачи равен минимуму двойственной.

Мы используем этот пример для иллюстрации доказательства теоремы о слабой двойственности. Предположим, что в прямой задаче линейного программирования мы хотим получить верхнюю границу целевой функции ${displaystyle 3x_{1}+4x_{2}}$ . Мы можем использовать ограничение, умноженное на некоторый коэффициент, скажем, y_1 . Для любого y_1 мы имеем: ${displaystyle y_{1}cdot (5x_{1}+6x_{2})=7y_{1}}$ . Теперь, если ${displaystyle y_{1}cdot 5x_{1}geqslant 3x_{1}}$ и ${displaystyle y_{1}cdot 6x_{2}geqslant 4x_{2}}$ , то ${displaystyle y_{1}cdot (5x_{1}+6x_{2})geqslant 3x_{1}+4x_{2}}$ , так что ${displaystyle 7y_{1}geqslant 3x_{1}+4x_{2}}$ . Следовательно, целевая функция двойственной задачи является верхней границей целевой функции прямой задачи.

Пример фермера[править | править код]

Рассмотрим фермера, который может выращивать пшеницу и ячмень на площади L, используя удобрения F и пестициды P.
Чтобы вырастить одну единицу пшеницы на единице площади, нужно использовать $F_{1}$ единиц удобрений и P_1 единиц пестицидов.

Прямой задачей будет решение фермера, сколько пшеницы ( $x_{1}$ ) и ячменя ( $x_{2}$ ) выращивать, если их продажные цены равны $S_{1}$ и $S_{2}$ за единицу.

Максимизировать:

${displaystyle S_{1}cdot x_{1}+S_{2}cdot x_{2}}$

(максимизировать доход от выращивания пшеницы и ячменя)

при ограничениях:

${displaystyle x_{1}+x_{2}leqslant L}$

(фермер не может использовать больше земли, чем у него есть)

${displaystyle F_{1}cdot x_{1}+F_{2}cdot x_{2}leqslant F}$

(фермер не может использовать больше удобрений, чем есть в наличии)

${displaystyle P_{1}cdot x_{1}+P_{2}cdot x_{2}leqslant P}$

(фермер не может использовать больше пестицидов, чем у него есть)

${displaystyle x_{1},x_{2}geqslant 0}$

(нельзя вырастить отрицательную величину зерна).

Для двойственной задачи предположим, что y единиц цены для каждой из этих видов продукта (входы) представлены группой планирования. Задачей группы планирования является минимизация полной стоимости производство продукции при заданных величинах потребления ресурсов с определением стоимости единицы ресурса (выход). Это соответствует следующей задаче линейного программирования:

Минимизировать

${displaystyle Lcdot y_{L}+Fcdot y_{F}+Pcdot y_{P}}$

(минимизировать полную стоимость производства продукции как «целевая функция»)

при ограничениях:

${displaystyle y_{L}+F_{1}cdot y_{F}+P_{1}cdot y_{P}geqslant S_{1}}$

(фермер должен получить не менее S₁ за единицу пшеницы)

${displaystyle y_{L}+F_{2}cdot y_{F}+P_{2}cdot y_{P}geqslant S_{2}}$

(фермер должен получить не менее S₂ за единицу ячменя)

${displaystyle y_{L},y_{F},y_{P}geqslant 0}$

(цены не могут быть отрицательными).

В матричной форме:

Минимизировать: ${displaystyle {begin{bmatrix}L&F&Pend{bmatrix}}{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}}$

при условиях: ${displaystyle {begin{bmatrix}1&F_{1}&P_{1}\1&F_{2}&P_{2}end{bmatrix}}{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}geqslant {begin{bmatrix}S_{1}\S_{2}end{bmatrix}},,{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}geqslant 0.}$

Прямая задача имеет дело с физическими количествами, когда все величины ограничены и цены на единицу продукции известны. Задача состоит в определении, какие количества продукта произвести, чтобы максимизировать суммарный доход. Двойственная задача имеет дело с экономическими величинами. Задача состоит в том, чтобы при фиксированных ценах на продукцию и известных потреблениях ресурсов определить, какую ценовую схему установить, чтобы минимизировать суммарные затраты.

Каждой переменной в пространстве прямой задачи соответствует неравенство в пространстве двойственной задачи. Каждому неравенству в пространстве прямой задачи соответствует переменная в пространстве двойственной задачи.

Коэффициенты, которые ограничивают неравенства в пространстве прямой задачи, используются для вычисления целевой функции в двойственном пространстве. Коэффициенты, используемые для вычисления целевой функции, в пространстве прямой задачи ограничивают неравенства в пространстве двойственной задачи.

Как прямая, так и двойственная задачи используют одну и ту же матрицу. В пространстве прямой задачи эта матрица выражает потребление физических величин, необходимых для производства выходного продукта. В пространстве двойственной задачи матрица выражает создание экономических значений, ассоциированных с выходным продуктом из множеств входных цен на единицу продукции.

Поскольку каждое неравенство может быть заменено на равенство и дополнительную переменную, это означает, что каждая переменная прямой задачи соответствует двойственной дополнительной переменной, а каждая двойственная переменная соответствует прямой дополнительной переменной. Это отношение позволяет нам говорить о взаимодополнительности дополнительных переменных.

Недопустимая задача[править | править код]

Задача линейного программирования может также быть неограниченной или недопустимой. Теория двойственности говорит нам, что:

Если прямая задача является неограниченной, то двойственная задача недопустима;
Если двойственная задача является неограниченной, то прямая задача недопустима^[11].

Однако может быть, что обе задачи, как двойственная, так и прямая, недопустимы. Вот пример:

Приложения[править | править код]

Теорема о максимальном потоке и минимальном разрезе является специальным случаем теоремы о сильной двойственности — максимизация потока является прямой задачей линейного программирования, а минимизация разреза является двойственной задачей линейного программирования. См. теорему Форда — Фалкерсона.

Другие теоремы, связанные с графами, могут быть доказаны с помощью теоремы о сильной двойственности, в частности, теорема Кёнига^[12].

Теорема о минимаксе^[en] для игр с нулевой суммой может быть доказана с помощью теоремы о сильной двойственности^[13].

Альтернативный алгоритм[править | править код]

Иногда можно найти более интуитивный способ получить двойственную задачу без применения матрицы задачи. Рассмотрим следующую задачу линейного программирования:

Минимизировать ${displaystyle sum _{i=1}^{m}c_{i}x_{i}+sum _{j=1}^{n}d_{j}t_{j}}$

при условиях

${displaystyle sum _{i=1}^{m}a_{ij}x_{i}+e_{j}t_{j}geqslant g_{j},1leqslant jleqslant n}$

${displaystyle f_{i}x_{i}+sum _{j=1}^{n}b_{ij}t_{j}geqslant h_{i},1leqslant ileqslant m}$

${displaystyle x_{i}geqslant 0,,t_{j}geqslant 0,1leqslant ileqslant m,1leqslant jleqslant n}$

Мы имеем условий и все переменные неотрицательны. Нам нужно определить двойственных переменных: y_j и s_i. Мы получаем:

Минимизировать ${displaystyle sum _{i=1}^{m}c_{i}x_{i}+sum _{j=1}^{n}d_{j}t_{j}}$

при условиях

${displaystyle sum _{i=1}^{m}a_{ij}x_{i}cdot y_{j}+e_{j}t_{j}cdot y_{j}geqslant g_{j}cdot y_{j},1leqslant jleqslant n}$

${displaystyle f_{i}x_{i}cdot s_{i}+sum _{j=1}^{n}b_{ij}t_{j}cdot s_{i}geqslant h_{i}cdot s_{i},1leqslant ileqslant m}$

${displaystyle x_{i}geqslant 0,,t_{j}geqslant 0,1leqslant ileqslant m,1leqslant jleqslant n}$

${displaystyle y_{j}geqslant 0,,s_{i}geqslant 0,1leqslant jleqslant n,1leqslant ileqslant m}$

Поскольку это задача минимизации, нам хотелось бы получить двойственную задачу, которая является нижней границей прямой задачи. Другими словами, нам хотелось бы, чтобы сумма всех правых частей ограничений была максимальной при условиях, что для каждой переменной прямой задачи сумма её коэффициентов не превосходит коэффициента в линейной функции. Например, x₁ появляется в n+1 ограничениях. Если мы суммируем коэффициенты ограничения, мы получим ${displaystyle a_{1,1}mathbf {y} _{1}+a_{1,2}mathbf {y} _{2}+dots +a_{1,n}mathbf {y} _{n}+f_{1}mathbf {s} _{1}}$ . Эта сумма должна не превосходить c₁. Как результат мы получаем:

Максимизировать ${displaystyle sum _{j=1}^{n}g_{j}y_{j}+sum _{i=1}^{m}h_{i}s_{i}}$

при ограничениях

${displaystyle sum _{j=1}^{n}a_{ij}y_{j}+f_{i}s_{i}leqslant c_{i},1leqslant ileqslant m}$

${displaystyle e_{j}y_{j}+sum _{i=1}^{m}b_{ij}s_{i}leqslant d_{j},1leqslant jleqslant n}$

${displaystyle y_{j}geqslant 0,,s_{i}geqslant 0,1leqslant jleqslant n,1leqslant ileqslant m}$

Вычисления выше предполагают, что задача представлена в стандартной форме. Это предположение не влияет на общность рассуждений, так как любая задача линейного программирования может быть приведена к стандартному виду.

Интерпретации в реальной жизни[править | править код]

Теорема двойственности имеет экономическую интерпретацию. Если мы интерпретируем прямую задачу линейного программирования как классическую задачу «распределения ресурсов», её двойственную задачу можно интерпретировать как задачу «оценки ресурсов»^[14]. См. статью Теневая цена^ru_en. Об экономической интерпретации двойственной задачи можно почитать также в книге Лунгу^[15].

Теорема двойственности имеет и физическую интерпретацию^[16].

Примечания[править | править код]

↑ Иногда используется термин Сопряжённая задача, как, например, в книге Юдина и Гольштейна (Юдин, Гольштейн 1969, 149) или в книге Лунгу (Лунгу 2005, 67). Во второй книге прямая задача именуется также основной задачей.
↑ Gartner, Matousek, 2006, с. 81–104.
↑ Юдин, Гольштейн, 1969, с. 150-152 Пункт 5.2.
↑ Юдин, Гольштейн, 1969, с. 157-159 Пункт 5.5.
↑ Gartner, Matousek, 2006, с. 85.
↑ Доказательство очень близкого утверждения, из которого вытекает данная теорема можно найти в книге Юдина и Гольштейна (Юдин, Гольштейн 1969, 159, Лемма 5.1)
↑ Gartner, Matousek, 2006, с. 81–83.
↑ Доказательство можно найти в книге Юдина и Гольштейна, где она именуется «первой теоремой двойственности» (Юдин, Гольштейн 1969, 164, Теорема 6.1)
↑ Gartner, Matousek, 2006, с. 87–89.
↑ Gartner, Matousek, 2006, с. 81–94.
↑ Юдин, Гольштейн, 1969, с. 162, Лемма 5.3.
↑ A. A. Ahmadi Lecture 6: linear programming and matching. Princeton University (2016). Архивировано 21 сентября 2018 года.
↑ Gartner, Matousek, 2006, с. sub.8.1.
↑ В книге Юдина и Гольштейна для теневых цен используется термин предварительные оценки (факторов производства).
↑ Лунгу, 2005, с. 68 Пункт 5.4.
↑ Gartner, Matousek, 2006, с. 86–87.

Литература[править | править код]

Jiri Matousek, Bernd Gärtner. Understanding and Using Linear Programming. — Springer, 2006. — С. 81–104. — (Universitext).
Юдин Д.Б., Гольштейн Е.Г. Линейное программирование (теория, методы и приложения). — Москва: «Наука», 1969.
Лунгу К.Н. Линейное программирование. Руководство к решению задач. — М.: ФИЗМАТЛИТ, 2005. — ISBN 5-9221-0631-7.

Источник

Видео урока:

Из занятия 1 имеем прямую задачу линейного программирования.

Прямая задача ЛП

Записываем матрицу прямой задачи:

Матрица прямой задачи ЛП

Транспонируем полученную матрицу и получаем матрицу двойственной задачи: ТРАНСП(C12:G16)

Матрица двойственной задачи ЛП

Двойственная задача запишется в виде:

Двойственная задача ЛП

Запишем обе задачи:

Пара двойственных задач ЛП

Запишем матрицы соответствия переменных прямых и двойственных задач:

Матрицы соответствия переменных прямой и двойственной задач

Единица по диагонали означает соответствие:

x1↔ y5

x2↔ y6

x3↔ y7

и т. д.

Подпишем соответствующие переменные к последней симплекс-таблице из урока 3.

Последняя симплекс-таблица

Видим, что значения двойственных переменных совпадают со значениями,

полученными нами через надстройку «поиск решения»

Анализ устойчивости

Значения целевых функций для оптимальных планов двойственных задач совпадают F min = f max = 30,667.

Значения Y6=3,3 и Y8=3,0333 означают, что при производстве одного вида продукции 2-го и 4-го вида значение целевой функции уменьшится на 3,3 и 3,0333 денежных единиц соответственно.

Y5=Y7=0 означает, что производство 1-го и 3-го видов продукции является наиболее эффективным.

Значения Y2=0,1 и Y3=0,267 означают, что при увеличении запасов 2-го и 3-го видов сырья на одну весовую единицу, значение целевой функции возрастёт на 0,1 и 0,267 денежных единиц соответственно. Так же это означает дефицитность этих видов ресурсов, так как оценки выше нуля.

Y1=Y4=0 – это означает, что ресурсы 1-го и 4-го видов не являются дефицитными и их увеличение никак не повлияет на значение целевой функции.

Эти выводы действительны в пределах интервалах устойчивости изменения ресурсов и коэффициентов целевой функции.

Надстройка «поиск решения» автоматически считает интервалы устойчивости для коэффициентов целевой функции и ресурсов. Интервалы устойчивости показаны в столбцах «допустимое увеличение» и «допустимое уменьшение».

В следующей статье мы рассмотрим определение интервалов устойчивости ресурсов и коэффициентов целевой функции на основании последней симплекс-таблице из занятия 3.

Материал подготовлен сайтом: https://pro-smysl.ru/

Онлайн помощь в решении задач, консультации, создание обучающих роликов.

Подписывайтесь на наши каналы:

https://vk.com/sm_smysl

https://www.youtube.com/@SMYS_L

Источник

Двойственная задача линейного программирования

Теорема двойственности

5.5. Двойственный симплексный метод

Двойственная задача линейного программирования

Основное неравенство теории двойственности

Критерий оптимальности Канторовича (достаточный признак оптимальности)

Теорема существования оптимальных планов пары двойственных задач

Первая теорема двойственности

Вторая теорема двойственности (о дополняющей нежесткости)

Третья теорема двойственности

Задача 1

Задача 2

Задача 3

Построение двойственной задачи[править | править код]

Векторные формулировки[править | править код]

Теоремы двойственности[править | править код]

Слабая двойственность[править | править код]

Сильная двойственность[править | править код]

Теоретическое приложение[править | править код]

Примеры[править | править код]

Простой пример[править | править код]

Пример фермера[править | править код]

Недопустимая задача[править | править код]

Приложения[править | править код]

Альтернативный алгоритм[править | править код]

Интерпретации в реальной жизни[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как я нашла интернет друга

Как найти рабочие дни в эксель

Секиро кукловод как найти

Добавить комментарий Отменить ответ